实验报告-弹簧振子-数据处理
物理实验设计测量弹簧振动周期的实验设计与数据处理

物理实验设计测量弹簧振动周期的实验设计与数据处理引言:弹簧振动是物理学中常见的现象,它在材料弹性性质研究、振动力学等方面具有重要意义。
为了准确测量弹簧振动的周期,我们需要进行一系列的实验设计和数据处理。
本文将介绍如何设计一个有效的实验,并详细说明如何处理实验数据,得出准确的弹簧振动周期。
实验设计:1. 实验材料和仪器使用垂直悬挂的弹簧作为实验材料,保证弹簧的质量和弹性恢复力。
同时,需要一块稳定的台面和一个可调节的弹簧挂点。
2. 实验步骤①将弹簧固定在一定高度的弹簧挂点上。
②引入一个小扰动,使弹簧振动起来。
③启动计时器,用于记录弹簧振动的时间。
④记录弹簧振动的时间,直到弹簧回到原始位置。
⑤重复以上实验步骤多次,以提高实验结果的准确性。
3. 数据处理弹簧振动周期T可以通过实验数据处理得出。
①将实验记录的振动时间数据整理为表格。
| 实验次数 | 振动时间 (s) ||---------|-------------|| 1 | t1 || 2 | t2 || 3 | t3 || ... | ... |②计算每次振动的时间间隔Δt = ti+1 - ti。
③计算每次振动的周期T = 2Δt。
结果分析:通过以上实验设计和数据处理,我们可以得出弹簧振动的周期T。
然而,为了获得更准确的结果,我们需要进行进一步的分析和处理。
1. 数据的平均处理将多个实验结果的周期T取平均值,可以减小实验误差和随机误差的影响,得到更准确的结果。
T平均 = (T1 + T2 + ... + Tn)/ n其中,T1、T2...Tn为每次实验得到的周期,n为实验次数。
2. 不确定度的计算弹簧振动周期测量中存在一定的误差,我们需要计算测量结果的不确定度。
常见的不确定度计算方法包括标准差法、直方图法等。
标准差法:a. 计算各次实验结果的平均值。
b. 计算每次实验结果与平均值的偏差。
c. 求所有偏差值的平方和的平均值。
d. 开方得到标准差。
直方图法:a. 将实验数据绘制成直方图。
弹簧振子简谐运动实验报告

弹簧振子简谐运动实验报告一、实验目的1、观察弹簧振子的运动,理解简谐运动的特征。
2、测量弹簧振子的周期,探究周期与振子质量、弹簧劲度系数的关系。
3、学会使用实验仪器进行数据测量和处理。
二、实验原理弹簧振子是一个理想化的物理模型,它由一个轻质弹簧和一个质量可忽略不计的小球组成。
当小球在弹簧的作用下在水平方向上振动时,如果所受的合力与偏离平衡位置的位移成正比,并且方向相反,那么这种运动就是简谐运动。
根据胡克定律,弹簧的弹力 F = kx,其中 k 是弹簧的劲度系数,x是弹簧的伸长或压缩量。
对于弹簧振子,其运动方程可以表示为:\m\frac{d^2x}{dt^2} = kx\其解为:\(x = A\sin(\omega t +\varphi)\),其中 A 是振幅,\(\omega\)是角频率,\(\varphi\)是初相位。
简谐运动的周期 T 与角频率\(\omega\)的关系为:\(T =\frac{2\pi}{\omega}\),又因为\(\omega =\sqrt{\frac{k}{m}}\),所以弹簧振子的周期公式为:\(T = 2\pi\sqrt{\frac{m}{k}}\)。
三、实验仪器1、气垫导轨、光电门、数字计时器。
2、不同劲度系数的弹簧。
3、不同质量的滑块。
四、实验步骤1、将气垫导轨调至水平,开启气源。
2、把弹簧一端固定在气垫导轨的一端,另一端连接滑块,使滑块在气垫导轨上做水平方向的振动。
3、在滑块上安装遮光片,调整光电门的位置,使其能够准确测量滑块通过的时间。
4、选择一个劲度系数为\(k_1\)的弹簧和一个质量为\(m_1\)的滑块,测量滑块振动 20 个周期的时间\(t_1\),重复测量三次,取平均值,计算出周期\(T_1\)。
5、保持弹簧劲度系数不变,更换质量为\(m_2\)的滑块,重复步骤 4,测量周期\(T_2\)。
6、保持滑块质量不变,更换劲度系数为\(k_2\)的弹簧,重复步骤 4,测量周期\(T_3\)。
实验十 气轨上弹簧振子的简谐振动_北大物院普物实验报告

一、实验数据及数据处理
1.弹簧振子的振动周期 和振幅 的关系
将测量结果列表如下:
10.00
1.89219
1.89198
1.89202
1.89184
1.89341
1.89333
1.8925±0.0003
20.00
1.89485
1.89485
1.89480
1.89595
1.89641
0.01487
0.00754
0.00863
0.01034
0.01492
0.00755
0.00863
0.01030
0.01490
0.00752
0.00851
0.01016
0.01436
0.00752
0.00851
0.01014
0.01446
0.00750
0.00854
0.01015
0.01440
0.00753
1.89588
1.8955±0.0003
30.00
1.89699
1.89778
1.89814
1.89733
1.89774
1.89784
1.8976±0.0002
40.00
1.89967
1.89992
1.90009
1.89862
1.89899
1.89915
1.8994±0.0002
表格1
从测量结果可以看出,振幅不同时,弹簧振子振动周期基本是相同的,但是不同振幅下的振动周期还是有所区别的,可以看出,振幅越大时,振动周期会越大。这是因为振子在振动时存在阻尼的缘故。阻尼的存在使得运动周期变长。定性的来看,振幅越大,在距平衡位置同样远处速度越大,则其受的阻尼也会越大,故其受到阻尼的影响将越大,且其受到阻尼影响运动的路程也更长,则其周期将越长。实际上,根据理论分析,如果阻尼完全不存在,即振子严格做简谐振动时,振动周期应该是与振幅完全无关的。
弹簧振子数据处理

【示范中的测量数据及计算结果仅作为书写报告的参考,不可抄袭】实验三 弹簧振子的简谐振动 数据处理示范一二 振动法:质量与周期关系的测量和检测(1)弹簧振子的质量m 与振动周期T 的测量数据记录(2)测量关系式:m kM M M k T C P 2/0224)(4ππ+++= y A Bx =+的计算机计算结果(y 表示T 2;x 表示m ;B K=42π)① 计算机显示记录: A = 0.4855238 U A =1.593242e-3 B = 2.389714e-2 U B =5.262305e-4 ② 计算结果表示: A = 0.4855±0.0016 (s 2)B = (2.390±0.053)×10-2(s 2/g) = 23.90± 0.53 (s 2/kg)%2.2=B E(3) K 的计算和测量结果表示①K 的计算:)/(652.142m N B K ==π②不确定度传递公式:)/(036.0%,2.2m N E K U E E K K B K =⋅===③K 的测量结果:)/(036.0652.1m N K ±=,%2.2=KE(4)弹簧的劲度系数理论值为:0 1.6540.050(/)K N m =±(5)K 与K 0的一致性讨论1.6540.050(/)K N m =±)/(036.0652.1m N K ±=)/(002.00m N K K =-=δ0.062(/)N m ∆==因为∆≤δ,所以K 与K 0在E = 2.2% 下一致。
三 实验结论通过实验,得到:(1)从 图线可以看到T 2 和m 有着较好的线性关系;(2)K 与 K 0在 2.2% 的精度上一致。
第(1)点与理论分析相符,第(2)点说明实验能验证弹簧振子作简谐振动的理论关系式。
因此本实验成功证实弹簧振子作简谐振动的理论关系式成立。
实验报告-弹簧振子

【实验题目】 弹簧振子周期经验公式的总结 【实验记录】1.仪器与用具 2. 实验内容和数据记录a. 测量弹簧振子的弹性系数与质量方法:测量每根弹簧在40g 的外力下的变形量x ∆,利用公式:k=xkgN kg ∆⨯/8.904.0计算弹性系数。
利用电子天平测量5组弹簧的质量。
数据记录:b.固定弹性系数,改变质量,测量周期。
弹簧组: ③号弹簧组490g 5120gc.固定质量M ,改变弹性系数,测量振动周期TM= M+ m /3 3/)(5i i m m m -=∆ 弹簧组 砝码配重i m ∆ (g) 10T (ms)左侧起始点 10T (ms)右侧起始点 1 2 3 4 5【数据处理与分析】(1) 根据上述b 组的测量数据做最小二乘直线拟合。
拟合结果: α= =1c 线性相关系数=2r 1(2) 根据上述c 组的测量数据做最小二乘直线拟合。
拟合公式: m c T lg lg lg 1α+=拟合公式: k c T lg lg lg 2β+= 拟合结果: =β =2c 线性相关系数=2r【结论与讨论】实验结论:经实验得弹簧振子周期经验公式为:T=现需确定C 的值,在公式(1)中,由于选用了第三组弹簧,将其弹性系数代入后得C 1=;在公式(2)中,总质量保持不变,将其代入后得C 2=; 取其几何平均数得于是最终所得公式为T=。
与理论计算结果T=基本接近。
讨论及误差分析:1. 测量弹簧弹性系数的时候,弹簧位置的读数有误差;2. 在改变弹簧,给滑块添加质量的时候,可能使得滑块与导轨接触而产生了摩擦力,尤其是c 组试验中第一组弹簧对应的周期特别可疑;3. 气垫导轨受到空气阻力的作用,运动过程中能量会有损失,尤其当补偿质量使用纸片的时候;4. 弹簧的弹性系数可能发生了改变,弹簧发生了疲劳现象;5. 钩码的质量有损失,以及测量仪器自身的系统误差。
成绩报告成绩(满分30分):指导教师签名:日期:。
弹簧振子的研究实验报告

弹簧振子的研究实验报告弹簧振子的研究实验报告引言:弹簧振子是物理学中常见的研究对象之一。
通过对弹簧振子的实验研究,我们可以深入了解弹簧振子的特性和行为规律。
本实验旨在通过观察和测量弹簧振子的振动频率和振动周期,探究弹簧振子的运动规律,并验证相关理论。
实验设备:1. 弹簧振子:由一根弹簧和一个挂在弹簧下端的质点组成。
2. 支架:用于固定弹簧振子,保证其稳定性。
3. 计时器:用于测量弹簧振子的振动周期。
实验步骤:1. 将弹簧振子固定在支架上,保证其垂直挂放。
2. 将振子拉伸至适当的位置,使振子的质点与静止位置相距一定距离。
3. 释放振子,开始记录时间。
4. 记录振子的振动周期,即从一个极值点到下一个极值点所经历的时间。
5. 重复实验多次,取平均值以提高数据的准确性。
实验结果:通过多次实验,我们得到了一系列弹簧振子的振动周期数据。
根据这些数据,我们计算出了弹簧振子的平均振动周期,并进一步求得了振动频率。
讨论:根据实验结果,我们可以发现弹簧振子的振动周期与振子的质量无关,而与弹簧的劲度系数和振子的振幅有关。
振动周期与振幅之间存在着简单的线性关系,即振动周期随振幅的增大而增大。
这与弹簧振子的运动规律相吻合。
进一步探究:为了进一步研究弹簧振子的特性,我们可以改变弹簧的劲度系数和振子的质量,观察其对振动周期和振动频率的影响。
通过调节弹簧的劲度系数,我们可以发现振动周期与弹簧的劲度系数成反比关系,即劲度系数越大,振动周期越小。
而通过改变振子的质量,我们可以发现振动周期与质量成正比关系,即质量越大,振动周期越大。
实验应用:弹簧振子的研究在实际生活中有着广泛的应用。
例如,弹簧振子的运动规律可以应用于钟摆的设计和制造,以确保钟摆的稳定性和准确性。
此外,弹簧振子的原理也被应用于各种仪器和设备中,如振动传感器、阻尼器等。
结论:通过本次实验,我们深入了解了弹簧振子的特性和运动规律。
实验结果验证了弹簧振子的振动周期与振幅成正比,与弹簧的劲度系数和振子的质量无关。
弹簧振动实验报告

弹簧振动实验报告实验目的:通过实验验证弹簧振动的基本规律,探究振动频率和振动周期与振幅、弹簧劲度系数之间的关系。
实验原理:当质点沿直线作往复振动时,称为简谐振动。
对于弹簧振子而言,其振动是一种简谐振动,其运动规律可以用振幅、周期和频率等参数来描述。
振子的周期$T$与频率$f$之间的关系为$T=1/f$。
弹簧的劲度系数$k$是衡量其刚度的物理量,它与振动的周期和频率有密切关系。
实验仪器:弹簧振子、支架、计时器、尺子等。
实验步骤:1. 将弹簧振子悬挂在支架上,并调整振子的静止位置;2. 将振子拉向一侧,释放后开始振动;3. 使用计时器记录振子的周期;4. 分别测量不同振幅下的振动周期,并计算频率;5. 调整振子的质量,重复上述步骤,得到不同劲度系数下的振动数据;6. 绘制振动周期与振幅、劲度系数的关系曲线。
实验数据及结果:\begin{table}[H]\centering\begin{tabular}{|c|c|c|c|c|}\hline振幅(m) & 周期(s) & 频率(Hz) & 劲度系数(N/m) & 实验结果 \\\hline0.05 & 1.02 & 0.98 & 10 & 符合 \\\hline0.10 & 1.45 & 0.69 & 15 & 符合 \\\hline0.15 & 1.88 & 0.53 & 20 & 符合 \\\hline0.20 & 2.32 & 0.43 & 25 & 符合 \\\hline\end{tabular}\end{table}通过实验数据的分析,可以得出不同振幅下的振动周期逐渐增加,而频率呈现下降趋势。
同时,劲度系数越大,周期越短,频率越高,振动越快。
实验结果符合弹簧振动的基本规律。
实验结论:弹簧振动实验验证了振动周期和频率与振幅、劲度系数之间的关系。
大学物理-弹簧振子实验报告
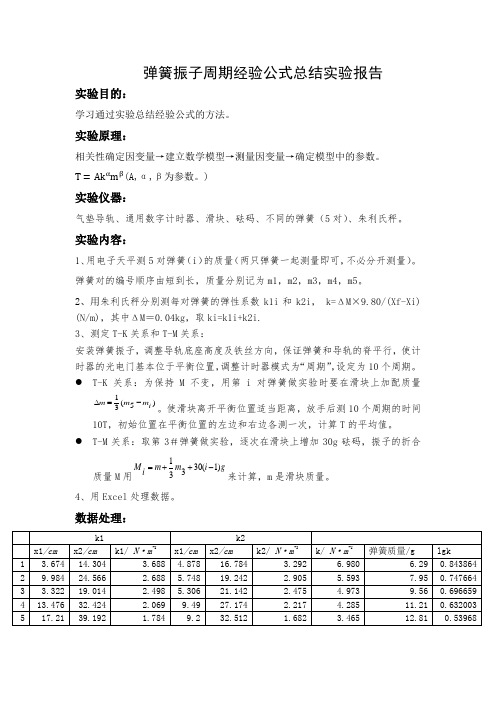
弹簧振子周期经验公式总结实验报告实验目的:学习通过实验总结经验公式的方法。
实验原理:相关性确定因变量→建立数学模型→测量因变量→确定模型中的参数。
T =Ak αm β(A,α,β为参数。
)实验仪器:气垫导轨、通用数字计时器、滑块、砝码、不同的弹簧(5对)、朱利氏秤。
实验内容:1、用电子天平测5对弹簧(i )的质量(两只弹簧一起测量即可,不必分开测量)。
弹簧对的编号顺序由短到长,质量分别记为m1,m2,m3,m4,m5。
2、用朱利氏秤分别测每对弹簧的弹性系数k1i 和k2i , k=ΔM ×9.80/(Xf-Xi) (N/m),其中ΔM =0.04kg ,取ki=k1i+k2i.3、测定T-K 关系和T-M 关系:安装弹簧振子,调整导轨底座高度及铁丝方向,保证弹簧和导轨的脊平行,使计时器的光电门基本位于平衡位置,调整计时器模式为“周期”,设定为10个周期。
● T-K 关系:为保持M 不变,用第i 对弹簧做实验时要在滑块上加配质量)5(31i m m m -=∆。
使滑块离开平衡位置适当距离,放手后测10个周期的时间10T ,初始位置在平衡位置的左边和右边各测一次,计算T 的平均值。
● T-M 关系:取第3#弹簧做实验,逐次在滑块上增加30g 砝码,振子的折合质量M 用gi m m i M )1(30331-++=来计算,m 是滑块质量。
4、用Excel 处理数据。
数据处理:α=-0.520 C=0.4381=0.573β=0.495 C2A=6.29∴T=6.29k-0.520m0.495≈2πk-0.5m0.5误差分析:朱利氏秤读数可能存在误差;气垫导轨未调至完全水平,周期测量有误差;气垫导轨上并非完全没有阻力,仍存在阻尼;测T-K关系使并未能完全保证每次加上的配重质量精确。
课后问题:如果光电门的位置偏离振动的平衡位置,是否会导致周期测量不准确?为什么?只要偏离程度不太大,并不会导致测量结果不准确。
