天线原理与设计习题集解答-第8-11章
天线原理与设计习题集解答第1章

天线原理与设计习题集第一章 天线的方向图(1-1) 如图 1 为一元天线,电流矩为Idz ,其矢量磁位表示为? 0 Idz j r,A ze4 r试导出元天线的远区辐射电磁场 E, H 。
(电磁场与电磁波 P163)图 1-1 (a) 元天线及坐标系 (b) 元天线及场重量取向解:利用球坐标中矢量各重量与直角坐标系中矢量各重量的关系矩阵A r s i n c o s s i n s i n c oA x sA c o s c o s c o s s i n sA y i nAs i nc o s0 A z因 A x A y 0 ,可得A rA z cosA A z sinA 0E j A由远场公式H1 ?Er可得Idzj r(V/m) E j2 r sin eHj Idz sin e j r(A/m)2 rE r EH r H(1-2) 已知球面波函数ejr/ r ,试证其知足颠簸方程: 2 22121j r2j r 2证明:r 2 r ( rr )r 2 r [(1j r )e ] r e则22(1-3) 如图 2 所示为两副长度为 2 的对称线天线,其上的电流分别为平均散布和三角形散布,试采纳元天线辐射场的叠加原理,导出两天线的远区辐射场E , H ,方向图函数 f ( , ) 和归一化方向图函数F ( , ) ,并分别画出它们在yoz 平面和 xoy 平面内的方向图的表示图。
解: (1) 天线上电流为平均散布时I ( z)0I , l z l将对称振子分为长度为 dz 的很多小段,每个小段可看作是一个元天线,以下列图所示。
距坐标原点 z 处的元天线的辐射电场为dEj I ( z)dz sin e j R j I 0 dz sin e j R2 R 2 R作远场近似,对相位 R r z cos ,对幅度 1/ R 1/ r ,且 e jRe j r e j zcos ,得dEje jrj zcosdz2 sin I 0er则远区总场为这些元天线的辐射场在空间某点的叠加,用积分表示为lj rlj rj l cosj l coseI 0e j zcos dzI 0eeeEdEjsinl j sinl2 r2 r j cosj 60I 0e j r sinr式中方向图函数为: f ( ) sin( l cos ) j 60I 0 e j r f ( )cos rsin( l cos ) sin( cos ) sin |l / 2 sincos cos平均电流散布的对称振子,其最大辐射方向在侧向。
2020年智慧树知道网课《天线原理(黑龙江联盟)》课后章节测试满分答案

绪论单元测试1【单选题】(2分)天线辐射的能量存在的形式是【】A.传导电流B.交变电磁场C.恒定磁场D.恒定电场2【单选题】(2分)关于发射机与天线的阻抗问题的描述,的是【】A.二者之间必须阻抗匹配B.匹配的好坏可以用阻抗的模值来衡量C.工作频带之外可以不管阻抗是否匹配D.匹配的好坏将影响功率的传输效率3【单选题】(2分)下列关于天线的描述的是【】A.天线对接收电磁波的频率是有选择的B.天线必须是一个电磁开放系统C.发射天线必须和源匹配D.只要是空间电磁波均能被天线完全接收4【单选题】(2分)接收天线与发射天线的作用是一个(①)的过程,同一副天线用作发射和用作接收的特性参数是(②)的。
接收天线特性参数的定义与发射天线是(③)的。
上述三处空白应依次填入【】A.①可逆、②不同、③不同B.①可逆、②相同、③不同C.①互易、②不同、③相同D.①互易、②相同、③相同5【单选题】(2分)下列天线分类法不一致的是【】A.全向天线、螺旋天线、行波天线B.电视天线、广播天线、遥测天线C.长波天线、短波天线、中波天线D.半波振子、短振子、全波振子第一章测试1【单选题】(2分)全向天线的固定底座上平面应与天线支架的顶端平行,允许误差()A.±10cmB.±11cmC.±15cmD.±12cm2【单选题】(2分)轴线为z轴的电基本振子,中心位于原点O;法矢量方向为z轴的小电流环,中心也位于原点O,则关于它们的E面和H面的叙述正确的是【】A.电基本振子H面为xoz,小电流环E面为xoyB.电基本振子E面为yoz,小电流环H面为xoyC.电基本振子H面为xoy,小电流环E面为xozD.电基本振子E面为yoz,小电流环H面为xoz3【单选题】(2分)电基本振子的辐射功率为PΣ=(①),辐射电阻RΣ=(②)。
上述两处空白应依次填入【】。
这里I为电流幅度,L为电流长度,λ为波长。
A.①60π2(IL/λ)2②120π2(L/λ)2B.①40π2(IL/λ)2②40π2(L/λ)2C.①80π2(IL/λ)2②80π2(L/λ)2D.①40π2(IL/λ)2②80π2(L/λ)24【单选题】(2分)有关自由空间中电基本振子的辐射场的说法正确的是【】A.波的传播速度为光速B.辐射方向上没有电场分量C.辐射远区场是均匀平面波D.波的传播方向上存在磁场分量5【单选题】(2分)下列说法正确的是【】A.磁导率的单位是S/mB.介电常数的单位是F/mC.电场强度的单位是N/mD.磁场强度的单位H/m6【单选题】(2分)下列哪个参数不是发射天线的电参数【】A.等效噪声温度B.输入阻抗C.有效高度D.增益第二章测试1【单选题】(2分)设对称振子总长度为2l,下列关于有效长度的计算正确的是【】。
天线原理与设计题库

天线原理与设计题库(总27页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--0(,)j re E Ef rβθθϕ-=0E ϕ=0r E ==w r P =max E max S E),(ϕθf m m ϕθ,r R a η00,θϕ0E 00(,)E θϕ00(,)D θϕ00(,)G θϕ22000(,)/E E θϕ(,)f θϕ00,θϕ00,θϕr R (,)f θϕe S4/λ 90=αvλ=)(z I=)(θf =)(θf =r R ()I z =r R =Ωθ=)(θa f =)(θa f =α=)(θa f),(0ϕθf ),(ϕθa f =),(ϕθfθ=m θα=m θ=m θd Z =s Z =d Z =s Zs E s H s J s M ˆns J s M sy E sx H = νf D 0ψ385.0/=D f 0ψcm D 75=0ψ s Z d Z 2/4s d Z Z η⋅=cos θ60πr Z =1111Z Z '+0ψ0/2ψπ<0/2ψπ=0/2ψπ>/4λΩH R H D 213H HopD R λ=α40m λ=o30∆=4sin λ∆1cos θ+0()sin (||)I z I l z β=-l z l -≤≤l1/1/R r →r R m I221122m r in in I R I R = sin()in m I I l β=2sin ()rin R R l β=(1) (2) (3) (4)c Zcoth()coth[(j )]in c c Z Z l Z l γαβ==+0(1j )c Z Z αβ=-102R Z α=(1) 0Z '0Z (2) 1R '1R(3) β'β1112r Z Z Z ⊥'=+1112r Z Z Z '=-12Z 'Z 'in Z /l λ金槽=H E 金槽=-E H(1) (2) (3) (4)/n l λ/2λ12g g g =⋅1g 2g1g 2g2g1g g(,)ˆ(,)j rj u e uEe rβψθϕθϕ-=Eˆu(,)E θϕ(,)ψθϕ (,)ψθϕ,θϕ(,)ψθϕ(,)ψθϕj 60j()rm I E e f rβθθ-=E H θϕη=222*22001||60ˆˆ()222m E I r r f rθθηη=⨯==W E H*1ˆ2r sPrds =⨯⋅⎰⎰E H 222200060()sin 2m I d f d ππϕθθθη=⎰⎰220260()sin rr mP R f d I πθθθ==⎰0E (,)E θϕ220(,)E E θϕr P in Pd α/2d λ= 0=α/2d λ= 180=α/4d λ= 90=αd λ= 0=α27.Γλλ/()a r r l R R R η=+r R l R Γr RRD f /0S 0SFM QM=2FM MP QM MP f+=+=cos FM rMP r ψ⎧=⎪⎨'=⎪⎩ cos 2r r f ψ''+=⇒21cos fr ψ'=+sin x r ψ'=2sin 1cos x fr ψψ'==+2x D =0ψψ=01()42f ctg D ψ= D f /0,0.252f D πψ<>fDfD0ψ0ψ4/λ=d /221j I I e π=1r Z0(,)()(,)T a f f f θϕθθϕ=0cos(cos /2)()sin f πθθθ=(,)2cos(/2)a f θϕψ=sin sin d ψβθϕα=+2/βπλ=/2απ=2cos[(sin sin 1)]4πθϕ=+/2ϕπ=cos(cos /2)()2cos[(sin 1)]sin 4E f πθπθθθ=⋅+ /2θπ=()2cos[(sin 1)]4H f πϕϕ=+2111121r I Z Z Z I =+/221/j I I e j π==1173.142.5Z j =+12Z 12(/0,/0.25)Z H d λλ==173.142.5(40.828.3)r Z j j j =++-Ω/2λm ∆()2sin(cos )H f h θβθ=/2h λ=2sin(sin )πϕ= sin(sin )1πϕ=sin 1/2m ϕ=o 30m m ϕ∆==2max 120rf D R =max 2f =Re()r r R Z =1112r Z Z Z =-1173.142.5Z j =+12(/0,/1)Z H d λλ===69.124.8r Z j =+Ω69.1r R =Ωm ∆o 30m ∆=()2sin(cos )H f h θβθ=22sin(sin )m h πλ=∆2|sin(sin )|1m h πλ∆=221sin 2m n h ππλ+∆=0,1,2,n =±±o 30m ∆=sin 1/2m ∆=/2h λ=2max 120rf D R =max 2f =Re()r r R Z =1112r Z Z Z =-1173.142.5Z j =+12(/0,/1)Z H d λλ===69.124.8r Z j =+Ω69.1r R =Ωm ∆/4λ(1)(2) (3)/4λcos(cos /2)(),0/2sin E f πθθθπθ=≤≤()1H f ϕ=11173.142.536.5521.2522r j Z Z j ⊥+===+Ω 2max 120120 3.2836.55r f D R ===λ1I 2I /212j I I e π-=0(,)()(,)T a f f f θϕθθϕ=cos(cos )2(,)sin f πθθϕθ=/4d λ=/2απ=-12(,)2cos(cos )22y d f βαθϕθ=-2cos[(sin sin 1)]4πθϕ=+/2ϕπ=/2cos(cos )2()(,)|2cos[(sin 1)]sin 4E T f f ϕππθπθθϕθθ===⋅+/2θπ=/2()(,)|12cos[(sin 1)]4H T f f θππθθϕϕ===⨯+/221111211121j r I Z Z Z Z Z e I π=+=+ /21111211()22j r r Z Z Z Z e π⊥==+ 1173.142.5()Z j =+Ω1240.828.3()Z j =-Ω1[73.1j42.5j(40.8j28.3)]2r Z ⊥=++-Ω2/2λ= /2H λ=21I I =r Z0()()()T a f f f θθθ=0cos(cos )2()sin f πθθθ=/2()2cos(cos )|2cos(cos )22a d d f λβπθθθ===2cos (cos )2()()2sin E T f f πθθθθ==/2()()|2E T f f θπθθ===2111211121m r m I Z Z Z Z Z I =+=+1173.142.5Z j =+Ω1226.420.2Z j =+Ω73.142.526.420.299.562.7r Z j j j =+++=+Ωcos(cos )cos()()sin f βθβθθ-=/2λ=cos(cos )1()sin f πθθθ+=22cos ()1cos(2)x x =+H/λ=0 H/λ=D/λ R 12 X 12 R 12 X 12 02cos (cos )2()2sin f πθθθ= 2120()T m f D R θ∑=/2()()|2T m T f f θπθθ===2Re()299.5199r R Z ∑==⨯=12042.4199D ⨯==8/3λ3/8d λ=12340I I I I I ==-=-=(,)2cos(cos )x x f d θϕβθ=cos sin cos x θθϕ=(,)2cos(cos )y y f d θϕβθ=cos sin sin y θθϕ=0()sin f θθ=0(,)()[(,)(,)]T x y f f f f θϕθθϕθϕ=-2sin [cos(sin cos )cos(sin sin )]d d θβθϕβθϕ=-/2θπ=()2[cos(cos )cos(sin )]H f d d ϕβϕβϕ=-4sin[(cos sin )]sin[(cos sin )]22ddββϕϕϕϕ-+-4/λ=d 2/,0,2/ππ-λλλλλ/210j I I e π=202I I =/230j I I e π-=/4d λ=0I01212,23(,)()(,)(,)T f f f f θϕθθϕθϕ=0cos(cos )2()sin f πθθθ= ()2cos(cos )22a d f βαθθ=-/2απ=12(,)2cos[(cos 1)]4y f πθϕθ=-, 12,23(,)2cos[(cos 1)]4y f πθϕθ=-cos sin sin y θθϕ=(1)/2ϕπ=2/2cos(cos )2()(,)|4cos [(sin 1)]sin 4E T f f ϕππθπθθϕθθ===⋅-/2θπ=2/2()(,)|4cos [(sin 1)]4H T f f θππθθϕϕ===-λλ23111121311r I IZ Z Z Z I I =++1112132j Z Z Z =-- Ω/2s λ=/4h λ=01212,12(,)()()(,)T f f f f θϕθθθϕ''=0cos(cos )2()sin f πθθθ=12()2cos(sin sin )2sf βθθϕ=12,12(,)2cos(cos )f h θϕβθ''=(1)/2θπ=/2()(,)|122cos(sin )2H T f f θππϕθϕϕ===⨯⨯0ϕ=0cos(cos )2()(,)|22cos(cos )sin 2E T f f ϕπθπθθϕθθ===⨯⨯(2)λλλλλλλ(3)11112111273.1j42.512.5j29.926.4j20.211.9j7.975.1j24.9r Z Z Z Z Z ''=+++=+--++--=+(4)0,/2ϕθπ==max /20(,)|4T T f f θπϕθϕ====12150.2j49.8r Z Z ∑==+22max 120120412.78Re()150.2T f D Z ∑⨯===/2s λ=/2h λ=01212,12(,)()()(,)T f f f f θϕθθθϕ''=0cos(cos )2()sin f πθθθ=12()2cos(cos )2s f βθθ= 12,12(,)2sin(sin cos )f h θϕβθϕ''=(5)/2θπ=/2()(,)|122sin(cos )H T f f θπϕθϕπϕ===⨯⨯0ϕ=0cos(cos )2()(,)|2cos(cos )2sin(sin )sin 2xz T f f ϕπθπθθϕθπθθ===⨯⨯(6)λλλλλλλ(7)11112111273.1j42.526.4j20.24j 17.79j8.986.5j36.1r Z Z Z Z Z ''=+--=+++----=+(8)|sin(cos )|1πϕ=o 60ϕ=/3,/2ϕπθπ==12173j72.2r Z Z ∑==+max /2/3(,)|4T T f f θπϕπθϕ====22max120120411.1Re()173T f D Z ∑⨯===o 15m ∆=01212,23(,)(,)(,)(,)(,)T jx f f f f f θϕθϕθϕθϕθϕ=20cos(cos )(,)sin x x f πθθϕθ=cos sin cos x θθϕ=0I 2πα=-1212,23(,)(,)2cos[(cos 1)]4y f f πθϕθϕθ==-cos sin sin y θθϕ=(,)2sin(cos )2jx f πθϕθ=/2ϕπ=2(,)14cos [(sin 1)]2sin(cos )42T f ππθϕθθ=⨯-⨯/2θπ=22cos(cos )()4cos [(sin 1)]00sin 4xy f πϕπϕϕϕ=⨯-⨯=o 9010j I I e =202I I =o9030j I I e -=11I I '=-22I I '=-33I I '=-33212111121311121311111r I I I I I Z Z Z Z Z Z Z I I I I I ''''''=+++++ 11121311121322Z jZ Z Z jZ Z '''=---++ 1173.142.5()Z j =+Ω12(/0,/0.25)40.828.3()Z H d j λλ===-Ω 13(/0,/0.5)12.529.9()Z H d j λλ===--Ω11(/0,/0.5)12.529.9()Z H d j λλ'===--Ω 12(/0,/0.56)20.122.0()Z H d j λλ'===--Ω 13(/0,/0.71)24.6 1.2()Z H d j λλ'===--Ω 173.142.52(40.828.3)2(12.529.9)2(20.122)24.6 1.2r Z j j j j j j j =+--+++----60.920.7()j =-Ω o 15m ∆=2(,)2sin(sin )jx f H πθϕλ=∆2|sin(sin )|1m H πλ∆=2sin 2m H ππλ∆=0.9664sin mH λλ==∆λ45m θ=±d ≤α≤()f ψ 0.52θ=1.7571|cos |m d cm λθ≤=+o cos 0.283149m d αβθπ≤==sin(/2)(),cos ,16sin(/2)N f d N ψψψβθαψ==-=o 0.52515.44Ndλθ==λ0.524o θ= α0.52514o Nd λθ==⇒1515120440.65N d λ===⨯⨯cos 0d βθα-=⇒o 2cos 0.65cos650.55d παβθλπλ==⨯⨯=o 0.6671|cos |1|cos60|m d λλλθ<==++sin()2()sin()2N F N ψθψ=cos d ψβθα=-E 5.02ϕH5.02ϕ⎪⎩⎪⎨⎧+=+=++dxdy ey x E A dE dxdy ey x E A dE y x j sy y x j sy θϕϕβϕθϕϕβθθϕθϕsin )sin cos (sin )sin cos (),()cos 1(cos ),()cos 1(sin r e j A r j λβ2-=707.0sin =u u39.1=u0ys E E =0ϕ=sin 0(1cos )j x H dE A E e dxdy βθθ=+90ϕ=sin 0(1cos )j y E dE A E e dxdy βθθ=+/2sin 00/2sin (1cos )(1cos )x x D x j x H y D x u E AE D e dx AE Su βθθθ=+=+⎰/2sin 00/2sin (1cos )(1cos )y y D y j y E x D yu E AE D e dy AE Su βθθθ=+=+⎰sin (1cos )sin (1cos )x H x yE y uF u u F u θθ⎧=+⎪⎪⎨⎪=+⎪⎩1cos θ+sin sin x H x yE y uF u u F u ⎧=⎪⎪⎨⎪=⎪⎩x y S D D =sin 2xx D u βθ=sin 2yy D u βθ=707.0sin =uu()()0.50.500.50.5sin 1.39251sin 1.39251xH H xy E E yD D D D πλθθλπλθθλ⋅⎧=⇒≈⎪⎪⎨⋅⎪=⇒≈⎪⎩0f 02ψ=02ψ00300/()25f MHz mm λ==01()42F ctg D ψ=⇒1o 02()233664Dtg Fψ-==⨯=⇒o 02132ψ= 01cos ..20lg 32S A dB ψ+==-2204()4441.324SDG g g ππλ===36.475G dB =02ψ1037s A dB =-+=- o E 1825.0=ϕo H 1625.0=ϕλ0.50.52215E H θθ==0.50.5254/15280/15E E H H D D θλθλ==⎧⎨==⎩⇒54/15115.280/15170.67E H D mmD mmλλ==⎧⎨==⎩ 22207.363303.422E E H H D R mm D R mm λλ⎧==⎪⎪⎨⎪==⎪⎩1/ 1.11/H EE HR b D R a D -==-E R /1.1275.84E H R R mm ==240.51123E HD D G πλ==20.9G dB =0f 0.10.122100E H θθ==00300/()75f MHz mm λ==0.100.10288/10023179/100E E H H D D θλθλ==⎧⎨=+=⎩⇒0088/1006679/(10031)85.87E H D mmD mmλλ==⎧⎨=-=⎩ 2020288288H Hm H E Em E D R D R ππψλππψλ⎧==⎪⎪⎨⎪==⎪⎩⇒2202196.632116.16HH E ED R mm D R mm λλ⎧==⎪⎪⎨⎪==⎪⎩1/31/H EE HR b D R a D -==-H R 3348.48H E R R mm ==d E D E220.02d D E d E D ⎛⎫== ⎪⎝⎭20lg40Ds D E SLL dB E ==-Ds E 0.01Ds DEE =20lg()20lg(0.010.02)30.46Ds dz D DE E SLL E E =+=+=-4030.469.5dB -= 10lg20lg 10.175T d D D G E G dB G E ⎛⎫∆==-=- ⎪⎝⎭T G D G/H G b λ/H R λ/H D λH D λH R λ21()3HH R Dλλ=/2H x D =H v H v H HH v222/2|224834H H H Hmx D H H HD D x R R R πϕβπλλπ=±====24G Sv πλ=H S bD =1()4H H Hv G b D λλπ=H v/E G a λ/E R λ/E D λE D λE R λ21()2EE R Dλλ=/2E y D =E v E v E λE λE v222/2|22482E E E Emy D E E ED D y R R R πϕβπλλπ=±====24G Sv πλ=E S aD =1()4E E Ev G a D λλπ=E v2120(,)(,)rf D R θϕθϕ=cos(cos )cos (,)sin l l f βθβθϕθ-=80%η=o 60θ=/2l βπ=cos(cos )2()sin f πθθθ=max /2()|1f f θπθ===73.1r R = 2max1200.8 1.31373.1f G D η==⨯=o o o60cos(cos60)2()|0.816sin 60f θπθ===o 601200.6659()| 1.0973.1D θθ=⨯==e S e L 204ee rL S R η=0120ηπ=r R2(,)(,)(,)||/2re re e i i P P S W E θϕθϕθϕη==2222||1||22()()A L re L L L L r L in V R P P I R R R X X ===+++L r R R =L in X X =-A e i V L E =22||||88i e A re r rE L V P R R ==204ee rL S R η=0Z014sin j r e H H r E H βϕθϕπθη-⎧=⎪⎨⎪=⎩ln |tan()|sin 2d C θθθ=+⎰ˆrˆr 0()()V r Z I r =()V r ()I r0000()4sin j r lH d V r E dl E rd e πθπθβθθθθηθθπθ---===⎰⎰⎰002ln(cot )42j r H e βηθπ-=0020()||cI r H dc H d πϕθθϕθθρϕ====⎰⎰0sin r ρθ=002sin |r H ϕθθπθ==02j rH e β-=dl rd θ=dc d ρϕ=000ln(cot )120ln(cot )22Z θθηπ==e S e L 204ee r L S R η=0120ηπ=r R e S 2()4e S D λπ=2max120rf D R =max 1cos()f l β=-202044eee r reL S S R R L ηη=⇒=202max4120ee L S Df η=⨯/2l λ=/2l βπ=max 1f =/e L λπ=0120ηπ=2()4e S D λπ=0cos ,02()0,nf f G G ψψπψ⎧<<⎪=⎨⎪⎩其它s E =op()s E ψ=2cos (2)f r ψ'=0()cos nf f G G ψψ=0()s E ψ=(0)s E =20020()cos cos (0)2ns s E E ψψψ=000()20lg40lg(cos )10lg(cos )(0)2s s s E A n E ψψψ==+n 0op ψψ=10s A dB ≈-。
天线原理与设计习题集解答_第8_11章

E
j e j r (1 cos ) ES e j sin ( x cos y sin ) dxdy 2 r S
(8-4) 试利用等效原理推证惠更斯面元的辐射场表达式。 (P188)
第九章 平面口径的绕射
(9-1) 从口径天线的一般远场公式如何得到矩形和圆形平面口径天线的远场表达式? 解:由惠更斯远场公式
口径场为均匀同相分布
E ys E0
①E 面和 H 面方向图函数 惠更斯矩形面元的辐射公式为
0:
dEH A(1 cos ) E0 e j ysin dxdy
90 : dEE A(1 cos ) E0e j xsin dxdy
Dy Dx 2 2 sin u x E AE ( 1 cos ) dy e j xsin dx AE0 (1 cos ) S 0 H ux Dy D x 2 2 Dy Dx 2 2 sin u y E E AE0 (1 cos ) dx e j ysin dy AE0 (1 cos ) S uy Dx Dy 2 2
3
(9-5) 设有一长度为 Dx,宽为 Dy 的矩形口径,如图所示。若口径场为均匀同相分 布,要求: ①导出 E 面和 H 面方向图函数; ②若口径较大,即 Dx 和 Dy 远大于波长时导出 2 0.5E 和 2 0.5 H 的表达式。
提示:惠更斯矩形面元的辐射场公式为
j ( x cos y sin ) sin dxdy dE A sin (1 cos ) E sy ( x, y )e j ( x cos y sin ) sin dxdy dE A cos (1 cos ) E sy ( x, y )e
天线原理与设计(王建)8PDF版

4π | Fmax |2
(6.8)
2
W = ∫ dϕ ∫
0
2π
π
0
π⎛ Z F (θ ) sin Z ⎞ 0 sin θ dθ = 2π ∫ ⎜ ⋅ ⎟ sin θ dθ 2 0 Fmax ⎝ sin Z 0 Z ⎠
2
4π Z 0 2 β L (ξ +1) / 2 sin Z 2 4π = ( ) ∫ ( ) dZ = g (Z0 ) β L ( ξ − 1) / 2 β L sin Z 0 Z βL
δ =π /N
(6.16)
当N=10时,正是如图中 红线所示的端射阵方向图, 这个方向图就是10单元强方 向性端射阵的方向图。
6.3.3 强方向性端射阵的方向性系数
由式(6.12) D = β L / g ( Z 0 ) ,取 g ( Z 0 ) = g min = 0.871 ,可得 强方向性端射阵的方向性系数为
(6.3) (6.4) (6.5) (6.6) (6.7)
链接
δ L = Nd , ξ = 1 + βd 端射阵方向图最大值出现在θ=0处,因此令 Z 0 = Z |θ =0 = β L(1 − ξ ) / 2 sin( Z 0 ) Fmax = Z0
由方向性系数公式
4π D = 2π = π 2 W d ϕ F ( θ )sin θ d θ ∫ ∫
βL 2π Nd Nd L De = = ⋅ = 7.213 ≃ 1.8 × (4 ) = 1.8D g ( Z 0 ) λ 0.871 λ λ
(6.17)
式中,D=4L/λ为普通端射阵的方向性系数。
6.3.4 强方向性端射阵的波瓣宽度
1. 主瓣零点宽度2θ0 由前面式(6.3),即
天线习题与答案
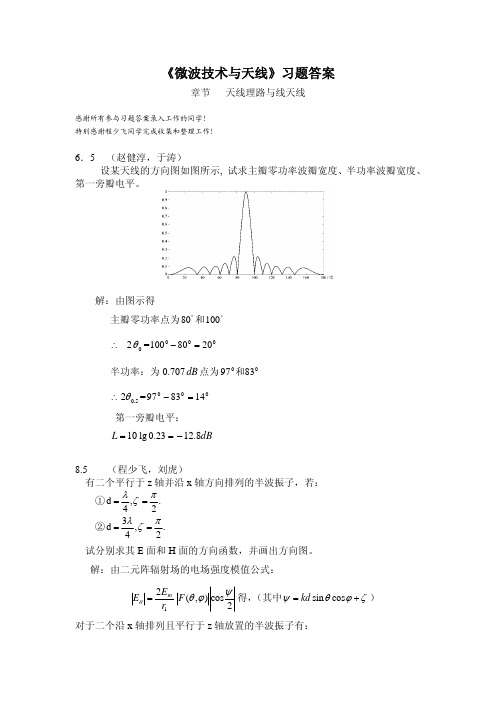
《微波技术与天线》习题答案章节 天线理路与线天线感谢所有参与习题答案录入工作的同学!特别感谢程少飞同学完成收集和整理工作!6.5 (赵健淳,于涛)设某天线的方向图如图所示, 试求主瓣零功率波瓣宽度、半功率波瓣宽度、第一旁瓣电平。
解:由图示得主瓣零功率点为和°80°100∴20θ=0002080100=−半功率:为0.707dB 点为008397和∴5.02θ=000148397=−第一旁瓣电平:10=L =23.0lg dB 8.12−8.5 (程少飞,刘虎)有二个平行于z 轴并沿x 轴方向排列的半波振子,若:①.2,4d πζλ== ②.2,43d πζλ== 试分别求其E 面和H 面的方向函数,并画出方向图。
解:由二元阵辐射场的电场强度模值公式:12r E E m =θ2cos ),(ψϕθF 得,(其中ζϕθψ+=cos sin kd ) 对于二个沿x 轴排列且平行于z 轴放置的半波振子有:2cos sin )cos 2cos(r E 2E 1mψθθπθ= (1) 当.2,4d πζλ==时代入上式可得:2cos sin )cos 2cos(r E 2E 1ψθθπθm= 令0=ϕ,得二元阵的E 面方向图函数为:)sin 1(4cos sin )cos 2cos()(F E θπθθπθ+= 令2πθ=,得二元阵的H 面方向图函数为:)cos 1(4cos )(F H ϕπϕ+=通过MATLAB 仿真得E 面和H 面方向图如下:(2) 当2,43πζλ==d 时,同理代入上式可得: E 面方向图函数为)sin 31(4cos sin )cos 2cos()(F E θπθθπθ+= H 面方向图函数为:)cos 31(4cos )(F H ϕπϕ+=由MATLAB 仿真得其E 面和H 面方向图如下:8.7 (于伟,陈修元)十二元均匀直线阵的各元间距为2λ,求:①天线阵相对于ϕ的归一化阵方向函数。
天线原理与设计习题集解答-第2章

第二章 天线的阻抗(2-1) 由以波腹电流为参考的辐射电阻公式:22030(,)sin r R d f d d ππϕθϕθθϕπ=⎰⎰计算对称半波天线的辐射电阻。
(提示:利用积分201cos ln(2)(2)xdx C Ci x πππ-=+-⎰,式中,0.577, 023.0)2(-=πCi )解:半波振子天线的辐射方向图函数为 cos(cos )2(,)sin f πθθϕθ=, 则 2222000cos (cos )301cos(cos )2sin 60(cos )sin 2(1cos )r R d d d ππππθπθϕθθθπθθ+==--⎰⎰⎰ 011130()[1cos(cos )](cos )21cos 1cos d ππθθθθ=+++-⎰01cos(cos )1cos(cos )15[](cos )1cos 1cos d ππθπθθθθ++=++-⎰01cos[(1cos )]1cos[(1cos )]15(cos )1cos 1cos d ππθπθθθθ-+--=++-⎰1cos[(1cos )]15[(1cos )](1cos )d ππθπθπθ-+=++⎰01cos[(1cos )]15[(1cos )](1cos )d ππθπθπθ--+--⎰201cos 215xdx xπ-=⨯⎰30[ln(2)(2)]C Ci ππ=+- 73.1()=Ω(2-2) 利用下式求全波振子的方向性系数rR f D ),(120),(2ϕθϕθ=, θβθβϕθsin cos )cos cos(),( -=f 若全波振子的效率为5.0=a η,求其最大增益的分贝数和3/πθ=时的方向性系数。
解:(1) 求增益(即最大辐射方向上的方向性系数与效率的积)全波振子半长度为/2l λ=,则cos(cos )1()sin f πθθθ+=,max /2()|2f f θπθ===,199r R =Ω2max 1201204 2.41199r f D R ⨯===0.5 2.41 1.205A G D η=⋅=⨯= (0.8)(2) 当3/πθ=时,cos(cos )123()33sin 3f ππθπ+==,则2/3120()1204|0.8041993r f D R θπθ===⨯=(2-3) 某天线以输入端电流为参考的辐射电阻和损耗电阻分别为Ω=4r R 和Ω=1L R ,天线方向性系数3,求天线的输入电阻in R 和增益G 。
天线原理与设计作业
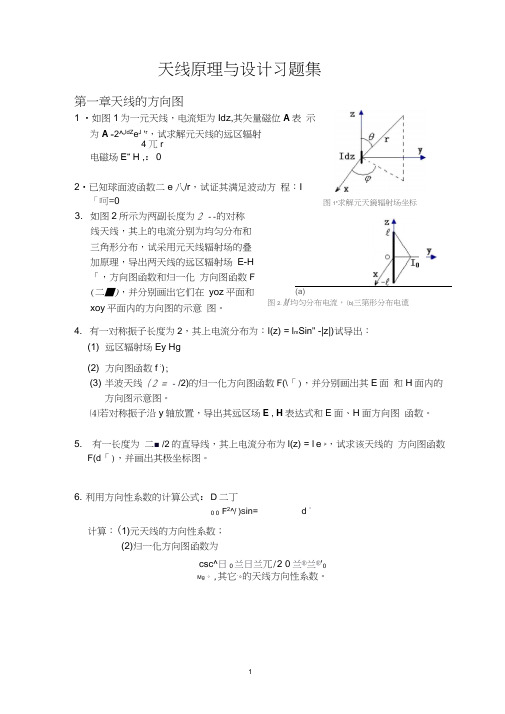
天线原理与设计习题集第一章天线的方向图1 •如图1为一元天线,电流矩为Idz,其矢量磁位A表示为A =2^o IdZ e J 'r,试求解元天线的远区辐射4兀r电磁场E“ H ,:02•已知球面波函数二e八/r,试证其满足波动方程:I 「呵=03. 如图2所示为两副长度为2 --的对称线天线,其上的电流分别为均匀分布和三角形分布,试采用元天线辐射场的叠加原理,导出两天线的远区辐射场E-H「,方向图函数和归一化方向图函数F(二■),并分别画出它们在yoz平面和xoy平面内的方向图的示意图。
(a)图2. M均匀分布电流,(b)三第形分布电谎4. 有一对称振子长度为2,其上电流分布为:l(z) = l m Sin" -|z|)试导出:(1) 远区辐射场Ey Hg(2) 方向图函数f :);(3) 半波天线{2 = -/2)的归一化方向图函数F(\「),并分别画出其E面和H面内的方向图示意图。
⑷若对称振子沿y轴放置,导出其远区场E , H表达式和E面、H面方向图函数。
5. 有一长度为二■ /2的直导线,其上电流分布为l(z) = l°e jz,试求该天线的方向图函数F(d「),并画出其极坐标图。
6. 利用方向性系数的计算公式:D二丁0 0F2^/)S in= d:计算:(1)元天线的方向性系数;(2)归一化方向图函数为csc^日0兰日兰兀/2 0兰®兰®'0Mg。
,其它,0的天线方向性系数。
图1*求解元天鏡辐射场坐标(3)归一化方向图函数为: F():)cos"日,0 兰日5 12,〔0 ,其它n=1和2时的天线方向性系数。
7•如图3所示为二元半波振子阵,两单元的馈电电流关系为h =12』必,要求导出二元阵的方向图函数仃(1「),并画出E面(xoy面)方向图的示意图。
8 •有三付对称半波振子平行排列在一直线上,相邻振子间距为d,如图4所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章口径天线的理论基础(8-1) 简述分析口径天线辐射场的基本方法。
答:把求解口径天线在远区的电场问题分为两部分:①. 天线的内部问题;②. 天线的外部问题;通过界面上的边界条件相互联系。
近似求解内部问题时,通常把条件理想化,然后把理想条件下得到的解直接地或加以修正后作为实际情况下的近似解。
这样它就变成了一个与外部问题无关的独立的问题了。
外部问题的求解主要有:辅助源法、矢量法,这两种是严格的求解方法;等效法、惠更斯原理法、几何光学法、几何绕射法,这些都是近似方法。
(8-2) 试述几何光学的基本内容及其在口径天线设计中的应用。
答:在均匀的媒质中,几何光学假设能量沿着射线传播,而且传播的波前(等相位面)处处垂直于射线,同时假设没有射线的区域就没有能量。
在均匀媒质中,射线为直线,当在两种媒质的分界面上或不均匀媒质传播时,便发生反射和折射,而且完全服从光的反射、折射定律。
BAl nds=⎰光程长度:在任何两个给定的波前之间,沿所有射线路径的光程长度必须相等,这就是光程定律。
''PdA P dA=应用:①. 可对一个完全聚焦的点源馈电的天线系统,求出它在给定馈源功率方向图为P(φ,ξ)时,天线口径面上的相对功率分布。
②. 对于完全聚焦的线源馈电抛物柱面天线系统,口径上的相对功率分布也可用同样类似的方法求解。
(8-3) 试利用惠更斯原理推证口径天线的远区场表达式。
解:惠更斯元产生的场:(1cos)2SPj rSSPjEdE erβθλ-⋅=⋅+⋅⋅222)()(zyyxxrSSSP+-+-=r , >>D (最大的一边)推广到球坐标系:sin cossin sincosx ry rz rθφθφθ=⋅⎧⎪=⋅⎨⎪=⎩r=,S Sx y r<<c o s )S P r =sin cos sin sin S S r x y θφθφ≈-⋅-⋅sin (cos sin )(1cos )2j r j x y S SjE e E e dxdy r ββθφφθλ-⋅⋅+∴=+⋅⎰⎰(8-4) 试利用等效原理推证惠更斯面元的辐射场表达式。
(P188)第九章 平面口径的绕射(9-1) 从口径天线的一般远场公式如何得到矩形和圆形平面口径天线的远场表达式? 解:由惠更斯远场公式j j (cos sin )sin j j (cos sin )sin jsin (1cos )2j cos (1cos )2rsy x y rsy x y E e dE e ds r E e dE e ds r ββϕϕθθββϕϕθϕϕθλϕθλ-+-+⎧=+⎪⎪⎨⎪=+⎪⎩可得矩形口径天线远场表达式j j (cos sin )sin j j (cos sin )sin j sin (1cos )(,)2j cos (1cos )(,)2r x y sy s r x y sy se E E x y edxdy r e E E x y e dxdy r ββϕϕθθββϕϕθϕϕθλϕθλ-+-+⎧=+⎪⎪⎨⎪=+⎪⎩⎰⎰⎰⎰ 圆形口径天线远场表达式ˆˆ11ˆˆˆ()s s s s s s s E E z E E ρϕϕρρϕρϕηη=+⎧⎪⎨=⨯=-+⎪⎩E H E j j sin cos()j j sin cos()j (1cos )(,)cos()(,)sin()2j (1cos )(,)sin()(,)cos()2r s s srs s s e E E E e d d r e E E E e d d r ββρθϕϕθρϕββρθϕϕϕρϕθρϕϕϕρϕϕϕρρϕλθρϕϕϕρϕϕϕρρϕλ-'--'-⎧'''''⎡⎤=+-+-⎪⎣⎦⎪⎨⎪'''''⎡⎤=+--+-⎣⎦⎪⎩⎰⎰⎰⎰(9-2) 试根据天线增益的定义,推证平面口径的增益和效率的表达式,并说明其物理意义。
解:已知口径电场分布为:E (,)sy y E x y ∧=口径面上磁场为:H =(,)sy E x y xη∧-则辐射功率为:()0211,22r sy s s P E H ds E x y ds η*=⨯=⎰⎰⎰⎰ 合成场的模:()()()cos sin 1cos ,,2j x y sy E E x y e ds rβϕϕθθϕλ++==⎰⎰理想电源辐射功率为:2022rP E r ηπ=由增益的定义:()()()22220,2,,rE r G E E P θϕπθϕθϕη==易求得:()()()()()2cos sin 22,1cos ,,j x y sysyE x y edsG E x y dsβϕϕπθθϕλ++=⎰⎰⎰⎰工程上,一般是求最大辐射方向(0θϕ==)的增益即:()()2222,44,sy syE x y ds G S E x y ds ππνλλ==⎰⎰⎰⎰ 效率为:22sy sy E dsS E dsν=⎰⎰⎰⎰物理意义:天线的增益表示在相同输入功率的条件下,某天线在给定方向上的辐射强度与理想点源天线在同一方向的辐射强度的比值。
天线的口径效率表示口径场不均匀时有效面积和实际口径面积之比,口径场越均匀效率越高。
(9-3) 试比较矩形口径和圆形口径在同相的均匀和坡度分布下的主瓣宽度,旁瓣电平和效率。
答:查表(P201)不管是矩形口径还是圆形口径(同相时),其主瓣宽度都随分布的不均匀性的加大而变宽,旁瓣电平和口径效率都随分布的不均匀性的加大而减小。
矩形口径与圆形口径(内切圆)相比,前者的波瓣宽度窄,副瓣电平高。
因它有效面积比圆形口径的有效面积大。
(9-4) 试述口径场相位分布对方向图和口径效率有何影响及对设计的要求。
答:一般来讲,口径场相位分布不同相的结果将使方向图的主瓣展宽、副瓣电平提高、增益降低。
工程设计中视具体情况而定。
对喇叭馈源来说,其口径边缘的最大相位偏差,8Hm Em πϕϕ≤对反射面天线凹凸不平引起的相位偏差4πϕ∆≤(9-5) 设有一长度为,宽为的矩形口径,如图所示。
若口径场为均匀同相分布,要求:①导出E 面和H 面方向图函数;②若口径较大,即和远大于波长时导出E 5.02ϕ和H 5.02ϕ的表达式。
提示:惠更斯矩形面元的辐射场公式为⎪⎩⎪⎨⎧+=+=++dxdy ey x E A dE dxdy ey x E A dE y x j sy y x j sy θϕϕβϕθϕϕβθθϕθϕsin )sin cos (sin )sin cos (),()cos 1(cos ),()cos 1(sin 式中,r e j A r j λβ2-=。
且当707.0sin =uu时,39.1=u 。
解:由公式⎪⎩⎪⎨⎧+=+=++dxdy ey x E A dE dxdy e y x E A dE y x j sy y x j sy θϕϕβϕθϕϕβθθϕθϕsin )sin cos (sin )sin cos (),()cos 1(cos ),()cos 1(sin 口径场为均匀同相分布 0ys E E =①E 面和H 面方向图函数惠更斯矩形面元的辐射公式为0ϕ=: sin 0(1cos )j y H dE A E e dxdy βθθ⋅⋅=+90ϕ=: sin 0(1cos )j x E dE A E e dxdy βθθ⋅⋅=+⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+=+=+=+=⎰⎰⎰⎰--⋅⋅--⋅⋅22220sin 022220sin 0sin )cos 1()cos 1(sin )cos 1()cos 1(xx y y y y xx D D D D y y y j E D D D D x x x j H u u SAE dy e dx AE E u u S AE dx e dy AE E θθθθθβθβ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⋅⎪⎪⎭⎫⎝⎛⋅+=⋅⎪⎭⎫⎝⎛⋅+=θλπθλπθθλπθλπθsin sin sin )cos 1(sin sin sin )cos 1(yy Ex x H D D F D D F 忽略1θ,因为、远大于波长λ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⋅⎪⎪⎭⎫⎝⎛⋅=⋅⎪⎭⎫⎝⎛⋅=θλπθλπθλπθλπs i n s i n s i n s i n s i n s i n y y E x x H DD F D D F当707.0sin =uu时,1.39 ()()⎪⎪⎩⎪⎪⎨⎧≈⇒=⋅≈⇒=⋅∴05.05.005.05.051239.1sin 51239.1sin yE E yxH H xD DD D λθθλπλθθλπ第十章 喇叭天线(10-1) 试述最佳角锥喇叭的定义和条件,并说明其物理意义。
答:最佳角锥喇叭是指使喇叭天线在其E 面和H 面尺寸均取最佳。
条件为:2222H Hop EEop D R D R λλ⎧=⎪⎪⎨⎪=⎪⎩物理意义为:当为最佳角锥喇叭时,其E 面和H 面增益均可达导最大。
(10-2) 试述喇叭天线口径场分布的特点和空气透镜天线的基本原理。
(10-3) 简要回答和证明扇形喇叭的口径场沿张开的口径方向为平方律相差。
解:图为H 面扇形喇叭的截面图,设 在喇叭内传播的是柱面波,当电磁波 传播到口径处时,其等相位线是以喇 叭张角虚顶点'O 为圆心,半径为R 的一段内切圆弧,若以口径面相位中心O 为参考点,则在偏离中心点的X 处波程差为()x δ,有()222R x R x δ+=+⎡⎤⎣⎦; ()22x x R R Rδ=-+=-+=; 设由虚顶点O ’发出的柱面波到达口径面偏离中心点为x 处的场为()(),j R x sy E E x y eβδ-+=若口径场为振幅均匀分布,取()0,j R E x y e E β-=,则 ()2200x j j x Rsy E E e E e ββδ--==(详见课件9.3节)(10-4) 设计一角锥喇叭天线,要求其半功率波瓣宽度2H E 5.05.02θθ==10°。
已知工作波长mm 8=λ,馈电波导尺寸a ×7.112×3.5562。
要求计算喇叭的口径尺寸,,长度,和天线增益。
解:由角锥喇叭半功率波瓣宽度00.500.5280254HH EE D D λθλθ⎧=⎪⎪⎨⎪=⎪⎩548010E H D D λλ⇒== 得 43.264E H D D =⎧⎨=⎩而 221116.6421170.6673E E H H D R D R λλ⎧=⋅=⎪⎪⎨⎪=⋅=⎪⎩检验:、 (馈电波导尺寸:525.9050.19⨯=⨯b a )1 1.111H EE HbR D a R D -==-1.11H E R R∴= 7.170667.1707.153754.153≈=≈=H E R R喇叭天线的尺寸:64,170.743.2,153.7H H E E D mm R mmD mm R mm====天线的增益:240.51276.86(24.4)H ED D G dB πλ⋅⋅==(10-5) 设计一作为标准增益的角锥喇叭天线,要求增益为15,工作波长cm 2.3=λ,馈电波导尺寸a ×b =22.86×10.162。
