最新人教版七年级数学上册第四章正多面体
最新人教版七年级数学上册全套PPT课件 第四章 几何图形初步 全章课件
底面是两个相同
侧面是一个
底面是一个多边形(三
的多边形(三角
扇 形,底
角形),侧面都是
形),侧面都是
面是一个圆
三角 形
长方 形
注意:同一个立体图形按照不同的方式展开,得到的平面图形是不一样的.
知识点三 由表面展开图描述多面体
一个多面体的底面通常有一个或两个,而侧面却有 很多.根据此特点,从判断多面体的底面入手,再分 析侧面,就能确定多面体的形状.
(2)把直角三角形以直角边所在直线为轴旋转一周，得到的立体 图形又是什么？以斜边所在直线为轴呢？你能画出示意图吗？
解：(2)把直角三角形以直角边所在直线为轴旋转一周 得到圆锥，以斜边所在直线为轴旋转一周得到两个圆 锥的组合体. 如图所示．
图4－1－22
解：(1)把长方形以长方形的一边所在直线为轴旋转一周，得 到的立体图形是圆柱．有两种情形，如图所示．
(2) 图中有几条线段，怎样表示它们？
(3) 射线 AB 和射线 AC 是同一条射线吗？
(4) 图中有几条射线？写出以点B为端点的射线.
AA
BB
CC
解：(1) 1条，直线AB或直线AC或直线BC；
(2) 3条，线段AB，线段BC，线段AC；
(3) 是；
(4) 6条.以B为端点的射线有射线BC、射线BA.
随堂演练
1. 如图是一个几何体的表面展开图,则该几何体是 ( C )
A.正方体 C.三棱柱
B.长方体 D.四棱锥
2.下列各图不是正方体表面展开图的是 ( C )
3.下列投影是平行投影的是 ( A )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
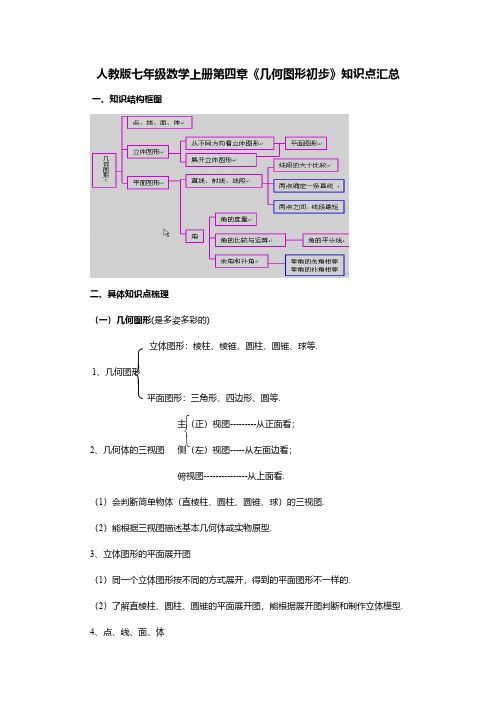
人教版七年级数学上册第四章《几何图形初步》知识点汇总
人教版七年级数学上册第四章《几何图形初步》知识点汇总一、知识结构框图二、具体知识点梳理（一）几何图形(是多姿多彩的)立体图形：棱柱、棱锥、圆柱、圆锥、球等.1、几何图形平面图形：三角形、四边形、圆等.主（正）视图---------从正面看；2、几何体的三视图侧（左）视图-----从左面边看；俯视图---------------从上面看.（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图.（2）能根据三视图描述基本几何体或实物原型.3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平面图形不一样的.（2）了解直棱柱、圆柱、圆锥的平面展开图，能根据展开图判断和制作立体模型.4、点、线、面、体(1)几何图形的构成点：直线与直线相交的点，是几何图形中最基本的图形。
线：面与面的交线是一条线，分为直线和曲线。
面：包围着体的是面，分为平面和曲面.体：几何体也简称体.(2)点运动成线，线运动成面，面运动成体。
(2)直线、射线和线段1、基本概念图形端点个数直线无直线a表示法直线AB（BA）作直线AB作法叙述做一条直线a制作射线ab作线段AB、连接AB延长线段AB延长叙述不能延长反向延长射线AB反向延长线段BA2、直线的性质有一条直线经过两点，并且只有一条直线。
缩写：两点确定一条直线。
3.画一条与已知线段相等的线段。
(1)测量方法。
(2)用尺子画图。
(4)比较线段的大小。
(1)测量方法。
(2)重叠法。
(5)线段的中点(二等分点)、三等分点和四等分点。
射线AB线段AB（BA）作线段a射线一个两个线段a线段定义：把一条线段平均分成两条相等线段的点叫做线段的中点.图形：AMB符号：若点M是线段AB的中点，则AM=BM=1AB，AB=2AM=2BM.26、线段的性质：两点的所有连线中，线段最短.简称：两点之间，线段最短.7、两点的距离：连接两点的线段长度叫做这两点的距离.8、点与直线的位置关系（1）点在直线上；（2）点在直线外.（三）角1.角：由两条有共同端点的射线组成的图形称为角。
人教版七年级数学上册第四章《几何图形初步》知识点汇总
⎧⎨⎩⎧⎨⎩人教版七年级数学上册第四章《几何图形初步》知识点汇总一、知识结构框图二、具体知识点梳理（一）几何图形(是多姿多彩的)立体图形：棱柱、棱锥、圆柱、圆锥、球等.1、几何图形平面图形：三角形、四边形、圆等.主（正）视图---------从正面看；2、几何体的三视图 侧（左）视图-----从左面边看；俯视图---------------从上面看.（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图.（2）能根据三视图描述基本几何体或实物原型.3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平面图形不一样的.（2）了解直棱柱、圆柱、圆锥的平面展开图，能根据展开图判断和制作立体模型.4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形.线：面和面相交的地方是线，分为直线和曲线.面：包围着体的是面，分为平面和曲面.体：几何体也简称体.（2）点动成线，线动成面，面动成体.（二）直线、射线、线段1、基本概念图形直线射线线段端点个数无一个两个表示法直线a直线AB（BA）射线AB线段a线段AB（BA）作法叙述作直线AB作直线a 作射线AB作线段a作线段AB、连接AB延长叙述不能延长反向延长射线AB延长线段AB反向延长线段BA 2、直线的性质经过两点有一条直线，并且只有一条直线. 简称：两点确定一条直线.3、画一条线段等于已知线段（1）度量法（2）用尺规作图法4、线段的大小比较方法（1）度量法（2）叠合法5、线段的中点（二等分点）、三等分点、四等分点等定义：把一条线段平均分成两条相等线段的点叫做线段的中点.图形：A M B符号：若点M 是线段AB 的中点，则AM=BM=AB ，AB=2AM=2BM.126、线段的性质：两点的所有连线中，线段最短.简称：两点之间，线段最短.7、两点的距离：连接两点的线段长度叫做这两点的距离.8、点与直线的位置关系 （1）点在直线上； （2）点在直线外.（三）角1、角：由公共端点的两条射线所组成的图形叫做角.2、角的表示法（四种）：∠1 ； ； ； .α∠β∠ABC ∠3、角的度量单位及换算4、角的分类：锐角、直角、钝角、平角、周角.5、角的比较方法 （1）度量法 （2）叠合法6、角的和、差、倍、分及其近似值7、画一个角等于已知角（1）借助三角尺能画出15°的倍数的角，在0～180°之间共能画出11个角.（2）借助量角器能画出给定度数的角.（3）用尺规作图法，可以作出任意给定的角.8、角的平线线定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做角的平分线.图形： 符号：9、互余、互补（1）若∠1+∠2=90°，则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角.（2）若∠1+∠2=180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角.（3）余（补）角的性质：同（等）角的余角相等. 同（等）角的补角相等.10、方向角（1）正方向；（2）北（南）偏东（西）方向；（3）东（西）北（南）方向.。
(名师整理)最新人教版数学七年级上册第4章第1节《立体图形与平面图形——点、线、面、体》精品课件
2
3
4
5
A
B
C
D
E
想一想：在你所熟悉的几何体中， 分别举例说明：
⑴全由曲面围成的几何体； ⑵全由平面围成的几何体； ⑶由平面和曲面围成的几何体； ⑷全由三角形围成的几何体
思考题：现有一条长为5cm，宽为
4cm的矩形，分别绕它的长，宽所在 直线旋转一周，得到不同的圆柱体， 他的体积分别为多少？谁的体积大？ 你得到怎么样的启示？
长方形 绕一边 旋转成 圆柱体
点是构成图形的基本元素
当电视画面的局部被放大后，你看到了什么 现象？分析这一现象，你能得出什么结论？
点、线、面、体经过运动 变化，形成多姿多彩世界。
填一填
1．人在雪地上走，他的脚印形成一条
__线_____，这说明了点__动__成__线 的数学原
理．
2．体是由__面_____围成的，面和面相交于 __线_____，线和线相交于__点____． 3．点动成___线_____，线动成__面____，面 动成__体_____．
点、线、面、体
1．可以从简单实物的外形中抽象出几何图形，并了解立体 图形与平面图形的区别； 2．会判断一个几何图形是立体图形还是平面图形，能准确 识别棱柱与棱锥． 3．能够画出从不同方向看一些常见的立体图形所得到的平 面图形,能够根据从不同方向看一个立体图形得到的平面图形, 想象并描述它的形状； 4．体会立体图形与平面图形的相互转化关系．
点
方是点
元素
点、线、面、体关系
点动成—— 线 线动成—— 面 面动成—— 体
体是由面围成 面与面相交成线 线与线相交成点
给我最大快乐的,不是已懂的知识, 而是不断的学习.
----高斯
4.几何图形是由_点__、_线______ 面 体 组成 、______、_______ 的。点___是组成图形的基本元素。
人教版数学七年级上册 第四章4.1.1立体图形的展开图
新知讲解
发现规律
1．沿立体图形的棱将立体图形剪开成平面图形，若干个平面 图形也可以围成一个多面体.
2．同一个立体图形沿不同的棱剪开，得到的平面展开图是不 一样的，就是说：同一个立体图形可以有多种不同的展开 图.
新知讲解
将一个正方体的表面沿某些棱剪开，能展成哪些平面 图形？与同伴进行交流．
友情提示： 1、沿着棱剪 2、展开后是一个图形
80.真正的闲，是心灵中超然物外；真正的忙，是工作里浑然忘我。真正的退，是处世时自然低调；真正的进，是做事中泰然担当。真正的静 ，是生命里寂然涤思；真正的动，是世路上毅然向前。真正的记，是脑海里珍藏印记；真正的忘，是微笑里坦荡无余。
71.成功与失败的分水岭可以用这几个字来表达——我没有时间。 57.不好用借口搪塞失败，不好让骄傲占据心灵。 26.同样的一瓶饮料，便利店里块钱，五星饭店里块。很多时候，一个人的价值取决于所在的位置。 98.哪怕此刻的生活有多糟糕，也总会有好转的一天。走过的生活并不完美，太完美的也就不是生活了！每人每天都在做一件事情：为了未来 而奋斗！固然结果不同，皆因我们平时的努力，每个今天我们都尽十分的努力，未来的成功就是必然！
蓝 黄
新知应用
例1 下列图形中，不是正方体
C
D
新知应用
例2 “坚” 在下，“就”在后，“胜”和“利”在哪里？
坚 持 就是
胜
“胜”在上，“利”在前.
一个多面体的展开图中， 在同一直线上的相邻的三个 线框中，首尾两个线框是立 体图形中相对的两个面.
利
新知应用
例3 下面图形是一些多面体的表面展开图，你能说出这些多面体 的名字吗?
75.你看着天空，才发现从七岁起陪着你的那个天空，一直都在你的头顶。然后，你最后一次的想，会不会云层的上头，真的有那一个城堡。 却又突然间觉得自己的这个想法很可笑。你终于是明白，原来生活比你想象的是艰难很多。
人教版七年级数学上册第四章《几何图形初步》知识点汇总
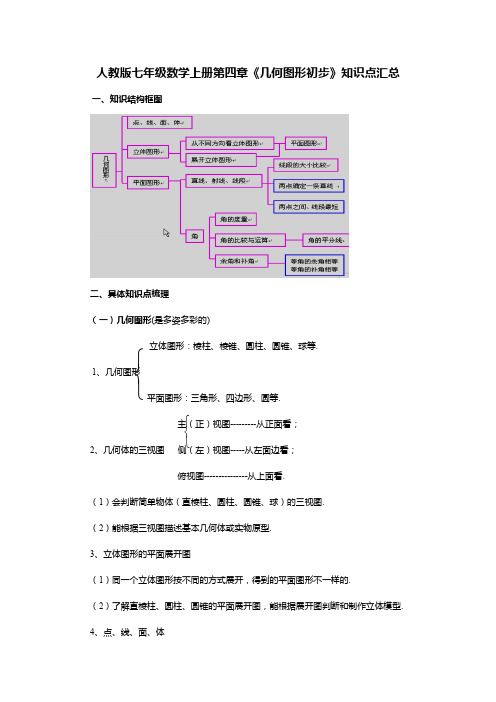
⎧⎨⎩⎧⎨⎩人教版七年级数学上册第四章《几何图形初步》知识点汇总一、知识结构框图二、具体知识点梳理（一）几何图形(是多姿多彩的)立体图形：棱柱、棱锥、圆柱、圆锥、球等. 1、几何图形 平面图形：三角形、四边形、圆等.主（正）视图---------从正面看； 2、几何体的三视图 侧（左）视图-----从左面边看；俯视图---------------从上面看.（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图.（2）能根据三视图描述基本几何体或实物原型.3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平面图形不一样的.（2）了解直棱柱、圆柱、圆锥的平面展开图，能根据展开图判断和制作立体模型.4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形.线：面和面相交的地方是线，分为直线和曲线.面：包围着体的是面，分为平面和曲面.体：几何体也简称体.（2）点动成线，线动成面，面动成体.（二）直线、射线、线段1、基本概念2、直线的性质经过两点有一条直线，并且只有一条直线. 简称：两点确定一条直线.3、画一条线段等于已知线段（1）度量法（2）用尺规作图法4、线段的大小比较方法（1）度量法（2）叠合法5、线段的中点（二等分点）、三等分点、四等分点等定义：把一条线段平均分成两条相等线段的点叫做线段的中点.图形：A M B符号：若点M 是线段AB 的中点，则AM=BM=12AB ，AB=2AM=2BM. 6、线段的性质：两点的所有连线中，线段最短.简称：两点之间，线段最短.7、两点的距离：连接两点的线段长度叫做这两点的距离.8、点与直线的位置关系 （1）点在直线上； （2）点在直线外.（三）角1、角：由公共端点的两条射线所组成的图形叫做角.2、角的表示法（四种）：∠1 ； α∠ ； β∠ ； ABC ∠.3、角的度量单位及换算4、角的分类：锐角、直角、钝角、平角、周角.5、角的比较方法 （1）度量法 （2）叠合法6、角的和、差、倍、分及其近似值7、画一个角等于已知角（1）借助三角尺能画出15°的倍数的角，在0～180°之间共能画出11个角.（2）借助量角器能画出给定度数的角.（3）用尺规作图法，可以作出任意给定的角.8、角的平线线定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做角的平分线. 图形： 符号：9、互余、互补（1）若∠1+∠2=90°，则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角.（2）若∠1+∠2=180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角.（3）余（补）角的性质：同（等）角的余角相等. 同（等）角的补角相等.10、方向角（1）正方向；（2）北（南）偏东（西）方向；（3）东（西）北（南）方向.。
七上数学第四章知识点总结人教版
七上数学第四章知识点总结人教版摘要：一、前言二、人教版七上数学第四章的知识点概述1.几何图形初步2.点、线、面的关系3.直线、射线、线段4.角的概念及分类5.角的度量6.三角形的性质和分类7.三角形的内角和定理8.四边形的性质和分类9.平行四边形的性质10.梯形的性质11.面积的计算三、重要公式和定理四、实际应用与例题解析五、总结与展望正文：一、前言人教版七上数学第四章主要涉及几何图形的初步知识，这对于培养学生空间观念和几何直观能力具有重要意义。
本章内容较为基础，但也为后续的几何学习打下良好基础。
二、人教版七上数学第四章的知识点概述1.几何图形初步：本章从最基本的点、线、面开始，让学生了解它们之间的关系，为后续的几何学习打下基础。
2.点、线、面的关系：点动成线，线动成面，面动成体。
学生需要理解并掌握这一基本关系。
3.直线、射线、线段：直线是无限延伸的，射线有一个起点，线段有两个端点。
理解它们的定义和性质有助于更好地理解几何图形。
4.角的概念及分类：角是由两条射线共同确定的图形，有锐角、直角、钝角等分类。
学生需要学会识别和分类各种角。
5.角的度量：角的大小可以用度数或弧度表示，学生需要熟练掌握角的度量方法。
6.三角形的性质和分类：三角形由三条边和三个顶点组成，根据边长和角度的不同，可以分为不等边三角形、等腰三角形和直角三角形等。
7.三角形的内角和定理：三角形三个内角的和等于180 度。
8.四边形的性质和分类：四边形由四条边和四个顶点组成，根据边长和角度的不同，可以分为矩形、平行四边形、菱形、梯形等。
9.平行四边形的性质：平行四边形的对边平行且相等。
10.梯形的性质：梯形有一对平行的边，另一对不平行的边。
11.面积的计算：本章介绍了三角形、平行四边形、梯形等图形的面积计算公式。
三、重要公式和定理1.三角形的面积公式：S = 1/2 * a * h，其中a 为底边长，h 为高。
2.平行四边形的面积公式：S = a * h，其中a 为底边长，h 为高。
七年级数学上册第四章几何图形初步4.1几何图形4.1.1立体图形与平面图形课件 新人教版
答案 B A是圆柱;B是棱柱;C是球;D是圆锥.
完整版ppt
21
2.与图中实物图相类似的立体图形按从左至右的顺序依次是 ( )
A.圆柱、圆锥、正方体、长方体 B.圆柱、球、正方体、长方体 C.棱柱、球、正方体、棱柱 D.棱柱、圆锥、棱柱、长方体
答案 B 与题图中实物图相类似的立体图形按从左至右的顺序依次 是圆柱、球、正方体、长方体.故选B.
有两个面(底面)是互相平 行的
底面是多边形;侧面形状 是四边形
底面是圆;侧面是曲面
有一个顶点
底面是多边形;侧面形状 是三角形
各侧面有一个公共顶点
完整版ppt
4
台体 球体
圆台 棱台
底面是圆;侧面是曲面
有两个面(底面)是互相平 行的
底面是多边形;侧面是梯 形
表面是曲面
完整版ppt
5
例1 如图4-1-1-1所示,请写出下列立体图形的名称.
答案 C 从不同方向看圆柱和棱柱,一定有长方形,故可排除A、B,从 不同方向看球,所看到的图形都是圆,故可排除D,只有C符合.
完整版ppt
34
知识点四 立体图形的展开图 13.(2018河北临西一中月考)下列平面图形中,不是正方体的展开图的是
()
答案 D 由四棱柱四个侧面和上下两个底面的特征可知,选项A,B,C 可以拼成一个正方体,而D选项,上底面不可能有两个,故不是正方体的 展开图.故选D.
完整版ppt
18
题型二 正方体的平面展开图 例2 图4-1-1-8是每个面上都有一个汉字的正方体的一种平面展开图, 那么在原正方体中和“国”字所在面相对的面上的汉字是 ( )
图4-1-1-8 A.钓 B.鱼 C.岛 D.中
完整版ppt
七年级数学上册第四章几何图形初步4.1几何图形4.1.2点、线、面、体课件(新版)新人教版
图4-1-2-2
图4-1-2-3 解析 A是由4旋转得到的,B是由2旋转得到的,C是由1旋转得到的,D是 由3旋转得到的. 点拨 利用面动成体这一性质解题.
题型二 探索几何体的顶点、棱、面之间的关系 例2 新年晚会会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立 体图形,多面体是其中的一部分,多面体中围成立体图形的每一个面都 是平的,没有曲的,如棱柱、棱锥等,如图4-1-2-4.
)
答案 B
5.如图,第二行的图形绕虚线旋转一周,便形成第一行的某个图形(几何 体),将对应的两个图末)圆柱是由长方形绕着它的一边所在直线旋 转一周得到的,那么图4-1-2-1是以下四个图形中的哪一个绕着直线旋转 一周得到的 ( )
图4-1-2-1
初中数学（人教版）
七年级 上册
第四章 几何图形初步
知识点 点、线、面、体
重要提示 (1)几何图形都是由点、线、面、体组成的,点是构成图形 的基本元素.点、线、面、体经过运动变化,就能组合成各种各样的几 何图形,形成多姿多彩的图形世界. (2)一般地,有曲面的几何体都可以由某个平面图形旋转得到.将一个平 面图形旋转成立体图形,既与平面图形的形状有关,也与平面图形旋转 时所绕的轴有关,因此在分析平面图形旋转后得到的立体图形时,要综 合分析平面图形的形状和旋转轴两个因素.
解析 分三种情况进行讨论. ①以8 cm长的边所在直线为轴,旋转得到的圆锥的体积V1= ×π×62×8=9 6π(cm3). ②以6 cm长的边所在直线为轴,旋转得到的圆锥的体积V2= ×π×82×6=1
1 3 1 3
28π(cm3).
③以10 cm长的边所在直线为轴,旋转得到的几何体是由两个同底面的 圆锥组成的,设圆锥底面的半径为r cm,则有 ×6×8= ×10×r,解得r=4.8.
人教版七年级数学上册第四章 《几何图形初步》课件
●
●
●
A
C
B
1
ACCB AB
2
或 AB=2AC=2CB
用一个大写字母表示点， 用二个大写字母表示线，
用三个大写字母表示角，
A
B
C
o
1
ABC
o
1
角度的转化： 1°=60′ 1′=60 〞 1°=3600 〞
角度的加减： 1.同种形式相加减； 2.度加（减）度；分加（减）分； 秒加（减）秒 3.超60进一；减一成60
谢谢观赏
You made my day!
我们，还在路上……
字母或用一个小写字母来表示. (3)线段的画法:可用直尺先量出线段的长度,
再画一条等于这个长度的线段.
下面的知识点你掌握了吗？
(4)线段的基本性质:两点之间线段最 短.
(5)两点间的距离:连结两点的线段的 长度,叫做这两点间的距离.
(6)线段的特点:有两个端点,不能向任 何一方伸展,可以度量,可以比较长短.
中学学科网
正视图 左（右）视图 俯视图
例：画出以下立体图形的三视图
正方体
长方体
三棱柱
四棱锥
三棱柱
五棱锥
归纳：正方体 的表面展开图 有以下11种。你能看 出有什么规律吗？
一
二
阶
四 一 型
三 一 型
梯 型
直线、射线、线段的比较
名称
直线
射线
线段
图形
表示法
a
A
BO C
线段AB 、线 射线OC、 段BA、线段a 射线l
知识点2：射线
(1)射线的概念:把线段向一方无限延伸所形成 的图形叫做射线.
(2)射线的表示方法:可用两个大写字母表示, 第一个大写字母表示它的端点;也可用一个 小写字母表示.
七年级数学上册 第四章 几何图形初步 4.1.1《立体图形与平面图形》课件2 (新版)新人教版
想一想
如果拼两个这样的三角形(等边三角形)
至少需要几条线段？ 三个呢？四个呢？
．．
1、本课学习了什么知识？ 2、本节课学会了什么方法？
➢ 新人教版数学七年级上册 第四章 几何图形初步
4.1.1 立体图形与平面图形(2)
苏轼
“横看成岭侧成峰” 一句中，蕴含了怎样的数学 道理？
立体图形
从正面看
主视图、左视图都是相等的长方形，俯视 图是圆，则该物体是 圆柱 。
用小立方块搭出符合下列三视图的几何体：
主视图
左视图
俯视图
1 21 1
俯视图
【探究】
1 . 如图是由几个小立方体所搭 几何体的俯视图，小正方形 中的数字表示在该位置小正 方体的个数。 你能摆出这个几何体吗？
试画出这个几何体的主视图 与左视图。
➢ 新人教版数学七年级上册 第四章 几何图形初步
4.1.1立体图形与平面图形(1)
到城雕
从古剪代纸 到现代 从长城 到立交
从植物 到动物
圆柱体
对于生活中的各种各样的物体，数学中关注的是 1、物体的形状(如方的、圆的等)； 2、物体的大小(如长度、面积、体积等) 3、物体的位置(如相交、垂直、平行等)。 它们的颜色、重量、材料等则是其他学科所关注。
如图图形是 __B_、__D_正方体的展开图．
A．
B．
C．
D．
5.小壁虎的选择：
如图：一只圆桶的下方有一只壁虎，上方有一只 蚊子，壁虎要想尽快吃到蚊子，应该走哪条路径？
●
●
● ●
通过本节课的学习，你掌握了什么本领？向大家汇 报一下！
作业：
1.教科书第122页习题4.1第6、7题.
2. 根据所学知识，帮老师做一个长方体形状的盒子.
人教版初一(七年级)数学上册课件-第四章 几何图形初步
Hale Waihona Puke 谜 语：落 到 水 中 看 不
千 条 线 万 条 线
见
1.把下面第一行的平面图形绕线旋转一周，便能形成第二 行的某个几何体，请用虚线连一连：
1
2
3
4
5
A
B
C
D
E
2.下图是一个长方体的模型，它有几个面，面和面相交的
地方形成了几条线？线和线相交成几个点？
·· ··
·· ·· 6个面
12条线
长方体
展开
圆柱
展开
圆锥
展开
棱柱
展开
如图所示，下面的图形分别是上面哪个立体图形的展开 图？把它们用线连起来.
1
2
3
4
A
B
C
D
想一想下列图形能围成什么立体图形？
1
2
圆
棱
柱
柱
3
4
圆
棱
锥
柱
用剪刀把桌上的正方体纸盒按任意方式沿棱展开，你 能得到哪些不同的展开图？比一比哪个小组的展开图的种 类更多.
你做对了吗？
1.下面是由六个正方形连在一起的图形，经折叠后能围 成正方体的图形有哪几个？
A
B
C
D
E
F
G
2.（武汉中考）如图所示，李老师办公桌上放着一个圆柱 形茶叶盒和一个正方体的墨水盒，小芳从上面看，看到的 图形是（ ）
答案：A
(A) (B)
(C) (D)
3.（宜宾中考）如图是由若干个大小相同的小正 方体堆砌而成的几何体．那么其三种视图中面积最小的 是（ ）
(A)正视图 (B)左视图 (C)俯视图 (D)三种一样 【解析】选B.正视图是由5个小正方形构成的平面图形； 左视图是由3个小正方形构成的平面图形；俯视图是由5个 小正方形构成的平面图形.
七年级数学上册第四章几何图形初步认识4.1.1 立体图形与平面图形 第2课时(图文详解)
人教版七年级数学上册第四章几何图形初步认识
5．长方形、正方形、圆等都是 平面 图形. 6．写出下列几何体的名称．
棱柱
棱锥
圆锥
人教版七年级数学上册第四章几何图形初步认识
7．下列图形中为圆柱的是（ D ）．
8．埃及金字塔类似于几何体（ C ）．
(A)圆锥 (B)圆柱 (C)棱锥 (D)棱柱
人教版七年级数学上册第四章几何图形初步认识
你做对了吗？
人教版七年级数学上册第四章几何图形初步认识
1.下面是由六个正方形连在一起的图形，经折叠后能围 成正方体的图形有哪几个？
A
B
C
D
E
F
G
人教版七年级数学上册第四章几何图形初步认识
2.（武汉中考）如图所示，李老师办公桌上放着一个圆柱 形茶叶盒和一个正方体的墨水盒，小芳从上面看，看到的 图形是（ ）
人教版七年级数学上册第四章几何图形初步认识
9．下列图形中不是立体图形的是（ D ）．
(A)球
(B)圆柱
(C)圆锥 (D)圆
人教版七年级数学上册第四章几何图形初步认识
10．小明为班级专栏设计了一个图案，如图所示，主 题是“我们喜爱合作学习”，请你也尝试用圆、扇形、 三角形、四边形、直线等为环保专栏设计一个图案， 并标明你的主题．
人教版七年级数学上册第四章几何图形初步认识
4.（宁波中考）骰子是一种特别的数字立方体(如图)，它
符合以下规则：相对两面的点数之和总是7.下面四幅图中
可以折成符合规则的骰子的是（ ）
(A)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正多面体
有一次一个平常的英国孩子詹姆斯，在醉心于制作多面体模型时，写信给父亲：“……我做了四面体、十二面体以及两个不知道名称的多面体．”他当时还是一个毫无名气的孩子．这些话意味着伟大物理学家詹姆斯·克拉克·麦克斯韦尔诞生了．想象一下，你们自己和你们亲人醉心于制作几何物体模型的情形．本书的这几页是家庭作业．新年临近，这是最欢乐和美丽的节日．除了传统的枫树装饰（炮仗和小挂灯）外，你们可以制作几何玩具．这是用彩色纸做成的正多面体模型．考察下图，在这图上画着四面体、正方体、八面体、十二面体和二十面体．它们的形状是完美的典型！
你们能觉察到一系列有趣的特点，也正是这些性质使它们得到了相应的名称．每一个正多面体的所有面都是相同的正多边形，在每一个顶点集聚着同样数量的棱，而相邻的面在相等角下毗连．
数一下每一个多面体具有的顶点数（V）、棱数（E）和面数（F），并且把结果记入表中．
在最后一栏，这些多面体得到的是同一个结果：V+F－E＝2．最令人惊奇的是它不仅对正多面体，而且对所有多面体都正确！
若有兴趣你们可以对某些胡乱取得的多面体进行验证．最伟大的数学家之一列昂纳德·欧拉（1707－1783）证明了这一令人惊叹的关系式，因此公式以他命名：欧拉公式．这位出生于瑞士的天才学者几乎整个一生居住在俄罗斯，我们完全有理由和自傲地将他引为自己的同胞．
正多面体还有一个特点．我们发现：正四面体有一性质：如果把它的每个面的中心作为新的多面体的顶点，那么我们重新得到一个正四面体．余下的4个正多面体恰可分成两对．正方体各面的中心组成一个正八面体，而正八面体各面的中心则组成正方体．同样，可以发生的另一对类似联系是正十二面体和正二十面体．
正多面体所具有的完美的形状和漂亮的数学规律使这五种几何物体具有某种神秘色彩，以致于很久以前它们就是神术者和占星家的必要伴侣．如果你们致力于正多面体的研究和制作，那么肯定会使你们感到欢乐和满意，甚至有可能在新的一年里给你带来好运气！
在下图中给出这些枞树上玩具的展开图．在制作模型时不要忘记在需要的地方留一片瓣膜为粘接用．
还有一种制作多面体模型的方法，不用胶水，由一些纸带编织而成．在嵌入最后一段纸带后，模型就具有刚性的结构．
下图展示了怎样用两条由4个三角形组成的纸带编织四面体．
按虚线屈折后又展开一条纸带，使得形成屈折处——“凹地”．把色纸盖在白纸带上，用白纸带折叠成四面体，使得有色三角形出现在它内部，随后用色纸带包裹四面体的两个面，并且把留下的三角形嵌入两个白三角形之间的裂缝中．图中给出一种用三条划分成5个正方形的纸带编织正方体的方法．
1.割出三条这样的纸带（白色、黑色、红色）．
2.折叠白色纸带．
3.用黑色纸带裹住它．
4.得到正方体，其前面和后面是白色的，而其余面是黑色的．
5．你从正方体背后让第三条（红色）纸带穿过白色和黑色纸带的缝隙，折
弯并且最终两个面也穿过正前方的白色面和黑色纸带之间的缝隙．
如果纸带是不同颜色的，那么所得的正方体有同样颜色的对面．在这种图上所展
示的方法的特点是：任何两条纸带彼此都没有钩住，而整个三条却钩住了．还有
另一种也是用纸带编制正方体的方法．在这种情况下每两条纸带是钩住的，而相
邻的一对面将是同一种颜色．独立地试试找出这第二种编制正方体的方法．
摘自《直观几何》。