层次分析法的具体步骤
层次分析法的具体步骤
层次分析法的具体步骤(1)建立层次结构模型如上所述,家纺纺织产业实施循环经济评价指标体系可被分为四层,最上层为最高层(目标层),即纺织企业循环经济各个方面的综合水平;第二层为准则层,即相互独立、分别隶属于总系统层的子系统;第三层为指数层,是对准则层的进一步细分和阐述;最底层为指标层,该层隶属于准则层,是对纺织企、Ek循环经济各个方面具体的评价指标。
在层次分析法巾多采用三层分析,即目标层、准则层和指标层。
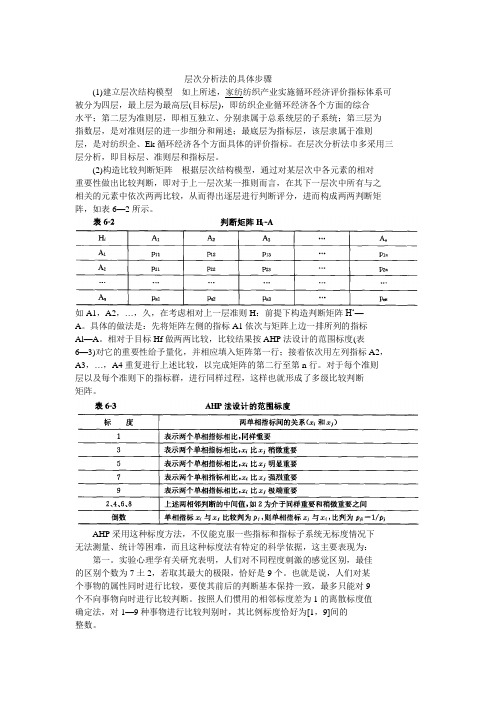
(2)构造比较判断矩阵根据层次结构模型,通过对某层次中各元素的相对重要性做出比较判断,即对于上一层次某一推则而言,在其下一层次中所有与之相关的元素中依次两两比较,从而得出逐层进行判断评分,进而构成两两判断矩阵,如表6—2所示。
如A1,A2,…,久,在考虑相对上一层准则H:前提下构造判断矩阵H‘—A。
具体的做法是:先将矩阵左侧的指标A1依次与矩阵上边一排所列的指标Al—A。
相对于目标Hf做两两比较,比较结果按AHP法设计的范围标度(表6—3)对它的重要性给予量化,并相应填入矩阵第一行;接着依次用左列指标A2,A3,…,A4重复进行上述比较,以完成矩阵的第二行至第n行。
对于每个准则层以及每个准则下的指标群,进行同样过程,这样也就形成了多级比较判断矩阵。
AHP采用这种标度方法,不仅能克服一些指标和指标子系统无标度情况下无法测量、统计等困难,而且这种标度法有特定的科学依据,这主要表现为:第一。
实验心理学有关研究表明,人们对不同程度刺激的感觉区别,最佳的区别个数为7土2,若取其最大的极限,恰好是9个。
也就是说,人们对某个事物的属性同时进行比较,要使其前后的判断基本保持一致,最多只能对9个不向事物向时进行比较判断。
按照人们惯用的相邻标度差为1的离散标度值确定法,对1—9种事物进行比较判别时,其比例标度恰好为[1,9]间的整数。
第二,人们在估计事物问区别时,习惯采用五种判断表述:相等、较强、强、4硼、绝对强。
若需要更高精度,还可在这五种相邻判断之间做出比较,这样共有9个等级。
(完整版)层次分析法步骤

层次分析法实例与步骤结合一个具体例子,说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策:层次分析法问题提出 市政部门管理人员需要对修建一项市政工程项目进行决策,可选择的方案是修建通往旅游 区的高速路(简称建高速路)或修建城区地铁(简称建地铁) 。
除了考虑经济效益外,还要考虑 社会效益、环境效益等因素,即是多准则决策问题,考虑运用层次分析法解决。
1. 建立递阶层次结构应用 AHP 解决实际问题,首先明确要分析决策的问题,并把它条理化、层次化,理出递 阶层次结构。
AHP 要求的递阶层次结构一般由以下三个层次组成::指问题的预定目标; :指影响目标实现的准则; :指促使目标实现的措施; 首先明确决策的目标,将该目标作为 这个目标要求是唯一的,即目标层只有一个元素。
然后找出影响目标实现的准则,作为目标层下的 准则层 因素,在复杂问题中,影响目标 实现的准则可能有很多,这时要详细分析各准则因素间的相互关系,即有些是主要的准则,有 些是隶属于主要准则的次准则,然后根据这些关系将准则元素分成不同的层次和组,不同层次 元素间一般存在隶属关系,即上一层元素由下一层元素构成并对下一层元素起支配作用,同一 层元素形成若干组,同组元素性质相近,一般隶属于同一个上一层元素(受上一层元素支配) 不同组元素性质不同,一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中,有时组的关系不明显,即上一层的若干元素同时对下一 层的若干元素起支配作用,形成相互交叉的层次关系,但无论怎样,上下层的隶属关系应该是 明显的。
最后分析为了解决决策问题(实现决策目标) 、在上述准则下,有哪些最终解决方案(措 施),并将它们作为 措施层 因素,放在递阶层次结构的最下面(最低层) 。
明确各个层次的因素及其位置,并将它们之间的关系用连线连接起来,就构成了递阶层次结构。
【案例分析】市政工程项目进行决策:建立递阶层次结构在市政工程项目决策问题中,市政管理人员希望通过选择不同的市政工程项目,使综合 效益最高,即决策目标是“合理建设市政工程,使综合效益最高” 。
层次分析法的实施——五步骤

准则层
C1 调动职工生产
积极性
C2 提高企业
技术水平
C3 改善职工物质
文化生活
方案层
P1 发奖金
P2 扩建福
利设施
P3 办学校
P4 建图书
馆或俱
乐部
P5 技术改造
. #;
A
C1
C2
…
Ck
(2)建立判断矩阵 C1
a12
a11
…
a1k
参见(P136)标度
C2
a21
a22
…
a2k
判断矩阵A-C:
Ck
ak1
对Wi进行归一化处理: Wi
Wi
n
Wj
j 1
(i, j 1,2, , n)
. #;
(4)层次总排序
所谓层次总排序就是针对最高层目标而言,本层次 各要素重要性的次序排序。
C层
P层 P1 P2 … Pn
因素及权重
C1
C2
1(1) 2(1) …
CK
k(1)
11(2) 12(2)
…
21(2) 22(2)
P5 0.046 0.263
0
0.172
方案 排序
4 3 1 5 2
P1
P2
发奖金 扩建福
利设施
P3
P4
P5
办学校 建图书 技术改造
馆或俱
乐部
. #;
3. 层次分析法
(1)分析复杂系统所包含的因素及其相互关系,形成多层次的分析 结构模型;
(2)将各要素及上层要素进行两两比较判断,得到其相对重要程度 的比较标度,建立判断矩阵;
方案层
方案1 方案2 方案3
层次分析法spss教程

层次分析法spss教程
层次分析法是一种用于多准则决策的方法,在SPSS软件中可以通过以下步骤进行:
1. 首先,导入数据。
数据应包括准则层和方案层的信息。
准则层是决策的准则,而方案层是待选择的各个方案。
2. 接下来,创建层次分析模型。
在SPSS软件中,可以使用层次分析法专用的插件进行创建。
选择“Analyze”->“Decision Trees”->“Analytic Hierarchy Process”。
3. 在创建模型时,需要确定决策的目标和准则。
设置准则的权重,权重表示每个准则对决策的重要程度。
在SPSS中,可以使用主观方法或客观方法来确定权重。
4. 设置方案的比较矩阵。
比较矩阵是用于比较各个方案在每个准则上的优劣程度。
在SPSS中,可以通过填写矩阵来完成方案的比较。
5. 进行一致性检验。
一致性检验用于检查比较矩阵的一致性,确保所选权重的合理性。
在SPSS中,可以通过CR值来判断一致性程度,CR值越接近0,表示一致性越好。
6. 根据准则权重和方案比较矩阵,计算各个方案的决策得分。
得分表示每个方案在总体考虑下的优劣情况。
在SPSS中,可以使用加权平均法来计算得分。
7. 最后,进行结果分析和决策选择。
根据各个方案的得分,可以进行排序和比较,选择最合适的方案。
需要注意的是,在使用层次分析法进行决策时,确保准则权重和比较矩阵的一致性是非常重要的。
此外,还需要进行灵敏度分析,检验准则权重的重要程度对最终决策结果的影响。
层次分析法及真题讲解

随机构造500个成对比较矩阵 A1,A2, ,A500
则可得一致性指标 C1,C I 2,I ,C5I00
R IC1 IC2 I C50 I 0 125 0 0 50 0 n
500
n 1
Saaty的结果如下
随机一致性指标 RI
n 1 2 3 4 5 6 7 8 9 10 11 RI 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51
定义一致性比率 : CR CI
RI
一般,当一致性比率 CR CI 0.1 时,认为 A
RI
的不一致程度在容许范围之内,有满意的一致性,通过 一致性检验。可用其归一化特征向量作为权向量,否则
要重新构造成对比较矩阵A,对 aij 加以调整。
“选择旅游地”中 准则层对目标的权 向量及一致性检验
最大特征根
j 1
层次总排序的一致性检验
设 B层 B1,B2, ,对Bn上层( 层)中因A素
Aj(j1,2, ,m )
的层次单排序一致性指标为 CI j ,随机一致性指为 ,
则层次RI 总j 排序的一致性比率为:
C R a a 1 1 C R1 1 IIa a2 2C R2 2 II a am m C Rm m II
0.3,0.24 ,06 .45 6可作为最后的决策依据。
即各方案的权重排序为 B3B1B2 又 B1,B2,B3 分别表示苏杭、北戴河、桂林,
故最后的决策应为去桂林。
2009 Problems High School Mathematical Contest in Modeling (HiMCM) Problem A: Water, Water Everywhere
层次分析法

这种方法既不单纯追求高深数学,又不片面地注重行为、逻辑、推理,而是把定性方法与定量方法有机地结 合起来,使复杂的系统分解,能将人们的思维过程数学化、系统化,便于人们接受,且能把多目标、多准则又难 以全部量化处理的决策问题化为多层次单目标问题,通过两两比较确定同一层次元素相对上一层次元素的数量关 系后,最后进行简单的数学运算。计算简便,并且所得结果简单明确,容易为决策者了解和掌握。
2.定量数据较少,定性成分多,不易令人信服
在如今对科学的方法的评价中,一般都认为一门科学需要比较严格的数学论证和完善的定量方法。但现实世 界的问题和人脑考虑问题的过程很多时候并不是能简单地用数字来说明一切的。层次分析法是一种带有模拟人脑 的决策方式的方法,因此必然带有较多的定性色彩。
3.指标过多时,数据统计量大,且权重难以确定
谢谢观看
计算步骤
ห้องสมุดไป่ตู้
计算步骤
1.建立层次结构模型
将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为最高层、中间层和最低层, 绘出层次结构图。最高层是指决策的目的、要解决的问题。最低层是指决策时的备选方案。中间层是指考虑的因 素、决策的准则。对于相邻的两层,称高层为目标层,低层为因素层。
2.构造判断(成对比较)矩阵
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Saaty等人提出 一致矩阵法,即不把所有因素放在一起比较,而是两两相互比较,对此时采用相对尺度,以尽可能减少性质不同 的诸因素相互比较的困难,以提高准确度。如对某一准则,对其下的各方案进行两两对比,并按其重要性程度评 定等级。为要素与要素重要性比较结果,表1列出Saaty给出的9个重要性等级及其赋值。按两两比较结果构成的 矩阵称作判断矩阵。判断矩阵具有如下性质:
层次分析法简介

在分配利润中,应拿出25.1%给 职工发奖金,21.8%用于扩建福 利设施,53.1%引进人才和设 备.
大学生毕业选择单位
1 1 1 1 2 1 1 1/ 2 1 1 / 4 1 / 4 1 / 5 1 1 1/ 3 2 2 2 4 4 5 1 3 3 1/ 2 1 1/ 2 3 1/ 2 1/ 3 1/ 3 1 1 1 1 1
层次分析法简介
层次分析法
在各领域以及日常生活中, 在各领域以及日常生活中,遇到一 些决策问题:选拔人才\评优\ 些决策问题:选拔人才\评优\工程 评标\选择旅游景点\购买衣服等. 评标\选择旅游景点\购买衣服等. 层次分析法--定性和量化相结 合的较科学的方法,由美国著名 的运筹学专家萨迪提出的.
所以单位C 所以单位C1,单位C2,单位C3的得 单位C 单位C 分分别是0 35 35, 40 40, 25 25, 分分别是0.35,0.40,0.25,故 该大学生应选择单位C 该大学生应选择单位C2.
层次分析法的基本步骤
1.建立层次结构 2.构造成比较矩阵 3.一致性检验
目标层---准则层; 准则层---方案层 目标层---准则层; 准则层---方案层
成对比矩阵是一致性矩阵,满足aij a jk = aik 如何检验一致性呢? 1)求A的最大特征值 λ . 2)若 λ = n ,则A是一致性矩阵.否则A 不是一致性矩阵,这时需检验可接受性. 如何检验呢?1)计算一致性指标 如何检验呢?1)计算一致性指标 CI = λ n n 1 2)查表确定 RI n 1 2 3 4 5 6 7 8 9 RI 0 0 0.580.90 1.12 1.24 1.32 1.41 1.45 3)计算一致性比例 CR = CI / RI 当 CR < 0.1 时,则A的不一致是可接受的, 否则需修改A
层次分析法

e1
1 4.511
0.778
0.172
,
3 0.665
0.4 6 7 e2 Ae1 0.565, e2 3.014,
1.9 9 1
01.55 0.471 e2 0.184, e3 0.559, e3 3.018,
0.661 1.988
0.156 0.473 e3 0.185, e4 0.561,
(4)定义未知参数 在这种问题中,运用层次分析法建立表达式 来表达未曾定义过的量。典型的例子是价值 工程,产品的价值V被定义为
VF C
其中F,C分别为产品的功能系数与成本系数, 它们可以用层次分析来定义。下面是一个 经济学例子。
例5 弹性系数的确定 经济学中有名的Cobb-Douglas生产函 数是
e (1,2,,n )T ,则权系数可取: wi i ,i 1,2,, n
在具体计算中,当
ek 与ek 1
接近到一定程度时,就取 e ek
例1 评价影视作品的水平, 用以下三个变量作评价指标 :
x1 教育性,x2 艺术性,x3 娱乐性
设有一名专家赋值:
x2 1, x3 5, x3 3
w1, w2 ,, wn
这 n 个常数便是权系数, 层次分析法给出了确定它们 的量化方法,其过程如下:
1.成对比较
从x1, x2,, xn中任取xi , xj ,比较它们
对y贡献的大小,给xi xj 赋值如下:
xi
xj
1,当认为“xi与x
贡献程度相同”时
j
xi
xj
3,当认为“xi比x
的贡献略大”时
x1
的概率估值为0.134+0.219+0.026=0.379,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
层次分析法的具体步骤
层次分析法是一种多因素决策方法,其具体步骤如下:
1. 确定决策目标:明确决策的目标,确定需要选择的方案或选项。
2. 列出准则:对于每个可选方案,列出与目标相关的准则或要素。
这些准则应该是可以量化的,例如成本、效益、质量等等。
3. 构建层次结构:将需要比较的准则按照层次结构排序。
通常情况下,决策目标位于最高层,准则位于下一级,再下一级是具体的备选方案。
这种结构可以用一个树状图表示。
4. 建立判断矩阵:对于每个准则与备选方案之间的重要程度或权重,依据专家意见和实际情况构建判断矩阵。
5. 计算权重向量:通过计算判断矩阵的特征向量,得到每个准则和备选方案的权重。
6. 一致性检验:对于每个准则和备选方案,验证其在判断矩阵中的数值是否一致。
若不一致,则需要对判断矩阵进行修正,重新计算权重向量,直至满足一致性要求为止。
7. 得出结论:根据各个备选方案的权重值,确定最优解或多个备选解,并进行评价和比较以做出最终决策。
总之,层次分析法可以帮助人们在复杂的多因素决策过程中,合理地评估各种因素的重要程度,提高决策的科学性和准确性。
