简单级数反应
简单级数反应的速率方程

简单级数反应的速率方程(1)一级反应动力学凡是反应速率与作用物浓度一次方成正比的反应为一级反应。
放射性元素的蜕变是典型的一级反应,如镭蜕变为氡和氦:Ra 22688→Rn 22286+He 42五氧化二氮的分解反应也是一级反应:N 2O 5→N 2O 4+21O 2 (1) 动力学方程 对于反应A → P ,速率方程为r = k [A] td d[A]-= k [A] 分离变量、积分,并利用初始条件:当t =0时,反应物A 的浓度为[A]0浓度与时间的关系为t k =[A][A]ln 0 )ex p([A]A][0t k -= 如果令[A]0= a ,至t 时刻反应物消耗的浓度为x ,那么转化率 y = x / a ,反应物剩余的浓度为a-x ,则上面的结果可以写成t k x a a =-ln 或 t k y =-11ln以上各式均为速率方程的积分式,都是一级反应的动力学方程。
对于气相一级反应,只要将浓度[A]用压力p A 替代,处理方法及动力学规律完全相同。
(2) 动力学特征① 线性关系 ln{[A]} 对t 作图应为一直线,其斜率等于 - k 。
这一特点在处理一级反应实验数据时尤其重要。
② 速率系数k 的量纲[时间]-1③ 半衰期 [A] = 2A][0或21==a x y (即反应物消耗了一半)所需的时间称为半衰期(half-life)21t一级反应的半衰期 kk t 693.02ln 21==可见,一级反应的半衰期与反应的速率系数k 成反比,而与反应物的起始浓度无关。
. 二级反应动力学(1) (单纯)二级反应动力学 对于反应2A → P ,速率方程为r = k 2 [A]2。
浓度对时间的微分方程: dt d[A]-= k [A]2(其中k=2k 2 ) 浓度与时间的关系为t k =-0A][1[A]1同样令[A]0= a ,至t 时刻反应物消耗的浓度为x (转化率 y = x / a ),反应物剩余的浓度为a -x ,则上面的结果可以写成 t k a x a =--11 或 t k y a y =-)1(对于气相反应,反应速率方程为 2A p k r p p '=,相应的微分方程为tp d d A -= k p 2A p (其中 k p =2p k ' ) 动力学方程为t k p p p =-0A,A 11 (单纯)二级反应动力学有如下两个特点:二级反应有如下一些特征:(1)二级反应速率与作用物浓度的二次方成正比,其速率常数单位为时间单位和浓度单位乘积的倒数;(2)二级反应的作用物浓度的倒数与时间成直线关系,直线的斜率为2k ;(3)二级反应的半衰期为速率常数和作用物初始浓度乘积的倒数。
华东理工大学《物理化学》课件7.1 简单级数反应

II. 动力学特性参数 7.9 动力学实验方法 7.10 动力学实验数据的处理 7.11 快速反应的实验方法* 7.12半经验方法*
III. 反应机理 7.13反应机理与速率方程 7.14 单分子反应* 7.15 微观可逆性和精细平衡原理*
化学动力学
研究各种因素对反应速率的影响规律的科学 。
✓反应物、产物、催化剂及其它物质的浓度; ✓系统的温度和压力; ✓光、电、磁等外场。
Ⅰ.化学动力学基本原理
7.2 化学反应的速率
0
B
B
B
d B1dnB
转化速率 反应速率
(V 恒定)
def d 1 dnB dt B dt
def 1 d 1 dnB V dt V BV dt
def 1 dcB cB dV B dt BV dt 1 dcB B dt
0
BHale Waihona Puke BBd B1dnB
消耗速率 生成速率
A
def
1 V
dnA dt
P
def
1 V
dnp dt
A
dcA dt
(V 恒定)
P
dcP dt
(V 恒定)
各种速率的特点和相互关系
、 ——与物质的选择无关 A , P ——与物质的选择有关
A P /V A P
0 N2 3H2 2NH 3
H HBr H2 Br
Br Br M Br2 M
复合反应 基元反应
H2 + I2 → 2HI
I2 M
2I M
H2 2I 2HI
化学动力学
宏观化学动力学——将基元反应和复合反应的 速率与浓度、温度、压力等联系起来,总结出 带有普遍意义的规律。 微观化学动力学——从微观的物质特性如分子 尺寸、几何构型,以及分子的平动、转动、振 动和电子的运动出发,研究态态反应,并运用 统计平均,得到基元反应的速率。
具有简单级数的反应[整理版]
![具有简单级数的反应[整理版]](https://img.taocdn.com/s3/m/d1dc7073ae1ffc4ffe4733687e21af45b307fead.png)
具有简单级数的反应化学反应中,表示反应速率与浓度之间的参数的关系,或表示浓度等参数与时间关系的方程称为化学反应的速率方程,也称为动力学方程。
在化学反应的速率方程中,各物浓度相的指数之代数和就称为该反应的级数。
在这些反应中存在具有简单级数的反应,以下就讨论这些具有简单级数的反应,介绍其速率方程式的微分式、积分式以及他们的速率常数k 的单位和半衰期等各自的特征。
一级反应:凡是反应速率只与物质浓度的一次方呈正比关系者称为一级反应。
设有以下一级反应 t=0 C A (0)=a C P (0)=0t=t C A =a-x C P =x 反应速率方程微分式有对其作不定积分得 ln(a-x)=-k 1t+C对其作定积分有 ln[a/(a-x)]= k 1tk 1=1/t ln[a/(a-x)]从反应物起始浓度a 和t 时刻的浓度a-x 即可算出速率常数k 1,一级反应的速率常数单位为1/(时间)。
取反应物消耗了一半所需时间作半衰期,则t 1/2=ln2/ k 1一级反应的特征有3点:1.速率常数的单位是时间的倒数;2.一级反应半衰期与反应物起始浓度无关;3.lnC A 与t 呈线性关系。
二级反应:反应速率和物质浓度的二次方成正比者称为二级反应。
通式为(1)A+B P+…… r= k 2[A][B](2)2A P+…… r= k 2[A] ²若A 和B 起始浓度相同,反应(1)的速率方程可写成dx/dt=k 2(a-x) ²移项作不定积分得: 1/(a-x)= k 2t+C作定积分得: 1/(a-x)-1/a= k 2tk 2=1/t*x/[a(a-x)]其半衰期为 t 1/2=1/k 2a二级反应的半衰期与一级反应不同,它与反应物的起始浓度成反比。
二级反应的特点:1.速率常数的单位是1/[(浓度)(时间)];2.半衰期与反应物的起始浓度成反比;3.1/(a-x)与t 呈线性关系。
若A 和B 起始浓度不相同则反应(1)的速率方程为dx/dt=k 2(a-x)(b-x)a 和b 分别为A 、B 起始浓度,x 为t 时刻已反应物质的量。
物理化学动力学测试卷

,
得此结论的理由是 基元反应的反应级数等于反应分子数
。
2.对峙反应 A
B,其正反应的速率可表示为: r 正=k1[A]
;逆
反应的速率为: r 逆=k-1[B] ,该对峙反应的净速率可表示为: r= r 正-r 逆
=k1[A]- k-1[B] ;当反应达到平衡时,正、逆反应速率常数之间的关系可表示为
k1[A]- k-1[B] 或 k1/ k-1 = [B]/ [A] =K
1
《动力学部分》题库及题解
一、填空题:
1.何为具有简单级数的反应:反应速率只与浓度有关,且组分级数和反应总级数
为零或正整数 ,某反应 A+B=P 为基元反应,则该反应的反应级数为: 二级 ,
该反应的反应速率与反应物浓度的关系可表示为 r=k[A][B]
,得此关系
的理由是 基元反应遵守质量作用定律 ,该反应的分子数为: 二
反应是……( D)
A.一级反应
B.二级反应
C.零级反应
D.3/2 级反应
∵3/2 级反应的 t = 2/k([A]01/2-[A]1/2/[A]01/2[A]1/2) t1/t 2=2.22≈2
10、若某反应进行完全所需的时间是有限的,且等于 c0/k,则此反应为……(C )
A.一级反应
B.二级反应
是:测 不同温度下的速率常数 k ,作 lnk~1/T 关系图,通过斜率求
得活化能。
4.某气体反应 A+B—→3C 的速率方程为 r ==kCαACβB,为确定α、β值在常温 下进行实验,当初始压力为 PA,0=102Pa,PB,0=105Pa 时,作反应的 lnPA~t(时间) 图为一直线,当初始压力为 PA,0= PB,0=5×102Pa 时,仍作反应的 lnPA~t 图仍为一 直线,则α= 1 ,β= 0 。(lnc~t 成直线关系的是一级反应)
简单级数反应的特点总结

简单级数反应的特点总结一、简单级数反应的动力学方程对于单向反应aA→P,若以[A]o,x,y分别表示反应物A的起始浓度,已反应的部分浓度及已反应的百分数,则其t 时刻的剩余浓度[A]应为:[A]=[A]o-ax=[A]o(1-y)而(一)一级反应反应速率与物种浓度成正比的反应为一级反应,其速率方程为:分离变量,积分,则得一级反应的动力学方程:或根据上述各式,可以看出一级反应具有下列特征:(1)若以ln{A] 对t作图,可得一斜率为(-ak),截距为ln[A]o的直线。
(2)若化学计量系数a=1,则可见,上式浓度项是以比值的形式出现的,因此任何与浓度成比例的物理量均可代替之而无须监测真实的浓度,且不影响k的值。
其量纲为(时间)-1,可用s-1,min-1或h-1等表示之。
(3)若y=1/2 ,即反应物浓度[A]降低到其初始值的一半所需时间称为"半衰期",以t1/2表示,则有表明半衰期与反应物的起始浓度无关。
(4)若定义反应物A的平均寿命为该反应物由开始反应到通过反应而消耗完全的平均经历时间,则其平均寿命为可见,若a=1,则一级反应的平均寿命的倒数即为其反应速率常数。
又由式容易看出,当=(ak)-1时,[A]=[A]o/e ,即反应物浓度下降到其起始值的1/e 。
这一关系提供了测量一级反应平均寿命的方法。
(二)二级反应二级反应有纯二级和混二级两种类型。
如果反应的计量方程为aA+bB+…→P+…则二种速率表示式分别为类型Ⅰ-d[A]/adt=k[A]2类型Ⅱ-d[A]/adt=k[A][B]先讨论类型Ⅰ。
对式移项,积分可得:由之可得纯二级反应具有如下特征:(1)若以1/[A] 对t 作图,可得一斜率为ak 的直线。
(2)若在不同的反应时间t1,t2,…t n测得反应物A的浓度是[A]1,[A]2,…[A]n,则([A]o-[A]1)/at1[A]o[A]1=([A]o-[A]2)/at2[A]o[A]2=…=([A]o-[A]n)/at n[A]o[A]n=k=常数(3)速率常数k的量纲为浓度-1·时间-1,常用单位为mol-1·dm3·s-1。
6-二级反应及其他简单级数反应

r=dx/dt=k(a-x)n
(3)半衰期的一般式:
t t1/ 2 , a x a,
1 2
1 1 1 kt n 1 n 1 1 n a (a x) 1 1 1 n 1 1 n 1 kt1/ 2 1 n a 1 2
x (y ) a
t1/2
1 k2 a
2006.1.1
二级反应的积分速率方程
1 a x 不定积分式: ln k2t 常数 a-b b x 1 b( a x ) 定积分式: ln k2t a - b a(b x)
C (3) 2A
(2)a b
定积分式:
x
0
x k2t a(a - 2 x)
t dx k2 dt 2 0 (a - 2 x)
2006.1.1
二级反应(a=b)的特点
1. 速率系数 k 的单位为[浓度] -1 [时间] -1 2. 半衰期与起始物浓度成反比 3.
t1/ 2
1 与 t 成线性关系。 ax
1 k2 a
引伸的特点: 对 a b 的二级反应, t1/ 2
三级反应(a=b=c)的特点
1.速率系数 k 的单位为[浓度]-2[时间]-1 2.半衰期 t1/ 2
3 2k 3 a 2
1 3. 2 与t 呈线性关系 (a x)
引伸的特点有:
t1/2:t3/4:t7/8=1:5:21
2006.1.1
零级反应
反应速率方程中,反应物浓度项不出现,
即反应速率与反应物浓度无关,这种反应称为
dx k0 dt
a t1 2k0 2
2006.1.1
零级反应的特点
简单级数反应

ln
dcA dt
ln
kA
ln
cA
ln
cD
ln
cE
需要解联立方程组, 才能求得各反应物的级数、、……和
反应速率kA。 实验中令某一反应物的浓度远小于其他各反应物的浓度,
此时可将其他各反应物浓度视为常数, 再用前述各种方法求得
这一反应物的级数。同理分别求得每一反应物的级数、、
一级反应特征:
①速率常数 k 的单位为:时间1(s1、min1、h1、d1等);
②lncA~ t 成线性关系,直线的斜率为kA, 截距为ln cA,0; ③经历相同的时间间隔后, 反应物浓度变化的分数相同;
④通常将反应物消耗一半所需的时间称为半衰期(half life),
记作t1/2。一级反应的半衰期为:
……及总反应级数n。
用微分法确定反应级数, 不仅适用于整数级数的反应, 也适
用于分数级数的反应。
三. 零级反应
反应速率与反应物浓度无关的反应是零级反应(zero order reaction)。零级反应的微分速率方程为:
r dcA k adt
或
rA
dcA dt
kA
将上式整理后作定积分:
cA cA,0
dcA
t
0 kAdt
积分后得:
cA,0cA=kAt
三. 零级反应
由ln t1/2~ln cA,0图中直线的斜率可求得反应级数n。
此法不限于用t1/2, 也可用反应进行到其他任意分数的时间。
二. 微分法
若反应微分速率方程具有如下的简单形式:
rA
dcA dt
物理化学答案——第九章-化学动力学基础
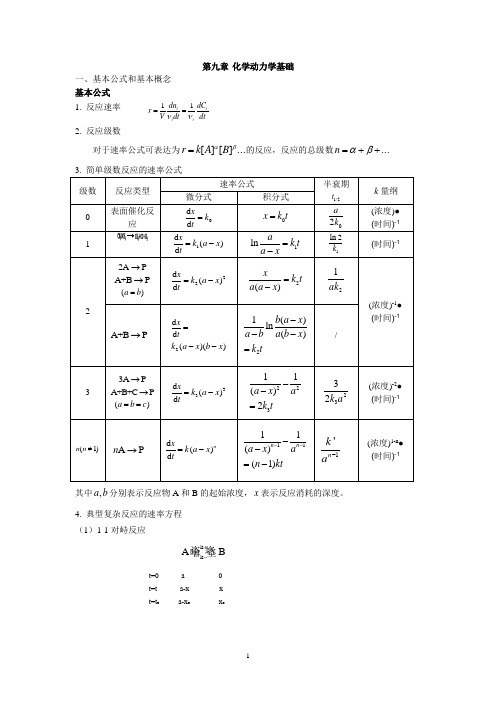
第九章 化学动力学基础一、基本公式和基本概念 基本公式 1. 反应速率 11i ii i dn dC r V dtdtνν==2. 反应级数对于速率公式可表达为...][][βαB A k r =的反应,反应的总级数...++=βαn 3. 简单级数反应的速率公式 级数 反应类型 速率公式半衰期 1/2tk 量纲微分式积分式0 表面催化反应0d d x k t =0x k t = 02a k (浓度)● (时间)-1 11d ()d x k a x t=-1lna k t a x=-1ln 2k(时间)-122A P→A +B P →()a b =22d ()d x k a x t=-2()x k t a a x =-21ak(浓度)-1●(时间)-1A +B P →2d d ()()xtk a x b x =--21()ln()b a x a b a b x k t---=/33A P→A +B +C P→()a b c ==33d ()d x k a x t=-22311()2a x a k t --=2332k a(浓度)-2● (时间)-1(1)n n ≠A P n →d ()d nx k a x t=-1111()(1)n n a x an kt----=-1'n k a-(浓度)1-n ● (时间)-1其中,a b 分别表示反应物A 和B 的起始浓度,x 表示反应消耗的深度。
4. 典型复杂反应的速率方程 (1)1-1对峙反应k k A B +-t=0 a 0 t=t a-x x t=t e a-x e x e速率方程: ()kk te e x x x e +--+-=(2)平行反应最简单的平行反应是由两个一级基元反应组成的平行反应:x=x 1+x 2速率方程:tk k aex a )(21+-=-产物B 和C 的浓度比由竞争反应的速率决定:2121k k x x = (3)连续反应最简单的连续反应是两个单向连续的一级反应:C B A kk −→−−→−21t=0 a 0 0 t=t x y z 速率方程:1k tx ae-=)(21121tk tk eek k a k y ----=]1[21121122tk tk ek k k ek k k a z ---+--=中间产物B 的浓度在反应过程中出现极大值:122)(21k k k m k k a y -=,出现极大值的时间为:2121)ln(k k k k tm-=5. 温度对反应速率的影响 (1)阿累尼乌斯经验公式2ln RTE dTk d a =阿累尼乌斯公式的指数函数式: RTE a Aek -=k 1k 2A a-xCx 2 B x 1(2)阿累尼乌斯活化能基元反应的活化能是活化分子的平均能量与所有分子平均能量之差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dc A = k A cA cD 其微分速率方程为: 其微分速率方程为: rA = dt
二. 二级反应
(1) 若反应物初浓度相等cA,0=cD,0, 则反应进行到任意时刻都有: 若反应物初浓度相等 则反应进行到任意时刻都有
c A = cD
其速率方程可简化为: 其速率方程可简化为 整理后作定积分: 整理后作定积分
二. 二级反应
二级反应特征: 二级反应特征 ①速率常数 k 的单位为:浓度1时间1 (mol1m3s1或 的单位为: mol1Ls1等); ②当cA,0=cD,0时, 1/cA~ t 成线性关系, 直线的斜率为kA, 截 成线性关系 直线的斜率为 距为1/cA,0; 距为 cD ,0 c A ~t 成线性关系 直线的斜率为 成线性关系, 当cA,0≠cD,0时, ln c A ,0 cD (cA,0cD,0)kA; 二级反应的半衰期: ③当cA,0=cD,0时, 二级反应的半衰期
t1/ 2
cA,0 = 2kA
四. 简单级数反应的速率方程小结
一些典型的简单级数反应的微分及积分速率方程及其特征见下表。 一些典型的简单级数反应的微分及积分速率方程及其特征见下表。表 级反应只列出了其微分速率方程为 的一种简单形式。 中n级反应只列出了其微分速率方程为dcA/dt=kAcAn的一种简单形式。 级反应只列出了其微分速率方程为 简单级数反应的速率方程小结
将上式整理后作定积分: 将上式整理后作定积分
或
cA
A,0
dc A rA = = kA dt
∫c
dc A =
∫0 k Adt
t
积分后得: 积分后得
cA,0cA=kAt
三. 零级反应
零级反应特征: 零级反应特征 的单位: ①速率常数 k的单位 浓度时间1 (molm3s1或molL1s1 的单位 浓度 等); 成线性关系, 直线的斜率为 截距为c ② cA~t 成线性关系 直线的斜率为kA, 截距为 A,0; ③零级反应的半衰期: 零级反应的半衰期
lnc -11.0 -11.5 -12.0 -12.5 -13.0 0 5 10 t /h 15 20
1 c0 t = ln = 6.7 h k c
图6-2
一. 一级反应
偶氮甲烷的气相分解反应CH3NNCH3(g)→ C2H6(g)+N2(g) 例2 偶氮甲烷的气相分解反应 为一级反应。在一温度为560 K的密闭容器中 CH3NNCH3的 的密闭容器中, 为一级反应。在一温度为 的密闭容器中 初压力为21.3 kPa, 1000秒钟后容器中的总压力为 秒钟后容器中的总压力为22.7 kPa, 求 初压力为 秒钟后容器中的总压力为 k及t1/2。 及 将气体视为理想气体, 在密闭容器中, 解: 将气体视为理想气体 在密闭容器中 反应物的初浓度 正比于它的初压力。 正比于它的初压力。
二. 二级反应
解: 先由上列数据计算出 ln 以 ln
c D ,0 c A c A ,0 c D
,
1.5
c D ,0 c A c A ,0 c D
作直线,见图。 对 t 作直线,见图。
ln [cB,0cA/(cA,0cB)]
1.0
直线的斜率为5.213×104 s1,则 × 直线的斜率为
0.5
1 1 = kt c A c A,0
整理后得: 整理后得
L0 Lt Lt = + L∞ c A,0kt
Lt与(L0Lt)/t为线性关系 直线的斜率为 为线性关系, 截距为L 为线性关系 直线的斜率为1/(cA,0k), 截距为 ∞。
二. 二级反应
由以上数据计算(L 如下: 由以上数据计算 0Lt)/t如下 如下 t/min 103L/S
3
40
6
50
60
70
80
[10 (L0-Lt)/t]/(S/min)
图6-4
三. 零级反应
反应速率与反应物浓度无关的反应是零级反应 反应速率与反应物浓度无关的反应是零级反应(zero order 零级反应 reaction)。零级反应的微分速率方程为 。零级反应的微分速率方程为:
dc A r= =k ad t
k = 斜率 A,0cD,0) =0.106 mol1Ls1。 斜率/(c
0.0
0
500 1000 1500 2000 2500 t (s)
图6-3Βιβλιοθήκη 二. 二级反应上例中的乙酸乙酯皂化反应, 例4 上例中的乙酸乙酯皂化反应 也可用电导法测定其速率常 数, 25℃时浓度都为 ℃时浓度都为0.0200 mol/L的CH3COOC2H5和NaOH溶液 的 溶液 以等体积混合, 在不同时刻测得混合后溶液的电导值L如下 如下,求反 以等体积混合 在不同时刻测得混合后溶液的电导值 如下 求反 应速率常数k。 应速率常数 。 t/min 103L/S 0 2.400 5 2.024 9 1.836 15 1.637 20 1.530 25 1.454
第四节 简单级数反应的速率方程
一. 一级反应
反应速率只与物质浓度的一次方成正比的反应称为一级反 反应速率只与物质浓度的一次方成正比的反应称为一级反 应(first order reaction) 。对一级反应 A t = 0 cA,0 t = t cA=cA,0-x 微分速率方程为: 微分速率方程为 将上式移项并积分: 将上式移项并积分 积分后得: 积分后得 G 0 cG
t1 / 2
1 = k A c A,0
二. 二级反应
乙酸乙酯皂化为二级反应: 例3 乙酸乙酯皂化为二级反应 CH2COOC2H5+NaOH → →CH3COONa+C2H5OH NaOH的初浓度为 A,0=0.00980 mol/L, CH3COOC2H5的初浓 的初浓度为c 的初浓度为 度为c 度为 D,0=0.00486 mol/L。25℃时用酸碱滴定法测得如下数据 。 ℃时用酸碱滴定法测得如下数据, 求速率常数k。 求速率常数 。 t/s 103cA/(mol/ L) 103cD/(mol/ L) 0 9.80 4.86 178 8.92 3.98 273 8.64 3.70 531 7.92 2.97 866 7.24 2.30 1510 1918 2401 6.45 1.51 6.03 1.09 5.74 0.80
[106(L0Lt)/t] (S/min)
0 2.400
5 2.024 75.20
9 1.836 62.67
15 1.637 50.87
2.2 2.0 10 Lt/S 1.8 1.6 1.4 30
20 1.530 43.50
25 1.454 37.84
作直线, 以Lt对(L0Lt)/t作直线 见图 , 作直线 直线的斜率为15.42 min。 直线的斜率为 。 1 1 k= = c A ,0 × 斜率 0.01 × 15.42 =6.486 mol-1Lmin-1 =0.1081 mol-1Ls-1 值一致。 与上例中所求得的 k 值一致。
图6-2
作直线回归见图, 解: (1)以ln c对t作直线回归见图 以 对 作直线回归见图 图中直线的斜率为 图中直线的斜率为0.0936 k=0.0936 h1, (2)由直线的截距得初浓度 由直线的截距得初浓度 c0=0.69 mg/100 ml 血液中四环素浓度降为0.37 mg/100 ml 血液中四环素浓度降为 所需的时间为: 所需的时间为 h1, 则:
二. 二级反应
cA,0cA=k′(L0Lt) ′ cA,0=k′(L0L∞) ′ k′=cA,0/(L0L∞) ′ 式中L 时的电导值, 时刻的电导值, 式中 0为 t =0时的电导值 Lt为 t 时刻的电导值 L∞为 t=∞ 即反 时的电导值 ∞ 应进行完毕时的电导值。将其代入该反应的积分速率方程式: 应进行完毕时的电导值。将其代入该反应的积分速率方程式
随着反应的进行, 溶液中电导率较大的OH离子逐渐 解: 随着反应的进行 溶液中电导率较大的 被电导率较小的CH3COO离子取代 溶液的电导值逐渐减小。 离子取代, 溶液的电导值逐渐减小。 被电导率较小的 在稀溶液中, 反应物浓度的减小与电导值的减小成正比: 在稀溶液中 反应物浓度的减小与电导值的减小成正比 cA,0cA=k′(L0Lt) ′ cA,0=k′(L0L∞) ′ k′=cA,0/(L0L∞) ′
c0 c0 p0 ln = ln = ln = kt c c0 x p0 ( p p0 ) 1 p0 k = ln = 6 .80 × 10 5 s 1 t 2 p0 p ln 2 4 t1/ 2 = = 1.02 × 10 s k
二. 二级反应
反应速率与一种反应物浓度的平方成正比, 或与两种反应 反应速率与一种反应物浓度的平方成正比 物浓度的乘积成正比的反应都是二级反应 物浓度的乘积成正比的反应都是二级反应(second order 二级反应 reaction)。 。 二级反应是一类常见的反应, 二级反应是一类常见的反应 溶液中的许多有机反应都符 合二级反应规律, 例如加成、取代和消除反应等。 合二级反应规律 例如加成、取代和消除反应等。 对二级反应: 对二级反应 A+D → →G
cA,0 ln = kAt cA,0 x
一. 一级反应
一级反应特征: 一级反应特征 的单位为: ①速率常数 k 的单位为:时间1(s1、min1、h1、d1等); 成线性关系,直线的斜率为 截距为ln ②lncA~ t 成线性关系,直线的斜率为kA, 截距为 cA,0; ③经历相同的时间间隔后, 反应物浓度变化的分数相同 经历相同的时间间隔后 反应物浓度变化的分数相同; 通常将反应物消耗一半所需的时间称为半衰期 半衰期(half life), ④ 通常将反应物消耗一半所需的时间称为 半衰期 记作t 一级反应的半衰期为: 记作 1/2。一级反应的半衰期为
dc A 2 rA = = kA cA dt
