(完整版)北师大版八年级三角形证明课后题汇总
北师大版八年级数学(下) 第一章 三角形的证明 第2节 等边三角形的性质
北师大版八年级数学（下）第一章三角形的证明第2课时等边三角形的性质例1：如图，△ABC是等边三角形，点D在AC边上，∠DBC＝35°，则∠ADB的度数为（）A．25°B．60°C．85°D．95°解：∠ADB＝∠DBC+∠C＝35°+60°＝95°．故选：D．练习：等边三角形的两个内角平分线所成的锐角是（）A．30°B．50°C．60°D．90°解：如图：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵BO、CO是两个内角的平分线，∴∠OBC＝∠OCB＝30°，在△OBC中，∠DOC＝∠OBC+∠OCB＝30°+30°＝60°．故选：C．作业：1．如图，在等边三角形ABC中，D是AC边上的点，延长BC到点E，使CE＝CD，则∠E的度数为（）A．15°B．20°C．30°D．40°解：∵△ABC是等边三角形，∴∠ACB＝60°，∵CD＝CE，∴∠E＝∠CDE，∵∠ACB＝∠E+∠CDE＝2∠E＝60°，∴∠E＝30°，故选：C．例2：如图，AD是等边三角形ABC的中线，AE＝AD，则∠EDC＝．解：∵AD是等边△ABC的中线，∴AD⊥BC，∠BAD＝∠CAD＝∠BAC＝×60°＝30°，∴∠ADC＝90°，∵AD＝AE，∴∠ADE＝∠AED＝＝75°，∴∠EDC＝∠ADC﹣∠ADE＝90°﹣75°＝15°．故答案为：15°．练习：如图，BD为等边△ABC的边AC上的中线，E为BC延长线上一点，且DB＝DE，若AB＝6cm，则CE＝cm．解：∵BD为等边△ABC的边AC上的中线，∴BD⊥AC，∵DB＝DE，∴∠DBC＝∠E＝30°∵∠ACB＝∠E+∠CDE＝60°∴∠CDE＝30°∴∠CDE＝∠E，即CE＝CD＝AC＝3cm．故填3．作业：2. 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝度．解：∵△ABC是等边三角形，∴∠C＝∠A＝60°，∵CG＝CD，∴∠GDC＝30°，∵DF＝DE，∴∠E＝15°．故答案为：15．例3：三个等边三角形的摆放位置如图所示，若∠1+∠2＝120°，则∠3的度数为（）A．90°B．60°C．45°D．30°解：如图，∵∠3+∠6+60°＝180°，∠2+∠4+60°＝180°，∠1+∠5+60°＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝540°﹣180°，∴∠3＝180°﹣（∠1+∠2）＝60°，故选：B．练习：如图，△ABC是等边三角形，BC＝BD，∠BAD＝20°，则∠BCD的度数为（）A．50°B．55°C．60°D．65°解：∵△ABC是等边三角形，∴AB＝BC，∠ABC＝60°，∵BC＝BD，∴AB＝BD，∠BAD＝∠ADB＝20°，∴∠ABD＝140°，∴∠CBD＝80°，又∵BC＝BD，∴∠BCD＝50°＝∠BDC，故选：A．作业：3. 如图，△ABC是等边三角形，BC⊥CD，且AC＝CD，则∠BAD的度数为（）A．50°B．45°C．40°D．35°解：∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∵BC⊥CD，∴∠BCD＝90°，∴∠ACD＝60°+90°＝150°，∵AC＝CD，∴∠DAC＝＝15°，∴∠BAD＝60°﹣15°＝45°．故选：B．例4：如图，在等边△ABC中，DA＝DC，DM⊥BC，垂足为M，E是BC延长线上的一点，CE＝CD．求证：MB＝ME．证明：连接BD．∵△ABC是等边三角形，且D是AC的中点，∴∠DBC＝∠ABC＝×60°＝30°，∠ACB＝60°，∵CE＝CD，∴∠CDE＝∠E，∵∠ACB＝∠CDE+∠E，∴∠E＝30°，∴∠DBC＝∠E＝30°，∴BD＝ED，△BDE为等腰三角形，又∵DM⊥BC，∴MB＝ME．练习：如图，△ABC是等边三角形，△ACE是等腰三角形，∠AEC＝120°，AE＝CE，F 为BC中点，连接AF．（1）直接写出∠BAE的度数为；（2）判断AF与CE的位置关系，并说明理由．解：（1）∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∵EA＝EC，∠AEC＝120°，∴∠EAC＝∠ECA＝30°，∴∠BAE＝∠BAC+∠CAE＝90°．故答案为90°．（2）结论：AF∥EC．理由：∵AB＝AC，BF＝CF，∴AF⊥BC，∵∠ACB＝60°，∠ACE＝30°，∴∠BCE＝90°，∴EC⊥BC，∴AF∥EC．作业：4．已知，如图，等边△ABC中，点D为BC延长线上一点，点E为CA延长线上一点，且AE＝DC，求证：AD＝BE．证明：在等边△ABC中，AB＝CA，∠BAC＝∠ACB＝60°，∴∠EAB＝∠DCA＝120°．在△EAB和△DCA中，，∴△EAB≌△DCA（SAS），∴AD＝BE．例5：已知：如图，等边三角形ABC中，D、E分别是BC、AC上的点，且AE＝CD．（1）求证：AD＝BE；（2）求：∠BFD的度数．解：（1）证明：∵△ABC是等边三角形，∴∠BAC＝∠C＝60°，AB＝CA，在△ABE和△CAD中，∴△ABE≌△CAD（SAS），∴AD＝BE（全等三角形对应边相等）；（2）解：∵△ABE≌△CAD（已证），∴∠ABE＝∠CAD（全等三角形对应角相等），又∵∠BFD＝∠BAD+∠ABE，∴∠BFD＝∠BAD+∠CAD＝∠BAC，又∠BAC＝60°，∴∠BFD＝60°．练习：已知，△ABC是等边三角形，D、E、F分别是AB、BC、AC上一点，且∠DEF＝60°．（1）如图1，若∠1＝50°，求∠2；（2）如图2，连接DF，若∠1＝∠3，求证：DF∥BC．解：（1）∵△ABC是等边三角形，∴∠B＝∠A＝∠C＝60°，∵∠B+∠1+∠DEB＝180°，∠DEB+∠DEF+∠2＝180°，∵∠DEF＝60°，∴∠1+∠DEB＝∠2+∠DEB，∴∠2＝∠1＝50°；（2）∵∠B+∠1+∠DEB＝180°，∠FDE+∠3+∠DEF＝180°，又∵∠B＝60°，∠DEF ＝60°，∠1＝∠3，∴∠FDE＝∠DEB，∴DF∥BC．作业：5．已知△ABC为等腰三角形，AC＝BC，△ACE为等边三角形．（1）如图①，若∠ABC＝70°，则∠CAB的大小＝（度），∠EAB的大小＝（度）；（2）如图②，△BDC为等边三角形，AE与BD相交于点F，求证：FA＝FB．解：（1）∵AC＝CB，∴∠ABC＝∠CAB＝70°，∵△ACE为等边三角形，∴∠CAE＝60°，∴∠EAB＝∠CAB﹣∠CAE＝70°﹣60°＝10°；故答案为：70，10．（2）证明：∵AC＝BC，∴∠CAB＝∠CBA，∵△ACE，△BDC都为等边三角形，∴∠CAE＝∠CBD＝60°，∴∠CAB﹣∠CAE＝∠CBA﹣∠CBD，即∠FAB＝∠FBA，∴FA＝FB．备用：在同一平面内，将两块正三角形的纸板的两个顶点重合在一起．（1）如图1重叠部分∠AOD＝30°，求∠COB的大小；（2）如图2重叠部分∠AOD＝15°，求∠COB的大小；（3）如图3，若两图形除O外没有重叠，∠AOD＝10°，求∠COB的大小；（4）求∠AOD和∠COB的数量关系．解：（1）∵△COD和△AOB为正三角形，∠AOD＝30°，∴∠COB＝∠COD+∠AOB﹣∠AOD＝60°+60°﹣30°＝90°；（2）∵△COD和△AOB为正三角形，∠AOD＝15°，∴∠COB＝∠COD+∠AOB﹣∠AOD ＝60°+60°﹣15°＝105°；（3）∵△COD和△AOB为正三角形，∠AOD＝10°，∴∠COB＝∠COD+∠AOB+∠AOD＝60°+60°+10°＝130°；（4）当∠AOD是两个角的重叠的角，则∠COB＝120°﹣∠AOD；当∠AOD是两个角的相离时的角，且∠AOD≤60°，则∠COB＝120°+∠AOD；当∠AOD是两个角的相离时的角，且∠AOD＞60°，则∠COB＝360°﹣（120°+∠AOD）＝240°﹣∠AOD．。
北师大版八年级数学(下) 第一章 三角形的证明 第5节 直角三角形的性质与判定
北师大版八年级数学（下）第一章三角形的证明第5节直角三角形的性质与判定例1：在△ABC中，∠A＝90°，∠B＝2∠C，则∠C的度数为（）A．30°B．45°C．60°D．30°或60°解：∵在△ABC中，∠A＝90°，∠B＝2∠C，∴2∠C+∠C＝90°，∴∠C＝30°，故选：A．练习：在Rt△ABC中，∠C＝90°，∠A﹣∠B＝50°，则∠A的度数为（）A．80°B．70°C．60°D．50°解：∵∠C＝90°，∴∠A+∠B＝90°，∵∠A﹣∠B＝50°，∴2∠A＝140°，∴∠A＝70°，故选：B．作业：1．直角三角形的一个锐角∠A是另一个锐角∠B的3倍，那么∠B的度数是（）A．22.5°B．45°C．67.5°D．135°解：设∠B＝x°，则∠A＝3x°，由直角三角形的性质可得∠A+∠B＝90°，∴x+3x＝90，解得x＝22.5，∴∠B＝22.5°，故选：A．例2：在下列条件中：①∠A+∠B＝∠C，②∠A：∠B：∠C＝1：2：3，③∠A＝90°﹣∠B，④∠A＝∠B＝∠C，⑤∠A＝2∠B＝3∠C中，能确定△ABC是直角三角形的条件有（）A．2个B．3个C．4个D．5个解：①因为∠A+∠B＝∠C，则2∠C＝180°，∠C＝90°，所以△ABC是直角三角形；②因为∠A：∠B：∠C＝1：2：3，设∠A＝x，则x+2x+3x＝180，x＝30°，∠C＝30°×3＝90°，所以△ABC是直角三角形；③因为∠A＝90°﹣∠B，所以∠A+∠B＝90°，则∠C＝180°﹣90°＝90°，所以△ABC 是直角三角形；④因为∠A＝∠B＝∠C，所以∠A+∠B+∠C＝∠C+∠C+∠C＝180°，则∠C＝90°，所以△ABC是直角三角形；⑤因为3∠C＝2∠B＝∠A，∠A+∠B+∠C＝∠A+∠A+∠A＝180°，∠A＝，所以△ABC为钝角三角形．所以能确定△ABC是直角三角形的有①②③④共4个，故选：C．练习：在下列条件中：①∠A＝∠B﹣∠C，②∠A﹣∠B＝90°，③∠A＝∠B＝2∠C，④∠A＝∠B＝∠C中，能确定△ABC是直角三角形的条件有（）A．1个B．2个C．3个D．4个解：①由∠A+∠B+∠C＝180°，∠A＝∠B﹣∠C得到：2∠B＝180°，则∠B＝90°，则△ABC是直角三角形，故符合题意；②∠A﹣∠B＝90°得到：∠A＞90°，则△ABC不是直角三角形，故不符合题意；③由∠A+∠B+∠C＝180°，∠A＝∠B＝2∠C得到：5∠C＝180°，则∠C＝36°，则∠A ＝∠B＝72°＜90°，则△ABC不是直角三角形，故不符合题意；④由∠A+∠B+∠C＝180°，∠A＝∠B＝∠C得到：∠C＝90°，则△ABC是直角三角形，故符合题意；综上所述，是直角三角形的是①④，共2个．故选：B．作业：2. 在下列条件中：①∠A+∠B＝∠C；②∠A：∠B：∠C＝1：2：3；③∠A＝2∠B＝3∠C；④∠A＝∠B＝∠C中，能确定△ABC是直角三角形的条件有（）A．1个B．2个C．3个D．4个解：①∠A+∠B＝∠C，是直角三角形；②∠A：∠B：∠C＝1：2：3，是直角三角形；③∠A＝2∠B＝3∠C，则设∠A＝x，∠B＝，∠C＝，则x++＝180°，解得x＝，∴∠A＝，，，∴△ABC不是直角三角形；④∠A＝∠B＝∠C，不是直角三角形，是等边三角形，能确定△ABC是直角三角形的条件有2个，故选：B．例3：在Rt△ABC中，斜边AB＝3，则AB2+BC2+CA2＝．解：∵△ABC为直角三角形，AB为斜边，∴AC2+BC2＝AB2，又AB＝3，∴AC2+BC2＝AB2＝9，则AB2+BC2+CA2＝AB2+（BC2+CA2）＝9+9＝18．故答案为：18练习：如图所示，在△ABC中，∠ABC＝90°，分别以AB、BC、AC为边向外作正方形，面积分别为225、400、S，则S为（）A．175B．600C．25D．625解：由勾股定理得，AB2+BC2＝AC2，则S＝25+400＝625，故选：D．作业：3. 已知△ABC中∠C＝90°，c为斜边，a、b为直角边，若a+b＝17cm，c＝13cm，则△ABC的面积为（）A．15cm2B．30cm2C．45cm2D．60cm2解：∵a+b＝17，∴（a+b）2＝289，∴2ab＝289﹣（a2+b2）＝289﹣c2＝289﹣169＝120∴ab＝30，故选：B．例4：如图，一块铁皮（图中阴影部分），测得AB＝3，BC＝4，CD＝12，AD＝13，∠B＝90°．求阴影部分的面积．解：如图，连接AC．∵△ABC中，∠B＝90°，AB＝3，BC＝4，∴AC＝＝5．∵CD＝12，AD＝13，AC＝5，∴AC2+CD2＝AD2，∴△ACD是直角三角形，∴S阴影＝S△ACD﹣S△ABC＝×5×12﹣×3×4＝30﹣6＝24．练习：如图，在Rt△ABD中，∠ABD＝90°，AD＝10，AB＝8．在其右侧的同一个平面内作△BCD，使BC＝8，CD＝2．求证：AB∥DC．证明：∵在Rt△ABD中，∠ABD＝90°，AD＝10，AB＝8，∴BD＝＝＝6，∵BC＝8，CD＝2，∴62+（2）2＝82，∴△BDC是直角三角形，∴∠BDC＝90°，∴∠ABD＝∠BDC，∴AB∥DC．作业：4. 如图所示，在四边形ABDC中，∠A＝90°，AB＝9，AC＝12，BD＝8，CD＝17．（1）连接BC，求BC的长；（2）判断△BCD的形状，并说明理由．解：（1）∵∠A＝90°，∴BC＝＝＝15；（2）△BCD是直角三角形，理由：∵BC2＝152＝225，BD2＝82＝64，CD2＝172＝289，∴BC2+BD2＝CD2＝289，∴△BCD是直角三角形．例5：如图，在正方形网格中，小正方形的边长为1，点A，B，C为网格的交点．（1）判断△ABC的形状，并说明理由；（2）求AB边上的高．解：（1）△ABC为直角三角形，理由：由图可知，，BC＝，AB＝＝5，∴AC2+BC2＝AB2，∴△ABC是直角三角形；（2）设AB边上的高为h，由（1）知，，BC＝，AB＝5，△ABC是直角三角形，∴＝，即＝h，解得，h＝2，即AB边上的高为2．练习：如图，在四边形ABCD中，AB＝3，BC＝4，CD＝12，AD＝13，∠B＝90°．（1）连接AC，求证：△ACD是直角三角形；（2）求△ACD中AD边上的高．解：（1）证明：连接AC，在Rt△ABC中，AC2＝AB2+BC2＝32+42＝25，∴AC＝5，∵CD＝12，AD＝13，∴AC2+CD2＝AD2，∴∠ACD＝90°，∴△ACD是直角三角形；（2）解：过点C作CH⊥AD于点H，则S△ACD＝AD×CH＝AC×CD，∴×13×CH＝×5×12，∴CH＝．作业：5.如图，在正方形网格中，小正方形的边长为1，A，B，C为格点（1）判断△ABC的形状，并说明理由．（2）求BC边上的高．解：（1）结论：△ABC是直角三角形．理由：∵BC2＝12+82＝65，AC2＝22+32＝13，AB2＝62+42＝52，∴AC2+AB2＝BC2，∴△ABC是直角三角形．（2）设BC边上的高为h．则有•AC•AB＝•BC•h，∵AC＝，AB＝2，BC＝，∴h＝．例6：写出命题“如果两个三角形全等，那么这两个三角形的周长相等”的逆命题．该逆命题是命题（填“真”或“假”）．解：“如果两个三角形全等，那么这两个三角形的周长相等．”写成它的逆命题：如果两个三角形的周长相等，那么这两个三角形全等，该逆命题是假命题，故答案为：如果两个三角形的周长相等，那么这两个三角形全等；假练习：“两直线平行内错角相等”的逆命题是命题．（填“真”或“假”）解：∵原命题的条件为：两直线平行，结论为：内错角相等，∴其逆命题为：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行，是真命题；故答案为：真．作业：6．已知命题“等腰三角形两腰上的高线相等”，它的逆命题是，该逆命题是命题．（“真”、“假”）．解：命题“等腰三角形两腰上的高线相等”的逆命题是“如果一个三角形两条边上的高线相等，那么这个三角形是等腰三角形”，是真命题，故答案为：如果一个三角形两条边上的高线相等，那么这个三角形是等腰三角形；真．。
1.2直角三角形——直角三角形的边角性质+练习课件+2023-—2024学年北师大版数学八年级下册
【点拨】
∵1 宣＝12矩，1 欘＝112宣，1 矩＝90°，∠A＝1 矩，
∠B＝1
欘
，
∴∠A
＝ 90°，
∠
B
＝
1
1 2
1 ×2
×90°＝
67.5°，
∴∠C＝90°－∠B＝90°－67.5＝22.5°.
3 (母题：教材P34复习题T5)若三角形三个内角的比为 1 ∶2 ∶3，则这个三角形是__直__角____三角形．
(2)若AE是△ABC的角平分线，AE，CD相交于点F，求证： ∠CFE＝∠CEF. 【证明】∵AE是△ABC的角平分线，∴∠DAF＝∠CAE. ∵∠FDA＝90°，∠ACE＝90°， ∴∠DAF＋∠AFD＝90°，∠CAE＋∠CEA＝90°. ∴∠AFD＝∠CEA. ∵∠AFD＝∠CFE， ∴∠CFE＝∠CEA，即∠CFE＝∠CEF.
解：如图②，延长 MN 至点 C′，使 NC′＝NC，连接 AC′， 则 AC′的长即为蚂蚁爬行的最短路程． 在 Rt△AMC′中，AM＝3×2＝6(cm)， MC′＝20＋2＝22(cm)． 由勾股定理，得 AC′2＝AM2＋MC′2＝62＋222＝520， 则 AC′＝2 130 cm. 答：蚂蚁需要爬行的最短路程是 2 130 cm.
∵∠C＝90°，∴∠4＋∠5＝90°. ∴∠3＋∠5＝90°，即∠FBG＝90°. 又∵DF⊥EG，DE＝DG，∴FG＝EF. 在Rt△FBG中，BG2＋BF2＝FG2，∴AE2＋BF2＝EF2.
【点方法】
欲证AE2＋BF2＝EF2，应联想到勾股定理，把AE， BF和EF转. 化. 为同一个直角三角形的三边．
【点拨】
∵直角三角形的三边a，b，c满足c>a>b，∴该直角三 角形的斜边为c，∴c2＝a2＋b2，∴c2－a2－b2＝0，∴S1＝ c2－a2－b2＋b(a＋b－c)＝ab＋b2－bc. ∵S2＝b(a＋b－c)＝ ab＋b2－bc，∴S1＝S2，故选C.
北师大版八年级下册三角形证明复习含答案
北师大版八年级下册三角形证明复习含答案三角形证明专题复习一．选择题（共15小题）1．如图，AB＝AC，AE＝EC＝CD，∠A＝60°，若EF＝2，则DF ＝（）A．3B．4C．5D．62．如图，已知△ABC的面积为8，在BC上截取BD＝BA，作∠ABC的平分线交AD于点P，连接PC，则△BPC的面积为（）A．2B．4C．5D．63．如图，已知△ABC，AB＝5，∠ABC＝60°，D为BC边上的点，AD＝AC，BD＝2，则DC＝（）A．0.5B．1C．1.5D．24．如图，△ABC中，∠B＝60°，AB＝8，点D在BC边上，且AD ＝AC．若BD＝，则CD的长为（）A．4B．C．5D．5．如图，△ABC中，AB＝AC，DE垂直平分AC，若△BCD的周长是14，BC＝6，则AC 的长是（）A．6B．8C．10D．146．如图，在△ABC中，∠ABC＝60°，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且，则线段BE的长为（）A．B．2C．3D．7．如图，在△ABC中，∠B＝90°，AB＝6，BC＝8，AD为∠BAC 的角平分线，则三角形ADC的面积为（）A．3B．10C．12D．158．如图，△ABC的一角被墨水污了，但小明很快就画出跟原来一样的图形，他所用定理是（）A．SAS B．SSS C．ASA D．HL9．如图，上午8时，一艘船从A处出发以15海里/小时的速度向正北航行，10时到达B处，从A、B两点望灯塔C，测得∠NAC＝42°，∠NBC＝84°，则B处到灯塔C的距离为（）A．15海里B．20海里C．30海里D．求不出来10．已知：如图，在△ABC中，AB＝AC，AB的垂直平分线DE，分别交AB，AC于点D，E．若AD＝3，BC＝5，则△BEC的周长为（）A．8B．10C．11D．1311．如图，∠MON＝60°，OA平分∠MON，P是射线OA上的一点，且OP＝4，若点Q是射线OM上的一个动点，则PQ的最小值为（）A．1B．2C．3D．412．如图，∠AOB＝60°，OC平分∠AOB，如果射线OA上的点E 满足△OCE是等腰三角形，那么∠OEC的度数不可能为（）A．120°B．75°C．60°D．30°13．已知实数a，b满足|a﹣2|+（b﹣4）2＝0，则以a，b的值为两边的等腰三角形的周长是（）A．10B．8或10C．8D．以上都不对14．如图，△ABC中，BO 平分∠ABC，CO平分∠ACB，M，N经过点O，且MN∥BC，若AB＝5，△AMN的周长等于12，则AC的长为（）A．7B．6C．5D．415．如图，在△ABC中，AB＝AD＝DC，∠BAD＝26°，则∠C的度数是（）A．36°B．38.5°C．64°D．77°二．填空题（共15小题）16．△ABC中，AD⊥BC于D，∠ACD＝60°，若AD＝2，AB＝2，则BC＝______．17．已知等腰三角形的周长是14，设其腰长是x，底边长是y，则y与x的函数关系式为y ＝______，自变量x的取值范围是______．18．如图，已知∠AOB＝30°，点P在边OA上，OP＝14，点E，F在边OB上，PE＝PF，EF＝6．若点D是边OB上一动点，则∠PDE ＝45°时，DF的长为______．19．如图，在等腰三角形ABC中，AB＝AC，∠B＝50°，D为BC 的中点，点E在AB上，∠AED＝70°，若点P是等腰三角形ABC的腰上的一点，则当△DEP是以∠EDP为顶角的等腰三角形时，∠EDP的度数是______．20．如图，D为△ABC中BC边上一点，AB＝CB，AC＝AD，∠BAD＝24°，则∠C＝______°．21．已知等腰三角形的底角为15°，腰长为8cm，则这个三角形的面积为______cm2．22．如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是______．23．如图，在△ABC中，AB＝AC，AB的垂直平分线交AB于点D，交AC于点E，若∠EBC ＝30°，则∠A的度数为______．24．如图，在△ABC中，∠C＝90°，∠ADC＝60°，∠B＝30°，若CD＝3cm，则BD＝______cm．25．如图，在△ABC中，BA＝BC，∠ABC＝120°，BD⊥BC交AC 于点D，BD＝1，则AC 的长______．26．在△ABC中，AB＝AD＝CD，且∠C＝40°，则∠BAD的度数为______．27．如图，在△ABC中，AD＝BD＝BC，若∠A＝x°，则∠ABC＝______度（用含x的代数式表示）．28．如图，在△ABC中，AC＝AD＝BD，∠B＝28°，则∠CAD的度数为______°．29．如图，点O是边长为2的等边三角形ABC内任意一点，且OD⊥AC，OE⊥AB，OF⊥BC，则OD+OE+OF＝______．30．如图，△ABC中，AD平分∠BAC，∠ACB＝3∠B，CE⊥AD，AC＝8，BC＝BD，则CE＝______．三．解答题（共20小题）31．如图，在Rt△ABC中，∠ACB＝90°，∠A＝36°，△ABC的外角∠CBD的平分线BE 交AC的延长线于点E．（1）求∠CBE的度数；（2）点F是AE延长线上一点，过点F作∠AFD＝27°，交AB的延长线于点D．求证：BE∥DF．32．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，分别交BC于点D、E，已知△ADE的周长5cm．（1）求BC的长；（2）分别连接OA、OB、OC，若△OBC的周长为13cm，求OA 的长．33．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，点P为AC的中点，点D为AB 边上一点，且AD＝PD，延长DP交BC的延长线于点E，若AB＝2，求PE的长．34．如图，△ABC是等边三角形，延长BC到E，使CE＝BC．点D是边AC的中点，连接ED并延长ED交AB于F求证：（1）EF⊥AB；（2）DE＝2DF．35．如图，在△ABC中，∠ACB＝110°，∠B＞∠A，D，E为边AB 上的两个点，且BD＝BC，AE＝AC．（1）若∠A＝30°，求∠DCE的度数；（2）∠DCE的度数会随着∠A度数的变化而变化吗？请说明理由．36．已知，△ABC是等边三角形，D、E、F分别是AB、BC、AC 上一点，且∠DEF＝60°．（1）如图1，若∠1＝50°，求∠2；（2）如图2，连接DF，若∠1＝∠3，求证：DF∥BC．37．在△ABC中，AB＝AC，点D是BC的中点，点E是AD上任意一点．（1）如图1，连接BE、CE，则BE＝CE吗？说明理由；（2）若∠BAC＝45°，BE的延长线与AC垂直相交于点F时，如图2，BD＝AE吗？说明理由．38．如图，三角形ABC中，AC＝BC，D是BC上的一点，连接AD，DF平分∠ADC交∠ACB的外角∠ACE的平分线于F．（1）求证：CF∥AB；（2）若∠DAC＝40°，求∠DFC的度数．39．如图，在△ABC中，∠C＝90°，∠B＝30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD＝3，求BD的长．40．如图，在△ABC中，∠BAC＝90°，BD平分∠ABC，CD∥AB 交BD于点D，已知∠1＝32°，求∠D的度数．41．如图，在△ABC中，AB＝AC，∠BAC＝100°，BD平分∠ABC，且BD＝AB，连接AD、DC．（1）求证：∠CAD＝∠DBC；（2）求∠BDC的度数．42．如图，点O是△ABC边AC上的一个动点，过O点作直线MN∥BC．设MN交∠ACB 的平分线于点E，交∠ACB的外角平分线于点F．（1）求证：OE＝OF；（2）若CE＝8，CF＝6，求OC的长．43．如图，在等边三角形ABC中，D是AB上的一点，E是CB延长线上一点，连结CD，DE，已知∠EDB＝∠ACD．（1）求证：△DEC是等腰三角形．（2）当∠BDC＝5∠EDB，BD＝2时，求EB的长．44．如图，在△ABC中，∠BAC＝120°，∠B＝40°，边AB的垂直平分线与边AB交于点E，与边BC交于点D．（1）求∠ADC的度数；（2）求证：△ACD为等腰三角形．45．如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC 于点E，过点E作EF∥BC交AB于点F．（1）若∠C＝36°，求∠BAD的度数．（2）求证：FB＝FE．46．如图，在△ABC中，∠ABC和∠ACB的平分线交于点O，过点O作EF∥BC，交AB 于E，交AC于F，若BE＝3，EF＝5，试求CF的值．47．如图，在△ABC中，AB＝AC，点D在线段BC上，AD＝BD，△ADC是等腰三角形，求△ABC三个内角的度数．48．如图，∠BAD＝90°，AB＝AC，AC的垂直平分线交BC于D．（1）求∠BAC的度数；（2）若AB＝10，BC＝10，求△ABD的周长．49．如图，已知∠1与∠2互为补角，且∠3＝∠B，（1）求证：EF∥BC；（2）若AC＝BC，CE平分∠ACB，求证：AF＝CF．50．如图，等边△ABC的边长为12，D为AB边上一动点，过点D作DE⊥BC于点E．过点E作EF⊥AC于点F．（1）若AD＝2，求AF的长；（2）当AD取何值时，DE＝EF？三角形证明专题复习参考答案与试题解析一．选择题（共15小题）1．解：如图，过点E作EG⊥BC，交BC于点G∵AB＝AC，∠A＝60°，∴△ABC是等边三角形，∴∠ACB＝60°，∵EC＝CD，∴∠CED＝∠CDE＝∠ACB＝30°，∴∠AEF＝30°，∴∠AFE＝90°，即EF⊥AB，∵△ABC是等边三角形，AE＝CE，∴BE平分∠ABC，∴EG＝EF＝2，在Rt△DEG中，DE＝2EG＝4，∴DF＝EF+DE＝2+4＝6；方法二、∵AB＝AC，∠A＝60°，∴△ABC是等边三角形，∴∠ACB＝60°，∵EC＝CD，∴∠CED＝∠CDE＝∠ACB＝30°，∵△ABC是等边三角形，AE＝CE，∴BE平分∠ABC，∴∠ABE＝∠CBE＝30°＝∠CDE，∴BE＝DE，∠BFD＝90°，∴BE＝2EF＝4＝DE，∴DF＝DE+EF＝6；故选：D．2．解：∵BD＝BA，BP是∠ABC的平分线，∴AP＝PD，∴S△BPD＝S△ABD，S△CPD＝S△ACD，∴S△BPC＝S△BPD+S△CPD＝S△ABD+S△ACD＝S△ABC，∵△ABC 的面积为8，∴S△BPC＝×8＝4．故选：B．3．解：过点A作AE⊥BC于点E，∵AD＝AC，∴E是CD的中点，在Rt△ABE中，AB＝5，∠ABC＝60°，∴BE＝，∵BD＝2，∴DE＝﹣2＝，∴CD＝1，故选：B．4．解：过点A作AE⊥BC，∵AD＝AC，∴E是CD的中点，∵∠B＝60°，AB＝8，在Rt△ABE中，BE＝4，∵BD＝，∴DE＝4﹣＝，∴CD＝5，故选：C．5．解：∵DE垂直平分AC，∴AD＝CD．∵△BCD的周长是14，BC＝6，∴AB＝BD+CD＝14﹣6＝8，∵AB＝AC，∴AC＝8．故选：B．6．解：连接BD，如图，∵DE＝DF，DE⊥AB，DF⊥BC，∴BD平分∠ABC，∴∠ABD＝∠ABC＝×60°＝30°，在Rt△BDE中，BE＝DE＝×＝3．故选：C．7．解：作DH⊥AC于H，如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，∴AC＝＝10，∵AD为∠BAC的角平分线，∴DB＝DH，∵×AB×CD＝DH×AC，∴6（8﹣DH）＝10DH，解得DH＝3，∴S△ADC＝×10×3＝15．故选：D．8．解：作△DEF，使DE＝AB，∠A＝∠D，∠E＝∠B，根据ASA定理可知，△DEF与原来的图形一样，他所用定理是ASA，故选：C．9．解：根据题意得：AB＝2×15＝30（海里），∵∠NAC＝42°，∠NBC＝84°，∴∠C＝∠NBC﹣∠NAC＝42°，∴∠C＝∠NAC，∴BC＝AB＝30海里．即从海岛B到灯塔C的距离是30海里．故选：C．10．解：∵AB的垂直平分线DE分别交AB、AC于点D、E，∴AE ＝BE，∵AD＝3，∴AB＝6，∴AE+EC＝AC＝AB＝6，∵BC＝5，∴△EBC的周长＝BC+BE+CE＝BC+AE+CE＝BC+AC＝6+5＝11；故选：C．11．解：作PQ′⊥OM于Q′，∵∠MON＝60°，OP平分∠MON，∴∠POQ′＝30°，∴PQ′＝OP＝2，由垂线段最短可知，PQ的最小值是2，故选：B．12．解：∵∠AOB＝60°，OC平分∠AOB，∴∠AOC＝30°，①当E在E1时，OE＝CE，∵∠AOC＝∠OCE＝30°，∴∠OEC＝180°﹣30°﹣30°＝120°；②当E在E2点时，OC＝OE，则∠OCE＝∠OEC＝（180°﹣30°）＝75°；③当E在E3时，OC＝CE，则∠OEC＝∠AOC＝30°；综上，∠OEC的度数不可能为60°，故选：C．13．解：根据题意得a﹣2＝0，b﹣4＝0，解得a＝2，b＝4，①a＝2是底长时，三角形的三边分别为4、4、2，∵4、4、2能组成三角形，∴三角形的周长为10，②a＝2是腰边时，三角形的三边分别为4、2、2，2+2＝4，不能组成三角形．综上所述，三角形的周长是10．故选：A．14．解：∵BO平分∠CBA，CO平分∠ACB，∴∠MBO＝∠OBC，∠OCN＝∠OCB，∵MN∥BC，∴∠MOB＝∠OBC，∠NOC＝∠OCB，∴∠MBO＝∠MOB，∠NOC＝∠NCO，∴MO＝MB，NO＝NC，∵AB＝5，△AMN的周长等于12，∴△AMN的周长＝AM+MN+AN＝AB+AC＝5+AC＝12，∴AC＝7，故选：A．15．解：在△ABC中，AB＝AD＝DC，∵在三角形ABD中，AB＝AD，∠BAD＝26°，∴∠B＝∠ADB＝（180°﹣26°）×＝77°，又∵AD＝DC，在三角形ADC中，∴∠C＝∠ADB＝77°×＝38.5°．故选：B．二．填空题（共15小题）16．解：∵AD⊥BC，∴∠ADC＝∠ADB＝90°，∵∠ACD＝60°，∴∠CAD＝30°，∵AD＝2，∴CD＝AD＝2，∵AB＝2，∴BD＝＝＝4，如图1，BC＝BD+CD＝6，如图2，BC＝BD﹣CD＝2，综上所述，BC＝6或2，故答案为：6或2．17．解：∵2x+y＝14，∴y＝14﹣2x，即x＜7，∵两边之和大于第三边∴x＞，综上可得＜x＜7故答案为：y＝﹣2x+14，＜x＜7．18．解：如图，过点P作PH⊥OB于点H，∵PE＝PF，。
北师大版八年级下册数学第一章 三角形的证明含答案
北师大版八年级下册数学第一章三角形的证明含答案一、单选题(共15题，共计45分)1、如图，△ABC中，AB＝AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则下面结论错误的是（）A.BF＝EFB.DE＝EFC.∠EFC＝45°D.∠BEF＝∠CBE2、如图，在△ABC中，∠C=90°，AD平分∠BAC，且DE⊥AB于E，DE=5，BC=11，则BD的长为( )A.5B.6C.7D.83、如图，在△ABC中，∠ACB＝90°，∠A＝20°．将△ABC绕点C按逆时针方向旋转得△A′B′C，且点B在A′B′上，CA′交AB于点D，则∠BDC的度数为（）A.40°B.50°C.60°D.70°4、如图，在△ABC中，AB=AC，D是BC中点，下列结论中不正确的是（）A. B. C. 平分 D.5、若等腰三角形一个外角等于100°，则它的顶角度数为（）.A.20°B.80°C.20°或80°D.无法确定6、等腰三角形中，，一边上的中线将这个三角形的周长分为和两部分，则这个等腰三角形的底边长为（）A.7B.7或11C.11D.7或107、如图，△ABC中，AB=AC，D，E，F分别在BC，AC，AB上，若BD=CE，CD=BF，则∠EDF（）A. 90°-∠AB. 90°-∠AC. 180°-∠AD. 180°-2∠A8、如图，在△ABC中，∠ACB为钝角。
用直尺和圆规在边AB上确定一点D。
使∠ADC=2∠B，则符合要求的作图痕迹是（）A. B. C.D.9、如图，在正方形ABCD中，点E，F分别在BC，CD上，且∠EAF=45°，将△ABE绕点A顺时针旋转90°，使点E落在点E'处，则下列判断不正确的是（）A.△AEE′是等腰直角三角形B.AF垂直平分EE'C.△E′EC∽△AFDD.△AE′F是等腰三角形10、如图，在等腰△ABC中，AB＝AC，∠A＝20°，AB上一点D，且AD＝BC，过点D作DE∥BC且DE＝AB，连接EC，则∠DCE的度数为（）A.80°B.70°C.60°D.45°11、如图，在□ABCD中，AB=5，BC=8，∠ABC，∠BCD的角平分线分别交AD于E和F，BE与CF交于点G，则△EFG与△BCG面积之比是（）A.5：8B.25：64C.1：4D.1：1612、如图，A，B，C三点在已知的圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是的中点，连接DB，DC，则∠DBC的度数为（）A.30°B.45°C.50°D.70°13、在等腰△ABC中，AB=AC=9，BC=6，DE是AC的垂直平分线，交AB、AC于点D、E，则△BDC的周长是（）A.6B.9C.12D.1514、以下列各组数据为边长，可以构成等腰三角形的是（）A.2，3，4B.5，5，10C.2，2，1D.1，2，315、如图，等腰三角形ABC的周长为21，底边BC=5，AB的垂直平分线DE交AB 于点D，交AC于点E，则△BEC的周长为（）A.13B.14C.15D.16二、填空题(共10题，共计30分)16、如图，已知钝角三角形ABC的面积为20，最长边AB=10，BD平分∠ABC，点M、N分别是BD、BC上的动点，则CM+MN的最小值为________．17、如图，菱形ABCD的边长是4，∠ABC＝60°，点E，F分别是AB，BC边上的动点（不与点A，B，C重合），且BE＝BF，若EG∥BC，FG∥AB，EG与FG相交于点G，当△ADG为等腰三角形时，BE的长为________.18、在△ABC中，如果AB=AC=10，cosB= ，那么△ABC的重心到底边的距离为________．19、如图，AE 是△ABC 的角平分线，AD⊥BC 于点D，若∠DAE=8°，∠C=36°，则∠BAC 的度数是________．20、在等腰△ABC中，AB=AC，∠B=40°，则∠A=________．21、如图，等腰三角形ABC中，AB＝AC，∠A＝40°，CD⊥AB于D，则∠DCB等于________.22、已知等腰三角形的一边长为9，另一边长为方程x2﹣8x+15=0的根，则该等腰三角形的周长为________．23、如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=3，则EF的长为________24、等腰三角形的底边长为6，底边上的中线长为4，它的腰长为________.25、如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为________．三、解答题(共5题，共计25分)26、已知：如图，在△ABC中，AB=AC，点D，E在边BC上，且BD=CE．求证：AD=AE．27、推理填空如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBC=∠F，求证：CE∥DF.请完成下面的解题过程.∵BD平分∠ABC，CE平分∠ACB（已知）∴∠DBC= ∠________，∠ECB= ∠________（角平分线的定义）又∵∠ABC=∠ACB（已知）∴∠________=∠________.又∵∠________=∠________（已知）∴∠F=∠________∴CE∥DF________.28、已知：在中，点是的中点，于点，平分，交的延长线于点，交于点．求证：．29、如图，CD平分∠ACB，DE∥BC，∠AED＝46°，求∠CDE的度数．30、如图，在△ABC中，CD=CA，CE⊥AD于点E，BF⊥AD于点F．求证：∠ACE=∠DBF．参考答案一、单选题(共15题，共计45分)1、B2、B3、C4、D5、C6、B7、A8、B9、D10、B11、D12、C13、D14、C15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)27、28、30、。
八年级数学下册第一章三角形的证明1.2教材习题课件新版北师大版
又∵AB=AD，∴AE=AF.
A
在△AEC和△AFC中，
E
F
∵AE=AF，∠EAC=∠FAC，AC=AC， B
D
∴△AEC≌△AFC(SAS)，
∴EC =FC.
∴这两根彩线的长度相等.
C
(2) 如果AE=1 AB，AF= 1 AD，那么彩线的长度相等吗？
如果AE=
1
3
AB，AF=
1
3
AD呢？由此你能得到什么结论？
(1) 分别在AB，AD的中点E，F处拉两根彩线EC，FC，
证明：这两根彩线的长度相等； (1)证明：如图，连接AC. 在△ABC和△ADC中，
A E B
F D
∵AB=AD，BC=DC，AC=AC，
∴△ABC≌△ADC(SSS)，
∴∠BAC=∠DAC.
C
∵E，F分别为AB，AD的中点，
∴AB=2AE，AD=2AF.
∵∠BDC=∠ABD+∠A,
A
∴∠A=∠BDC－∠ABD=2x°－x°=x°.
∵∠A+∠ABC+∠C=180°，
D
∴x+2x+2x=180．解得x=36 ∴∠A=36°.
B
C
2. 已知：如图，在△ABC中，AB=AC，D为BC的中点，
点E，F分别在AB和AC上，并且AE=AF.
求证：DE=DF.
A
八（下）数学教材习题
习题 1.2
1. 如图，在△ABC中，AB=AC，BD平分∠ABC，交AC
于点D. 若BD=BC，则∠A等于多少度？
解：设∠ABD=x°，
A
∵BD平分∠ABC，
∴∠ABC=2∠ABD=2x°. ∵AB=AC， ∴∠C=∠ABC=2x°.
北师大版八年级数学下册第一章 三角形的证明练习(包含答案)
第一章三角形的证明一、单选题1．已知等腰三角形的一个角等于42°，则它的底角为：（）A．42°B．69°C．69°或84°D．42°或69°2．等腰三角形的两条边长分别为9cm和12cm，则这个等腰三角形的周长是()A．30cm B．33cm C．24cm或21cm D．30cm或33cm 3．如图所示，V ABC是等边三角形，且BD=CE，∠1=15︒，则∠2的度数为（）A．15︒B．30°C．30°D．60︒4．下列各组线段能构成直角三角形的是（）A．1,2,3B．7,12,13C．5,8,10D．15,20,255．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP的长不可能是()A．3.5B．4.2C．5.8D．76．如图，在V ABC中，∠A=90︒,∠C=30︒,PQ垂直平分BC，与AC交于点P,下列结论正确的是（）． ∠ △°A ． PC < 2P AB ． PC > 2P AC ． AB < 2P AD ． AB > 2P A7．在联欢会上，有 A 、B 、C 三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在 ∆ABC 的（）A ．三边中垂线的交点C ．三条角平分线的交点B ．三边中线的交点D ．三边上高的交点8 如图所示，Rt△ABC 中， C 90° △AB 的垂直平分线 DE 交 BC 于 D ，交 AB 于点 E .当∠B 30时，图中一定不相等的线段有()△A ．AC △AE BEC ．△CD DEB ．AD △BDD ．AC △BD9．如图，△ABC 中，AB ＝5，AC ＝4，以点 A 为圆心，任意长为半径作弧，分别交 A B 、AC于 D 和 E ，再分别以点 D 、E 为圆心，大于二分之一 DE 为半径作弧，两弧交于点 F ，连接AF 并延长交 BC 于点 G ，GH ⊥AC 于 H ，GH ＝2，则△ABG 的面积为（ ）A．4B．5C．9D．1010．已知：如图，点D，E分别在△ABC的边AC和BC上，AE与BD相交于点F，给出下面四个条件：①∠1=∠2；②AD=BE；③AF=BF；④DF=EF，从这四个条件中选取两个，不能判定△ABC是等腰三角形的是（）A．①②B．①④C．②③D．③④二、填空题11．如图，已知在∆ABC中，AB=AC，点D在边BC上，要使BD=CD，还需添加一个条件，这个条件是_____________________．（只需填上一个正确的条件）12．如图是一块菜地，已知AD=8米，CD=6米，∠D=90︒,AB=26米，BC=24米．则这块菜地的面积是_____．13．如图，在V ABC中，AC=BC，分别以点A和点C为圆心，大于1AC长为半径画2弧，两弧相交于点M、N，连接MN分别交BC、AC于点D、E，连接AD．若∠B=70︒，则∠BAD的度数是_____度．14．如图，∆ABC中，∠BAC=90︒，AD⊥BC，∠ABC的平分线BE交AD于点F，AG 平分∠DAC．给出下列结论：①∠BAD=∠C；②∠EBC=∠C；③AE=AF；④FG//AC；⑤EF=FG．其中正确的结论是______．三、解答题15．如图，在△ABC中，AB＝AC，D为BC上一点，∠B＝30°，连接AD．（1）若∠BAD＝△45°，求证：ACD为等腰三角形；（△2）若ACD为直角三角形，求∠BAD的度数．16．如图，已知O是等边三角形ABC内一点，D是线段BO延长线上一点，且OD=OA，∠AOB=120︒，求∠BDC的度数．17．如图，一架2.5m长的梯子AB斜靠在一竖直墙AO上，这时AO为2.4m．（1）求OB的长度；（2）如果梯子底端B沿地面向外移动0.8m到达点C，那么梯子顶端A下移多少m？△18．如图，在ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，分别交BC于点D、E，已知△ADE的周长5cm．（1）求BC的长；（2）分别连接OA、OB、△OC，若OBC的周长为13cm，求OA的长．19．如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°.以点D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN.(1)求证：MN＝BM＋NC；(2)△求AMN的周长．答案1．D 2．D 3．D 4．D 5．D 6.C.△， ，△， △﹣ △， △﹣ ﹣ △，△， △，△， △﹣ ﹣ △﹣ ﹣ 7．A8．D9．B10．C11．AD ⊥BC12．96△△△13．3014．①③④15．（1） AB=AC B=30°B= C=30°BAC=180°30°﹣30°=120°， BAD=45°CAD= BAC BAD=120° 45°=75°△， ADC= B+ BAD=75° ADC= CADAC=CD△即 ACD 为等腰三角形；（2）有两种情况： △当 ADC=90°△时，B=30°BAD= ADC B=90° 30°=60°；△当 CAD=90°△时， BAD= BAC CAD=120° 90°=30°；△即 BAD 的度数是 60°或 30°．⎨∠BAO = ∠CAD16．∵∠AOB=120°，∴∠AOD=60°∵AO=OD ，∴△AOD 是等边三角形∴ ∠BAC = 60︒ ， AB = AC∵△ABC 是等边三角形，∴∠BAC=60°，AB=AC∴∠BAC=∠OAD ，∴∠BAO+△OAC=△OAC+△CAD△∴∠BAO= CAD在△BAO 和△CAD 中⎧ AO = AD ⎪⎪ ⎩AB = AC∴ ∆ABO ≌ ∆ACD∴ ∠AOB = ∠ADC = 120︒△ ∠BDC = ∠ADC - ∠ADO = 60︒17.（1）解：在 Rt ∆AOB 中，由勾股定理OB 2 = AB 2 - AO 2= 2.52 - 2.4 2= 0.49∴ OB = 0.49 = 0.7（2）设梯子的 A 端下移到 D ， OC = 0.7 + 0.8 = 1.5∴在Rt∆OCD中，由勾股定理∴OD2=CD2-DC2=2.52-1.52=4∴OD=4=2∴顶端A下移了：2.4=2=0.4m18.解：（1）∵DM是线段AB的垂直平分线，∴DA＝DB，同理，EA＝EC，∵△ADE的周长5，∴AD+DE+EA＝5，∴BC＝DB+DE+EC＝AD+DE+EA＝5（cm）；（△2）∵OBC的周长为13，∴OB+OC+BC＝13，∵BC＝5，∴OB+OC＝8，∵OM垂直平分AB，∴OA＝OB，同理，OA＝OC，∴OA＝OB＝OC＝4（cm）．19.解：(1)∵△BDC是等腰三角形，且∠BDC＝120°，∴∠BCD＝∠DBC＝30°.∵△ABC是等边三角形，∴∠ABC＝∠BCA＝60°，∴∠DBA＝∠DCA＝90°，延长AB至F，使BF＝CN，连接DF，由SAS△可证BDF≌△CDN，∴∠BDF＝∠CDN，DF＝DN，∵∠MDN＝60°，∴∠FDM＝∠BDM＋∠CDN＝60°，由SAS△可证DMN≌△DMF，∴MN＝MF＝MB＋BF＝MB＋CN(2)由(1)知MN＝MB＋CN，∴△AMN的周长为AM＋AN＋MN＝AM＋MB＋AN＋CN＝AB＋AC＝6。
(完整版)北师大版八年级三角形证明课后题汇总
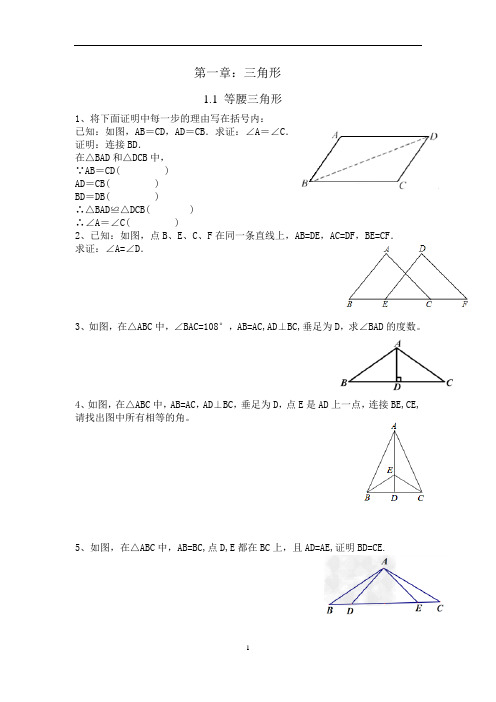
1.1 等腰三角形1、将下面证明中每一步的理由写在括号内：已知：如图，AB＝CD，AD＝CB．求证：∠A＝∠C．证明：连接BD．在△BAD和△DCB中，∵AB＝CD( )AD＝CB( )BD＝DB( )∴△BAD≌△DCB( )∴∠A＝∠C( )2、已知：如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．3、如图，在△ABC中，∠BAC=108°，AB=AC,AD⊥BC,垂足为D，求∠BAD的度数。
4、如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，点E是AD上一点，连接BE,CE,请找出图中所有相等的角。
5、如图，在△ABC中，AB=BC,点D,E都在BC上，且AD=AE,证明BD=CE.1、如图，在△ABC中，AB=AC,BD平分∠ABC,交AC于点D.若BD=BC,则∠A等于多少度？2、已知：如图，在△ABC中，AB=AC,D为BC中点，点E,F分别在AB和AC尚，并且AE=AF.求证：DE=DF3、已知：如图，D，E分别是等边三角形ABC的两边AB,AC上的点，且AD=CE。
求证：CD=BE4、如图，在一个风筝ABCD中，AB=AD,BC=DC⑴分别在AB,AD的中点E,F处拉两根彩线EC,FC.证明:这两根彩线的长度相等。
⑵如果AE=1/3AB,AF=1/3AD,那麼彩线的长度相等吗?如果AE=1/4AB,AF=1/4AD呢?由此你能得到什麼结论?1、已知：如图，∠CEA是△ABC的外角，AD平行BC，且∠1=∠2.求证：AB=AC.2、已知：如图，在△ABC中，AB=AC，点E在CA的延长线上，EP垂直于BC，垂足为P，EP交AB于点F。
求证：△AEF是等腰三角形。
3、如图，一艘船从A处出发，以18kn的速度向北航行，经过10h到处B处。
分别从A，B望灯塔C，测得∠NAC＝42°，∠NBC＝84°．求从B处到灯塔C 的距离．1、已知：如图，△ABC是等边三角形，与BC平行的直线分别交AB和AC于点D,E, 求证：△ADE是等边三角形。
北师大版数学八年级下册：第一章《三角形的证明》含详细答案
北师大版八年级下册数学第一章三角形的证明一．选择题（共12小题）1．（2014•遂宁）如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC 长是（）A．3B．4C．6D．52．（2014•台湾）如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24 B．30 C．32 D．363．（2014•安顺）已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b﹣13）2=0，则此等腰三角形的周长为（）A．7或8 B．6或1O C．6或7 D．7或104．（2014•宁波）如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）A．2.5 B．C．D．25．（2014•甘井子区一模）如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为14cm，则△ABC 的周长为（）6．（2014•本溪一模）如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=10cm，则AC等于（）A．10cm B．8cm C．5cm D．2.5cm7．（2013•西宁）如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2B．C．D．8．（2013•滨城区二模）如图，△ABC中，∠B=40°，AC的垂直平分线交AC于D，交BC于E，且∠EAB：∠CAE=3：1，则∠C等于（）A．28°B．25°C．22.5°D．20°9．（2013•澄江县一模）若一个等腰三角形至少有一个内角是88°，则它的顶角是（）A．88°或2°B．4°或86°C．88°或4°D．4°或46°10．（2012•泰安）如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）A．3B．3.5 C．2.5 D．2.811．（2011•成华区二模）如图，在Rt△ABC中，∠ACB=30°，CD=4，BD平分∠ABC，交AC于点D，则点D到A．1B．2C．D．12．（2006•威海）如图，在△ABC中，∠ACB=100°，AC=AE，BC=BD，则∠DCE的度数为（）A．20°B．25°C．30°D．40°二．填空题（共6小题）13．（2014•长春）如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为_________．14．（2013•泰安）如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是_________．15．（2013•沈阳模拟）如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠BAC=70°，则∠CAE=_________．16．（2012•通辽）如图，△ABC的三边AB、BC、CA长分别为40、50、60．其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO=_________．17．（2012•广东模拟）在△ABC中，已知AB=AC，DE垂直平分AC，∠A=50°，则∠DCB的度数是_________．18．（2009•临沂）如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB=_________度．三．解答题（共12小题）19．（2014•翔安区质检）如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，求△ABD的周长．20．（2014•长春模拟）如图，D为△ABC边BC延长线上一点，且CD=CA，E是AD的中点，CF平分∠ACB交AB于点F．求证：CE⊥CF．21．（2014•顺义区一模）如图，在四边形ABCD中，∠B=∠D=90°，∠C=60°，BC=4，CD=3，求AB的长．22．（2013•湘西州）如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．23．（2012•重庆模拟）如图，已知△ABC和△ABD均为直角三角形，其中∠ACB=∠ADB=90°，E为AB的中点，求证：CE=DE．24．（2010•攀枝花）如图所示，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD 于点F．点E是AB的中点，连接EF．（1）求证：EF∥BC；（2）若△ABD的面积是6，求四边形BDFE的面积．25．（2009•大连二模）如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，CE⊥BD于点E．求证：AD=BE．26．（2007•宜宾）已知；如图，在△ABC中，AB=BC，∠ABC=90度．F为AB延长线上一点，点E在BC上，BE=BF，连接AE、EF和CF．（1）求证：AE=CF；（2）若∠CAE=30°，求∠EFC的度数．27．（2006•韶关）如图，在△ABC中，AB≠AC，∠BAC的外角平分线交直线BC于D，过D作DE⊥AB，DF⊥AC 分别交直线AB，AC于E，F，连接EF．（1）求证：EF⊥AD；（2）若DE∥AC，且DE=1，求AD的长．28．如图，Rt△ABC中，∠C=90°，AC=6，∠A=30°，BD平分∠ABC交AC于点D，求点D到斜边AB的距离．29．如图，在△ABC中，∠CAB=90°，AB=3，AC=4，AD是∠CAB的平分线，AD交BC于D，求BD的长．30．如图，四边形ABCD中，AB=BC，AB∥CD，∠D=90°，AE⊥BC于点E，求证：CD=CE．北师大版八年级下册数学第一章三角形的证明参考答案与试题解析一．选择题（共12小题）1．（2014•遂宁）如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC 长是（）A．3B．4C．6D．5考点：角平分线的性质．专题：几何图形问题．分析：过点D作DF⊥AC于F，根据角平分线上的点到角的两边距离相等可得DE=DF，再根据S△ABC=S△ABD+S△ACD列出方程求解即可．解答：解：如图，过点D作DF⊥AC于F，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，∴DE=DF，由图可知，S△ABC=S△ABD+S△ACD，∴×4×2+×AC×2=7，解得AC=3．故选：A．点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．2．（2014•台湾）如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（）A．24 B．30 C．32 D．36根据等边对等角可得∠CBP=∠BCP，然后利用三角形的内角和等于180°列出方程求解即可．解答：解：∵直线M为∠ABC的角平分线，∴∠ABP=∠CBP．∵直线L为BC的中垂线，∴BP=CP，∴∠CBP=∠BCP，∴∠ABP=∠CBP=∠BCP，在△ABC中，3∠ABP+∠A+∠ACP=180°，即3∠ABP+60°+24°=180°，解得∠ABP=32°．故选：C．点评：本题考查了线段垂直平分线上的点到两端点的距离相等的性质，角平分线的定义，三角形的内角和定理，熟记各性质并列出关于∠ABP的方程是解题的关键．3．（2014•安顺）已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b﹣13）2=0，则此等腰三角形的周长为（）A．7或8 B．6或1O C．6或7 D．7或10考点：等腰三角形的性质；非负数的性质：偶次方；非负数的性质：算术平方根；解二元一次方程组；三角形三边关系．分析：先根据非负数的性质求出a，b的值，再分两种情况确定第三边的长，从而得出三角形的周长．解答：解：∵|2a﹣3b+5|+（2a+3b﹣13）2=0，∴，解得，当a为底时，三角形的三边长为2，3，3，则周长为8；当b为底时，三角形的三边长为2，2，3，则周长为7；综上所述此等腰三角形的周长为7或8．故选：A．点评：本题考查了非负数的性质、等腰三角形的性质以及解二元一次方程组，是基础知识要熟练掌握．4．（2014•宁波）如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）A．2.5 B．C．D．2考点：直角三角形斜边上的中线；勾股定理；勾股定理的逆定理．理列式求出AF，再根据直角三角形斜边上的中线等于斜边的一半解答即可．解答：解：如图，连接AC、CF，∵正方形ABCD和正方形CEFG中，BC=1，CE=3，∴AC=，CF=3，∠ACD=∠GCF=45°，∴∠ACF=90°，由勾股定理得，AF===2，∵H是AF的中点，∴CH=AF=×2=．故选：B．点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，正方形的性质，勾股定理，熟记各性质并作辅助线构造出直角三角形是解题的关键．5．（2014•甘井子区一模）如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为14cm，则△ABC 的周长为（）A．18cm B．22cm C．24cm D．26cm考点：线段垂直平分线的性质．分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=CD，然后求出△ABD的周长=AB+BC，再求出AC的长，然后根据三角形的周长公式列式计算即可得解．解答：解：∵DE是AC的垂直平分线，∴AD=CD，∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，∵AE=4cm，∴AC=2AE=2×4=8cm，∴△ABC的周长=AB+BC+AC=14+8=22cm．故选B．点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，求出△ABD的周长=AB+BC是解题的关键．6．（2014•本溪一模）如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=10cm，则AC等于（）A．10cm B．8cm C．5cm D．2.5cm考点：线段垂直平分线的性质；勾股定理．专题：探究型．分析：连接AD，先由三角形内角和定理求出∠BAC的度数，再由线段垂直平分线的性质可得出∠DAB的度数，根据线段垂直平分线的性质可求出AD的长及∠DAC的度数，最后由直角三角形的性质即可求出AC的长．解答：解：连接AD，∵DE是线段AB的垂直平分线，BD=15，∠B=15°，∴AD=BD=10，∴∠DAB=∠B=15°，∴∠ADC=∠B+∠DAB=15°+15°=30°，∵∠C=90°，∴AC=AD=5cm．故选C．点评：本题考查的是直角三角形的性质及线段垂直平分线的性质，熟知线段垂直平分的性质是解答此题的关键．7．（2013•西宁）如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）A．2B．C．D．考点：角平分线的性质；含30度角的直角三角形；直角三角形斜边上的中线；勾股定理．分析：由OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，易得△OCP是等腰三角形，∠COP=30°，又由含30°角的直角三角形的性质，即可求得PE的值，继而求得OP的长，然后由直角三角形斜边上的中线等于斜边的一半，即可求得DM的长．解答：解：∵OP平分∠AOB，∠AOB=60°，∴∠AOP=∠COP=30°，∵CP∥OA，∴∠AOP=∠CPO，∴∠COP=∠CPO，∴OC=CP=2，∵∠PCE=∠AOB=60°，PE⊥OB，∴∠CPE=30°，∴CE=CP=1，∴PE==，∴OP=2PE=2，∵PD⊥OA，点M是OP的中点，∴DM=OP=．故选：C．点评：此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质．此题难度适中，注意掌握数形结合思想的应用．8．（2013•滨城区二模）如图，△ABC中，∠B=40°，AC的垂直平分线交AC于D，交BC于E，且∠EAB：∠CAE=3：1，则∠C等于（）A．28°B．25°C．22.5°D．20°考点：线段垂直平分线的性质．专题：计算题．分析：设∠CAE=x，则∠EAB=3x．根据线段的垂直平分线的性质，得AE=CE，再根据等边对等角，得∠C=∠CAE=x，然后根据三角形的内角和定理列方程求解．解答：解：设∠CAE=x，则∠EAB=3x．∵AC的垂直平分线交AC于D，交BC于E，∴AE=CE．∴∠C=∠CAE=x．根据三角形的内角和定理，得∠C+∠BAC=180°﹣∠B，即x+4x=140°，x=28°．则∠C=28°．故选A．点评：此题综合运用了线段垂直平分线的性质、等腰三角形的性质以及三角形的内角和定理．9．（2013•澄江县一模）若一个等腰三角形至少有一个内角是88°，则它的顶角是（）A．88°或2°B．4°或86°C．88°或4°D．4°或46°考点：等腰三角形的性质．分析：分88°内角是顶角和底角两种情况讨论求解．解答：解：88°是顶角时，等腰三角形的顶角为88°，88°是底角时，顶角为180°﹣2×88°=4°，综上所述，它的顶角是88°或4°．故选C．点评：本题考查了等腰三角形的两底角相等的性质，难点在于要分情况讨论．10．（2012•泰安）如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）A．3B．3.5 C．2.5 D．2.8考点：线段垂直平分线的性质；勾股定理；矩形的性质．专题：计算题．分析：根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE，设CE=x，表示出ED的长度，然后在Rt△CDE中，利用勾股定理列式计算即可得解．解答：解：∵EO是AC的垂直平分线，∴AE=CE，设CE=x，则ED=AD﹣AE=4﹣x，在Rt△CDE中，CE2=CD2+ED2，即x2=22+（4﹣x）2，解得x=2.5，即CE的长为2.5．故选：C．点评：本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，勾股定理的应用，把相应的边转化为同一个直角三角形的边是解题的关键．11．（2011•成华区二模）如图，在Rt△ABC中，∠ACB=30°，CD=4，BD平分∠ABC，交AC于点D，则点D到BC的距离是（）A．1B．2C．D．考点：角平分线的性质；含30度角的直角三角形；勾股定理．分析：根据直角三角形两锐角互余求出∠ABC=60°，再根据角平分线的定义求出∠ABD=∠DBC=30°，从而得到∠DBC=∠ACB，然后利用等角对等边的性质求出BD的长度，再根据直角三角形30°角所对的直角边等于斜边的一半求出AD，过点D作DE⊥BC于点E，然后根据角平分线上的点到角的两边的距离相等解答即可．解答：解：∵Rt△ABC中，∠ACB=30°，∴∠ABC=60°，∵BD平分∠ABC，∴∠ABD=∠DBC=30°，∴∠DBC=∠ACB，∴BD=CD=4，在Rt△ABD中，∵∠ABD=30°，∴AD=BD=×4=2，过点D作DE⊥BC于点E，则DE=AD=2．故选B．点评：本题考查了角平分线上的点到角的两边的距离相等的性质，30°角所对的直角边等于斜边的一半的性质，以及等角对等边的性质，小综合题，但难度不大，熟记各性质是解题的关键．12．（2006•威海）如图，在△ABC中，∠ACB=100°，AC=AE，BC=BD，则∠DCE的度数为（）A．20°B．25°C．30°D．40°考点：等腰三角形的性质．专题：几何图形问题．分析：根据此题的条件，找出等腰三角形，找出相等的边与角度，设出未知量，找出满足条件的方程．解答：解：∵AC=AE，BC=BD∴设∠AEC=∠ACE=x°，∠BDC=∠BCD=y°，∴∠A=180°﹣2x°，∠B=180°﹣2y°，∵∠ACB+∠A+∠B=180°，∴100+（180﹣2x）+（180﹣2y）=180，得x+y=140，∴∠DCE=180﹣（∠AEC+∠BDC）=180﹣（x+y）=40°．故选D．点评：根据题目中的等边关系，找出角的相等关系，再根据三角形内角和180°的定理，列出方程，解决此题．二．填空题（共6小题）13．（2014•长春）如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为15．考点：角平分线的性质．专题：几何图形问题．分析：要求△ABD的面积，现有AB=7可作为三角形的底，只需求出该底上的高即可，需作DE⊥AB于E．根据角平分线的性质求得DE的长，即可求解．解答：解：作DE⊥AB于E．∵AD平分∠BAC，DE⊥AB，DC⊥AC，∴DE=CD=3．∴△ABD的面积为×3×10=15．故答案是：15．点评：此题主要考查角平分线的性质；熟练运用角平分线的性质定理，是很重要的，作出并求出三角形AB边上的高时解答本题的关键．14．（2013•泰安）如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是2．考点：含30度角的直角三角形；线段垂直平分线的性质．分析：根据同角的余角相等、等腰△ABE的性质推知∠DBE=30°，则在直角△DBE中由“30度角所对的直角边是斜边的一半”即可求得线段BE的长度．解答：解：∵∠ACB=90°，FD⊥AB，∴∠ACB=∠FDB=90°，∵∠F=30°，∴∠A=∠F=30°（同角的余角相等）．又∵AB的垂直平分线DE交AC于E，∴∠EBA=∠A=30°，∴直角△DBE中，BE=2DE=2．故答案是：2．点评：本题考查了线段垂直平分线的性质、含30度角的直角三角形．解题的难点是推知∠EBA=30°．15．（2013•沈阳模拟）如图，△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，若∠BAC=70°，则∠CAE=55°．考点：角平分线的性质．分析：首先过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，由△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，易证得AE是∠CAH的平分线，继而求得答案．解答：解：过点E作EF⊥BD于点F，作EG⊥AC于点G，作EH⊥BA于点H，∵△ABC的外角∠ACD的平分线CE与内角∠ABC平分线BE交于点E，∴EH=EF，EG=EF，∴EH=EG，∴AE是∠CAH的平分线，∵∠BAC=70°，∴∠CAH=110°，∴∠CAE=∠CAH=55°．故答案为：55°．点评：此题考查了角平分线的性质与判定．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．16．（2012•通辽）如图，△ABC的三边AB、BC、CA长分别为40、50、60．其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO=4：5：6．考点：角平分线的性质．专题：压轴题．分析：首先过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，由OA，OB，OC是△ABC的三条角平分线，根据角平分线的性质，可得OD=OE=OF，又由△ABC的三边AB、BC、CA长分别为40、50、60，即可求得S△ABO：S△BCO：S△CAO的值．解答：解：过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，∵OA，OB，OC是△ABC的三条角平分线，∴OD=OE=OF，∵△ABC的三边AB、BC、CA长分别为40、50、60，∴S△ABO：S△BCO：S△CAO=（AB•OD）：（BC•OF）：（AC•OE）=AB：BC：AC=40：50：60=4：5：6．故答案为：4：5：6．点评：此题考查了角平分线的性质．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．17．（2012•广东模拟）在△ABC中，已知AB=AC，DE垂直平分AC，∠A=50°，则∠DCB的度数是15°．考点：线段垂直平分线的性质；等腰三角形的性质．分析：由DE垂直平分AC，∠A=50°，根据线段垂直平分线的性质，易求得∠ACD的度数，又由AB=AC，可求得∠ACB的度数，继而可求得∠DCB的度数．解答：解：∵DE垂直平分AC，∴AD=CD，∴∠ACD=∠A=50°，∵AB=AC，∠A=50°，∴∠ACB=∠B==65°，∴∠DCB=∠ACB﹣∠ACD=15°．故答案为：15°．点评：此题考查了线段垂直平分线的性质与等腰三角形的性质．此题比较简单，注意数形结合思想的应用．18．（2009•临沂）如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB=72度．考点：线段垂直平分线的性质；菱形的性质．专题：计算题．分析：欲求∠CPB，可根据菱形、线段垂直平分线的性质、对称等方面去寻求解答方法．解答：解：先连接AP，由四边形ABCD是菱形，∠ADC=72°，可得∠BAD=180°﹣72°=108°，根据菱形对角线平分对角可得：∠ADB=∠ADC=×72°=36°，∠ABD=∠ADB=36度．EP是AD的垂直平分线，由垂直平分线的对称性可得∠DAP=∠ADB=36°，∴∠PAB=∠DAB﹣∠DAP=108°﹣36°=72度．在△BAP中，∠APB=180°﹣∠BAP﹣∠ABP=180°﹣72°﹣36°=72度．由菱形对角线的对称性可得∠CPB=∠APB=72度．点评：本题开放性较强，解法有多种，可以从菱形、线段垂直平分线的性质、对称等方面去寻求解答方法，在这些方法中，最容易理解和表达的应为对称法，这也应该是本题考查的目的．灵活应用菱形、垂直平分线的对称性，可使解题过程更为简便快捷．三．解答题（共12小题）19．（2014•翔安区质检）如图，已知DE是AC的垂直平分线，AB=10cm，BC=11cm，求△ABD的周长．考点：线段垂直平分线的性质．分析：先根据线段垂直平分线的性质得出AD=CD，故可得出BD+AD=BD+CD=BC，进而可得出结论．解答：解：∵DE垂直平分，∴AD=CD，∴BD+AD=BD+CD=BC=11cm，又∵AB=10cm，∴△ABD的周长=AB+BC=10+11=21（cm）．点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．20．（2014•长春模拟）如图，D为△ABC边BC延长线上一点，且CD=CA，E是AD的中点，CF平分∠ACB交AB于点F．求证：CE⊥CF．考点：等腰三角形的性质．专题：证明题．分析：根据三线合一定理证明CF平分∠ACB，然后根据CF平分∠ACB，根据邻补角的定义即可证得．解答：证明：∵CD=CA，E是AD的中点，∴∠ACE=∠DCE．∵CF平分∠ACB，∴∠ACF=∠BCF．∵∠ACE+∠DCE+∠ACF+∠BCF=180°，∴∠ACE+∠ACF=90°．即∠ECF=90°．∴CE⊥CF．点评：本题考查了等腰三角形的性质，顶角的平分线、底边上的中线和高线、三线合一．21．（2014•顺义区一模）如图，在四边形ABCD中，∠B=∠D=90°，∠C=60°，BC=4，CD=3，求AB的长．考点：含30度角的直角三角形；相似三角形的判定与性质．专题：计算题．分析：延长DA，CB，交于点E，可得出三角形ABE与三角形CDE相似，由相似得比例，设AB=x，利用30角所对的直角边等于斜边的一半得到AE=2x，利用勾股定理表示出BE，由BC+BE表示出CE，在直角三角形DCE中，利用30度角所对的直角边等于斜边的一半得到2DC=CE，即可求出AB的长．解答：解：延长DA，CB，交于点E，∵∠E=∠E，∠ANE=∠D=90°，∴△ABE∽△CDE，∴=，在Rt△ABE中，∠E=30°，设AB=x，则有AE=2x，根据勾股定理得：BE==x，∴CE=BC+BE=4+x，在Rt△DCE中，∠E=30°，∴CD=CE，即（4+x）=3，解得：x=，则AB=．点评：此题考查了相似三角形的判定与性质，含30度直角三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．22．（2013•湘西州）如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．考点：角平分线的性质；勾股定理．分析：（1）根据角平分线性质得出CD=DE，代入求出即可；（2）利用勾股定理求出AB的长，然后计算△ADB的面积．解答：解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=DE，∵CD=3，∴DE=3；（2）在Rt△ABC中，由勾股定理得：AB===10，∴△ADB的面积为S△ADB=AB•DE=×10×3=15．点评：本题考查了角平分线性质和勾股定理的运用，注意：角平分线上的点到角两边的距离相等．23．（2012•重庆模拟）如图，已知△ABC和△ABD均为直角三角形，其中∠ACB=∠ADB=90°，E为AB的中点，求证：CE=DE．考点：直角三角形斜边上的中线．专题：证明题．分析：由于AB是Rt△ABC和Rt△ABD的公共斜边，因此可以AB为媒介，再根据斜边上的中线等于斜边的一半来证CE=ED．解答：证明：在Rt△ABC中，∵E为斜边AB的中点，∴CE=AB．在Rt△ABD中，∵E为斜边AB的中点，∴DE=AB．∴CE=DE．点评：本题考查的是直角三角形的性质：在直角三角形中，斜边上的中线等于斜边的一半．24．（2010•攀枝花）如图所示，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD 于点F．点E是AB的中点，连接EF．（1）求证：EF∥BC；（2）若△ABD的面积是6，求四边形BDFE的面积．考点：等腰三角形的性质；三角形中位线定理；相似三角形的判定与性质．专题：几何综合题．分析：（1）在等腰△ACD中，CF是顶角∠ACD的平分线，根据等腰三角形三线合一的性质知F是底边AD的中点，由此可证得EF是△ABD的中位线，即可得到EF∥BC的结论；（2）易证得△AEF∽△ABD，根据两个相似三角形的面积比（即相似比的平方），可求出△ABD的面积，而四边形BDFE的面积为△ABD和△AEF的面积差，由此得解．解答：（1）证明：∵在△ACD中，DC=AC，CF平分∠ACD；∴AF=FD，即F是AD的中点；又∵E是AB的中点，∴EF是△ABD的中位线；∴EF∥BC；（2）解：由（1）易证得：△AEF∽△ABD；∴S△AEF：S△ABD=（AE：AB）2=1：4，∴S△ABD=4S△AEF=6，∴S△AEF=1.5．∴S四边形BDFE=S△ABD﹣S△AEF=6﹣1.5=4.5．点评：此题主要考查的是等腰三角形的性质、三角形中位线定理及相似三角形的判定和性质．25．（2009•大连二模）如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，CE⊥BD于点E．求证：AD=BE．考点：直角三角形全等的判定；全等三角形的性质．专题：证明题．分析：此题根据直角梯形的性质和CE⊥BD可以得到全等条件，证明△ABD≌△BCE，然后利用全等三角形的性质证明题目的结论．解答：证明：∵AD∥BC，∴∠ADB=∠DBC．∵CE⊥BD，∴∠BEC=90°．∵∠A=90°，∴∠A=∠BEC．∵BD=BC，∴△ABD≌△BCE．∴AD=BE．点评：本题考查了直角三角形全等的判定及性质；此题把全等三角形放在梯形的背景之下，利用全等三角形的性质与判定解决题目问题．26．（2007•宜宾）已知；如图，在△ABC中，AB=BC，∠ABC=90度．F为AB延长线上一点，点E在BC上，BE=BF，连接AE、EF和CF．（1）求证：AE=CF；（2）若∠CAE=30°，求∠EFC的度数．考点：等腰三角形的性质；全等三角形的判定与性质．专题：计算题；证明题．分析：根据已知利用SAS判定△ABE≌△CBF，由全等三角形的对应边相等就可得到AE=CF；根据已知利用角之间的关系可求得∠EFC的度数．解答：（1）证明：在△ABE和△CBF中，∵，∴△ABE≌△CBF（SAS）．∴AE=CF．（2）解：∵AB=BC，∠ABC=90°，∠CAE=30°，∴∠CAB=∠ACB=（180°﹣90°）=45°，∠EAB=45°﹣30°=15°．∵△ABE≌△CBF，∴∠EAB=∠FCB=15°．∵BE=BF，∠EBF=90°，∴∠BFE=∠FEB=45°．∴∠EFC=180°﹣90°﹣15°﹣45°=30°．点评：此题主要考查了全等三角形的判定方法及等腰三角形的性质等知识点的掌握情况；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．27．（2006•韶关）如图，在△ABC中，AB≠AC，∠BAC的外角平分线交直线BC于D，过D作DE⊥AB，DF⊥AC 分别交直线AB，AC于E，F，连接EF．（1）求证：EF⊥AD；（2）若DE∥AC，且DE=1，求AD的长．考点：角平分线的性质；全等三角形的判定与性质；线段垂直平分线的性质．专题：几何综合题；压轴题．分析：（1）根据AD是∠EAF的平分线，那么DE=DF，如果证得EA=FA，那么我们就能得出AD是EF的垂直平分线，那么就证得EF⊥AD了．因此证明EA=FA是问题的关键，那么就要先证得三角形AED和AFD全等．这两个三角形中已知的条件有∠EAD=∠FAD，一条公共边，一组直角，因此两三角形全等，那么就可以得出EA=AF了．（2）要求AD的长，在直角三角形AED中，有了DE的值，如果知道了∠ADE或∠EAD的度数，那么就能求出AD了．如果DE∥AC，那么∠EAC=90°，∠EAD=45°，那么在直角三角形AED中就能求出AD的长了．解答：（1）证明：∵AD是∠EAF的平分线，∴∠EAD=∠DAF．∵DE⊥AE，DF⊥AF，∴∠DEA=∠DFA=90°又AD=AD，∴△DEA≌△DFA．∴EA=FA∵ED=FD，∴AD是EF的垂直平分线．即AD⊥EF．（2）解：∵DE∥AC，∴∠DEA=∠FAE=90°．又∠DFA=90°，∴四边形EAFD是矩形．由（1）得EA=FA，∴四边形EAFD是正方形．∵DE=1，∴AD=．点评：本题考查了全等三角形的判定，角平分线的性质，线段垂直平分线的性质等知识点．本题中利用全等三角形得出线段相等是解题的关键．。
北师大版数学八下三角形的证明练习题含答案
北师大版数学八年级下册第一章三角形的证明1.1.等腰三角形的性质同步课时练习题1．如图，下列条件中，不能证明△ABC≌△DCB的是( )A．AB＝DC，AC＝DBB．AB＝DC，∠ABC＝∠DCBC．BO＝CO，∠A＝∠DD．AB＝DC，∠DBC＝∠ACB2．如图，△ABC≌△DEF，BE＝4，AE＝1，则DE的长是( )A．5 B．4 C．3 D．23. 如图，在△ABC中，AB＝AD＝DC，∠B＝70°，则∠C的度数为( )A．35° B．40° C．45° D．50°4. 如图，在等腰△ABC中，AB＝AC，BD⊥AC，∠ABC＝72°，则∠ABD等于( )A．36° B．54° C．18° D．64°5. 如图，在△ABC中，AB＝AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E＝35°，则∠BAC等于( )A．40° B．45° C．60° D．70°6. 如图，在△ABC中，AB＝AC，AD平分∠BAC，则下列结论错误的是( )A．∠B＝∠C B．AD⊥BCC．∠BAD＝∠CAD＝∠C D．BD＝CD7. 如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠C的度数为( )A．35° B．45° C．55° D．60°8. 如图，在△PAB中，PA＝PB，M，N，K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK，若∠MKN＝44°，则∠P的度数为( )A．44° B．66° C．88° D．92°9. 如图，在△ABC中，AD⊥BC，垂足为D，AD＝BD＝CD，则下列结论错误的是( )A．AB＝AC B．AD平分∠BAC C．AB＝BC D．∠BAC＝90°10. 如图，在△ABC中，D为AB上一点，E为BC上一点，且AC＝CD＝BD＝BE，∠A＝50°，则∠CDE的度数为( )A．50° B．51° C．51.5° D．52.5°11. 如图，在△ABC中，∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝____．12. 如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D.(1)若∠BAC＝80°，则∠BAD＝____；(2)若AB＋CD＝12 cm，则△ABC的周长为____ cm.13. 如图，点D，E在△ABC的边BC上，AB＝AC，BD＝CE. 求证：AD＝AE.14. 如图，在△ABC中，AB＝AC，AD平分∠BAC，点M，N分别在边AB，AC上，AM＝2MB，AN＝2NC，求证：DM＝DN.15. 如图，在△ABC中，AB＝AC，AD⊥BC，CE⊥AB.AE＝CE，求证：(1)△AEF≌△CEB；(2)AF＝2CD.16. 如图，AB＝AE，BC＝DE，∠B＝∠E，点F是CD的中点．求证：AF⊥CD.1.1参考答案：1---10 DAABA CCDCD 11. 312. (1) 40° (2) 2413. 证明：∵AB ＝AC ，∴∠B ＝∠C ，在△ABD 和△ACE 中，AB ＝AC ，∠B ＝∠C ，BD ＝CE ，∴△ABD ≌△ACE (SAS )，∴AD ＝AE14. 证明：∵AM ＝2MB ，AN ＝2NC ，∴AM ＝23AB ，AN ＝23AC.又∵AB ＝AC ，∴AM ＝AN.∵AD 平分∠BAC ，∴∠BAD ＝∠CAD. 在△AMD 和△AND 中，AM ＝AN ，∠MAD ＝∠NAD ，AD ＝AD ， ∴△AMD ≌△AND (SAS )，∴DM ＝DN15. 解：(1)∵AD ⊥BC ，CE ⊥AB ，∴∠DFC ＋∠DCF ＝90°，∠B ＋∠DCF ＝90°，∴∠B ＝∠DFC ，又∵∠DFC ＝∠EFA ，∴∠B ＝∠EFA.在△AEF 和△CEB 中，∠EFA ＝∠B ，∠FEA ＝∠BEC ＝90°，AE ＝CE ，∴△AEF ≌△CEB (AAS )(2)∵△AEF ≌△CEB ，∴AF ＝BC.∵AB ＝AC ，AD ⊥BC ，∴BD ＝CD ，∴BC ＝2CD ，∴AF ＝2CD16. 证明：连接AC ，AD ，在△ABC 和△AED 中，AB ＝AE ， ∠B ＝∠E ，BC ＝ED ，∴△ABC ≌△AED (SAS )， ∴AC ＝AD.又∵点F 是CD 的中点，∴AF ⊥CD1.2 直角三角形同步练习题1．如图，在平行线a、b之间放置一块直角三角板，三角板的顶点A、B分别在直线a、b上，则∠1＋∠2的值为()A．90° B．85°C．80° D．60°2．如图，直线AB∥CD，∠B＝50°，∠C＝40°，则∠E等于()A．70° B．80°C．90° D．100°3．下列四组线段中，能组成直角三角形的是()A．a＝1，b＝2，c＝3 B．a＝2，b＝3，c＝4 C．a＝2，b＝4，c＝5 D．a＝3，b＝4，c＝5 4．由下列条件不能判定△ABC是直角三角形的是()A．∠A＝37°，∠C＝53°B．∠A－∠C＝∠BC．∠A∶∠B∶∠C＝3∶4∶5D．∠A∶∠B∶∠C＝2∶3∶55．下列说法中，正确的是()A．每个命题都有逆命题B．每个定理都有逆定题C．真命题的逆命题是真命题D．假命题的逆命题是假命题6．如图，△ABC中，AB＝AC，AD是∠BAC的平分线，已知AB＝5，AD＝3，则BC 的长为()A ．5B ．6C ．8D ．107．如图，一艘轮船位于灯塔P 的北偏东60°方向，与灯塔P 的距离为30海里的A 处，轮船沿正南方向航行一段时间后，到达位于灯塔P 的南偏东30°方向上的B 处，则此时轮船所在位置B 处与灯塔P 之间的距离为( )A ．60海里B ．45海里C ．203海里D ．303海里8．如图，Rt △ABC 中，AB ＝9，BC ＝6，∠B ＝90°，将△ABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，则线段BN 的长为( )A.53B.52 C ．4D ．59．下列命题中，其逆命题成立的是 (只填写序号)①同旁内角互补，两直线平行；②如果两个角是直角，那么它们相等；③如果两个实数相等，那么它们的平方相等；④如果三角形的三边长a 、b 、c (c 为最长边)满足a 2＋b 2＝c 2，那么这个三角形是直角三角形．10．已知c －10＋|a －6|＋(b －8)2＝0，则以a 、b 、c 为三边的三角形是 .11．在△ABC 中，AB ＝13cm ，AC ＝20cm ，BC 边上的高为12cm ，则△ABC 的面积为 cm 2.12．如图所示，某公路一侧有A 、B 两个送奶站，C 为公路上一供奶站，CA 和CB 为供奶路线，现已测得AC ＝8km ，BC ＝15km ，AB ＝17km ，∠1＝30°，若有一人从C 处出发，沿公路边向右行走，速度为2.5km/h ，问：多长时间后这个人距B 送奶站最近？13．如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．14．如图所示，在等腰直角三角形ABC中，∠ABC＝90°，D为AC边上的中点，过D点作DE⊥DF，交AB于E，交BC于F.若AE＝4，FC＝3.求EF长．1.2答案：1---8 ACDCA CDC 9. ①④ 10. 直角三角形 11. 126或6612. 解：过B 作BD ⊥CD 于D ，在△ABC 中，AC ＝8，BC ＝15，AB ＝17，∴AC 2＋BC 2＝AB 2，∴△ABC 为直角三角形，∵∠1＝30°，∴∠BCD ＝60°，∴∠CBD ＝30°，∴CD ＝12BC ＝7.5km ，∴时间为7.5÷2.5＝3h.13. 解：连接AC .∵∠B ＝90°，∴AC ＝AB 2＋BC 2＝32＋42＝5，在△ACD 中，AC 2＋CD 2＝52＋122＝169.AD 2＝132＝169，∴AC 2＋CD 2＝AD 2，∴∠ACD ＝90°，∴S四边形ABCD ＝S △ABC ＋S △ACD ＝12AB ·BC ＋12AC ·CD ＝12×3×4＋12×5×12＝36.14. 解：连接BD .∵△ABC 是等腰直角三角形，D 是AC 边上的中点，∴∠A ＝∠ABD ＝∠CBD ＝45°，∴AD ＝BD ，∵AD ＝DC ，∴BD ⊥AC ，∴∠ADB ＝90°，∵DE ⊥DF ，∴∠EDF ＝∠ADB ＝90°，∴∠ADE ＝∠BDF ，∴△ADE ≌△BDF ，∴AE ＝BF ＝4，同理BE ＝CF ＝3，在Rt △BEF 中，EF ＝BE 2＋BF 2＝5.1．3 线段的垂直平分线同步训练题1．如图，已知线段a、h，作等腰△ABC，使AB＝AC，且BC＝a，BC边上的高AD ＝h.张红的作法是：①作线段BC＝a；②作线段BC的垂直平分线MN，MN与BC 相交于点D；③在直线MN上截取线段h；④连接AB、AC，则△ABC为所求的等腰三角形．上述作法的四个步骤中，你认为有错误的一步是()A．①B．②C．③D．④2．如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC 于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为()A．4cm B．3cmC．2cm D．1cm3．如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是.4．如图，在锐角三角形ABC中，∠BAC＝60°，边AC、AB的垂直平分线交于点O，交AC、AB于点D、E，则∠BOC等于.5．在△ABC中，AB＝AC，AB的垂直平分线与AC所在的直线相交所得到的锐角为50°，则∠B等于.6．如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在()A．在AC、BC两边高线的交点处B．在AC、BC两边中线的交点处C．在∠A、∠B两内角平分线的交点处D．在AC、BC两边垂直平分线的交点处7．如图，点D在BC上，DE⊥AB，DF⊥AC，垂足分别为E、F，DE＝DF.求证：AD 垂直平分EF.8．如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．9．如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F.若BF＝3cm.求BC.10. 如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.求∠ECD的度数；11．线段垂直平分线上的点到这条线段两个端点的距离.12．如图，已知线段AB.(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹，不要求写作法)；(2)在(1)中所作的直线l上任意取的两点M、N(在线段AB的上方)，连接AM、AN、BM、BN.求证：∠MAN＝∠MBN.答案:1. C2. C3. 50°4. 120°5. 70°或20°6. D7. 证明：∵DE ⊥AB ，DF ⊥AC ，∴∠AED ＝∠AFD ＝90°，∵DE ＝DF ，AD ＝AD ，∴Rt △AED ≌Rt △AFD ，∴AE ＝AF ，∴AD 垂直平分EF.8. 证明：∵E 是BD 垂直平分线上一点，∴EB ＝ED ，∴∠B ＝∠D ，∵∠ACB ＝90°，∴∠A ＝90°－∠B ，∠CFD ＝90°－∠D ，∵∠B ＝∠D ，∴∠CFD ＝∠A ，∵∠AFE ＝∠CFD ，∴∠AFE ＝∠A ，∴EF ＝EA ，∴点E 在AF 的垂直平分线上． 9. 解：连接AF ，∵AB ＝AC ，∠BAC ＝120°，∴∠B ＝∠C ＝30°，∵EF 垂直平分AB ，∴BF ＝AF ，∴∠B ＝∠BAF ＝30°，∴∠CAF ＝∠BAC －∠BAF ＝120°－30°＝90°，在Rt △ACF 中，∠C ＝30°，∴AF ＝12CF ，∴CF ＝2AF ，∵AF ＝BF ，∴CF＝2BF.∴BC ＝3BF ＝3×3＝9(cm)． 10. 解：∠ECD ＝36° 11. 相等12. 解：(1)画图略 (2)∵点M 、N 在线段AB 的垂直平分线上，∴MA ＝MB ，NA ＝NB ，∴∠MAB ＝∠MBA ，∠NAB ＝∠NBA ，∴∠MAB －∠NAB ＝∠MBA －∠NBA ，∴∠MAN ＝∠MBN.1.４角平分线同步测试题1. 如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA ＝2，则PQ的最小值为( )A．1 B．2 C．3 D．42．如图，在△ABC中，∠C＝90°，∠B＝30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE＝1，则BC等于( )A. 3 B．2 C．3 D.3＋23．如图，AB∥CD，O为∠BAC，∠ACD的平分线的交点，OE⊥AC，垂足为E，若OE＝2 cm，则AB与CD间的距离为( )A．2 cm B．3 cm C．4 cm D．5 cm4. 如图，AB∥CD，AD⊥DC，AE⊥BC，垂足分别为D，E，∠DAC＝35°，AD＝AE，则∠B等于( )A．50° B．60° C．70° D．80°5. 如图，△ABC是等边三角形，P是∠ABC的平分线上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q.若BF＝2，则PE的长为( )A．2 B．2 3 C. 3 D．36．在△ABC中，∠C＝90°，O为△ABC三条角平分线的交点，OD⊥BC于点D，OE⊥AC于点E，OF⊥AB于点F，且AB＝10 cm，BC＝8 cm，AC＝6 cm，则点O到三边AB，AC，BC的距离分别为( )A．2 cm，2 cm，2 cm B．3 cm，3 cm，3 cmC．4 cm，4 cm，4 cm D．2 cm，3 cm，5 cm7．如图，O为△ABC内任意一点，OD⊥AB于点D，OE⊥AC于点E，OF⊥BC于点F，若OD＝OE＝OF，连接OA，OB，OC，下列结论不一定正确的是( )A．△BOD≌△BOF B．∠OAD＝∠OBF C．∠COE＝∠COF D．AD＝AE 8．如图，在△ABC中，∠C＝90°，∠B＝30°，DE垂直平分AB，交BC于点D，垂足为E.则下列结论错误的是( )A．DE＋BD＝BC B．BD＝2CD C．BE＋DE＝BC D．BE＋AC＝AB 9．如图，在△ABC中，∠B，∠C的平分线交于点O，OD⊥AB于点D，OE⊥AC于点E，则OD与OE的大小关系是( )A．OD＞OE B．OD＝OE C．OD＜OE D．无法确定10. 在Rt△ABC中，∠C＝90°，若BC＝10，AD平分∠BAC交BC于点D，且BD∶CD ＝3∶2，则点D到线段AB的距离为____．11. 如图，在△ABC中，∠BAC＝60°，点D在BC上，DE⊥AB于点E，DF⊥AC 于点F，且DE＝DF，若DE＝4，则AD＝____．12．如图，已知DB⊥AN于点B，交AE于点O，OC⊥AM于点C，且OB＝OC，若∠EAN ＝25°，则∠ADB＝____．13. 如图，在△ABC中，∠ABC＝120°，∠C＝26°，且DE⊥AB，DF⊥AC，DE＝DF，则∠ADC的度数为____．14. 如图，BO，CO分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3.若△ABC 的周长是22，则△ABC的面积是____．15. 如图，AB＝AC，PB＝PC，PD⊥AB，PE⊥AC，垂足分别是D，E.求证：PD＝PE.16. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB ＝4，求AC的长．1.4参考答案：1---9 BCCCC ABCB10. 411. 812. 40°13. 137°14. 3315. 证明：连接AP，∵AB＝AC，PB＝PC，AP＝AP，∴△ABP≌△ACP(SSS)，∴∠BAP＝∠CAP，又∵PD⊥AB，PE⊥AC，∴PD＝PE(角平分线上的点到这个角的两边的距离相等)16. 解：过点D作DF⊥AC，∵AD是∠BAC平分线，DE⊥AB，∴DF＝DE＝2，∵S△ABD＝4×22＝4，∴S△ACD＝7－4＝3，∴2AC2＝3，即AC＝3。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.1 等腰三角形1、将下面证明中每一步的理由写在括号内：已知：如图，AB＝CD，AD＝CB．求证：∠A＝∠C．证明：连接BD．在△BAD和△DCB中，∵AB＝CD( )AD＝CB( )BD＝DB( )∴△BAD≌△DCB( )∴∠A＝∠C( )2、已知：如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．3、如图，在△ABC中，∠BAC=108°，AB=AC,AD⊥BC,垂足为D，求∠BAD的度数。
4、如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，点E是AD上一点，连接BE,CE,请找出图中所有相等的角。
5、如图，在△ABC中，AB=BC,点D,E都在BC上，且AD=AE,证明BD=CE.1、如图，在△ABC中，AB=AC,BD平分∠ABC,交AC于点D.若BD=BC,则∠A等于多少度？2、已知：如图，在△ABC中，AB=AC,D为BC中点，点E,F分别在AB和AC尚，并且AE=AF.求证：DE=DF3、已知：如图，D，E分别是等边三角形ABC的两边AB,AC上的点，且AD=CE。
求证：CD=BE4、如图，在一个风筝ABCD中，AB=AD,BC=DC⑴分别在AB,AD的中点E,F处拉两根彩线EC,FC.证明:这两根彩线的长度相等。
⑵如果AE=1/3AB,AF=1/3AD,那麼彩线的长度相等吗?如果AE=1/4AB,AF=1/4AD呢?由此你能得到什麼结论?1、已知：如图，∠CEA是△ABC的外角，AD平行BC，且∠1=∠2.求证：AB=AC.2、已知：如图，在△ABC中，AB=AC，点E在CA的延长线上，EP垂直于BC，垂足为P，EP交AB于点F。
求证：△AEF是等腰三角形。
3、如图，一艘船从A处出发，以18kn的速度向北航行，经过10h到处B处。
分别从A，B望灯塔C，测得∠NAC＝42°，∠NBC＝84°．求从B处到灯塔C 的距离．1、已知：如图，△ABC是等边三角形，与BC平行的直线分别交AB和AC于点D,E, 求证：△ADE是等边三角形。
2、屋梁的一部分如图所示，其中BC⊥AC，∠A＝30º，AB＝7.4m，点D是AB的中点，且DE⊥AC，垂足为E，求BC的长。
3、如图，△ABC是等边三角形，过它的三个顶点分别作对边的平行线，得到一个新的三角形DEF，△DEF是等边三角形吗？你还能找到其他的等边三角形吗？点A，B，C分别是EF，ED，FD的中点吗？请证明你的结论．（2）如果△DEF是等边三角形，点A，B，C分别是EF，ED，FD的中点，那么△ABC是等边三角形吗？请证明你的结论．4、证明：在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
5、如图，ABCD是一张长方形纸片，且AD=2AB，沿过点D的折痕将A角翻折，使得点A落在BC上（如图中的点A、），折痕交AB于点E，那么∠ADE等于多少度？你能证明你的结论吗？（利用第4题的结论）1、如图，在四边形ABCD中，AB平行CD，E为BC上的一点，且∠BAE=45°，2、一个直角三角形屋梁如图所示，其中BC⊥AC，∠A=30°，AB=10m， CB₁⊥AB, B₁C₁⊥AC,垂足分别为B₁,C₁,那么BC的长是多少？B₁C₁呢？3、小红想测量离A处30m的大树的高度，她站在A处仰望树顶B，仰角为30°（即∠BDE=30°），已知小红身高1.52m．求大树的高度．4、如图，正四棱柱的底面边长为5cm，侧棱长为8cm，一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面到顶点C′处吃食物. 那么它需要爬行的最短路程的长是多少？5、DE⊥AC已知：如图，点D是△ABC的BC边上的中点，DE⊥AC于E，DF⊥AB于F，且DE=DF．求证：△ABC是等腰三角形．6、已知：如图，AB=CD,DE⊥于AC，BF⊥AC，垂足分别为E、F,且DE=BF。
求证：（1）AE=CF;（2）AB⁄⁄CD.7、如图所示，把矩形ABC D沿对角线B D折叠，点C落在点F处，若AB＝12 c m，BC＝16c m．（1）求A E的长；（2）求重合部分的面积．8、如图所示，把矩形纸片ABC D沿EF折叠，使点B落在边A D上的点B′处，点A落在点A′处．（1）求证B′E＝B F；（2）设A E＝a，AB＝b，B F＝c，试猜想a，b，c之间的一种关系，并给出证明．3.1线段的垂直平分线1、如图，在△ABC中，AB=AC,∠BAC=120°，AB的垂直平分线交AB于点E，交BC于点F，连接AF，求∠AFC的度数。
2、如图，在△ABC中，已知AC=27，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长等于50，求BC的长。
3、如图，A、B表示两个仓库，要在A、B一侧的河岸边建造一个码头，使它到两个仓库的距离相等，码头应建在什么位置？你能画图说明吗？4、如图所示，在△ABC中，∠A＝90°，AC＝8 cm，AB＝6 cm，BC边的垂直平分线DE 交BC于E，交AC于D，求△ABD的周长．5、如图所示，∠BAC＝∠ABD，AC＝BD，点O是AD，BC的交点，点E是AB的中点．试判断OE和AB的位置关系，并给出证明．4.1角平分线1、已知，如图，OC是∠AOB的平分线,点P在OC上，PD⊥OA,PE⊥OB，垂足分别为D,E. 求证：PD=PE.2、已知：如图，OC是∠AOB的平分线，P是OC上的一点，PD⊥OA，PE⊥OB，垂足分别为D、E，点F是OC上的另一点，连接DF，EF．求证：DF=EF．3、如图，在△ABC中，∠BAC=60°，点D在BC上，AD=10，DE⊥AB，DF⊥AC,垂足分别为E和F，且DE=DF,求DE的长。
4、如图，在三角形ABC中，AC=BC，∠A=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E。
（1）已知CD=4cm，求AC的长；（2）求证AB=AC+CD5、如图，在Rt△ABC中，∠ACB=90°，∠B=60°，AD，CE是角平分线，AD与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为M，N．求证：FE=FD．6、已知：如图，∠C=90°，∠B=30°，AD是△ABC的角平分线。
求证：BD=2CD。
7、已知：如图，△ABC的外角∠CBD和∠BCE的平分线相较于点F.求证：点F在∠DAE的平分线上。
8、已知：如图，P是∠AOB平分线上的一点，PC垂直OA，PD垂直于OB，垂足分别为C，D,求证：（1）OC=OD（2）OP是CD的垂直平分线。
三角形证明单元总复习1、已知：如图，在三角形ABC中，AB=AC，点D，E分别在边AC，AB上，且三角形ABD=三角形ACE，BD与CE相交于点O。
求证：（1）OB=OC。
（2）BE=CD。
2、已知：如图，BD，CE是△ABC的高，且BD=CE。
求证：△ABC是等腰三角形。
3、在△ABC中，已知∠A,∠B,∠C的度数之比是1：2：3，AB=3，求AC的长。
4、已知：如图，AN⊥OB，BM⊥OA，垂足分别为N,M，OM=ON,BM与AN相交于点P,求证：PM=PN。
5、如图，在△ABC中，∠C=90°，∠A=30°，AB的垂直平分线分别交AB，AC于点D、E。
求证AE=2CE.6、如图，在四边形BCDE中，∠C=∠BED=90°，∠B=60°，延长CD，BE，两线交于点A，已知CD=2,DE=1,求Rt△ABC的面积。
7、如图，在三角形ABC中，∠B=64°，∠BAC=72°，D为BC上一点，DE交AC 于点F,且AB=AD=DE，连接AE,∠E=55°。
请判断△AFD的形状，并说明理由（证明）。
联系拓广8、如图，在△ABC中，AB=AC,AB的垂直平分线交AB于点D，交AC于点E。
已知△BCE的周长为8，AC-BC=2，求AB与BC的长。
《三角形的证明》课外巩固培优练习题1、如图，OC 是∠AOB 的平分线，P 是OC 上一点，PD ⊥OA 于D ，PE ⊥OB 于E ，F 是OC 上另一点，连接DF 、EF 。
求证：DF=EF2、如图，AF 平分∠BAC ，P 是AF 上任一点，过P 向AB 、AC 作垂线PD 、PE ，D 、E 分别为垂足，连结DE ， 求证：AF 垂直平分DE 。
3、如图，点D 是等边△ABC 边AB 上的一点，AB=3AD ，DE⊥BC 于点E ，AE 、CD 相交于点F ． （1）求证：△ACD≌△BAE；（2）请你过点C 作CG⊥AE，垂足为点G ，探究CF 与FG 之间的数量关系，并证明．4、如图，已知AB=AC ，BD=CD ，DE ⊥AB 于E ，DF ⊥AC 于F 。
求证：DE=DF5、如图，在△ABC 中，AD 为∠BAC 的平分线，FE 垂直平分AD ，E 为垂足，EF 交BC 的延长线于F ， A B C E P D F AD E CB求证：∠CAF ＝∠B6、如图，在Rt △ABC 中，∠C ＝90°E 为AB 的中点，且DE ⊥AB 于F ，∠CAD ︰∠BAD ＝1︰2， 试求∠B 和∠BAC 的度数。
7、如图，在△ABC 中，∠ACB ＝90°，D 是BC 延长线上一点，BD 的垂直平分线交AB 于P ，PD 交AC 于E ，求证：点P 也在AE 的垂直平分线上8、如图所示，已知AD//BC ，AE 平分∠DAB ，BE 平分∠ABC ，直线DC 过点E 交AD 于点D ，交BC 于点C ，求证：（1）E 为DC 的中点；（2）AD ＋BC=AB.2、如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，•求证：•BC=3AD.A C D EA B C PD E F3、 ABC ∆中，120A AC AB =∠=，，AB 的中垂线交AB 于D ，交CA 延长线于E ，求证：BC 21DE =。
5、在等边ΔABC 中，AE=CD ，BG ⊥AD ，求证：BP=2PG 。
6、已知：如图6，在△ABC 中，AD 是高，CE 是中线。
DC=BE ，DG ⊥CE ，G 为垂足。
求证：（1）G 是CE 的中点；（2）∠B=2∠BCE 。
7、如图7，在△ABC 中，∠C=2∠B ，D 是BC 上的一点，且AD ⊥AB ，点E 是BD 的中点，连AE 。
求证：（1）∠AEC=∠C ；（2）求证：BD=2AC 。
9、如图，在ABC ∆中，︒=∠90ACB ，︒=∠30CAB ，以AC 、AB 为边在ABC ∆外侧作等边ACD ∆和等边ABE ∆，连结DE 交AB 于F .求证：EFDF12、如图4，△ABC中，AD平分∠BAC，E、F分别在BD、AD上，且DE＝CD，EF＝AC．求证：EF∥AB．13、如图5，△ABC中，AB=AC，∠ABD=∠CBD，BD⊥DE于D，DE交BC于E，求证：CD=12 BE．14．如图2，在Rt△ABC中，∠C=900，AD∥BC，∠CBE=12∠ABE，求证：DE=2AB图4FCDEBAMBAD图5BA DCEF图2。