(完整版)第4章杆梁结构的有限元分析原理
合集下载
有限元分析基础(推荐完整)

图1-5 驾驶室受侧向力应力云图
图1-6 接触问题结构件应力云图
10
第一章 概述
图1-7 液压管路速度场分布云图
图1-8 磨片热应力云图
图1-9 支架自由振动云图
11
第二章 结构几何构造分析
2.1 结构几何构造的必要性 2.2 结构计算基本知识 2.3 结构几何构造分析的自由度与约束 2.4 自由度计算公式
(1)结点: ① 铰结点;② 刚结点;③ 混合结点。 (2)支座: ① 活动铰支座;② 固定铰支座 ;
③ 固定支座 ;④ 定向支座
15
第二章 结构几何构造分析
2.2.2 结构的分类与基本特征
(1) 按结构在空间的位置分 结构可分为平面结构和空间结构两大类
(2) 按结构元件的几何特征分 ① 杆系结构: 梁、拱、桁架、刚架、桁构结构等 。 ② 板壳结构 ③ 实体结构实体结构的长、宽、高三个尺寸都很 大,具有同一量级。 ④ 混合结构
d. 超静定结构中的多余约束破坏后,结构仍然保持 几何不变性,因而仍有一定的承载能力, 不致整个结构 遭受破坏。
e. 超静定结构由于具有多余的约束,因而比相应的 静定结构具有较大的刚度和稳定性, 在载荷作用下,内 力分布也较均匀,且内力峰值也较静定结构为小。
18
第二章 结构几何构造分析
2.2.3 结构对称性的利用
对称结构在正对称载荷下,对称轴截面上只能产生 正对称的位移,反对称的位移为零;对称结构在反对称 载荷下,对称轴截面上只有反对称的位移,正对称的位 移为零。 (1) 具有奇数跨的刚架
① 正对称载荷作用
(a) 对称刚架
(b) 变形状态分析
(c) 对称性利用
图2-22对称性利用示意图
19
[工学]第四章-杆单元和梁单元
![[工学]第四章-杆单元和梁单元](https://img.taocdn.com/s3/m/9641e3285bcfa1c7aa00b52acfc789eb172d9e36.png)
坐标系中,取杆单元的左端点为坐标原点,图4-2为任取的一
个杆单元。
P1, u1
P2 , u2
E,A,l
1
2
图 4-2 杆单元
对于两个节点的杆单元,存在如下节点力和节点位移的关系
式
P1 P2
k
e
u1 u2
(4.1)
其中, k称e 为单元刚度矩阵
4.1 杆件系统的有限元分析方法
(2)确定位移模式
6
2
4.2.1 平面悬臂梁问题的解析分析
将悬臂梁的右端受载荷W处的横坐标x=l代入以上两式,得 右端受载荷截面的转角和挠度分别为
B
v'B
WL2 2EI
fB
vB
WL3 3EI
(2)平面悬臂梁的弹性力学求解
(4.25)
末端受集中载荷作用的平面悬臂梁的位移场可以用以下多项
式表示
x方向:
u(x, y) Wy 6Lx 3x2 y2 6EI
对于图4.1所示结构
第一个单元:
δ(1)
uu12
K (1)
E(1) A(1) l (1)
1 1
1
1
P (1)
R1 R2
4.1 杆件系统的有限元分析方法
第二个单元:
δ(2)
uu23
K (2)
E(2) A(2) l (2)
1 1
1
1
P (2)
FR32
整体结构的总势能是所有单元的势能的和,即
4.1 杆件系统的有限元分析方法
杆件只承受轴向力,可以视为一种特殊的梁单元,本节将采 用有限元法来分析杆件系统,以下给出规范的有限元法中关于杆 单元的推导过程,以及整个杆系的求解过程。
第四讲结构力学有限元分析

z q x y
1/3
1/3
1/3
几何模型
有限元分析
微分方程描述: 板单元: 采用adini板单元,adini矩形板单元是基于经典薄板理论的板单元,其广义内力和广义应变的定义是
M x M M y M xy
其广义应力应变关系是: 其中:
M Dκ
y 2w 2 x x x 2w x κ y 2 y y xy y 2 w x 2 x y x y
d d du du d 2v d 2v d 2w d 2w 0 [ EA dx dx EI z dx2 dx2 EI y dx2 dx2 GI x dxx dxx ]dx
l
单元刚度矩阵对应 微分方程弱形式中 的左端项
单元载荷向量:
LOAD = +[u]*dfx +[v]*dfy +[w]*dfz +[v/x]*rmz +[w/x]*rmy +[anx]*rmx
如下图所示,空间1m*1m*0.02m的方板,y方向有两根加强梁,四边固支,板受向下的均布力q的 作用,板的材料参数为E=210GPa;v=0.3;thick=0.02m;q=-1000N;梁的材料参数为E=210GPa; v=0.3;A=7.5e-3m2;Ix=15.62e-6m4;Iy=14.06e-6m4;Iz=15.6e-7m4分析板的变形情况。
0 0 0 0 0
l
l
l
l
l
l dv dw dx m y ( x) dx 0 dx dx
梁结构ELAB1.0软件实现 工程建模
1/3
1/3
1/3
几何模型
有限元分析
微分方程描述: 板单元: 采用adini板单元,adini矩形板单元是基于经典薄板理论的板单元,其广义内力和广义应变的定义是
M x M M y M xy
其广义应力应变关系是: 其中:
M Dκ
y 2w 2 x x x 2w x κ y 2 y y xy y 2 w x 2 x y x y
d d du du d 2v d 2v d 2w d 2w 0 [ EA dx dx EI z dx2 dx2 EI y dx2 dx2 GI x dxx dxx ]dx
l
单元刚度矩阵对应 微分方程弱形式中 的左端项
单元载荷向量:
LOAD = +[u]*dfx +[v]*dfy +[w]*dfz +[v/x]*rmz +[w/x]*rmy +[anx]*rmx
如下图所示,空间1m*1m*0.02m的方板,y方向有两根加强梁,四边固支,板受向下的均布力q的 作用,板的材料参数为E=210GPa;v=0.3;thick=0.02m;q=-1000N;梁的材料参数为E=210GPa; v=0.3;A=7.5e-3m2;Ix=15.62e-6m4;Iy=14.06e-6m4;Iz=15.6e-7m4分析板的变形情况。
0 0 0 0 0
l
l
l
l
l
l dv dw dx m y ( x) dx 0 dx dx
梁结构ELAB1.0软件实现 工程建模
杆梁结构的有限元分析原理

e
下面考察该简单问题的FEA求解过程。 (1) 离散化
两个杆单元,即:单元①和单元②
(2) 单元的特征及表达
对于二结点杆单元,设该单元的位移场为 么它的两个结点条件为
,那
设该单元的位移场具有模式(考虑两个待定系数)
利用结点条件,可以确定系数a0和a1,即
将系数a0和a1代入
,可将
表达成结点位移(u1, u2)的关系,即
其中, 为整体坐标系下的单元刚度矩阵, 为 整体坐标系下的结点力,即
由最小势能原理(针对该单元),将 对待定的 结点位移向量 取一阶极小值,有整体坐标系中 的刚度方程
对于本节给出的杆单元,具体有
4.3.3 空间问题中杆单元的坐标变换
就空间问题中杆单元,局部坐标系下的结点位移还 是 而整体坐标系中的结点位移为
这时由全部结点位移[0 u2 u3]分段所插值 出的位移场为全场许可位移场。
由最小势能原理(即针对未知位移u2和u3求 一阶导数),有
可解出
(5) 计算每个单元的应变及应力
在求得了所有的结点位移后,由几何方程
可求得各单元的应变
由方程 可求得各单元的应力
(6) 求结点1的支反力
就单元 ①的势能,对相应的结点位移求极值,可以 建立该单元的平衡方程,即
其中
由一维问题几何方程和物理方程,则该单元 的应变和应力为
其中
单元的势能
其中 叫做单元刚度矩阵。
叫做单元结点外载。
在得到“特征单元”的单元刚度矩阵和单元 结点外载后,就可以计算该单元的势能,因 此,计算各单元的矩阵 和 是一个关 键,下面就本题给出了个单元的 和 。
具体就单元①,有 单元①的结点位移向量
(5) 单元的刚度方程
杆梁结构的有限元法

l
[K]e l[B]T EA[B]dx 0
[K ]e
AE l
1 1
1
1
3-2 杆单元刚度矩阵
如图为只受扭转的杆单
y
元。同上分析,只需将
相应的变量和符号进行
xi
替换,可得扭力杆的刚
度矩阵:
M xi
xj
M xj
x
Fe Mix
T
M jx
假设杆只承受扭矩,只有绕轴线扭转变
M j , j
x
Fjy ,v j
F e Fiy
Mi
Fjy
T
M j
e vi
i
vj
T
j
1、位移函数
v 1 2x 3x2 4x3
据材料力学可知,转角与扰度存在如下关系:
dv dx
2
23x
3 4 x2
3-3 纯弯曲梁单元刚度矩阵
刚度矩阵为:
杆单元扩大刚度矩阵
K e K e K e
1
2
弯曲梁单元扩大刚度矩阵
1 0 0 1 0 0
0 0 0 0 0 0
0 0 0 0 0
12 6l
0 12
6l
=
EA l
0
0 1
0 0
0 0
EI z l3
4l2 0 6l 2l2
载荷突变点必须设置节点
3
1
2
截面变化点必须设置节点
4
5
3-2 杆单元刚度矩阵
由于杆梁问题有解析解,所以杆梁单元无需假设近似函数作为 位移函数,其刚度矩阵可直接按材料力学的基本公式,建立平 衡推得,如绪论介绍的实例所示。但为了统一有限元分析的格 式,这里仍按有限元的基本格式推导,其结果是相同的,亦即 杆梁单元的有限元解是精确解。
杆梁结构有限元分析
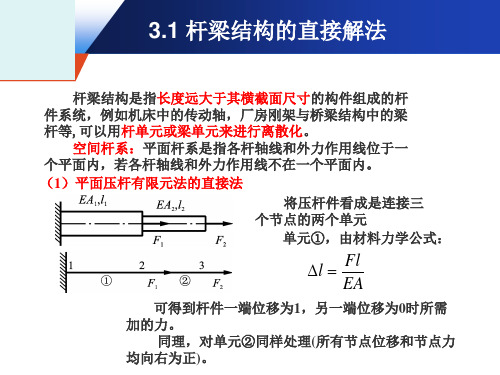
3.1 杆梁结构的直接解法
机械分社
(1)平面压杆有限元法的直接法
由节点平衡有: 即有:
U1(1)u1 U1(1)u2 N1
U
u (1)
21
(U
(2 2
)
U
(1) 2
)u2
U
(2 2
)u3
F1
U
(2 3
)
u2
U
(2 3
)
u3
F2
EA1 l1
u1
EA1 l1
u2
N1
EA1 l1
u1
( EA1 l1
3.1 杆梁结构的直接解法
机械分社
杆梁结构是指长度远大于其横截面尺寸的构件组成的杆 件系统,例如机床中的传动轴,厂房刚架与桥梁结构中的梁 杆等,可以用杆单元或梁单元来进行离散化。
空间杆系:平面杆系是指各杆轴线和外力作用线位于一 个平面内,若各杆轴线和外力作用线不在一个平面内。 (1)平面压杆有限元法的直接法
单元刚度矩阵每一列元素表示一组平衡力系,对于平面 问题,每列元素之和为零。
3.1 杆梁结构的直接解法
机械分社
(2)平面梁单元有限元法的直接法 2)节点位移与节点力之间的关系
Ui
Vi
k11
k21
M i U j
k31
k41
V
j
M j
k51
k61
他们在轴和轴的投影之和等于零:
vi
6EI l2
i
12EI l3
vj
6EI l2
j
M
j
6EI l2
vi
2EI l
i
6EI l2
vj
4EI l
杆梁结构的有限元分析原理

对剪切变形的影响
3.1 理论
只考虑剪切变形
变形后轴线切向与变形前轴角 γxz 其中 ψ (x) 为只考虑梁弯曲理论中的线性单元转角. 假设 : 截面上均匀分布剪应变
弯曲产生的位移:
9
内部力
其中假设
10
实际上τxz采用以下形式:
其中变量与z相关。 为了确定截面的不均匀剪应力分布,引入因素k修正剪应 力:
BEAM44 3-D Elastic Tapered Unsymmetric Beam This element allows a different unsymmetrical geometry at each end and permits the end nodes to be offset from the centroidal axis of the beam
除非ψ是常数(没有弯曲变形),否则, dw/dx-ψ不会为零。这种现象称为剪切闭锁。 shear-locking
17
几种方法避免产生剪切闭锁
减缩积分
数值积分采用比精确积分要求少的积分点数
假设剪切应变 替代插值函数
举例说明
18
19
Timoshenko 梁 (采用精确积分)
20
采用缩减积分
形成总体刚度矩阵
点坐标、约束条件等;
形成结点荷载向量
(3)单元数据:如单元编号、单 元结点序号、单元的材料特性、
引入约束条件
几何特性等;
求解方程组,输出结点位移
(4)载荷数据:包括集中载荷、 计算单元应力,输出结果 分布载荷等。
结束
37
2、单元分析
(1)各单元的bi,ci(i,j,m) , 面积A;
30
杆梁的有限元分析
(e)
由虚位移原理得: 由虚位移原理得:
[q *(e) ]T F (e) = ∫∫∫ ε *T σdV
V
将应力矩阵和应变矩阵带入上式得: 将应力矩阵和应变矩阵带入上式得:
[q *(e) ]T F (e) = ∫∫∫[q *(e) ]T [ B (e) ]T S (e) q (e) dV
V
[q *(e) ]T F (e) = [q *(e) ]T ( ∫∫∫[ B (e) ]T S (e) dV )q (e)
(1)
K=[K](1)+[K](2)
( 2)
k13 k 23 k33
1.2 杆系结构的有限元分析
(1) 杆 单 元 的 坐 标 变 化
θ
在工程实际中, 在工程实际中,杆单元可能处于整体坐标系中任意一个位 如图所示。 置,如图所示。这需要将原来在局部坐标系中所得到的单元表 达等价的变化到整体坐标系中, 达等价的变化到整体坐标系中,这样不同位置的单元才有公共 的坐标基准,以便对各个单元进行组集。 的坐标基准,以便对各个单元进行组集。
0 cos θ
下面推导整体坐标系下的刚度方程。 下面推导整体坐标系下的刚度方程。其表达式同前面一维 的表述,将位移、力表述为整体坐标系下的形式, 的表述,将位移、力表述为整体坐标系下的形式,有
A( e ) E ( e ) L( e )
(e) (e) 1 − 1 δ i Fi − 1 1 δ ( e ) = F ( e ) j j
− 2 u2 0 4 6 10 = 10 × − 2 2 u 3 u2 = 0.2 × 10 −3 m, u3 = 0.75 ×10 −3 m
求节点1的支反力: 求节点 的支反力: 的支反力 由单元1的方程,代入节点 、 的位移 的位移, 由单元 的方程,代入节点1、2的位移, 的方程
由虚位移原理得: 由虚位移原理得:
[q *(e) ]T F (e) = ∫∫∫ ε *T σdV
V
将应力矩阵和应变矩阵带入上式得: 将应力矩阵和应变矩阵带入上式得:
[q *(e) ]T F (e) = ∫∫∫[q *(e) ]T [ B (e) ]T S (e) q (e) dV
V
[q *(e) ]T F (e) = [q *(e) ]T ( ∫∫∫[ B (e) ]T S (e) dV )q (e)
(1)
K=[K](1)+[K](2)
( 2)
k13 k 23 k33
1.2 杆系结构的有限元分析
(1) 杆 单 元 的 坐 标 变 化
θ
在工程实际中, 在工程实际中,杆单元可能处于整体坐标系中任意一个位 如图所示。 置,如图所示。这需要将原来在局部坐标系中所得到的单元表 达等价的变化到整体坐标系中, 达等价的变化到整体坐标系中,这样不同位置的单元才有公共 的坐标基准,以便对各个单元进行组集。 的坐标基准,以便对各个单元进行组集。
0 cos θ
下面推导整体坐标系下的刚度方程。 下面推导整体坐标系下的刚度方程。其表达式同前面一维 的表述,将位移、力表述为整体坐标系下的形式, 的表述,将位移、力表述为整体坐标系下的形式,有
A( e ) E ( e ) L( e )
(e) (e) 1 − 1 δ i Fi − 1 1 δ ( e ) = F ( e ) j j
− 2 u2 0 4 6 10 = 10 × − 2 2 u 3 u2 = 0.2 × 10 −3 m, u3 = 0.75 ×10 −3 m
求节点1的支反力: 求节点 的支反力: 的支反力 由单元1的方程,代入节点 、 的位移 的位移, 由单元 的方程,代入节点1、2的位移, 的方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
讨论2:由前面的步骤,我们也可以直接将各个单元的刚 度矩阵按照节点编号的对应位置来进行装配,即在未处理边 界条件之前,先形成整体刚度矩阵。
Kq P
其物理意义是,表示在未处理边界条件前的基于节点描述 的总体平衡关系。在对该方程进行位移边界条件的处理后就 可以求解,这样与先处理边界条件再求系统势能的最小值所 获得的方程完全相同。
1 qeT BT EBqe Aele
2
P1u1 P2u2
写成矩阵形式为
e 1 qeT BT EBqe Aele
2
P1u1 P2u2
1 2
u1
u2
1 le
1
1
EAel e
1 le
1
1
u1 u2
P1
P2
u1 u2
1 2
u1
EAe
u2
le EAe
le
EAe
le
基本变量为:
节点 位移
(1)
内部各
点位移
(2)
(3)
应变
应力
完整的求解过程
1)离散化 该构件由两根杆件做成,因此可以自然离散成2个杆单元。
假定以这类单元位移的特征为两个端点位移,就这两个离散 单元给出节点编号和单元编号。
单元1:i=1,j=2 单元2:i=2,j=3
2)单元分析
单元位移模式:u(x)=a0+a1x
1 2
u1
EA1
u2
l1 EA1
l1
EA1
l1
EA1
u1 u2
R1
l1
0
u1 u2
1 2
u2
EA2
u3
l2 EA2
l2
EA2
l2
EA2
u2 u3
0
l 2
1 2
u1
u2
EA1
l1
u3
EA1 l1
0
EA1 l1
EA1 l1
EA2 l2
EA2 l2
E le
1
1
ui u j
简记为 Sqe 应力矩阵或者是应力转换矩阵
势能的表达
e U e W e
1 2
e ij ij d
P1u1 P2u2
1 2
le 0
Bq e
T
Sqe
Aedx
P1u1
P2u2
1 2
le qeT BT EBqe Aedx
0
P1u1 P2u2
1 2
u2
u3
EA1
l1
EA2 l2
EA2 l2
EA2 l2
EA2
u2 u3
0
l 2
F3
u2 u3
5)建立刚度方程
由于上式是基于许可位移场的表达的系统势能,这是由全
部节点位移分段所插值出的位移场为全场许位移场,且基本
未知量为节点位移,根据最小势能原理(即针对未知位移求
一阶导数)有
本章主要内容
4.1有限元分析的完整过程 4.2有限元分析的基本步骤及表达式 4.3杆单元及其坐标变换 4.4梁单元及其坐标变换
4.1有限元分析的完整过程
E1=E2=2E7Pa A1=A2=2cm2 l1=l2=10cm
P3为10N作用下二杆结构的变形。
问题的解题思路: 1)用标准化的分段小单元来逼近原结构 2)寻找能够满足位移边界条件的许可位移场 3)基于位移场的最小势能原理来求解
单元节点条件:u(0)=u1, u(1)=u2
从而得:
a0 ui ,
a1
uj
ui le
i
1,
j
2
回代得
u(x) a0 a1x
ui
u j ui le
x
1
x le
ui
x le
u
j
Niui N ju j
写成矩阵形式为
q Niu Nqe
N
ju
ui u j
形函数矩阵
其中Ni,Nj是形函数。
可得支反力大小。
以上是一个简单结构有限元方法求解得完整过程,对于 复杂结构,其求解过程完全相同,由于每一个步骤都具备 标准化和规范性的特征,所以可以在计算机上编程而自动 实现。
讨论1:对于一个单元的势能取极值,所得到的方程为 节点的位移和节点力之间的关系,也称为单元的平衡关系, 由此可以求出每一个单元所受的节点力。
第4章 杆系结构的有限元分析原理
杆梁单元概述
讨论杆梁单元和由它们组成的平面和空间杆梁结构系统. 从构造上来说其长度远大于其截面尺寸的一维构件 承受轴力或扭矩的杆件称为杆 杆梁问题都有精确解 承受横向力和弯矩的杆件称为梁 平面桁架 平面刚架 连续梁 空间刚架 空间桁架等 变截面杆和弯曲杆件
EA1 EA2
l1
l2
EA2
l2
EA2
l2
EA2
u2 u3
0
F3
l2
6)求解节点位移
将结构参数和外载荷代入上式有
3EA2
l2
EA2 l2
EA2 l2
EA2
u2 u3
0
F3
l2
2E4
3 1
1
1
u2 u3
0 10
求解得(单位m)
u2 u3
2.5E 7.5E
根据几何方程可得应变的表达
x
du dx
a1
1 le
u j ui
写成矩阵形式为
Niu
N
ju
ui u j
1 le
1
1
ui u j
简记为 Bqe
几何函数矩阵或者是应变转换矩阵
根据物理方程可得应力的表达
x
E
du dx
E le
u j ui
写成矩阵形式为
E Niu
N
ju
ui u j
N
ju
2
ui u j
2
E l2
1
1
uu32
0.1Mpa
9)计算支反力
对于单元势能的表达,对其取极值有
K eqe Pe
具体地对于单元1,有
EA1 1 l1 1
1
1
u1 u2
R1
ห้องสมุดไป่ตู้
P2
其中R1是节点1的支反力,P2是单元1的节点2所受的力,即
单元2对该节点的作用力,将前面求得的节点位移代入上式
EAe
u1 u2
P1
le
P2
u1 u2
1 qeTK eqe PeTqe 2
刚度矩阵
节点力列阵
3)离散单元的装配
在得到各个单元的势能表达式后,需要进行离散单元的装配,以求 出整个系统的总势能,对于该系统,总势能包括两个单元部分
e 1 2
1 q1T K1q1 q2T K 2q2 P1Tq1 P2Tq2 2
4 4
7)计算单元应变
1 Niu
N
ju
ui u j
1
1 l1
1
1
u1 u2
2.5E 3
2 Niu
N
ju
2
ui u j
2
1 l2
1
1
uu32
5E 3
8)计算单元应力
1 E Niu
N
ju
ui u j
1
E l1
1
1
uu12
0.05Mpa
2 E Niu
0
EA2 l2
EA2
u1 u2 u3
R1
0
u1
F3
u2
u3
l2
F3
u2 u3
4)边界条件的处理
处理边界条件是获取可能位移场,将左端的约束条件,
即u1=0代入上式可以得到简化的势能表达式
e 1 2
1 q1T K1q1 q2T K 2q2 P1Tq1 P2Tq2 2
