三元一次方程组及应用
人教版七年级数学下册三元一次方程组(提高) 典型例题(考点)讲解+练习(含答案).doc

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】三元一次方程组(提高)知识讲解责编:杜少波【学习目标】1.理解三元一次方程(或组)的含义;2.会解简单的三元一次方程组;3. 会列三元一次方程组解决有关实际问题.【要点梳理】要点一、三元一次方程及三元一次方程组的概念1.三元一次方程的定义:含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1,2a-3b+4c=5等都是三元一次方程.要点诠释:(1)三元一次方程的条件:①是整式方程,②含有三个未知数,③含未知数的项的最高次数是1次.(2) 三元一次方程的一般形式:ax+by+cz+d=0,其中a、b、c不为零.2.三元一次方程组的定义:一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组. 要点诠释:(1) 三个方程中不一定每一个方程中都含有三个未知数,只要三个方程共含有三个未知量即可.(2)在实际问题中含有三个未知数,当这三个未知数同时满足三个相等关系时,可以建立三元一次方程组求解.要点二、三元一次方程组的解法解三元一次方程组的一般步骤(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;(2)解这个二元一次方程组,求出两个未知数的值;(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;(4)解这个一元一次方程,求出最后一个未知数的值;(5)将求得的三个未知数的值用“{”合写在一起.要点诠释:(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”.使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.其思想方法是:(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.要点三、三元一次方程组的应用列三元一次方程组解应用题的一般步骤:1.弄清题意和题目中的数量关系,用字母(如x,y,z)表示题目中的两个(或三个)未知数;2.找出能够表达应用题全部含义的相等关系;3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;4.解这个方程组,求出未知数的值;5.写出答案(包括单位名称).要点诠释:(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.(3)一般来说,设几个未知数,就应列出几个方程并组成方程组.【典型例题】类型一、三元一次方程及三元一次方程组的概念1.下列方程组不是三元一次方程组的是().A.12236x yy zy+=⎧⎪+=-⎨⎪=⎩B.24013xy xxy z⎧-=⎪+=⎨⎪-=-⎩C.2231xyx z=⎧⎪=-⎨⎪-=⎩D.1321y xx zy z-=-⎧⎪+=⎨⎪-=⎩【思路点拨】根据三元一次方程组的定义来求解,对A、B、C、D四个选项进行一一验证.【答案】B【解析】解:由题意知,含有三个相同的未知数,每个方程中含未知数的项的次数都是1次,并且一共有三个方程,叫做三元一次方程组.A、满足三元一次方程组的定义,故A选项错误;B、x2-4=0,未知量x的次数为2次,∴不是三元一次方程,故B选项正确;C、满足三元一次方程组的定义,故C选项错误;D、满足三元一次方程组的定义,故D选项错误;故选B.【总结升华】三元一次方程组中的方程不一定都是三元一次方程,并且有时需对方程化简后再根据三元一次方程组的定义进行判断.类型二、三元一次方程组的解法2. (2015春•苏州校级期末)若x:y:z=2:7:5,x﹣2y+3z=6,求的值.【思路点拨】根据x:y:z=2:7:5,设x=2k,y=7k,z=5k,代入x﹣2y+3z=6得出方程,求出方程的解,即可求出x、y、z的值,最后代入求出即可.【答案与解析】解:∵x:y:z=2:7:5,∴设x=2k,y=7k,z=5k,代入x﹣2y+3z=6得:2k﹣14k+15k=6,解得:k=2,∴x=4,y=14,z=10,∴==0.18.【总结升华】若某一方程是比例形式,则先引入参数,后消元. 举一反三:【变式】解方程组:2:3,:4:5,2329x y y z x y z =⎧⎪=⎨⎪-+=⎩①②③【答案】解:由①,得3x =2y ,即23x y =, ④ 由②,得5y =4z ,即54z y =,⑤把④、⑤代入③,得21522934y y y -+=.解得y =12.⑥把⑥代入④,得x =8,把⑥代入⑤,得z =15.所以原方程组的解为8,12,15.x y z =⎧⎪=⎨⎪=⎩【:三元一次方程组 409145 例3】3.已知方程组354x y a y z a z x a +=⎧⎪+=⎨⎪+=⎩①②③的解使得代数式x-2y+3z 的值等于-10,求a 的值.【思路点拨】由题意可知,此方程组中的a 是已知数,x 、y 、z 是未知数,先解方程组,求出x ,y ,z(含有a 的代数式),然后把求得的x 、y 、z 代入等式x-2y+3z =-10,可得关于a 的一元一次方程,解这个方程,即可求得a 的值. 【答案与解析】解法一: ②-①,得z-x =2a ④③+④,得2z =6a ,z =3a把z =3a 分别代入②和③,得y =2a ,x =a .∴ 23x a y a z a =⎧⎪=⎨⎪=⎩.把x =a ,y =2a ,z =3a 代入x-2y+3z =10得 a-2×2a+3×3a =-10. 解得53a =-. 解法二:①+②+③,得2(x+y+z)=12a .即x+y+z=6a ④④-①,得z =3a ,④-②,得x =a ,④-③,得y =2a .∴ 23x a y a z a =⎧⎪=⎨⎪=⎩,把x =a ,y =2a ,z =3a 代入x-2y+3z =10得 a-2×2a+3×3a =-10. 解得53a =-. 【总结升华】当方程组中三个方程的未知数的系数都相同时,可以运用此题解法2中的技巧解这类方程组.【:三元一次方程组409145 例4】 举一反三:【变式】若 303340x y z x y z -+=⎧⎨--=⎩①② ,则x :y :z = .【答案】15:7:6类型三、三元一次方程组的应用4.(2016春•洛江区期末)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息: 营业员A :月销售件数200件,月总收入2400元; 营业员B :月销售件数300件,月总收入2700元;假设营业员的月基本工资为x 元,销售每件服装奖励y 元. (1)求x 、y 的值;(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?【思路点拨】(1)根据题意可以列出相应的二元一次方程组,从而可以得到x 、y 的值; (2)由题意可以列出相应的不等式,从而可以得到某营业员至少需要卖出服装的件数; (3)由题意可得相应的三元一次方程组,通过变形即可得到问题的答案. 【答案与解析】 解:(1)由题意,得,解得即x 的值为1800,y 的值为3;(2)设某营业员当月卖服装m 件,由题意得,1800+3m ≥3100,解得,,∵m 只能为正整数, ∴m 最小为434,即某营业员当月至少要卖434件;(3)设一件甲为a元,一件乙为b元,一件丙为c元,则,将两等式相加得,4a+4b+4c=720,则a+b+c=180,即购买一件甲、一件乙、一件丙共需180元.【总结升华】本题考查三元一次方程组的应用、二元一次方程组的应用、一元一次不等式的应用,解题的关键是明确题意,列出相应的方程组或不等式.举一反三:【变式】(2015•黄冈中学自主招生)有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需()A.1.2元B.1.05元C.0.95元D.0.9元【答案】B.解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,根据题意得,②﹣①得x+y+z=1.05(元).初中奥数题试题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么 ( )A.a,b都是0 B.a,b之一是0C.a,b互为相反数 D.a,b互为倒数2.下面的说法中正确的是 ( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式3.下面说法中不正确的是 ( )A. 有最小的自然数 B.没有最小的正有理数C.没有最大的负整数 D.没有最大的非负数4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号 B.a,b异号 C.a>0 D.b>05.大于-π并且不是自然数的整数有 ( )A.2个 B.3个 C.4个 D.无数个6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
三元一次方程组及其应用(学生用教案无答案)

三元一次方程组及其应用要点一、三元一次方程及三元一次方程组的概念1. 三元一次方程的定义:含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1,2a-3b+4c=5等都是三元一次方程.要点诠释:(1)三元一次方程的条件:①是整式方程,②含有三个未知数,③含未知数的项的最高次数是1次.(2) 三元一次方程的一般形式:ax+by+cz+d=0,其中a、b、c不为零.2.三元一次方程组的定义:一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组.要点诠释:(1) 三个方程中不一定每一个方程中都含有三个未知数,只要三个方程共含有三个未知量即可.(2) 在实际问题中含有三个未知数,当这三个未知数同时满足三个相等关系时,可以建立三元一次方程组求解要点二、三元一次方程组的解法解三元一次方程组的一般步骤(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;(2)解这个二元一次方程组,求出两个未知数的值;(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;(4)解这个一元一次方程,求出最后一个未知数的值;(5)将求得的三个未知数的值用“{”合写在一起.要点诠释:(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”.使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.其思想方法是:(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法要点三、三元一次方程组的应用列三元一次方程组解应用题的一般步骤:1.弄清题意和题目中的数量关系,用字母(如x,y,z)表示题目中的两个(或三个)未知数;2.找出能够表达应用题全部含义的相等关系;3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;4.解这个方程组,求出未知数的值;5.写出答案(包括单位名称).要点诠释:(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.(3)一般来说,设几个未知数,就应列出几个方程并组成方程组类型一、三元一次方程及三元一次方程组的概念1. 下列方程组不是三元一次方程组的是().A. B. C.D.类型二、三元一次方程组的解法2. 解三元一次方程组3. 已知方程组的解使得代数式x-2y+3z的值等于-10,求a的值.【巩固训练】:知识点1.三元一次方程组的概念1.下列是三元一次方程组的是( )A.⎩⎨⎧2x =5,x 2+y =7,x +y +z =6B.⎩⎪⎨⎪⎧3x -y +z =-2,x -2y +z =9,y =-3C.⎩⎨⎧x +y -z =7,xyz =1,x -3y =4D.⎩⎨⎧x +y =2,y +z =1,x +z =9知识点2.三元一次方程组的解法2.将三元一次方程组⎩⎨⎧5x +4y +z =0,①3x +y -4z =11,②x +y +z =-2,③经过步骤①-③和③×4+②消去未知数z 后,得到的二元一次方程组是( )A.⎩⎨⎧4x +3y =2,7x +5y =3B.⎩⎨⎧4x +3y =2,23x +17y =11C.⎩⎨⎧3x +4y =2,7x +5y =3D.⎩⎨⎧3x +4y =2,23x +17y =113.对于方程组⎩⎨⎧x +y +z =6,①y -z =4,②x -y -2z =3.③(1)若先消去x ,可得含y ,z 的方程组是__ __;(2)若先消去y ,可得含x ,z 的方程组是__ 或 或 __;(3)若先消去z ,可得含x ,y 的方程组是__ 或 或 __.知识点3.利用三元一次方程组求待定系数4.当x =0,1,-1时,二次三项式ax 2+bx +c 的值分别为5,6,10,则a =__ __,b =__ __,c =__ __.5.在等式y =ax 2+bx +c 中,当x =-1时,y =4;当x =2时,y =4;当x =1时,y =2.(1)求a ,b ,c 的值;(2)当x =-2时,求y 的值.知识点4.三元一次方程组的简单应用6.某次知识竞赛共出了30道试题,评分标准如下:答对一题加4分,答错一题扣1分,不答记0分,已知小丰同学不答的题比答错的题多3道,他的总分为81分,则他答对了( )A .19道题B .20道题C .21道题D .22道题【易错点】忽略集中消同一未知数导致不会解三元一次方程组.7.解下列三元一次方程组:(1)⎩⎨⎧2x +y =4,①x +3z =1,②x +y +z =7;③ (2)⎩⎨⎧x +z -3=0,①2x -y +2z =2,②x -y -z =-3.③8、如图所示,已知前两架天平两端保持平衡.要使第三架天平两端保持平衡,则应在天平的右托盘上放__ __个圆形物品.9.有一个三位数,它的十位上的数字等于个位上的数字与百位上的数字的和,个位上的数字与十位上的数字之和等于8,百位上的数字与个位上的数字对调后所得的三位数比原来的三位数大99.求原来的三位数.10.某汽车在相距70 km的甲、乙两地往返行驶,因为行驶中有一坡度均匀的小山,该汽车从甲地到乙地需要2.5 h,而从乙地到甲地需要2.3 h,假设汽车在平地、上坡、下坡的行驶过程中的时速分别为30 km,20 km,40 km.问:从甲地到乙地的过程中,平地路、上坡路、下坡路各为多少千米.11.小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入y元.(1)求x,y的值;(2)若营业员小丽某月的总收入不低于3 800元,那么小丽当月至少要卖服装多少件?(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需315元;如果购买甲1件,乙2件,丙3件共需285元.求某顾客想购买甲、乙、丙各一件共需多少元.【作业】:一、选择题1. 下列方程组中是三元一次方程组的是( ).A .2258232a b c a b c ++=⎧⎪=⎨⎪+=⎩B .2222225810x y y z x z ⎧+=⎪+=⎨⎪+=⎩C .1141171110x y y z z x⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩ D .::3:4:524x y z x y z =⎧⎨++=⎩ 2. 已知方程370x y --=,231x y +=,9y kx =-有公共解,则k 的值为( ).A. 3B.4C.0D.-13. 下列说法正确的是( ).A.方程3220x y z ++=有唯一组解.B.若x 、y 、z 是非负数,则三元一次方程3x+5y+2z =0只有一组解.C. 方程4x+y+2z =7是三元一次方程.D.三元一次方程组有且只有一组解.4.已知代数式2ax bx c ++,当x =-1时,其值为4;当x =1时,其值为8;当x =2时,其值为25;则当x =3时,其值为 ( ).A .1个B .2个C .3个D .4个5.一对夫妇现在年龄的和是其子女年龄和的6倍,他们两年前年龄和是子女两年前年龄和的10倍,6年后,他们的年龄和是子女6年后年龄和的3倍,则这对夫妇共有( )个子女.A .1个B .2个C .3个D .4个6.为了奖励进步较大的学生,某班决定购买甲、乙、丙三种钢笔作为奖品,其单价分别为4元、5元、6元,购买这些钢笔需要花60元;经过协商,每种钢笔单价下降1元,结果只花了48元,那么甲种钢笔可能购买( ) .A .11支B .9支C .7支D .5支二、填空题7. 若12||(1)5210b a a x y z +--++=是一个三元一次方程,那么a =_______,b =________.8.已知2234x y y z x z +++===-,则x+2y+z =________. 9.当a =________时,方程组352,2718x y a x y a -=⎧⎨+=-⎩的解x 、y 互为相反数. 10.已知303340x y z x y z -+=⎧⎨--=⎩,则x :y :z =________. 11.有甲、乙、丙三种商品,如果购甲3件、乙2件、丙1件共需315元;购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需________元钱.12. 方程x+2y+3z =14 (x <y <z)的正整数解是 .三、解答题13.解方程组:(1):3:2:5:466x y y z x y z =⎧⎪=⎨⎪++=⎩ (2)3222311410x y x x y z x y z ++=⎧⎪++=⎨⎪--=-⎩14. 已知等式(27)(38)810-+-=+对于一切有理数x都成立,求A,B的值.A B x A B x15.某工程由甲、乙两队合作需6天完成,厂家需付甲、乙两队共8700元,乙、丙两队合作需10天完,此时厂家需付甲、丙成,厂家需支付乙、丙两队共8000元;甲、丙两队合作5天完成全部工程的23两队共5500元.(1)求甲、乙、丙各队单独完成全部工程各需多少天?(2)若要不超过15天完成全部工程,问由哪队单独完成此项工程花钱最少?请说明理由.。
三元一次方程组(基础)知识讲解

三元一次方程组(基础)知识讲解【学习目标】1.理解三元一次方程(或组)的含义;2.会解简单的三元一次方程组;3. 会列三元一次方程组解决有关实际问题.【要点梳理】要点一、三元一次方程及三元一次方程组的概念1.三元一次方程的定义含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1,2a-3b+4c=5等都是三元一次方程.要点诠释:(1)三元一次方程的条件:①是整式方程,②含有三个未知数,③含未知数的项的最高次数是1次.(2) 三元一次方程的一般形式:ax+by+cz+d=0,其中a、b、c不为零.2.三元一次方程组的定义一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组. 要点诠释:(1) 三个方程中不一定每一个方程中都含有三个未知数,只要三个方程共含有三个未知量即可.(2)在实际问题中含有三个未知数,当这三个未知数同时满足三个相等关系时,可以建立三元一次方程组求解.要点二、三元一次方程组的解法解三元一次方程组的一般步骤(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;(2)解这个二元一次方程组,求出两个未知数的值;(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;(4)解这个一元一次方程,求出最后一个未知数的值;(5)将求得的三个未知数的值用“{”合写在一起.要点诠释:(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”.使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.其思想方法是:(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.要点三、三元一次方程组的应用列三元一次方程组解应用题的一般步骤1.弄清题意和题目中的数量关系,用字母(如x,y,z)表示题目中的两个(或三个)未知数;2.找出能够表达应用题全部含义的相等关系;3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;4.解这个方程组,求出未知数的值;5.写出答案(包括单位名称).要点诠释:(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.(3)一般来说,设几个未知数,就应列出几个方程并组成方程组.【典型例题】类型一、三元一次方程及三元一次方程组的概念1.下列方程组中是三元一次方程组的是( )A .2102x y y z xz ⎧-=⎪+=⎨⎪=⎩B .111216y xz y x z⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩ C .123a b c d a c b d +++=⎧⎪-=⎨⎪-=⎩ D .18120m n n t t m +=⎧⎪+=⎨⎪+=⎩ 【答案】D【解析】A 选项中21x y -=与2xz =中未知数项的次数为2次,故A 选项不是;B 选项中1x ,1y ,1z不是整式,故B 选项不是;C 选项中有四个未知数,故C 选项不是;D 项符合三元一次方程组的定义.【总结升华】理解三元一次方程组的定义要注意以下几点:(1)方程组中的每一个方程都是一次方程;(2)一般地,如果三个一次方程合起来共有三个未知数,它们就能组成一个三元一次方程组.类型二、三元一次方程组的解法2. (韶关)解方程组275322344y x x y z x z =-⎧⎪++=⎨⎪-=⎩①②③【思路点拨】方程①是用未知数x 表示y 的式子,将①代入②可得二元一次方程组.【答案与解析】解:将①代入②得:5x+3(2x -7)+2z =2,整理得:11x+2z =23 ④由此可联立方程组34411223x z x z -=⎧⎨+=⎩③④,③+④×2得:25x =50,x =2.把x =2分别代入①③可知:y =-3,12z =.所以方程组的解为2312x y z ⎧⎪=⎪=-⎨⎪⎪=⎩.【总结升华】解三元一次方程组的思想仍是消元,是用加减消元法,还是用代入消元法,要根据方程组的特征来确定,一定要选择较简便的方法.【高清课堂:三元一次方程组 409145 例1】举一反三: 【变式】解方程组: 【答案】解:①+②得:5311x y +=④ ①×2+③得:53x y -=⑤由此可得方程组:531153x y x y +=⎧⎨-=⎩④⑤④-⑤得:48y =,2y =将2y =代入⑤知:1x =将1x =,2y =代入①得:3z =所以方程组的解为:123x y z =⎧⎪=⎨⎪=⎩【高清课堂:三元一次方程组409145 例2(2)】3. 解方程组23520x y z x y z ⎧==⎪⎨⎪++=⎩①②【答案与解析】 解法一:原方程可化为:253520x z y z x y z ⎧=⎪⎪⎪=⎨⎪⎪++=⎪⎩①②③ 由①③得:25x z =,35y z = ④ 将④代入②得:232055z z z ++=,得:10z = ⑤ 2334823x y z x y z x y z -+=⎧⎪+-=⎨⎪+-=-⎩①②③将⑤代入④中两式,得:2210455x z ==⨯=,3310655y z ==⨯= 所以方程组的解为:4610x y z =⎧⎪=⎨⎪=⎩解法二:设235x y z t ===,则2,3,5x t y t z t ===③ 将③代入②得:23520t t t ++=,2t =将2t =代入③得:2224x t ==⨯=,3326,55210y t z t ==⨯===⨯=所以方程组的解为:4610x y z =⎧⎪=⎨⎪=⎩【总结升华】对于这类特殊的方程组,可根据其方程组中方程的特点,采用一些特殊的解法(如设比例系数等)来解.举一反三:【变式】(2015秋•德州校级月考)若三元一次方程组的解使ax+2y+z=0,则a 的值为( )A .1B .0C .﹣2D .4【答案】B . 解:,①+②+③得:x+y+z=1④,把①代入④得:z=﹣4,把②代入④得:y=2,把③代入④得:x=3,把x=3,y=2,z=﹣4代入方程得:3a+4﹣4=0,解得:a=0.类型三、三元一次方程组的应用4. (2015春•黄陂区校级月考)购买铅笔7支,作业本3本,圆珠笔1支共需3元;购买铅笔10支,作业本4本,圆珠笔1支共需4元,则购买铅笔11支、作业本5本圆珠笔2支共需 元.【思路点拨】首先假设铅笔的单价是x 元,作业本的单价是y 元,圆珠笔的单价是z 元.购买铅笔11支,作业本5本,圆珠笔2支共需a 元.根据题目说明列出方程组,解方程组求出a 的值,即为所求结果.【答案】5.【解析】解:设铅笔的单价是x元,作业本的单价是y元,圆珠笔的单价是z元.购买铅笔11支,作业本5本,圆珠笔2支共需a元.则由题意得:,由②﹣①得3x+y=1,④由②+①得17x+7y+2z=7,⑤由⑤﹣④×2﹣③得0=5﹣a,解得:a=5.【总结升华】本题考查了列三元一次不定方程组解实际问题的运用,在解决实际问题时,若未知量较多,要考虑设三个未知数,但同时应注意,设几个未知数,就要找到几个等量关系列几个方程.举一反三:【变式】现有面值为2元、1元和5角的人民币共24张,币值共计29元,其中面值为2元的比1元的少6张,求三种人民币各多少张?【答案】解:设面值为2元、1元和5角的人民币分别为x张、y张和z张.依题意,得24122926x y zx y zx y++=⎧⎪⎪++=⎨⎪⎪+=⎩①②③把③分别代入①和②,得21813232x zx z+=⎧⎪⎨+=⎪⎩④⑤⑤×2,得6x+z=46 ⑥⑥-④,得4x=28,x=7.把x=7代入③,得y=13.把x=7,y=13代入①,得z=4.∴方程组的解是7134xyz=⎧⎪=⎨⎪=⎩.答:面值为2元、l元和5角的人民币分别为7张、13张和4张.。
三元一次方程组解应用题专项练习88题(有答案) ok

三元一次方程组解应用题专项练习88题(有答案)1.为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.2.有三种物品,每件的价格分别是2元、4元和6元,现在用60元买这三种物品(三种物品均需买到),总数共买16件,而钱要恰好用完,则价格为6元的物品最多买几件?价格为2元的物品最少买几件?3.琪琪、倩倩、斌斌三位同学去商店买文具用品.琪琪说:“我买了4支水笔,2本笔记本,10本作文本共用了19元.”倩倩说:“我买了2支水笔,3本笔记本,10本练习本共用了20元.”斌斌说:“我买了12本练习本,8本作文本共用了10元;作文本与练习本的价格是一样哦!”请根据以上内容,求出笔记本,水笔,练习本的价格.4.某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台5000元、B型每台4000元、C型每台3000元,某中学现有资金100000元,计划全部用从这家电脑公司购进30台两种型号的电脑,请你设计几种不同的购买方案供这个学校选择,并说明理由.5.已知△ABC的周长为48cm,最长边与最短边之差为14cm,另一边与最短边之和为25cm,求△ABC各边的长.6.已知某体育公司有A型、B型、C型三种型号的健身器材,其中价格分别是A型每台5000元、B型每台3000元、C型每台2000元.某单位计划将87000元钱全部用于从该公司购进其中两种不同型号的健身器材36台.请你设计几种不同的购买方案供学校选择,并说明理由.7.大约1500年以前,我国古代数学家张丘建在他编写的《张丘建算经》里,曾经提出并解决了“百钱买百鸡”这个有名的数学问题,通俗地讲就是下例:今有公鸡每只五个钱,母鸡每只三个钱,小鸡每个钱三只.用100个钱买100只鸡,问公鸡、母鸡、小鸡各买了多少只?8.有收录机、钢笔和书包三种物品,若购买收录机3台,钢笔6支,书包2个共需302元,若购买收录机5台,钢笔11支,书包3个共需508元,则购买收录机、钢笔、书包各一个需要_________元.9.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:家电名称空调彩电冰箱工时产值(千元) 4 3 2问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)10.甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,所给的枚数等于乙,丙原来各有的邮票数;然后依同样的游戏规则再由乙送给甲,丙现有的邮票数,最后由丙送给甲,乙现有的邮票数.互相送完后,每人恰好各有64枚.你能知道他们原来各有邮票多少枚吗?说出你的思考过程.11.某公园门票规定为:每人20元,30人以上的团体购票,每人18元,每30人优惠1人免费(不足30人的余数不优惠).今有甲、乙、丙三支旅游团前来参观,若甲、乙两旅游团合起来作为一个团体购票,应购门票3834元,若乙、丙两旅游团合起来作为一个团体购票,应购门票4788元,若甲、丙两旅游团合起来作为一个团全购票,应购门票5220元,求三个旅游团共有多少人?12.一辆客车、一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等,走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上客车,问再过几分钟,货车追上了客车?13.江堤边发生管涌,江水不断涌到堤边一原本干凅的池塘,假定每分钟涌出的水量相同,如果用两台抽水机抽水,40分钟可以抽完池塘里的蓄水;如果用4台抽水机抽水,16分钟可以抽完;如果要在10分钟内将池塘里的蓄水抽完,那么至少需要抽水机多少台?14.编号为1到25的25个弹珠被分放在两个篮子A和B中.15号弹珠在篮子A中,把这个弹珠从篮子A移至篮子B中,这时篮子A中的弹珠号码数的平均数等于原平均数加,篮子B中弹珠号码数的平均数也等于原平均数加.问原来在篮子A中有多少个弹珠?15.2011年3月10日12时58分云南盈江县发生5.8级地震,有1.8万人等待安置.如图(1)是某中学学生捐款情况制成的条形图,图(2)是该中学学生人数分布统计表.(1)该校共有学生_________人;(2)该校学生平均每人捐款_________元(精确到0.01元);(3)在得知灾区急需帐篷后,学校立即与厂家联系购买帐篷送往灾区.已知用9万元刚好可以从厂家购进帐篷500顶.该厂家生产三种不同规格的帐篷,出厂价分别为甲种帐篷每顶150元,乙种帐篷每顶210元,丙种帐篷每顶250元.①若学校同时购进其中两种不同规格的帐篷,则学校的购买方案有哪几种?②若学校想同时购进三种不同规格的帐篷,必须每种帐篷都有,而且帐篷10顶打包成一件,所以每种帐篷数都要求是10的倍数.请你研究一下是否可行?如果可行请给出符合条件的设计方案;若不可行,请说明理由.某中学学生数分布表年级初一初二初三人数493 479 47816.某电器公司计划装运甲、乙、丙三种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电)下表所示为装运甲、乙、丙三种家电的台数及利润.(1)若用8辆汽车装运乙、丙两种家电190台到A地销售,问装运的汽车各多少辆?(2)计划用20辆汽车装运甲、乙、丙三种家电720台到B地销售,如何安排装运,可使公司获得36.6万元的利润?甲乙丙每辆汽车能装满的台数40 20 30每台家电可获利润(万元) 0.05 0.07 0.0417.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需34.5元;若购甲4件,乙10件,丙1件,共需42.00元,现在购甲、乙、丙各一件共需多少元?18.某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、乙、丙三种摩托车,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3200元,可获利320元.10万元资本全部用完.(1)请你帮助该商场设计进货方案;(2)从销售利润上考虑,应选择哪种方案?19.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:农作物品种每公顷需劳动力每公顷需投入资金水稻4人1万元棉花8人1万元蔬菜5人2万元已知该农场计划在设备投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工有工作,而且投入的资金正好够用?20.某单位职工在植树节时去植树,甲、乙、丙三个小组共植树50株,乙组植树的株数是甲、丙两组的和的,甲组植树的株数恰是乙组与丙组的和,问每组各植树多少株?21.现有A、B、C三种型号的产品出售,若售A3件,B2件,C1件,共得315元;若售A1件,B2件,C3件,共得285元.问售出A、B、C各一件共得多少元?22.一头猪卖银币,一头山羊卖银币,一头绵羊卖银币,有人用100个银币买了100头牲畜,问买了猪、山羊、绵羊各几头?23.根据下面的等式,求出妈妈买回来的鱼、鸡、菜各花了多少钱?鸡+鸭+鱼+菜=35.4元鸡+鱼+菜=20.4元鸭+鱼+菜=21.4元鸭+菜=17元.24.新学期开学了,小丽买了10本练习本、4支铅笔、1块橡皮共花去16.8元;小华买了9本练习本、5支铅笔、3块橡皮共花去18.2元;小明练习本、铅笔、橡皮想各买一件,请你帮他算算共需多少钱?25.某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?26.在第29届北京奥运会上,中国体育健儿共获得奖牌100枚,令国人振奋,世界瞩目,下面是两位同学的对话:小明:太厉害了,我们在金牌榜上居第一位,金牌比银牌的2倍还多9块!小华:是呀,我们的银牌也不少啊,只比铜牌少7块!你知道我们共获得金牌、银牌、铜牌各多少块吗?27.某体育彩票经销商计划从省体育彩票中心购进彩票20000张.已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.若经销商同时购进两种不同型号的彩票20000张,共用去45000元,请你设计出几种不同的进票方案供经销商选择,并说明理由.28.有甲、乙、丙三种货物,若购甲3件、乙7件、丙1件共需315元;若购甲4件、乙10件、丙1件共需420元.问购甲、乙、丙各5件共需多少元?29.已知,甲乙丙三个数的和为26,甲数比乙数大1,甲数的两倍与丙数的和比乙数大18,求这三个数.30.一对夫妇现在年龄的和是其子女年龄和的6倍,他们两年前年龄和是子女两年前年龄和的10倍,6年后他们的年龄和是子女6年后年龄和的3倍,问这对夫妇共有多少个子女?31.王明在超市用74元钱买了苹果、梨、香蕉三种水果共15.5/kg,苹果比梨多2kg,已知苹果5元/kg,梨5.5元/kg,香蕉4元/kg.王明买了苹果、梨、香蕉各多少/kg?32.已知甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的等于丙数的.求这三个数.33.某选择题共有10小题,评分标准如下:选对得4分,选错倒扣2分,不选得0分.已知小王选择题的得分是28分,且选对的题数是选错题数的4倍,问小王选对、选错、不选的题各有几个?34.一个三位数,各位数字和为6,百位数字是个位数字的2倍,将原数个位数字与百位数字对调后得的数比原数小198,求这个三位数.35.从甲地到乙地,先平路再上坡后下坡,汽车在平路上每小时行走30千米,上坡路每小时行28千米,下坡路每小时行走35千米.甲、乙两地路程是142千米,从甲到乙用4小时,而乙到甲用4小时42分钟,求这段路的上坡路,下坡路,平路有多少千米?36.学校决定对数学竞赛优胜者进行奖励,获胜者共25人,其中获省里奖的每人奖励价值为200元的奖品,获得市里奖的每人奖励价值50元的奖品,共花去2000元,那么你知道获得省、市奖的学生各有多少人?37.从A地到B地骑车要走上坡、下坡、平路三个路段,全程9km,某人上坡每小时4千米,下坡每小时8千米,平路每小时6千米,如图,他从A地到B地用了1小时,从B到A地用了1小时,求A地到B地,上坡、下坡、平路各是多少千米?38.三人合办一企业,共投资143万元,投资最多的与投资最少的钱数的比为5:3,问第三个人最多投资多少万元?最少投资多少万元?39.某班参加一次智力竞赛,共a,b,c三题,每题或者得满分或者得0分.其中题a满分20分,题b、题c满分分别为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a 的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,问这个班的平均成绩是多少分?40.某城市有一段马路需要整修,这段马路的长不超过3500米.今有甲、乙、丙三个施工队,分别施工人行道、非机动车道和机动车道.他们于某天零时同时开工,每天24小时连续施工.若干天后的零时,甲完成任务;几天后的18时,乙完成任务,自乙队完成的当天零时起,再过几天后的8时,丙完成任务,已知三个施工队每天完成的施工任务分别为300米、240米、180米,问这段路面有多长?41.某农场300名职工种51公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每亩所需工人数和预计产值如下表所示,设水稻、蔬菜和棉花的种植面积分别为x公顷、y公顷和z公顷.(1)用含x的式子表示y和z;(2)若总产值p(万元)满足:360≤p≤370,且x、y、z均为正整数,这个农场怎样安排三种农作物的种植面积才能取得最优效益?农作物每公顷所需人数每公顷预计产值水稻 4 4.5万元蔬菜8 9万元棉花 5 7.5万元42.有三个乒乓球代表队,不同的代表队队员之间都要进行一场比赛,同一代表队的队员互不比赛,参加比赛的三个代表队共有10名队员,共比赛了31场,求每个代表队各有几名队员?43.某电器商场欲用9万元购进某种品牌的电冰箱50台,已知该品牌的电冰箱有甲、乙、丙三种不同型号,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.商场销售一台电冰箱的获利情况分别为:甲种150元,乙种200元,丙种250元.(1)若商场准备同时购进其中两种不同型号的电冰箱,请你设计出最佳进货方案;(2)若商场准备同时购进三种不同型号的电冰箱,请你设计出最佳进货方案.44.某公司董事会决定拨出40万元款项作为奖金,全部用于奖励本年度评出的一、二、三等奖的职工,原定一等奖每人5万元,二等奖每人3万元,三等奖每人2万元.定好一、二、三等奖的人数后,为了重奖对公司有突出贡献的人,改为一等奖每人15万元,二等奖每人4万元,三等奖每人1万元(仍正好把40万元奖励完),问该公司本年度获得一、二、三等奖的职工分别有多少人?45.有甲、乙、丙三种零件,若购甲种零件3件,乙种零件7件,丙种零件1件,共需315元,或购甲种零件4件,乙种零件10件,丙种零件1件,共需420元.问购甲、乙、丙各1件共需多少元?46.甲乙两邮递员分别从A,B两地同时以匀速相向而行,甲比乙多走了18千米(km),相遇后甲走4.5小时到达B地,乙走8小时到A地,求A,B两地的距离.47.从两个重量分别为12千克(kg)和8千克,且含铜的百分数不同的合金上切下重量相等的两块,把所切下的每块和另一块剩余的合金放在一起,熔炼后两个合金含铜的百分数相等.求所切下的合金的重量是多少千克?48.一个三位数,如果把它的个位数字与百位数字交换位置,那么所得的新数比原数小99,且各位数字之和为14,十位数字是个位数字与百位数字之和.求这个三位数.49.某人乘汽车,他看到第一块里程碑上写着一个两位数(表示千米);经过1小时,他看到第二块里程碑写的两位数恰好是第一块里程碑上的数字互换了;又经过1小时,他看到第三块里程碑上写着一个三位数,这个三位数恰好是第一块里程碑上的两位数中间加上一个0,问汽车的速度是多少?50.今有浓度为5%,8%,9%的甲、乙、丙三种盐水分别为60克,60克,47克,现要配制浓度为7%的盐水100克,问甲种盐水最多可用多少克?最少可用多少克?51.甲、乙、丙三个容器中盛有含盐比例不同的盐水.若从甲、乙、丙中各取出重量相等的盐水,将它们混合后就成为含盐10%的盐水;若从甲和乙中按重量之比为2:3来取,混合后就成为含盐7%的盐水;若从乙和丙中按重量之比为3:2来取,混合后就成为含盐9%的盐水.求甲、乙、丙三个容器中盐水含盐的百分数.52.有三块合金,第一块是60%的铝和40%的铬,第二块是10%的铬和90%的钛,第三块是20%的铝、50%的铬和30%的钛,现将它们铸成一块含钛45%的新的合金,问在新的合金中,铬的百分比为多少?53.已知:青铜含有80%的铜、4%锌和16%锡,而黄铜是铜和锌的合金.今有黄铜和青铜的混合物一块,其中含有74%的铜、16%锌和10%锡.求黄铜含有铜和锌之比.54.某市为了节约用水,规定:每户每月用水量不超过最低限量am3时,只付基本费8元和定额损耗费c元(c≤5);若用水量超过am3时,除了付同上的基本费和损耗费外,超过部分每1m3付b元的超额费.根据上表的表格中的数据,求a、b、c.55.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,问:(1)如果放牧16头牛,几天可以吃完牧草?(2)要使牧草永远吃不完,至多放牧几头牛?56.若干人参加智力竞赛游戏,一共有3道题:第1题20分,后两道每道均为25分.每个人对每道题,要么答对得满分,要么答错得0分.结束时的统计结果是:每个人至少答对了1题,3题全答对的只有1人,答对两题的有15人;且答对第1题与答对第2题的人数和为29,答对第2题与答对第3题的人数和为20,答对第1题与答对第3题的人数和为25.求这次竞赛的平均成绩.57.组装甲、乙、丙3种产品,需用A、B、C3种零件.每件甲需用A、B各2个;每件乙需用B、C各1个;每件丙需用2个A和1个C.用库存的A、B、C3种零件,如组装成p件甲产品、q件乙产品、r件丙产品,则剩下2个A和1个B,C恰好用完.求证:无论怎样改变生产甲、乙、丙的件数,也不能把库存的A、B、C3种零件都恰好用完.58.有一水库,在单位时间内有一定量的水流进,同时也向外放水,按现在的进出水量,水库中的水可使用40天,因最近在水源的地方降雨,流入水库的水量增加20%,如果放水量增加10%,则仍可使用40天,如果按原来的放水量放水,可使用多少天?59.从两个重量分别为7千克和3千克,且含铜百分数不同的合金上切下重量相等的两块,把切下的每一块和另一块剩余的合金放在一起,熔炼后两块合金含铜百分数相等,求所切下的合金的重量是多少?60.教师节,甲、乙、丙三个班的学生到花店买花送给自己的班主任.已知甲班买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;乙班买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元.若丙班买上面三种花各3枝,求丙班应付多少元.61.初一年级共举行了24次数学测验,共出了426道考题,每次出题数有25道,有20道,也有16道,问:其中考25道题的测验举行了多少次?62.合肥寿春中学和合肥滨湖寿春中学系同属合肥寿春教育品牌之下的两大核心办学机构,今年同时招生.计划两校共招初一新生45个班共1800人,合肥寿春中学只招小班,合肥滨湖寿春中学招收小班和大班,且小班数量是大班数量的2倍.小班每班36人,大班每班人数在70﹣75人间,求两校计划各招多少班?63.有一片牧场,草每天都在匀速生长(草每天增长量相等).如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草,设每头牛吃草的量是相等的,问如果放牧16头牛,几天可以吃完牧草.64.7公斤桃子的价钱等于1公斤苹果和2公斤梨的价钱,7公斤苹果的价钱等于10公斤梨和1公斤桃子的价钱,则购买12公斤苹果所需的钱可以购买梨_________公斤.65.小鹏对八年级甲、乙、丙三个班的女生进行统计,他发现甲班比乙班女生多4人,乙班比丙班女生多1人;如果把甲班的第一组调至乙班,乙班的第一组调至丙班,丙班的第一组调至甲班,则三个班的女生人数恰好相等;已知丙班第一组共有2个女生,设甲班原有女生x人.(1)原来乙班有女生_________人,丙班有女生_________人(用x的代数式表示)(2)若设甲班第一组有y名女生,乙班第一组有z名女生,请你用代数式分别表示出调整后甲,乙,丙各班的女生人数.(3)问甲、乙两班第一组各有几个女生?66.某个商店出售ABC三种生日贺卡,已知A种贺卡每张0.5元,B种贺卡每张1元,C种贺卡每张2.5元.营业员统计三月份的经营情况如下:三种贺卡共卖出150张,收入合计180元,则该商店3月份出售C种贺卡至少多少张?67.某人用15元钱买了20张邮票,其中有1元,8角,2角的邮票.问他可能有多少种不同的买法?68.某专卖店有A、B、C三种袜子,若买A种4双、B种7双、C种1双共需26元;若买A种5双、B种9双,C种1双共需32元,问A、B、C三种袜子各买1双共需多少元?69.兴隆货车配货站有长途货车若干辆,计划要装运A、B、C三种不同型号的商品.已知每辆长途货车的容积为38m3,每件A种型号商品的体积为3m3,每件B种型号商品的体积为4m3,每件C种型号商品的体积为6m3.(1)每辆货车安排装运A、B、C三种型号商品,使货车刚好装满,则有几种装运方案?(2)如果装运每件A种型号商品运费50元,装运每件B种型号商品运费60元,装运每件C种型号商品运费65元,货主应选择哪种方案装运比较省钱?70.过年时,小刚领来家做客的表弟到文具店购物,他用自己50元的“压岁钱”给表弟买了圆珠笔、铅笔和方格本三种文具共100件.已知一支圆珠笔5元,一支铅笔0.1元,一个方格本1元,那么,这100件文具中,三种文具各多少?71.现有三包杂拌糖,由甲、乙、丙三种水果糖按不同比例混合而成.第一包中含甲种水果糖60%和乙种水果糖40%,第二包中含乙种水果糖10%和丙种水果糖90%,第三包中含甲种水果糖20%、乙种水果糖50%和丙种水果糖30%.先从三包中各取适量杂拌糖,重新混合,得到1千克含丙种水果糖45%的杂拌糖.(1)试用新得到的杂拌糖中所含第一包杂拌糖的质量表示其中所含第二包杂拌糖的质量;(2)求新杂拌糖中所含第二包杂拌糖的质量范围.72.甲组同学每人有28个核桃,乙组同学每人有30个核桃,丙组同学每人有31个核桃,三组的核桃总数是365个,问三个小组共有多少名同学?73.今有公鸡每只五个钱,母鸡每只三个钱,小鸡每个钱三只.用100个钱买100只鸡,问公鸡、母鸡、小鸡各买了多少只?74.某市为鼓励节约用水,对自来水妁收费标准作如下规定:每月每户用水中不超过10t部分按0.45元/吨收费;超过10t而不超过20t部分按每吨0.8元收费;超过20t部分按每吨1.50元收费,某月甲户比乙户多缴水费7.10元,乙户比丙户多缴水费3.75元,问甲、乙、丙该月各缴水费多少?(自来水按整吨收费)75.某地区举办初中数学联赛,有A,B,C,D四所中学参加,选手中,A,B两校共16名;B,C两校共20名;C,D两校共34名,并且各校选手人数的多少是按A,B,C,D中学的顺序选派的,试求各中学的选手人数.76.甲、乙、丙三人共解出100道数学题,每人都解出其中的60道题,将其中只有1人解出的题叫做难题,3人都解出的题叫做容易题,试问:难题多还是容易题多?(多的比少的)多几道题?77.四十只脚的蜈蚣和三个头的龙在同一个笼中,共有26个头和298只脚,如果40只脚的蜈蚣只有一个头,那么三个头的龙有几只脚?78.五个人要完成某项工作,如果甲、乙、丙三人同时工作需6小时;甲、丙、戊三人同时工作需3小时;甲、丙、丁三人同时工作需7.5小时;乙、丙、戊同时工作,需用5小时,问五个人同时工作需用多少小时完成?79.永强加工厂接到一批订单,为完成订单任务,需用a米长的材料440根,b米长的材料480根,可采购到的原料有三种,一根甲种原料可截得a米长的材料4根,6米长的材料8根,成本为60元;一根乙种原料可截得a米长的材料6根,b米长的材料2根,成本为50元;一根丙种原料可截得a米长的材料4根,b米长的材料4根,成本为40元.问怎样采购,可使材料成本最低?80.某人家的电话号码是八位数,将前四位数组成的数与后四位数组成的数相加得14405,将前三位数组成的数与后五位数组成的数相加得16970,求此人家的电话号码.81.已知甲、乙、丙三人.甲单独做一件工作的时间是乙丙两人合作做这件工作所用时间的a倍,乙独做这件工作是甲丙两人合作做这件工作的b倍.求丙单独做这件工作是甲乙两人合作做这件工作所需时间的几倍?82.有一水池,池底有泉水不断涌出,要将满池的水抽干,用12台水泵需5小时,用10台水泵需7小时,若要在2小时内抽干,至少需水泵几台?83.汽车在相距74千米的甲、乙两地之间往返行驶,因行程有一坡度均匀的小山,该汽车从甲地到乙地需要2小时30分钟,从乙地到甲地需要2小时48分钟,已知汽车在平地每小时行驶30千米,上坡路每小时行驶20千米,下坡每小时行驶40千米,求甲地到乙地地行驶过程中平路、上坡、下坡各是多少?。
第9课时 《三元一次方程组及应用题》导学案
第9课时 《三元一次方程组及应用题》导学案 知识目标:1、通过解三元一次方程组进一步掌握代入消元、加减消元思想; 2、会根据相等关系列三元一次方程组解应用题。
能力目标:1、掌握消元思想; 自主学习(我愿学,我会学) 阅读课本111页“三元一次方程组解法举例”到114页,回答下列问题。
1、方程组中含有 个 的未知数,每个方程中含未知数的 的 都是1,并且一共有 个方程,这样的方程组叫做三元一次方程组。
2、根据概念,请写出一个三元一次方程组: 3、解三元一次方程组的基本思路是:通过 法或 法进行消元,把“三元”化为“ ”,使解三元一次方程组转化为解 ,进而转化为解 。
这与解二元一次方程组的思路是一样的。
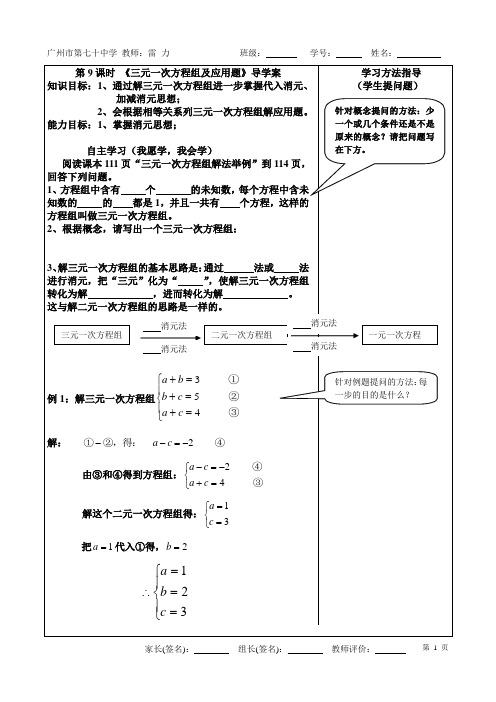
例1:解三元一次方程组⎪⎩⎪⎨⎧=+=+=+③②①453c a c b b a 解: ④②,得:①2-=--c a由③和④得到方程组:⎩⎨⎧=+-=-③④42c a c a 解这个二元一次方程组得:⎩⎨⎧==31c a 把1=a 代入①得,2=b⎪⎩⎪⎨⎧===∴321c b a学习方法指导 (学生提问题)三元一次方程组 二元一次方程组 一元一次方程 消元法 消元法 消元法 消元法 针对概念提问的方法:少一个或几个条件还是不是原来的概念?请把问题写在下方。
针对例题提问的方法:每一步的目的是什么?练习:解方程组:⎪⎩⎪⎨⎧=+=+=+321x z z y y x⎪⎩⎪⎨⎧=+=--=-472392x z z y y x例2:书本112页例题1,针对每一步进行思考,它们的作用是什么?练习:在正面做课本114页第1题的(1),第2题的(1)应用题:1、 一个三位数,个位、百位上的数字的和等于十位上的数字,百倍上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14.求这个三位数。
分析:由“个位、百位上的数字的和等于十位上的数字”可得到相等关系: 由“百倍上的数字的7倍比个位、十位上的数字的和大2”可得到相等关系: 由“个位、十位、百位上的数字的和是14”可得到相等关系: , 这三种关系都体现着这种类型是:“和差倍分”类型的问题。
三元一次方程组(提高)知识讲解

三元一次方程组(提高)知识讲解责编:康红梅【学习目标】1.理解三元一次方程(或组)的含义;2.会解简单的三元一次方程组;3. 会列三元一次方程组解决有关实际问题.【要点梳理】要点一、三元一次方程及三元一次方程组的概念1.三元一次方程的定义:含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1,2a-3b+4c=5等都是三元一次方程.要点诠释:(1)三元一次方程的条件:①是整式方程,②含有三个未知数,③含未知数的项的最高次数是1次.(2) 三元一次方程的一般形式:ax+by+cz+d=0,其中a、b、c不为零.2.三元一次方程组的定义:一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组. 要点诠释:(1) 三个方程中不一定每一个方程中都含有三个未知数,只要三个方程共含有三个未知量即可.(2)在实际问题中含有三个未知数,当这三个未知数同时满足三个相等关系时,可以建立三元一次方程组求解.要点二、三元一次方程组的解法解三元一次方程组的一般步骤(1)利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组;(2)解这个二元一次方程组,求出两个未知数的值;(3)将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程;(4)解这个一元一次方程,求出最后一个未知数的值;(5)将求得的三个未知数的值用“{”合写在一起.要点诠释:(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”.使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程.其思想方法是:(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.要点三、三元一次方程组的应用列三元一次方程组解应用题的一般步骤:1.弄清题意和题目中的数量关系,用字母(如x,y,z)表示题目中的两个(或三个)未知数;2.找出能够表达应用题全部含义的相等关系;3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;4.解这个方程组,求出未知数的值;5.写出答案(包括单位名称).要点诠释:(1)解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.(2)“设”、“答”两步,都要写清单位名称,应注意单位是否统一.(3)一般来说,设几个未知数,就应列出几个方程并组成方程组.【典型例题】类型一、三元一次方程及三元一次方程组的概念1.下列方程组不是三元一次方程组的是().A.12236x yy zy+=⎧⎪+=-⎨⎪=⎩B.24013xy xxy z⎧-=⎪+=⎨⎪-=-⎩C.2231xyx z=⎧⎪=-⎨⎪-=⎩D.1321y xx zy z-=-⎧⎪+=⎨⎪-=⎩【思路点拨】根据三元一次方程组的定义来求解,对A、B、C 、D四个选项进行一一验证.【答案】B【解析】解:由题意知,含有三个相同的未知数,每个方程中含未知数的项的次数都是1次,并且一共有三个方程,叫做三元一次方程组.A、满足三元一次方程组的定义,故A选项错误;B 、x2-4=0,未知量x的次数为2次,∴不是三元一次方程,故B选项正确;C、满足三元一次方程组的定义,故C选项错误;D、满足三元一次方程组的定义,故D选项错误;故选B.【总结升华】三元一次方程组中的方程不一定都是三元一次方程,并且有时需对方程化简后再根据三元一次方程组的定义进行判断.类型二、三元一次方程组的解法2.(2015春•苏州校级期末)若x:y:z=2:7:5,x﹣2y+3z=6,求的值.【思路点拨】根据x:y:z=2:7:5,设x=2k,y=7k,z=5k,代入x﹣2y+3z=6得出方程,求出方程的解,即可求出x 、y、z的值,最后代入求出即可.【答案与解析】解:∵x:y:z=2:7:5,∴设x=2k,y=7k,z=5k,代入x﹣2y+3z=6得:2k﹣14k+15k=6,解得:k=2,∴x=4,y=14,z=10,∴==0.18.【总结升华】若某一方程是比例形式,则先引入参数,后消元.举一反三:【变式】解方程组:2:3,:4:5,2329x y y z x y z =⎧⎪=⎨⎪-+=⎩①②③【答案】解:由①,得3x =2y ,即23x y =, ④ 由②,得5y =4z ,即54z y =,⑤ 把④、⑤代入③,得21522934y y y -+=. 解得y =12.⑥把⑥代入④,得x =8,把⑥代入⑤,得z =15.所以原方程组的解为8,12,15.x y z =⎧⎪=⎨⎪=⎩【高清课堂:三元一次方程组 409145 例3】3.已知方程组354x y a y z a z x a +=⎧⎪+=⎨⎪+=⎩①②③的解使得代数式x -2y+3z 的值等于-10,求a 的值.【思路点拨】由题意可知,此方程组中的a 是已知数,x 、y 、z 是未知数,先解方程组,求出x ,y ,z (含有a 的代数式),然后把求得的x 、y 、z 代入等式x -2y+3z =-10,可得关于a 的一元一次方程,解这个方程,即可求得a 的值.【答案与解析】解法一: ②-①,得z-x =2a ④③+④,得2z =6a ,z =3a把z =3a 分别代入②和③,得y =2a ,x =a .∴ 23x a y a z a =⎧⎪=⎨⎪=⎩.把x =a ,y =2a ,z =3a 代入x -2y+3z =10得a -2×2a+3×3a =-10.解得53a =-. 解法二:①+②+③,得2(x+y+z )=12a .即x+y+z=6a ④④-①,得z =3a ,④-②,得x =a ,④-③,得y =2a .∴ 23x a y a z a =⎧⎪=⎨⎪=⎩,把x =a ,y =2a ,z =3a 代入x -2y+3z =10得a -2×2a+3×3a =-10.解得53a =-. 【总结升华】当方程组中三个方程的未知数的系数都相同时,可以运用此题解法2中的技巧解这类方程组.【高清课堂:三元一次方程组409145 例4】举一反三:【变式】若 303340x y z x y z -+=⎧⎨--=⎩①② ,则x :y :z = . 【答案】15:7:6类型三、三元一次方程组的应用4. (凉山)甲、乙、丙三块地,草长得一样密,一样快,甲地133公顷可供12头牛吃4周;乙地10公顷可供21头牛吃9周,求丙地24公顷可供几头牛吃18周?【思路点拨】本题草地上原有一些草,其数量不知,草地上的草还在不停地生长,但生长的速度不知道,因此解题时应把原有的草量、草的生长速度及每头牛每周的食草量用字母表示,设成辅助未知数,再根据题意便可列出方程组.【答案与解析】解:设每公顷草地原有牧草akg ,每周每公顷草地生长草bkg ,每头牛每周吃草ckg ,丙地24公顷地可供x 头牛吃18周.根据题意得10104412331091092124182418a b c a b c a b xc ⎧+⨯=⨯⎪⎪⎨+⨯=⨯⎪⎪⎩+⨯=⨯①②③由①②得545910a cbc ⎧=⎪⎪⎨⎪=⎪⎩代入③,得x =36. 答:丙地24公顷可供36头牛吃18周.【总结升华】用三元一次方程组解答实际问题的方法与用二元一次方程组解答实际问题的方法类似,根据题目给出的条件寻找相等关系是利用方程解应用题的重要一环.举一反三:【变式】(2015•黄冈中学自主招生)有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需()A.1.2元B.1.05元C.0.95元D.0.9元【答案】B.解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,根据题意得,②﹣①得x+y+z=1.05(元).。
初中数学三元一次方程组及其应用专题培优练习(解析版)
点睛:本题考查了解三元一次方程组,利用了消元的思想,熟练掌握运算法则是解本题的关键.
5.A
【解析】
【分析】
方程组两方程相减求出 x-z 的值,原式变形后代入计算即可求出值.
【详解】
{ 解:
������ + ������ + ������ = 5① 4������ + ������ ‒ 2������ = 2②
C.﹣7
D.7
x y z 7 6.已知实数 x,y,z 满足 4x y 2z 2 ,则代数式 3(x﹣z)+1 的值是( )
A.﹣2
B.﹣4
C.﹣5
D.﹣6
7.对于三元一次方程组,我们一般是先消去一个未知数,转化为二元一次方程组求解。那么在解
2x y z 9
详解:(1)设需甲车型 x 辆,乙车型 y 辆,得:
5x+8y=120 400x+500 y=8200 ,
x=8
解得
y=10
.
答:分别需甲车型 8 辆,乙车型 10 辆.
(2)设需甲车型 x 辆,乙车型 y 辆,丙车型 z 辆,得:
x+y+z=16 5x+8y+10z=120 , 消去 z 得 5x+2y=40, x=8 2 y ,
10.解方程组:
2x 3y 16
(1)
x
4
y
13
(代入法)
5x 6 y 3 (2) 7x 4 y 9 (加减法)
x y z 4 (3) 2x y z 3
3x 2 y 3z 5
11.为了组织一个 50 人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人 间、单人间三种,收费标准是三人间每人每晚 20 元,二人间每人每晚 30 元,单人间每人每晚 50 元,旅游团共住 20 间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.
初中数学:三元一次方程组及其应用(原卷版)
2022-2023学年浙教版七年级数学下册精选压轴题培优卷专题04三元一次方程组及其应用名:___________班级:___________考号:___________、选择题(每题2分,共20分)1.(本题2分)(2023·全国·七年级专题练习)6321324x y z x y z x y z的解是( )A .115325515x y zB .95365515x y zC .215x y zD .431x y z2.(本题2分)(2023秋·江苏苏州·七年级校考阶段练习)将下表从左到右在每个小格子中都填入一个整数,使得其中任意四个相邻格子中所填整数之和都相等,则第2022个格子中的数字是()3a b c1 02…A .3B .2C .0D .13.(本题2分)(2023·全国·七年级专题练习)购买铅笔7支,作业本3本,圆珠笔1支共需3元;购买铅笔10支,作业本4本,圆珠笔1支共需4元,则购买铅笔11支,作业本5本,圆珠笔2支共需( )A .4.5元B .5元C .6元D .6.5元4.(本题2分)(2023·全国·七年级专题练习)已知123x y z是方程组237ax by by cz cx az 的解,则a b c 的值为( )A .3B .2C .1D .05.(本题2分)(2022春·河南南阳·七年级统考期中)我们探究得方程2x y 的正整数解只有1组,方程3xy 的正整数解只有2组,方程4x y 的正整数解只有3组,……,那么方程9x y z 的正整数解的组数是( )A .27B .28C .29D .306.(本题2分)(2022秋·安徽·七年级周测)已知1,5,6x yy z x z ,则x y z 等于( )A .6B .7C .8D .97.(本题2分)(2022秋·安徽·七年级周测)有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需315元;若购甲4件,乙10件,丙1件,共需420元.现在购买甲、乙、丙各1件,共需()A .105元B .210元C .170元D .不能确定8.(本题2分)(2023春·七年级课时练习)已知方程组234113720x y m x y m的解x ,y 使32521x y m 成立,则m 的值是( )A .0B .12C .1D .29.(本题2分)(2019春·湖南长沙·七年级统考期中)已知方程组4520430x y z x y z(xyz≠0),则x :y :z 等于( )A .2:1:3B .3:2:1C .1:2:3D .3:1:210.(本题2分)(2022春·全国·七年级假期作业)解方程组3423126x y z x y z x y z①②③时,第一次消去未知数的最佳方法是()A .加减法消去x ,将①-③×3与②-③×2B .加减法消去y ,将①+③与①×3+②C .加减法消去z ,将①+②与③+②D .代入法消去x ,y ,z 中的任何一个、填空题(每题3分,共20分)11.(本题2分)(2023春·七年级课时练习)已知x ,y ,z 满足438324xyz,且212x y z ,则x____________.12.(本题2分)(2023·全国·七年级专题练习)我国的经济总量已居世界第二,人民富裕了,很多家庭都拥有多种车型.小明家有A、B、C三种车型,已知3辆A型车的载重量与4辆B型车的载重量之和刚好等于2辆C型车的载重量;4辆B型车的载重量与1辆C型车的载重量之和刚好等于6辆A型车的载重量.现有一批货物,原计划用1辆C型车5次可全部运完,由于C型车另有运输任务,现在安排1辆A型车单独装运9次,余下的货物由1辆B型车单独装运刚好可以全部运完,则B型车需单独装运____次(每辆车每次都满载重量).13.(本题2分)(2023春·七年级课时练习)某校用一笔钱来购买A,B两种奖品,若购买24个A种奖品和14个B种奖品则差30元,若购买20个A种奖品和18个B种奖品则余20元,那么用这笔钱购买28个A种奖品和10个B种奖品差_________元.14.(本题2分)(2022春·重庆·七年级重庆十八中校考期中)中午放学后,有a个同学在学校一食堂门口等候进食堂就餐,由于二食堂面积较大,所以配餐前二食堂等待就餐的学生人数是一食堂的2倍,开始配餐后,仍有学生继续前来排队等候就餐,设一食堂排队的学生人数按固定的速度增加,且二食堂学生人数增加的速度是一食堂的2倍,两个食堂每个窗口阿姨配餐的速度是一样的,一食堂若开放12个配餐窗口,则需10分钟才可为排队就餐的同学配餐完毕;二食堂若开放20个配餐窗口,则14分钟才可为排队就餐的同学配餐完毕;若需要在15分钟时刚好配餐完毕,则两个食堂需要同时一共开放_________个配餐窗口.15.(本题2分)(2023春·七年级单元测试)小华和小慧到校门外文具店买文件,小华购铅笔2支,练习本2本,圆珠笔1支,共付9元钱;小慧购同样铅笔1支,练习本4本,圆珠笔2支,共付12元钱,若小明去买与她们一样的购铅笔1支、练习本2本、圆珠笔1支,他需付______元钱.16.(本题2分)(2021春·重庆·七年级期末)为隆重庆祝建党一百周年,某学校欲购买A,B,C三种花卉各100束装饰庆典会场.已知购买4束A花卉,7束B花卉,1束C花卉,共用45元;购买3束A花卉,5束B花卉,1束C花卉,共用35元.则学校购买这批装饰庆典会场的花卉一共要用__元.17.(本题2分)(2022秋·重庆·七年级重庆南开中学校考期末)北京冬奥会志愿者招募迎来全球申请热潮,赛会志愿者将在北京赛区、延庆赛区、张家口赛区的竞赛场馆开展志愿服务,北京赛区、延庆赛区、张家口赛区的志愿者人数之比为5∶3∶2.随着赛事的调整,各赛区的志愿者人数均要增加,其中等于其余两个赛区增加的总人数的34,则增加后北京赛区志愿者人数占所有赛区增加后的总人数的1837.为使延庆赛区、张家口赛区增加后的志愿者人数之比为6∶5,则延庆赛区增加的志愿者人数与各赛区增加的志愿者总人数之比是______.18.(本题2分)(2022春·江苏·七年级专题练习)幻方,又称为九宫格,最早起源于中国,是一种中国传统游戏.如图1,它是在33 的9个格子中填入9个数,使得每行、每列及对角线上的3个数之和都相等.在如图2所示幻方中,只填了5个用字母表示的数,根据每行、每列及对角线上的3个数之和都相等,则右上角“x ”所表示的数应等于_______.19.(本题2分)(2023春·七年级课时练习)重庆市举行了中学生足球联赛,共赛17轮(即每队均需比赛17场),记分办法是胜一场得3分,平一场得1分,负一场得0分.若文德中学足球队的积分为16分,且踢平场数是所负场数的整数倍,且胜、平、负的场数各不相同.则文德中学足球队共负____场.20.(本题2分)(2022春·江苏·七年级专题练习)已知x ,y ,z 满足方程组207450x y z x y z,则::x y z____.、解答题(共60分)21.(本题8分)(2022秋·广东广州·七年级广州大学附属中学校考期中)计算:(1) 422311(1){[()0.412)}532;(2)223232332[232323)3234343443;(3)解方程0.10.20.50.10.40.7x y x y;(4)解方程224x y z y z x z x y.22.(本题8分)(2023春·七年级课时练习)某校开展校园科技节系列活动,校学生会代表小明到文具店购买文具作为奖品.(1)小明第一次购买若干个文具袋作为奖品,这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话图,求小明原计划购买文具袋多少个?(2)小明第二次购买钢笔和签字笔共50支作为补充奖品,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予8折优惠,钢笔和签字笔合计288元,问小明购买了钢笔和签字笔各多少支?(3)如果小明用48元去购买单价为3元的铅笔,单价为8元的钢笔,单价为5元的笔记本若干(三样都要买,把48元恰好用完),问有哪几种购买方案?23.(本题8分)(2021春·浙江杭州·七年级校考期中)阅读理解:已知实数x ,y 可满足35x y……①,237xy ……②,求4x y 和75x y 值,仔细观察未知数系数之间的关系,如由①-②可得42x y ,由2 ①②可得7519x y .这就是通常说的“整体思想”.尝试利用“整体思想”,解决下列问题:(1)已知二元一次方程组28210x y x y,则x y ___________,x y ___________;(2)买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,求购买5支铅笔、5块橡皮5本日记本共需多少元?(3)对于实数x ,y ,定义新运算:x y ax by c ,其中a ,b ,c 是常数,等式右边是实数运算.已知3515 ,4728 ,求11 的值.24.(本题6分)(2023春·七年级单元测试)在求代数式的值时,可以用整体求值的方法,化难为易.例:已知32475310x y z x y z①②,求x y z 的值.解:①2 得:6428x y z ③② ③得:2x y z ∴x y z 的值为2.(1)已知231056726x y z x y z,求345x y z 的值;(2)马上期中了,班委准备把本学期卖废品的钱给同学们买期中奖品,根据商店的价格,购买40本笔记本、20支签字笔、4支记号笔需要488元.通过还价,班委购买了80本笔记本、40支签字笔、8支记号笔,只花了732元,请问比原价购买节省了多少钱?25.(本题6分)(2023春·七年级课时练习)某工程由甲、乙两队合做6天完成,厂家需付甲、乙两队共4350元;乙、丙两队合做10天完成,厂家需付乙、丙两队共4750元;甲、丙两队合做5天完成全部工程的23,厂家需付甲、丙两队共2750(1)求甲、乙、丙各队单独完成全部工程各需多少天?(2)若工期要求不超过20天完成全部工程,问可由哪队单独完成此项工程花钱最少?请说明理由.26.(本题8分)(2022秋·湖南长沙·七年级校考阶段练习)两个小伙伴共带100只鸡蛋去卖,一个带得多,一个带得少,但卖了同样的价钱,一个对另一个说:“如果我有你那么多鸡蛋,我能卖15元.”另一个说:“如果我有你那么多鸡蛋,只能卖263元.”问两人各有多少鸡蛋?希望你有尽可能简单的解答.27.(本题8分)(2022春·江苏扬州·七年级统考期末)阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的一个代数式的值.如以下问题:已知实数x 、y 满足35x y,237xy ,求4x y 和75x y 的值.本题常规思路是将35x y①,237x y ②联立组成方程组,解得x 、y 的值再代入欲求值的代数式得到答案.常规思路计算量比较大,其实本题还可以仔细观察两个方程未知数系数之间的关系,通过适当变形整体求得代数式的值,如由①-②可得42x y ,由①+②×2可得7519x y .这样的解题思想就是通常所说的“整体思想”.解决问题:(1)已知二元一次方程组2425x y x y,则x y ______,x y ______;(2)试说明在关于x 、y 的方程组3453x y ax y a中,不论a 取什么实数,x y 的值始终不变;(3)某班级组织活动购买小奖品,买3支铅笔、5块橡皮、1本笔记本共需21元,买4支铅笔、7块橡皮、1本笔记本共需28元,则购买10支铅笔、10块橡皮、10本笔记本共需多少元?28.(本题8分)(2022·江苏·七年级假期作业)阅读感悟:有些关于方程组的问题,要求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x 、y 满足35x y①,237x y ②,求4x y 和75x y 的值.本题常规思路是将①②两式联立组成方程组,解得x 、y 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得42x y ,由①+②×2可得7519x y .这样的解题思想就是通常所说的“整体思想”.解决问题:(1)已知二元一次方程组2728x y x y,则x y _______,x y _______;(2)某班级组织活动购买小奖品,买20支水笔、3块橡皮、2本记事本共需35元,买39支水笔、5块橡皮、3本记事本工序62元,则购买6支水笔、6块橡皮、6本记事本共需多少元?(3)对于实数x 、y ,定义新运算:*x ya x by c ,其中a 、b 、c 是常数,等式右边是通常的加法和乘法运算.已知3*515 ,4*728 ,那么1*1 _______.。
三元一次方程组及其应用
三元一次方程组要点突破【三元一次方程的概念】三元一次方程组就是含有三个未知数,并且含有的未知数的项都是1次的整式方程。
【三元一次方程组的概念】一般地,由三个一次方程组成,并且含有三个未知数的方程组叫做三元一次方程组。
【三元一次方程组的解法】(1)三元一次方程组与二元一次方程组同属于一次方程组,解二元一次方程组基本思想是消元,通过代入法或加减法使二元化成一元,未知转化为已知,受它的启发,解三元一次方程组也通过代入或加减消元,使三元化为二元或一元,转化为我们已经熟悉的问题。
(2)三元一次方程组解题的基本步骤:①利用代入法或加减法,把方程组中的一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组。
②解这个二元一次方程组,求得两个未知数的值;③将这两个未知数的值代入原方程中较简单的一个方程,求出第三个未知数的值,把这三个数写在一起的就是所求的三元一次方程组的解。
例 解方程组2636315764949x y z x y z x y z ++=⎧⎪++=⎨⎪-+=⎩①②③课时达优:1、解方程组3232411751x y z x y z x y z -+=⎧⎪+-=⎨⎪+-=⎩若要使运算简便,消元的方法应选取( )A 、先消去xB 、先消去yC 、先消去zD 、以上说法都不对2、将三元一次方程组⎪⎩⎪⎨⎧-=++=-+=++③②①21143045z y x z y x z y x ,经过步骤①-③和③×4+②消去未知数z后,得到的二元一次方程组是( )A 、⎩⎨⎧=+=+357234y x y xB 、⎩⎨⎧=+=+111723234y x y xC 、⎩⎨⎧=+=+357243y x y xD 、⎩⎨⎧=+=+111723243y x y x3、方程组11x yz xy z+=-⎧⎪+=⎨⎪+=⎩的解是( ).A、11xyz=⎧⎪=⎨⎪=-⎩B、11xyz=⎧⎪=-⎨⎪=⎩C、11xyz=⎧⎪=⎨⎪=⎩-D、11xyz=⎧⎪=⎨⎪=⎩-4、解下列方程组(1)3743225x yy zx z-=-⎧⎪+=⎨⎪-=-⎩(2)491731518232x zx y zx y z-=⎧⎪++=⎨⎪++=⎩(3)76710020320x y zx y zx y z++=⎧⎪-+=⎨⎪+-=⎩(4)2439325115680x y zx y zx y z++=⎧⎪-+=⎨⎪++=⎩5、甲、乙、丙三数之和是26,甲数比乙数大1,甲数的两倍与丙数的和比乙数大18 求这三个数?6.甲、乙两位同学解方程组232ax bycx y+=⎧⎨-=-⎩,甲解得正确答案为11xy=⎧⎨=-⎩,乙因抄错了c的值,解得26xy=⎧⎨=⎩,求aacb-的值7.学校的篮球数比排球数的2倍少3个,足球数与排球数的比是2:3,三种球共41个,求三种球各有多少?8.在第29届奥运会上,中国健儿共获得100枚奖牌,金牌比银牌的2倍还多9块,银牌比铜牌少7块,问金牌、银牌、铜牌各多少块?9.某足球联赛一个赛季共进行26场比赛(即每队均赛26场),其中胜一场得三分,平一场得一分,负一场得0分.某队在这个赛季中平局的场数比负的场数多7场,结果共得34分.这个队在这个赛季中胜、平、负各多少场?。
了解三元一次方程组的解法及应用
了解三元一次方程组的解法及应用在数学中,方程是一个含有未知数的等式,而方程组则是由多个方程组成的一组等式。
其中,三元一次方程组指的是含有三个未知数的一组方程。
了解和掌握三元一次方程组的解法及应用,对于解决实际问题和提升数学能力都具有重要意义。
一、三元一次方程组的解法1. 代入法代入法是解三元一次方程组的一种常用方法。
首先,从其中一个方程中解出一个未知数,然后将其代入其他方程中,得到一个二元方程组。
接着,再使用二元方程组的解法求出另外两个未知数的值。
最后,将求得的两个未知数代入原方程中,求出第三个未知数的值。
2. 消元法消元法是另一种解三元一次方程组的常用方法。
通过将方程组中的某一方程乘以适当的数,使得方程组中某一未知数的系数相等,然后将这两个方程相减,从而消去该未知数。
接着,将得到的新方程与其他方程相加或相减,继续消去另一个未知数。
最后,将求得的两个未知数代入原方程中,求出第三个未知数的值。
二、三元一次方程组的应用1. 几何问题三元一次方程组在几何问题中有广泛的应用。
例如,在三维空间中,可以通过三元一次方程组来求解平面与直线的交点、直线与直线的交点等。
这些问题常常涉及到坐标系、向量和几何关系等概念,通过解方程组可以得到准确的结果。
2. 经济问题三元一次方程组在经济学中也有重要的应用。
例如,在市场经济中,供求关系是一个复杂的问题。
通过建立三元一次方程组,可以求解出市场平衡点,即供给与需求相等的点。
这对于决策者来说,可以提供重要的参考,帮助他们做出合理的经济决策。
3. 物理问题三元一次方程组在物理学中也有广泛的应用。
例如,在运动学中,可以通过三元一次方程组来求解物体的运动轨迹、速度和加速度等。
这些问题涉及到时间、距离和速度等概念,通过解方程组可以得到物理量之间的关系,进而进行科学的分析和预测。
三、三元一次方程组的挑战尽管三元一次方程组具有广泛的应用,但在实际问题中,解方程组并不总是一件容易的事情。
有时,方程组可能没有解,或者有无穷多个解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9、某种商品的进价是1000元,售价为1500元,由于销售情况不好,商店决定降价出售,但又要保证利润不低于5%,那么商店最多降多少元出售此商品?
10、商场按标价销售某商品,每件可获利45元,按标价的8.5折销售8件与将标价降价35元销售12件的利润相同。求该商品的进价和标价各多少元?
2、小明手头有12张面额分别为1元,2元,5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元,2元,5元纸币各多少张.
3、甲、乙、丙三个数的和是35,甲数的2倍比乙数大,乙数的 等于丙数的 ,求这三个数.
4、体育商店足球打6折出售,是指按原价的%出售,如果这种足球的原价是80元,则现价是元,比原价便宜____元。
13、李大叔今年五月购买了一台彩电和一台洗衣机,根据“家电下乡”的补贴标准:农户每购买一件家电,国家按每件家电售价13%电的售价比洗衣机的售价高1000元,求彩电和洗衣机的售价各是多少?
14、为了拉动内需,广东启动“家电下乡”活动。某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出960台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1228台。
(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别多少台?
(2)若Ⅰ型冰箱每台2298元,Ⅱ型冰箱1999元,政府按每台冰箱价格的13%给补贴,问:活动后一个月销售给农户的1228台Ⅰ型冰箱和Ⅱ型冰箱,政府共补贴多少元?(保留两个有效数字)
15、下面是某周甲乙两种股票的收盘价:
某人在该周内持有若干甲乙两种股票,若按照两种股票每天收盘价计算(不计手续费,税费等),该人账户星期二比星期一获利200元,星期三比星期二获利1300元,问该人持有甲乙两种股票各多少股?
A、4B、10C、11D、12
6、已知∣x-8y∣+2(4y-1)2+3∣8z-3x∣=0,求x+y+z的值.
7、解方程组
(1)(2)
3、知识拓展
1、一对夫妇现在年龄的和是其子女年龄和的6倍,他们两年前年龄和是子女两年前年龄和的10倍,6年后他们的年龄和是子女6年后年龄和的3倍,问这对夫妇共有多少个子女?
三元一次方程组及应用
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
三元一次方程组及应用
1、知识体系
1、概念:含有三个未知数,并且含有未知数的项的次数都是1的方程叫做三元一次方程。由三个三元一次方程组成的叫做三元一次方程组。
2、解方程组 ,若要使运算简便,消元的方法应选取( )
A、先消去xB、先消去y C、先消去zD、以上说法都不对
3、已知 ,则x∶y∶z=___________.
4、若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值为()
A、2B、3 C、4D、5
5、若方程组的解x与y相等,则a的值等于()
18、某人以两种形式一共储蓄了8000元人民币,其中甲种储蓄的年利率为10%,乙种储蓄的年利率为12%,一年后共得利息860元整,问甲、乙两种储蓄各多少元?
19、将________吨含铁72%和________吨含58%的铁矿石混合后配成含铁64%的铁矿石70吨.
(四)储蓄问题(银行利率问题)
利息=本金×利率 本息和=本金+利息
=本金×(1+利率)
利息税=利息×利息税率 所得金额=本息和-利息税
(五)浓度问题:
溶质=溶液×浓度百分数 溶液=溶质+溶剂
m溶液=m溶质+m溶剂
m溶质=m溶液×m浓度百分数
=(m溶质+m溶剂)×浓度百分数
二、知识巩固
1、 已知代数式ax2+bx+c,当x=-1时,其值为4;当x=1时,其值为8;当x=2时,其值为25;则当x=3时,其值为_______.
5、一支铅笔进价每支0.5元,零售每支0.8元,每支铅笔的利润是_________元,利润率是_________.
6、某商品的每件销售利润是72元,进价是120,则售价是__________元.4、某商品利润率13﹪,进价为50元,则利润是________元.
7、随着计算机技术的迅猛发展,电脑价格大幅度下降,某品牌电脑今年每台售出价格为4200元,比去年降低了30%,问去年该品牌电脑每台售出价为多少元?
利润=成本×利润率 亏损额=成本×亏损率
售价=标价× 售价=进价×(1+利润率)
总价=单价×数量 数量之和=甲商品+乙商品+丙商品
(二)增长率或百分比的问题
增长(降低)率问题:
增长量=原有量×增长率 现有量=原有量+增长量
=原有量×(1+增长率)
减少量=原有量×降低率 现有量=原有量-减少量
=原有量×(1-降低率)
16、小李以两种形式分别储蓄了2000元和1000元,一年后全部取出,扣除利息所得税后可得利息43.92元,以知这两种储蓄年利率的和为3.24%,问这两种储蓄的年利率各是多少?
17、某商业银行今年现有存款4600万元,与2008年同期相比,定期存款增加了25%,活期存款减少了25%,存款总额增加了15%,2008年有定期存款多少万元?活期存款多少万元?
11、某商场购进商品后,均加价10%作为销售价。现商场搞优惠促销活动,决定由顾客抽奖确定折扣。某顾客购买甲、乙两种商品分别抽到7折和9折,共付款399无。已知这两种商品原销价之各为490元。问这两种商品的进价分别为多少元?
12、工厂去年的利润(总产值—总支出)为200万元.今年总产值增加了20%,总支出比去年减少了10%,今年的利润为780万元.问去年总产值、总支出各是多少万元?
2、方法:代入消元法、加减消元法。先消掉一个未知数,化成二元一次方程组。
3、基本关系量:
(一)销售问题:
·基 本 量:
成本(进价)、售价(实售价)、
利润(亏损额)、利润率(亏损率)
·基本关系:
盈利:售价>进价 利润=售价-进价>0
亏损:售价<进价 利润=售价-进价<0
利润=售价-成本 亏损额=成本-售价、
