数学建模追逐问题
数学建模追逐问题

实验追逐问题L问题提出在图8. 4中,假设正方形ABCD的四个顶点处各站人.在集时刻,四人同时以匀速v 沿顺时针方向追逐卜一个人,并且在任意时刻他们绘终保持追逐的方向是对准追逐目柿"例如、A追逐D任惫时刻A始终向着B追+可Wiil'nJJ四人的运动轨迹将按蛭旋删线状汇合于中心O.怎样证明呢?有两种证明方法.一是分别求出四人的运动轨迹曲纯解析式"求证艸条曲线在某时刻相交[一乩力一方丛则是用计律机模拟将四人的运动轨迹H观地去示在图形上*2.建亡模型及模拟方法模拟步骤;1)建立平面直箱坐标系.2)以时间间3进行采样,在毎一时H+算每个人在卜一时t+加时的坐标.3)不妨设屮的追遂对象是乙,在时MtlbL甲的酸标为(兀$),乙的坐标旳仕2小) + 屮在t+ 3 时的坐标为(”丫1 + cos^j^ +1込『虹口&1Jt屮cos# 二一用inf 二一= J(x2-^i)2 +(v2 - Vi)2a d ~ ~同珅,乙在T+At时的砸标为(x2 4- vAt cos0.y2 +皿f sin &) *4选取足够小的At,模拟到d <vAf时为止.5)连接四人在齐时刻的位社,就得到濟求的轨迹*连纯系统模拟的特点是首先选定一个时间步K (迪常是零间距的)i JC次按时何顺用推进*每推进一个时间步长,就对系统的活动和状态按预定的规则和冃的进行考察"分析r II 算、记录,亘到预定模拟结束条件(通常是时间条件)为止.Matlab程序如下:%取v=1,t=12,A,B,C,D 点的坐标分另为(0, 10), (10, 10) , (10, 0), (0, 0)v=1;dt=0.05;d=20;x=[0 0 0 10 10 10 10 0];x(9)=x(1);x(10)=x(2);holdaxis('equal')axis([0 10 0 10]);for k=1:2:7plot(x(k),x(k+1),'.')endwhile(d>0.1)for i=1:2:7d=sqrt((x(i)-x(i+1))A2+(x(i+1)-x(i+3))A2);x(i)=x(i)+v*dt*(x(i+2)-x(i))/d;x(i+1)=x(i+1)+v*dt*(x(i+3)-x(i+1))/d;plot(x(i),x(i+1),'.')endx(9)= x(1); x(10)= x(2);endhold运行结果如下:狼追击兔子的问题狼追击兔子问题是欧洲文艺复兴时代的著名人物达■芬奇提出的一个数学问题。
数学建模-微分解法-狗追狼问题

数学建模微分作业烟台大学文经学院解:设狼在A 点登岛,此时狗在O 点,以OA 为X 轴建立直角坐标系如下:设t 时刻时,狗到达M 点,其速度1v 分解如上图,则易得2221y x v v v +=(1)。
在极坐标下,狗跑到点M (ρ,θ),分解后对应的直角坐标上有:cos x t ρω=,sin y t ρω=设狼的角速度为ω,由题意知狼、狗、圆心始终在一条直线上,所以狼与狗的角速度相等,且2v Rω=。
分析M 点有:cos sin x dx d v t t dt dtρωρωω==-(2), sin cos y dy d v t t dt dtρωρωω==+(3) 将(2)(3)式带入(1)式得22221d v dt ρωρ⎛⎫=+ ⎪⎝⎭,即d dtρ=解得dt =两边同乘ω得 2221ρωρωω-=v d dt=2221ρωρ-vd=221211ρωωρvv d -两边积分得221211ρωωρωvv d dt -=⎰⎰得1arcsin C t v ωθω⎛⎫+=⎪⎝⎭当0=t 时,0ρ= 所以0=C所以1sin vρθω=(3)根据 222ρ=+y x (4) ()s i n c o s x y ρθθ+=+(5)根据(3)(4)(5)得()221sin cos v x y x y a θθω+=+-又cos x ρθ=R v 2=ω 所以21122v R v y v y y x ==+ω算得狗的运动轨迹方程为 222112222v v x y R R v v ⎛⎫⎛⎫+-=⎪ ⎪⎝⎭⎝⎭ 则该圆必过圆心,且与X 轴相切,所以狗运动的圆心必在Y 轴。
综上所述有以下三种情况: 第一种:当1222v Rv <即12v Rv <时,狗追不上狼。
第二种 当1222v Rv =,即12v Rv =时,狗在B 点追上狼。
第三种:2221Rv v >,即21Rv v >时,狗在C 点追上狼。
数学追赶问题计算公式

数学追赶问题计算公式在咱们学习数学的过程中,有一个特别有趣的知识点,那就是追赶问题。
说起这个追赶问题啊,它就像是一场你追我赶的比赛,充满了挑战和乐趣。
咱们先来说说追赶问题常见的计算公式。
比如说,有甲和乙两个人,甲在前面跑,速度是 V1 ,乙在后面追,速度是 V2 ,开始的时候两人相距 S ,经过时间 t 后乙追上了甲。
那这个时候,追赶问题的基本公式就是:S = (V2 - V1)×t 。
这个公式看起来简单,但是用起来可大有学问。
咱们来举个例子哈,有一天我在公园里散步,看到两个小朋友在玩追逐游戏。
前面的小朋友小明跑得挺快,速度大概是 3 米每秒,后面的小朋友小刚速度能达到 4 米每秒。
一开始他们相距 10 米,那小刚啥时候能追上小明呢?咱们就可以用这个公式来算算。
首先,V1 就是小明的速度 3 米每秒,V2 是小刚的速度 4 米每秒,S 是 10 米。
代入公式就是:10 = (4 - 3)×t ,算一下就知道 t = 10 秒。
也就是说,10 秒后小刚就能追上小明啦。
再比如说,在公路上,一辆汽车 A 以 60 千米每小时的速度行驶,另一辆汽车 B 以 80 千米每小时的速度追赶,两车一开始相距 50 千米。
那 B 车追上 A 车需要多长时间?同样的,V1 是 60 千米每小时,V2 是80 千米每小时,S 是 50 千米。
代入公式 50 = (80 - 60)×t ,算出 t = 2.5 小时。
追赶问题可不只是在这些简单的例子里出现哦。
想象一下,在田径赛场上,长跑运动员之间的追逐;或者是在动物世界里,猎豹追捕羚羊的场景,其实都能用到咱们这个追赶问题的计算公式。
而且啊,在实际生活中,追赶问题的应用也特别广泛。
就像咱们坐地铁的时候,两列地铁先后出发,可能就会存在追赶的情况;还有物流运输中,不同速度的货车送货,也可能涉及到追赶的时间计算。
总之,这个数学中的追赶问题计算公式虽然简单,但用处可真不小。
追逐问题

实验1 追逐问题实验问题四个人甲、乙、丙、丁分别位于边长为10米的正方形ABCD 的四个顶点处.在某一时刻,四人同时出发以匀速v 按顺时针方向跑向下一个人.在行进过程中,如果他们始终保持对准目标,问他们的追逐路线是怎样的?试用计算机求出追逐过程中每个人的行进轨迹.符号说明t :追逐的时间,单位为秒t0:开始追逐的时间,单位为秒tn :终止追逐的时间,单位为秒(x1,y1): 甲在t 时刻处于的坐标位置(x2,y2): 乙在t 时刻处于的坐标位置(x3,y3): 丙在t 时刻处于的坐标位置(x4,y4): 丁在t 时刻处于的坐标位置问题分析与求解建立如图坐标系,则有甲在t=0时刻处于的坐标位置为(0,0)、乙在t=0时刻处于的坐标位置为(0,10)、丙在t=0时刻处于的坐标位置为(10,10)、丁甲在t=0时刻处于的坐标位置为(10,0)。
为了用计算机模拟追逐过程中每个人的行进轨迹,考虑追逐在发生较小时间间隔情况下,每个人的变化位置。
先考虑甲追乙的情况:在时刻t ,甲的坐标为(x1,y1), 乙的坐标为(x2,y2),则甲乙之间的距离 22)21()21(y y x x d -+-=按题意,甲乙位置坐标的连线确定了甲的追逐方向θ1,显然有dx x y y x x x x 12)21()21(121cos 22-=-+--=θdy y y y x x y y 12)21()21(121sin 22-=-+--=θx当追逐又延续了时间间隔∆t 后,假设时间间隔∆t 较小,有甲的坐标变为 (x1+v ∆tcos θ1,y1+v ∆tsin θ1)类似地,有在在时刻由t 变到t+∆t 时,乙的坐标变为:(x2+v ∆tcos θ2,y2+v ∆tsin θ2)22)23()23(232cos y y x x x x -+--=θ 22)23()23(232sin y y x x y y -+--=θ丙的坐标变为:(x3+v ∆tcos θ3,y3+v ∆tsin θ3)22)43()43(343cos y y x x x x -+--=θ 22)43()43(343sin y y x x y y -+--=θ丁的坐标变为:(x4+v ∆tcos θ4,y4+v ∆tsin θ4)22)41()41(414cos y y x x x x -+--=θ 22)41()41(414sin y y x x y y -+--=θ设开始追逐的时间t0=0,将整个追逐时间分为n 等份,每一个时间采样间隔为∆t =tn/n,这样我们可以在每个追逐的时间进行∆t 后利用如上公式依次算出每个人位置变化的坐标,然后用小直线段分别连接每个人的位置坐标,画出相应的图形就可以看到计算机模拟出的追逐路线。
数学建模-猎狗追兔子问题

数学建模论文《数学建模》(2014春)课程期末论文摘要(一)对于问题一:自然科学中存在许多变量,也有许多常量,而我们要善于通过建立合适的模型找到这些变量之中的不变量。
猎狗追赶兔子的问题是我们在生活中常见的实例,而题目把我们生活中的普通的例子抽象成为高等数学中微分方程的例子,通过对高阶微分方程的分析,建立微分方程模型,并用数学软件编写程序求解,得出结论,解决生活中常见的实际问题。
(二)对于问题二:学习使用matlab进行数学模型的求解,掌握常用计算机软件的使用方法。
关键词微分方程导数的几何意义猎狗追兔子数学建模数学软件一、问题重述如图1所示,有一只猎狗在B 点位置,发现了一只兔子在正东北方距离它250m 的地方O 处,此时兔子开始以8m/s 的速度正向正西北方向,距离为150m 的洞口A 全速跑去. 假设猎狗在追赶兔子的时候,始终朝着兔子的方向全速奔跑。
请回答下面的问题:⑴ 猎狗能追上兔子的最小速度是多少? ⑵ 在猎狗能追上兔子的情况下,猎狗跑过的路程 是少?⑶ 假设猎狗在追赶过程中,当猎狗与兔子之间的距离为30m 时,兔子由于害怕导致奔跑速度每秒减半, 而狗却由于兴奋奔跑速度每秒增加0.1倍,在这种情 况下回答前面两个问题。
二、问题分析与假设在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶,所以可以建立平面直角坐标系,通过导数联立起猎狗运动位移,速度和兔子的运动状态。
1.假设兔子的运动是匀速的。
2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。
3.猎狗的运动时匀速或者匀变速的。
4.猎狗运动时总是朝向兔子。
三、模型的建立及求解3.1 符号规定1.(x ,y ):猎狗或者兔子所在位置的坐标。
2. t :从开始到问题结束经过的时间。
3. a:猎狗奔跑的路程。
4. v:猎狗的奔跑速度。
3.2 模型一的建立与求解猎狗能够抓到兔子的必要条件:猎狗的运动轨迹在OA 要有交点以OA 为y 轴,以OB 为x 轴建立坐标系,则由图有O(0,0),A(0,150),B(250,0),兔子的初始位置0点,而猎狗初始位置是B 点,t (s )后猎狗到达了C (x ,y ),而兔子到达了D (0,8t ),则有CD 的连线是猎狗运动轨迹的一条切线,由导数的几何意义有:NW8dy y tdx x-=dav dt =da =三式联立消去t ,得到;设:若猎狗可以追上兔子则有当兔子在OA,猎狗在OB 之间运动时此方程有解,设:得到:得到:两式联立相加得到:1.如果q=1即v=8 m/s 得到所以此情况无交点,所以v=8m/s 猎狗无法追上兔子; 2.如果q<1即v>8m/s 得到此情况有交点,所以有可能能够追上兔子,如果要追上兔子需要y<=150; 解得到: 即所以这种情况下能够追上的最小速度是 .3.如果q>1 利用上式得到,所以这种情况不能追上兔子。
数学建模实验报告大小圆追击问题

数学建模实验报告一.实验题目第一题:设一个小圆在大圆内无滑动的滚动,用Matlab变编程探讨小圆上或小圆内一点的运动轨迹。
问题分析:由题目条件可知,小圆在大圆内无滑动滚动,所以对于小圆与大圆的初始接触点来说,该点滑动的弧长即为小圆滚动的路程。
由此便可以联系小圆与大圆。
首先,分析目标点。
若对小圆上一点进行观察,对于任意两点,从它不再与大圆接触到再一次与大圆接触,其运动轨迹必然是相同的(仅讨论轨迹弧线的形状,初末位置不做要求)。
所以,我们可以以初始位置时的接触点来考察运动轨迹。
若对小圆内(非圆心)一点进行考察,则其轨迹必与其在小圆上的对应点相似。
故可以先计算出小圆上对应点的轨迹,然后缩放移动即可。
若对小圆圆心进行考察,则易知其轨迹必为一圆。
分析完成后,下面开始讨论轨迹的计算方法。
由于除圆心外,轨迹是类似于摆线的一条曲线,所以用参数方程进行求解。
具体做法是以大圆圆心为原点,建立一个直角坐标系。
由于小圆的初始位置与小圆上或小圆内一点的运动轨迹无关,所以,我们不妨设小圆与大圆初始位置时的接触点在X轴正半轴上。
之后再以小圆的圆心建立一个直角坐标系。
对于这个坐标系里的任一点,可以利用向量的计算方法,由于大圆圆心和小圆圆心连线的向量是可求的,所以可将该点投影到以大圆圆心建立的坐标系中。
在计算该点的参数方程时,可使用公式l=Ra,a为圆心角。
先求出该点在以小圆圆心为原点的坐标系中的参数方程,然后投影至另一坐标系中即可。
若观察的是圆上一点,则只需将原程序中的小圆半径换成该点到小圆圆心的距离即可。
具体计算过程如下:Matlab代码:h=0.1;q=0:h:20*pi;R=5;r=3; d=2;v=-R/r;xR=R*cos(q);yR=R*sin(q);xrh=(R-r)*cos(q);yrh=(R-r)*sin(q);xr=xh+d*cos(v*q+q);yr=yh+d*sin(v*q+q);plot(xh,yh,xx,yy,xz,yz);结果截图:绿色为大圆,半径10,蓝色为小圆圆心轨迹,小圆半径为3,红色为小圆上一点轨迹。
饿狼追兔问题数学建模

饿狼追兔问题数学建模数学建模饿狼追兔问题摘要本文研究饿狼追兔问题,是在给定狼兔相对位置,以及兔子巢穴位置的情况下求解的,狼的速度是兔子速度两倍,在不考虑其他任何因素的情况下研究狼能否追上兔子的问题。
首先,我们对问题进行了适当的分析,然后根据已知条件建立了狼的运动轨迹微分模型。
其次,根据建好的模型,运用MATLAB编程,然后仿真画出了饿狼和野兔的运动轨迹图。
再次,用解析方法将建立的模型求解,并给出该问题的结论,准确的回答题目。
最后,用数值方法求解,将所求与前面所求进行对比,也给出结论,回答题目。
并将两种方法做相应比较。
结论:野兔可以安全回巢关键词:算法高阶常微分方程§1.1问题的提出在自然界中,各种生物都有它的生活规律,它们钩心斗角,各项神通,在饿狼追野兔的工程中,饿狼的速度是野兔的二倍,但是野兔有自己的洞穴,野兔在跑到自己洞穴之前被狼捉住,野兔就将会成为饿狼的囊中之物;如果野兔在饿狼捉住自己之前跑回到自己的洞穴,那么野兔就保住小命,得以生还。
图1-1-1为饿狼追野兔的两条曲线,其中绿线表示野兔,图中的箭头表示的是野兔的奔跑方向,野兔从远点开始沿y轴正方向运动,其洞穴在坐标为(0,60)的位置;红线为饿狼的运动轨迹,,图中的剪头表示饿狼追逐野兔的方向,饿狼从坐标为(100,0)的方向追逐野兔,饿狼的速度是野兔速度的二倍。
建立数学模型需研究一下几个问题:(1)设野兔的速度我v0,饿狼的速度为v1,野兔的奔跑方向是沿y轴正方向奔跑,而饿狼的方向是一直指向野兔的方向,即饿狼的运动的轨迹某一时候的切线指向同一时刻的野兔的位置。
建立饿狼追野兔的运动轨迹微分模型。
(2)根据建立的饿狼运动轨迹得微分模型,作出饿狼与野兔的运动轨迹图形。
(3)用解析方法求解,即根据第二步作出的饿狼渔业突地运动轨迹图形,分析兔子能否安全回到巢穴,即野兔的运动曲线与饿狼的运动曲线的交点是在点(0,60)-野兔巢穴的上面还是下面。
四只乌龟追逐问题
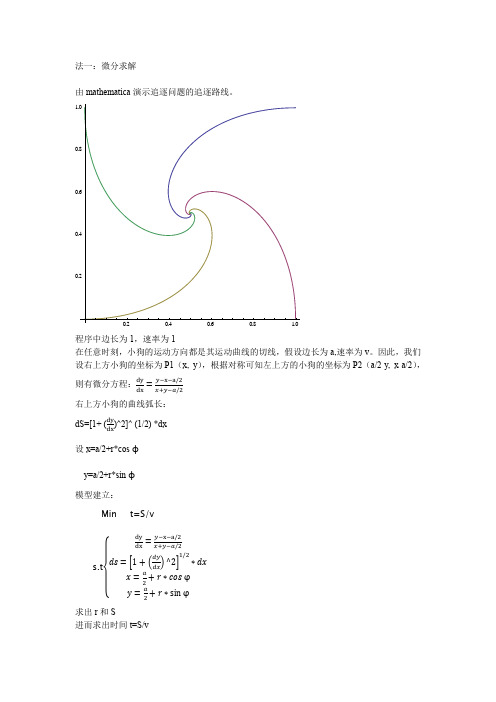
已知4只小狗可拓展模型为n只小狗的追逐问题,即模型为边长为a的n边形,最后在中心点相遇。
dS=[1+ ( )^2]^ (1 Nhomakorabea2) *dx
设x=a/2+r*cosφ
y=a/2+r*sinφ
模型建立:
Min t=S/v
s.t
求出r和S
进而求出时间t=S/v
法二:看图求解
每个时刻,四只小狗所在四点总是圆的四等分点,此圆的半径不断缩小,最后到达中心。每只小狗速度可分解为一个向心速度及一个切向速度,切向速度不改变圆的半径,半径的改变取决于向心速度。运动速度v已知,所以向心速度是它的 ,又由于从顶点到中心的路程为边长的 ,所以时间t=( =a/v
法一:微分求解
由mathematica演示追逐问题的追逐路线。
程序中边长为1,速率为1
在任意时刻,小狗的运动方向都是其运动曲线的切线,假设边长为a,速率为v。因此,我们设右上方小狗的坐标为P1(x,y),根据对称可知左上方的小狗的坐标为P2(a/2-y, x-a/2),则有微分方程:
右上方小狗的曲线弧长:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验追逐问题
Matlab程序如下:
%取v=1,t=12,A,B,C,D点的坐标分另为(0,10),(10,10),(10,0),(0, 0) v=1;
dt=0.05;
d=20;
x=[0 0 0 10 10 10 10 0];
x(9)=x(1);
x(10)=x(2);
hold
axis('equal')
axis([0 10 0 10]);
for k=1:2:7
plot(x(k),x(k+1),'.' )
end
while(d>0.1)
for i=1:2:7
d=sqrt((x(i)-x(i+1))^2+(x(i+1)-x(i+3))^2);
x(i)=x(i)+v*dt*(x(i+2)-x(i))/d;
x(i+1)=x(i+1)+v*dt*(x(i+3)-x(i+1))/d;
plot(x(i),x(i+1),'.')
end
x(9)= x(1);
x(10)= x(2);
end
hold
运行结果如下:
狼追击兔子的问题狼追击兔子问题是欧洲文艺复兴时代的著名人物达.芬奇提出的一个数学问题。
当一个兔子正在它的洞穴南面60码处觅食时,一只恶狼出现在兔子正东的100码处。
当两只动物同时发现对方以后,兔子奔向自己的洞穴,狼以快于兔子一倍的速度紧追兔子不放。
狼在追赶过程中所形成的轨迹就是追击曲线。
狼是否会在兔子跑回洞穴之前追赶上兔子?
为了研究狼是否能够追上兔子,可以先考虑求出狼追兔子形成的追击曲线,然后根据曲线来确定狼是否能够追上兔子。
可以对狼与兔子的追击过程通过计算机进行模拟,然后从模拟结果获取。
模拟程序如下,程序文件名sim_langtu.m:
function sim_langtu
%《狼兔追击问题》
%(离散模拟)
%这里没有具体考虑狼、兔的具体速度
%主要通过二者的速度倍速关系及方向向量奔跑过程
Q=[0 0];%兔子坐标
P=[100 0];%狼坐标
PQ=Q-P;%狼兔方向向量
step =1;%模拟步长:兔子奔跑的距离,step越小就越精确
count = 60/step;%以兔子的奔跑距离划分
PQ=PQ/norm(PQ)*step;%归一化,单位向量
trackP=P;
trackQ=Q;
for k=1:count;
P = P + 2*PQ;%2倍速度
Q = Q + step*[0 1];%[0 1]为兔子奔跑方向的单位方向向量
PQ = Q - P;
trackP(1+k,:)=P;
trackQ(1+k,:)=Q;
PQ=PQ/norm(PQ)*step;%归一化,单位向量
dis= sqrt(sum((P-Q).^2));
plot(trackP(:,1),trackP(:,2),'*',Q(1),Q(2),'rp',0,60,'r+' );
pause(0.5)
end%for
dis%兔子到达窝边时,狼兔之间的距离
P %兔子到达窝边时,狼的坐标
Q %兔子到达窝边时,兔子的坐标
(二)模拟程序运行结果
dis =
7.0619
P =
1.6805 53.1410
Q =
0 60
注:如果修改程序中的step赋值,则结果稍有不同。
程序结束后,输出狼兔的位置图如下。
通过下图可以直观的看到,当兔子回到窝边时,狼还与兔子有一段距离,这表示兔子成功逃脱。
