人教版几何模型基本图形编辑版

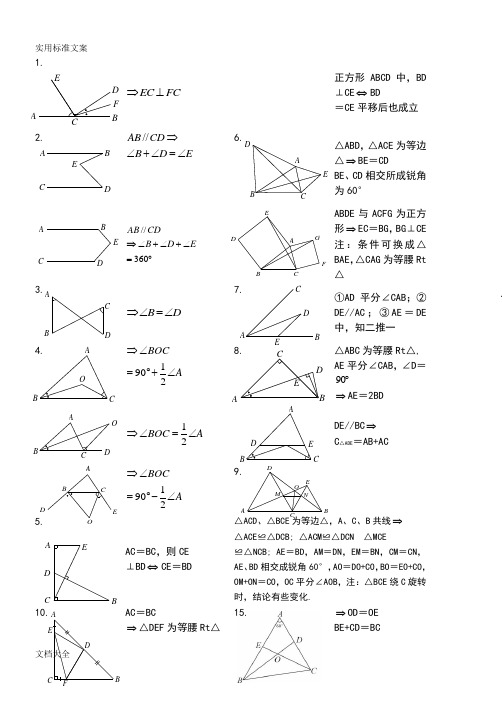
ABC DEA C DBE A BC DDABDEFGDABCEADC BECN OMDAE BA DE FBOEA BCDA1. EC FC ⇒⊥正方形ABCD 中，BD ⊥CE ⇔BD ＝CE 平移后也成立2. //AB CD B D E⇒∠+∠=∠6.△ABD ，△ACE 为等边△⇒BE ＝CD BE 、CD 相交所成锐角为60° //360AB CDB D E ⇒∠+∠+∠=︒ABDE 与ACFG 为正方形⇒EC ＝BG ，BG ⊥CE 注：条件可换成△BAE ，△CAG 为等腰Rt △ 3. B D ⇒∠=∠7.①AD 平分∠CAB ；②DE//AC ；③AE ＝DE 中，知二推一1902BOCA⇒∠=︒+∠ 8.△ABC 为等腰Rt △,AE 平分∠CAB ，∠D ＝90︒⇒AE ＝2BD12BOC A ⇒∠=∠DE//BC ⇒C △ADE ＝AB+AC1902BOCA⇒∠=︒-∠ 9.5.AC ＝BC ，则CE ⊥BD ⇔CE ＝BD△ACD 、△BCE 为等边△，A 、C 、B 共线⇒ △ACE ≌△DCB; △ACM ≌△DCN △MCE≌△NCB; AE ＝BD ，AM ＝DN ，EM ＝BN ，CM ＝CN ，AE 、BD 相交成锐角60°，AO ＝DO+CO ，BO ＝EO+CO ，OM+ON ＝CO ，OC 平分∠AOB ，注：△BCE 绕C 旋转时，结论有些变化.10.AC ＝BC⇒△DEF 为等腰Rt △15.⇒OD ＝OEBE+CD ＝BCA ABCD21D CBAE FE F A ′B ′C′O ABCDAD BCEFE FMA C DB F MGAB C DE45︒FEA BCD ⇒PB+PC ＝2PD∠ABP+∠C ＝180°16.AD ＝CD⇔CD ＝BD ⇔AD ＝BDAB ＝AC⇒AE+BE ＝BC17.⇒∠A ＝∠B或∠A+∠B ＝180°12.AC ＝BC⇒∠ADC ＝∠BDF ； CF+DF ＝AD18.⇒DE+BF ＝EFAE 平分∠DEF ，AF 平分∠BFE13.⇒CD ＝CE ＝BGCEFD 为菱形∠2＝2∠1⇒AF ＝BC+CF14.AB ＝AC⇒DE+DF ＝BM （钝角△也成立）⇒AE+CF ＝CDEF ＝OES 四边形OEBF ＝14a 2等腰梯形⇒EF+EG ＝CM⇒BE+DF=AEEFDCBAGHA B CDE FE B A CDA BCNM DF AB CE H 1ADBCB ACD EFEC BADAB CDFEA BCDEFABCDEF1A BCDE G AD19.BF=AD ⇔BF ⊥AD⇒∠1＝∠B△ADC ∽△CDB ∽△ACB AC 2=AD·AB BC 2＝BD·BA AC·BC ＝AB·CD CD 2＝AD·BDBF=AC ⇔BF ⊥AC25.∠C ＝∠D⇔△ABC ∽△ADE ⇔AB·AD ＝AC·AE 20.中点四边形EFGH 至少是 ，取决于AC 、BD 的关系，EF ，EH 的关系对应AC 、BD 的关系26.∠B ＝∠E⇔△ADE ∽△ACB ⇔AD·AB ＝AC·AE 21. 梯形ABCD 中： ①AE ＝BE ；②AD+BC ＝CD ； ③DE ⊥CE ，知二推一27.⇒DF ＝EF22. ⇒AM 2+BN 2＝MN 228.2AE AFED BF⇒=23. AD ＝BC ＝a ，BF ＝CF ⇒HF+HD ＝a29. ⇒EF//ADEF ＝12(BC －AD)24.∠1＝∠C⇔△ADE ∽△ACB ⇔AD·AB ＝AE·AC 30.⇒AN DGAM BC=∠1＝∠BO MDCB AE N OFABCDENMOD C B AFAE N A B C D E M a aM ABODEMEA CN B D F EB C D A M PABN DC⇔△ADC ∽△ACB ⇔∠ADC ＝∠ACB⇔AC 2=AD·AB 31. DE//BC ⇒DN ＝EN ，BM ＝CM 35.⇒AO ＝2DOBO ＝2EOCO ＝2FO⇒MO ＝NO 112AD BC MN+=⇒AB BM BNAC CM CN==32. ⇒DM BN EM CN = 当DM ＝EM 时， 则BN ＝CN 37.⇒222OD DE a +=222OD DE a +=同上33.⇒111AB CD EF +=34.AD ＝DC ，PN//BD⇒PN+MN ＝2BDAB ＝AC⇒PE+PF ＝2ADMAO BCP1半弧所对的圆心角等于整弧所对的圆心角 AOC APB ⇒∠=∠2（1）五元素：①CD 过圆心O ；②CD ⊥AB ；③AM ＝BM ；④ ADBD ＝；⑤ AC BC ＝中，知二推三。

注：由①③推另三，需附加条件AB 不是直径。

（2）图形中弦长、半径、弦心距、弓高已知两个量，则另二可求。

3D CB OA ME FG2EC FD AE FG AE BF OM⇒==+= 若AB 、EF 相交，则|AE —BF|＝2OM⇓EC FC AE FG AE BF AB⇒==+= 411802C AOB ⇒∠=︒-∠OB A5. 共斜边的两直角三角形，四个顶点在同一圆上。

BACDDCAB6①△任意两边之积等于第三边上的高与其外接圆直径之积。

如：AB ·AC ＝AD ·2R （钝角△也适用）； ②正弦定理：2sin BCR BAC=∠（不能直接用，可构造以直径为斜边的Rt △，利用三角函数求。

）7DC AEF B//CD EF ⇒812OE BC ⇒=FM 的延长线平分AC9M F EOABC DAM CM FM ⇒== AC ＝EC21212CD AE AC AM AE AD AB OM BF ====10BD CD ⇒= △ABE ∽△ADC ∽△CDE△ABD ∽△AEC ∽△BED BD 2＝CD 2＝DE ·DA AB ·AC ＝AE ·AD AE ·DE ＝BE ·CD*2cos AB ACBAD AD+=∠若I 为△ABC 内心，则BT ＝CD ＝ID ，关注∠BAC 为特殊角时图形的特殊性、及相关比值。

11HE M O FDCBAHD FD ⇒= CH ⊥ABH 点关于AC 的对称点在圆上，H 点关于AB 的对称点在AB 上， 12OM AH =12ABD ＝CD ⇔AD 平分△CAE13①AD ⊥CD ；②AC 平分△DAB ； ③DC 切⊙O 于C中，知二推一。

14PD PO PM PN ⇒=△PDM ∽△PNOCA 平分∠PCD △OND ∽△OPN15EFOCBA D1902BOC A ⇒∠=︒+∠2/1902ABC ABCBO DEr S C DEF A∆∆⊥=∠=︒-∠⇓EA2a b cr +-⇒=16abr a b⇒=+（注AC 与BC 不一定相等）17⇒①BO ⊥OA ；②RQ 切⊙O 于Q 。

③RP ＝RQ 中，知二推一⇒OR 可上、下平移，Q 也可在AB 上 18⇒AB+CD ＝AD+BC22AP BP r OP⇒=-P22PA PB OP r⇒=-20B AE BF CG DG⇒==211(180)2PDEC PA PBDOE P∆⇒=+∠=︒-∠22 BE BD⇒=△PBD∽△PCE △PBE∽△PAD△PBA∽△PCB BE·BD＝AD·CE若AC是直径，则△ADP＝45°*若△BDE为等腰Rt△或等边△时，上述结论有些变化。

AC EC⇒=CB＝CGF为△ABC的内心其它同前（10）题24D①AD平分∠BAC；②BC//MN；③MN切⊙O于D中，知二推一。

25①EA切⊙O于A；②AE//CF；③AP＝EP中，知二推一。

2622cosAC AG AFFC FE CECFAFA AC⇒=+==∠。