人教版几何模型基本图形
6.1几何图形 (课件)人教版(2024)数学七年级上册

(1)展开图全是长方形或正方形时,要考虑长方体或正
方体;
(2)展开图中有三角形时,要考虑三棱柱或棱锥;
(3)展开图中有长方形(或正方形)和圆时,要考虑圆柱;
(4)展开图中有扇形时,要考虑圆锥.
感悟新知
知4-练
6-1.[期末·北京大兴区] 如图是由下列哪个立体图形展开得 到的?( B ) A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
( B) A.1 种 C.3 种
B.2 种 D.4 种
感悟新知
知4-练
例 8 [立德树人 家国情怀]小红通过学习中国现代史了解到遵义 会议是中国共产党成立以来,第一次独立自主地运用马列
主义基本原理解决自己的路线、方针和政策问题的会议. 如图6.1-11,她将路线、方针、政策六个字分别填写在正 方体的展开图上,折叠成正方体后,
▲▲▲
综合应用创新
题型 2 列代数式表示实际问题
例 12 [新趋势 学科内综合]如图6.1-18,这是一个正方体的 表面展开图,且正方体相对面上的两个数互为相反数.
综合应用创新
(1)a=__3__,b=_-__1_,c=__5__; 解题秘方:根据正方体的表面展开图特点找到a,b,c 相对应的数字,再根据相反数的概念即可解题. 解:由正方体的表面展开图特点可知,a 与-3 相对,b 与1 相对,c 与-5 相对. 因为正方体相对面上的两个数 互为相反数,所以a=3,b=-1,c=5 .
点:线• 和• 线• 相• 交• 的地方是点.
感悟新知
2. 点、线、面、体的关系
知5-讲
感悟新知
知5-讲
特别解读
1. 几何中的点只有位置,没有大小;线只有长短,没
有粗细;面只有大小,没有薄厚.
三角形全等几何模型(一线三等角)(人教版)(学生版) 2024-2025学年八年级数学上册专项突破

专题12.11三角形全等几何模型(一线三等角)第一部分【知识点归纳】【知识点一】一线三直角模型1.基本图形题型特征:如图1,在直线BC上出现三个直角,如图中∠B=∠ACE=∠D=90°图1图2图3解题方法:只要题目再出现一组等边(AB=CD或BC=DE或CA=CE),可证△ABE≌△ECD(AAS 或ASA)结论延伸1:如图2,两个直角三角形在直线两侧时,同样成立结论延伸2:图1中连接AE,得到如图3,可得以下结论:(1)四边形ABDE为直角梯形;AB+DE=BC(上底+下底=高)【知识点二】一线三等角模型图4图5题型特征:如图4,图形的某条线段上出现三个相等的角,如图中∠B=∠ACE=∠D解题方法:只要题目再出现一组等边(BA=CD或BC=DA或CA=DC),必证△ABC≌△CDE(AAS或ASA)结论延伸:如图5,两个三角形在直线两侧时,同样成立第二部分【题型展示与方法点拨】【题型1】直接用“一线三直角”模型求值或证明【例1】(23-24八年级上·安徽合肥·期末)如图,在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C ,且AD MN ⊥,BE MN ⊥,垂足分别为D E 、.(1)求证:ADC CEB ≌;(2)若3cm =AD ,5cm BE =,求四边形ABED 的面积.【变式1】(23-24八年级上·湖北武汉·阶段练习)如图,小虎用10块高度都是3cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC BC =,90ACB ∠=︒),点C 在DE 上,点A 和B 分别与木墙的顶端重合,则两堵木墙之间的距离DE 的长度为()A .30cmB .27cmC .21cmD .10cm【变式2】(23-24九年级下·重庆开州·阶段练习)如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D 为BC 上一点,连接AD .过点B 作BE AD ⊥于点E ,过点C 作CF AD ⊥交AD 的延长线于点F .若5BE =,2CF =,则EF 的长度为.【题型2】直接用“一线三等角”模型求值或证明【例2】(23-24八年级上·新疆昌吉·期中)已知ABC 是直角三角形,90BAC AB AC ∠=︒=,,直线l 经过点A ,分别过点B 、C 向直线l 作垂线,垂足分别为D 、E(1)如图a ,当点B 、C 位于直线l 的同侧时,证明:ABD CAE≌(2)如图b ,锐角ABC 中,AB AC =,直线l 经过点A ,点D 、E 分别在直线l 上,点B ,C 位于l 的同一侧,如果CEA ADB BAC ∠=∠=∠,请找到图中的全等三角形,并写出线段ED EC 、和DB 之间的数量关系【变式1】(21-22八年级上·浙江温州·期中)如图,在△ABC 中,AB =AC =9,点E 在边AC 上,AE 的中垂线交BC 于点D ,若∠ADE =∠B ,CD =3BD ,则CE 等于()A .3B .2C .94D .92【变式2】(23-24七年级下·吉林长春·期中)如图,在ABC 中,AB AC =,AB BC >,点D 在边BC 上,且2CD BD =,点E 、F 在线段AD 上.CFD BED BAC ∠=∠=∠,ABC 的面积为18,则ABE 与CDF 的面积之和.【题型3】构造“一线三直角”模型求值或证明【例3】(23-24八年级上·山西吕梁·期末)数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系问题情境:如图1,三角形纸片ABC 中,90ACB ∠=︒,AC BC =.将点C 放在直线l 上,点A ,B 位于直线l 的同侧,过点A 作AD l ⊥于点D初步探究:(1)在图1的直线l 上取点E ,使BE BC =,得到图2,猜想线段CE 与AD 的数量关系,并说明理由;(2)小颖又拿了一张三角形纸片MPN 继续进行拼图操作,其中90MPN ∠=︒,MP NP =.小颖在图1的基础上,将三角形纸片MPN 的顶点P 放在直线l 上,点M 与点B 重合,过点N 作NH l ⊥于点H .如图3,探究线段CP ,AD ,NH 之间的数量关系,并说明理由【变式1】(23-24八年级上·新疆喀什·期中)如图,906AC AB BD ABD BC ==∠=︒=,,,则BCD △的面积为()A .9B .6C .10D .12【变式2】(20-21七年级下·黑龙江哈尔滨·期末)如图,在ABC 中,90ABC ∠=︒,过点C 作CD AC ⊥,且CD AC =,连接BD ,若92BCD S = ,则BC 的长为.【题型4】“一线三直(等)角”模型的延伸与拓展【例4】如图,A 点的坐标为(0,3),B 点的坐标为(-3.0),D 为x 轴上的一个动点,AE ⊥AD ,且AE=AD ,连接BE 交y 轴于点M(1)若D点的坐标为(-5.0),求E点的坐标:(2)求证:M为BE的中点(3)当D点在x轴上运动时,探索:OMBD为定值【变式1】(23-24八年级上·陕西西安·阶段练习)勾股定理被誉为“几何明珠”.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图所示,把一个边长分别为3,4,5的三角形和三个正方形放置在大长方形ABCD中,则该长方形中空白部分的面积为()A.54B.60C.100D.110【变式2】已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是.第三部分【中考链接与拓展延伸】1、直通中考【例1】(2021·四川南充·中考真题)如图,90BAC ∠=︒,AD 是BAC ∠内部一条射线,若AB AC =,BE AD ⊥于点E ,CF AD ⊥于点F .求证:AF BE =.【例2】(2023·重庆·中考真题)如图,在Rt ABC △中,90BAC ∠= ,AB AC =,点D 为BC 上一点,连接AD .过点B 作BE AD ⊥于点E ,过点C 作CF AD ⊥交AD 的延长线于点F .若4BE =,1CF =,则EF 的长度为.2、拓展延伸【例1】(22-23八年级下·河南洛阳·期中)综合与实践数学活动课上,老师让同学们以“过等腰三角形顶点的直线”为主题开展数学探究.(1)操作发现:如图甲,在Rt ABC △中,90BAC ∠=︒,且AB AC =,直线l 经过点A .小华分别过B 、C 两点作直线l 的垂线,垂足分别为点D 、E .易证ABD CAE △△≌,此时,线段DE 、BD 、CE 的数量关系为:;(2)拓展应用:如图乙,ABC 为等腰直角三角形,90ACB ∠=︒,已知点C 的坐标为(2,0)-,点B 的坐标为(1,2).请利用小华的发现直接写出点A 的坐标:;(3)迁移探究:①如图丙,小华又作了一个等腰ABC ,AB AC =,且90BAC ∠≠︒,她在直线l 上取两点D 、E ,使得BAC BDA AEC ∠=∠=∠,请你帮助小华判断(1)中线段DE 、BD 、CE 的数量关系是否变化,若不变,请证明;若变化,写出它们的关系式并说明理由;②如图丁,ABC 中,2AB AC =,90BAC ∠≠︒,点D 、E 在直线l 上,且BAC BDA AEC ∠=∠=∠,请直接写出线段DE 、BD 、CE 的数量关系.【例2】(22-23八年级上·广东惠州·期中)如图1,90ACB AC BC AD CE BE CE ∠==⊥⊥,,,,垂足分别为D ,E .(1)若 2.5cm 1.7cm AD DE ==,,求BE 的长.(2)在其它条件不变的前提下,将CE 所在直线变换到ABC 的外部(如图2),请你猜想AD DE BE ,,三者之间的数量关系,并证明你的结论;(3)如图3,将(1)中的条件改为:在ABC 中,AC BC =,D ,C ,E 三点在同一条直线上,并且有BEC ADC BCA α∠=∠=∠=,其中α为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由.。
人教版初中数学一年级上册《几何图形- 点、线、面、体》图文课件

线 动 成 面
直角三角形绕一直 角边旋转成圆锥体
长方形绕一边旋 转成圆柱体
点动成—— 线 线动成—— 面
面动成—— 体
(动态)
体是由面围成 面与面相交成线 线与线相交成点
(静态)
练一练:把下面第一行的平面图形绕线 旋转一周,便能形成第二行的某个几何 体,请用虚线连一连:
1
2
3
4
5
A
B
C
D
2.老师叫小明在地上画圆圈,并交给了他两件东西:
一支粉笔和一根细绳,小明很快画好了,你知道他
是怎样画的吗?
从中体现了怎样的数学知识?
3. ①飞机飞行表演在空中留下漂亮的“彩 带”,用数学知识解释为: 点动成。线
②把一张纸对折,形成一条折痕,用数学知 识解释为: 面面相交形。成线
● 你学到了什么?
1、多姿多彩的图形是由点、线、面、体组 成。点是构成图形的基本元素。
面与面相交的地方形成线
点
点
天上的星星、地图上的城市等都给我们以点的形象。
线和线相交的地方是点。
练一练:下图是一个长方体的模型,它 有几个面?面和面相交的地方形成了几 条线?线和线相交成几个点?
·· ·· ·· ··
6个面 12条线 8个点
几何图形是由点、线、面、体组成的
点动成线
点 动 成 线
E
为什么北 京市在右 边地图上 几乎占了 整个版面
点无大小 北京市地图
为什么在 左边地图 上北京只 是一个点
点
是构成图形 的基本元素
点、线、面、体经过运动 变化,形成多姿多彩世界。
点、线、面、体经过运动 变化,形成多姿多彩世界。
点、线、面、体经过运动 变化,形成多姿多彩世界。
九年级数学几何模型

九年级数学几何模型一、相似三角形模型。
1. A字模型。
- 基本图形:在三角形ABC中,DE平行于BC,则三角形ADE相似于三角形ABC。
- 性质:对应边成比例,即(AD)/(AB)=(AE)/(AC)=(DE)/(BC)。
- 应用:在很多几何证明和计算中,若已知平行关系和部分线段长度,可以利用此模型求出其他线段的长度。
例如,已知AD = 2,AB = 5,BC = 6,求DE的长度。
根据(DE)/(BC)=(AD)/(AB),可得DE=(AD× BC)/(AB)=(2×6)/(5)=(12)/(5)。
2. 8字模型。
- 基本图形:若有四边形ABDC,其中AB与CD相交于点E,则三角形AEC相似于三角形BED。
- 性质:(AE)/(BE)=(CE)/(DE),并且AE× DE = BE× CE。
- 应用:在求解线段比例关系或者证明线段乘积相等时经常用到。
比如在一个几何图形中,已知AE = 3,BE = 4,CE = 6,求DE的长度。
根据AE× DE = BE×CE,可得DE=(BE× CE)/(AE)=(4×6)/(3)=8。
3. 母子相似三角形模型(射影定理模型)- 基本图形:在直角三角形ABC中,∠ ACB = 90^∘,CD垂直于AB于点D。
则三角形ACD相似于三角形ABC,三角形BCD相似于三角形BAC,三角形ACD相似于三角形CBD。
- 性质:- 在三角形ACD与三角形ABC中,AC^2=AD× AB。
- 在三角形BCD与三角形BAC中,BC^2=BD× AB。
- 在三角形ACD与三角形CBD中,CD^2=AD× BD。
- 应用:在涉及直角三角形中的线段长度计算和比例关系证明时非常有用。
例如,在直角三角形ABC中,∠ ACB = 90^∘,CD垂直于AB,AD = 2,DB = 8,求AC 的长度。
新人教版七年级数学上册《几何图形初步》精品课件(共37张PPT)

四棱柱 五棱柱
六棱柱
圆锥
锥体
三棱锥
棱锥
四棱锥 五棱锥
六棱锥
认识多面体
若围成立体图形的面是平的面,这样的立体图形又称为多面体
著名的欧拉公式:
多面体可以按面数V来+分F类-E,=如2下列图形中:
V:点、 E:棱、 F:面
四面体
六面体
八面体
正视图 从正面看
• 观察 • 立体图
三视图
左视图 从左面看 俯视图 从上面看
D
O
使DB=2CD,延长DC到A,使AC= 1 CB, C
若AB=10,则CD= ______
2
A CD
B
用一个大写字母表示点,1.当角的顶点处只有一个角时,可用表示 用二个大写字母表示线,顶 2.在点顶的点一处个加大上写弧字线母注表上示数; 字; 用三个大写字母表示角,3.在顶点处加上弧线注上希腊字母.
练 习: ⑺在以O为端点的两条射线上,分别取线段OA 、OB二等分OA 、OB,分别得 中点M、N,连结A、B并连结M、N。
• 2.如图:用所给的字母表示图中分别有直线_____,射线
B
______________,线段____
A
DE
CD 、CE、AB
AC DC E
3.填空:⑴如果两条直线有一个公共点,那么这两
A
B
C
o
1
ABC
o
1
1周角=3600 1平角=1800 小于平角的角按角的大小分类
▪ 锐角:小于直角的角; ▪ 直角:平角的一半(900); ▪ 钝角:大于直角且小于平角的角.
角度的转化: 1°=60′ 1′=60 〞 1°=3600 〞
角度的加减: 1.同种形式相加减; 2.度加(减)度;分加(减)分; 秒加(减)秒 3.超60进一;减一成60
人教版几何模型基本图形
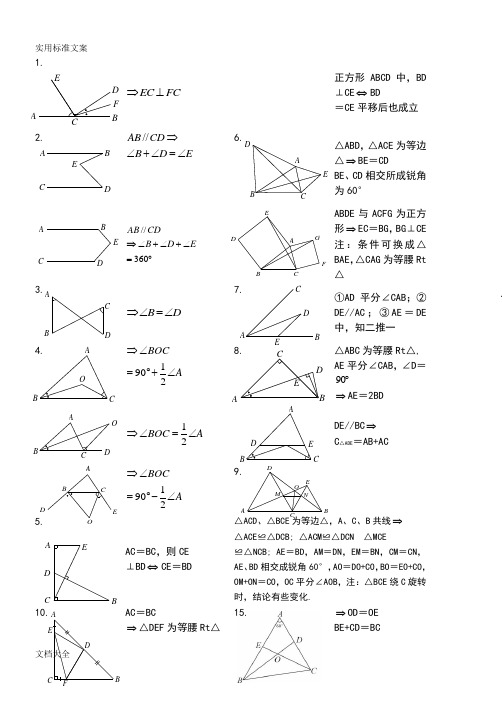
A BC DEAC DBEABCDDABDEFGD AB CEADCBECNOMDAEC BAEFBOEABCDA1.EC FC⇒⊥正方形ABCD中,BD⊥CE⇔BD=CE平移后也成立2. //AB CDB D E⇒∠+∠=∠6.△ABD,△ACE为等边△⇒BE=CDBE、CD相交所成锐角为60°//360AB CDB D E⇒∠+∠+∠=︒ABDE与ACFG为正方形⇒EC=BG,BG⊥CE注:条件可换成△BAE,△CAG为等腰Rt△3.B D⇒∠=∠7.①AD平分∠CAB;②DE//AC;③AE=DE中,知二推一1902BOCA⇒∠=︒+∠8. △ABC为等腰Rt△,AE平分∠CAB,∠D=90︒⇒AE=2BD12BOC A⇒∠=∠DE//BC⇒C△ADE=AB+AC1902BOCA⇒∠=︒-∠9.AC=BC,则CE⊥BD⇔CE=BD△ACD、△BCE为等边△,A、C、B共线⇒△ACE≌△DCB; △ACM≌△DCN △MCE≌△NCB; AE=BD,AM=DN,EM=BN,CM=CN,AE、BD相交成锐角60°,AO=DO+CO,BO=EO+CO,OM+ON=CO,OC平分∠AOB,注:△BCE绕C旋转时,结论有些变化.10. AC=BC⇒△DEF为等腰Rt△15. ⇒OD=OEBE+CD=BCA ABCD21D CBAE FE F A ′B ′C′O ABCDAD BCEFE FMA C DB F MGAB C DE45︒FEABCD ⇒PB+PC =2PD ∠ABP+∠C =180°16.AD =CD ⇔CD =BD ⇔AD =BDAB =AC⇒AE+BE =BC17.⇒∠A =∠B或∠A+∠B =180°12.AC =BC⇒∠ADC =∠BDF ; CF+DF =AD18. ⇒DE+BF =EFAE 平分∠DEF ,AF 平分∠BFE13.⇒CD =CE =BG CEFD 为菱形∠2=2∠1 ⇒AF =BC+CF14.AB =AC⇒DE+DF =BM (钝角△也成立)⇒AE+CF =CDEF OES 四边形OEBF =14a 2等腰梯形 ⇒EF+EG =CM⇒BE+DF=AEEFDCBAGHA B CDE FE B A CDABCNM DF AB CE H 1ADBCB ACDEFEC BADAB CDFEA BCDEFABCDEFA 19.BF=AD ⇔BF ⊥AD⇒∠1=∠B△ADC ∽△CDB ∽△ACB AC 2=AD ·AB BC 2=BD ·BAAC ·BC =AB ·CD CD 2=AD ·BD BF=AC ⇔BF ⊥AC25.∠C =∠D⇔△ABC ∽△ADE ⇔AB ·AD =AC ·AE 20.中点四边形EFGH 至少是,取决于AC 、BD 的关系,EF ,EH 的关系对应AC 、BD 的关系26.∠B =∠E⇔△ADE ∽△ACB ⇔AD ·AB =AC ·AE21. 梯形ABCD 中: ①AE =BE ; ②AD+BC =CD ;③DE ⊥CE ,知二推一27.⇒DF =EF22. ⇒AM 2+BN 2=MN 228.2AE AFED BF⇒=23.AD =BC =a ,BF =CF⇒HF+HD =a29. ⇒EF//ADEF =12(BC -AD)OMDCB AE N OFABCDENMOD C B A N A B C D EM aaM ABODE MEA CN B D FEB C D A1D CBA G E ABCDM FA24.∠1=∠C⇔△ADE ∽△ACB ⇔AD ·AB =AE ·AC 30.⇒AN DGAM BC=∠1=∠B⇔△ADC ∽△ACB ⇔∠ADC =∠ACB ⇔AC 2=AD ·AB31.DE//BC⇒DN =EN , BM =CM35.⇒AO =2DO BO =2EO CO =2FO⇒MO =NO112AD BC MN +=⇒AB BM BNAC CM CN==32.⇒DM BN EM CN = 当DM =EM 时, 则BN =CN37.⇒222OD DE a += 222OD DE a +=同上33.⇒111AB CD EF+=34.AD =DC ,PN//BD ⇒PN+MN =2BDP FAB CDE MAO BCPAB =AC⇒PE+PF =2AD1半弧所对的圆心角等于整弧所对的圆心角 AOC APB ⇒∠=∠2(1)五元素:①CD 过圆心O ;②CD ⊥AB ;③AM =BM ;④AD BD =;⑤AC BC =中,知二推三。
人教版七年级上数学教学课件第四章几何图形全章

谜 语
:
落 到 水 中 看 不
千 条 线 万 条 线
见
1.把下面第一行的平面图形绕线旋转一周,便能形成第二 行的某个几何体,请用虚线连一连:
1
2
3
4
5
A
B
C
D
E
2.下图是一个长方体的模型,它有几个面,面和面相交的
地方形成了几条线?线和线相交成几个点?
·· ··
·· ·· 6个面
12条线
从上面看 从正面看
从左面看
从上面看 从正面看
从上面看 从左面看
从正面看
从正面看
从左面看
从上面看
利用骰子,摆成下面的图形,分别从正面、左面、上 面观察这个图形,各能得到什么平面图形?
从正面看
从上面看 从左面看
请你从不同角度观察,下列立体图形各是 什么图形?
把你手中的立体图形沿棱展开,看它的平面展开图是什 么?
➢(2)直线的表示方法是怎样呢? a
画一条直 线CF
AB
直线AB 或直线 a
线段
线段的表示方法:
a
A
B
在我们的日常生活 中有哪些有关“线 段”的形象的例子?
线段AB (线段BA)或线段a 画一画:画出线段b
b
射线
线段向一个方向无限延伸就形成了一条射线.
a
O
A
射线0A 或射线 a
射线0A和射线AO是 同一射线吗?
(B)圆柱
(C)圆锥 (D)圆
10.小明为班级专栏设计了一个图案,如图所示,主 题是“我们喜爱合作学习”,请你也尝试用圆、扇形、 三角形、四边形、直线等为环保专栏设计一个图案, 并标明你的主题.
几何图形的基本模型

几何图形的基本模型【典型例题】模型一:双子型(手拉手模型)——全等(1)等边三角形条件:ΔOAB, ΔOCD均为等边三角形。
结论:①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=600④OE平分∠AED ⑤点E在ΔOAB的外接圆上(2)等腰直角三角形条件:ΔOAB, ΔOC D均为等腰直角三角形。
结论:①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=900 ④OE平分∠AED ⑤点E在ΔOAB的外接圆上(3)任意等腰三角形条件:ΔOAB, ΔOCD均为等腰三角形。
结论:①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=∠A0B ④OE平分∠AED(或∠AED的外角)⑤点E在ΔOAB的外接圆上例题:(1)如图①,△ABC中,AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰三角形ABD,ACE,分别取BD,CE,BC的中点M、N、G,连接GM、GN,线段GM与GN数量关系是;位置关系是(2)如图②,把等腰三角形ABC换为一般的锐角三角形,AB﹥AC,其中,其它条件不变,上述结论还成立吗?请说明理由。
(3)如图③,在(2)的基础上,又作了进一步的探究,向△ABC的内侧分别作等腰直角三角形ABD、ACE,其它条件不变,试判断△GMN的形状,并给与证明。
模型二:双子型(手拉手模型)——相似(1)一般情况条件:CD ∥AB(ΔOCD ∽ΔOAB ),将ΔOCD 旋转至右图位置结论:右图中①ΔOCD ∽ΔOAB⇔ΔOAC ∽ΔOBD ②延长AC 交BD 于点E ,必有∠AEB=∠AOB ③点E 在ΔOAB 的外接圆上。
(2) 特殊情况条件:CD ∥AB (ΔOCD ∽ΔOAB ), ∠AOB=∠COD=900将ΔOCD 旋转至右图位置结论:右图中①ΔOCD ∽ΔOAB ⇔ΔOAC ∽ΔOBD ②延长AC 交BD 于点E ,必有∠AEB=900(BD ⊥AC )③连接AD,BC ,则S ABCD =12AC ×BD ④OD OC =OBOA =tan ∠OCD ⑤点E 在ΔOAB 的外接圆上(A,O,E,B 四点共圆) ⑥必有AD 2+BC 2=AB 2+CD 2例题:以平面上一点O 为直角顶点,分别画出两个直角三角形,记作△AOB 和△COD ,其中∠ABO=∠DCO=300(1)点E 、F 、M 分别是AC 、CD 、DB 的中点,连接FM 、EM. ① 如图1,当点D 、C 分别在AO 、BO 的延长线上时,FMEM =② 如图2,将图1中△AOB 的绕点O 沿顺时针方向旋转α角(00<α<600),其他条件不变,判断FM EM的值是否发生变化,并对你的结论进行证明(3) 如图3,若B0=3√3,点N 在线段OD 上,且NO=2.点P 是线段AB 上的一个动点,在将ΔOAB 绕点0旋转过程中,线段PN 长度的最小值为 ,最大值为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
C D
E
A C D
B
E A B
C D
E
A B C
D
O
A
B
C
D
E
F
G
D
A
B
C
E
A
D
C B
E
E A
C
D
B
N O
M
D
A
E C
B
F
A B
C
D
E F E D B
A
A B C O A
B C D
O
E
A B
C
D A
B C
D E
A
1.
EC FC ⇒⊥
正方形ABCD 中,BD ⊥CE ⇔BD =CE 平移后也成立
2. B D E
∠+∠=∠
6.
△ABD ,△ACE 为等边△⇒BE =CD BE 、CD 相交所成锐角为60° //360AB CD
B D E ⇒∠+∠+∠=︒
ABDE 与ACFG 为正方形⇒EC =BG ,BG ⊥CE 注:条件可换成△BAE ,△CAG 为等腰Rt △ 3. B D ⇒∠=∠ 7.
①AD 平分∠CAB ;②DE//AC ;③AE =DE 中,知二推一
4.
1
902
BOC
A
⇒∠=︒+∠ 8.
△ABC 为等腰Rt △,
AE 平分∠CAB ,
∠D =90︒
⇒AE =2BD
1
2
BOC A ⇒∠=∠
DE//BC ⇒
C △ADE =AB+AC
1
902
BOC
A
⇒∠=︒-∠ 9.
5.
AC =BC ,则CE ⊥BD ⇔CE =BD
△ACD 、△BCE 为等边△,A 、C 、B 共线⇒ △ACE ≌△DCB; △ACM ≌△DCN △MCE
≌△NCB; AE =BD ,AM =DN ,EM =BN ,CM =CN ,AE 、BD 相交成锐角60°,AO =DO+CO ,BO =EO+CO ,OM+ON =CO ,OC 平分∠AOB ,注:△BCE 绕C 旋转时,结论有些变化.
10.
AC =BC
⇒△DEF 为等腰Rt △ 15.
⇒OD =OE BE+CD =BC
F M
D
G A B C E A
B
C
D
2
1
D C
B
A
E F
E F A ′
B ′
C
′
O A
B
C
D
A
D B
C
F
A P
C B
100︒
B C
A
E
E F
M
A C D
B F M
G
A
B C D
45︒
F
E
A B
C
D 11.
⇒PB+PC =2PD ∠ABP+∠C =180°
16.
AD =CD
⇔CD =BD ⇔AD =BD
AB =AC
⇒AE+BE =BC
17.
⇒∠A =∠B
或∠A+∠B =180°
12.
AC =BC
⇒∠ADC =∠BDF ; CF+DF =AD
18.
⇒DE+BF =EF
AE 平分∠DEF ,AF 平分∠BFE
13.
⇒CD =CE =BG CEFD 为菱形
∠2=2∠1
⇒AF =BC+CF
14.
AB =AC
⇒DE+DF =BM (钝角△也成立)
⇒AE+CF =CD
EF =2OE
S 四边形OEBF =
14
a 2
等腰梯形
⇒EF+EG =CM
⇒BE+DF=AE
1
A
C
A
B C
D
F
E
1
A B
C
D
E 1
D
C
B
A G E A
B
C
D
M F
19.
BF=AD ⇔BF ⊥AD
⇒∠1=∠B
△ADC ∽△CDB ∽△ACB AC 2=AD·AB BC 2=BD·BA 少是 24.
∠1=∠C
⇔△ADE ∽△ACB ⇔AD·AB =AE·AC 30.
⇒
AN DG
AM BC
=
∠1=∠B
⇔△ADC ∽△ACB
P F
A
B C D
E M P
A
B
N D
C
⇔∠ADC =∠ACB ⇔AC 2=AD·AB
AD =DC ,PN//BD
⇒PN+MN =2BD
AB =AC
⇒PE+PF =2AD
4
1
1802
C AOB ⇒∠=︒-∠
O
B A
C
5. 共斜边的两直角三角形,四个顶点在同一圆上。
B
A
C
D
D
C
A
B
10
BD CD ⇒= △ABE ∽△ADC ∽△CDE
△ABD ∽△AEC ∽△BED BD 2=CD 2=DE ·DA AB ·AC =AE ·AD AE ·
DE =BE ·CD
*
2cos AB AC
BAD AD
+=∠
若I 为△ABC 内心,则BT =CD =ID ,关注∠BAC 为特殊角时图形的特殊性、及相关比值。
14
PD PO PM PN ⇒=
△PDM ∽△PNO
CA 平分∠PCD △OND ∽△OPN
15
1
90BOC A ⇒∠=︒+∠
18
⇒AB+CD =AD+BC
19
22
AP BP r OP
⇒=-
△PBA∽△PCB BE·BD=AD·CE
若AC是直径,则△ADP=45°
*若△BDE为等腰Rt△或等边△时,上述结论有些变化。
23
AC EC
⇒=CB=CG F为△ABC的内心
其它同前(10)题
AC。
