空间直角坐标系 空间两点间的距离公式
4-3-1、2 空间直角坐标系和空间两点间的距离公式 67张

第四章
4.3
4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
画法
在平面上画空间直角坐标系Oxyz时,一般使 ∠xOy=_______,∠yOz=90° 135°
图示
第四章
4.3
4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
本书建立的坐标系都是右手直角坐标系,即 说 明 在空间直角坐标系中,让右手拇指指向x轴的 正方向,食指指向y轴的正方向,如果中指指 向z轴的正方向,则称这个坐标系为右手直角 坐标系.
第四章 4.3 4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
自主预习 阅读教材P134~137,完成下列问题. 1.空间直角坐标系 以空间中两两______且相交于一点O的三条直线分 垂直 定 义 别为x轴、y轴、z轴,这时就说建立了空间直角坐
原点 标系Oxyz,其中点O叫做坐标_____,x轴、y轴、z 坐标轴 轴叫做________.通过每两个坐标轴的平面叫做 坐标平面 ________,分别称为xOy平面、yOz平面、zOx平面
第四章 圆的方程
成才之路 ·数学 ·人教A版 · 必修2
课前自主预习 课堂基础巩固 思路方法技巧 课后强化作业 名师辨误做答
第四章
4.3
4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
课前自主预习
第四章
4.3
4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
温故知新 1.平面直角坐标系内的点的对称问题
第四章 4.3 4.3.1 、4.3.2
成才之路 ·数学 ·人教A版 · 必修2
命题方向
4.3.2 空间两点间的距离公式3

2
2 2 2 (7 4) (1 3) (2 1) 14, =
M 2 M 3 = (5 7)2 (2 1)2 (3 2)2 6,
2
M 3 M 1 = (4 5)2 (3 2)2 (1 3)2 6,
2
所以 M2 M3 = M3 M1 ,
提示:在空间中,到定点 的距离等于定长的点的轨 迹是 以原点为球心,
z
P
O y
半径长为 r 的球面.
x
2.如果是空间中任意一点P1(x1,y1,z1)到点P2 (x2,y2,z2)之间的距离公式会是怎样呢? 提示:如图,设P1(x1,y1,z1)、P2(x2,y2,z2) 是空间中任意两点,且点P1(x1,y1,z1)、 P2(x2,y2,z2) 在xOy平面上的射影分别为M,N, 那么M,N的坐标为M(x1,y1, 0), N(x2,y2,0).
2 2
即 (0 4)2 (0 1)2 ( z 7)2 (3 0)2 (5 0)2 (2 z)2
14 解之得 z 9
14 (0, 0, ). 9
所以所求点的坐标是
【变式练习】 在z轴上求一点M,使点M 到A(1,0,2)与点B(1, -3,1)的距离相等. 答案:(0, 0, 3)
x z
P2 P1
O
M1 N1 M M2
H N2 y N
2 2 MN = (x x ) +(y y ) . 在xOy平面上, 2 1 2 1
过点P1作P2N的垂线,垂足为H,
则 MP1 = z1 ,NP2 = z2 , 所以 HP2 = z2 - z1 .
在RtΔP1HP2中,
P1H = MN = (x2 - x1 ) +(y 2 - y 1 ) ,
2.空间两点间的距离公式
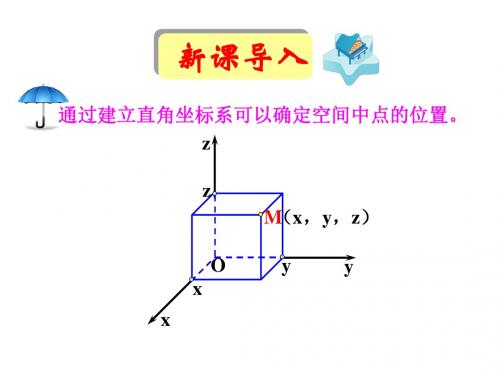
通过建立直角坐标系可以确定空间中点的位置。 z z
M (x,y,z)
O x x y y
如何计算空间两点之间的距离?
4.3.2 空间两点间的 距离公式
思考
类比平面两点间距离公式的推导,你能猜想一下 空间两点 P1 ( x1,y1,z1 ), P2 ( x2 , y2 , z2 ) 间的距离公式吗? 平面内两点P1(x1,y1), P2(x2,y2) 的距离公式
|P1Q1|=|x1-x2|; |Q1R1|=|y1-y2|;|R1P2|=|z1-z2|
|P1P2|2=|P1Q1||2+|Q1R1|2+|R1P2|2
| P1P2 | (x1 x 2 )2 (y 1 y 2 )2 (z1 z 2 )2
空间内两点 P1 (x1 , y1 , z1 ), P2 (x2 , y 2 , z 2 )的距离公式是:
| AB | (10 4) 2 ( 1 1) 2 (6 9) 2 7 | BC | (4 2) 2 (1 4) 2 (9 3) 2 7 | AC | (10 2) 2 ( 1 4) 2 (6 3) 2 98
因为 7 7 98,
所以
| OP |
x2 y2 z 2
思考
如果|OP|是定长r,那么 x2 y 2 z 2 r2 表示什 么图形? z
O
x y
表示以原点为球心,r为半径的球体。
空间任意两点间的距离. R2 z S2 O x Q1 y Q2
P2 (x2,y2,z2) S1 P1 (x1,y1,z1) R1
| P1 P2 | ( x2 x1 ) 2 ( y2 y1 ) 2
测量坐标计算公式大全

测量坐标计算公式大全一、两点间距离公式(平面直角坐标系)设两点坐标分别为A(x_1,y_1),B(x_2,y_2),则两点间的距离d为:d = √((x_2 - x_1)^2+(y_2 - y_1)^2)例如,A(1,2),B(4,6),则x_1 = 1,y_1=2,x_2 = 4,y_2 = 6d=√((4 - 1)^2+(6 - 2)^2)=√(3^2 + 4^2)=√(9+16)=√(25) = 5二、中点坐标公式(平面直角坐标系)设两点坐标分别为A(x_1,y_1),B(x_2,y_2),则AB中点M的坐标为(x_m,y_m),其中。
x_m=(x_1 + x_2)/(2)y_m=(y_1 + y_2)/(2)例如,A( - 2,3),B(4,-1),则中点M的坐标为。
x_m=(-2+4)/(2)=1y_m=(3+(-1))/(2)=1即中点M(1,1)三、直线的斜率公式(平面直角坐标系)设直线上两点坐标为A(x_1,y_1),B(x_2,y_2)(x_1≠ x_2),则直线AB的斜率k 为:k=(y_2 - y_1)/(x_2 - x_1)例如,A(1,2),B(3,6),则k=(6 - 2)/(3 - 1)=(4)/(2)=2四、直线的点斜式方程(平面直角坐标系)已知直线过点(x_0,y_0),斜率为k,则直线方程为y - y_0=k(x - x_0)例如,直线过点(1,3),斜率k = 2,则直线方程为y-3 = 2(x - 1),即y=2x+1五、平面直角坐标系中坐标旋转公式。
设点P(x,y)绕原点旋转θ角后得到点P'(x',y')x'=xcosθ - ysinθy'=xsinθ + ycosθ六、极坐标与直角坐标的转换公式。
1. 直角坐标(x,y)转换为极坐标(ρ,θ)ρ=√(x^2 + y^2)θ=arctan(y)/(x)(x≠0)2. 极坐标(ρ,θ)转换为直角坐标(x,y)x = ρcosθy=ρsinθ七、空间直角坐标系中两点间距离公式。
《空间两点间的距离公式》名师课件2

当 x=87时,|AB|有最小值 57= 735.
此时 A87,277,97,B1,272,67.
例题讲解
例2、已知A(1,-2,11),B(4,2,3) ,C(6,-1,4),求证其连线组成的三角 形为直角三角形。
证明:利用两点间距离公式,由
| AB | 89,| AC | 75,| BC | 14
巩固训练
1、(1)已知两点 P(1,0,1)与 Q(4,3,-1). ①求 P、Q 之间的距离; ②求 z 轴上的一点 M,使|MP|=|MQ|. (2)已知 A(x,5-x,2x-1),B(1,x+2,2-x),求|AB|取最小 值时,A、B 两点的坐标,并求此时的|AB|. 解:
(1)①|PQ|= (1-4)2+(0-3)2+(1+1)2= 22. ②设 M(0,0,z)由|MP|=|MQ|, 得(-1)2+02+(z-1)2=42+32+(-1-z)2, 所以 z=-6.所以 M(0,0,-6).
空间两点间的距离公式
复习引入
如何计算空间两点之间的距离?
复习引入
1.在平面直角坐标系中两点间 的距离公式是什么?
复习引入
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式
| P1P2 | (x2 x1 )2 (y2 y1 )2
y
P1
o
x
P2
复习引入
2.类比平面两点间的距离公式,你 能猜想出在空间直角坐标系中两点 间的距离公式吗?
|BC|= (6-4)2+(-1-2)2+(4-3)2= 14, 所以|AC|2+|BC|2=|AB|2,故△ABC 为直角三角形.
例题讲解
例1、(2)如图所示,正方体的棱长为1,以正方体的同一顶点上
已知两个坐标点求距离的公式

已知两个坐标点求距离的公式介绍在几何学中,已知两个点的坐标,我们经常需要计算它们之间的距离。
这种距离计算在物理学、地理学、计算机图形学等领域中都有广泛的应用。
本文将介绍两个坐标点之间距离计算的基本公式。
直角坐标系下的两点距离计算在直角坐标系中,我们可以通过两个点的坐标来计算它们之间的距离。
设两个点的坐标分别为A(x1, y1)和B(x2, y2)。
根据勾股定理,我们可以使用以下公式计算两个点之间的距离d:d = √((x2 - x1)² + (y2 - y1)²)其中x2、x1、y2和y1分别代表点B和A的x坐标和y坐标。
示例假设点A的坐标为(2, 3),点B的坐标为(5, 7),我们可以使用上述公式计算它们之间的距离。
将坐标代入公式中,可以得到:d = √((5 - 2)² + (7 - 3)²)= √(3² + 4²)= √(9 + 16)= √25= 5因此,点A和点B之间的距离为5。
三维空间中的两点距离计算对于三维空间中的点,我们可以通过类似的方法计算它们之间的距离。
假设点A的坐标为(x1, y1, z1),点B的坐标为(x2, y2, z2),我们可以使用以下公式计算它们之间的距离:d = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)同样,我们可以通过将点A和点B的坐标代入公式来计算它们之间的距离。
总结已知两个坐标点,我们可以使用勾股定理来计算它们之间的距离。
根据坐标点所在的空间维度不同,我们可以使用二维或三维距离公式来计算距离。
这些公式在各种领域中都有着重要的应用,例如计算两个物体之间的距离、城市之间的距离等。
在实际应用中,我们可以使用计算机编程语言中提供的数学库函数来直接计算距离,这样可以更加方便和高效地进行坐标点距离的计算。
希望本文对你计算两个坐标点之间的距离有所帮助!。
用4.3.2空间两点间的距离公式

2 2
2 2
∵P3与P1关于原点O对称,P4与P2关于原点O对称.
dx dy dz
y z
2 0
2 0 2 0 2 0
O x
x z
2 0 2 0
x y
规律:谁没有,就等于谁.
练 5 .点P(2,3,5)到平面xOy的距离为________ . 1. 习 5
[解析]
d=|z|=5.
6.已知点M到三个坐标平面的距离都是1,且点M的三个 2.
[答案] .(1,1,1)或(-1,-1,-1) 坐标同号,则点M的坐标为________
3 解: M的坐标为 (4, ,5) 2 5 N的坐标为 (4,3, ) 2
(0,0,5) (4,0,5) (4,3,5)
(0,3,5)
3 AC与BO交点的坐标 (2, ,0) 2
3 5 AC1与A1C的交点的坐标 (2, , ) 2 2
(0,3,0)
(0,0,0)
(4,0,0) (4,3,0)
练 7.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为D1D、BD的 1 习 中点,G在棱CD上,且CG= CD,H为C1G的中点,试建立适当的坐标系, 写出E、F、G、H点的坐标. 4 z (0,0,1) 解:如图所示,以D为原点,DA所在直线为x 轴,DC所在直线为y轴,DD1所在直线为z轴 建立空间直角坐标系. (1,0,1)
(2)求EF的长.
空间中两点的距离公式PPT教学课件

10
(一)齿teeth
作用:捕食,不能 咀嚼。
硬骨鱼类的齿:可 分为颌齿、腭齿、 犁齿、咽齿等。 统称为口腔齿。
犁齿和腭齿的有无,
左右下咽齿是否
分离或愈合等常
作为分类标志之
11
咽齿
鲤科鱼类的第五鳃弓 的角鳃骨特别扩大,特称 为咽骨或下咽骨,咽骨上 长的齿,就是咽齿。
胰脏分泌胰蛋白酶、胰脂肪酶及胰淀粉酶, 能消化分解蛋白质、脂肪和醣类,为十分重 要的消化酶类。胰脏产生的消化酶通过胰31管
胃腺(gastric gland)
圆口类及肺鱼类无特殊分化的胃腺,其余鱼类 胃腺一般均存在。少数无胃鱼类如鲤科、隆 头鱼科等无胃腺。
胃腺分泌胃蛋白酶,分解食物中的蛋白质。凶 猛的肉食性鱼类的胃蛋白酶的活性特别高。
Y 型:盲囊部明显突出,贲门部、幽门 部及盲囊部分界明显,如拟沙丁鱼、鳀及鳗 鲡等鱼类的胃。
卜型:盲囊部特别延长而发达,幽门部22较
四、肠(intestine)
软骨鱼类板鳃亚纲的肠可明显分出小肠和大 肠,小肠又可分为十二指肠及回肠。大肠 可分为结肠和直肠。
硬骨鱼类及全头类的肠的末端以肛门开口体 外,板鳃亚纲肠管末端则以肛门开口于泄 殖腔。
X
§4.3.1 空间中两点的距离公式
1
(1) 在空间直角坐标系中,任意一点 P(x,y,z)到原点的距离:
z
| OP | x2 y2 z2
O x
P(x,y,z)
y
P`(x,y,0)
2
(1) 在空间直角坐标系中,任意两点 P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:
| P1P2 | (x1 x2 )2 ( y1 y2 )2 (z1 z2 )2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由题意可知 C(3,3,0),D(0,3,0), ∵|DD1|=|CC1|=|AA1|=2, ∴C1(3,3,2),D1(0,3,2), ∵N 为 CD1 的中点,
3 ∴N2,3,1.
[探究共研型]
空间两点间的距离
探究 1 已知两点 P(1,0,1)与 Q(4,3,-1),请求出 P、Q 之间的距离.
【提示】 |PQ|= 1-42+0-32+1+12= 22.
探究 2 的坐标.
上述问题中,若在 z 轴上存在点 M,使得|MP|=|MQ|,请求出点 M
【提示】 设 M(0,0,z),由|MP|=|MQ|, 得(-1)2+02+(z-1)2=42+32+(-1-z)2, ∴z=-6.∴M(0,0,-6).
[再练一题] 1.在棱长都为 2 的正三棱柱 ABCA1B1C1 中,建立恰当的空间直角坐标系, 并写出三棱柱 ABCA1B1C1 各顶点的坐标.
【解】
取 BC,B1C1 的中点分别为 O,O1,连接 OA,OO1,
3 根据正三棱柱的几何性质,OA,OB,OO1 两两互相垂直,且 OA= 2 ×2 = 3,
任意一点 Px,y,z,关于原点对称的点是 P1-x,-y,-z;关于 x 轴 横轴对称的点是 P2x,-y,-z;关于 y 轴纵轴对称的点是 P3-x,y,-z; 关于 z 轴竖轴对称的点是 P4-x,-y,z;关于 xOy 平面对称的点是 P5x,y, -z;关于 yOz 平面对称的点是 P6-x,y,z;关于 xOz 平面对称的点是 P7x, -y,z.,求对称点的问题可以用“关于谁对称,谁保持不变,其余坐标相反”的 口诀来记忆.
(2) 在空间直角坐标系中,在 yOz 平面上的点的坐标一定可写成 (0 , b , c ) .( ) ) )
(3)在空间直角坐标系中,在 Oz 轴上的点的坐标可记作(0,0,c).( (4)在空间直角坐标系中,在 xOz 平面上的点的坐标是(a,0,c).(
【解析】 (1)错误.x 轴上的点的坐标是纵坐标与竖坐标都为 0. (2)、(3)、(4)正确.
【精彩点拨】 对照空间点的对称的规律直接写出各点的坐标.
【自主解答】
(1)由于点 P 关于 x 轴对称后,它在 x 轴的分量不变,在 y
轴、z 轴的分量变为原来的相反数,所以对称点坐标为 P1(-2,-1,-4). (2)由于点 P 关于 xOy 平面对称后,它在 x 轴、y 轴的分量不变,在 z 轴的分 量变为原来的相反数,所以对称点坐标为 P2(-2,1,-4). (3)设对称点为 P3(x,y,z),则点 M 为线段 PP3 的中点, 由中点坐标公式,可得 x=2×2-(-2)=6, y=2×(-1)-1=-3,z=2×(-4)-4=-12, 所以 P3 的坐标为(6,-3,-12).
【答案】 -7 或 13
[小组合作型]
空间中点的坐标的确定
在棱长为 1 的正方体 ABCDA1B1C1D1 中,E、F 分别是 D1D、BD 1 的中点,G 在棱 CD 上,且 CG=4CD,H 为 C1G 的中点,试建立适当的坐标系, 写出 E、F、G、H 的坐标.
【精彩点拨】 求点的坐标.
要求点的坐标,需求得横、纵、竖坐标的值,即确定出所
画法
在平面上画空间直角坐标系 Oxyz 时,一般使∠xOy=____ ,∠yOz 135° =90°
图示
右手直角坐标系,即在空间直角坐标系中, 本书建立的坐标系都是____
y 轴的正方向, x 轴的正方向, 说明 让右手拇指指向__ 食指指向__ 中指指向
__ z 轴的正方向,则称这个坐标系为右手直角坐标系
【答案】 (1)× (2)√ (3)√ (4)√
教材整理 2 空间两点间的距离公式 阅读教材 P136“练习”以下至 P137 部分,完成下列问题.
2 2 2 x + y + z 1.点 P(x,y,z)到坐标原点 O(0,0,0)的距离|OP|=__________.
2 . 任 意 两 点 P1(x1 , y1 , z1) , P2(x2 , y2 , z2) 间 的 距 离 |P1P2| =
2 2 2 x - x + y - y + z - z 1 2 1 2 1 2 ______________________________.
在空间直角坐标系中,A(-1,2,3),B(2,1,m),若|AB|= 110,则 m 的值 为________.
【解析】 |AB|= -1-22+2-12+3-m2 = 110, ∴(3-m)2=100,3-m=± 10. ∴m=-7 或 13.
[构建· 体系]
1.点 A(-1,2,1)在 x 轴上的投影点和在 xOy 平面上的投影点的坐标分别为 ( ) A.(-1,0,1),(-1,2,0) B.(-1,0,0),(-1,2,0) C.(-1,0,0),(-1,0,0) D.(-1,2,0),(-1,2,0)
【解析】 点 A(-1,2,1)在 x 轴上的投影点的横坐标是-1,纵坐标、竖坐标 都为 0, 故为(-1,0,0), 点 A(-1,2,1)在 xOy 平面上横、 纵坐标不变且竖坐标是 0, 故为(-1,2,0).
M 是 A1C1 的三分之一分点且靠近 A1 点, ∴M(1,1,2).由两点间距离公式,得 |MN|= 21 = 2 .
3 -12+3-12+1-22 2
利用空间两点间的距离公式求线段长度问题的一般步骤为:
[再练一题] 3. 如图 432 所示, 直三棱柱 ABCA1B1C1 中, |C1C|=|CB|=|CA|=2, AC⊥CB, D,E 分别是棱 AB,B1C1 的中点,F 是 AC 的中点,求 DE,EF 的长度.
【解析】 由|AB|= 6-42+2+72+z-12 =11, 解得 z=7 或-5.
【答案】 7 或-5
5.(2016·威海高一检测)VABCD 为正四棱锥,O 为底面中心,若 AB=2, VO=3,试建立空间直角坐标系,并确定各顶点坐标.
【解】
以底面中心 O 为坐标原点,建立如图所示空间直角坐标系.
【自主解答】
建立如图所示的空间直角坐标系.点 E 在 z 轴上,它的 x
1 DD1 的中点,故其坐标为0,0,2.
坐标、y 坐标均为 0,而 E 为
1 1 由 F 作 FM⊥AD、FN⊥DC,由平面几何知 FM=2、FN=2,则 F 点
1 1 坐标为2,2,0. 3 3 点 G 在 y 轴上,其 x、z 坐标均为 0,又 GD=4,故 G 点坐标为0,4,0.
[基础· 初探] 教材整理 1 空间直角坐标系
阅读教材 P134~P135“例 1”以上部分,完成下列问题. 1.空间直角坐标系 以空间中两两____ 垂直且相交于一点 O 的三条直线分别为 x 轴、y 轴、 定义 z 轴,这时就说建立了空间直角坐标系 Oxyz,其中点 O 叫做坐标
原点,x 轴、y 轴、z 轴叫做______ 坐标轴.通过每两个坐标轴的平面叫做 ____ zOx 平面 坐标平面,分别称为 xOy 平面、yOz 平面、____ ________
【答案】 A
3.已知 A(3,2,-4),B(5,-2,2),则线段 AB 中点的坐标为________.
【解析】 设中点坐标为(x0,y0,z0), 3+5 2-2 -4+2 则 x0= 2 =4,y0= 2 =0,z0= 2 =-1, ∴中点坐标为(4,0,-1).
【答案】 (4,0,-1)
4.设 A(4,-7,1),B(6,2,z),|AB|=11,则 z=________.
如图 431 所示, 在长方体 ABCDA1B1C1D1 中, |AB|=|AD|=3, |AA1| =2,点 M 在 A1C1 上,|MC1|=2|A1M|,N 在 D1C 上且为 D1C 的中点,求线段 MN 的长度.
图 431
【精彩点拨】 先建立空间直角坐标系,求出点 M、N 的坐标,然后利用 两点间的距离公式求解.
1 1 由 H 作 HK⊥CG 于 K,由于 H 为 C1G 的中点,故 HK=2、CK=8.
7 1 7 ∴DK=8.故 H 点坐标为0,8,2.
1.建立空间直角坐标系时应遵循以下原则 (1)让尽可能多的点落在坐标轴上或坐标平面内; (2)充分利用几何图形的对称性. 2.求某点的坐标时,一般先找出这一点在某一坐标平面上的射影,确定其 两个坐标,再找出它在另一轴上的射影(或者通过它到这个坐标平面的距离加上 正负号),确定第三个坐标.
【答案】 B
2.在空间直角坐标系中,点 P(3,4,5)与 Q(3,-4,-5)两点的位置关系是 ( ) A.关于 x 轴对称 B.关于 xOy 平面对称 C.关于坐标原点对称 D.以上都不对
【解析】 点 P(3,4,5)与 Q(3,-4,-5)两点的横坐标相同,而纵、竖坐标 互为相反数,所以两点关于 x 轴对称.
阶 段 一
4.3 4.3.1 4.3.2Βιβλιοθήκη 空间直角坐标系 空间直角坐标系
阶 段 三
空间两点间的距离公式
阶 段 二
学 业 分 层 测 评
1.了解空间直角坐标系的建系方式.(难点) 2. 能在空间直角坐标系中求出点的坐标和已知坐标作出点. (重点、 易错点) 3.理解空间两点间距离公式的推导过程和方法.(难点) 4.掌握空间两点间的距离公式,能够用空间两点间距离公式解决简单的问 题.(重点)
∵V 在 z 轴正半轴上,且|VO|=3,它的横坐标与纵坐标都是零, ∴点 V 的坐标是(0,0,3).而 A、B、C、D 都在 xOy 平面上, ∴它们的竖坐标都是零. 又|AB|=2, ∴A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),V(0,0,3).
