结构力学 第八章
合集下载
结构力学第八章 影 响 线

与其他截面上的弯矩无关。
(4) 绘制规定不同 MC的影响线中的正弯矩画在基线的上方, 负弯矩画在基线的下方,标明正负号。
★第三节
结点荷载作用下梁的影响线
(1)支座反力FRA和FRB的影响线
(2)MC的影响线 C点正好是结点。
(3) MD的影响线 (4) FQCE的影响线 力,以FQCE表示。 MD的影响线如图8-5c所示。 在结点荷载作用下,主梁在C、E两点之间
3.弯矩影响线作法 由此得简支梁作弯矩影响线简易作法:先作一基线,在基线对
应所作弯矩影响线截面处作一竖线,其值为ab/l,连接A、B两
端,即为此截面弯矩的影响线,如图8-2e所示。 弯矩影响系数其量纲为L,单位为m
3.弯矩影响线作法 【例8-1】试用静力法绘制图8-3所示外伸梁的FAy、FBy、FQC、 MC 、FQD、MD的影响线。 【解】(1)绘制反力FAy、FBy的影响线。取A点为坐标原点,横 坐标x向右为正。当荷载F=1作用于梁上任一点x时,分别求得 反力FAy、FBy的影响线方程为
这就是FRB的影响线方程。由此方程知,FRB的影响线是一条
直线。在A点,x=0,FRA=0。在B点,x=1,FRB=1。利用这 两个竖距便可以画出FRB的影响线,如图8-2b所示。
(2) 支座反力FRA影响线作法 将FP=1放在任意位置,距A点为x。由平衡条件 解得 这就是FRA的影响线方程。由此方程知,FRA的影响线也是一
1.支座反力的影响线 (1) 支座反力FRB影响线作法 如图8-2a所示简支梁,将FP=1放 将FP=1放在任意位置,距A点为x。
在任意位置,距A点为x。
(2) 支座反力FRA影响线作法
(1) 支座反力FRB影响线作法 如图8-2a所示简支梁,将FP=1放在任意位置,距A点为x。 由平
第八章 结构力学

上一页 下一页 返回
第一节钢筋混凝土平面楼盖概述
在高层建筑中,楼盖宜现浇;对抗震设防的建筑,当高度 >=50m时,楼盖应采用现浇;当高度<= 50m时,在顶层、刚性 过渡层和平面复杂或开洞过多的楼层,也应采用现浇楼盖。 随着商品混凝土、泵送混凝土以及工具式模板的广泛使用, 钢筋混凝土结构,包括楼盖在内,大多采用现浇的方式。 日前,我国装配式楼盖主要用在多层砌体房屋,特别是多层 住宅中。在抗震设防区,有限制使用装配式楼盖的趋势。装 配整体式楼盖是提高装配式楼盖刚度、整体性和抗震性能的 一种改进措施,最常见的方法是在板面做40mm厚的配筋现 浇层。 (3)按是否预加应力情况,楼盖可分为钢筋混凝土楼盖和预 应力混凝土楼盖两种。预应力混凝土楼盖用得最普遍的是无 钻结预应力混凝土平板楼盖;当柱网尺寸较大时,预应力楼盖 可有效减小板厚,降低建筑层高。
上一页 下一页 返回
第二节单向板肋梁楼盖的设计
④跨数超过五跨的连续梁、板,当各跨荷载相同且跨度相差 不超过10%时,可按五跨的等跨连续梁、板计算。 (2)为减少计算工作量,结构内力分析时,常常不是对整个结 构进行分析,而是从实际结构中选取有代表性的某一部分作 为计算的对象,称为计算单元。 楼盖中对于单向板,可取1m宽度的板带作为其计算单元, 在此范围内,即图8-3中用阴影线表示的楼面均布荷载便是该 板带承受的荷载,这一负荷范围称为从属面积,即计算构件 负荷的楼面面积。 主、次梁截面形状都是两侧带翼缘(板)的T形截面,每侧翼 缘板的计算宽度取与相邻梁中心距的一半。次梁承受板传来 的均布线荷载,主梁承受次梁传来的集中荷载,由上述假定 ③可知,一根次梁的负荷范围以及次梁传给主梁的集中荷载 范围如图8-3所示。
第一节钢筋混凝土平面楼盖概述
在高层建筑中,楼盖宜现浇;对抗震设防的建筑,当高度 >=50m时,楼盖应采用现浇;当高度<= 50m时,在顶层、刚性 过渡层和平面复杂或开洞过多的楼层,也应采用现浇楼盖。 随着商品混凝土、泵送混凝土以及工具式模板的广泛使用, 钢筋混凝土结构,包括楼盖在内,大多采用现浇的方式。 日前,我国装配式楼盖主要用在多层砌体房屋,特别是多层 住宅中。在抗震设防区,有限制使用装配式楼盖的趋势。装 配整体式楼盖是提高装配式楼盖刚度、整体性和抗震性能的 一种改进措施,最常见的方法是在板面做40mm厚的配筋现 浇层。 (3)按是否预加应力情况,楼盖可分为钢筋混凝土楼盖和预 应力混凝土楼盖两种。预应力混凝土楼盖用得最普遍的是无 钻结预应力混凝土平板楼盖;当柱网尺寸较大时,预应力楼盖 可有效减小板厚,降低建筑层高。
上一页 下一页 返回
第二节单向板肋梁楼盖的设计
④跨数超过五跨的连续梁、板,当各跨荷载相同且跨度相差 不超过10%时,可按五跨的等跨连续梁、板计算。 (2)为减少计算工作量,结构内力分析时,常常不是对整个结 构进行分析,而是从实际结构中选取有代表性的某一部分作 为计算的对象,称为计算单元。 楼盖中对于单向板,可取1m宽度的板带作为其计算单元, 在此范围内,即图8-3中用阴影线表示的楼面均布荷载便是该 板带承受的荷载,这一负荷范围称为从属面积,即计算构件 负荷的楼面面积。 主、次梁截面形状都是两侧带翼缘(板)的T形截面,每侧翼 缘板的计算宽度取与相邻梁中心距的一半。次梁承受板传来 的均布线荷载,主梁承受次梁传来的集中荷载,由上述假定 ③可知,一根次梁的负荷范围以及次梁传给主梁的集中荷载 范围如图8-3所示。
结构力学(龙驭球)第八章_2023年学习资料

第八章位移法总结-当C点有水平向右的侧移△时,B点将沿垂直于AB杆-的方向运动(图d,其中△,和∠之间具有 定的几何-关系。-△B-袋C-B3-1求△和△2之间的几何关系。取BC杆研究(图e,-发生侧移后,B点移至 1,C点移至C1。△B在BC杆上的水-平投影为BB2=∠Bc0s45°。-仅从水平方向观察可以看出BC杆由 来的位置平移至B,C1-的位置,由于杆件不伸长,因此有BB2=CC1-即-∠Bc0s45°=△2-又由于B 3是BB1在垂直BC杆方向的投影,因此-BB3=∠BSin45°=△2
第八章位移法总结-由平衡条件求出系数k和自由项F:P:-4解方程求4;-注意:一切计算-5按叠加原理计算杆 弯矩。-都是在基本结构上进-M=M△+M2△2+…Mn△n+M,-行别-三、几个值得注意的问题-1.位移法 适用条件-1位移法既可以求解超静定结构,也可以求解静定结-构;-2既可以考虑弯曲变形,也可以考虑轴向和剪切 -3可以用于梁、刚架、桁架、拱、组合结构等各种类-型的结构;-4从材料性质看,只能用于弹性材料。
第八章位移法总结-2作M2图。由以上叙述可知BC杆两端有相对侧移BB3,-因此在图中-d-△B-e-2=-k12-3E1△,-12E1-B☑-6E1/n2-12E1/2-而AB杆两端的相对侧移为BB3,因此-6 2E1-M BA-W2
第八章位移法总结-3求k2=k12,k22。由M2图易得-6EI-k12=k21=-f-△2=】-6E1/ 2-8-B段-EVL-6E1/2-A户工-6EM/I 2-12E/n2-12EI/213-求k22时取图f 的BC杆为隔离体(图g,由-∑Mc=0,能求出轴力FN。-36E1-再由∑F,=0求出k22=
第八章-位移法总结-2利用与位移相应的隔离体的平衡条件建立平衡方程:-3解方程求出结点位移;-4将结点位移 入杆端力方程从而求出杆端内力。-2.基本体系法-基本体系法是利用附加约束的基本原理建立位移法典型-方程。骤-:-1确定基本未知量。将原结构有角位移和线位移的-结点分别加上阻止转动的刚臂和阻止移动的支座链杆,附刚臂和附加支座链杆数之和即为位移法的基本未知量:-2由附加约束上约束力为零的条件,建立位移法方程-k4+F =0Gj=1,2.…,n):-3在基本结构上分别绘制在各附加约束分别产生单位-位移4;=1下向变形的情况下,当竖柱平行时,无-论梁是水平的还是倾斜的,梁都产生平动,因而各 柱顶有相同的水平线位移。图a中A、C点的水平位-移相同,结构只有一个位移未知量人。
结构力学 第八章 作业参考答案
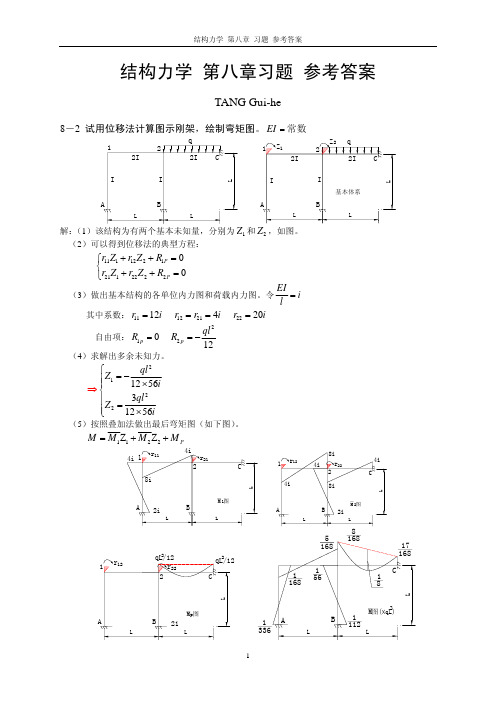
基本体系
D
Z2
B
2I 2FL/9 I
M图
D
L
B
A
L
B
2FL/9
A
L
FL/9
B
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。令 其中系数: r11 = 14i 自由项: R1 p = 0 (4)求解出多余未知力。
4
1m
E
E
E r12 2I
4m
I
I
4m
I
I
1m
0.75 E
1m
结构力学 第八章 习题 参考答案
(2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。 其中系数: r11 = r22 =
8-7 试用位移法计算连续梁,绘制弯矩图。 EI = 常数
A Z1 B 6m 6m
基本体系
Z1 C 6m
A B 6m 6m C 6m
D
D
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
D
Z2
B
2I 2FL/9 I
M图
D
L
B
A
L
B
2FL/9
A
L
FL/9
B
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。令 其中系数: r11 = 14i 自由项: R1 p = 0 (4)求解出多余未知力。
4
1m
E
E
E r12 2I
4m
I
I
4m
I
I
1m
0.75 E
1m
结构力学 第八章 习题 参考答案
(2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
(3)做出基本结构的各单位内力图和荷载内力图。 其中系数: r11 = r22 =
8-7 试用位移法计算连续梁,绘制弯矩图。 EI = 常数
A Z1 B 6m 6m
基本体系
Z1 C 6m
A B 6m 6m C 6m
D
D
解: (1)该结构为有两个基本未知量,分别为 Z1 和 Z 2 ,如图。 (2)可以得到位移法的典型方程:
⎧r11Z1 + r12 Z 2 + R1P = 0 ⎨ ⎩r21Z1 + r22 Z 2 + R2 P = 0
结构力学上第8章 位移法

(非独立角位移) l FQBA
M AB M BA
F 3i A 3i M AB l 0
3、一端固 FQAB
A
B1
B
l
F M AB i A i B M AB F M BA i A i B M BA
(非独立线位移)
q B EI C L
Z1
q B
EI C
Z2 4i
Z1=1
EI A 原结构
L
=
Z2=1
EI A qL2 8 基本体系
=
3i
M1图×Z1 2i
+
6EI L2 6EI M2图×Z2 L2
+
qL2 8 MP图
在M1、M2、MP三个 图中的附加刚臂和链杆 中一定有约束反力产生, 而三个图中的反力加起 来应等于零。
M
q
应用以上三组转角位移方程,即可求出三种基本的单跨超 静定梁的杆端弯矩表达式,汇总如下:
F 1)两端固定梁 M AB 4i A 2i B 6i M AB
M BA
l F 2i A 4i B 6i M BA l
2)一端固定另一端铰支梁
F M AB 3i A 3i M AB l M BA 0 3)一端固定另一端定向支承梁 F M AB i A i B M AB
3
2
1
结点转角的数目:7个
独立结点线位移的数目:3个
D
E
A
B
C
C
D
刚架结构,有两个刚结点D、E, 故有两个角位移,结点线位移由铰 结体系来判断,W=3×4-2×6=0, 铰结体系几何不变,无结点线位移。
A
B
结构力学第八章

M BA
6i 2i A l
18
2)
MAB EI A i l
MAB
B
M AB
A
EI i l
A
A
B
3i 3i A l
MAB
3)
MAB i EI
MBA
A
l
A
B
A
EI i l
MBA
A
B
M AB i A M BA i A
19
三、固端弯矩
单跨超静定梁在荷载作用下产生的杆端弯矩称 为固端弯矩。固端弯矩以顺时针方向为正,逆时 针方向为负。 1. 两端固定梁 q
16
3. 一端固定、一端滑动支座的梁
MAB
EI
MBA
A
A
B
EI i l
M AB i A
M BA i A
17
4. 等截面直杆只要两端的杆端位移对应相同, 则相应的杆端力也相同。
EI MBA A i l
MAB MAB
1)
A
B
A
EI MBA A i l
B
M AB
6i 4i A l
2 D 0
30
k12 k12 B 2i A
1 B 0
k22 4i 3i D i E
B 0 k12=2i k22 4i D
2i
C
M2图
2 D 1( )
i
3i
k22=Байду номын сангаасi
31
2)建立位移法方程 上述刚度系数实质上是刚结点附加转动约束产 生的反力矩,由于原结构并没有附加转动约束, 各附加转动约束上的反力矩之和应等于零,据此 可以建立位移法典型方程。
第八章 -结构力学

二、结构位移计算的一般公式
由叠加原理:
i
总位移⊿=叠加每个微段变形在该点(A)处引起的微小
i
位移d⊿
d (M N Q )ds
l
如果结构由多个杆件组成,则整个结构变形引起某点
的位移为: (M N Q )ds
l
若结构的支座还有给定位移,则总的位移为:
( M N Q )ds Rkck (9-6)
虚功方程:
1 m M d 0
m M d
例3、悬臂梁在截面B处由于某种原因产生相对
剪位移d,试求A点在i-i方向的位移 Q。
B
d
B
解:①、在B截面处加
i
机构如图(将实际位移状态
A
Q
明确地表示为刚体体系的位 移状态)。
i
②、A点加单位荷载 FP=1,在铰B处虚设一对剪
A
Q
力Q(为保持平衡)
Q 1sin
➢ ① NP, QP , MP是荷载作用下,结构各截面上
的轴力,剪力,弯矩。注意这是在实际状态下的
内力。
➢ ②E,G材料的弹性模量和剪切弹性模量。
➢ ③A,I杆件截面的面积和惯性矩。
➢ ④EA,GA , EI杆件截面的抗拉,抗剪,抗弯
1、广义力与广义位移
作功的两方面因素:力、位移。
与力有关的因素,称为广义力S。
与位移有关的因素,称为广义位移Δ。 广义力与广义位移的关系是:它们的乘积是虚功。
即:W=PΔ
1)广义力是单个力,则广义位移是沿此力作用线 方向的线位移。 2)广义力是一个力偶,则广义位移是它所作用的 截面的转角β,即角位移。
mA
Δ A
B
P
Bm B
2、虚功
结构力学第八章

1、分层法 刚架在竖向荷载作用下,计算结果有以下两个特点:
1)结点的位移主要是转角,侧移很小; 2)作用在某根梁上的荷载主要对本层及上下柱子有影响, 对其它层杆件的影响很小。
为了简化计算,由此作如下假设: 1)在竖向荷载作用下,忽略刚架的侧移; 2)作用在梁上的荷载只对本层梁及上下层的柱子有影响。
§9-5
=
原结构
-M
A状态
+
B状态
在结点上加一个 反向的力矩。
A状态的内力——固端弯矩 (P281) 查表计算
B状态的内力——分配弯矩 用力矩分配法计算
§8-1
单结点的力矩分配法
例1:用力矩分配法计算图示连续梁。 FP=2kN q=1kN/m q FP L=4m EI EI A C L/2 L/2 B L 4/7 3/7 分配系数
无剪力分配法
FP FP
FP
FP
FP
FP
FP FP
=
(b)正对称
+
(c)反对称 可取半刚 架计算。
取
(d)半刚架
C
C’
(a)原结构
分解为正、 反对称问题
弯矩等于零, 不必计算
有侧移的柱剪力是 静定的,可用无剪 力分配法计算。
§9-4
无剪力分配法
对图示有侧移刚架,则不能直接应用无剪力分配法。 因竖柱AB、CD既不是两端无线位移杆件,也不是剪力静 定杆件,不符合无剪力分配法的应用条件。
4i 4 M13 M M 8i 8
分母是围绕“1”结点每个 单元的转动刚度之和
§8-1
力矩分配法的基本概念
2 EI M 1 EI EI 4
L
回代,得:
2i 1 M 31 2 i 1 M M 13 8i 2 i M 21 i 1 M M 12 8i M 41 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
wmax 0.0202 0.76 1 = = < l 4 150 150
解、将均布载荷分解为沿轴线方向和垂直于轴线方向的两个分力,可得: qx = q sin α ; 距离 B 端为 x 的截面上的轴力和弯矩分别为
q y = q cos α
M=
该截面的最大压应力为
q y lx 2
−
qy x2 2
=
q ( lx − x 2 ) cos α 2
σ
所以该点最大切应力为: τ max =
8-16、铁道路标圆信号板,装在外径 D=60mm 的空心圆柱上,所受的最大风载 p=2kN/m2,[σ]=60MPa。试 按第三强度理论选定空心柱的厚度。
解、结构的危险截面为空心柱的固定端,截面的弯矩和扭矩分别为
M = 2×
π × 0.52
4
× 0.8 = 0.314(kN .m);
当中性轴为①时,中性轴的截矩为: 偏心力作用点的位置为:
a y = −0.3; az → ∞ ;
z
②
iz2 0.019333 ey = − = − = 0.0644(m), ay −0.3
当中性轴为②时,中性轴的截矩为: 偏心力作用点的位置为:
iz2 ez = − = 0 az
①
a y = 0.4; az = −0.4 ;
解、将外载荷分解为沿 y 和 z 方向的力,可得
q y = q cos 300 = 2 × cos 300 = 1.732kN / m qz = q sin 300 = 2 × sin 300 = 1kN / m
梁的最大弯矩发生在梁的中间截面,值分别为
M zmax =
max My
1.732 × 42 = 3.464 ( kN .m ) 8 8 q z l 2 1× 4 2 = = = 2 ( kN .m ) 8 8 =
8-10、受拉构件形状如图,己知截面尺寸为 40mm×5mm,承受轴向拉力 F=l2kN。现拉杆开有切口,如不 计应力集中影响,当材料的[σ]=100MPa 时,试确定切口的最大许可深度,并绘出切口截面的应力变 化图。
38MPa
100 MPa A-A 截面应力分布图
解、由于切口的存在,在切口截面载荷为偏心力,切口截面上的轴力和弯矩分别为
第八章
组合变形习题答案
第八章、组合变形
8-1、14 号工字钢悬臂梁受力情况如图所示。已知 l=0.8m,F1=2.5kN,F2=1.0kN,试求危险截面上的最大 正应力。 解、危险截面为固定端 A 截面,该截面上的弯矩为
F1l 2 = 2.5 × 0.8 + 2.5 × 0.4 = 3 ( kN .m ) M zmax = F1l +
上述一元三次方程手算求解比较困难,下面给出 Maple 软件计算的结果和图形。 restart:solve(94.25*D^3-1200*D-1842=0,D);
-2.086581942 − .5739138538 I, -2.086581942 + .5739138538 I, 4.173163884
6 6
6
( Pa )
最大拉应力的表达式为
6q ( lx − x ) cos α qx sin α F M σ= z− N = − Wz A 2bh 2 bh
2
最大拉应力的位置为
x0 =
+
l h − tan α = 1.981m 2 6
6 6
最大拉应力的值为: σ max = 5.196 × 10 − 0.0991× 10 = 5.097 × 10
6
( Pa )
2
第八章
组合变形习题答案
8-6、砖砌烟囱高 h=30m,底截面 m-m 的外径 d1=3m,内径 d2=2m,自重 P1=2000kN,受 q=1kN/m 的风力 作用。试求: (1) 烟囱底截面上的最大压应力; (2) 若烟囱的基础埋深 h0=4m,基础及填土自重按 P2=1000kN 计算,土壤的许用压应力[σ]=0.3MPa, 圆形基础的直径 D 应为多大? 注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。 解、 (1)底面 m-m 截面上的弯矩和轴力分别为
2
, FN = qx x = qx sin α
6q ( lx − x ) cos α qx sin α F M + σ= z+ N = Wz A 2bh 2 bh
上式对 x 求导,可得取得最大压应力的位置为
x0 =
l h + tan α = 2.019m 2 6
−
可得最大压应力为: 将 x0 代入正应力的表达式, σ max = 5.1967 × 10 + 0.101×10 = 5.297 × 10
3 3 2⎤ ⎡1 ⎤ ⎡1 I zC = ⎢ ( 4a )( 2a ) + ( 4a )( 2a ) a 2 ⎥ + ⎢ a ( 4a ) + ( 4a )( a )( 2a ) ⎥ = 32a 4 ⎣12 ⎦ ⎣12 ⎦ 1 1 3 I yC = ( 2a )( 4a ) + ( 4a ) a 3 = 11a 4 12 12
所以该点的主应力为
σ ma+ ⎜ ⎟ + τ 2 = 11.734 + 21.699 = 33.43( MPa ) 2 ⎝2⎠
2
2
⎛σ ⎞ = σ 2 = − ⎜ ⎟ + τ 2 = 11.734 − 21.699 = −9.93( MPa) 2 ⎝2⎠ 1 (σ 1 − σ 3 ) = 21.68( MPa) 2
T = 2×
π × 0.52
4
× 0.6 = 0.236(kN .m)
根据第三强度理论,可知
σr =
3
32 M 2 + T 2 32 M 2 + T 2 4 σ α ≤ ⇒ ≤ 1 − [ ] π D 3 (1 − α 4 ) π D 3 [σ ]
F := 12000 ; h :=
1 1 ; b := ; s := 100000000 25 200
solve(3*F*x/(b*(h-x)**2)+F/(b*(h-x))<s,x);
⎛ 8 − 3 6 ⎞ ⎞, RealRange⎛ Open⎛ 8 + 3 6 ⎞, ∞ ⎞ RealRange⎛ ⎜ ⎟⎟ ⎜ ⎜ ⎟ ⎟ ⎜ −∞, Open⎜ ⎜ 125 125 ⎟ ⎟ ⎜ ⎜ 125 125 ⎟ ⎟ ⎝ ⎝ ⎠⎠ ⎝ ⎝ ⎠ ⎠
M=
qh 2 = 450(kN .m), FN = 2000kN 2
因此,烟囱底截面上的最大压应力为
σ max =
M FN + = W A
32 × 450 × 103 4 × 2000 ×103 + ⎡ ⎛ 2 ⎞ 4 ⎤ π × ( 32 − 22 ) 3 π × 3 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝3⎠ ⎦ ⎥ ⎣
32 × 3.2 ×103 × 90 ×10−3 正应力为: σ = = 23.468 × 106 ( Pa) 3 −9 π × 50 × 10
切应力为: τ =
16 × 3.2 ×10 ×140 × 10 π × 503 × 10−9
3
−3
τ
σ
= 18.253 × 106 ( Pa)
5
第八章
组合变形习题答案
根据工字形截面的特点,可知,截面的最大弯曲正应力为
σ max
8-2、受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为α=30o, 如图所示。己知该梁材料的弹性模量 E=10GPa;梁的尺寸为 l=4m,h=160mm;b=120mm;许用应力 [σ]=l20MPa;许可挠度[w]=l/1150。试校核梁的强度和刚度。
两个联合作用下的最大挠度为
wmax =
根据刚度条件要求,可得
(w ) + (w )
max 2 y
max 2 z
= 0.0202(m)
8-4、图示一楼梯木斜梁的长度为 l=4m,截面为 0.1m×O.2m 的矩形,受均布荷载作用,q=2kN/m。试作梁的 轴力图和弯矩图,并求横截面上的最大拉应力和最大压应力。
wy =
5q y l 4 384 EI z
=
12 × 5 ×1.732 × 103 × 44 = 0.0141(m) 384 × 10 × 109 ×120 × 1603 × 10−12
1
第八章
组合变形习题答案
qz 作用下最大挠度为
wy =
5qz l 4 12 × 5 × 1× 103 × 44 = = 0.0145(m) 384 EI y 384 × 10 ×109 × 160 ×1203 × 10−12
max My = F2 l = 1.0 × 0.8 = 0.8 ( kN .m )
14 号工字钢的抗弯截面模量分别为
Wz = 102cm3 ;
Wy = 16.1cm3
max 3 × 103 0.8 ×103 M zmax M y = + = + = 79.1× 106 ( Pa ) −6 −6 102 × 10 16.1×10 Wz Wy
qyl2
根据矩形截面的特点,可得梁的最大正应力为
σ max =
max M zmax M y 6 × 3.464 ×103 6 × 2 × 103 + = + = 11.97 × 106 ( Pa ) −9 −9 2 2 Wz Wy 120 ×160 ×10 160 ×120 × 10
qy 作用下最大挠度为
M=
Fx ; 2
FN = F
所以,偏心截面处的最大拉应力和所对应的强度条件为
