简单回归数据
SPSS教程-简单回归分析-案例及结果解释
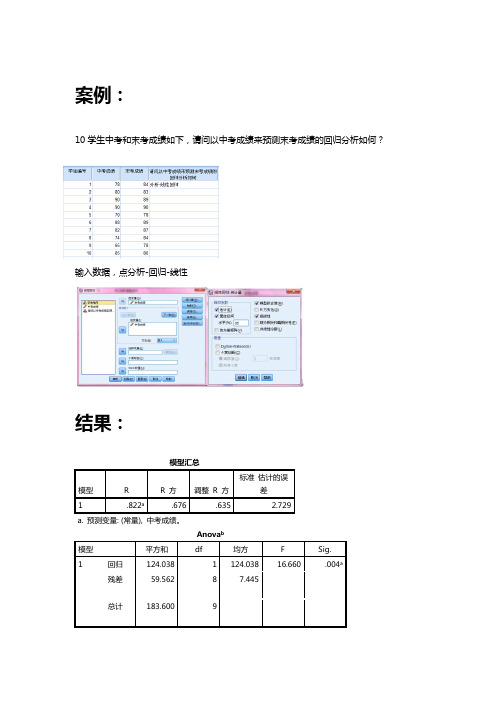
案例:
10学生中考和末考成绩如下,请问以中考成绩来预测末考成绩的回归分析如何?输入数据,点分析-回归-线性
结果:
模型汇总
模型R R 方调整R 方标准估计的误
差
1 .822a.676 .635 2.729
a. 预测变量: (常量), 中考成绩。
Anova b
模型平方和df 均方 F Sig.
1 回归124.038 1 124.038 16.660 .004a
残差59.562 8 7.445
总计183.600 9
R平方的F检验为16.660,达显著水平。
系数估计:个别变量,B,beta及显著性检验。
中考变量beta为0.822,达显著水平。
结果分析:
以中考成绩预测末考成绩,为单一回归分析,由于数学基础相同,简单回归与相关分析的主要结果相同。
Pearson相关系数、Multiple R与Beta皆为0.822,这几个系数的检验值均相同,达显著水平。
R平方则提供回归变异量,显示中考成绩预测末考成绩有63.5%的解释力,F(1,8)=16.66,p=0.004,显示该解释力具有统计上的意义。
系数估计的结果指出,中考成绩能够有效预测末考成绩,beta系数达0.822(t=4.082, p=0.004), 表示中考成绩越高,末考成绩越好。
简单回归分析计算例

【例9-3】-【例9-8】 简单回归分析计算举例利用例9-1的表9-1中已给出我国历年城镇居民人均消费支出和人均可支配收入的数据,(1)估计我国城镇居民的边际消费倾向和基础消费水平。
(2)计算我国城镇居民消费函数的总体方差S2和回归估计标准差S。
(3)对我国城镇居民边际消费倾向进行置信度为95%的区间估计。
(4)计算样本回归方程的决定系数。
(5)以5%的显著水平检验可支配收入是否对消费支出有显著影响;对Ho :β2=0.7,H1:β2<0.7进行检验。
(6)假定已知某居民家庭的年人均可支配收入为8千元,要求利用例9-3中拟合的样本回归方程与有关数据,计算该居民家庭置信度为95%的年人均消费支出的预测区间。
解:(1)教材中的【例9-3】Yt =β1+β2Xt +u t将表9-1中合计栏的有关数据代入(9.19)和(9.20)式,可得:2ˆβ =2129.0091402.57614 97.228129.009 1039.68314)-(-⨯⨯⨯=0.6724 1ˆβ=97.228÷14-0.6724×129.009÷14=0. 7489 样本回归方程为:tY ˆ=0.7489+0.6724Xt 上式中:0.6724是边际消费倾向,表示人均可支配收入每增加1千元,人均消费支出会增加0.6724千元;0.7489是基本消费水平,即与收入无关最基本的人均消费为0.7489千元。
(2)教材中的【例9-4】将例9-1中给出的有关数据和以上得到的回归系数估计值代入(9.23)式,得:∑2te=771.9598-0.7489×97.228-0. 6724×1039.683=0.0808将以上结果代入(9.21)式,可得: S2=0.0808/(14-2)=0.006732 进而有: S=0.006732=0.082047(3)教材中的【例9-5】 将前面已求得的有关数据代入(9.34)式,可得:2ˆβS =0.082047÷14/129.0091402.5762)(-=0.0056 查t分布表可知:显著水平为5%,自由度为12的t分布双侧临界值是2.1788,前面已求得0.6724ˆ2=β,将其代入(9.32)式,可得: 0560.01788.20.67240560.01788.26724.02⨯+≤≤⨯-β 即:0.68460.66022≤≤β(4)教材中的【例9-6】 r2=1 -SST SSE= 1- 96.72520.0808 = 0.9992 上式中的SST是利用表9-1中给出的数据按下式计算的:SST=∑2t Y -(∑Yt )2/n=771.9598-(97.228)2÷14=96.7252(5)教材中的【例9-7】首先,检验收入对消费支出是否有显著影响,提出假设 Ho :β2=0,H1:β2≠0。
医学统计学简单线性回归和线性相关

1、答:实验数据为:图一实验数据图首先得到散点图,观察身高与肺死腔容积是否具有线性关系。
Graph-Scatter/Dot-simple scatter,x图二15名儿童身高与肺死腔容积散点图从图中可知,肺死腔容量随着身高增加而增加,且呈直线变化趋势。
回归方程的截距和系数求解为:Analyze-Regression-Linear,将y放入Dependent, x放入Independent中,结果为:图三回归系数和截距结果图从上图得,截距为-89.771,回归系数为1.069.回归系数等于0的假设检验:建立假设、确定检验水准α。
H0:β=0,即儿童的身高与肺死腔容积无直线关系。
H1:β≠0,即儿童的身高与肺死腔容积有直线关系。
检验水准α=0.05计算检验统计量F值,确定P值。
图四方差齐性结果图从上图得,F=42.629,概率P<0.05,即拒绝H0,接受H1,可认为儿童的身高与肺死腔容积有直线关系。
证明:由图三和图四可得,t b=6.529=√F=6.529。
估计回归系数的95%置信区间:Analuze-Regression-Linear-save,勾上Mean,结果如下,图五总体回归系数置信区间得总体回归系数95%置信区间为(13.664,109.797)。
2、答:实验数据为:图一实验数据图首先得到散点图,观察凝血时间与凝血酶浓度是否具有线性关系。
Graph-Scatter/Dot-simple scatter,x变量放入X Axis,与y变量放入Y Axis,OK.结果如下,图二15名健康成人凝血时间与凝血酶浓度散点图从图中可知,凝血酶浓度随着凝血时间增加而减少,且呈直线变化趋势。
其次进行双变量正态检验:对x进行正态检验,结果为,图三 x变量正态检验结果图从上图可知,概率P>0.05,即x变量服从正态变量。
以凝血酶浓度和凝血时间作直线回归,并进行残差分析。
Analyze-Regression-Linear,将y放入Dependent, x放入Independent中,结果为:图四回归系数和截距结果图从上图得,截距为2.816,回归系数为-0.123.并且从上图得,概率P<0.05,即拒绝H0,接受H1,可认为凝血时间与凝血酶浓度有直线关系。
简易回归模型案例 数据集

简易回归模型案例数据集
假设我们有一个简单的回归模型案例,我们需要一个数据集来
进行分析。
我们可以使用一个虚拟的数据集来说明这个案例。
假设
我们想要建立一个回归模型来预测学生的考试成绩(因变量)与他
们每周学习时间(自变量)之间的关系。
我们可以创建一个包含学生ID、学习时间和考试成绩的数据集。
例如,我们有10个学生的数据,他们的学习时间和考试成绩如下:
学生ID 学习时间(小时)考试成绩。
1 5 80。
2 7 85。
3 3 75。
4 6 88。
5 4 79。
6 8 92。
7 5 81。
8 7 87。
9 4 77。
10 6 89。
这个数据集包括了学生的学习时间和他们对应的考试成绩。
我们可以使用这个数据集来建立一个简单的回归模型,来预测学生的考试成绩。
在这个案例中,我们可以使用学习时间作为自变量,考试成绩作为因变量。
我们可以使用简单的线性回归模型来建立它们之间的关系,模型可以表示为,考试成绩= β0 + β1学习时间+ ε。
其中,β0是截距,β1是斜率,ε是误差项。
我们可以使用这个数据集来估计β0和β1的值,然后建立回归方程,最终用于预测学生的考试成绩。
当然,这只是一个简单的示例数据集和回归模型案例。
在实际应用中,数据集的大小和复杂度会更大,回归模型的建立也会更加细致和复杂。
但是通过这个简单的案例,我们可以初步了解回归模型的应用和建立过程。
简单线性回归模型的公式和参数估计方法以及如何利用模型进行

简单线性回归模型的公式和参数估计方法以及如何利用模型进行数据预测一、简单线性回归模型的公式及含义在统计学中,线性回归模型是一种用来分析两个变量之间关系的方法。
简单线性回归模型特指只有一个自变量和一个因变量的情况。
下面我们将介绍简单线性回归模型的公式以及各个参数的含义。
假设我们有一个自变量X和一个因变量Y,简单线性回归模型可以表示为:Y = α + βX + ε其中,Y表示因变量,X表示自变量,α表示截距项(即当X等于0时,Y的值),β表示斜率(即X每增加1单位时,Y的增加量),ε表示误差项,它表示模型无法解释的随机项。
通过对观测数据进行拟合,我们可以估计出α和β的值,从而建立起自变量和因变量之间的关系。
二、参数的估计方法为了求得模型中的参数α和β,我们需要采用适当的估计方法。
最常用的方法是最小二乘法。
最小二乘法的核心思想是将观测数据与模型的预测值之间的误差最小化。
具体来说,对于给定的一组观测数据(Xi,Yi),我们可以计算出模型的预测值Yi_hat:Yi_hat = α + βXi然后,我们计算每个观测值的预测误差ei:ei = Yi - Yi_hat最小二乘法就是要找到一组参数α和β,使得所有观测值的预测误差平方和最小:min Σei^2 = min Σ(Yi - α - βXi)^2通过对误差平方和进行求导,并令偏导数为0,可以得到参数α和β的估计值。
三、利用模型进行数据预测一旦我们估计出了简单线性回归模型中的参数α和β,就可以利用这个模型对未来的数据进行预测。
假设我们有一个新的自变量的取值X_new,那么根据模型,我们可以用以下公式计算对应的因变量的预测值Y_new_hat:Y_new_hat = α + βX_new这样,我们就可以利用模型来进行数据的预测了。
四、总结简单线性回归模型是一种分析两个变量关系的有效方法。
在模型中,参数α表示截距项,β表示斜率,通过最小二乘法估计这些参数的值。
简单线性回归模型

简单线性回归模型线性回归是统计学中一个常见的分析方法,用于建立自变量与因变量之间的关系模型。
简单线性回归模型假设自变量与因变量之间存在线性关系,可以通过最小二乘法对该关系进行拟合。
本文将介绍简单线性回归模型及其应用。
一、模型基本形式简单线性回归模型的基本形式为:y = β0 + β1x + ε其中,y为因变量,x为自变量,β0和β1为常数项、斜率,ε为误差项。
二、模型假设在使用简单线性回归模型之前,我们需要满足以下假设:1. 线性关系假设:自变量x与因变量y之间存在线性关系。
2. 独立性假设:误差项ε与自变量x之间相互独立。
3. 同方差性假设:误差项ε具有恒定的方差。
4. 正态性假设:误差项ε符合正态分布。
三、模型参数估计为了估计模型中的参数β0和β1,我们使用最小二乘法进行求解。
最小二乘法的目标是最小化实际观测值与模型预测值之间的平方差。
四、模型拟合度评估在使用简单线性回归模型进行拟合后,我们需要评估模型的拟合度。
常用的评估指标包括:1. R方值:衡量自变量对因变量变异的解释程度,取值范围在0到1之间。
R方值越接近1,说明模型对数据的拟合程度越好。
2. 残差分析:通过观察残差分布图、残差的均值和方差等指标,来判断模型是否满足假设条件。
五、模型应用简单线性回归模型广泛应用于各个领域中,例如经济学、金融学、社会科学等。
通过建立自变量与因变量之间的线性关系,可以预测和解释因变量的变化。
六、模型局限性简单线性回归模型也存在一些局限性,例如:1. 假设限制:模型对数据的假设比较严格,需要满足线性关系、独立性、同方差性和正态性等假设条件。
2. 数据限制:模型对数据的需求比较高,需要保证数据质量和样本的代表性。
3. 线性拟合局限:模型只能拟合线性关系,无法处理非线性关系的数据。
简单线性回归模型是一种简单且常用的统计方法,可以用于探索变量之间的关系,并进行预测和解释。
然而,在使用模型时需要注意其假设条件,并进行适当的拟合度评估。
如何在Excel中使用Regression进行回归分析
如何在Excel中使用Regression进行回归分析回归分析是一种用于研究变量之间关系的统计技术。
在Excel中,你可以使用Regression函数进行回归分析,通过拟合数据点的回归线来预测因变量。
本文将详细介绍如何在Excel中使用Regression函数进行简单线性回归和多元线性回归分析。
一、简单线性回归分析简单线性回归分析适用于只有一个自变量和一个因变量的情况。
以下是在Excel中进行简单线性回归分析的步骤:1. 准备数据首先,将需要进行回归分析的数据录入Excel表格中。
通常,自变量应该在A列,而因变量应该在B列。
2. 插入回归分析工具点击Excel菜单栏中的"数据"选项卡,然后点击“数据分析”按钮。
如果在"数据分析"中找不到“回归”选项,请先点击“加载项”按钮,然后勾选“分析工具包”,最后点击“确认”。
3. 选择回归分析工具在“数据分析”对话框中,选择“回归”,然后点击“确定”。
4. 设置输入和输出范围“输入X范围”设置为自变量的数据列。
选择“标签”选框,并选择“输出范围”。
点击“确定”。
5. 分析回归结果在指定的输出范围中,Excel将显示回归分析的结果,包括截距、斜率、相关系数等。
二、多元线性回归分析多元线性回归分析适用于有多个自变量和一个因变量的情况。
以下是在Excel中进行多元线性回归分析的步骤:1. 准备数据同样地,将需要进行回归分析的数据录入Excel表格中。
自变量应该在不同的列,而因变量应该在单独的列中。
2. 插入回归分析工具同样地,点击Excel菜单栏中的"数据"选项卡,然后点击“数据分析”按钮。
确保你已经加载了“分析工具包”。
3. 选择回归分析工具在“数据分析”对话框中,选择“回归”,然后点击“确定”。
4. 设置输入和输出范围“输入X范围”设置为所有自变量的数据列。
选择“标签”选框,并选择“输出范围”。
点击“确定”。
简单回归和二元回归的标准误
简单回归和二元回归的标准误一、简单回归的标准误1.简单回归的定义简单回归是指通过一个自变量(X)来预测一个因变量(Y)的关系。
这种关系可以用线性方程来表示,即Y = aX + b,其中a和b分别为斜率和截距。
2.简单回归的公式简单回归的残差(e)公式为:e = Y - (aX + b)。
3.简单回归的标准误计算方法简单回归的标准误(SE)是通过计算残差的平方和(RSS)来得到的,公式为:SE = sqrt(RSS/n),其中n为观测值的数量。
二、二元回归的标准误1.二元回归的定义二元回归是指通过两个自变量(X1,X2)来预测一个因变量(Y)的关系。
这种关系可以用线性方程来表示,即Y = a1X1 + a2X2 + b。
2.二元回归的公式二元回归的残差(e)公式为:e = Y - (a1X1 + a2X2 + b)。
3.二元回归的标准误计算方法二元回归的标准误(SE)是通过计算残差的平方和(RSS)来得到的,公式为:SE = sqrt(RSS/n),其中n为观测值的数量。
三、简单回归和二元回归的标准误应用1.数据处理与分析在进行简单回归和二元回归分析时,首先需要收集相关数据,然后利用统计软件(如SPSS、R等)进行线性回归分析。
在分析过程中,会得到回归系数、截距、残差等统计量。
2.结果解读与应用标准误可以用来衡量模型的拟合效果。
较低的标准误表明模型预测较为准确,较高的标准误则说明模型预测存在较大误差。
在实际应用中,我们可以根据具体情况选择合适的模型。
同时,通过比较不同模型的标准误,可以优选拟合效果较好的模型。
简单回归和二元回归的标准误为我们提供了评估模型质量的指标,有助于我们在实际问题中选择合适的回归模型。
回归方法进行数据统计分析
回归方法进行数据统计分析回归方法是一种常用的数据统计分析方法,它用于探究变量之间的关系,并预测一个变量对其他相关变量的响应。
回归分析通常用于预测因变量的值,并确定自变量对因变量的贡献程度。
在本文中,我将详细介绍回归方法的原理、应用、优势和限制。
首先,回归方法的原理是建立一个数学模型来描述自变量与因变量之间的关系。
这个模型可以用线性方程、非线性方程或其他函数来表示。
线性回归是最简单且最常用的回归方法之一。
其基本形式是Y = β₀+ β₁X₁+ β₂X₂+ ... + βₙXₙ,其中Y 是因变量,X₁~Xₙ是自变量,β₀~βₙ是待求的系数。
通过估计这些系数,可以推断自变量对因变量的影响大小。
回归方法有着广泛的应用领域。
在经济学中,回归分析可用于评估经济指标之间的关系,比如GDP与人口增长率之间的关系。
在市场营销中,回归分析可用于预测销售额与广告投入、促销活动等因素之间的关系。
在医学领域,回归分析可用于研究药物剂量与疗效之间的关系。
在环境科学中,回归分析可用于分析气候因素对植物生长的影响。
总而言之,回归方法可以在各个学科领域进行统计分析和预测。
回归方法具有一些优势。
首先,它提供了一种量化分析变量之间关系的方法,可以帮助我们理解变量之间的因果关系。
其次,回归分析可以用于预测未来或不存在的数据,帮助我们做出决策和制定策略。
第三,回归方法在样本数据较多时具有较高的准确性和可信度,可以提供较为准确的结果。
最后,回归分析的结果易于解释和理解,可以帮助我们传达统计推断的结论。
然而,回归方法也有一些局限性。
首先,回归分析是基于现有数据的分析方法,对数据质量要求较高。
如果数据存在缺失、离群点或非线性关系,可能会影响回归分析的结果。
其次,回归方法只能揭示相关性,而不能确定因果关系。
即使存在显著相关性,在解释这种关系时也需要慎重。
此外,回归模型的选择和变量的解释都需要主观判断,可能存在一定的不确定性。
在进行回归分析时,我们应该注意一些关键点。
简单线性回归的分析步骤
简单线性回归的分析步骤简单线性回归是一种统计分析技术,通常用于确定两个变量之间的相关性和影响,以及预测一个变量响应另一个变量的变化。
这种分析技术可以帮助组织分析影响某个变量的原因,以更好地开发这些变量之间的关系。
简单线性回归分析可以帮助组织采取有效的管理和决策措施。
本文将介绍简单线性回归分析的六个步骤:第一步:定义回归模型简单线性回归中有两个变量:自变量(X)和因变量(Y),并假设存在线性关系。
变量之间的关系可以表示为方程:Y = +X+εα要求估计的参数,ε模型中的噪声。
第二步:收集数据简单线性回归的第二步是收集数据。
数据收集是回归分析的核心,是建立回归模型的基础,决定了估计参数的准确性。
因此,在收集数据的时候需要注意数据的准确性,也要注意数据量。
数据量越大,分析结果越准确。
第三步:检查数据在收集数据之后,需要检查数据,检查数据中是否存在缺失值,异常值等情况。
缺失值可能影响数据分析的准确性,而异常值可能会降低模型的准确性和复杂度。
此外,还需要检查自变量和因变量之间是否存在多重共线性。
第四步:拟合模型简单线性回归的第四步是拟合模型。
在拟合模型的时候,可以使用最小二乘法或最小平方根法来拟合模型。
最小二乘法可以获得最佳拟合参数,而最小平方根法可以获得更准确的拟合参数。
第五步:诊断模型简单线性回归的第五步是诊断模型。
诊断模型旨在检测模型的正确性。
此时,可以检查不变的残差、残差的自相关性、残差的正态性、残差的均值和方差,以及多元共线性、自变量的偏性和因变量的偏性等。
这些检查有助于验证模型的准确性和可靠性。
第六步:模型检验最后一步是模型检验。
模型检验旨在测试模型的可靠性。
模型检验可以使用拟合优度检验、显著性检验或者F-检验来完成。
拟合优度检验用于测量模型中变量的可预测性,而显著性检验用于检验参数的显著性,而F-检验用于检验拟合的精确度。
综上所述,简单线性回归分析有六个步骤:定义回归模型,收集数据,检查数据,拟合模型,诊断模型,以及模型检验。
