一元线性回归方程
1一元线性回归方程
i =1 n
i =1 n
2
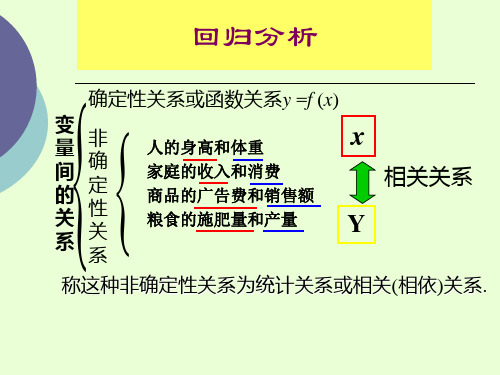
Lxy = ∑( Xi − X ) (Yi −Y )
i=1
ˆ ˆ β0 = Y − β1 X ˆ Lxy β1 = Lxx
二、OLS回归直线的性质 回归直线的性质
ˆ (1)估计的回归直线 Yi )
(2) )
ˆ ˆ = β 0 + β 1X i
前三个条件称为G-M条件 条件 前三个条件称为
§1.2 一元线性回归模型的参数估计
普通最小二乘法( Squares) 普通最小二乘法(Ordinary Least Squares) OLS回归直线的性质 OLS回归直线的性质 OLSE的性质 OLSE的性质
一、普通最小二乘法
对于所研究的问题, 对于所研究的问题,通常真实的回归直线 E(Yi|Xi) = β0 + β1Xi 是观 测不到的。可以通过收集样本来对真实的回归直线做出估计。 测不到的。可以通过收集样本来对真实的回归直线做出估计。
Y
55 80 100 120140 160
X
二、随机误差项εi的假定条件 随机误差项
为了估计总体回归模型中的参数,需对随机误差项作出如下假定: 为了估计总体回归模型中的参数,需对随机误差项作出如下假定: 假定1: 假定 :零期望假定:E(εi) = 0。 。 假定2: 假定 :同方差性假定:Var(εi) = σ 2。 假定3: 假定 :无序列相关假定:Cov(εi, εj) = 0, (i ≠ j )。 。 假定4: 假定 : εi 服从正态分布,即εi ∼ N (0, σ 2 )。 。
以下设 x 为自变量(普通变量 Y 为因变量(随机变 普通变量) 普通变量 随机变 量) .现给定 x 的 n 个值 x1,…, xn, 观察 Y 得到相应的 n 个 值 y1,…,yn, (xi ,yi) i=1,2,…, n 称为样本点 样本点. 样本点 以 (xi ,yi) 为坐标在平面直角坐标系中描点,所得到 的这张图便称之为散点图 散点图. 散点图
一元线性回归方程

Upper 95% 238.4541 -118.508
第二十六页,编辑于星期六:十三点 五十五分。
Y
140 120 100
80 60 40 20
0 0
X Variable 1 Line Fit Plot
0.2
0.4
0.6
0.8
1
X Variable 1
Y 预测 Y
1.2
第二十七页,编辑于星期六:十三点 五十五分。
i 1
y )2
第八页,编辑于星期六:十三点 五十五分。
散点图
以(xi ,yi)为坐标在平面直角坐标系中描 点,所得到的这张图便称之为散点图.
第九页,编辑于星期六:十三点 五十五分。
北京市城市居民家庭生活抽样调查表1
Y:人均收入
14 12 10 8 6 4 2 0
1976
1978
1980 1982 1984
第二节
一元线性回归方程
第一页,编辑于星期六:十三点 五十五分。
一 回归直线方程
两个变量之间的线性关系,其回归模型为:
yi a bxi i
y称为因变量,x称为自变量, 称为随
机扰动,a,b称为待估计的回归参数, 下标i表示第i个观测值。
第二页,编辑于星期六:十三点 五十五分。
对于回归模型,我们假设:
4.代入样本信息,F落入否定域则否定原假设,
线性关系显著;落入接受域则接受原假设,
线性关系不显著.
第二十一页,编辑于星期六:十三点 五十五分。
相关系数检验法:
1.提出原假设:H0:b=0;
2.选择统计量 R lxy lxxl yy
3.对给定的显著性水平α,查临界值rα (n-2),
一元线性回归

12.9 一元线性回归以前我们所研究的函数关系是完全确定的,但在实际问题中,常常会遇到两个变量之间具有密切关系却又不能用一个确定的数学式子表达,这种非确定性的关系称为相关关系。
通过大量的试验和观察,用统计的方法找到试验结果的统计规律,这种方法称为回归分析。
一元回归分析是研究两个变量之间的相关关系的方法。
如果两个变量之间的关系是线性的,这就是一元线性回归问题。
一元线性回归问题主要分以下三个方面:(1)通过对大量试验数据的分析、处理,得到两个变量之间的经验公式即一元线性回归方程。
(2)对经验公式的可信程度进行检验,判断经验公式是否可信。
(3)利用已建立的经验公式,进行预测和控制。
12.9.1 一元线性回归方程 1.散点图与回归直线在一元线性回归分析里,主要是考察随机变量y 与普通变量x 之间的关系。
通过试验,可得到x 、y 的若干对实测数据,将这些数据在坐标系中描绘出来,所得到的图叫做散点图。
例1 在硝酸钠(NaNO 3)的溶解度试验中,测得在不同温度x (℃)下,溶解于100解 将每对观察值(x i ,y i )在直角坐标系中描出,得散点图如图12.11所示。
从图12.11可看出,这些点虽不在一条直线上,但都在一条直线附近。
于是,很自然会想到用一条直线来近似地表示x 与y 之间的关系,这条直线的方程就叫做y 对x 的一元线性回归方程。
设这条直线的方程为yˆ=a+bx 其中a 、b 叫做回归系数(y ˆ表示直线上y 的值与实际值y i 不同)。
图12.11下面是怎样确定a 和b ,使直线总的看来最靠近这几个点。
2.最小二乘法与回归方程在一次试验中,取得n 对数据(x i ,y i ),其中y i 是随机变量y 对应于x i 的观察值。
我们所要求的直线应该是使所有︱y i -yˆ︱之和最小的一条直线,其中i y ˆ=a+bx i 。
由于绝对值在处理上比较麻烦,所以用平方和来代替,即要求a 、b 的值使Q=21)ˆ(i ni iyy-∑=最小。
一元线性回归方程的建立

第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这(i=1,2,3,…,n)。
这样,我们就可以用残差平种偏差称为残差,记为e i方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为: (2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
一元线性回归方程的应用

第四节一元线性回归方程的应用回归方程最主的应用就是用它进行估计或预测。
只要r2≠1,估计误差就不可避免。
因而在应用回归方程时,需要对估计的误差以及与之相联系的一些问题有所了解。
一、回归方程的建立与预测(或估计)对于一组X、Y的数据,我们可以建立回归方程,有了y对X的回归方程,也就找到了X与y之间变化的数量关系,对于任意一个X值都可估计出与之对应的y值。
一)回归方程的建立例下面是20名工作人员的智商和某一次技术考试成绩,根据这个结果求出考试成绩对智商的回归方程。
如果另有一名工作人员智商为120,则估计一下若让他也参加技术考试,将会得多少分?解:经检验两者具有线性关系计算得:X与Y的均值:107 71标准差:13.69 11.63 r=0.86代入公式则回归方程为:NO 智商X成绩Y估计Y'NO智商X成绩Y估计Y'1 89 55 57.86 11 84 53 54.212 97 74 63.7 12 121 82 81.223 126 87 84.87 13 97 58 63.74 87 60 56.4 14 101 60 66.625 119 71 79.76 15 92 67 60.056 101 54 66.62 16 110 80 73.197 130 90 87.79 17 128 85 86.338 115 73 76.84 18 111 73 73.929 108 67 71.73 19 99 71 65.1610 105 70 69.54 20 120 90 80.49二)回归方程的检验1.方差分析法SSR=1997.48 SST=2705.14 SSE=707.66F=MSR/MSE=(SSR/dfR)/(SSE/dfE)= 1997.48 /(707.66/18)=50.81查表F(1,18)=8.28(0.01) 或 4.41(0.05) 结果显著2.回归系数法SX=13.69 SY=11.63 b=0.73 r=0.86三)用回归方程进行预测若X=120,代入回归方程得=80.5就是说,这位工作人员虽没参加技术考试,但根据他的智商,估计其技术考试的分数应该为80.5。
(完整word版)一元线性回归方程的建立分析

第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)我们称(2-1-1)式为回归方程,a与b是待定常数,称为回归系数。
从理论上讲,(2-1-1)式有无穷多组解,回归分析的任务是求出其最佳的线性拟合。
二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这种偏差称为残差,记为e i(i=1,2,3,…,n)。
这样,我们就可以用残差平方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为:(2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
三、正规方程组根据微分中求极值的方法可知,Q(a,b)取得最小值应满足(2-1-3)由(2-1-2)式,并考虑上述条件,则(2-1-4)(2-1-4)式称为正规方程组。
一元线性回归模型及参数估计

但是,随机误差项的方差的估计量是不同的。
解或然方程
sm2
L*
= n
2sm2
+1
2sm4
S(Yi
bˆ0
bˆ1Xi)2
=0
即可得到sm2的最大或然估计量为:
sˆm2
1 =nS(Yi
bˆ0
bˆ1Xi)2
s P (Y i)=
1 e2s 1m 2(Y ibˆ0bˆ1X i)2 2
i= 1,2,… ,n
因为Yi 是相互独立的,所以 Y 的所有样本观测值的联合概率, 也即或然函数(likelihood function)为:
L(bˆ0,bˆ1,sm2) = P(Y1,Y2,,Yn)
=
1
e 1 2sm2
S(Yi
,当
Q对
b$ 、 0
b$ 的一阶偏导数为 1
0 时, Q 达到最小。即
Q
bˆ 0 Q
bˆ1
=0 =0
(
( bˆ
bˆ
0
0 +
+ bˆ1 X bˆ1 X i
i
Yi ) Yi ) X
= i
0 =
0
SYi SYi X i
= nbˆ0 + bˆ1SX i
=
bˆ0 SX i
+
bˆ1S
X
2 i
解得:
bˆ0 = Y bˆ1X
bˆ1
=
nSYi Xi SYiSXi nSXi2 (SXi )2
由于
bˆ 0
、bˆ 的估计结果是从最小二乘原理得到的,故称为 1
一元线性回归方程的建立
第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型,它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论,我们不仅可以掌握有关一元线性回归的知识,而且可以从中了解回归分析方法的基本思想、方法和应用。
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响,测定了不同氮含量时铁合金溶液初生奥氏体析出温度,得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标,把初生奥氏体析出温度作为纵坐标,将这些数据标在平面直角坐标上,则得图2-1-1,这个图称为散点图。
从图2-1-1可以看出,数据点基本落在一条直线附近。
这告诉我们,变量X与Y的关系大致可看作是线性关系,即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上,因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素,诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系,可以作线性拟合(2-1-1)我们称(2-1-1)式为回归方程,a与b是待定常数,称为回归系数。
从理论上讲,(2-1-1)式有无穷多组解,回归分析的任务是求出其最佳的线性拟合。
二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值,那么实际测量值y i与回归值i之间存在着偏差,我们把这种偏差称为残差,记为e i(i=1,2,3,…,n)。
这样,我们就可以用残差平方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为:(2-1-2) 所谓最小二乘法,就是选择a和b使Q(a,b)最小,即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数,所以它的最小值总是存在的。
下面讨论的a和b的求法。
三、正规方程组根据微分中求极值的方法可知,Q(a,b)取得最小值应满足(2-1-3)由(2-1-2)式,并考虑上述条件,则(2-1-4)(2-1-4)式称为正规方程组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
父母高,子女也高;父母矮,子女也矮。给定父母的身高,子女 平均身高趋向于“回归”到 全体人口的平均身高。
➢ 回归的现代释义
回归分析用于研究一个变量关于另一个(些)变量的具
体依赖关系的计算方法和理论。
inflation a b
1
unemployment
商品需求函数: Q a bP
Yi
E(Y|Xi) = 0 + 1 Xi
Yˆi ˆ0 ˆ1Xi
(估计的)样本回归模型:
Yi ˆ0 ˆ1Xi ei
其中ei是第i次观测的残差
Y2
e2 Y1 u2
e1 u1
Yˆi ˆ0 ˆ1Xi
u3
e3
Y3
Xi
三、参数估计——最小二乘法
对于所研究的经济问题,通常总体回归直线 E(Yi|Xi) = 0 + 1Xi 是
通常总体回归函数E(Y) = 0+ 1X是观测不到的,利用样本得到的是 对它的估计,即对0和1的估计。令{(Xi,Yi):i=1,…,n}表示从总体中抽取
的一个样本容量为n的随机样本,对于每个i,可以写出:
Yi 0 1Xi ui 其中ui是第i次观测的误差项
(估计的)样本回归函数:
第二章 一元线性回归模型
回归的含义 一元回归模型的建立 参数估计——最小二乘法 随机误差项的古典假定 最小二乘估计量的性质 最小二乘估计量的概率分布 回归系数的显著性检验与置信区间 用样本可决系数检验回归方程的拟合优度 案例分析
一、回归的含义
➢ 回归概念的提出
Francis Galton最先使用“回归(regression)”。
回归元(regressor)。
➢ 回归分析中的因果关系和其他条件不变的概念
在多数对经济理论的检验中(包括对公共政策的评价),经济 学家的目标就是要退订一个变量(比如受教育程度)对另一个 变量(如犯罪率或工人的生产率)具有因果效应(causal effect)。有时可能会很简单就能发现两个或多个变量之间存 在很强的联系,但除非能得到某种因果关系,否则这种联系很 难令人信服。
其他条件不变(ceteris paribus):意味着“其他(相关因 素保持不变)”的概念,它在因果分析中有重要的作用。
这个概念看似简单,但是除非在极为特殊的条件下,很难实现 多数经验研究中的一个关键问题是:要做出一个因果推断,是
否能使其他足够多的因素保持不变呢?
只要方法得当,用计量经济方法可以模拟一个其他条件不变的 实验——通过对模型进行假定。
生产函数: ln Q ln A ln K ln L
菲利普斯曲线:
拉弗曲线: Tax a b(TR)2
➢ 回归的现代释义
等式左边的变量被称为
等式右边的变量被称为
被解释变量(explained variable) 解释变量(explanatory variable)
观测不到的。可以通过收集样本来对总体(真实的)回归直线做出估计。
样本回归模型: Yi ˆ0 ˆ1Xi ei
样本回归直线: Yˆi ˆ0 ˆ1Xi
其中: Yˆi 为Yi的估计值(拟合值); ˆ0, ˆ1 为 0 , 1 的估计值;
我们可以通过建立一个如下的关于Y和X的方程来解决上述三个问 题
总体回归模型
Y= 0 + 1 X+ u
其中: Y——被解释变量; X——解释变量;
u——随机误差项;表示除X之外其他影响Y的因素,一元回 归分析 将除X之外的其他所有影响Y的因素都看成了无法观测 的因素
0,1—回归系数(待定系数或待估参数) 1是斜率系数,是主要的研究对象 0 是常数项,也被称作截距参数,很少被当做分析的核心
二、一元线性回归模型
回归分析都是从如下假设前提开始的:Y和X是代表某个总 体的变量,我们感兴趣的是“用X解释Y”或“研究Y如何随 X而变化”在写出用X解释Y的模型时,面临三个问题 Y和X的函数关系是怎么样的? 如何考虑其他影响Y的因素呢? 我们如何才能确信我们得到的是,是在其他条件不变情况下 的Y和X之间的关系?
因变量 (dependent variable)
自变量(independent variable)
响应变量(response variable)
控制变量(control variable)
被预测变量(predicted variable) 预测变量(predictor variable)
回归子(regressand)
为解决上面提到的第三个问题,及如何在忽略其他因素的同时, 又得到其他因素不变情况下X对Y的影响呢?这需要我们对无法观测 的u和X之间的关系加以约束,并且只有如此,才能从一个随机样本 数据中获得β0和β1的可靠估计量。
➢ E(u)=0 即无法观测的因素的平均值为零,不会对结果产生影响
➢ E(u|X)=0 根据X的不同把总体划分为若干部分,每个部分中无法 观测的因素都具有想通的平均值,且这个共同的平均值 必然等于整个总体中u的平均值,即u是均值独立的。
根据上面的假定对原模型取期望得:
E(Y|X)=E[(0+1X+u)|X] =0+1X+E(u|X)= 0+1X
总体回归函数 (直线) E(Y|Xi) = 0+1X
总体回归函数E(Y|X)是X的 一个线性函数,它表示Y中可以 由X解释的部分,线性意味着X 变化一个单位,Y的期望改变β1 个单位。对于任意给定的X值, Y的分布都是以E(Y|X)为中心的。
