1.2.3《简单复合函数的导数》课件
合集下载
简单复合函数的导数 课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册

2
解:令u
t- ,
3
2
2
2
则函数y 18sin( t - )可以看作y 18sin u和u
t - 的复合函数.
3
2
3
2
y't y'u u't
2
2
(18sin u )' ( t )' 12 cos( t ).
3
2
3
2
2
y't 12 cos( t ),
1
1
3x)'=3 ×(3x)'= ,
(ln3 )'e -(ln3 )(e )'
∴y'=
1
-ln3
e
=
(e )2
=
1-ln3
.
e
(2)y'=(x 1 + 2 )'=x' 1 + 2 +x( 1 + 2 )'
= 1 + 2 +
2
1+ 2
=
(1+2 2 ) 1+ 2
[ f ( x) g ( x)]' f '( x) g ( x) f ( x) g '( x)
f '( x) g ( x) f ( x) g '( x)
f ( x)
[
]'
2
[
g
(
x
)]
g ( x)
[cf ( x)]' cf '( x)
我们学习过基本初等函数,如指数函数、对数函数、幂函数、三角函数、
解:令u
t- ,
3
2
2
2
则函数y 18sin( t - )可以看作y 18sin u和u
t - 的复合函数.
3
2
3
2
y't y'u u't
2
2
(18sin u )' ( t )' 12 cos( t ).
3
2
3
2
2
y't 12 cos( t ),
1
1
3x)'=3 ×(3x)'= ,
(ln3 )'e -(ln3 )(e )'
∴y'=
1
-ln3
e
=
(e )2
=
1-ln3
.
e
(2)y'=(x 1 + 2 )'=x' 1 + 2 +x( 1 + 2 )'
= 1 + 2 +
2
1+ 2
=
(1+2 2 ) 1+ 2
[ f ( x) g ( x)]' f '( x) g ( x) f ( x) g '( x)
f '( x) g ( x) f ( x) g '( x)
f ( x)
[
]'
2
[
g
(
x
)]
g ( x)
[cf ( x)]' cf '( x)
我们学习过基本初等函数,如指数函数、对数函数、幂函数、三角函数、
课件10:1.2.3 导数的四则运算法则

,
特别地当 f(x)=1 时有g(1x)′= -gg′2((xx))
.
知识2:复合函数的导数 问题导思 已知函数 y=2x+π6+sin x,y=sin2x+π6,y=ln(x+2). 这三个函数都是复合函数吗? 答:函数 y=sin2x+6π,y=ln(x+2)是复合函数,函数 y =2x+6π+sin x 不是复合函数.
本节内容结: (1)y=cos(2x-1); (2)y=2xe-x. 解:(1)y′=-sin(2x-1)·(2x-1)′=-2sin(2x-1). (2)y′=(2x)′e-x+2x(e-x)′=2e-x-2xe-x.
类型3:导数运算法则的综合应用
例3:求过点(1,-1)与曲线f(x)=x3-2x相切的直线方程.
例 1:求下列函数的导数. (1)y=x4-2x2-3x+3; (2)y=xx2++33; (3)y=(x+1)(x+2)(x+3);(4)y=xtan x.
解:(1)y′=(x4-2x2-3x+3)′=4x3-4x-3 (2)y′=xx2++33′ =(x+3)′(x2+(3)x2+-3()x+2 3)(x2+3)′ =-(xx22-+63x)+23.
(3)函数 y=log2(1-x)可看作函数 y=log2u 和 u=1-x 的复 合函数, ∴ yx =5 yu · ux =5(log2u)′·(1-x)′ =u-ln52=(x-15)ln 2.
(4)函数y=sin3x可看作函数y=u3和u=sin x的复合 函数,函数y=sin 3x可看作函数y=sin v和v=3x的 复合函数. ∴y′x=(u3)′·(sin x)′+(sin v)′·(3x)′ =3u2·cos x+3cos v =3sin2x cos x+3cos 3x.
高中数学苏教版选修2-2第一章1.2.3复合函数的导数课件

小结 : • ⑴复合函数的求导,要注意分析复合函数的结 构,引入中间变量,将复合函数分解成为较简单的 函数,然后再用复合函数的求导法则求导; • ⑵复合函数求导的基本步骤是:
分解——求导——相乘——回代
天气影响身体,身体决定思想,思想左右心情。 当你飞黄腾达的时候,你的朋友知道你是谁;当你穷困潦倒的时候,你才知道你的朋友是谁。 生命的路是进步的,总是沿着无限的精神三角形的斜面向上走,什么都阻止他不得。 勤奋好学会使你更优秀!——王光凤 世上的事,不如己意者,那是当然的。 衷心的说一句:承诺就像“操他妈”一样,经常说,却很难做得到。 人只要不失去方向,就不会失去自己。 稗子享受着禾苗一样的待遇,结出的却不是谷穗。 活在当下,别在怀念过去或者憧憬未来中浪费掉你现在的生活。 人生里面总是有所缺少,你得到什么,也就失去什么,重要的是你应该知道自己到底要什么。追两只兔子的人,难免会一无所获。 无所求则无所获。 有时候读书是一种巧妙地避开思考的方法。——赫尔普斯
解 : ysinu,u2x.
切 y 线 的 sin 斜 u 率 ku 2 6c o c o ss u 2 1 2 2 2 6 c o s 1 2 .x 6 .
而切点坐标为12,23,
切 线 的 方 程 为 y 2 3 1 x 1 2 ,即 y x 2 3 1 2 .
和 函 数 u2x复 合 而 成 .
求导
相乘
回代
复合函数的求导法则:
一般地,若 yfu,uaxb,则
函数 f22fxx的 f导 x数是?
对于一般的复合函数,结论也成立 。
例题讲解
课堂练习 1、求下列函数的导数:
课堂练习 1、求下列函数的导数:
课堂练习 1、求下列函数的导数:
课堂练习
2020学年高中数学第1章导数及其应用1.2导数的运算1.2.3简单复合函数的导数课件苏教版选修2_2

判断复合函数的复合关系的一般方法是从外向里分析,最外层的 主体函数结构是以基本函数为主要形式,各层的中间变量结构也 都是基本函数关系,这样一层一层分析,最里层应是关于自变量 x 的基本函数或关于自变量 x 的基本函数经过有限次四则运算而 得到的函数.
1.指出下列函数的复合关系: (1)y=cos( 3x+1);(2)y=e3x2+2;(3)y=(1+15x)3.
第1章 导数及其应用
1.2.3 简单复合函数的导数
第1章 导数及其应用
1.了解复合函数的概念,掌握复合函数的求导法则. 2.能够利用复合函数的求导法则,并结合已经学过的公式、法则 进行一些简单复合函数的求导(仅限于形如 f(ax+b)的导数).
1.复合函数的概念 由基本初等函数复合而成的函数,称为复合函数.如 y=sin 2x 由 y=sin u 及 u=_2_x__复合而成. 2.复合函数的求导法则 若 y=f(u),u=ax+b,则 yx′=__y_u_′·_u_x_′ _____,即 yx′=___y_u_′·_a___. 其中 yx′,yu′分别表示 y 关于 _x__的导数及 y 关于_u__的导数.
1.函数 y=(3x-2)2 的导数 y′=________. 解析:y′=2(3x-2)·(3x-2)′=6(3x-2). 答案:18x-12
2.若 f(x)=sin3x+π4,则 f′π4=________. 解析:f′(x)=3cos3x+π4,所以 f′π4=-3. 答案:-3
3.设曲线 y=eax 在点(0,1)处的切线与直线 x+2y+1=0 垂直, 则 a=________. 解析:由题意知 y′|x=0=aeax|x=0=a=2. 答案:2
(2)设 y=cos u,u=53π-7x.
江苏省2020年高二数学第12讲 简单复合函数的导数 课件

(2) y
=
ln(2 x )由y
=
ln
u及u=2x复合而成,yⅱu =
ቤተ መጻሕፍቲ ባይዱ
1 u
, ux
=
2,
yⅱu ?ux
2, u
又y
=
ln(2x)= ln
x
+ ln
2,
yⅱx =
1 x
=
yu
?u?x符合猜想.
2.3法则论证
对于y = (3x - 1)2, yu = u2,ux = 3x - 1 yⅱx = 6(3x - 1),yu = 2u,u?x = 3
核心任务
如何获得复合函数的求导法则?
如何理解复合函数的求导法则? 如何运用复合函数的求导法则?
01 简单复合函数的定义 ------研究对象的确定
1.1复合函数的概念
由基本初等函数复合而成的函数,称为复合函数. 如y = ln(5x +1)由y = ln u及u = 5x +1复合而成. y = f (j (x))由y = f (u)及u =j (x)复合而成.
考察特殊的位置:x =1时,u = 2 思考:此时yⅱ x =12,yu = 4,u?x = 3分别代表什么含义?
y¢x =12表示此时y增加的速度是x增加速度的12倍, yu¢= 4表示此时y增加的速度是u增加速度的4倍, u¢x = 3表示此时u增加的速度是x增加速度的3倍.
2.2法则归纳
若y = f (u),u = ax +b,则yⅱ x = yu ?u?x,即 yⅱ x = yu ?a
例2:求下列函数的导数
(1) y = (2x - 3)3
(2) y = 1 3x - 1
(1) y = (2x - 3)3可由y = u3及u = 2x - 3复合而成,从而
1.2.3复合函数求导ppt
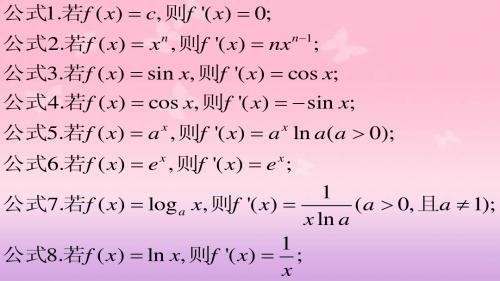
我们遇到的许多函数都 可以看成是由两个函数 经过 " 复合" 得到的, 例如, 函数y 2 x 3 由y u 2和u 2 x 3
2
" 复合" 而成, 等等.
一般地, 对于两个函数 y f u 和u g x , 如果通过变量 u, y可以表示成 x的函数, 那么称这个函数为函数 y f u 和 u g x 的复合函数 (com posite fun ction), 记作y f g x .
' ' ' yx yu ux ln u 3x 2 ' '
即y对x的导数等于 y对u的导数与 u对x的导数的乘积 .
1 3 3 . u 3x 2
例4
求下列函数的导数
2
1 y 2 x 3 ; 2 y e 0.05 x 1 ; 3 y sin x 其中 , 均为常数.
复合函数y f g x 的导数和函数 y f u , u g x 的
' ' ' 导数间的关系为 yx yu ux .
' yx 表示y对x的导数
由此可得 , y ln3 x 2 对x的导数等于 y ln u对u的 导数与u 3x 2对x的导数的乘积 ,即
练习2、求下列函数的导数。
1、y=x5+sinx-7x 2、y=6x-cosx+log7x 3、y=ex+lnx+9x7 4、y=4ex-2cosx+7sinx
一、复习与引入:
求函数y=(3x-2)2的导数. 可以把平方式展开,利用导数的四则运算法则,再 求导. 思考: 能否用其它的办法求导呢? 又如函数 f x ln x 的导数是什么 ? 函数 f x ln 3x 2 的导数又是什么呢?
课件13:1.2.3 导数的四则运算法则
x .
题型二 复合函数的求导运算
例 2 求下列函数的导数:
(1)y=(2x-1)4;
(2)y=102x+3;
(3)y=sin4x+cos4x.
[解] (1)令 u=2x-1,则 y=u4,
因为 yx′=yu′·ux′=4u3·(2x-1)′=4u3·2=8(2x-1)3.
(2)令 u=2x+3,则 y=10u,所以 yx′=yu′·ux′=10u·ln10·(2x+3)′=2ln10·102x+3.
答案:ln x+1
题型探究
题型一 应用求导法则求导数
例 1 求下列函数的导数:
(1)y=x4+3x3-2x-5; (3)y=sinx x;
(2)y=xlog3x; (4)y=x-sin2xcos2x.
[解] (1)y′=(x4+3x3-2x-5)′=(x4)′+(3x3)′-(2x)′-5′=4x3+9x2-2.
2.设 f(x)=sin x-cos x,则 f(x)在 x=π4处的导数 f′π4=(
)
A. 2
B.- 2
C.0 答案:A
D.
2 2
3.已知 f(x)=1+1 x,则 f′(x)等于(
)
A.1+1 x
B.-1+1 x
C.(1+1 x)2
D.-(1+1 x)2
答案:D
4.函数 y=xln x 的导数为________.
跟踪训练 若函数 f(x)=exx在 x=c 处的导数值与函数值互为相反数, 求 c 的值. 解:由于 f(x)=exx,所以 f(c)=ecc, 又 f′(x)=ex·xx2-ex=ex(xx-2 1),所以 f′(c)=ec(cc-2 1). 依题意知 f(c)+f′(c)=0,所以ecc+ec(cc-2 1)=0,所以 2c-1=0 得 c=12.
湘教版高中同步学案数学选择性必修第二册精品课件 第1章 导数及其应用 1.2.3 简单复合函数的求导
2
f'(x)= .
2-1
2
3
f'(x0)=
=1,解得 x0= .故选
2 0 -1
2
1 2 3 4 5 6
B.
5.曲线y=(x2-2x)ln 2x在点(1,-ln 2)处的切线方程为 x+y+ln 2-1=0
.
解析 由函数y=(x2-2x)ln 2x,可得y'=(2x-2)ln 2x+x-2,所以当x=1时y'=-1,所求
新函数.
பைடு நூலகம்2.复合函数求导法则的三个关注点:
(1)分析复合函数的复合关系是由哪些基本初等函数复合而成,适当选定中
间变量;
(2)分步计算中的每一步都要明确是对哪个变量求导,而其中特别要注意的
是中间变量;
(3)根据基本函数的求导公式及导数的运算法则,求出各函数的导数,并把
中间变量转换成自变量的函数.
自主诊断
1.判断正误.(正确的画“√”,错误的画“×”)
(1)函数 f(x)= x-1可以看作是由 f(x)=√u 和 u=x-1 复合而成的.( √ )
(2)函数y=sin 2x的导数为y'=cos 2x.( × )
2.[北师大版教材习题]写出下列函数的中间变量,并利用复合函数的求导
法则分别求出函数的导数:
则yx'=yu'·ux'=2u·(-2)=-4(-2x+1)=8x-4.
π
(2)y=sin(2x+3 );
解 设 y=sin
π
u,u=2x+ ,
3
则 yx'=yu'·ux'=cos
π
课件11:1.2.3 导数的四则运算法则
本节内容结束 更多精彩内容请登录:
1.2.3 导数的四则运算法则
学习目标 (1)能利用导数的运算法则和基本初等函数的导数公式 求简单函数的导数; (2)理解并掌握复合函数的求导法则.
知识导学 一、导数的四则运算法则 1.函数和(或差)的求导法则 若f(x),g(x)是可导的,则(f(x)+g(x))′=f′(x)+g′(x),(f(x) -g(x))′=f′(x)-g′(x). 注意:(1)设f(x),g(x)是可导的,则(f(x)±g(x))′= f′(x)±g′(x),即两个函数的和(或差)的导数,等于这两 个函数的导数的和(或差).
解:(1)y′=4x3-9x2+4x-4. (2)y′=x′cosx+x(cosx)′=cosx-xsinx. (3)y′=(sin2x)′=(2sinxcosx)′=(2sinx)′cosx+2sinx(cosx)′ =2cos2x-2sin2x=2cos2x. (4)y′=(tanx+cotx)′=csoinsxx′+csoinsxx′ =cos2cxo+s2sxin2x+-sins2ixn-2xcos2x=co1s2x-sin12x
归纳总结 (1)熟练掌握和运用函数的和、差、积、商的导数公式, 并进行简单、合理的运算,注意运算中公式运用的准确 性. (2)灵活运用公式,化繁为简,如小题(2)这种类型,展开 化为和、差的导数比用积的导数简单容易.
练一练 1.求下列函数的导数: (1)y=x4-3x3+2x2-4x-1; (2)y=xcosx; (3)y=sin2x; (4)y=tanx+cotx; (5)y=x2lnx+lo1gax(a>0 且 a≠1,x>0).
(2)对任意有限个可导函数,有(f1(x)±f2(x)±…±fn(x))′ =f1′(x)±f2′(x)±…±fn′(x).
简单复合函数的导数 课件
(2)函数 = −.+ 可以看作函数 = 和 = −. + 的复合函数.根
据复合函数的求导法则,有
′ = ′ ∙ ′ = ′ ∙ −. + ′ = −. = −. −.+
(3)函数 = ln(2 − 1) 可以看作函数 = ln 和 = 2 − 1 的复合函数.根据
(2)令 u=ex+x2,则 y=ln u,
ex+2x
1 x 2
1
x
y′x=y'u·u′x=u·(e +x )′= x
·
(e
+2x)= x
.
2
2
e +x
e +x
例3 某个弹簧振子在振动过程中的位移y(单位:mm)关于时间t(单位:
s)的函数满足关系式为 = (
− ) . 求函数y在t=3s 时的导数,并解
个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)). 且 ˊ = ˊ · ˊ .
复
合
函
数
求
导
分层——选择中间变量,写出
构成它的内、外层函数
求导——分别求内、外层函数对
应变量的导数
代回——把中间变量回代
相乘——把上述求导的结果相乘
课后提升
3
1.下列求导运算正确的是( B)A.( + )′ = +
5.2 导数的运算
思 考
=
(1
+
)
的导数呢?
如何求函数 = (1 + ) 的导数呢?
3
= (1 + )3 = 3 + 3 2 + 3 + 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求 导 相 乘
2 cos 2 x
从而有
y ' x y 'u u ' x
回 代
建构数学 一般地,我们有u=ax+b时,有 若 y=f(u),u=ax+b,则
y ' x y 'u u ' x
即: y ' x y 'u a
• 对于一般的复合函数,结论也成立 。 • 复合函数的求导法则 • 复合函数对自变量的导数,等于已 知函数对中间变量的导数,乘以中间变 量对自变量的导数 ,即 y ' y ' u '
[
f ( x) g ( x)
]
f ( x ) g ( x ) f ( x ) g ( x ) g ( x)
2
其中 g ( x ) 0
复合函数:
由几个函数复合而成的函数,叫复合函数. 由函数 y f (u ) 与 u
( x ) 复合而成
的函数一般形式是
y f [ ( x )]
2 3
( 3 ) y e ; ( 4 ) y lP(π,0)处的 切线方程。
小结 : • ⑴复合函数的求导,要注意分析复 合函数的结构,引入中间变量,将复 合函数分解成为较简单的函数,然后 再用复合函数的求导法则求导; • ⑵复合函数求导的基本步骤是: • 分解——求导——相乘——回代
x u x
复合函数求导的基本步骤是:
(1)分解 (2)求导 (3)相乘 (4)回代
数学运用
例1.试说明下列函数是怎样复合而成的,并求 下列函数的导数:
(1) y ( 2 x 3 ) ; ( 2 ) y ln( 5 x 1)
3
(3) y
1 3x 1
; ( 4 ) y cos( 1 2 x )
法则3:两个函数的积的导数,等于 第一个函数的导数 乘 以第二个函数
加上第一个函数乘以第二个函数
的导数
[ f ( x ) g ( x )] f ( x ) g ( x ) f ( x ) g ( x ).
法则4 :两个函数的商的导数,等于分
子的导数与分母的积,减去分母的导数 与分子的积,再除以分母的平方,即:
,其中u称为中间变量.
目前我们所研究的简单复合函数的导数 仅限于形如f(ax+b)的复合函数
问题探究: 求函数 y (3 x 2) 的导数 。
2
方法一:
y x [(3 x 2) ] (9 x 12 x 4) 18 x 12
2 2
方法二:将函数 y (3 x 2)
数学运用
练习:试说明下列函数是怎样复合而成的, 并求下列函数的导数:
(1) y (2 x ) ; y sin x ; (2)
2 2
(3) y cos(
4
x ) y ln sin(3 x-1) (4)
例3.写出由下列函数复合而成的函数,并 求它们的导数。 2 y cos u ⑴ u 1 x
x 0
y x A( x )
f ( x ) A ( x )
法则1: 两个函数的和(或差)的 导数,等于这两个函数的导数的和 (或差),即:
[ f ( x ) g ( x )] f ( x ) g ( x ).
法则2:
[ Cf ( x ) ] C f ( x ).( C 为常数 )
看作是函数
2
2
y u 和函数 u 3 x 2
u (3 x 2) 3 x
复合函数,并分别求对应变量的导数如下:
yu (u ) 2u
2
两个导数相乘,得
y u u x 2 u 3 2 (3 x 2 ) 3 18 x 12
从而有
y ' x y 'u u ' x
问题探究: 考察函数
y sin 2 x
2 x )
;
的导数 。
一方面 : y sin 2 x 2 sin x cos x
y (sin x
( 2 sin x cos x ) 2 (sin x ) cos x 2 sin x (cos x ) 2 cos
2
x 2 sin
2
x
2 cos 2 x
另一方面: 将函数 看作是函数
y sin 2 x y sin u 和函数 u 2 x
分 解
复合函数,并分别求对应变量的导数如下:
y u (sin u ) cos u u ( 2 x ) 2 x
x 两个导数相乘,得 y u u (cos u ) 2
简单复合函数 的导数
知识回顾:基本求导公式:
(1)( kx b ) k , 特殊的: C 0 (C 为常数 )
( 2 )( x ) x
'
x ' x
1
( 为常数)
(3)( a ) a lna(a 0, 且 a 1)
( 4 )( log a x )
'
1 xlna
( a 0 , 且 a 1)
(5 )( e ) e
x '
'
x
(6)(lnx)
'
'
1 x
( 7 )( sinx ) cosx
(8)(cosx)
sinx
根据导数的概念,求函数导数的过程可以 用下面的流程图来表示
给定函数 y f ( x )
计算 y x f( x x) f( x ) x
;
⑵
.
y ln u
,
u ln x
,
解:⑴ ⑵
y cos( 1 x )
2 2
y 2 x sin( 1 x )
y ln(ln x ) 1 y ( x ln x )
例4.求y=(2x+1)5在x=1处的切线方程。
• 1、求下列函数的导数:
(1) y ( 2 x 3 ) ; ( 2 ) y (1 3 x ) ;
