制动系统建模、仿真及ABS控制器设计
单轮ABS建模与仿真_k

单轮ABS 建模与仿真一、理论分析与数学建模汽车在制动过程中,当制动器制动力大于轮胎-道路附着力时,车轮就会抱死滑移。
只有汽车具有足够的制动器制动力,同时地面又能提供较大的附着力时,汽车才能获得较好的制动效果。
在汽车制动时,除车轮旋转平面的纵向附着力外,还有垂直于车轮旋转平面的侧向附着力。
在汽车制动过程中,纵向附着力决定汽车的纵向运动,影响汽车的制动距离;侧向附着力决定汽车的侧向运动,影响汽车的方向稳定性和转向操纵能力。
当汽车匀速行驶时,实际车速V (即车轮中心的纵向速度)与车轮速度v ω (即车轮滚动的圆周速度)相等,车轮在路面上的运动为纯滚动运动。
然而,在汽车实际运行过程中,当驾驶员踩下制动踏板后,在制动器摩擦力矩的作用下,车轮的角速度减小,实际车速与车轮速度之间就会产生一个速度差,轮胎与地面之间就会产生相对滑移。
轮胎滑移的程度用滑移率slip 来表示。
车轮滑移率是指实际车速v ω与车轮速度w ω之差同实际车速v ω的比值,公式如下。
vw slip ωω-=1 当v ω=w ω时,滑移率slip=0,车轮自由滚动;当w ω=0时,滑移率slip=1,车轮完全抱死滑移;当v ω>w ω时,滑移率0<slip<1,车轮既滚动又滑移。
试验证明,在地面附着条件差(例如在冰雪路面上制动)的情况下,由于道路附着力很小,使可以得到的最大地面制动力减小。
因此,在制动踏板力(或制动分泵压力)很小时,地面制动力就会达到最大附着力,车轮就会抱死滑移。
在制动过程中,车轮抱死滑移的根本原因是制动器制动力大于轮胎-道路附着力。
滑移率大于理想滑移率后的区域称为非稳定制动区域或非稳定区,如图所示。
横向附着系数是研究汽车行驶稳定性的重要指标之一。
横向附着系数越大,汽车制动时的方向稳定性和保持转向控制的能力越强。
当滑移率为零时,横向附着系数最大;随着滑移率的增加,横向附着系数逐渐减小。
当车轮抱死时,横向附着系数接近于零,汽车将失去方向稳定性和转向控制能力,其危害极大。
轿车制动系建模与仿真及ABS控制策略

关键词:制动力分配,制动性能仿真,实验,ABS 控制策略
第
I
页
上海交通大学硕士学位论文
ABSTRACT
MODELING AND SIMULATION OF AUTOCAR BRAKING SYSTEM AND ABS CONTROL STRATEGY
ABSTRACT
At first, this thesis analyzed the braking system theoretically, working principle and characteristic of braking force regulate fitting was expounded. Second,based on analysis, this thesis presents the braking force distribution rationality evaluation mathematics model and the braking performance computer simulation mathematics model. Then, a computer program was designed based on the mathematics model. The program is built by Matlab. The computer program can improve the design efficiency and made them achieve the optimal project. In this thesis, with the program, the braking force distribution of the Haiyiu-MB autocar was rationality evaluated and the braking performance of the autocar was simulation calculated. At the same time, the result was testified by some tests. Finally, this thesis describes the fundamental principle of ABS controlling and discuss several control methods of ABS in common use, emphasis on the logic gate control. In brief, the study of this thesis is directive and practical for the design of the autocar braking system. Keywords: braking force distribution, braking performance simulation, Test, Anti-lock brake controlling.
汽车ABS系统的PID控制策略及仿真分析.

汽车 ABS 系统的 PID 控制策略及仿真分析*李香桂(甘肃畜牧工程职业技术学院 , 甘肃武威 733006摘要 :运用汽车动力学理论 , 建立了 PID 控制器模型、制动时整车动力学模型、车轮模型。
提出了以滑移率为控制目标的 ABS 系统的控制仿真分析 , 将 PID 控制器应用于单个 ABS 系统控制研究 , 以车轮滑移率为控制目标 , 通过轮速与车速传感器采集汽车速度、车轮转速 , 计算出汽车各轮胎实际滑移率 , 与期望滑移率进行比较后 , 将二者的偏差作为 PID 控制器的输入量 ,反复调节控制器的控制参数 , 使其实际滑移率始终处于最佳滑移率附近 , 通过PID 控制最终使汽车在最佳滑移率所对应的地面制动力下进行制动。
关键词 :汽车 ; ABS ; 控制 ; 仿真分析中图分类号 :U463文献标识码 :A文章编号 :1007-4414(2011 05-0020-03PID control strategy and simulation analysis of ABS systermLi Xiang -gui(Gansu vocational and technical college of animal husbandry , Wuwei Gansu 733006, ChinaAbstract :In this thesis , using vehicle dynamics theory , PID controller model , dynamic model of vehicle braking , the wheel model are established.The simulation ofABS control system which is aimed at the slip ratio is proposed.PID controller is used in the individual ABS system , the control objective is slip rate of wheel.The actual slip ratio is calculated through the wheel speed and vehicle speed which is acquired by the sensor.Compared the actual slip rate with the expected slip ratio , The deviation of them is put in the PID controller.In the end , the actual slip ratio is always near the best slip rate , by repeatedly adjusting the control parameters.At last , the motor vehicle is braked with the best power which is corresponding to the best slip rate .Key words :car ; ABS ; control ; simulation analysis1课题研究的必要性防抱制动系统 ABS (Anti -lock Braking System ,在汽车制动时能根据轮胎与路面间附着力 , 自动调节车轮制动力大小 , 防止车轮抱死滑移 , 保证汽车侧向稳定性和转向操纵性 , 同时缩短制动距离。
基于MATLAB的汽车ABS制动过程仿真

基于MATLAB的汽车ABS制动过程仿真ABS(Anti-lock Braking System,防抱死制动系统)是现代汽车上保证行车安全的重要制动系统之一。
ABS制动系统可以避免在制动时车轮抱死,从而提高了制动效果和稳定性。
为了深入理解ABS制动系统的工作原理和性能,本文将基于MATLAB软件进行汽车ABS制动过程的仿真。
一、建立模型和假设为了实现ABS制动过程的仿真,需要建立一个基于MATLAB 的系统模型。
该系统模型需要考虑以下几个方面:1. 汽车的运动方程。
2. 轮胎与地面的接触力,即摩擦力。
3. 制动器与车轮的接触力。
4. ABS控制器的控制策略。
在仿真过程中,假设车辆在制动前以一定的速度匀速行驶,制动时四个车轮的制动和抱死状态是相同的。
二、模型搭建在MATLAB界面中,首先利用simulink模块搭建模型。
模型如下:模型中包含了车辆运动方程、轮胎地面接触力、制动器与车轮接触力等模块。
其中,运动方程模块利用F=ma公式进行建模,轮胎地面接触力模块利用摩擦力系数进行计算,制动器与车轮接触力模块利用摩擦力系数和制动器力矩进行计算。
在模型中,还有制动器控制器模块,负责制动器的控制与调节。
制动器控制器可以采用PID算法或滑模控制算法来控制制动器的开闭和力矩大小。
三、仿真过程在进行仿真过程中,需要确定以下参数:1. 初始车速度v0=80km/h。
2. 初始刹车踏板角度θ=0。
3. 制动器摩擦力系数μs=0.7。
4. 刹车片初期转动半径r=0.05m。
在进行仿真操作前,应先在程序中设定好各参数,再设定仿真时间和仿真步长。
由于ABS制动过程会使用到控制器,因此应首先进行控制器的设计和仿真。
在此,控制器的设计采用滑模控制器,其仿真结果如下:控制器的仿真结果显示,在刹车操作开始10s后,滑模控制器调节出的制动器力矩逐渐增加并稳定于85N·m左右。
随着控制器的调节,车轮抱死现象得以解决、保持ABS制动状态下使车辆具备更好的稳定性和制动效果。
ABS的simulink仿真分析详细步骤
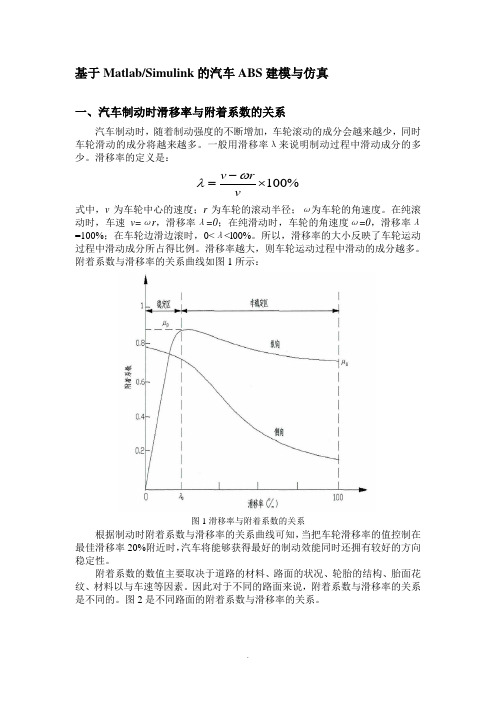
基于Matlab/Simulink 的汽车ABS 建模与仿真一、汽车制动时滑移率与附着系数的关系汽车制动时,随着制动强度的不断增加,车轮滚动的成分会越来越少,同时车轮滑动的成分将越来越多。
一般用滑移率λ来说明制动过程中滑动成分的多少。
滑移率的定义是:100%v r vωλ-=⨯式中,v 为车轮中心的速度;r 为车轮的滚动半径;ω为车轮的角速度。
在纯滚动时,车速v=ωr ,滑移率λ=0;在纯滑动时,车轮的角速度ω=0,滑移率λ=100%;在车轮边滑边滚时,0<λ<l00%。
所以,滑移率的大小反映了车轮运动过程中滑动成分所占得比例。
滑移率越大,则车轮运动过程中滑动的成分越多。
附着系数与滑移率的关系曲线如图1所示:图1滑移率与附着系数的关系根据制动时附着系数与滑移率的关系曲线可知,当把车轮滑移率的值控制在最佳滑移率20%附近时,汽车将能够获得最好的制动效能同时还拥有较好的方向稳定性。
附着系数的数值主要取决于道路的材料、路面的状况、轮胎的结构、胎面花纹、材料以与车速等因素。
因此对于不同的路面来说,附着系数与滑移率的关系是不同的。
图2是不同路面的附着系数与滑移率的关系。
图2 不同路面的附着系数与滑移率的关系路面峰值附着系数滑动附着系数沥青或混凝土(干)0.75沥青(湿)0.5—0.7 0.45—0.6混凝土(湿)0.8 0.7砾石0.6 0.55土路(干)0.68 0.65土路(湿)0.55 0.4—0.5雪(压紧)0.2 0.15冰0.1 0.07表1 各种路面上的平均附着系数二、汽车ABS原理汽车ABS作为一种主动安全装置,它可以通过调节车轮制动压力将汽车前后车轮的滑移率控制在最佳滑移率附近,使汽车在获得最大地面制动力的同时拥有良好的方向稳定性。
1、汽车ABS的控制原理在常见的ABS 系统中,每个车轮上各安装一个转速传感器,将有关各车轮转速的信号输入电子控制装置ECU)。
电子控制装置ECU)根据各车轮转速传感器输入的信号对各个车轮的运动状态进行监测和判定,并形成相应的控制指令。
汽车制动控制系统ABSEBD设计与仿真

第28卷第2期2020年6月山东交通学院学报JOURNAL OF SHANDONG JIAOTONG UNIVERSITYVol.28No.2Jun.2020DOI:10.3969/j.issn.1672-0032.2020.02.001汽车制动控制系统ADS/EDD设计与仿真王健>,杨君>,于蓬2!,郑金凤21.山东交通学院汽车工程学院,山东济南250357;2.山东明宇新能源技术有限公司,山东济南271100摘要:为提高汽车的制动性能,采用汽车防抱死制动系统(anti-locked braking system,ADS)与电子制动力分配(electronis brake force distribution,EBD)系统联合控制制动系统的方法。
设计基于滑模控制的ADS和基于模糊控制的EBD系统。
分别在干、湿沥青路面2种条件下对ABS/EBD系统进行仿真分析。
结果表明:设计的ABS/ EDD控制系统能充分利用ABS和EBD的优点,大大提高汽车的制动效能。
关键词:ABS/EBD;滑模控制器;模糊控制器;滑移率中图分类号:U463.5文献标志码:A文章编号:1672-0032(2020)02-0001-08引用格式:王健,杨君,于蓬,等.汽车制动控制系统ABS/EBD设计与仿真[J].山东交通学院学报,2020,28(2): 1-8.WANG Jian,YANG Jun,YU Peng,et aO.ABS/EBD design and simulation of automotive brake controO system[J].JournaS of Shandong Jiaotong University,2020,28(2):1-8.0引言汽车紧急制动,特别是在附着系数较低的路面上紧急制动时,汽车防抱死制动系统(anti-locked braking system,ABS)可以防止前后车轮抱死拖滑,在保证汽车具有转向功能的同时,防止汽车不发生甩尾侧滑等危险情况,保持汽车的制动稳定性,且可以缩短制动距离(1-)%电子制动力分配(electronic brake force distribution,EBD)系统作为ABS的子系统,可以在车辆制动时控制制动力在各轮间的分配,更好地利用各轮的附着系数[4-11]%国内大多数ABS采用逻辑门限值控制,通过大量试验确定各门限值,对系统的控制很不稳定[12-14]%本文ABS采用滑模变结构控制,该方法是针对非线性和参数不确定性系统的控制方法[15-17],具有很好的鲁棒性%EBD系统采用模糊控制,该方法对系统中的参数变化、外界干扰、系统非线性等具有很强的鲁棒性%通过建立1/2车辆动力学模型、设计基于滑模变结构控制的ABS控制器和基于模糊控制的EBD控制器,在不同路面上进行ABS/EBD系统的仿真验证,以期提高车辆的制动性能%1车辆动力学模型为了设计ABS&EBD控制器以及进行系统动力学仿真,需建立车辆动力学模型%为便于建模,对车辆收稿日期:2020-04-02基金项目:国家自然科学基金项目(61803231);山东省重点研发计划(2017GGX50109);山东交通运输厅科技计划(2018B66);山东省高等学校科技计划项目(J17KB024);山东省高等学校青创科技支持计划(2020KJJ002);山东交通学院博士科研启动资金资助项目(BS2017001)第一作者简介:王健(1986$),男,山东潍坊人,工学博士,副教授,主要研究方向为汽车智能驾驶、主动安全,E-mail:wangjian1987228@0*通信作者简介:于蓬(1986—),男,济南人,工学博士,高级工程师,主要研究方向为新能源汽车集成及产业化,E-mail:t_ y_yupeng@。
汽车ABS系统的建模与仿真
汽车ABS系统的建模与仿真基于Matlab/Simulink的汽车建模与仿真摘要本文所研究的是基于Matlab/Simulink的汽车防抱死刹车系统(ABS)的仿真方法,本方法是利用了Simulink所提供的模块建立了整车的动力学模型,轮胎模型,制动系统的模型和滑移率的计算模型,采用的控制方法是PID控制器,对建立的ABS的数学模型进行了仿真研究,得到了仿真的曲线,将仿真曲线与与没有安装ABS系统的制动效果进行对比。
根据建立的数学模型分析,得到ABS系统可靠,能达到预期的效果。
关键词ABS 仿真建模防抱死系统 PIDModeling and Simulation of ABS System of AutomobilesBased onMatlab/SimulinkAbstractA method for building a Simulator of ABS base on Matlab/Simulink is presented in this paper.The single wheel vehicle model was adopted as a research object in the paper. Mathematical models for an entire car, a bilinear tire model, a hydraulic brake model and a slip ratio calculation model were established in the Matlab/Simulink environment. The PID controller was designed. The established ABS mathematical model was simulated and researched and the simulation curves were obtained. The simulation results were compared with the results without ABS. The results show that established models were reliable and could achieve desirable brake control effects.Key wordsABS; control; modeling; simulation;Anti-lock Braking System;PID1.概述随着载重车辆动力性的不断提高,客观上也对车辆的制动性能与驱动性能提出了越来越高的要求。
ABS控制器设计及仿真
汽车ABS控制器设计及其仿真摘要:ABS(Anti-lock Braking System)防抱死制动系统,通过安装在车轮上的传感器发出车轮将被抱死的信号,控制器指令调节器降低该车轮制动缸的油压,减小制动力矩。
关键字:ABS 控制系统仿真一.ABS控制系统简介。
汽车制动性能主要是三个方面:⑴制动效能,即制动距离与制动减速度;⑵制动效能的恒定性,即摩擦材料的抗热衰性能;⑶制动时汽车的方向稳定性,即制动时汽车不发生跑偏、侧滑及失去转向性能。
汽车维持直线行驶或按预定弯道行驶的能力。
而制动性能主要是有汽车轮胎的制动性能决定的。
ABS系统是一种能防止车轮被抱死而导致车身失去控制的安全装置,全称防抱死刹车系统。
我们知道,当车轮抱死滑移时,车轮与路面间的侧向附着力将完全消失。
如果是前轮(转向轮)制动到抱死滑移而后轮还在滚动,汽车将失去转向能力(跑偏)。
如果是后轮制动到抱死而前轮还在滚动,即使受到不大的侧向干扰力,汽车也将产生侧滑(甩尾)现象。
这些都极容易造成严重的交通事故。
因此,汽车在制动时不希望车轮制动到抱死滑移,而是希望车轮制动到边滚边滑的运动状态。
从已有的实验中可以知道[1],如图1所示,汽车车轮的滑动率在15%-20%时,轮胎与路面有最大的纵向附着系数,此时侧向附着系数也较大,因此,为了充分发挥轮胎与路面间这种潜在的附着能力,目前的许多中高级轿车及大客车和重型货车上均装备了防抱死制动装置(Antilock Braking System),简称ABS.汽车电控防抱死制动系统的主要功用有:(1)在任何制动情况下驾驶员应能保持对行驶车辆的控制。
(2)在任何制动情况下应能保持汽车转向时的操纵性和制动时的稳定性。
(3)当左,右车轮处于不同附着系数路面或者路面附着系数突然变化时能够进行调整控制。
(4)能够缩短制动距离,提高汽车制动效能。
(5)制动噪声小,工作安全可靠,一但防抱死制动系统失效时,自检系统能显示报警,而由机械制动系统来承担汽车制动作用。
防抱死制动系统仿真
600
800
1000
1200
1400
1600
1800
制动时间(x10-2s)
重庆理工大学 系统建模与仿真 13
100 G(s) TB.s 1
重庆理工大学 系统建模与仿真 10
防抱死制动系统(ABS)
8.仿真曲线:
swich=1,ABS制动
速度曲线 紫色:车轮身速度 黄色:车轮速度
滑移率曲线 黄色:实际滑移率
重庆理工大学
系统建模与仿真
11
防抱死制动系统(ABS)
9.仿真曲线:
swich=0,非ABS制动
重庆理工大学 系统建模与仿真 6
防抱死制动系统(ABS)
4.单轮制动数学模型:
v v Rr
slip 1 w / v
v
Vv
Rr
f (slip)
Ff F
dVv m Ff dt dw I F f Rr Tb dt
重庆理工大学 系统建模与仿真
Tb
防止“除零”而采取的措施: 1.0 – u(1) / (u(2) + (u(2) == 0) * eps)
必定非零!
重庆理工大学 系统建模与仿真 9
防抱死制动系统(ABS)
7.Simulink模型精讲
bangbang 控制器原理:
1, Uk 1, En 0 En 0
制动系液压管路:一阶惯性环节
Ff
Fz
7
防抱死制动系统(ABS)
5.Simulink模型:
重庆理工大学
系统建模与仿真
8
防抱死制动系统(ABS)
6.基本模块介绍:
1. 2. 3. 4. 传递函数 Transfer Fcn Continuous 查找表 Lookup TableLoopup Tables 积分器(限幅)Integrator Continuous 终止仿真 Stop Sinks
制动系统建模、仿真及ABS控制器设计
制动系统建模、仿真及ABS控制器设计专业:车辆工程姓名:汤兴贤学号:200620103918一、源程序:m=300;rd=0.25;Iw=12;ki=4500;kd=5000;Ts=0.05;s0=0.2;uh=0.8;ug=0.6;smin=0.18;smax=0.22;g=9.8;u(1)=30;w(1)=120;Tb(1)=600;j=1;while u(j)>0sb(j)=1-rd*w(j)/u(j); %计算当前滑移率if sb(j)>smaxTb(j+1)=Tb(j)-kd*Ts; %制动器减压elseif sb(j)<sminTb(j+1)=Tb(j)+ki*Ts; %制动器增压else Tb(j+1)=Tb(j); %制动器保压endif sb(j)<=s0v(j)=uh*sb(j)/s0; %计算附着系数else v(j)=(uh-ug*s0)/(1-s0)-(uh-ug)*sb(j)/(1-s0); %计算附着系数endFxb=v(j)*m*g; %计算地面制动力w1(j)=(Fxb*rd-Tb(j+1))/Iw; %计算角加速度u1(j)=Fxb/m; %计算加速度u(j+1)=u(j)-u1(j)*Ts %计算车速w(j+1)=w(j)+w1(j)*Ts; %计算角速度j=j+1;end;t1=0:0.05:(j-1)*Ts; %(j-1)*Ts为采样时间t2=0:0.05:(j-2)*Ts; %(j-2)*Ts为从开始制动到角速度为零之间的时间figure(1)plot(t1,u)xlabel('时间/s'),ylabel('速度/s')axis([0,5,0,30]);hold onplot(t1,w*rd);title('车轮前进速度与车轮线速度关系曲线');text(2,20,'车轮前进速度');text(1.5,10,'车轮线速度');figure(2)plot(t2,sb);title('ABS控制的滑移率时域仿真结果');xlabel('时间/s'),ylabel('滑移率')axis([0,4.5,0,1]);图100.10.20.30.40.50.60.70.80.91ABS 控制的滑移率时域仿真结果时间/s 滑移率图2051015202530时间/s 速度/s 车轮前进速度与车轮线速度关系曲线从线性化的路面附着系数与车轮滑移率关系曲线知道,车轮的滑移率sb在0.2左右时纵向附着系数最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录1. 动力学建模 ....................................................................................... - 1 -2. 分段线性的轮胎模型....................................................................... - 1 -3. 控制算法............................................................................................ - 2 -4. 仿真流程及参数输入....................................................................... - 2 -5. 实例分析............................................................................................ - 3 -6. MATLAB 仿真过程 ......................................................................... - 4 -6.1.逻辑门限值控制器................................................................... - 4 -6.2.模糊控制器................................................................................ - 8 -6.2.1模糊控制器设计.............................................................. - 8 -6.2.2模糊控制matlab仿真过程........................................ - 10 -6.3.PID控制器.............................................................................. - 14 -通过两自由度单轮模型为例,介绍在MATLAB 环境下的控制系统力学建模、ABS 控制器设计及仿真分析过程。
1. 动力学建模某车辆简化后的制动力学模型如右图所示。
其中单轮模型质量m ,车轮滚动半径rd ,车轮转动惯量为Iw ,车辆旋转角速度为ω,车轮轮心前进速度为uw ,地面制动力为Fxb 。
作用于车轮的制动力矩为Tb 。
若忽略空气阻力与车轮滚动阻力,则系统的运动方程如下: w xb d b td I F r T d ω=- (1) xb tdu mF d ω= (2) 式中,地面制动力Fxb 等于地面作用于车轮的法向反力Fx 与路面附着系数μ的乘积,其中μ为制动滑移率Sb 的函数。
2. 分段线性的轮胎模型根据第三章中介绍的有关轮胎纵向特性的内容,路面附着系数与车轮滑移率之间存在一定的非线性关系。
如果用两段直线近似表示路面附着-滑移曲线,可得到分段线性化的附着系数μ与车辆滑移率s b 的关系(即所谓的“Dugoff ”模型),如下图所示。
其表达式如下:11h b b oo h g o h g bb oo o S S S S S SS S S S μμμμμμμ⎧=≤⎪⎪⎨--⎪=->⎪--⎩(3)式中,μb 为峰值附着系数;μg 为车轮完全抱死时(即Sb=1)时的路面附着系数;So 为峰值附着系数所对应的滑移率。
图1 单轮制动力模型图2 线性化的路面附着系数与车轮滑移率关系曲线3.控制算法这里以门限值控制算法为例,说明ABS控制器设计及制动系统力学的仿真过程。
采用门限制控制算法的基本思想是保证车轮滑移率在最理想的范围之内。
制动开始后,随着制动压力的升高车轮转速ω相应减小,车轮出现滑移;当车轮滑移率达到理想范围上限值Smax时,减小制动压力;随着制动压力的减小,直至减小到滑移率下限值Smin时再增大制动压力。
循环往复这一过程直至车辆停止。
因此,在ABS控制器起作用的过程中,滑移率总是保持在理想的范围内,从而保证车辆的最佳制动性能及行驶方向控制的稳定性。
4.仿真流程及参数输入由上可知,ABS控制器所用到的一些控制参数有:1)由路面附着系数μ与滑移率S b的关系曲线所表示的轮胎模型;2)滑移率控制上限S max、下限S min;3)车辆模型参数及初始车速μωo;4)制动器油压增长率k i和减小率k d等。
根据分析可知,控制逻辑实现的关键是计算当前车轮滑移率S b(t)并与预先确定的上限值(S max,S min)进行比较,来判断对制动液压控制系统的增压或减压操作,控制流程如图3所示。
5.实例分析图3 仿真流程单轮制动动力模型参数由表1给出。
设式图2定义的路面附着系数分别为μh=0.8,μg=0.6.以门限值控制算法设计ABS控制器,使车轮滑移率S b保持在最优值(S opt附近),这里令S min=0.18,S max=0.22。
根据表1给出的模型参数及附着系数,按照图3所示的控制流程采用m语言编制仿真程序。
需要指出的是,表1给出的制动系统控制参数仅作为参考,系统设计过程中可根据需要适当调整,已获得满意的结果。
表1 单轮ABS制动力学模型参数6.MATLAB仿真过程6.1.逻辑门限值控制器Matlab代码如下:clearclc%% 输入初始参数m=300; %车轮质量rd=0.25; %车轮动力半径Iw=12; %车轮转动惯量u0=30; %初始车速w0=120; %初始角速度Tb0=600; %初始制动力矩ki=4500; %制动油压增长率 kd=5000; %制动油压减少率 dt=0.05; %采样时间u(1)=u0; %设置车速数组变量 w(1)=w0; %设置轮速数组变量 Tb(1)=Tb0; %设置制动压力数组变量 s(1)=0; %设置滑移率数组变量 Fxb(1)=0; %设置地面制动力数组变量 %% 滑移率逻辑门控制 i=1;while(u(i)>0)s(i+1)=(u(i)-w(i)*rd)/u(i); %计算滑移率if s(i+1)<0.2 %计算纵向附着系数 mu=4*s(i+1); elsemu=0.85-0.25*s(i+1); endFxb(i+1)=m*9.8*mu; %计算地面制动力if s(i+1)<0.18 %与滑移率门限值比较,确定制动力矩 Tb(i+1)=Tb(i)+ki*dt; elseif s(i+1)>0.22 Tb(i+1)=Tb(i)-kd*dt; elseTb(i+1)=Tb(i); enddw=(Fxb(i+1)*rd-Tb(i+1))/Iw; %计算车轮角加速度 du=-Fxb(i+1)/m; %计算车身加速度 u(i+1)=u(i)+du*dt; %计算下一时刻车速 w(i+1)=w(i)+dw*dt; %计算下一时刻轮速 i=i+1; endt=0:dt:(i-1)*dt; plot(t,[u' w'*rd]) figure() plot(t,Fxb,t,Tb) figure() plot(t,s) 运行结果如下:逻辑门控制器1) 制动器制动力矩与地面制动力随时间变化曲线0.51 1.52 2.53 3.54 4.5时间t/s制动力制动力变化曲线2) 滑移率随时间变化曲线00.51 1.52 2.53 3.54时间t/s滑移率滑移率变化曲线3) 车速与轮速随时间变化曲线0.51 1.52 2.53 3.54 4.5时间t/s速度m /s车速与轮速变化曲线可以看出:● 基于滑移率的逻辑门限值控制器,可以限制滑移率在给定的最佳滑移率附近波动,汽车完全停止时,车速为零,滑移率趋于无穷大,所以在仿真时间最后一段,滑移率有较大波动。
● 制动器制动力矩在滑移率控制器的控制下,可以完成增压、保压、减压动作,防止车轮过早抱死,减小制动距离。
6.2.模糊控制器6.2.1模糊控制器设计1)输入量模糊化●为简化,仅选取滑移率偏差e作为输入量,当最佳滑移率选为0.2时,滑移率偏差范围为【-0.2,0.8】,经过适当变化,使e的变化范围为【-6,6】,以便于控制。
●为简化,仅选取三个语义词【N,Z,P】,即正、零、负。
分别定义各自的隶属度函数,进行模糊化,如下图:2)输出量反模糊化●选取制动器制动力矩改变量为输出量,取值范围设定为【-1,+1】。
同样,为简化,选取三个语义词【I,K,D】,即增压、保压、减压。
并定义相应隶属度函数,如下图:3)模糊规则●由于仅有一个输入量,且仅选取三个语义词,只需定义三条模糊规则,如下图:4)控制曲线●观察制动器制动力矩改变量与滑移率偏差的关系6.2.2模糊控制matlab仿真过程程序如下:clearclc%% 输入初始参数m=300; %车轮质量rd=0.25; %车轮动力半径Iw=12; %车轮转动惯量u0=30; %初始车速w0=120; %初始角速度Tb0=600; %初始制动力矩ki=4500; %制动油压增长率kd=5000; %制动油压减少率dt=0.05; %采样时间u(1)=u0; %设置车速数组变量w(1)=w0; %设置轮速数组变量Tb(1)=Tb0; %设置制动压力数组变量s(1)=0; %设置滑移率数组变量Fxb(1)=0; %设置地面制动力数组变量dtp(1)=0; %设置地面制动力变化量数组变量%% 模糊控制i=1;while(u(i)>0)s(i+1)=(u(i)-w(i)*rd)/u(i); %计算滑移率if s(i+1)<0.2 %计算纵向附着系数 mu=4*s(i+1); elsemu=0.85-0.25*s(i+1); endFxb(i+1)=m*9.8*mu; %计算地面制动力e=12*(s(i+1)-0.5); %将滑移率偏差范围转化到【-6,6】 abs=readfis('abs_fzy2.fis'); %调用设计好的模糊控制器 dtp(i+1)=evalfis(e,abs); %输出制动器制动力矩变化量Tb(i+1)=Tb(i)+2*5000*dtp(i+1)*dt; %计算制动器制动力矩 dw=(Fxb(i+1)*rd-Tb(i+1))/Iw; du=-Fxb(i+1)/m; u(i+1)=u(i)+du*dt; w(i+1)=w(i)+dw*dt; i=i+1; end %% 绘图 t=0:dt:(i-1)*dt; plot(t,[u' w'*rd]) figure() plot(t,Fxb,t,Tb) figure() plot(t,s) figure() plot(t,dtp)模糊控制器运行结果:1) 模糊控制器输出,即Tb 的变化量00.51 1.52 2.53 3.54 4.5-0.6-0.4-0.20.20.40.60.8时间t/s变化率模糊控制器输出(Tb 变化量)2) 地面制动力与制动器制动力矩0.51 1.52 2.53 3.54 4.5-50005001000150020002500时间t/s制动力制动力变化曲线3) 滑移率0.050.10.150.20.250.30.350.4时间t/s滑移率滑移率变化曲线4) 车速与轮速0.51 1.52 2.53 3.54 4.5-5051015202530时间t/s速度m /s车速与轮速变化曲线6.3.PID 控制器● PID 控制器的设计选取滑移率s 的偏差e 作为输入,若选定最佳滑移率为0.2,则e=s-0.2;输出量为制动器制动力矩的变化量dtp 。
