系统建模与仿真设计报告一
基于witness的系统建模与仿真实验报告
多路径生产仿真模型S11085240007 物流工程一、实验名称:多路径生产仿真模型二、实验目的1)了解结合路径path的系统设计。
2)熟悉系统元素Part、Machine、Buffer、Variable、Labor、Attribute的用法。
3)深入研究系统元素Machine的用法。
4)研究机器、缓冲区结合路径以及劳动者之间协作所形成系统的运行效率。
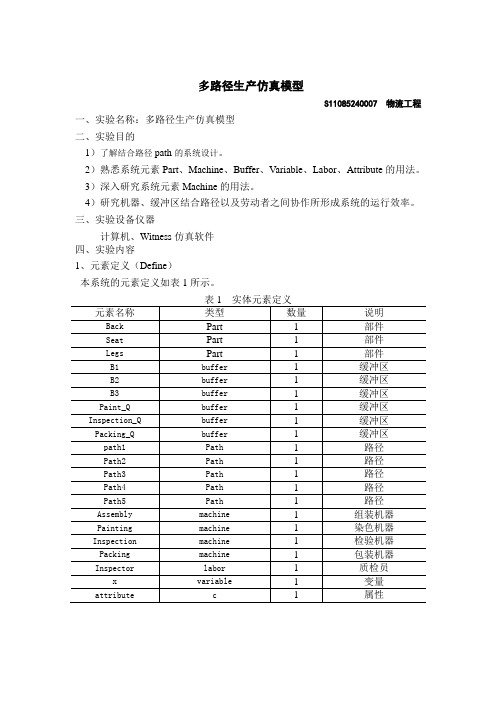
三、实验设备仪器计算机、Witness仿真软件四、实验内容1、元素定义(Define)本系统的元素定义如表1所示。
表1 实体元素定义元素名称类型数量说明Back Part 1 部件Seat Part 1 部件Legs Part 1 部件B1buffer 1 缓冲区B2buffer 1 缓冲区B3buffer 1 缓冲区Paint_Q buffer 1 缓冲区Inspection_Q buffer 1 缓冲区Packing_Q buffer 1 缓冲区path1Path 1 路径Path2Path 1 路径Path3Path 1 路径Path4Path 1 路径Path5Path 1 路径Assembly machine 1 组装机器Painting machine 1 染色机器Inspection machine 1 检验机器Packing machine 1 包装机器Inspector labor 1 质检员x variable 1 变量attribute c 1 属性2、元素可视化(Display)设置各个实体元素的显示特征定义设置如下图所示3、元素细节(Detail)设计1对Part各元素细节设计●可视化效果设定●属性定义:seat.Arrival Type=Activeseat.inter Arrival=2.0back.Arrival Type=Activeback.inter Arrival=2.0legs.Arrival Type=Activelegs.inter Arrival=2.0●规则定义:seat’s output Rules:PUSH to B1back’s output Rules:PUSH to B2legs’ output Rules:PUSH to B32对Buffer各元素细节设计display 选项中对话框对buffer icon 、name、part queue属性进行设置;3对Machine各元素的细节设计属性定义:Assembly.Type=AssemblyAssembly.Cycle Time=6.0Assembly. Input Quantity=3;!机器Assembly的输入零部件数量为3个;规则定义:Assembly.Input Rules(From):MATCH/ANY B1 #(1)B2 #(1)B3 #(1) !匹配缓冲区B1、B2、B3中的任意类型的part各一个;Assembly.Output Rules(To):PUSH to Paint_Q Using Path !通过路径将成品送至缓冲区Paint_Q;活动定义:Assembly.actions on finish:3.1)对machine元素Assembly的详细定义:属性定义:♦Assembly.Type=Assembly♦Assembly.Cycle Time=6.0♦Assembly. Input Quantity=3;!机器Assembly的输入零部件数量为3个;规则定义:Assembly.Input Rules(From):♦MATCH/ANY B1 #(1)B2 #(1)B3 #(1) !匹配缓冲区B1、B2、B3中的任意类型的part各一个;Assembly.Output Rules(To):♦PUSH to Paint_Q Using Path !通过路径将成品送至缓冲区Paint_Q;活动定义:Assembly.actions on finish:♦ICON = 115!通过变换图标,表示seat、back、legs组装成了一把白色椅子;3.2)对machine元素inspection的详细定义:属性定义:♦inspection.Type=Single♦inspection.Cycle Time=3.0♦bor=Inspector规则定义:inspection.Input Rules(From):♦PULL from Inspection_Q !从缓冲区Inspection_Q中提取零件加工;inspection.Output Rules(To):♦PERCENT /189 Packing_Q Using Path 90.00 ,Paint_Q With Inspector Using Path 10.00 !产生随机概率,以90%的概率通过检测,使用路径移向Packing_Q,进行打包;以10%的概率检测出油漆有质量问题,需要人工搬运,通过路径送回缓冲区Paint_Q,排队重新油漆。
生产系统建模与及仿真实验报告

生产系统建模与及仿真实验报告实验一Witness仿真软件认识一、实验目的1、学习、掌握Witness仿真软件的主要功能与使用方法;2、学习生产系统的建模与仿真方法。
二、实验内容学习、掌握Witness仿真软件的主要功能与使用方法三、实验报告要求1、写出实验目的:2、写出简要实验步骤;四、主要仪器、设备1、计算机(满足Witness仿真软件的配置要求)2、Witness工业物流仿真软件。
五、实验计划与安排计划学时4学时六、实验方法及步骤实验目的:1、对Witness的简单操作进行了解、熟悉,能够做到基本的操作,并能够进行简单的基础建模。
2、进一步了解Witness的建模与仿真过程。
实验步骤:Witness仿真软件是由英国lanner公司推出的功能强大的仿真软件系统。
它可以用于离散事件系统的仿真,同时又可以用于连续流体(如液压、化工、水力)系统的仿真。
目前已成功运用于国际数千家知名企业的解决方案项目,有机场设施布局优化、机场物流规划、电气公司的流程改善、化学公司的供应链物流系统规划、工厂布局优化和分销物流系统规划等。
◆Witness的安装与启动:➢安装环境:推荐P4 1.5G以上、内存512MB及以上、独立显卡64M以上显存,Windows98、Windows2000、Windows NT以及Windows XP的操作系统支持。
➢安装步骤:⑴将Witness2004系统光盘放入CD-ROM中,启动安装程序;⑵选择语言(English);⑶选择Manufacturing或Service;⑷选择授权方式(如加密狗方式)。
➢启动:按一般程序启动方式就可启动Witness2004,启动过程中需要输入许可证号。
◆Witness2004的用户界面:➢系统主界面:正常启动Witness系统后,进入的主界面如下图所示:主界面中的标题栏、菜单栏、工具栏状态栏等的基本操作与一般可视化界面操作大体上一致。
这里重点提示元素选择窗口、用户元素窗口以及系统布局区。
控制工程实训课程学习总结基于MATLAB的系统建模与仿真实验报告

控制工程实训课程学习总结基于MATLAB 的系统建模与仿真实验报告摘要:本报告以控制工程实训课程学习为背景,基于MATLAB软件进行系统建模与仿真实验。
通过对实验过程的总结,详细阐述了系统建模与仿真的步骤及关键技巧,并结合实际案例进行了实验验证。
本次实训课程的学习使我深入理解了控制工程的基础理论,并掌握了利用MATLAB进行系统建模与仿真的方法。
1. 引言控制工程是一门应用广泛的学科,具有重要的理论和实践意义。
在控制工程实训课程中,学生通过实验来加深对控制系统的理解,并运用所学知识进行系统建模与仿真。
本次实训课程主要基于MATLAB软件进行,本文将对实验过程进行总结与报告。
2. 系统建模与仿真步骤2.1 确定系统模型在进行系统建模与仿真实验之前,首先需要确定系统的数学模型。
根据实际问题,可以选择线性或非线性模型,并利用控制理论进行建模。
在这个步骤中,需要深入理解系统的特性与工作原理,并将其用数学方程表示出来。
2.2 参数识别与估计参数识别与估计是系统建模的关键,它的准确性直接影响到后续仿真结果的可靠性。
通过实际实验数据,利用系统辨识方法对系统的未知参数进行估计。
在MATLAB中,可以使用系统辨识工具包来进行参数辨识。
2.3 选择仿真方法系统建模与仿真中,需要选择合适的仿真方法。
在部分情况下,可以使用传统的数值积分方法进行仿真;而在其他复杂的系统中,可以采用基于物理原理的仿真方法,如基于有限元法或多体动力学仿真等。
2.4 仿真结果分析仿真结果的分析能够直观地反映系统的动态响应特性。
在仿真过程中,需对系统的稳态误差、动态响应、鲁棒性等进行综合分析与评价。
通过与理论期望值的比较,可以对系统的性能进行评估,并进行进一步的优化设计。
3. 实验案例及仿真验证以PID控制器为例,说明系统建模与仿真的步骤。
首先,根据PID控制器的原理以及被控对象的特性,建立数学模型。
然后,通过实际实验数据对PID参数进行辨识和估计。
设计报告--005---直接序列扩频系统的SIMULINK建模与仿真

直接序列扩频系统的SIMULINK建模与仿真一.直接扩频发射机系统设数据传输率为100 bps,扩频码片速率为2000chip/s,采用m序列作为扩频序列,以BPSK为调制方式。
试建立扩频系统仿真模型并仿真观察其数据波形、扩频输出波形以及扩频调制输出的频谱。
仿真模型如图5-1所示。
Bernoulli Binary Generator用于产生数据流,其采样时间设置为0.01s,这样输出的数据速率为100bps。
PN Sequence Generator用于产生伪随机扩频序列,其采样时间设置为0.0005s,这样输出的码片速率为2000chip/s。
为了使扩频模块(乘法器)上的数据采样速率相同,需要对数据流进行升速率处理。
Unipolar yo Bipolar Converter用于完成数据和扩频序列的双极性变换。
乘法器输出就是扩频输出,其码速率等于采样速率,即每个采样点代表一个码片。
扩频输出信号以BPSK方式进行调制。
模型中采用了调制的等效低通模型来实现,调制输出信号是复信号,采样率为2000次/s。
调制也可采用通带模型来实现。
为了使频谱观察范围达到4kHz,需要被观察信号的采样率达到8000次/s,为此,以升速率模块配合采样保持模块将调制输出信号采样率提高到8000次/s。
图5-1 直接扩频发射机仿真系统模型仿真执行后,两个频谱仪将分别显示扩频前后的信号频谱,采用BPSK调制的等效低通模型时,调制前后的功率频谱相同,如图5-2所示。
可见,数据信号的带宽约100Hz,其功率峰值约为20dB处,而扩频输出信号带宽展宽了20倍,为2kHz,而功率峰值下降到约7dB处。
仿真输出的时域波形结果如图5-3所示,图中显示了数据流、PN序列以及扩频输出信号的波形,当数据为+1时,扩频输出就是对应的PN序列,当数据为-1时,扩频输出是PN序列的反相结果。
图5-2 直接扩频发射机扩频前后的信号频谱仿真结果分析:图5-2分别为扩频之前与扩频之后的频谱图,由图可知,数据信号的带宽约100Hz,其功率峰值约为20dB处,而扩频输出信号带宽展宽了20倍,为2kHz,而功率峰值下降到约7dB处。
系统建模与仿真实验报告

系统建模与仿真实验报告系统建模与仿真实验报告1. 引言系统建模与仿真是一种重要的工程方法,可以帮助工程师们更好地理解和预测系统的行为。
本实验旨在通过系统建模与仿真的方法,对某个实际系统进行分析和优化。
2. 实验背景本实验选择了一个电梯系统作为研究对象。
电梯系统是现代建筑中必不可少的设备,其运行效率和安全性对于整个建筑物的使用体验至关重要。
通过系统建模与仿真,我们可以探索电梯系统的运行规律,并提出优化方案。
3. 系统建模为了对电梯系统进行建模,我们首先需要确定系统的各个组成部分及其相互关系。
电梯系统通常由电梯、楼层按钮、控制器等组成。
我们可以将电梯系统抽象为一个状态机模型,其中电梯的状态包括运行、停止、开门、关门等,楼层按钮的状态则表示是否有人按下。
4. 仿真实验在建立了电梯系统的模型之后,我们可以通过仿真实验来模拟系统的运行过程。
通过设定不同的参数和初始条件,我们可以观察到系统在不同情况下的行为。
例如,我们可以模拟电梯在高峰期和低峰期的运行情况,并比较它们的效率差异。
5. 仿真结果分析通过对仿真实验结果的分析,我们可以得出一些有价值的结论。
例如,我们可以观察到电梯在高峰期的运行效率较低,这可能是由于大量乘客同时使用电梯导致的。
为了提高电梯系统的运行效率,我们可以考虑增加电梯的数量或者改变乘客的行为规则。
6. 优化方案基于对仿真结果的分析,我们可以提出一些优化方案来改进电梯系统的性能。
例如,我们可以建议在高峰期增加电梯的数量,以减少乘客等待时间。
另外,我们还可以建议在电梯内设置更多的信息显示,以便乘客更好地了解电梯的运行状态。
7. 结论通过本次实验,我们深入了解了系统建模与仿真的方法,并应用于电梯系统的分析和优化。
系统建模与仿真是一种非常有用的工程方法,可以帮助我们更好地理解和改进各种复杂系统。
在未来的工作中,我们可以进一步研究和优化电梯系统,并将系统建模与仿真应用于更多的实际问题中。
8. 致谢在本次实验中,我们受益于老师和同学们的帮助与支持,在此表示诚挚的感谢。
系统建模与仿真上机报告

系统建模与仿真实验报告实验题目:库存系统建模与仿真设计指导老师:学生:时间:系统建模与仿真实验报告一、实验目的:本次实验是在学习完离散事件系统建模与仿真的课堂理论后的实际操作试验,可以很好的运用和巩固学过的知识,同时也是对学习的检验。
希望在试验中了解仿真中相关的随机统计模型;能够运用Witness对运营系统分析、建模、仿真运行、结果分析及提出评价和改善建议。
二、试验环境:本次试验是在充分分析所给出的题目后,对题目的要求建立仿真模型,主要运用witness仿真软件运行所建立的模型并分析所得的结果,然后在修改调整的基础上得到最优化的结果。
三、题目:库存系统建模与仿真设计课题系统描述:顾客进入订货服务台的到达间隔时间服从均值为10分钟的负指数分布,首次到达时刻点为0。
一个工作人员接受并检查顾客的订单、收取费用,总共花费时间为UNIFORM (8, 10)分钟。
完成这个步骤后,订单被随机送给两个仓库人员之一(每个仓库人员都有50%的概率得到一个顾客的订单),仓库人员帮顾客找到订购的货物,花费的时间为UNIFORM (16, 20)分钟。
每个仓库人员只为持有分配给他的订单的顾客提供服务。
顾客拿到货物之后离开系统。
对此系统建立仿真模型,并运行5 000分钟,观察顾客的平均系统逗留时间和最大系统逗留时间等。
一位聪明、年轻的工程师建议,不要为仓库人员指派其服务的顾客,而是让两位仓库人员按照“先到先服务”的原则直接为任意一位前来的顾客服务。
对此系统建立仿真模型,也运行5000分钟,将结果与前面的进行比较。
四、建模与仿真步骤如下:1.元素定义:分别对顾客、工作人员、仓库人员的类型、数量定义,完成仿真模型如下图:2.元素可视化的设置:2.1对顾客进行设置如下图:(顾客进入订货服务台的到达间隔时间服从均值为10分钟的负指数分布)2.2对工作人员进行设置如下图:2.2.1对50%的概率设置:2.2.2仓库工作人员花费时间分布设置:(仓库人员帮顾客找到订购的货物,花费的时间为UNIFORM (16, 20)分钟)2.2.3对仓库人员进行设置如下图:对仓库人员1设置:2.2.4对仓库人员2设置:3.运行结果如下图:五、运行结果分析:通过对以上的运行结果观察可以发现,检查人员的使用效率是49.32%,仓库取货员1的使用效率是45.96%,仓库取货员2 的使用效率是52.20%,可以发现在这种随即分配顾客的模式下,造成顾客有很多的等待和人员效率的分配不合理,就是在随机分配下,可能会由于某个取货人员在某个时间分得了较多的顾客而又在花费较多的时间寻找货物,此时就会造成后面的顾客排队等候,使交货期明显延长,交货效率低下。
生产物流系统建模仿真实验报告

系统建模仿真实验报告一、实验目的 (1)二、实验内容及要求 (2)三、实验内容与步骤 (2)生产制造系统建模与仿真基础知识研究: (2)建立实验模型: (2)系统建模及初步的仿真运行调试: (3)四、系统仿真与分析 (5)五、实验心得 (11)一、实验目的本实验围绕生产物流实验系统展开,进行制造系统的建模、仿真分析与设计优化研究实践。
重点研究运用仿真软件Flexsim,对生产物流实验系统的生产运行过程进行建模、仿真和分析,并进行系统改造的方案论证。
二、实验内容及要求对照实验系统,参考有关系统资料及参考案例,在对系统的基本布局、工作特点、工作流程、及实验生产设备等进行详细研究的基础上,运用Flexsim工具进行建模,并对其生产过程进行仿真。
通过仿真分析了解有关生产实验系统方案是否满足预期运行目标的需要,并且针对仿真生产过程中所表现出来的缺陷与瓶颈问题,提出改进方案。
最终完成对于该生产系统的整体产能及物流运作分析,为系统改造决策提供参考依据。
三、实验内容与步骤生产制造系统建模与仿真基础知识研究:结合有关实验系统的生产运作原型,深入研究制造系统的运作控制,及其系统建模与仿真相关知识;熟悉掌握Flexsim建模仿真工具及其安装运行环境,为具体的实验与分析应用做好前期的理论与技术知识准备。
建立实验模型:本实验所涉及的是一个柔性制造系统的生产线(如图1-1所示),它主要有四条流水线组成,同时加工两种不同原材料(以下称原材料a和原材料b),最后把加工后的两种半成品和另一种原材料(以下称原材料c)装配起来,成为成品d。
在模型中,设有存放原材料a、b和成品d的组合式货架,存放原材料c的货栈,它们分别通过堆垛机和AGV小车与生产线相联通,组成系统。
具体物流过程简述如下:(1) 组合式货架用来存放待加工的原材料和成品,货架配备堆垛机,用于从货架上取下原材料,并运到生产线上进行加工。
货架上混合存放a、b两种货物,堆垛机随机取出货物,放入出货台。
仿真软件操作实验报告(3篇)

第1篇实验名称:仿真软件操作实验实验目的:1. 熟悉仿真软件的基本操作和界面布局。
2. 掌握仿真软件的基本功能,如建模、仿真、分析等。
3. 学会使用仿真软件解决实际问题。
实验时间:2023年X月X日实验地点:计算机实验室实验器材:1. 仿真软件:XXX2. 计算机一台3. 实验指导书实验内容:一、仿真软件基本操作1. 打开软件,熟悉界面布局。
2. 学习软件菜单栏、工具栏、状态栏等各个部分的功能。
3. 掌握文件操作,如新建、打开、保存、关闭等。
4. 熟悉软件的基本参数设置。
二、建模操作1. 学习如何创建仿真模型,包括实体、连接器、传感器等。
2. 掌握模型的修改、删除、复制等操作。
3. 学会使用软件提供的建模工具,如拉伸、旋转、镜像等。
三、仿真操作1. 设置仿真参数,如时间、步长、迭代次数等。
2. 学习如何进行仿真,包括启动、暂停、继续、终止等操作。
3. 观察仿真结果,包括数据、曲线、图表等。
四、分析操作1. 学习如何对仿真结果进行分析,包括数据统计、曲线拟合、图表绘制等。
2. 掌握仿真软件提供的分析工具,如方差分析、回归分析等。
3. 将仿真结果与实际数据或理论进行对比,验证仿真模型的准确性。
实验步骤:1. 打开仿真软件,创建一个新项目。
2. 在建模界面,根据实验需求创建仿真模型。
3. 设置仿真参数,启动仿真。
4. 观察仿真结果,进行数据分析。
5. 将仿真结果与实际数据或理论进行对比,验证仿真模型的准确性。
6. 完成实验报告。
实验结果与分析:1. 通过本次实验,掌握了仿真软件的基本操作,包括建模、仿真、分析等。
2. 在建模过程中,学会了创建实体、连接器、传感器等,并能够进行模型的修改、删除、复制等操作。
3. 在仿真过程中,成功设置了仿真参数,启动了仿真,并观察到了仿真结果。
4. 在分析过程中,运用了仿真软件提供的分析工具,对仿真结果进行了数据分析,并与实际数据或理论进行了对比,验证了仿真模型的准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设计一产生十种不同分布的独立的随机数一、设计内容及要求任务:产生十种不同分布的独立的随机数,并进行检验。
要求:对随机数进行的统计性检验包括频率检验、参数检验、独立性检验。
二、设计环境及工具Windows7、MatlabR2010b三、设计思想及方法(1) 在对雷达系统进行仿真时,首当其冲的问题就是对电磁环境的仿、真。
其中无用的电磁信号包括三大类,即杂波、噪声和干扰,在模拟仿真时相比于有用的电磁信号也是不可或缺的。
其所谓的仿真就是在已知随机变量的统计特性及其参数的情况下,研究如何在计算机上产生服从给定统计特性和参数的随机变量。
(2) 在雷达、导航、声呐、通信和电子对抗等系统中,应用最多的概率统计模型还是正态分布或高斯分布、指数分布、瑞利分布、莱斯分布或广义瑞利分布、韦尔分布、对数-正态分布、m分布、拉普拉斯分布、复合k分布等。
(3) 在这些随机总体中畸形随机抽样,实际上都是以[0,1]区间上的均匀分布随机总体为基础的。
原则上讲,只要已知[0,1]区间上的均匀分布随机数序列,总可以通过某种方法(数学方法)来获得某已知分布的简单子样。
只要给定的均匀分布随机数列满足均匀且相互独立打的要求,经过严格的数学变换或者严格的数学方法,所产生的任何分布的简单子样都会满足具有相同总体分布和相互独立的要求。
四、设计过程及结果本次设计的十种随机数包括均匀分布、高斯分布、指数分布、广义指数分布、瑞利分布、广义瑞利分布、韦尔分布、拉普拉斯分布、柯西分布和2χ分布,使用Matlab 完成设计并给出具体的参数,代码附在最后。
1.均匀分布已知随机变量ε在[0,1]区间上服从均匀分布,则有概率密度函数 1,01()0,x f x ≤≤⎧=⎨⎩其他 其分布函数为0,0F(),01x x x x x <⎧⎪=≤≤⎨⎪≥⎩1,1在计算机上利用数学方法产生随机数的方法有平方取中法、移位寄存器法和各种同余法等,这里我们采用剩同余法产生均匀随机序列,其递推公式为1(mod )n n x x M λ+=通常取2k M =,k 为计算机的尾数字长021b x =+,b 为正整数,x 初始值须为奇数323a λ=±,a 为正整数(1) 所谓频率检验就是检验随机数序列的观测频数与理论频数的差异是否显著。
详细的论述见教材P24,只要给定一个显著水平α,就可以确定二者之间的差异程度,α一般取值为0.05或0.01。
为了有效的进行统计检验,N 值最好大于100,在雷达仿真中,通常1024N ≥。
(2) 随机数的参数检验是随机数分布的各个参数的观测值与理论值的差异是否显著,本设计的检验只包括一二阶矩和方差的检验。
详细的论述见教材P25。
(3) 独立性检验就是检验随机数序列中前后各数的统计相关性是否异常,通常包括相关系数检验,联列表检验和连检验等,我们这里只进行相关系数的检验。
详细的论述见教材P26,需要注意的是通常取50N j ->,这样就可以根据给定的显著水平α及正态分布表查处临界值了。
(4) 如此根据上述,本次设计的均匀分布的参数分布为:显著水平α取0.05,相应的频率检验中区间分为50k =组,取2χ分布的自由度为39(参考)时的临界值为254.572χ=;参数检验时相应的正态分布显著水平为0.05时的临界值为 1.96z α=;独立性检验时N 取值为100000点,取10050N j -=>,满足条件。
用Matlab 实现上述的100000点的均匀分布随机数的仿真并实现三种统计检验,结果如下图所示:图1. 100000点均匀分布直方图相应的检验结果为:从上述检验结果可以看出,本设计产生的[0,1]区间上的均匀分布的随机数序列通过了各项检验。
由于均匀分布是以下9种其他分布的基础,即可以用均匀分布序列通过一定的数学变换得到,若均匀分布通过检验,则基于此产生的其他分布也必定能通过相关的检验,故下述的分布均是由通过检验的均匀分布变换得到,本身就不再进行检验了。
2.高斯分布高斯分布即正态分布,其概率密度函数为221()()exp()22x f x μσπσ-=-(1) 本次设计中的高斯分布是通过近似抽样法产生,即假设有N 个相互独立的随机变量12,,...,N u u u ,它们有相同的分布,其均值()i E u m =,方差2()i D u σ=,根据中心极限定理,这N 个随机变量之和服从高斯分布,详细论述见教材P81。
(2) 这里我们取独立的随机变量i u 为均匀分布,通常其数目N 至少要大于8,这里我们将N 取为12,则高斯随机变量为121(6)j i i y u u σ==-+∑为简便起见,其中u 取0,σ取1,仿真结果如下图所示图2. 100000点高斯分布直方图其中共检验了32组参数相同且相互独立的均匀分布,取其中符合要求的12组仿真生成高斯变量。
3.指数分布指数分布的概率密度函数为 1,0()0,0x e x f x x λλ-⎧≥⎪=⎨⎪<⎩(1) 指数分布的仿真采用直接抽样法,详细论述见教材P74,即知道某一分布的概率密度函数,就可以由其积分形式构成[0,1]区间上的均匀分布从而得到其随机变量。
(2) 由均匀分布得到的指数的随机变量的表达式为1ln i i y u λ=- 其中i u 即为均匀分布随机变量,参数λ取8。
仿真结果如下图所示:图3. 100000点高斯分布直方图高斯分布的检验包括之后的7个检验与第一个均匀分布完全相同不再赘述。
4.广义指数分布广义指数分布的概率密度函数为0()exp[()]f x x s I =-+式中s 是信噪比,由教材P95-96的论述可以得到最终的广义指数分布的的随机变量抽样表达式为12ln )i i i x u u s π=-++其中s 是输入信噪比,1i u 、2i u 均为[0,1]区间上的均匀分布,仿真时取信噪比为2,方针的结果如下图所示图4. 100000点广义指数分布直方图5.瑞利分布瑞利分布的概率密度函数为222()exp(),02xx f x x σσ=-≥ 式中,σ是瑞利分布的参量,但不是其均方根值。
利用直接抽样法得到瑞利分布的随机变量,具体的公式变换详见P77-78,最后得到瑞利分布直接抽样公式为2ln i i u ξσ=-其中σ是瑞利分布的参量,取1/2 ,i u 为[0,1]区间上的均匀分布,仿真结果如下图所示图5. 100000点瑞利分布直方图6.广义瑞利分布广义瑞利信号就是所谓的莱斯信号,它是将一个恒值信号叠加在两个相互独立正交的高斯随机变量值上,并取其矢量和而构成的。
其概率密度函数为220222()exp()()2rr a ar f x I σσσ+=- σ为随机变量r 的分布参数,a 为常数(1) 因此,只要在正态分布总体中抽取两个相互独立的均值为0的正态分布随机数,再在其中一个加上个常数a ,便可获得广义瑞利分布的随机数。
由P94论述得到其分布的表达式为22()i i i r x a y =++式中i x 、i y 均为正态分布,且相互独立,a 为常数值(2) 仿真时,取a 为2,结果如下图所示图6. 100000点广义瑞利分布直方图7.韦尔分布服从三参量的韦尔分布的概率密度函数为1()()exp(())0,0,0a a n n a x x x x f x a b x b b b---=->>≤<∞ 式中,n x 、a 、b 是韦尔分布的位置参量、形状参量和标度参量。
利用直接抽样法得到韦尔分布的随机变量,具体的公式变换详见P77-78,最后得到韦尔分布直接抽样公式为ln a i n i x b u ξ=+-其中公式中位置参数n x 取3,形状参量a 取3,标度参量b 取2, i u 为[0,1]区间上的均匀分布,仿真结果如下图所示图7. 100000点韦尔分布直方图8.拉普拉斯分布拉普拉斯分布的概率密度函数为|)|exp(2)(m x a a x f la --=式中m 为均值,a 为形状参数。
为简便起见这里只考虑m 为0,a 为1的情况,即|)|exp(21)(x x f -= 可以看出,该分布为双指数分布,则得出有两个相同指数分布随机变量之差服从拉普拉斯分布的结论,最后有)ln(21ii i u u =ξ 式中1,2i i u u 为 [0,1]区间的均匀分布随机数。
仿真时,直接调用产生两个均匀分布随机序列即可,结果如下图所示图8. 100000点拉普拉斯分布直方图9.柯西分布柯西分布有概率密度函数 21()(1)cau f x x π=+其中均值()0E x =,方差不存在。
随机数产生公式 a u b i i +-=)]21(tan[πξ式中:i u 为[0,1]区间的均匀分布随机数。
仿真时参数a 、b 分别取,0、1,结果如下图所示图9. 100000点柯西分布直方图10.2χ分布 2χ分布的概率密度函数为21221exp(),02()2()20,0nn x x x n f x p x χ+⎧->⎪⎪=⎨⎪⎪≤⎩ 根据正态分布之平方和为2χ分布这一基本原理,可以直接获得2χ分布随机变量抽样21()nj j n x ξ==∑ 式中j x 是采样间相互独立地均值为0,方差为1的正态分布随机变量:n 是2χ分布的自由度,则可以看出自由度n 是决定该分布的唯一分布参量。
这里为方便起见,取自由度为4,则其为两个指数分布之和的分布,仿真结果为图10. 自由度为4的2 分布直方图五、附录0.均匀分布function u=evenlydis(a,b,m,N) %³ËͬÓà·¨lam=8*a-3;M=pow2(m);x=zeros(1,N);x(1)=pow2(b)+1;for i=2:N;y=lam*x(i-1);x(i)=mod(y,M);endu=x/M;end1.分布检验function result=check(x)%¼ìÑéÏîÄ¿°üÀ¨:ƵÂʼìÑé,Ò»½×¾Ø,¶þ½×¾Ø,·½²î,¶ÀÁ¢ÐÔ; N=length(x);%%%%%%%%%%%%%ƵÂʼìÑé,»ñµÃͳ¼ÆÁ¿A%%%%%%%%%%%%%L=50; %Ö±·½Í¼Éϵļä¸ô´óСA=0;n=zeros(1,L);for i=1:Nfor j=1:Lif(x(i)>=(j-1)*1/L)&&(x(i)<=j*1/L) %Ƶ¶Èͳ¼Æn(j)=n(j)+1;endendendfor i=1:LA=A+((n(i)-N/L)^2)/(N/L); %¶ÔÖ±·½Í¼ÉϵÄÿ¸ö¼ä¸ôÈ¡µÄ´ó·½²î¶øÒÑend%%%%%%%%%%%%%²ÎÊý¼ìÑé,»ñµÃͳ¼ÆÁ¿Z1,Z2,Z%%%%%%%%%%%%% M1=0;M2=0;for i=1:NM1=M1+x(i);M2=M2+x(i)^2;endM1=M1/N;M2=M2/N;S=M2-M1+1/4;Z1=sqrt(12*N)*(M1-1/2);%Ò»½×¾Øͳ¼ÆÁ¿Z2=1/2*sqrt(45*N)*(M2-1/3);%¶þ½×¾Øͳ¼ÆÁ¿Z=(sqrt(180*N))*(S-1/12);%·½²îͳ¼ÆÁ¿%%%%%%%%%%%%%¶ÀÁ¢ÐÔ¼ìÑé,»ñµÃÏà¹ØϵÊýͳ¼ÆÁ¿p%%%%%%%%%% %%%?j=N-100; %ͨ³£È¡N-j>50¼´¿É£¬´Ë´¦È¡100sum=0;for i=1:(N-j)sum=sum+x(i)*x(j+i);endp=(sum/(N-j)-M1*M1)/S*sqrt(N-j); %%%%%%%%%%%%%¸ù¾ÝÒÔÉÏͳ¼ÆÁ¿£¬¼ìÑéËæ»úÐòÁÐxÄÜ·ñͨ¹ý¼ìÑé%%%%%%%%%%%%%ALPHA=0.05; %ÏÔÖøˮƽGuass_Value=1.96; %±ê×¼Õý̬·Ö²¼ÏÔÖøˮƽΪ5%µÄÁÙ½çÖµLamenda_Value=54.572; %×ÔÓɶÈΪ39µÄx^2·Ö²¼ÏÔÖøˮƽΪ5 %µÄÁÙ½çÖµ%%%%%ÏÔʾ½á¹û%%%%%%%if(abs(A)<Lamenda_Value)&&(abs(Z1)<Guass_Value)&&(abs(Z 2)<Guass_Value)&&(abs(Z)<Guass_Value)&&(abs(p)<Guass_ Value)disp('¾ùÔÈ·Ö²¼Í¨¹ý¼ìÑé');result=1;elsedisp('¾ùÔÈ·Ö²¼Î´Í¨¹ý¼ìÑé'); %֮ǰעÊ͵ôµÄÔ-ÒòÊÇʲôresult=0;enddisp('ͨ¹ý¼ÆË㣬½á¹ûÈçÏ£º');disp(' ƵÂʼìÑé Ò»½×¾Ø ¶þ½×¾Ø ·½²îÏà¹ØϵÊý ×ÔÓÉ¶È ÏÔÖøÐÔˮƽ ÁÙ½çÖµ1 ÁÙ½çÖµ2'); disp([A,Z1,Z2,Z,p,39,ALPHA,Guass_Value,Lamenda_Value] );end2.高斯分布function z=guassdis(a,b,m,u,sigma,N)%¸Ãº¯ÊýÓÃÀ´²úÉú¸ß˹ÐòÁÐ%º¯Êýµ÷ÓÃÐÎʽΪz=GuassDist(s,u,sigma,N)%sΪ¾ùÓë·Ö²¼µÄa%bΪ¾ùÓë·Ö²¼µÄb%mΪ¾ùÓë·Ö²¼µÄm%uΪ¸ß˹·Ö²¼µÄ¾ùÖµ%sigmaΪ¸ß˹·Ö²¼µÄ·½²îundis=zeros(12,N);i=1;x0=b;z=zeros(1,N);seed=zeros(1,12);%%%%%%%²úÉú12¸ö¶ÀÁ¢µÄͨ¹ý¼ìÑéµÄ[0,1]Çø¼ä¾ùÔÈ·Ö²¼µÄËæ»úÐòÁУ¬³¤¶ÈΪN%%%%%%%%%while(i<=12)undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));while(s==0)x0=x0+1;undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));endseed(i)=x0;x0=x0+1;i=i+1;enddisp('¾ùÓë·Ö²¼µÄbµÄֵΪ£º');disp(seed);for i=1:Nfor j=1:12z(i)=z(i)+undis(j,i);endz(i)=z(i)-6;z(i)=z(i)*sigma+u;endend3.指数分布function z=expdis(a,b,lamda,m,N)%¸Ãº¯ÊýÓÃÀ´²úÉú²ÎÊýΪlamdaµÄÖ¸Êý·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN? %sΪ¾ùÔÈ·Ö²¼µÄa?%...%lamdaΪָÊý·Ö²¼µÄ²ÎÊýz=zeros(1,N);x0=b;%%%%%%%%%%%%Ê×ÏȲúÉúͨ¹ý¼ìÑéµÄ[0,1]Çø¼äµÄ¾ùÔÈ·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN%%%%%%%%%%%%%%?undis=evenlydis(a,x0,m,N);s=check(undis);while(s==0)x0=x0+1;undis=evenly(a,x0,m,N);s=check(undis);endfor i=1:Nz(i)=-log(undis(i))/lamda;endend4.广义指数分布function z=eexpdis(a,b,sn,m,N)%¸Ãº¯ÊýÓÃÀ´²úÉú²ÎÊýΪsnµÄ¹ãÒåÖ¸Êý·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN %snΪÊäÈëÐÅÔë±È?%aΪ¾ùÓë·Ö²¼µÄ³õʼ²ÎÊý%...undis=zeros(2,N);i=1;x0=b;z=zeros(1,N);%%%%%%%²úÉú2¸ö¶ÀÁ¢µÄͨ¹ý¼ìÑéµÄ[0,1]Çø¼ä¾ùÔÈ·Ö²¼µÄËæ»úÐòÁУ¬³¤¶ÈΪN%%%%%%%%%?while(i<=2)undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));while(s==0)x0=x0+1;undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));endx0=x0+1;i=i+1;endfor i=1:Nz(i)=(-log(undis(1,i)))+2*sqrt(-sn*log(undis(1,i)))*c os(2*pi*undis(2,i))+sn;endend5.瑞利分布function z=rayleighdis(a,b,m,sigma,N)%¸Ãº¯ÊýÓÃÀ´²úÉú²ÎÊýΪsigmaµÄÈðÀû·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN? %aΪ¾ùÔÈ·Ö²¼³õʼ²ÎÊýz=zeros(1,N);x0=b;%%%%%Ê×ÏȲúÉúͨ¹ý¼ìÑéµÄ[0,1]Çø¼äµÄ¾ùÔÈ·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN%%%%%undis=evenlydis(a,x0,m,N);s=check(undis);while(s==0)x0=x0+1;undis=evenlydis(a,x0,m,N);s=check(undis);endfor i=1:Nz(i)=sigma*sqrt((-2)*log(undis(i)));endend6.广义瑞利分布function z=erayleighdis(a,b,m,n,N)%GYRelayDist?²úÉú¹ãÒåÈðÀû·Ö²¼Ëæ»úÊýÐòÁÐundis=zeros(2,N);i=1;x0=b;M1=zeros(1,N);M2=zeros(1,N);z=zeros(1,N);%%%%%%%²úÉú2¸ö¶ÀÁ¢µÄͨ¹ý¼ìÑéµÄ[0,1]Çø¼ä¾ùÔÈ·Ö²¼µÄËæ»úÐòÁУ¬³¤¶ÈΪN%%%%%%%while(i<=2)undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));while(s==0)x0=x0+1;undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));endx0=x0+1;i=i+1;endfor i=1:NM1(i)=sqrt(-2*log(undis(1,i))).*cos(2*pi*(undis(2,i)) );M2(i)=sqrt(-2*log(undis(1,i))).*sin(2*pi*(undis(2,i)) );z(i)=sqrt((M1(i)+n)^2+M2(i)^2);end7.韦尔分布function z=vaildis(a,b,m,xn,beta,lamda,N)%¸Ãº¯ÊýÓÃÀ´²úÉúΤ¶û·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN%sΪ¾ùÔÈ·Ö²¼µÄa?%...%lamdΪΤ¶û·Ö²¼µÄ²ÎÊýz=zeros(1,N);x0=b;%%%%%%%%%%%%Ê×ÏȲúÉúͨ¹ý¼ìÑéµÄ[0,1]Çø¼äµÄ¾ùÔÈ·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN%%%%%%%%%%%%%%?undis=evenlydis(a,x0,m,N);s=check(undis);while(s==0)x0=x0+1;undist=evenly(a,x0,m,N);s=check(undist);endfor i=1:Nt=1/lamda;y=-log(undis(i));z(i)=xn+beta*power(y,t);endend8.拉普拉斯分布function z=laplacedis(a,b,m,N)%¸Ãº¯ÊýÓÃÀ´²úÉú³¤¶ÈΪNµÄLaplacian·Ö²¼Ëæ»úÐòÁÐ?%bΪ³õʼ¾ùÔÈ·Ö²¼µÄ²ÎÊýundis=zeros(2,N);i=1;x0=b;z=zeros(1,N);%%%%%%%²úÉú2¸ö¶ÀÁ¢µÄͨ¹ý¼ìÑéµÄ[0,1]Çø¼ä¾ùÔÈ·Ö²¼µÄËæ»úÐòÁУ¬³¤¶ÈΪN%%%%%%%%%?while(i<=2)undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));while(s==0)x0=x0+1;undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));endx0=x0+1;i=i+1;endfor i=1:Nz(i)=log(undis(1,i)/undis(2,i));endend9.柯西分布function z=cauchydis(a,b,m,beta,lamda,N)%¸Ãº¯ÊýÓÃÀ´²úÉú²ÎÊýΪa,bµÄ¿ÂÎ÷·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN?%²ÎÊýaΪλÖòÎÊý;²ÎÊýbΪÐÎ×´²ÎÊý?%µ÷ÓÃÐÎʽΪz=CauchyDist(s,a,b,N)??z=zeros(1,N);x0=b;%%%%%%%%%%%%Ê×ÏȲúÉúͨ¹ý¼ìÑéµÄ[0,1]Çø¼äµÄ¾ùÔÈ·Ö²¼Ëæ»úÐòÁÐ,³¤¶ÈΪN%%%%%%%%%%%%%%?undis=evenlydis(a,x0,m,N);s=check(undis);while(s==0)x0=x0+1;undis=evenlydis(a,x0,m,N);s=check(undis);endfor i=1:Nz(i)=beta*tan(pi*(undis(i)-1/2))+lamda;endend10.2 分布function z=x2dis(a,b,m,n,N)%GYRelayDist?²úÉú¹ãÒåÈðÀû·Ö²¼Ëæ»úÊýÐòÁÐundis=zeros(n+1,N);i=1;x0=b;z=zeros(1,N);%%%%%%%²úÉú2¸ö¶ÀÁ¢µÄͨ¹ý¼ìÑéµÄ[0,1]Çø¼ä¾ùÔÈ·Ö²¼µÄËæ»úÐòÁУ¬³¤¶ÈΪN%%%%%%%while(i<=n+1)undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));while(s==0)x0=x0+1;undis(i,:)=evenlydis(a,x0,m,N);s=check(undis(i,:));endx0=x0+1;i=i+1;endfor i=1:Nfor j=1:nz(i)=z(i)+(sqrt(-2*log(undis(j,i))).*cos(2*pi*undis(j +1,i)))^2;endendend。
