直角三角形斜边上的中线
斜边中线定理推导

斜边中线定理推导摘要:1.斜边中线定理的概念2.斜边中线定理的推导过程3.斜边中线定理的应用正文:【1.斜边中线定理的概念】斜边中线定理,又称为直角三角形斜边中线定理,是指在直角三角形中,斜边的中线等于另外一条直角边的一半。
这个定理在我国初中数学课程中就会接触到,是直角三角形性质中一个非常基础且重要的定理。
【2.斜边中线定理的推导过程】斜边中线定理的推导过程主要分为两个步骤:步骤一:作图。
在直角三角形ABC 中,假设∠C=90°,AB 为斜边,CD 为AB 的中线,AE 为BC 的延长线,AF 为AC 的延长线,交于点E。
步骤二:证明。
根据三角形的全等条件,我们可以证明Rt△ADC≌Rt△AEB,具体如下:(1)∠ADC=∠AEB,因为它们都是对直角三角形的补角;(2)DC=EB,因为CD 是AB 的中线,所以DC=EB;(3)∠CAD=∠EBA,根据同理,它们都是对直角三角形的补角。
既然有两个三角形的三个对应角相等,且对应边长相等,那么根据三角形全等的SAS(边- 角-边)条件,我们可以得出Rt△ADC≌Rt△AEB。
【3.斜边中线定理的应用】斜边中线定理在实际应用中,主要体现在以下几个方面:(1)计算。
在直角三角形中,如果知道斜边和斜边的中线,可以很方便地计算出另外两条直角边的长度。
(2)证明。
在几何证明中,斜边中线定理可以作为一个基本的工具,帮助我们证明一些更复杂的几何问题。
(3)解决实际问题。
在一些实际问题中,可能会涉及到直角三角形的斜边和斜边的中线,这时候斜边中线定理就可以派上用场。
“直角三角形斜边上的中线”的性质及其应用
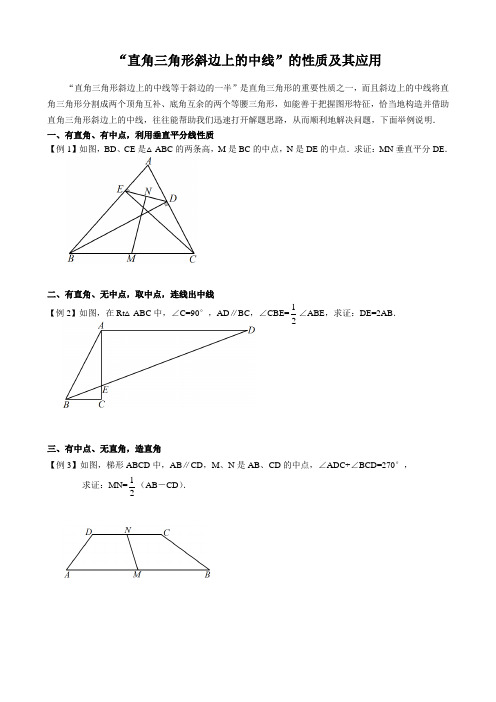
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,利用垂直平分线性质【例1】如图,BD 、CE 是△ABC 的两条高,M 是BC 的中点,N 是DE 的中点.求证:MN 垂直平分DE .二、有直角、无中点,取中点,连线出中线【例2】如图,在Rt △ABC 中,∠C=90°,AD ∥BC ,∠CBE=21∠ABE ,求证:DE=2AB .三、有中点、无直角,造直角【例3】如图,梯形ABCD 中,AB ∥CD ,M 、N 是AB 、CD 的中点,∠ADC+∠BCD=270°,求证:MN=21(AB -CD ).四、逆用性质解题【例4】如图,延长矩形ABCD 的边CB 至E ,使CE=CA ,P 是AE 的中点.求证:BP ⊥DP .【习题练习】1、如图,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E ,求证:CD=21BE .2、如图,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的中点,求证:AB=2DM .3、如图,在四边形ABCD 中,∠DAB=∠DCB=90°,点M 、N 分别是BD 、AC 的中点.确定MN 、AC 的位置关系.直角三角形斜边上中线性质的应用一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图,在Rt △BAC 中,∠BAC=90°,D 为BC 的中点,则BC 21AD =.2、性质的拓展:如图:因为D 为BC 中点,所以BC 21DC BD ==, 所以AD=BD=DC=BC 21, 所以∠1=∠2,∠3=∠4,因此∠ADB=2∠1=2∠2,∠ADC=2∠3=2∠4.因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、21倍关系求值 例1、如图,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、如图,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点.(1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于G .求证:AG=DG .3、证明角相等及角的倍分关系例3、已知,如图,在△ABC中,∠BAC 90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE.例4、已知:如图,在△ABC中,AD是高,CE是中线。
直角三角形斜边上的中线应用题目

直角三角形斜边上的中线应用题目
直角三角形是一种特殊的三角形,其中一个角为直角(90度角)。
在直角三角形中,斜边是指与直角的两条边不重合的另外那条边。
斜边上的中线是指从斜边中点垂直于斜边的线段。
直角三角形斜边上的中线有很多应用,下面是一些题目:
1. 题目一:
已知一个直角三角形的斜边长为10cm,求斜边上的中线的长度。
解答:
由于直角三角形中,斜边的一半就是中线的长度。
所以,中线的长度为10cm的一半,即5cm。
2. 题目二:
已知一个直角三角形的斜边长为12cm,中线的长度为6cm,求与中线相交的直角三角形两个直角边的长度。
解答:
由于中线是斜边的一半,所以斜边的长度是中线的两倍,即12cm。
因此,直角边的长度可以使用勾股定理求解。
设一个直角边为x,则另一个直角边为12-x。
根据勾股定理,我们可以得到以下方程:
x^2 + (12-x)^2 = 12^2
化简方程后,求解x的值,即可得到另一个直角边的长度。
这些题目是直角三角形斜边上的中线应用题目的一些例子。
通过解答这些题目,我们可以更深入地理解直角三角形的性质和中线的应用。
在解题过程中,可以运用勾股定理和直角三角形的基本性质,加深对数学知识的理解和应用能力。
希望以上内容对您有所帮助,如有其他问题,请随时提问。
直角三角形斜边上的中线的性质及其应用

“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半” 是直角三角形的重要性质之一, 而且斜边上的中线将直角三角形分割成两个顶角互补、 底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线, 往往能帮助我们迅速打开解题思路, 明. 一、有直角、有中点,连线出中线,用性质 例1.如图1 , BD N 是DE 的中点.试问:猜想:MN B 直平分 1ME MD 在 Rt △ BEC 中,•••点 M 是斜边BC 的中点,• ME^ BC,又 NE = ND •2直线MN 是线段DE 的垂直平分线,• NMLDE 即 MN 垂直平分 DE. 评析:题目中给出了三角形的两条高与两个中点, 联想“直角三角形斜边上的中线等于斜边的一半” ,证明:DE 的中点F ,连AF ,贝U AF=FD 」DE,所以/ DAF=Z ADF,又因为 AD// BC,所以/ CBE Z ADF, 21又因为/ CBEd Z ABE 所以/ ABF=/ AFB,所以 AF=AB 即 DE=2AB2评析:本题是有直角、无中点的情况,这时要取直角三角形的斜边上的中点,再连结该点与直角顶 点,然后用性质来解决问题.三、有中点、无直角,造直角,用性质 PM 交DC 于 K 下证N 和K 重合,贝U P 、N M 三点共线,PDC △ PAB 斜边上的中线,• PN=CN=DlN=CD PM=BM=D M=AB,2 2•••/ PNC=2/ PDN=2/ A Z PMB Z PKC=2/ A, •/ PNC / PKC •- N 、K 重合,问题便迎刃而解. 2△ ABF 均为等腰三角形,由此结论得证. CE 是厶ABC 的两条高,M 是BC 的中点,MN 与 DE 有什么关系?证明你的猜想.DE.证明:如图:连接例 3.如图 3,梯形 ABCD 中, AB// CD M / ADC+Z BCD=270,1求证:MN — (AB-CD .2证明:延长AD BC 交于 •••/ APB=9(°,连结 PN 连结P,vZ ADC y BCD=270,••• PN PM 分别是直角三角形△ B• MN=PM-PN= (AB-CD).2评析:本题只有中点,而没有直角,这时要想方设法构造直角,应用性质,而条件中正好有角的关系“Z ADC-Z BCD=270 ” ,这样问题就易以解决了四、逆用性质解题例4.如图4,延长矩形ABCD的边CB至E,使CE=CA , P是AE的中点.求证:BP丄DP .证明:如图3,连结BD交AC于点0,连结PO,•••四边形ABCD 是矩形,••• A0=0C=0B=0D ,1 1••• PA=PE ,• P0= — EC ,T EC=AC , • P0= — BD ,2 2即0P=0B=0D , • BP丄DP.评析:“直角三角形斜边上的中线等于斜边的一半”这个性质是众所周知的,而它的逆定理往往被大家所忽视,本题就是利用这个性质构造厶PBD ,请同学们试一试吧!1. 如图5,A ABC中, AB=AC 厶1求证:CD= BE22. 如图6,A ABC中,/ B=2/ C, 中点,求证:AB=2DM证BD边的中线等于BD的一半.1. 提示:结论中的BE是直角三角形的斜边,由半”,故应取BE的中点F,连结DF,只需证明1— BE应想到“直角三角形斜边上的中线等于斜边的一2DC=DF,即证/ C=Z DFC2 .提示:取AB的中点N,连结DN、MN即可.直角三角形斜边上中线性质的应用直角三角形斜边上中线的性质是直角三角形的一个重要性质, 同时也是常考的知识点. 它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。
直角三角形斜边中线证明

直角三角形斜边中线证明对于一个直角三角形,以斜边为直径可以画出一个内切圆,如下图所示:[插入图片]设该直角三角形的斜边为 c ,直角边为 a ,另一直角边为 b 。
由内切圆的性质可知,圆心 O 位于斜边中点 M 上。
[插入图片]接下来我们来证明斜边中线 OM 的长度等于直角边的一半。
首先,根据勾股定理可知:a^2 + b^2 = c^2再根据正弦定理可知:$\frac{a}{\sin A} = \frac{c}{\sin C} $$\frac{b}{\sin B} = \frac{c}{\sin C} $其中 A 为直角所在的角,B 为另一个角,C 为斜边所对的角。
因为斜边为直径的圆内角和为180度,所以C=90度。
将上面两个式子带入,可得:a = c $\sin A$b =c $\sin B$将斜边 c 写成 a 和 b 的平方和的形式,可得:c^2 = a^2 + b^2将 a 和 b 分别用 c 的正弦值表示,可得:c^2 = (c $\sin A$)^2 + (c $\sin B$)^2化简可得:$\sin ^2 A + \sin ^2 B = 1 $利用三角余弦定理,可得:$\cos C = \cos 90° = 0$而 $\cos C = \frac{a^2 + b^2 - c^2}{2 a b}$带入可得:$\frac{a^2 + b^2 - c^2}{2 a b} = 0$进一步化简可得:a^2 + b^2 = c^2这与最开始的勾股定理相同,因此我们得到了一个等式,即:$\sin ^2 A + \sin ^2 B = 1 $同时成立。
接下来考虑直角三角形斜边中线 OM 。
由三角形中线定理可知,直角三角形 CMO 的斜边长度为 $\frac{c}{2}$ ,所以我们只需要证明 OM 与直角边 a 的长度相等即可。
考虑三角形 OMC 。
由于三角形 CMO 的斜边长度为$\frac{c}{2}$ ,而圆心 O 位于斜边中点 M 上,所以 OM 也等于$\frac{c}{2}$ 。
直角三角形斜边中线定理 (3)

直角三角形斜边中线定理直角三角形是一种特殊的三角形,其中一个角度为90度。
直角三角形的边可分为三种:斜边、邻边和对边。
直角三角形具有许多特性和性质,其中之一就是直角三角形斜边中线定理。
定理描述直角三角形斜边中线定理指出:直角三角形斜边上的中线等于斜边的一半。
换句话说,如果在一个直角三角形中,连接斜边的中点与直角顶点的直线段,那么这个直线段的长度等于斜边的一半。
下面是该定理的数学表达式:设直角三角形的斜边长度为c,斜边上的中线长度为m,则有:m = c / 2定理证明我们可以通过几何和代数的方法来证明直角三角形斜边中线定理。
几何证明设直角三角形的斜边为AC,斜边上的中线为BM,并连接顶点A和中点B。
首先,我们可以通过斜边上的中线构造一个三角形ABM。
根据直角三角形的性质,A和C分别为直角三角形ABM的直角顶点和斜边上的另一个顶点。
由于三角形ABM是直角三角形,我们可以利用勾股定理来求解等式AB和BM的关系。
根据勾股定理,直角三角形ABM的斜边AB的平方等于直角边AM的平方加上直角边BM的平方:AB² = AM² + BM²因为直角三角形ABM是等腰三角形(与斜边等长),所以直角边AM的长度等于斜边AC的一半(即AM=c/2),我们将其带入等式中化简:AB² = (c/2)² + BM²继续化简:AB² = c²/4 + BM²由于AB = AC(直角边)和AC = c(斜边),我们可以将AB替换为c,即:c² = c²/4 + BM²继续化简并整理:3c²/4 = BM²通过移项操作,得到:BM² = 3c²/4我们可以取开根号来求解BM的长度:BM = √(3c²/4) = (√3c) / 2接下来,我们将BM的长度与斜边的一半进行比较:BM = (√3c) / 2 c / 2我们可以发现,BM的长度等于斜边的一半(c/2),这证明了直角三角形斜边中线定理。
专题12 直角三角形斜边上的中线(解析版)

专题12 直角三角形斜边上的中线【考点归纳】(1)性质:在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)(2)定理:一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.该定理可一用来判定直角三角形.【好题必练】一、选择题1.(2020秋•贵阳期末)如图,在长为10的线段AB上,作如下操作:经过点B作BC⊥AB,使得BC=AB;连接AC,在CA上截取CE=CB;在AB上截取AD=AE,则AD的长为()A.5﹣5B.10﹣5C.10﹣10D.5+5【答案】A【解析】解:∵AB=10,BC=AB,∴BC=5,由勾股定理得:AC=5,∵CE=BC=5,∴AD=AE=AC﹣CE=5﹣5.故选:A.2.(2020秋•仪征市期末)A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在()A.AB中点B.BC中点C.AC中点D.∠C的平分线与AB的交点【答案】A.【解析】解:∵AB2=10002=1000000,BC2=6002=360000,AC2=8002640000,∴AB2=BC2+AC2,∴△ABC为以AB为斜边的直角三角形,当点P在AB的中点时,CP=AB=P A=PB,故选:A.3.(2020秋•莲湖区期末)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB 的长为4.8km,则M,C两点间的距离为()A.1.2km B.2.4km C.3.6km D.4.8km【答案】B.【解析】解:∵公路AC,BC互相垂直,∴∠ACB=90°,∵M为AB的中点,∴CM=AB,∵AB=4.8km,∴CM=2.4(km),即M,C两点间的距离为2.4km,故选:B.4.(2020秋•新华区校级月考)如图所示,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥BC,E为垂足,AC=AB,图中为60°的角有()A.2个B.3个C.4个D.5个【答案】D.【解析】解:在Rt△ABC中,∠ACB=90°,AC=AB,∴∠B=30°.∵D是AB的中点,∴BD=CD.∴∠DCB=∠B=30°.又∵DE⊥BC于E,∴∠BDE=∠CDE=60°.∴∠ACD=90°﹣30°=60°.∴△ACD为等边三角形.∴∠ADC=∠DAC=∠ACD=∠CDE=∠BDE=60°.故选:D.5.(2020秋•嵊州市期中)直角三角形的两条直角边为3,4,则这个直角三角形斜边上的中线长为()A.5B.2.5C.3.5D.4.5【答案】B【解析】解:由勾股定理得:直角三角形的斜边长是=5,所以=2.5,故选:B.6.(2020秋•高州市期中)如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=()A.2B.3C.4D.6【答案】D【解析】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,∴AE=CE=10,∵AD=2,∴DE=8,∵CD为AB边上的高,在Rt△CDE中,CD===6,故选:D.二、填空题7.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=20,则CD=.【答案】10【解析】解:∵∠ACB=90°,CD是斜边AB上的中线,∴CD=AB=10,故答案为:10.8.如图,直角三角形ABC中,∠ACB=90°,∠B=36°,D是AB的中点,ED⊥AB交BC于E,连接CD,则∠CDE:∠ECD=.【答案】1:2.【解析】解:∵∠ACB=90°,∠B=36°,D是AB的中点,∴CD=DB,∴∠ECD=∠B=36°,∴∠CDB=180°﹣∠ECD﹣∠B=180°﹣36°﹣36°=108°,∵ED⊥AB,∴∠EDB=90°,∠CDE=∠CDB﹣∠EDB=108°﹣90°=18°,∠CDE:∠ECD=1:2.故答案为1:2.9.(2020春•南岗区校级期中)如图,已知在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB=DC.则∠BAC的度数为°.【答案】105【解析】解:取CD的中点E,连接AE,在Rt△ADC中,DE=EC,∴AE=CD=ED=EC,∴∠EAC=∠C=25°,∴∠AED=∠EAC+∠C=50°,∵AE=ED,∴∠EAD=∠EDA=65°,∵AB=DC,AE=CD,∴AB=AE,∴∠BAE=80°,∴∠BAC=∠BAE+∠EAC=105°,故答案为:105.10.在Rt△ABC中,∠ACB=90°,如果斜边AB上的中线CD=4cm,那么斜边AB=cm.【答案】8【解析】解:∵在Rt△ABC中,斜边AB上的中线CD=4cm,∴AB=2CD=8cm.故答案为:8.11.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=.【答案】90°【解析】解:连接EB、ED,∵∠ABC=90°,E是AC的中点,∴BE=AC,同理,DE=AC,∴EB=ED,又F是BD的中点,∴EF⊥BD,∴∠EFO=90°,故答案为:90°.三、解答题12.如图,在△ABC中,AB=AC,BD平分∠ABC,AD⊥BD于点D.(1)若∠C=74°,求∠BAD的度数;(2)点E为线段AB的中点,连接DE.求证:DE∥BC.【答案】(1)解:∵AB=AC,∴∠ABC=∠C=74°,∵BD平分∠ABC,∴∠ABD=∠ABC=37°,∵AD⊥BD,∴∠BAD=90°﹣37°=53°;(2)证明:在Rt△ADB中,点E为线段AB的中点,∴ED=EB∴∠EBD=∠EDB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠EDB=∠CBD,∴DE∥BC.【解析】(1)根据等腰三角形的性质得到∠ABC=∠C=74°,根据角平分线的定义、三角形内角和定理计算即可;(2)根据直角三角形的性质得到ED=EB根据等腰三角形的性质得到∠EBD=∠EDB,根据平行线的判定定理证明结论.13.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连结ED,求△EDC的面积.【答案】(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=EG.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.【解析】(1)连接DE,根据直角三角形的性质得到DE=AB=AE,根据等腰三角形的性质证明结论;(2)作EF⊥BC于F,根据题意求出BD,根据等腰三角形的性质求出DF,根据勾股定理求出EF,根据三角形的面积公式计算,得到答案.14.如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.(1)求证:DC=BE;(2)若∠AEC=72°,求∠BCE的度数.【答案】(1)证明:∵DG垂直平分CE,∴DE=DC,∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线,∴DE=BE=AB,∴DC=BE;(2)∵DE=DC,∴∠DEC=∠DCE,∴∠EDB=∠DEC+∠BCE=2∠BCE∵DE=BE∴∠B=∠EDB,∴∠B=2∠BCE,∴∠AEC=3∠BCE=72°,∴∠BCE=24°.【解析】(1)根据线段垂直平分线的性质得到DE=DC,根据直角三角形斜边上的中线是斜边的一半得到DE=BE=AB,证明结论;(2)根据等腰三角形想的性质得到∠DEC=∠DCE,根据三角形的外角性质列式计算即可.15.如图.△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,点E是BD的中点,连结AE.(1)求证:BD=2AC;(2)若AE=6.5,AD=5,那么△ABE的周长是多少?【答案】(1)证明:∵AD⊥AB,∴∠BAD=90°,又点E是BD的中点,∴EA=BD=EB,∴∠EAB=∠EBA,∴∠AEC=2∠B,又∠C=2∠B,∴∠AEC=∠C,∴AE=AC,∴BD=2AC;(2)解:∵∠BAD=90°,点E是BD的中点,∴BD=2AE=13,EA=EB=6.5,由勾股定理得,AB===12,∴△ABE的周长=AB+AE+BE=12+6.5+6.5=25.【解析】(1)根据直角三角形的性质得到EA=BD=EB,根据等腰三角形的性质和三角形的外角的性质证明;(2)根据直角三角形的性质分别求出BC和BE,根据勾股定理求出AB,根据三角形的周长公式计算.16.已知:如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:MN⊥BD.【答案】证明:连接DM,BM,∵∠ABC=∠ADC=90°,M是AC的中点,∴DM=AC,BM=AC,∴DM=BM,又N是BD的中点,∴MN⊥BD.【解析】连接DM,BM,根据直角三角形的性质得到DM=AC,BM=AC,得到DM=BM,根据等腰三角形的三线合一证明.11/ 11。
直角三角形斜边中线定理

此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!
∵BE中点F ∴∠ABD=∠DBC=∠BDF
∠DFC=∠ABC ∵∠ABC=∠C ∴∠DFC=∠C ∴DF=DC ∴DF=1/2BE ∴CD=1/2BE
如图△ABC中,∠B=2∠C,AH为高,M是BC边的中点. 求证:AB=2HM.
取AC中点D,连HD,MD ∴MD∥AB,MD=1/2AB HD=1/2AC ∴∠C=∠DHM ∴∠B=∠ADH ∠CAB=∠CDM ∴∠HDM=∠C=∠DHM ∴DM=HM ∴AB=2HM
2
延长CD至点E 连接EA、EB
如图,在△ABC中,D是BC上的点,AD=AB,点F
是BD的中点,点E是AC上一点,且AE=EF,AC=6.
求EF的ห้องสมุดไป่ตู้.
∵AF⊥BC,AE=EF ∴∠EAF=∠EFA,∠C=90°∠EFA
∠EFC=90°-∠EFA ∴∠C=∠EFC,EF=EC ∴E为AC中点,AC=6,EF=3
如图,在△ABC中,AD是高,CE是中线,DC=BE, DF⊥CE,F为垂足. 求证:(1)F是CE的中点;(2)∠B=2∠BCE.
∵DE=1/2AB=AE=BE=CD ∵DF⊥CE ∴F为BC中点
ED=BE ∴∠B=∠EDB=2∠BCE
角平分线+斜边中线
如图,在△ABC中,AB=AC ,BD平分∠ABC,BD 与AC交于点D,DE⊥BD,DE与BC交于点E,猜想并 证明BE与CD的数量关系.
中 点 的 辅 助 倍长中线 线
三线合一
中位线定理 直角三角形斜边中线定理
直角三角形斜边中线的定义
直角三角形斜边中点和直角顶点的连线 叫做直角三角形斜边中线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
B
E D
A B
A
D
C
E
B
C
A
D
“直角三角形斜边上的中线”的性质及其应用
性质:
几何语言:
相关结论:
习题重现一
1、如图,△ABC 是直角三角形, CD 是斜边AB 上的中线。
①AB=10cm,CD 的长为多少cm? ②CD=2cm ,则AB 的长为多少?
2、已知:如图,C 为AB 的中点,90AEB ADB ︒
∠=∠=,连结CD ,CE ,DE.
求证:△CDE 为等腰三角形
归纳一:有直角,有中点; 拓展提升
如图,已知△ADG 中,AB ⊥BD 于B ,CD ⊥AC 于C ,E 为AD 的中点,点F 是BC 的中点, EF 与BC 有什么位置关系?请说明理由.
习题重现二 3、如图,在△ABC 中,点D 在边BC 上,且90BAD ︒
∠=,BD=2AC, 25B ︒
∠= , 求 的
度数.
归纳二:有直角,无中点; 拓展提升
已知:如图,在Rt △ABC 中,90C ︒∠= , , AD//BC,
求证:DE=2AB
G
F
C
B C ∠ABE CBE ∠=∠2
1
E
B
D A
C
习题重现三
4、如图,已知 AB=AC ,D ,E 分别是 BC ,AC 上的中点 求证:AB=2DE
归纳三:有中点,无直角; 拓展提升
如图,在四边形ABCD 中,DC//AB ,M ,N 是AB ,DC 的中点,90A B ︒
∠+∠= 求证:1
()2
MN AB DC =-
练习
1.如图,∠ABC=∠ADC=Rt ∠,E 是AC 的中点,则( ) A 、 21∠>∠ B 、21∠<∠ C 、 21∠=∠ D 、无法判断
2. 如图,在△ABC 中,∠C=2∠B ,D 是BC 上的一点,且AD ⊥AB ,点E 是BD 的中点,连接AE ,若AE=6.5,AD=5, 则AC= △ABE 的周长是
3. 已知:如图,在△ABC 中,AD 是高,CE 是AB 边上的中线,且DC=BE . 求证:∠B=2∠BCE .
4. 已知:如图,在△ABC 中,D 是BC 上的点,AD=AB ,E 、F 分别是AC 、BD 的中点,AC=6.求EF 的长.
A
D
C。
