速度加速度矢量图解
第3.3节 用矢量方程图解法作运动分析

c
速度多边形的用途 由两点的速度求构件上任意点的速度 C A 例如,求BC中间点E的速度VE 时,bc上 中间点e为E点的影像,连接pe就是VE a p ω E B
e b
c
2、同一构件上两点加速度之间的关系 设已知角速度ω ,A点加速度,求B点的加速度 A B两点间加速度之间的关系有: A
BA
C ω B aB
2 2 2
方向:顺时针
+ω +ω +ω
4 4 4
= μ aa’b’ = μ a a’c’ = μ a b’c’ A p’ ω α aA C
B
aB
得:a’b’/ lAB=b’c’/ lBC= a’ c’/ lCA
∴△a’b’c’∽△ABC
p’a’b’c’-加速度多边形(或速度 图解), p’-极点 加速度多边形的特性: ①联接p’点和任一点的向量代表该 点在机构图中同名点的绝对加速 度,指向为p’→该点。
VB B
2
VB B
2
1
1
VB
2
2
B(B1,B2)
vB2 vB1 vB2B1
VB
1
1
A
ω1
VB B
2
VB B
2
1
1
VB
:
aB2 aB1 a k B2B1 a r B2B1
2
2
B(B1,B2)
VB
aB1 a n B1 a t B1
等速
1
1
A
ω1
④极点p’代表机构中所有加速度为零的点。 用途:根据相似性原理由两点的加速度求任 意点的加速度。 例如,求BC中间点E的加速度aE 时,b’c’上中间
高中物理加速度(共15张PPT)

关,加速度与速度变化量无直接关系,不能 只要加速度与速度的方向相同,就是加速;
定义:平均加速度指速度变化量与发生这一变化所用时间的比值.
直互判断大小关系. 加速度反映了速度变化的大小。
它表示在这段时间内速度平均变化的快慢.
第11页,共15页。
加速度方向与速度方向的关系
加速度方向与速度方向相同:速度增加即物 体做加速运动.
加速度方向与速度方向相反:速度减小即物 体做减速运动.
进一步归纳为:只要加速度的方向与速度方 向相同,物体就做加速运动;加速度的方向 与速度方向相反,物体就做减速运动;加速 度的方向与速度的方向无直接关系,不能单 从加速度的正、负来判断物体是加速还是减 速运动.必须与初速度相结合综合考虑.
第13页,共15页。
课堂练习
3.关于物体运动的加速度和速度的关系,以 下说法中正是( )B A.速度越大,加速度也一定越大。 B.速度变化很快,加速度一定很大。 C.加速度的方向保持不变,速度的方向也一 定不变。 D.加速度就是速度的增加量。
第14页,共15页。
课堂练习
4.由a=△V/△t可得与△VC成正比。 B.物体的加速度大小由△DV决定。 的方向与△V的方向相同。 D.△V/△t叫速度的变化率,就是加速度。
第10页,共15页。
速度、速度变化量与加速度的区别
的方向与△V的速方向相度同。 变化量与加速度的区别
速度、速度变化量与加速度的区别
由a=△V/△t及△V=a△t可知,加速度是速 如何判断物体做的是加速运动还是减速运动
总与初速度的方向一致。
速度是描述物体运动快慢的物理量,它等于位移于时间的比值;
度的变化率而不是速度的变化量;加速度表 哪个物体速度变化的快?怎样进行比较?
矢量方程图解法作速度加速度分析

2、作图方法
具体方法为图解矢量方程。
基础知识:一个矢量有大小和方向两个要素。
用图解的方法一个矢量方程可以求出两个未知要素(包括大小和
方向均可以)。
例题:
C B
A P
A BC
大小 ? √ ?
方向 √ √ √
A BC
大小 √ √ ?
方向 √ √ ?
二、同一构件上两点之间的速度和加速度关系
8
8
B
3
P23 (P24)
2
4
C P34
1
A P12
(b) P13
8
P23 B 3 P34
2
A P12
1
4
P24 C P14
8
(d)
P13
3
A
M P23B
Vm
P24
2 A P12
1
C4
P14 P34
8
青岛滨海学院教师教案 §3-3 用矢量方程图解法作机构的速度及加速度分析
一、矢量方程图解法的基本原理及作图法
注意:速度影像只能应用于同一构件上的各点。 总结:
1) 一个矢量方程最多只能求解两个未知量; 2) P 称为极点,它代表机构中所有构件上绝对速度为零的点;
青岛滨海学院教师教案
(速度多边形中仅此一点,它可能对应机构中多个点:机架上的点或构件的绝 对瞬心点)
3)由 P 点指向速度多边形中任一点的矢量代表该点的绝对速度大小和方 向;
们可以得到:
(B1 B2 ) B
1 2
VB2 VB1 VB2B1
青岛滨海学院教师教案
aB2
a B1
aBr 2B1
2加速度及矢量的方向性

2.加速度一、 加速度的大小 1.公式: 2.v-t 图像例1、在数学上,定义直线的斜率 k=y 2-y i /x 2-x i =tan a , a 为直线与横轴的倾斜角。
(1) 求出 K a = ____ k B = _______ k c = _________ k D = _________ (2) 从图中观察出,斜率越大则直线的倾 ~ 二、 加速度的方向1. 与速度变化方向相同 2•与速度方向可以相同(加速),可以相反(减速) 例题2•图为一物体做直线运动的 v — t 图象,则在0〜t 1和t |〜t 2时间内( )A •速度方向相同,加速度方向相同B •速度方向相同,加速度方向相反C .速度方向相反,加速度方向相同D .速度方向相反,加速度方向相反三、加速度与速度及速度变化量的关系 1 .意义上对比:2 .联系点:例题3.下列关于质点运动的速度和加速度的说法中不可能 的是()A .速度变化很大,加速度很小B .速度变化很快,加速度很小C .速度向东,加速度向西D .速度向东,加速度向北四、矢量方向的表示方法1. 做题之前规定正方向(一般规定初速度方向为正方向)2. 与正方向相同则矢量为正值,与正方向相反则矢量为负值。
3. 题目中若给的适量是大小为多少时,应考虑矢量的多种可以性 例题4.一个质点,初速度的大小为2 m/s ,末速度的大小为 4 m/s ,贝U ()A .速度改变量的大小可能是 8 m/sB .速度改变量的大小可能是 1 m/sC .速度改变量的方向可能与初速度方向相同D .速度改变量的方向可能与初速度方向相反 练习1 .关于做直线运动的物体的加速度方向,下列判断正确的是 ( ) A.加速度的方向就是速度的方向 B .加速度的方向就是位移的方向 C. 当物体做加速运动时,加速度的方向与速度的方向相同 D. 当物体做减速运动时,加速度的方向与速度的方向相同 2. 关于加速度的概念,下列说法正确的是 ( ) A.加速度就是加出来的速度 B .加速度反映了速度变化的大小 C.加速度反映了速度变化的快慢 D .加速度为正值,表示速度的大小一定越来越大3. 如图所示是汽车中的速度计,某同学在汽车中观察速度计指针位置的变化,开始时指针指示在如图甲所示的位置, 经过5s 后指针指示在如图乙所示的位置,若汽车做匀加速直线运动,那么它在这 段时间内的加速度大小约为 ( )2 2A. 8.0 m/sB. 5.1 m/s _ 2 2C. 2.2 m/sD. 1.6 m/s4.关于速度与加速度的说法,错误的是 ( A.速度增大时,加速度不一定增大 B. C.速度改变量越大,加速度越大D.5.某物体以2 m/s 2的加速度做匀加速直线运动,则该物体( )A.任意1s 的末速度都是该1s 初速度的2倍B .任意1s 的末速度都比该 C.任意1s 内的平均速度都比前 1s 内的平均速度大 2m/s D.任意1s 的初速度都比前1s 的末速度大2m/s 6.两物体都作匀变速直线运动,在给定的时间间隔内,位移的大小决定于( )A.谁的加速度越大,谁的位移一定越大;B.谁的初速度越大,谁的位移一定越大;C.谁的末速度越大,谁的位移一定越大;D.谁的平均速度越大,谁的位移一定越大7. 我们知道,要拍打蚊子不是一件容易的事,当我们看准蚊子停留的位置,拍打下去时,蚊子早就不知飞向何方了, 这是因为蚊子在感受到突然袭击而飞走时,具有很大的( )A.速度 B .加速度 C .速度的改变量 D .位移&甲、乙两个物体沿同一直线向同一方向运动时,取物体的初速度方向为正,甲的加速度恒为 为一31s 初速度大2m/s)速度减小时,加速度不一定减小 加速度与速度的大小及方向无关2 m/s 2,乙的加速度恒|k「n/h|200220Q 160 • 60^ W '20 200 0 恢 m/hl 220m/s2,则下列说法中正确的是()A .两物体都做加速直线运动,乙的速度变化快B .甲做加速直线运动,它的速度变化快C.乙做减速直线运动,它的速度变化率大 D .甲的加速度比乙的加速度大9. 一个质点做方向不变的直线运动,加速度的方向始终与速度方向相同,但加速度大小逐渐减小直至为零,在此过程中()A .速度逐渐减小,当加速度减小到零时,速度达到最小值B .速度逐渐增大,当加速度减小到零时,速度达到最大值C.位移逐渐减小,当加速度减小到零吋,位移将不再减小D .位移逐渐增大,当加速度减小到零时,位移将不再增大10. 一质点以初速度v o沿x轴正方向运动,已知加速度方向沿x轴正方向,在加速度a的值由零逐渐增大到某一值后再逐渐减小到零的过程中,该质点()A .速度先增大后减小直到加速度等于零为止B .速度一直在增大直到加速度等于零为止C.位移先增大后减小直到加速度等于零为止 D .位移一直在增大直到加速度等于零为止11. 火车紧急刹车时,在30 s内速度从108 km/h均匀减小到零,求此过程中火车的加速度。
用矢量方程图解法作机构的速度及加速度分析

b2
ω3=v pb3/LBC,顺时针方向
加速度关系a ① 加速度关系
A
r B3B2
aB3 = a
大小 方向 ak
n B3
+a
t B3
= aB2 + a
+a
k B3B2
1 2 B
ω1
? ω23LBC ? ω21LAB ? 2vB3B2ω3 ? B→C ⊥CB B→A // //BC √ 转过90 沿ω3转过 °
方程不可解 方程可解 G C F E
D
vG = vB + vGB = vC + vGC = vG 大小 ? √ ? ? √ ? 方向 ? √ √ √ √ ?
● 重合点应选已知参数较多的点(一般为铰链点) 。 重合点应选已知参数较多的点(一般为铰链点) 选C点为重合点 点为重合点 v C 3 = v C 4 + v C 3C 4 ? ? 大小 ? 方向 ? √ √
c b
p
角速度 ω=vBA/LBA=v ab/l AB,顺时针方向 / , 同理 ω=v ca/l CA / ω=v cb/lCB / 因此 ab/AB=bc/BC=ca/CA / / / 于是 abc∽ABC
速度多边形 c b 速度极点 速度零点) (速度零点) C A
ω
a
B
p
●
●
●
●
速度多边形( 速度多边形(Velocity polygon)的性质 ) 联接p点和任一点的向量代表该点在 联接 点和任一点的向量代表该点在 机构图中同名点的绝对速度, 机构图中同名点的绝对速度 , 指向 C 为p→该点。 →该点。 A 联接任意两点的向量代表该两点 ω 机构图中同名点的相对速度, 在 机构图中同名点的相对速度 , 指向与速度的下标相反。 指向与速度的下标相反 。 如 bc代 代 a 表 vCB 而不是vBC 。 常用相对速度 而不是 来求构件的角速度。 来求构件的角速度。 abc∽ABC,称abc为ABC的速 ∽ , 为 的速 c 度影像( ) 度影像(Velocity image),两者相似 b 且字母顺序一致, 且字母顺序一致 , 前者沿 ω方向转 过90。 速度极点 极点p代表机构中所有速度为 速度极点 代表机构中所有速度为 零的点的影像。 零的点的影像。
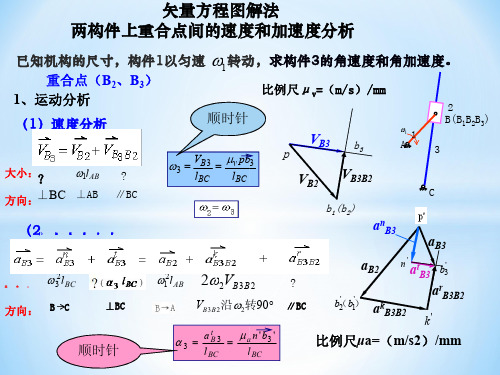
机械原理(2015春)矢量方程图解法 两构件上重合点间的速度和加速度分析
a = a + a + a 则
k
r
c1
c2
c1c2
c1c2
w a = 2 V k
c1c2
2 c1c2
4 例题:已知构件1的运动,求: vC 、vD及 w2、w5和a5
(1)速度分析
v D = v B + v DB
大小 ? √
?
方向 ? √
√
v C = v B + v CB
?
√
?
√
√
√
vC = mv pc (m s) vCB = mv bc (m s)
.
p
VB3
b3
VB2
VB3B2
b1(b2)
w1 1
A
3
C
(2)
加
速
度
分
析
a n B3 a B3
大
小
:
w 32 l BC
方向: B C
⊥BC
顺时针
w12l AB
2w2VB 3 B 2
VB 3 B 2沿w 2转90°
a3
=
a
t B
3
l BC
=
m a n 'b3 ' l BC
?
∥BC
a B2
n ' atB3 b3'
当牵连运动为平动( w1 = 0)则无科氏加速度。
v CB = w 2 l BC
p w 2
=
v CB l BC
=
m v bc l BC
(逆)
这里用速度影像求vD
选重合点:E(E4、E5)
VC
VD d
VB
b
加速度、s-t图像和v-t图像

精心整理高一秋季第二次课加速度、s-t图像和v-t图像1加速度:表示速度改变快慢的物理量,它等于速度的变化量与发生这一变化所用时间的比值2表达式:a=△v/△t=(vt -v)/t(vt表示末速度,v表示初速度)3单位:m/s2或m.s-24矢量性:加速度的方向与速度变化量△v的方向相同5a=△v/△t所求的应是△t内的平均加速度,若△t很短,也可近似看成瞬时加速度1物体做直线运动的加速度大小、方向都不变,这种运动叫做2分为:匀加速直线运动和匀减速直线运动取初速度方向为正时:vt >v,a>0,加速度为正,表示加速度方向与初速度方向相同;vt <v,a<0,加速度为负,表示加速度方向与初速度方向相反。
3匀变速直线运动的特点:(1)加速度大小、方向都不变(2)加速度不变,所以相等时间内速度的变化一定相同△v=a△t(3)在这种运动中,平均加速度与瞬时加速度相等1.下列说法中正确的是()A.物体有加速度,其速度一定变大B.物体的加速度越大,其速度一定越大C.物体的加速度越大,其速度变化越快D.物体的加速度越大,其速度变化越大2.做匀变速直线运动的物体,其加速度的方向()A.与初速度方向相同B.与末速度方向相同C.与运动方向相同D.与速度变化量的方向相同3.甲、乙两个物体在同一直线上沿正方向运动,判断正确的是()A.甲的加速度小于乙的加速度B.甲做匀加速直线运动,乙做匀减速直线运动C.甲的速度比乙的速度变化慢D.甲、乙在不相等时间内速度变化可能相等4A.物体在某时刻运动速度很大,而加速度为零B.物体在某时刻运动速度很小,而加速度很大CD5.ABCD6)ABCD73m/s,经过1s后速度大小为4m/s,该质点的A.1m/s2B.3m/s2C.5m/s2D.7m/s28.某物体做变速直线运动,其加速度方向不变,大小逐渐减小到零,该物体的运动情况可能是()A.速度不断增大,最后达到最大,并以此速度做匀速直线运动B.速度不断减小,最后达到最小,并以此速度做匀速直线运动C.速度不断减小,又不断增大,最后做匀速直线运动D.速度不断增大,又不断减小,最后做匀速直线运动9.做匀加速直线运动的物体,加速度为2m/s2,它的意义是()A.物体在任一秒末的速度是该秒初的速度的2倍B.物体在任一秒末速度比该秒初的速度大2m/sC.物体在任一秒的初速度比前一秒的末速度大2m/sD.物体在任一秒的末速度比前一秒的初速度大2m/s10.物体正在沿x轴做直线运动,可能出现的情况是()A.加速度沿+x方向逐渐增大,速度沿+x方向逐渐减小B.加速度沿+x方向逐渐减小,速度沿+x方向逐渐减小C.加速度沿-x方向逐渐增大,速度沿-x方向逐渐减小D.加速度沿-x方向逐渐减小,速度沿-x方向逐渐增大11.根据给出的速度、加速度的正负,对下列运动性质的判断不正确的是()A.v0<0,a<0,物体做加速运动B.v0<0,a>0,物体先做加速运动,后做减速运动C.v0>0,a<0,物体先做减速运动,后做加速运动D.v0>0,a=0,物体做匀速运动知识点二、图像一、s-t图像(t轴表示时间,s轴表示位移)1.斜率:表示速度;斜率越大,速度越大;1.如图是做直线运动的甲、乙物体的位移—时间图象,由图象可知错误的是()A.甲起动的时间比乙早t1秒B.当t=t2时两物体相遇C.当t=t2时两物体相距最远D.当t=t3时两物体相距S0米2.某质点沿东西方向做直线运动,其位移~时间图象如右图所示。
矢量方程图解法作速度加速度分析

青 岛 滨 海 学 院 教 师 教 案 课 题 教 学 目 的 要 求 教 学 重 点 教 学 难 点
C B A
A BC
大小 ? √ ? 方向 √ √ √
P
A BC
大小 √ √ ? 方向 √ √ ? 二、同一构件上两点之间的速度和加速度关系 已知:四杆机构 ABCDE 机构的位置如图所示,各个构件的长度已知,原 动件 1 的角速度 1 ,求: VC 、 VE 、 a C 、 a E 、 2 、 3 、 2 、 3 ?
青 岛 滨 海 学 院 教 师 教 案
解:1、求速度和角速度
VC VB VCB
大小 ? lABω ? 方向 ⊥CD ⊥AB ⊥BC → VC
VE VB VEB VC VEC
大小 方向 ?
1l AB ?
√
? → VE
? √
⊥BE √ ⊥EC
2
VCB V , 方向:顺时针 3 C ,,逆时针 (方向判定采用矢量平移) l BC lCD
4
2
4 2 a EC l EC 2 2
∴ aCB : a EB : a EC lCB : l EB : l EC
∴ bc : be : ce BC : EB : EC 即 bce 和 BCE 相似, 称 bce 为
BCE 的加速度影像。 注意:只用于同一构件上。 小结:首先讲解上次作业中出现问题较多的部分;然后讲授矢量方程图解 法的基本原理和作图方法,接着用例题讲解了同一构件上两点之间的速度和加 速度关系的求解方法和步骤。 作业:P44 3-6 (利用 3-6 原题的已知条件,采用这节课讲解的矢量方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若求w1,即 的方向
量出 若待求w1: 的方向 。
量出
总结:
注:在哥氏加速度中的W 具体指的是相对的还是绝对的?(后边跟大家讲)
(3)w 是由速度求出的
(4)比例尺=实际尺寸/图上尺寸
两种:做机构示意图的简图 做矢量图(速度 加速度)加速度:
其中 故 W 恒定 则
(1)法向加速度公式: 所以反过来看W 是否可求?切向加速度公式 只
能未知 切向求
(2)一个等式必须首尾相接或者看角标来连线 (其实首尾相接更可靠)
二、速度、加速度影像
(1)、影像别名为相似图形 故满足对应角相等 对应边成比例(作图技巧) 且对应字母顺序一致
(2)、同一构件 (相似保证了它是刚体)(考判断)
一、基础知识:
若已知w1,方向与w1转向一致
做图:P 点出发 沿着 的方向做出 若:w1已知 方向与w1转向一致 做图: 从 出发 沿着 的方向做出:
注:这里的 若以B 为参考点 就是 若以D 为参考
点
试写出: ?
?矢量图解(1)
2020年4月14日22:31
讨论:
(1)形成三点不共线的影像:转向一样 利用相似=角度相同
(2)形成三点共线的影像:对应边成比例时一定注意对应起点 (3)若矢量图中量出“长度=0” 则会出现“点集中”
注意:图形选择:选择已知量对应的点的图形 例如:求C 求C。
