1998年全国高考
1998年全国高考试卷及答案
1998年普通高等学校招生全国统一考试物理测试一、本题共12小题;每小题5分,共60分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。
全部选对的得5分,选不全的得2分,有选错或不答的得0分。
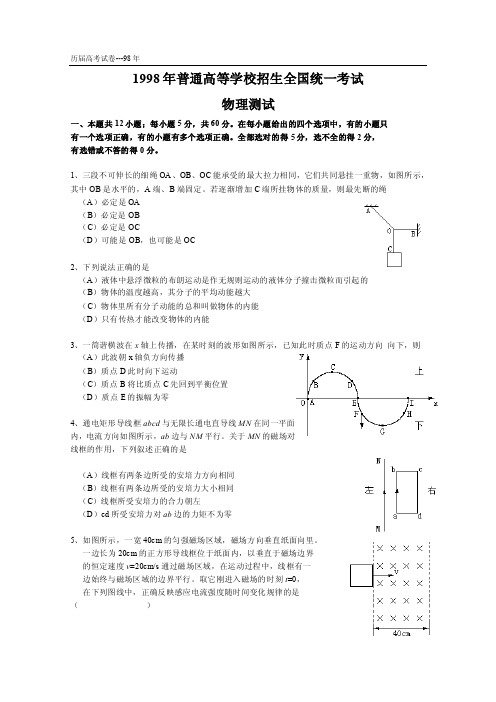
1、三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB是水平的,A端、B端固定。
若逐渐增加C端所挂物体的质量,则最先断的绳(A)必定是OA(B)必定是OB(C)必定是OC(D)可能是OB,也可能是OC2、下列说法正确的是(A)液体中悬浮微粒的布朗运动是作无规则运动的液体分子撞击微粒而引起的(B)物体的温度越高,其分子的平均动能越大(C)物体里所有分子动能的总和叫做物体的内能(D)只有传热才能改变物体的内能3、一简谐横波在x轴上传播,在某时刻的波形如图所示,已知此时质点F的运动方向向下,则(A)此波朝x轴负方向传播(B)质点D此时向下运动(C)质点B将比质点C先回到平衡位置(D)质点E的振幅为零4、通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与NM平行。
关于MN的磁场对线框的作用,下列叙述正确的是(A)线框有两条边所受的安培力方向相同(B)线框有两条边所受的安培力大小相同(C)线框所受安培力的合力朝左(D)cd所受安培力对ab边的力矩不为零5、如图所示,一宽40cm的匀强磁场区域,磁场方向垂直纸面向里。
一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行。
取它刚进入磁场的时刻t=0,在下列图线中,正确反映感应电流强度随时间变化规律的是()6、天然放射性元素Th(钍)经过一系列α衰变和β衰变之后,变成Pb(铅)。
下列论断中正确的是(A)铅核比钍核少24个中子(B)铅核比钍核少8个质子(C)衰变过程中共有4次α衰变和8次β衰变(D)衰变过程中共有6次α衰变和4次β衰变7、一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,金属球上感应电荷产生的电场在球内直径上a、b、c三点的场强大小分别为E a、E b、E c,三者相比,(A)E a最大(B)E b最大(C)E c最大(D)E a=E b=E c8、一细束平行光经玻璃三棱镜折射后分解为互相分离的三束光,分别照射到相同的金属板a、b、c上,如图所示。
1998年高考

1998年高考1998年,是中国高考历史上一个重要的年份。
这一年,无数学子为了实现自己的人生梦想而奋斗着。
回顾1998年的高考,可以说是一部略带曲折的史诗。
无数学子提前一年就开始准备,努力备战。
他们在各个角落的考试辅导班中汗水如雨,他们每晚熬夜背诵各种知识点,他们为了获得一份满意的成绩而忍受着各种压力。
考场上,学子们紧张而又充满期待地迈入考场。
这是一个决定他们未来的舞台,他们在这个瞬间,感受到了前所未有的压力和挑战。
但是他们坚定地面对着,一道道题目被他们解决,一篇篇作文被他们完成,他们用自己的努力去书写人生。
在1998年的高考中,许多学子们遇到了各种困难和挫折。
有的因为生病而错过了考试,有的因为紧张而无法集中注意力,有的因为面对考题而觉得无从下手。
然而,这些困难并没有阻挡他们前进的脚步。
他们用自己那颗坚毅的心去克服困难,勇往直前。
终于,1998年高考落下帷幕。
学子们背负着自己满意或遗憾的成绩走出考场,面对未来的选择和挑战。
他们用自己的努力,用自己的汗水,为未来的人生打下了坚实的基础。
1998年的高考,是一个充满回忆的年份。
对于那些经历过考场的人们来说,这一年将会永远留在他们的记忆中。
那时的他们,年轻而富有朝气,他们在考场上奋斗着,为了自己的梦想。
如今,已经过去了二十多年。
那些参加当年高考的学子们,早已步入了各自的人生道路。
他们或许成为了医生、工程师、教师,或许成为了企业家、演员、作家。
无论他们走向何方,都会牢牢记得,那个充满挑战的1998年。
1998年的高考,是一段浓缩的人生经历。
在这个历史节点上,一代学子们用青春和梦想,书写了属于自己的辉煌篇章。
无论结果如何,他们都是伟大的,因为他们敢于追求梦想,勇敢面对困难。
或许,这篇文章里没有明确的标题,但是无法掩饰的是那个年代特有的精神和情感。
那是一群年轻人的青春年华,在历经了高考这一道艰难的考验后,他们终将展翅高飞。
1998年试题全国高考数学试题及参考答案
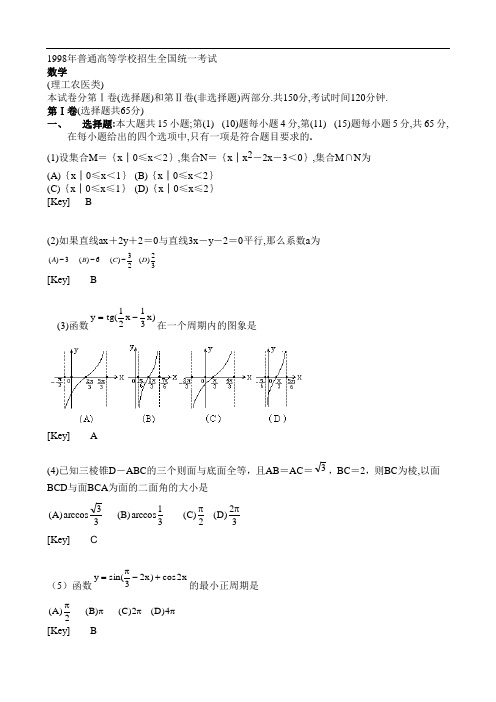
1998年普通高等学校招生全国统一考试 数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟. 第Ⅰ卷(选择题共65分)一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合M ={x │0≤x <2},集合N ={x │x 2-2x -3<0},集合M ∩N 为 (A){x │0≤x <1} (B){x │0≤x <2} (C){x │0≤x ≤1} (D){x │0≤x ≤2} [Key] B(2)如果直线ax +2y +2=0与直线3x -y -2=0平行,那么系数a 为32)(23)(6)(3)(D C B A ---[Key] B(3)函数)x 31x 21(tg y -=在一个周期内的图象是[Key] A(4)已知三棱锥D -ABC 的三个则面与底面全等,且AB =AC =3,BC =2,则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是32)D (2)C (31arccos)B (33arccos)A (ππ[Key] C(5)函数x2cos )x 23sin(y +-π=的最小正周期是 ππππ4)D (2)C ()B (2)A ([Key] B(6)满足arccos(1-x)≥arccosx 的x 的取值范围是]1,21)[(]21,0)[(]0,21)[(]21,1)[(D C B A --[Key] D(7)将y =2x 的图象(A)先向左平行移动1个单位 (B)先向右平行移动1个单位 (C)先向上平行移动1个单位 (D)先向下平行移动1个单位 再作关于直线y =x 对称的图象,可得到函数y =log 2(x +1)的图象.[Key] D(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是ππππ200)(50)(225)(220)(D C B A[Key] C(9)曲线的参数方程⎪⎩⎪⎨⎧-=-=2111t y tx (t 是参数,t ≠0),它的普通方程是 11)(1)1(1)()1()2()(1)1()1)((2222+-=--=--==--x xy D x y C x x x y B y x A[Key] B(10)函数y =cos 2x -3cosx +2的最小值为6)(41)(0)(2)(D C B A -[Key] B(11)椭圆C 与14)2(9)3(22=-+-y x 椭圆关于直线x +y =0对称,椭圆C 的方程是 (A) 19)3(4)2(22=+++y x (B) 14)3(9)2(22=-+-y x(C) 14)3(9)2(22=+++y x (D) 19)3(4)2(22=-+-y x[Key] A(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是337)(637)(32)(332)(ππππD C B A[Key] D(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式 ①f(b)-f(-a)>g(a)-g(-b); ②f(b)-f(-a)<g(a)-g(-b); ③f(a)-f(-b)>g(b)-g(-a); ④f(a)-f(-b)<g(b)-g(-a), 其中成立的是(A)①与④ (B)②与③ (C)①与③ (D)②与④ [Key] C(14)不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是 (){}20<<x x A (){}5.20<<x x B (){}60<<x x C (){}30<<x x D[Key] C(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有 (A)150种 (B)147种 (C)144种 (D)141种[Key] D(16)已知92⎪⎪⎭⎫⎝⎛-x x a 的展开式中x 3的系数为49,常数a 的值为_________. [Key] 4(17)已知直线的极坐标方程22)4sin(=+πθρ则极点到该直线的距离是_______。
1998年全国高考数学试题

1998年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题共65分)一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合M={x │0≤x<2},集合N={x │x 2-2x-3<0},集合M ∩N 为(A){x │0≤x<1} (B){x │0≤x<2}(C){x │0≤x ≤1} (D){x │0≤x ≤2}[Key] B(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a 为32)(23)(6)(3)(D C B A ---[Key] B(3)函数)x 31x 21(tg y -=在一个周期内的图象是[Key] A(4)已知三棱锥D-ABC 的三个则面与底面全等,且AB=AC=3,BC=2,则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是32)D (2)C (31arccos )B (33arccos )A (ππ[Key] C(5)函数x 2cos )x 23sin(y +-π=的最小正周期是ππππ4)D (2)C ()B (2)A ([Key] B(6)满足arccos(1-x)≥arccosx 的x 的取值范围是]1,21)[(]21,0)[(]0,21)[(]21,1)[(D C B A --[Key] D(7)将y=2x 的图象(A)先向左平行移动1个单位 (B)先向右平行移动1个单位(C)先向上平行移动1个单位 (D)先向下平行移动1个单位再作关于直线y=x 对称的图象,可得到函数y=log 2(x+1)的图象.[Key] D(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是ππππ200)(50)(225)(220)(D C B A[Key] C(9)曲线的参数方程⎪⎩⎪⎨⎧-=-=2111t y t x (t 是参数,t ≠0),它的普通方程是11)(1)1(1)()1()2()(1)1()1)((2222+-=--=--==--x x y D x y C x x x y B y x A[Key] B(10)函数y=cos 2x-3cosx+2的最小值为6)(41)(0)(2)(D C B A -[Key] B(11)椭圆C 与14)2(9)3(22=-+-y x 椭圆关于直线x+y=0对称,椭圆C 的方程是 (A) 19)3(4)2(22=+++y x(B) 14)3(9)2(22=-+-y x (C) 14)3(9)2(22=+++y x (D) 19)3(4)2(22=-+-y x[Key] A(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是337)(637)(32)(332)(ππππD C B A[Key] D(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式①f(b)-f(-a)>g(a)-g(-b); ②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a); ④f(a)-f(-b)<g(b)-g(-a),其中成立的是(A)①与④ (B)②与③ (C)①与③ (D)②与④[Key] C(14)不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是 (){}20<<x x A (){}5.20<<x x B (){}60<<x x C (){}30<<x x D[Key] C(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有(A)150种 (B)147种 (C)144种 (D)141种[Key] D(16)已知92⎪⎪⎭⎫ ⎝⎛-x x a 的展开式中x 3的系数为49,常数a 的值为_________. [Key] 4(17)已知直线的极坐标方程22)4sin(=+πθρ则极点到该直线的距离是_______。
1998年全国高考历史试题及其参考答案

1998年全国高考历史试题及其参考答案一、选择题:本大题共34小题,每小题1.5分,共51分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
1、半坡人和河姆渡人生活的共同点是A、普遍使用打制石器B、制造陶器C、种植栗、水稻D、饲养猪、水牛2、屈原被楚王流放的主要原因是A、反对君主专制B、要求革新图强C、主张抵抗秦军D、《离骚》触怒权贵3、下列我国古代衣着织物三种原料使用的先后顺序是A、丝棉麻B、麻棉丝C、丝麻棉D、麻丝棉4、下列战国时期的城市中,既是诸侯国都城又是冶铁中心的是A、邯郸B、大梁C、临淄D、宛5、中央政府管辖玉门关和阳关以西、天山南北地区最早的行政、军事机构是A、黑水都督府B、西域都护府C、北庭都护府D、安西都护府6、唐太宗说:“自古皆贵中华,贱夷狄,朕独爱之如一。
”他在位期间最能体现这一思想的重大举措是①与叶蕃和亲,送去手工业品和医药、生产技术书籍②在东突厥建都督府,由突厥人自己管理③册封皮罗阁为云南王,把手工业技术传到南诏④接待渤海人来长安学习汉族文化A、①②B、①③C、②③④D、①②③④7、右图所示犁耕法始见于A、春秋B、战国C、西汉D、唐8、元朝漕运路线最北的一段河道是A、广通渠B、通惠河C、会通河D、胶莱河9、《资政新篇》没有实行的根本原因是A、太平天国是农民革命政权B、处于紧张的战争环境C、太平天国未能推翻清政权D、缺乏必要的社会条件10、下列对中法战争和中日甲午战争结局相同之处的表述,不正确的是A、中国战败,被迫签订不平等条约B、清政府妥协退让,导致丧权辱国C、中国对交战方输华货物的税率给予优惠D、中国允许交战方在规定范围内对华投资11、戊戌变法运动突出的历史功绩在于A、挽救民族危亡B、推动政治改革C、发展社会经济D、促进思想启蒙12、下列对义和团“扶清灭洋”的口号的评价,不正确的是A、具有朴素的爱国意识B、带有笼统排外性质C、导致对清政府放松警惕D、反映了中国社会的主要矛盾13、保路运动的主要目的是A、要求铁路干线改为商办B、收回用于筑路的股款C、收回被清政府出卖的铁路权利D、反对举借外债举办铁路14、下列各国,在鸦片战争后割占过中国领土的有①英国②法国③德国④俄国⑤日本A、①④⑤B、①③④⑤C、①②④⑤D、①②③④⑤15、第一次国共合作得以实现的条件有①中国共产党需要团结各种力量作为革命同盟军②中国国民党在各政党中“比较是革命的民族派”③共产国际提出了实行国共合作的建议④“打倒列强除军阀”成为全国人民的共同愿望A、①②B、①②③C、①②④D、①②③④16、下列事件发生的先后顺序是①西安事变②一·二八抗战③华北事变④一二·九运动A、③④②①B、④②①③C、②③④①D、①②④③17、井冈山根据地的建立与巩固A、开辟了农村包围城市、武装夺取政权的道路B、是土地革命战争时期开始的标志C、是中国共产党独立领导武装斗争的开端D、确立了党对军队的绝对领导18、下列各项,周恩来直接领导或参加的是①上海工人第三次武装起义②南昌起义③广州起义④八七会议⑤红军第四次反“围剿”⑥遵义会议A、①②⑤⑥B、②③⑤⑥C、①③④⑥D、①②③④19、百团大战作战区域涉及的主要抗日根据地是A、陕甘宁、晋绥、晋冀豫B、晋冀豫、晋绥、晋察冀C、陕甘宁、山东、晋察冀D、晋察冀、山东、晋冀豫20、1946年制定的《中华民国宪法》是伪宪法,因为A、它直接恶化了国共关系B、国民党召开“国民大会”是非法的C、违反《和平建国纲领》D、它旨在使蒋介石独裁统治合法化21、建国以后,人民政府没收国民政府财产和官僚资本,这一措施A、兼有旧民主主义革命和新民主主义革命性质B、属于新民主主义革命性质C、兼有新民主主义革命和社会主义革命性质D、属于社会主义革命性质22、邓小平说:“一九七七年和一九七八年,中国还处于徘徊状态。
1998年高考部分试题

1998年普通高等学校招生全国统一考试英语National Matriculation English Test(NMET 98)本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至13页。
第二卷1至4页。
共150分。
考试时间120分钟。
第一卷(三大题,共95分)注意事项:1.答第一卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
3.考试结束后,考生将本试卷和答题卡一并交回。
Ⅰ. 单项填空(共25小题,每小题1分;满分25分)A)从A 、B、C、D中找出其划线部分与所给单词的划线部分读音相同的选项。
例:haveA. gaveB. saveC. hatD. made答案是C。
1.proveA. stoneB. routeC. stoveD. hook2. anxiousA. branchB. conclusionC. dangerousD. tongue3. breatheA. healthB. deafC. increaseD. pleasure4. achieveA. researchB. chemistC. techniqueD. stomach5. silverA. silentB. prettyC. tinyD. rejectB)从A、B、C、D四个选项中,选出可以填入空白处的最佳答案。
例:We ______ last night, but we went to the concert instead.A. must have studiedB. might studyC. should have studiedD. would study答案是C。
6.—Can you come on Monday or Tuesday?—I‟m afraid _____ day is possible.A. eitherB. neitherC. someD. any7. —You haven‟t been to Beijing, have you?—______. How I wish to go there!A. Yes, I haveB. Yes, I haven‟tC. No, I haveD. No, I haven‟t8. I hate ____ when people talk with their mouths full.A. itB. thatC. theseD. them9. Dr. Black comes from either Oxford or Cambridge, I ca n‟t remember ______.C. whichD. that10. —Nancy is not coming tonight.—But she _______!A. promiseB. promisedC. will promiseD. had promised11. If I had ______, I‟d visit Europe, stopping at all the small interesting place.A. a long enough holidayB. an enough long holidayC. a holiday enough longD. a long holiday enough12. Nobody noticed the thief slip into the house because the lights happened to ____.A. be put upB. give inC. be turned onD. go out13. —When can I come for the photos? I need them tomorrow afternoon.—They ____ be ready by 12:00.A. canB. shouldC. mightD. need14. Professor White has written some short stories, but he is ______ known for his plays.A. the bestB. moreC. betterD. the most15. —Can I get you a cup of tea?—_______.A. That‟s very nice of youB. With pleasureC. You can, pleaseD. Thank you for the tea16. Why do you want a new job _____ you‟ve got such a good one already?A. thatB. whereC. whichD. when17. They ______ the train until it disappeared in the distance.A. sawB. watchedC. noticedD. observed18. _____ it with me and I‟ll see what I can do.A. When leftB. LeavingC. If you leaveD. Leave19. —I stayed at a hotel while in New York.—Oh, did you? You ______ with Barbara.A. could have stayedB. could stayC. would stayD. must have stayed20. Shirley _____ a book about China last year but I don‟t know whether she has finished it.A. has writtenB. wroteC. had writtenD. was writing21. You‟ll find this map of great _____ in helping you to get round London.A. priceB. costC. valueD. usefulness22. It was only when I reread his poems recently ______ I began to appreciate their beauty.A. untilB. that23. Cleaning women in big cities usually get ____ by the hour.A. payB. payingC. paidD. to pay24. —Hi, Tracy, you look tired.—I am tired. I _____ the living room all day.A. paintedB. had paintedC. have been paintingD. have painted25. European football is played in 80 countries, _____ it the most popular sport in the world.A. makingB. makesC. madeD. to makeⅡ. 完形填空(共25小题,每小题1分;满分25分)阅读下面短文,掌握其大意,然后从26~50各题所给的四个选项中,选出一个最佳答案。
1998年全国卷高考文科数学真题及答案
1998年全国卷高考文科数学真题及答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试120分钟.第Ⅰ卷(选择题共65分)一.选择题:本大题共15小题;第(1)-(10)题每小题4分,第(11)-第(15)题每小题5分,65分.在每小题给出四项选项,只一项符合题目要求的(1) sin600º( )(A)21 (B) -21 (C) 23 (D) -23 (2) 函数y =a |x |(a >1)的图像是 ( )(3) 已知直线x =a (a >0)和圆(x -1)2+y 2=4相切,那么a 的值是( )(A) 5 (B) 4 (C) 3 (D) 2 (4) 两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直的充要条件是( )(A) A 1A 2+B 1B 2=0 (B) A 1A 2-B 1B 2=0 (C)12121-=B B A A (D) 12121=A A BB (5) 函数f (x )=x1( x ≠0)的反函数f -1(x )= ( ) (A) x (x ≠0) (B) x 1(x ≠0) (C) -x (x ≠0) (D) -x 1(x ≠0)(6) 已知点P(sin α-cos α,tg α)在第一象限,则[ 0,2π]内α的取值范围是 ( )(A) (432ππ,)∪(45ππ,) (B) (24ππ,)∪(45ππ,) (C) (432ππ,)∪(2325ππ,) (D) (24ππ,)∪(ππ,43) (7) 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面积展开图扇形的圆心角为( )(A) 120º (B) 150º (C) 180º (D) 240º (8) 复数-i 的一个立方根是i ,它的另外两个立方根是( )(A)2123±I (B) -2123±I (C) ±2123+I (D)±2123-i(9) 如果棱台的两底面积是S,S′,中截面的面积是S0,那么( )(A) 2SSS'+=(B) S0=SS'(C) 2S0=S+S′(D) SSS'=22(10) 2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共( )(A) 6种 (B) 12种 (C) 18种 (D) 24种(11) 向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图像如右图所示,那么水瓶的形状是( )(12) 椭圆31222yx+=1的焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是( )(A) ±43(B) ±23(C) ±22(D) ±43(13) 球面上有3个点,其中任意两点的球面距离都等于大圆周长为61,经过这3个点的小圆的周长为4π,那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D) 3(14) 一个直角三角形三内角的正弦值成等比数列,其最小内角的正弦值为( )(A)251-(B)2252-(C)215-(D)2252+(15) 等比数列{a n}的公比为-21,前n项的和S n满足∞→nlim S n=11a,那么11a的值为( )(A)3± (B)±23 (C) 2± (D) 26± 二.填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.(16) 设圆过双曲线116922=-y x 的一个顶点和一个焦点,圆心在双曲线上,则圆心到双曲线中心距离是__________(17) (x +2)10(x 2-1)的展开的x 10系数为____________(用数字作答)(18) 如图,在直四棱柱A 1B 1C 1D 1-ABCD 中,当底面四边形ABCD 满足条件____________时,有A 1C ⊥B 1D 1.(注:填上你认为正确的一种条件即可,不必考试所有可能的情形)(19) 关于函数f (x )=4sin(2x +3π)(x ∈R ),有下列命题 ①y =f (x )的表达式可改写为y =4cos(2x -6π);②y =f (x )是以2π为最小正周期的周期函数;③y =f (x )的图像关于点⎪⎭⎫⎝⎛-06,π对称; ④y =f (x )的图像关于直线x =-6π对称.其中正确的命题的序号是______ (注:把你认为正确的命题的序号都.填上.) 三.解答题:本大题共6小题;共69分.解答应写出文字说明、证明过程或演算步骤. (20) (本小题满分10分)设a ≠b ,解关于x 的不等式a 2x +b 2(1-x )≥[ax +b (1-x )]2.21) (本小题满分11分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,设a +c =2b ,A -C=3π,求sin B 的值.以下公式供解题时参考:2cos2sin2sin sin ϕθϕθϕθ-+=+, 2sin2cos2sin sin ϕθϕθϕθ-+=-,2cos 2cos 2cos cos ϕθϕθϕθ-+=+, 2sin 2sin 2cos cos ϕθϕθϕθ-+-=-.(22) (本小题满分12分)如图,直线l 1和l 2相交于点M ,l 1 ⊥l 2,点N ∈l 1.以A 、B 为端点的曲线段C 上的任一点到l 2的距离与到点N 的距离相等.若△AMN 为锐角三角形,|AM |=17,|AN |=3,且|BN |=6.建立适当的坐标系,求曲线C 的方程.(23) (本小题满分12分)已知斜三棱柱ABC -A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直,∠ABC =90º,BC =2,AC=23,且AA 1 ⊥A 1C ,AA 1= A 1 C 1.(Ⅰ)求侧棱A 1A 与底面ABC 所成角的大小; (Ⅱ)求侧面A 1 ABB 1 与底面ABC 所成二面角的大小; (Ⅲ)求侧棱B 1B 和侧面A 1 ACC 1的距离.(24) (本小题满分12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱.污水从A 孔流入,经沉淀后从B 孔流出.设箱体的长度为a 米,高度为b 米.已知流出的水中该杂质的质量分数与a ,b 的乘积ab 成反比.现有制箱材料60平方米.问当a ,b 各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A 、B 孔的面积忽略不计).(25) (本小题满分12分)已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=100. (Ⅰ)求数列{b n }的能项b n ; (Ⅱ)设数列{a n }的通项a n =lg(1+nb 1),记S n 是数列{a n }的前n 项的和.试比较S n 与21lg b n +1的大小,并证明你的结论.1998年普通高等学校招生全国统一考试 数学试题(文史类)参考解答及评分标准一.选择题:本题考查基本知识和基本运算.第(1)-(10)题每小题4分,第(11)-(15)题每小题5分.满分65分.(1) D (2) B (3) C (4) A (5) B (6) B (7) C (8) D (9) A (10) B (11) B (12) A (13) B (14) C (15) D 二.填空题:本题考查基本知识和基本运算.每小题4分,满分16分.(16)316(17) -5120 (18) AC ⊥BD ,或任何能推导出这个条件的其他条件.例如ABCD 是正方形,菱形等 (19)①,③注:第(19)题多填、漏填的错填均给0分. 三.解答题:(20)本小题主要考查不等式基本知识,不等式的解法.满分10分. 解:将原不等式化为(a 2-b 2)x +b 2≥(a -b )2x 2+2(a -b )bx +b 2, 移项,整理后得 (a -b )2(x 2-x ) ≤0, ∵ a ≠b 即 (a -b )2>0, ∴ x 2-x ≤0, 即 x (x -1) ≤0.解此不等式,得解集 {x |0≤x ≤1}.(21) 本小题考查正弦定理,同角三角函数基本公式,诱导公式等基础知识,考查利用三角公式进行恒等变形的技能及运算能力.满分11分.解:由正弦定理和已知条件a +c =2b 得sin A +sin C =2sin B .由和差化积公式得B CA C A sin 22cos 2sin 2=-+. 由A +B +C =π,得 2)sin(C A +=2cos B,又A -C =3π,得23cos 2B =sin B ,∴23cos 2B =2sin 2B cos 2B .∵ 0<2B <2π, 2cos B ≠0,∴sin2B =43, 从而cos2B =2sin 12B -=413 ∴ sin B =⨯23413=839(22) 本小题主要考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想.考查抛物线的概念和性质,曲线与方程的关系以及综合运用知识的能力.满分12分.解法一:如图建立坐标系,以l 1为x 轴,MN 的垂直平分线为y 轴,点O 为坐标原点.依题意知:曲线段C 是以点N 为焦点,以l 2为准线的抛线段的一段,其中A 、B 分别为C 的端点.设曲线段C 的方程为y 2=2px (p >0),(x A ≤x ≤x B ,y >0),其中x A ,x B 分别为A ,B 的横坐标,P =|MN |.所以 M (-2P ,0),N (2P,0). 由 |AM |=17,|AN |=3得(x A +2P )2+2Px A =17, ① (x A -2P )2+2Px A =9. ②由①、②两式联立解得x A =P4,再将其代入①式并由p >0解得⎩⎨⎧==14A x p 或⎩⎨⎧==22Ax p . 因为△AMN 是锐角三角形,所以2P>x A ,故舍去⎩⎨⎧==22A x p .∴ P =4,x A =1.由点B 在曲线段C 上,得x B =|BN |-2P=4. 综上得曲线段C 的方程为y 2=8x (1≤x ≤4,y >0).解法二:如图建立坐标系,分别以l 1、l 2为x 、y 轴,M 为坐标原点. 作AE ⊥l 1,AD ⊥l 2,BF ⊥l 2,垂足分别为E 、D 、F . 设 A (x A ,y A )、B (x B ,y B )、N (x N ,0). 依题意有x A =|ME|=|DA|=|AN|=3, y A =|DM |=22DA AM -=22,由于△AMN 为锐角三角形,故有x N =|AE |+|EN |=4.=|ME |+22AE AN -=4X B =|BF |=|BN |=6.设点P (x ,y )是曲线段C 上任一点,则由题意知P 属于集合 {(x ,y )|(x -x N )2+y 2=x 2,x A ≤x ≤x B ,y >0}. 故曲线段C 的方程y 2=8(x -2)(3≤x ≤6,y >0).(23) 本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,棱柱的性质,空间的角和距离的概念,逻辑思维能力、空间想象能力及运算能力.满分12分.注:题中赋分为得到该结论时所得分值,不给中间分. 解:(Ⅰ)作A 1D ⊥AC ,垂足为D ,由面A 1ACC 1⊥面ABC ,得A 1D ⊥面ABC ,∴ ∠A 1AD 为A 1A 与面ABC 所成的角. ∵ AA 1⊥A 1C ,AA 1=A 1C ,∴ ∠A 1AD=45º为所求.(Ⅱ)作DE ⊥AB ,垂足为E ,连A 1E ,则由A 1D ⊥面ABC ,得A 1E ⊥AB . ∴∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角.由已知,AB ⊥BC ,得ED ∥BC .又D 是AC 的中点,BC =2,AC =23,∴ DE =1,AD =A 1D =3,tg A 1ED=DEDA 1=3. 故∠A 1ED=60º为所求.(Ⅲ) 作BF ⊥AC ,F 为垂足,由面A 1ACC 1⊥面ABC ,知BF ⊥面A 1ACC 1. ∵ B 1B ∥面A 1ACC 1,∴ BF 的长是B 1B 和面A 1ACC 1的距离. 在Rt △ABC 中,2222=-=BC AC AB ,∴ 362=⋅=AC BC AB BF 为所求. (24) 本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力,考查建立函数关系、不等式性质、最大值、最小值等基础知识.满分12分.解法一:设y 为流出的水中杂质的质量分数,则y =abk,其中k >0为比例系数,依题意,即所求的a ,b 值使y 值最小.根据题设,有4b +2ab +2a =60(a >0,b >0), 得 aab +-=230 (0<a <30=, ① 于是 aa a k ab k y +-==230226432+-+-=a a k⎪⎭⎫ ⎝⎛+++-=264234a a k()2642234+⋅+-≥a a k18k =当a +2=264+a 时取等号,y 达最小值.这时a =6,a =-10(舍去). 将a =6代入①式得b =3.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小. 解法二:依题意,即所求的a ,b 的值使ab 最大. 由题设知 4a +2ab +2a =60 (a >0,b >0) 即 a +2b +ab =30 (a >0,b >0). ∵ a +2b ≥2ab , ∴ 22ab +ab ≤30,当且仅当a =2b 时,上式取等号. 由a >0,b >0,解得0<ab ≤18.即当a =2b 时,ab 取得最大值,其最大值18. ∴ 2b 2=18.解得b =3,a =6.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.(25) 本小题主要考查等差数列基本概念及其通项求法,考查对数函数性质,考查归纳,推理能力以及用数学归纳法进行论证的能力.满分12分.解:(Ⅰ)设数列工{b n }的公差为d ,由题意得b 1=1,10b 1+d2)110(10-=100.解得 b 1=1,d =2.∴ b n =2n -1. (Ⅱ)由b n =2n -1,知S n =lg(1+1)+lg(1+31)+…+lg(1+121-n ) =lg[(1+1)(1+31)· … ·(1+121-n )],21lg b n +1=lg 12+n . 因此要比较S n 与21lg b n +1的大小,可先比较(1+1)(1+31)· … ·(1+121-n )与12+n 的大小.取n =1有(1+1)>112+⋅,取n =2有(1+1)(1+31)>112+⋅ 由此推测(1+1)(1+31)· … ·(1+121-n )>12+n . ①若①式成立,则由对数函数性质可判定:S n >21lgb n +1. 下面用数学归纳法证明①式. (i)当n =1时已验证①式成立.(ii)假设当n =k (k ≥1)时,①式成立,即 (1+1)(1+31)· … ·(1+121-k )>12+k ,那么,当n =k +1时, (1+1)(1+31)· … ·(1+121-k )(1+1)1(21-+k )>12+k (1+121+k ) =1212++k k (2k +2).∵ [1212++k k (2k +2)]2-[32+k ]2=123848422+++++k k k k k=121+k >0, ∴1212++k k (2k +2) >32+k =()112++k .因而 (1+1)(1+31)· … ·(1+121-k )(1+121+k )>1)1(2++k . 这就是说①式当n =k +1时也成立.由(i),(ii )知①式对任何正整数n 都成立.由此证得:S n >21lg b n +1.。
1998年全国高考理科数学试题及其解析
1998年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试120分钟.第Ⅰ卷(选择题共65分)一.选择题:本大题共15小题;第1—10题每小题4分,第11— 15题每小题5分,共65分.在每小题给出的四个选项中,只有一项是符合题目要求的(1) sin600º( )(A)21 (B) -21(C) 23 (D) -23(2) 函数y =a |x |(a >1)的图像是( )(3) 曲线的极坐标方程ρ=4sin θ化成直角坐标方程为( )(A) x 2+(y +2)2=4 (B) x 2+(y -2)2=4 (C) (x -2)2+y 2=4 (D) (x +2)2+y 2=4 (4) 两条直线A 1x +B 1y +C 1=0,A 2x +B 2y +C 2=0垂直的充要条件是( )(A) A 1A 2+B 1B 2=0 (B) A 1A 2-B 1B 2=0 (C)12121-=B B A A (D) 12121=A A B B(5) 函数f (x )=x1( x ≠0)的反函数f -1(x )= ( ) (A) x (x ≠0) (B) x 1(x ≠0) (C) -x (x ≠0) (D) -x1(x ≠0)(6) 已知点P (sin α-cos α,tg α)在第一象限,则在)20[π,内α的取值是 ( )(A) (432ππ,)∪(45ππ,) (B) (24ππ,)∪(45ππ,) (C) (432ππ,)∪(2345ππ,) (D) (24ππ,)∪(ππ,43) (7) 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为 ( )(A) 120º (B) 150º (C) 180º (D) 240º (8) 复数-i 的一个立方根是i ,它的另外两个立方根是( )(A)2123± i (B) -2123± i (C) ±2123+ i (D) ±2123-i (9) 如果棱台的两底面积分别是S ,S ′,中截面的面积是S 0,那么( )(A) 2S S S '+=0 (B) S 0=S S '(C) 2 S 0=S +S ′ (D) S S S '=22(10) 向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图像如下图所示,那么水瓶的形状是( )(11) 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共有( )(A) 90种 (B) 180种 (C) 270种 (D) 540种(12) 椭圆31222y x +=1的焦点为F 1和F 2,点P 在椭圆上,如果线段PF 1的中点在y 轴上,那么|P F 1|是|P F 2|的( )(A) 7倍 (B) 5倍 (C) 4倍 (D) 3倍 (13) 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过这3个点的小圆的周长为4π,那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D) 3(14) 一个直角三角形三内角的正弦值成等比数列,其最小内角为( )(A) arccos215- (B) arcsin215- (C) arccos251- (D) arcsin 251-(15) 在等比数列{a n }中,a 1>1,且前n 项和S n 满足∞→n lim S n =11a ,那么a 1的取值范围是( ) (A)(1,+∞) (B)(1,4) (C) (1,2) (D)(1,2)第Ⅱ卷(非选择题共85分)二、填空题:本大题共4小题;每小题4分,共16分.把答案填在题中横线上.16.设圆过双曲线116922=-y x 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是_________17.(x +2)10(x 2-1)的展开式中x 10的系数为____________(用数字作答)18.如图,在直四棱柱A 1B 1C 1 D 1-ABCD 中,当底面四边形ABCD 满足条件____________时,有A 1 C ⊥B 1 D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)19.关于函数f (x )=4sin(2x +3π)(x ∈R ),有下列命题: ①由f (x 1)= f (x 2)=0可得x 1-x 2必是π的整数倍; ②y =f (x )的表达式可改写为y =4cos(2x -6π); ③y =f (x )的图像关于点(-6π,0)对称; ④y =f (x )的图像关于直线x =-6π对称.其中正确的命题的序号是_______ (注:把你认为正确的命题的序号都.填上.) 三、解答题:本大题共6小题;共69分.解答应写出文字说明,证明过程或演算步骤. (20)(本小题满分10分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,设a +c =2b ,A -C=3π.求sin B 的值. 以下公式供解题时参考: sin θ+sin ϕ =2sin2ϕθ+cos2ϕθ-, sin θ-sin ϕ=2cos2ϕθ+sin2ϕθ-,cos θ+cos ϕ=2cos 2ϕθ+cos 2ϕθ-, cos θ-cos ϕ=-2sin 2ϕθ+sin 2ϕθ-.(21)(本小题满分11分)如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1.以A,B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=17,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.(22)(本小题满分12分)如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出.设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比.现有制箱材料60平方米.问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计).(23)(本小题满分12分)已知斜三棱柱ABC -A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直,∠ABC =90º,BC =2,AC=23,且AA 1 ⊥A 1C ,AA 1= A 1 C .Ⅰ.求侧棱A 1A 与底面ABC 所成角的大小;Ⅱ.求侧面A 1 ABB 1 与底面ABC 所成二面角的大小; Ⅲ.求顶点C 到侧面A 1 ABB 1的距离.(24)(本小题满分12分)设曲线C 的方程是y =x 3-x ,将C 沿x 轴、y 轴正向分别平行移动t 、s 单位长度后得曲线C 1.Ⅰ.写出曲线C 1的方程; Ⅱ.证明曲线C 与C 1关于点A (3t ,2s)对称; Ⅲ.如果曲线C 与C 1有且仅有一个公共点,证明s =43t -t 且t ≠0.(25)(本小题满分12分)已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=145. Ⅰ.求数列{b n }的通项b n ; Ⅱ.设数列{a n }的通项a n =log a (1+nb 1)(其中a >0,且a ≠1),记S n 是数列{a n }的前n 项和.试比较S n 与31log a b n +1的大小,并证明你的结论.1998年普通高等学校招生全国统一考试数学试题(理工农医类)参考答案一、选择题(本题考查基本知识和基本运算.)1.D 2.B 3.B 4.A 5.B 6.B 7.C 8.D 9.A 10.B 11.D 12.A 13.B 14.B 15.D 二、填空题(本题考查基本知识和基本运算.)16.31617.179 18.AC ⊥BD ,或任何能推导出这个条件的其他条件.例如ABCD 是正方形,菱形等 19.②,③ 三、解答题20.本小题考查正弦定理,同角三角函数基本公式,诱导公式等基础知识,考查利用三角公式进行恒等变形的技能及运算能力.解:由正弦定理和已知条件a +c =2b 得 sin A +sin C =2sin B .由和差化积公式得2sin 2C A +cos 2CA -=2sinB . 由A +B +C =π 得 sin 2C A +=cos 2B,又A -C =3π 得 23cos 2B=sin B ,所以23cos 2B =2sin 2B cos 2B. 因为0<2B <2π,cos 2B≠0, 所以sin2B =43, 从而cos2B =4132sin 12=-B 所以sinB=83941323=⨯.21.本小题主要考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想.考查抛物线的概念和性质,曲线与方程的关系以及综合运用知识的能力.解法一:如图建立坐标系,以l 1为x 轴,MN 的垂直平分线为y 轴,点O 为坐标原点.依题意知:曲线段C 是以点N 为焦点,以l 2为准线的抛物线的一段,其中A ,B 分别为C 的端点.设曲线段C 的方程为y 2=2px (p >0),(x A ≤x ≤x B ,y >0),其中x A ,x B 分别为A ,B 的横坐标,p =|MN |. 所以 M (2p -,0),N (2p,0). 由|AM |= 17 ,|AN |=3 得(x A +2p )2+2px A =17, ① (x A -2p)2+2px A =9. ②由①,②两式联立解得x A =p4.再将其代入①式并由p >0解得 ⎩⎨⎧==⎩⎨⎧==.2,2;1,4AA x p x p 或 因为ΔAMN 是锐角三角形,所以2p> x A ,故舍去⎩⎨⎧==22A x p 所以p =4,x A =1.由点B 在曲线段C 上,得x B =|BN |-2p=4. 综上得曲线段C 的方程为y 2=8x (1≤x ≤4,y >0).解法二:如图建立坐标系,分别以l 1、l 2为x 、y 轴,M 为坐标原点. 作AE ⊥ l 1,AD ⊥ l 2,BF ⊥ l 2,垂足分别为E 、D 、F . 设A (x A ,y A )、B (x B ,y B )、N (x N ,0).依题意有x A =|ME |=|DA |=|AN |=3, y A =|DM |=2222=-DAAM,由于ΔAMN 为锐角三角形,故有 x N =|ME |+|EN | =|ME |+22AE AN -=4x B =|BF |=|BN |=6.设点P (x ,y )是曲线段C 上任一点,则由题意知P 属于集合{(x ,y )|(x -x N )2+y 2=x 2,x A ≤x ≤x B ,y >0}.故曲线段C 的方程为y 2=8(x -2)(3≤x ≤6,y >0).22.本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力,考查建立函数关系、不等式性质、最大值、最小值等基础知识.解法一:设y 为流出的水中杂质的质量分数,则y =abk,其中k >0为比例系数.依题意,即所求的a ,b 值使y 值最小.根据题设,有4b +2ab +2a =60(a >0,b >0), 得 b =aa+-230(0<a <30). ① 于是 y =ab k =aaa k+-230226432+-+-=a a k ⎪⎭⎫ ⎝⎛+++-=264234a a k≥()2642234+⋅+-a a k18k =, 当a +2=264+a 时取等号,y 达到最小值. 这时a =6,a =-10(舍去). 将a =6代入①式得b =3.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小. 解法二:依题意,即所求的a ,b 的值使ab 最大. 由题设知 4b +2ab +2a =60(a >0,b >0),即 a +2b +ab =30(a >0,b >0). 因为 a +2b ≥2ab 2, 所以 ab 22+ab ≤30, 当且仅当a =2b 时,上式取等号. 由a >0,b >0,解得0<ab ≤18.即当a =2b 时,ab 取得最大值,其最大值为18. 所以2b 2=18.解得b =3,a =6.故当a 为6米,b 为3米时,经沉淀后流出的水中该杂质的质量分数最小.23.本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,棱柱的性质,空间的角和距离的概念,逻辑思维能力、空间想象能力及运算能力.Ⅰ.解:作A 1D ⊥AC ,垂足为D ,由面A 1ACC 1⊥面ABC ,得A 1D ⊥面ABC , 所以∠A 1AD 为A 1A 与面ABC 所成的角. 因为AA 1⊥A 1C ,AA 1=A 1C , 所以∠A 1AD =45º为所求.Ⅱ.解:作DE ⊥AB ,垂足为E ,连A 1E ,则由A 1D ⊥面ABC ,得A 1E ⊥AB . 所以∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角. 由已知,AB ⊥BC ,得ED ∥BC . 又D 是AC 的中点,BC =2,AC =23, 所以DE =1,AD =A 1D =3, tg ∠A 1ED =DEDA 1=3. 故∠A 1ED =60º为所求.Ⅲ.解法一:由点C 作平面A 1ABB 1的垂线,垂足为H ,则CH 的长是C 到平面A 1ABB 1的距离.连结HB ,由于AB ⊥BC ,得AB ⊥HB . 又A 1E ⊥AB ,知HB ∥A 1E ,且BC ∥ED , 所以∠HBC =∠A 1ED =60º 所以CH =BC sin60º=3为所求. 解法二:连结A 1B .根据定义,点C 到面A 1ABB 1的距离,即为三棱锥C -A 1AB 的高h . 由ABC A AB A C V V --=11锥锥得D A S h S ABC B AA 131311∆∆=, 即 322312231⨯⨯=⨯h 所以3=h 为所求.24.本小题主要考查函数图像、方程与曲线,曲线的平移、对称和相交等基础知识,考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力.Ⅰ.解:曲线C 1的方程为y =(x -t )3-(x -t )+s .Ⅱ.证明:在曲线C 上任取一点B 1(x 1,y 1).设B 2(x 2,y 2)是B 1关于点A 的对称点,则有2221t x x =+, 2221sy y =+. 所以 x 1=t -x 2, y 1=s -y 2.代入曲线C 的方程,得x 2和y 2满足方程:s -y 2=(t -x 2)3-(t -x 2),即 y 2=(x 2-t )3-(x 2-t )+ s , 可知点B 2(x 2,y 2)在曲线C 1上.反过来,同样可以证明,在曲线C 1上的点关于点A 的对称点在曲线C 上. 因此,曲线C 与C 1关于点A 对称.Ⅲ.证明:因为曲线C 与C 1有且仅有一个公共点,所以,方程组⎪⎩⎪⎨⎧+---=-=st x t x y xx y )()(33有且仅有一组解.消去y ,整理得3tx 2-3t 2x +(t 3-t -s )=0, 这个关于x 的一元二次方程有且仅有一个根. 所以t ≠0并且其根的判别式Δ=9t 4-12t (t 3-t -s )=0.即 ⎩⎨⎧=--≠.0)44(,03s t t t t所以 t t s -=43且 t ≠0. 25.本小题主要考查等差数列基本概念及其通项求法,考查对数函数性质,考查归纳、推理能力以及用数学归纳法进行论证的能力.解:Ⅰ.设数列{b n }的公差为d ,由题意得⎪⎩⎪⎨⎧=-+=.1452)110(1010,111d b b 解得⎩⎨⎧==.3,11d b 所以 b n =3n -2.Ⅱ.由b n =3n -2,知S n =log a (1+1)+ log a (1+41)+…+ log a (1+231-n ) = log a [(1+1)(1+41)……(1+231-n )], 31log a b n +1= log a 313+n . 因此要比较S n 与31log a b n +1的大小,可先比较(1+1)(1+41)……(1+231-n )与313+n 的大小.取n =1有(1+1)>3113+⋅,取n =2有(1+1)(1+41)>3123+⋅, ……由此推测(1+1)(1+41)……(1+231-n )>313+n . ① 若①式成立,则由对数函数性质可断定:当a >1时,S n >31log a b n +1. 当0<a <1时,S n <31log a b n +1. 下面用数学归纳法证明①式.(ⅰ)当n =1时已验证①式成立.(ⅱ)假设当n =k (k ≥1)时,①式成立,即(1+1)(1+41)……(1+231-k )>313+k . 那么,当n =k +1时,(1+1)(1+41)……(1+231-k )(1+()2131-+k )>313+k (1+131+k ) =13133++k k (3k +2). 因为()[]333343231313+-⎥⎦⎤⎢⎣⎡+++k k k k ()()()()22313134323+++-+=k k k k ()013492>++=k k , 所以13133++k k (3k +2)>().1134333++=+k k 因而(1+1)(1+41)……(1+231-k )(1+131+k )>().1133++k 这就是说①式当n=k +1时也成立.由(ⅰ),(ⅱ)知①式对任何正整数n 都成立.由此证得:当a >1时,S n >31log a b n +1. 当0<a <1时,S n <31log a b n +1.。
1998年全国高考数学试题及答案解析
第 1 页 共 10 页 1998年普通高等学校招生全国统一考试
数学
(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共65分)
一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设集合M={x │0≤x<2},集合N={x │x 2-2x-3<0},集合M ∩N 为
(A){x │0≤x<1} (B){x │0≤x<2}
(C){x │0≤x ≤1} (D){x │0≤x ≤2}
[Key] B
(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a 为
32
)(23
)(6)(3)(D C B A ---
[Key] B
(3)函数
)x 31x 21(tg y -=在一个周期内的图象是
[Key] A
(4)已知三棱锥D-ABC 的三个则面与底面全等,且AB=AC=3,BC=2,则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是
32)D (2)C (31
arccos )B (33
arccos )A (ππ
[Key] C
(5)函数x 2cos )x 23sin(y +-π=的最小正周期是
ππππ
4)D (2)C ()B (2)A (
[Key] B。
1998年高考数学试题及答案(全国理)
1998年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题共65分)一、选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、sin600°的值是23.D 23.C 21.B 21.A --[Key] D2、函数)1a (a y |x |>=的图象是[Key] B3、曲线的极坐标方程θ=ρsin 4化成直角坐标方程为A . 4)2y (x 22=++B .4)2y (x 22=-+ C . 4y )2x (22=+- D .4y )2x (22=++[Key] B4、两条直线0C y B x A ,0C y B x A 222111=++=++垂直的充要条件是A . 0B B A A 2121=+B . 0B B A A 2121=-C . 1B B A A 2121-=D . 1B B A A 2121=[Key] A5、函数)0x (x 1)x (f ≠=的反函数=-)x (f 1A . x(x ≠0)B . )0x (x 1≠C . -x(x ≠0)D .)0x (x 1≠- [Key] B6、已知点)tg ,cos (sin P αα-α在第一象限,则在)2,0(π内α的取值范围是A . )45,()43,2(ππ⋃ππ B . )45,()2,4(ππ⋃ππ C . )23,45()43,2(ππ⋃ππ D . ),43()2,4(ππ⋃ππ[Key] B °7、已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为A .120°B .150°C .180°D .240°[Key] C8、复数-i 的一个立方根是i ,它的另外两个立方根是A . i 2123±B .i 2123±-C .i 2123+± D . i 2123-± [Key] D9、如果棱台的两底面积分别是S , S',中截面的面积是S 0,那么A . 'S S +=22B . S 'S S =0C . 'S S S +=02D . S 'S S 220=[Key] A10、向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图象如右图所示,那么水瓶的形状是[Key] B11、3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有A .90种B .180种C .270种D .540种[Key] D12、椭圆131222=+y x 的焦点为F 1和F 2,点P 在椭圆上,如果线段PF 1的中点在y 轴上,那么|PF 1|是|PF 2|的A .7倍B .5倍C .4倍D .3倍[Key] A13、球面上有3个点,其中任意两点的球面距离都等于大圆周长的1/6,经过这3个点的小圆的周长为4π,那么这个球的半径为A . 34B .32C .2D .3[Key] B14、一个直角三角形三内角的正弦值成等比数列,其最小内角为A . 215arccos -B . 215arcsin -C . 251arccos- D . 251arcsin - [Key] B15、在等比数列{a n }中,a 1>1,且前n 项和S n 满足11lim a S n n =∞→,那么a 1的取值范围是A .(1,+∞)B .(1,4)C .(1,2)D .(1,2)[Key] D16、设圆过双曲线116922=+y x 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是 _______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1998年全国高校招生物理统考试题一.本题共12小题;每小题5分,共60分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。
全部选对的得5分,选不全的得2分,有选错或不答的得0分。
1.如图所示,三段不可伸长的细绳OA、OB、OC,能承受的最大拉力相同,它们共同悬挂一重物,其中OB是水平的,A端、B端固定。
若逐渐增加C端所挂物体的质量,则最先断的绳()。
(A)必定是OA (B)必定是OB(C)必定是OC (D)可能是OB,也可能是OC2.下列说法正确的是()(A)液体中悬浮微粒的布朗运动是作无规则运动的液体分子撞击微粒而引起的(B)物体的温度越高,其分子的平均动能越大(C)物体里所有分子动能的总和叫做物体的内能(D)只有传热才能改变物体的内能3.一简谐横波在x轴上传播,在某时刻的波形如图所示,已知此时质点F的运动方向向下,则()(A)此波朝x轴负方向传播(B)质点D此时向下运动(C)质点B将比质点C先回到平衡位置(D)质点E的振幅为零4.通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与MN平行。
关于MN的磁场对线框的作用,下列叙述正确的是()(A)线框有两条边所受的安培力方向相同(B)线框有两条边所受的安培力大小相同(C)线框所受安培力的合力朝左(D)cd所受安培力对ab边的力矩不为零5.如图所示,一宽40cm的匀强磁场区域,磁场方向垂直纸面向里。
一边长为20cm的正方形导线框位于纸面内,以垂直于磁场边界的恒定速度v=20cm/s通过磁场区域,在运动过程中,线框有一边始终与磁场区域的边界平行。
取它刚进入磁场的时刻t=0,在下列图线中,正确反映感应电流强度随时间变化规律的是()6.天然放射性元素23290Th(钍)经过一系形α衰变和β衰变之后,变成20882Pb(铅)。
下列论断中正确的是()(A)铅核比钍核少24个中子(B)铅核比钍核少8个质子(C)衰变过程中共有4次α衰变和8次β衰变(D)衰变过程中共有6次α衰变和4次β衰变7.一金属球,原来不带电,现沿球的直径的延长线放置一均匀带电的细杆MN,如图所示,金属球上感应电荷产生的电场在球内直径上a、b、c三点的场强大小分别为E a、E b、E c,三者相比()(A)E a最大(B)E b最大(C)E c最大(D)E a=E b=E c8.一细束平行光经玻璃三棱镜折射后分解为互相分离的三束光,分别照射到相同的金属板a、b、c上,如图所示。
已知金属板b有光电子放出,则可知()(A)板a一定不放出光电子(B)板a一定放出光电子(C)板c一定不放出光电子(D)板c一定放出光电子9.处于基态的氢原子在某单色光束照射下,只能发出频率为ν1、ν2、ν3的三种光,且ν1<ν2<ν3,则该照射光的光子能量为()(A)hν1(B)hν2(C)hν3(D)h(ν1+ν2+ν3)10.在光滑水平面上,动能为E0、动量的大小为p0的小钢球1与静止小钢球2发生碰撞,碰撞前后球1的运动方向相反。
将碰撞后球1的动能和动量的大小分别记为E1、p1,球2的动能和动量的大小分别记为E2、p2,则必有()(A)E1<E0(B)p1<p0(C)E2>E0(D)p2>p011.图示的两种电路中,电源相同,各电阻器阻值相等,各电流表的内阻相等且不可忽略不计。
电流表A1、A2、A3和A4读出的电流值分别为I1、I2、I3和I4。
下列关系式中正确的是()(A)I1=I3(B)I1<I4(C)I2=2I1(D)I2<I3+I412.图中两单摆摆长相同,平衡时两摆球刚好接触。
现将摆球A 在两摆线所在平面内向左拉开一小角度后释放,碰撞后,两摆球分开各自做简谐运动,以m A 、m B 分别表示摆球A 、B 的质量,则()(A )如果m A >m B ,下一次碰撞将发生在平衡位置右侧(B )如果m A <m B ,下一次碰撞将发生在平衡位置左侧(C )无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧(D )无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧二.本题共5小题;每小题4分,共20分。
把答案填在题中的横线上。
13.一理想变压器,原线圈匝数n 1=1100,接在电压220V 的交流电源上。
当它对11只并联的“36V ,60W ”灯泡供电时,灯泡正常发光。
由此可知该变压器副线圈的匝数n 2=_____,通过原线圈的电流I 1=_____A 。
14.如图所示,一储油圆桶,底面直径与桶高均为d 。
当桶内无油时,从某点A 恰能看到桶底边缘上的某点B 。
当桶内油的深度等于桶高一半时,在A 点沿AB 方向看去,看到桶底上的C 点,C 、B 相距14d 。
由此可得油的折射率n =______;光在油中传播的速度v =_____m/s 。
(结果可用根式表示)15.如图,质量为2m 的物块A 与水平地面的摩擦可忽略不计,质量为m 的物块B 与地面的摩擦系数为μ。
在已知水平推力F 的作用下,A 、B 作加速运动。
A 对B 的作用力为_______。
16.A 、B 两带电小球,A 固定不动,B 的质量为m 。
在库仑力作用下,B 由静止开始运动。
已知初始时,A 、B 间的距离为d ,B 的加速度为a 。
经过一段时间后,B 的加速度变为14a ,此时A 、B 间的距离应为________。
已知此时B 的速度为v ,则在此过程中电势能的减少量为________。
17.来自质子源的质子(初速度为零),经一加速电压为800kV 的直线加速器加速,形成电流强度为1mA 的细柱形质子流。
已知质子电荷e =1.60×10-19C 。
这束质子流每秒打到靶上的质子数为_______。
假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距l 和4l 的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n 1和n 2,则n 1/n 2=_______。
三.本题共3小题;其中第19题5分,其余的每题6分,共17分。
把答案填在题中的横线上或按题目要求作图。
18.在LC 振荡电路中,如已知电容C ,并测得电路的固有振荡周期T ,即可求得电感L 。
为了提高测量精度,需多次改变C 值并侧得相应的T 值。
现将测得的六组数据标示在以C 为横坐标、T 2为纵坐标的坐标纸上,即图中用“×”表示的点。
(1)T、L、C的关系为_________。
(2)根据图中给出的数据点作出T2与C的关系图线。
(3)求得的L值是___________。
19.某学生做“验证牛顿第二定律”的实验在平衡摩擦力时,把长木板的一端垫得过高,使得倾角偏大。
他所得到的a-F关系可用下列哪根图线表示?图中a是小车的加速度,F是细线作用于小车的拉力。
答:_________。
20.用图示的电路测定未知电阻R x的值。
图中电源电动势未知,电源内阻与电流表的内阻均可忽略不计,R为电阻箱。
(1)若要测得R x的值,R至少需要取_________个不同的数值。
(2)若电流表每个分度表示的电流值未知,但指针偏转角度与通过的电流成正比,则在用此电路测R x时,R至少需取_______个不同的数值。
(3)若电源内阻不可忽略,能否应用此电路测量R x?答:_________。
四.本题共5小题,53分,解答应写出必要的文字说明、方程式和重要演算步骤。
只写出最后答案的不能得分。
有数值计算的题,在答案中必须明确写出数值和单位。
21.(9分)宇航员站在一星球表面上的某高处,沿水平方向抛出一个小球。
经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。
若抛出时的初速增大到2倍,则抛出点与落地点之间的距离为3L。
已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。
求该星球的质量M。
22.(9分)活塞把密闭气缸分成左、右两个气室,每室各与U形管压强计的一臂相连。
压强计的两臂截面处处相同。
U 形管内盛有密度为ρ=7.5×102kg/m 3的液体。
开始时左、右两气室的体积都为V 0=1.2×10-2m 3,气压都为p 0=4.0×103Pa ,且液体的液面处在同一高度,如图所示。
现缓缓向左推进活塞,直到液体在U 形管中的高度差h =40cm 。
求此时左、右气室的体积V 1、V 2。
假定两气室的温度保持不变。
计算时可以不计U 形管和连接管道中气体的体积。
23.(11分)如图所示,在x 轴上方有垂直于xy 平面向里的匀强磁场,磁感应强度为B ;在x 轴下方有沿y 轴负方向的匀强电场,场强为E 。
一质量为m ,电量为-q 的粒子从坐标原点O 沿着y 轴正方向射出。
射出之后,第三次到达x 轴时,它与点O 的距离为L 。
求此粒子射出时的速度v 和运动的总路程s (重力不计)。
24.(12分)如图所示,L 为薄凸透镜,点光源S位于L 的主光轴上,它到L 的距离为36cm ;M 为一与主光轴垂直的挡光圆板,其圆心在主光轴上,它到L 的距离为12cm ;P 为光屏,到L 的距离为30cm 。
现看到P 上有一与挡光板同样大小的圆形暗区ab 。
求透镜的焦距。
25.(12分)一段凹槽A 倒扣在水平长木板C 上,槽内有一小物块B ,它到槽两内侧的距离均为12L ,如图所示。
木板位于光滑水平的桌面上,槽与木板间的摩擦不计,小物块与木板间的摩擦系数为μ。
A 、B 、C 三者质量相等,原来都静止。
现使槽A 以大小为v 0的初速向右运动,已知v 0<2μgL 。
当A 和B 发生碰撞时,两者速度互换。
求:(1)从A 、B 发生第一次碰撞到第二次碰撞的时间内,木板C 运动的路程。
(2)在A 、B 刚要发生第四次碰撞时,A 、B 、C 三者速度的大小。
答案一.不定项选择题1.A2.AB 3.AB 4.BC 5.C 6.BD 7.C 8.D 9.C 10.ABD 11.BD 12.CD二.填空题13.180,3 14.102,610×107 15.F +2μmg 316.2d ,12mv 217.6.25×1015,2 三.本题共17分。
其中第19题5分,其余的每题6分。
18.(1)T =2πLC (1分)(2)如图,图线应为一条直线,数据点尽可能靠近直线且均匀分布在直线两侧。
(如画出的不是直线,或没有画,就不给(2)、(3)两问的5分。
)(2分)(3)答数在0.0351H ~0.0389H 范围内给3分;若不在以上范围内,但在0.0333H ~0.0407H 范围内给1分。
有效数字位数不对扣1分。
19.C (5分)20.(1)2(2分)(2)2(3分)(3)不能(1分)四.计算题21.解:设抛出点的高度为h ,第一次平抛的水平射程为x ,则有x 2+h 2=L 2 ①由平抛运动规律得知,当初速增大到2倍,其水平射程也增大到2x ,可得 (2x )2+h 2=(3L )2②由①、②解得 h =L/3 设该星球上的重力加速度为g ,由平抛运动的规律,得h =gt 2/2由万有引力定律与牛顿第二定律,得GMm/R 2=mg式中m 为小球的质量,联立以上各式,解得M =23LR 23Gt 222.解:以p 1、V 1表示压缩后左室气体的压强和体积,p 2、V 2表示这时右室气体的压强和体积。
