角动量守恒定律
角动量守恒定律

角动量守恒定律角动量守恒定律,也称转动动量守恒定律,是描述旋转系统中物体角动量守恒的物理定律。
它是在伽利略与牛顿的基础上,由欧拉和拉格朗日等人发展起来的。
它表明,在无外力矩作用下,一个封闭系统的总角动量守恒。
在物理学中,角动量是描述物体旋转运动的物理量。
一个物体的角动量等于其自转角速度和惯性矩的乘积。
考虑一个刚性物体,其围绕某个轴心旋转。
此时,物体的角动量L等于其自转惯性矩I和角速度ω的积,即L=Iω。
这个公式可以用来描述物体的旋转状态。
在没有外力矩作用的情况下,物体的角动量守恒。
也就是说,在这种情况下,刚体自身的角速度和惯性矩不会发生改变。
这个定律可以由牛顿第二定律的角动量形式推导出来。
当一个刚体受到外部力矩时,他的角动量就会发生变化。
这个变化量等于力矩与旋转时间的积。
一个封闭系统中的物体,在没有外部力矩作用时,总角动量守恒,即所有物体的角动量的代数和不变。
如果物体中有某一个物体受到外部力矩,那么这个物体的角动量就会发生变化,但是,由于总系y运中的总力矩为零,所以其他物体的角动量将以相反的方式发生变化,以保证总角动量守恒。
一个典型的例子是一个旋转跳板启动一个跳跃者,高度和角速度的变化取决于跳板和跳跃者的质量和形状。
在这个过程中,跳板和跳跃者的角动量守恒,因为在计算角速度和角动量时,两个物体的总和是不变的。
总之,角动量守恒定律是一种重要的动力学基本定律。
它说明,封闭系统中的角动量总和保持不变。
在硬物体的运动中往往非常有用,可以帮助计算速度、加速度和其他涉及运动的数值。
在工程学和物理学中,它被广泛地应用于旋转系统、制药生产,以及其他需要涉及转动的领域。
角动量定理 角动量守恒定律

量守恒。
13
第3章动量与角动量
例2 发射一宇宙飞船去考察一 质量为 M 、半径为 R 的行 星, 当飞船静止于空间距行星中心 4 R 时,以速度v 0发射一
质量为 m 的仪器。要使该仪器恰好掠过行星表面。 求 θ角及着陆滑行的初速度。 解 引力场(有心力) 系统的机械能守恒
m
r0
v0
v
R
OM
质点的动量矩守恒 1 GMm 1 2 GMm 2 mv 0 mv 2 r0 2 R
求 此时刻质点对三个参考点的动量矩
d1
m v
d3
d2
解
4
LA d1mv LB d1mv LC 0
第3章动量与角动量
B
C
二、力对定点的力矩 定义 为力对定点O的力矩 M r F 大小: M r F sin
方向:垂直 r , F 组成的平面 M ML2T 2 SI Nm 量纲:
r r r M r F 0
L
r L mvrsin m rsin t 1 r r rsin S 2 2m 2m t t
12
r r r L r m C
r r F
r
m
掠面 速度
行星对太阳的位矢在相等 的时间内扫过相等的面积
i i
L Li ri Pi
P2 r2 o
P 1
r1
质点系对参考点O 的动量矩就是质点系所有质点对同一参 考点的动量矩的矢量和
dLi 2. 质点系的动量矩定理 M i dt i i M M i ri Fi ri fi
角动量 角动量守恒定律

h
vN2 2g
1 2g
3mvM m 6m
2
h
3m m 6m
2
19
4-3 角动量 角动量守恒定律
第四章 刚体转动
P104例3 质量很小长度为l 的均匀细杆, 可绕过其中心
O 并与纸面垂直的轴在竖直平面内转动 . 当细杆静止于
水l/4平处位, 置并时背,离有点一O只向小细虫杆以的速端率点vvA0 0垂爬直行落. 设在小距虫点与O细为杆
14
4-3 角动量 角动量守恒定律
比较 动量
F
dP dt
t2
Fdt ΔP
t1
F 0 P 0
F
P
mv
力 动量
t2
Fdt 力的冲量
t1
第四章 刚体转动
角动量
M
dL dt
t2
Mdt ΔL
t1
LMMrrp0F角L力动矩量0或或角动力量矩
其角速度为ω, 求齿轮啮合后两圆盘的角速度.
解: 系统角动量守恒
J11 J22 (J1 J2)
J11 J22
(J1 J2 )
16
4-3 角动量 角动量守恒定律
第四章 刚体转动
P103例2 一杂技演员 M 由距水平跷板高为 h 处自由下
落到跷板的一端 A, 并把跷板另一端的演员 N 弹了起来.
R
x
26
dP
F dt
t2
Fdt ΔP
t1
F 0 P 0
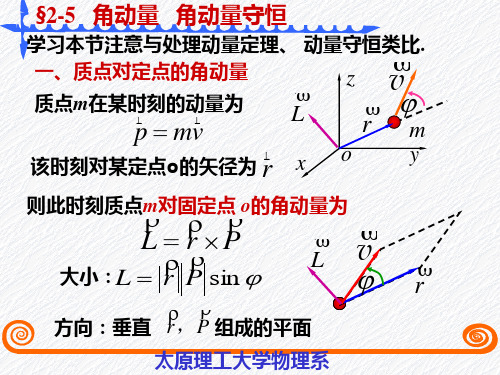
§2-5角动量定理 角动量守恒定律
太原理工大学物理系
L r P
在直角坐标系中
L ( xi yj zk ) ( Px i Py j Pz k )
L x y z
i j k p x p y p z
太原理工大学物理系
L
v
方向:垂直 r ,P 组成的平面
太原理工大学物理系
r
讨论: 1) 同一质点相对于不同的点,角动量不同。 2) 在说明质点的角动量时,必须指明是对哪个 点而言的。
3)质点以角速度作半径为r的圆运动,相对 圆心的角动量
L = mvr
L
p
mr J
2
o r
2)在具体的坐标系中,角动量在各坐标轴的分 量称作对轴的角动量。力矩在各坐标轴的分量, 称作对轴的力矩。
L Lx i Ly j Lz k L 是质点对o点的角动量
Lx Ly Lz
分别是质点对x、y、z轴的角动量.
M M x i M y j M z k M 是力对o点的力矩
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt dt dt
dr 由速度定义 v dt
v p 0 dL dp d r (r p) dt dt dt
i
ri fi 质点系受到的内力矩的矢量和
i
矩
太原理工大学物理系
可以证明:内力对定点的力矩之和为零,即
ri fi 0
i
质点系内的重要结论之三
角动量角动量守恒定律

dr r
l
I r dm
2 m
R2
R1
2 l r dr
3
l
2
4 ( R2 R14 )
m 圆筒的体密度 2 , R2 R, I m R2 2 若R1 R2 R, I m R2
1 2 I m( R2 R12 ) 2
刚体绕OZ轴转动的角动量
a)力矩、角动量都是瞬时量,它们只能针对某 注意: 一时刻而言,它们都不是时间的累积效应。 b)力矩、角动量都是相对量,都必须指明它们 是相对于哪个轴或哪个点。 强调:对于刚体的定轴转动,我们只能用角动量来 描述,而不能用动量来描述。
8
3.转动惯量 1 .定义 刚体对固定轴的转动惯量等于各质元质量与其至 转轴的垂直距离的平方的乘积之和。
I ( Δmiri2 )
I是描述刚体转动惯性大小的物理量。
刚体的转动惯量与哪些物理量有关? ①.与刚体质量有关。 ②.与质量对轴的分布有关。 ③.与轴的位置有关。 在(SI)中,I 的单位:kgm2 量纲:ML2
9
2 .转动惯量的计算
Δmiri2 ) Ii 分立质点系 I (
质量连续分布的刚体
10
例2:半径为 R 质量为 M 的圆环,绕垂直于圆环平面 的质心轴转动,求转动惯量I。 解:分割质量元 dm圆环上各质量元到轴的距离相等,
M
I
0
R dm R
2
2 M 0
2 dm MR M
绕圆环质心轴的转动惯量为
o
R
dm
I MR
2
例2:在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的质点,可绕 o 轴转动,求:质点系的转动惯量I。 解:由转动惯量的定义
5.5 角动量守恒定律
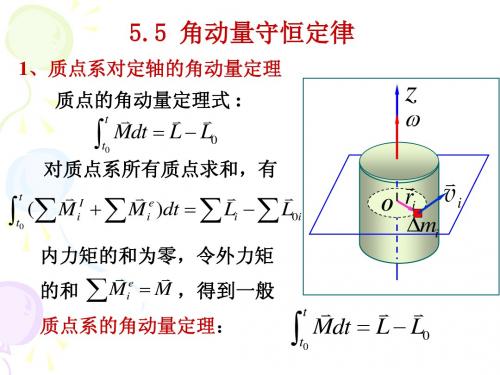
例题1 : 一粒子弹水平射入一静止悬杆的下端,穿出 后速度损失 3 / 4,求子弹穿出后棒的角速度 。已知轴处自由 。
解:以 f 代表杆对子弹的阻力,对子弹有: fdt m(v v0 ) 3mv0 / 4
子弹对杆的冲量矩为:
l f dt J f ldt
若 M 0 ,则
L J 常量
——刚体定轴转动的角动量守恒定律
讨论
内力矩不改变系统的角动量.
在冲击等问题中
M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律. 刚体(或刚体组系统)角动量守恒的三种情况: ①J 不变(刚体),角速度ω的大小和方向均不变 ②J 可变(质点系),ω亦可变,但Jω乘积不变 ③刚体组的角动量守恒
a
v
m
3mva 2 2 m' l 3ma
射入竿后,以子弹、细杆和 地球为系统 ,机械能守恒 .
o
30
a
1 1 2 2 2 ( ml ma ) 2 3 l mga(1 cos 30) mg (1 cos 30) 2
2 2 v g (2 3 )( m l 2ma )( m l 3ma ) 6 ma
质点系的角动量定理:
t
t0
Mdt L L0
质点系的角动量定理:
t
t0
Mdt L L0
O
ri
mi
z
该矢量式向固定转轴(如 z轴) 的投影,得一个标量式,即
vi
t
t0
M z dt Lz L0 z
相对某固定轴,质点系所受的角冲量等于系统 角动量的增量。——质点系对定轴的角动量定理。
§2-3 角动量守恒定律

γ
v lz r
O
)
θ
M z = M cos γ
= r F sin θ cos γ
y
3
x
二、
角动量和角动量定理
z
1、角动量 (angular momentum) 设质点的质量、位矢、速度 v v p v r、 v、 。 和动量分别为 m 、 质点相对参考点O的角动量定义为
v mv
v r
)
)
4
θ
v v w r1 , r2 , L , rn
v L = v li =
质点系的角动量为所有质点的角动量的矢量之 和,即
∑
n
i =1
∑
n
i =1
v v ri × m i v i
10
对每个质点,根据角动量定理列方程 v v v v v dln d l1 v dl2 M1 = ,M 2 = , ⋅ ⋅⋅ , M n = dt dt dt
即
v l = 恒矢量
若作用于质点的合力对参考点的力矩始终为零, 则质点对同一参考点的角动量将保持恒定。 注意: (1)这也是自然界普遍适用的一条基本规律。 v v v v v (2) M = 0,可以是r = 0,也可以是F = 0, 还可能是r 与F 同向或反向,例如有心力情况。 8
如果作用于质点的合力矩不为零,而合力矩沿Oz 轴的分量为零,则
v 当 ∑M =0 时
v L = 恒矢量
如果外力对参考点O的力矩的矢量和始终等于零, 那么质点系对同一参考点的角动量不随时间变化。 当
∑M
z
= 0 时 Lz = 恒量
上式称为质点系对轴的角动量守恒定律。
12
观察发现, 宇宙中存在着大大小小各种层次的天体 系统, 它们都具有旋转的盘状结构, 并且系统中的天体 基本上都朝同一方向转动, 无论是太阳系、银河系以 及众多的河外旋涡星系都是如此,这种现象的形成是 天体系统遵从角动量守恒定律的必然结果。
角动量守恒

角动量守恒角动量守恒定律是指系统所受合外力矩为零时系统的角动量保持不变。
角动量守恒定律是物理和自然界的一条重要定律。
它在日常生活、天体物理、微观物理和工程中都有广泛的应用。
例如,角动量守恒定律可以很好地解释开普勒天体运行第二定律、陀螺效应等。
当一个质点绕原点运动时,它的角动量L=RP。
这里,R是质点相对于原点的位置向量;P是质点的线性动量;而表示矢量积。
具有一定质量的物体绕一固定轴转动,它的角动量L可表示为这个物体的惯性矩I和它的角速度向量w的乘积,即L=Iw。
角动量又称为动量矩,是一个矢量,是位矢叉乘于动量。
定理也称动量矩定理。
表述角动量与力矩之间关系的定理。
对于质点,角动量定理可表述为:质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
对于质点系,由于其内各质点间相互作用的内力服从牛顿第三定律,因而质点系的内力对任一点的主矩为零。
利用内力的这一特性,即可导出质点系的角动量定理:质点系对任一固定点O的角动量对时间的微商等于作用于该质点系的诸外力对O点的力矩的矢量和。
由此可见,描述质点系整体转动特性的角动量只与作用于质点系的外力有关,内力不能改变质点系的整体转动情况。
定理应用角动量守恒定律是物理和自然界的一个重要定律,它在日常生活、天体物理、微观物理和工程等许多方面都有广泛的应用。
例如:当滑冰者手臂收缩时,自我旋转滑冰者的转动速度就会加快。
用角动量守恒定律也可解析中子星有很高的转动速率等。
另外,角动量守恒定律也是陀螺效应的原因。
角动量守恒定律反映了质点和质点系围绕一点或一轴运动的普遍规律。
如一质量为 m的质点受指向固定中心O的向心力F的作用,因力F对O点的力矩为零,根据牛顿第二定律可推得质点对O点的角动量守恒,Lo=rmv=常矢量,此常矢量决定于运动的起始条件,r为质点对于O点的矢径,v为质点的速度。
如将太阳看成固定中心,行星看成质点,则角动量守恒表明行星轨道必在一平面上。
矢径在相等的时间内扫过的面积相等,这就是开普勒行星运动三定律之一—开普勒第二定律角动量守恒也是微观物理学中的重要基本规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理》作业 No.4 角动量守恒定律
一、选择题
1.已知地球的质量为m,太阳的质量为M,地心与日心的距离为R,引力常数为G,则地球绕太阳作圆周运动的角动量为
[ ](A) (B) (C) (D)
2.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如图所示。
今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?
[ ](A) 角速度从小到大,角加速度从大到小 ;
(B) 角速度从小到大,角加速度从小到大 ;
(C) 角速度从大到小,角加速度从大到小 ;
(D) 角速度从大到小,角加速度从小到大。
3. 两个均质圆盘A和B密度分别为和,若>,但两圆盘质量与厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为和,则
[ ](A) > (B) >
(C) = (D) 、哪个大,不能确定
4.有两个力作用在一个有固定转轴的刚体上:
(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;
(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;
(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;
(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零。
在上述说法中:
[ ](A) 只有(1)是正确的。
(B) (1)、(2)正确,(3)、(4)错误。
(C) (1)、(2)、(3)都正确,(4)错误。
(D) (1)、(2)、(3)、(4)都正确。
5.关于力矩有以下几种说法:
(1) 对某个定轴而言,内力矩不会改变刚体的角动量。
(2) 作用力和反作用力对同一轴的力矩之和必为零。
(3) 质量相等、形状和大小不同的两个物体,在相同力矩的作用下,它
们的角加速度一定相等。
在上述说法中,
[ ](A) 只有(2)是正确的; (B) (1)、(2)是正确的;
(C) (2)、(3)是正确的; (D) (1)、(2)、(3)都是正确的。
6.一圆盘正绕垂直于盘面的水平光滑固定轴O转动,如图射来两个质量相同、速度大小相同,方向相反并在一条直线上的子弹,子弹射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘的角速度
[ ](A) 增大 (B) 不变 (C) 减小 (D) 不能确定
二、填空题
1. 一质量为m的质点沿着一条空间曲线运动,该曲线在直角坐标系下的定义式为,其中皆为常数。
则此质点所受的对原点的力矩= ;该质点对原点的角动量= 。
2.一长为l、质量可以忽略的直杆,两端分别固定有质量为2m和m的小球,杆可绕通过其中心O且与杆垂直的水平
光滑固定轴在铅直平面内转动。
开始杆与水平方
向成某一角度,处于静止状态,如图所示。
释放
后,杆绕O轴转动,则当杆转到水平位置时,该系
统所受的合外力矩的大小M = __ ,
此时该系统角加速度的大小= 。
3.半径为R、具有光滑轴的定滑轮边缘绕一细绳,绳的下端挂一质量为m的物体,绳的质量可以忽略,绳与定滑轮之间无相对滑动,若物
体下落的加速度为a,则定滑轮对轴的
转动惯量J = 。
4. 在一水平放置的质量为m、长度为l的均匀细杆上,套着一个质量也为m的套管B(可看作质点),套管用细线拉住,它到竖直的光滑固定
轴OO′的距离为,杆和套管所组成的系统以角速度绕OO′轴转动,如图所示。
若在转动过程中细线被拉断,套管将沿着杆滑动。
在套管滑动过程中,该系统转动的角速度与套管轴的距离x的函数关系为 __。
(已知杆本身对OO′轴的转动惯量为)
三、计算题
0115-1. 有一半径为R的圆形平板放在水平桌面上,平板与水平桌面的摩擦系数为μ,若平板绕通过其中心且垂直板面的固定轴以角速度开始旋转,它将在旋转几圈后停止?
0563-2.一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的质量为,均匀分布在其边缘上。
绳子的A端有一质量为M的人抓住了绳端,而在绳的另一端B系了一质量为的重物,如图。
设人从静止开始以相对绳匀速向上爬时,绳与滑轮间无相对滑动,求B端重物上升的加速度。
(已知滑轮对过滑轮中心且垂直于轮面转动的轴的转动惯量)
0784-3.如图所示,一半径为R的匀质小木球固结在一长度为l的匀质细棒的下端,且可绕水平光滑固定轴O转动,今有一质量为m,速度为的子弹,沿着与水平面成角的方向射向球心,且嵌于球心。
已知小木球、细棒对通过O水平轴的转动惯量的总和为J。
求子弹嵌入球心后系统的共同角速度。
4. 一匀质细棒长为2l,质量为m,以与棒长方向相垂直的速度在光滑水平面内平动时,与前方一固定的光滑支点O发生完全非弹性碰撞。
碰撞点位于棒中心的一方处,如图所示。
求棒在碰撞后的瞬时绕点O转动的角速度。
(细棒绕通过其端点且与其垂直的轴转动时的转动惯量为,式中的m和l分别为棒的质量和长度。
)
答案:
一、选择题:①A、②A、③B、④B、⑤B、⑥C
二、填空题
1、0
2、mgl/2 2g/(3l)
3、
4、
三、计算题
1、设圆板旋转n圈后停止,由下面六个式子可得:
2、由于人与重物在一根绳子上,线加速度大小均为,方向相反。
再分别有牛二律:……① M是人的质量。
……②
另外,对滑轮有转动定律:
……③
因绳与滑轮无相对滑动:…………④
由以上四式解出:
3、以细棒、小球及子弹为系统,子弹射入时,系统所受合外力矩为零,故系统角动量守恒。
