完整版小升初数学专项训练 几何篇 答案
六年级下册数学试题-小升初专题训练-几何专题题库含答案
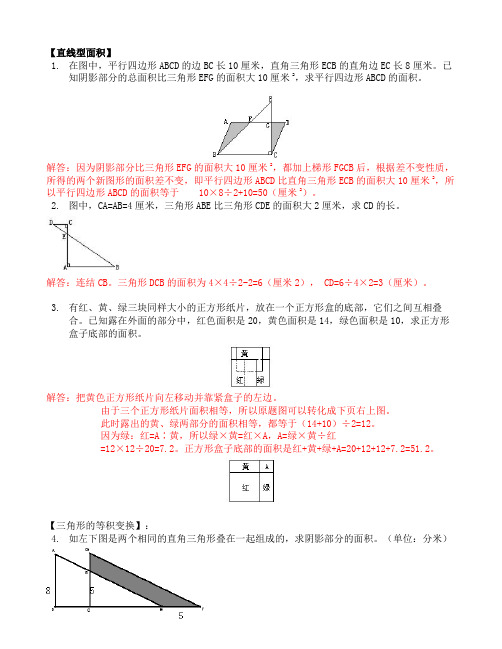
【直线型面积】1.在图中，平行四边形ABCD的边BC长10厘米，直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10厘米2，求平行四边形ABCD的面积。
解答：因为阴影部分比三角形EFG的面积大10厘米2，都加上梯形FGCB后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边形ABCD比直角三角形ECB的面积大10厘米2，所以平行四边形ABCD的面积等于10×8÷2+10=50（厘米2）。
2.图中，CA=AB=4厘米，三角形ABE比三角形CDE的面积大2厘米，求CD的长。
解答：连结CB。
三角形DCB的面积为4×4÷2-2=6（厘米2）， CD=6÷4×2=3（厘米）。
3.有红、黄、绿三块同样大小的正方形纸片，放在一个正方形盒的底部，它们之间互相叠合。
已知露在外面的部分中，红色面积是20，黄色面积是14，绿色面积是10，求正方形盒子底部的面积。
解答：把黄色正方形纸片向左移动并靠紧盒子的左边。
由于三个正方形纸片面积相等，所以原题图可以转化成下页右上图。
此时露出的黄、绿两部分的面积相等，都等于（14+10）÷2=12。
因为绿：红=A∶黄，所以绿×黄=红×A，A=绿×黄÷红=12×12÷20=7.2。
正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2。
【三角形的等积变换】：4.如左下图是两个相同的直角三角形叠在一起组成的，求阴影部分的面积。
（单位：分米）答案：32.5平方分米。
拓展：如图所示，已知正方形ABCD和正方形EFGC，且正方形EFGC的边长为6厘米，请问图中阴影部分面积是多少？答案：18平方厘米。
5.如图所示，在平行四边形ABCD中，DE=EF=FC,BG=GD.已知三角形GEF的面积是4平方厘米，求平行四边形的面积。
六年级下册数学试题-小升初分班考试数学之几何 人教版(含答案)
一、几何图形的相关概念及基本公式1、点、线、面、体；直线、射线、线段、角；长方形（体）、正方形（体）、平行四边形、三角形、题型、多边形、圆与扇形、圆柱、圆锥、轴对称图形2、平面图形的周长、面积公式，立体图形的侧面积、表面积、体积公式3、定理、结论：三角形内角和、三角形三边关系、勾股定理、一笔画、格点图形面积公式（毕克定理）4、几何计数二、巧求周长和面积1、通过平移、旋转、翻折（对称）、割补等手段将图形转化成比较好求的形状2、利用差不变原理将图形转化3、利用面积之比与边长之比的关系解题三、几何五大模型1、等高模型及变型（如一半模型、鸟头模型等）2、风筝模型（也叫蝴蝶模型）3、相似三角形（金字塔模型、沙漏模型）4、题型比例关系（题型蝴蝶模型）5、燕尾模型四、长方体正方体及侧面展开图、圆柱圆锥【例 1】如图，阴影部分是正方形，则最大长方形的周长是_ _____厘米．知识框架例题精讲3 几何10答案: 30【练习】 如图7-20，在直角梯形ABCD 中，三角形ABE 和三角形CDE 都是等腰直角三角形，且BC=20厘米，那么直角梯形ABCD 的面积是多少？答案: 200平方厘米【例 2】 如图，有一块长方形的草坪，长20米，宽10米，现要在草坪上铺设两条宽1米的小路，则剩下草坪的面积是________平方米.答案: 171【练习】 一块矩形场地被一条路隔成甲、乙两块，甲乙的面积之比为3:8，尺寸如图，甲的面积是＿＿＿＿。
21122乙甲答案: 60【例 3】 如图，一个梯形，面积为45，AB=10，高为6，则△AOB 的面积是___________.OCDA答案: 20【练习】如图，梯形ABCD的上底AD长5厘米，下底BC长12厘米，腰CD的长为8厘米，过B点向CD作出的垂线BE的长为9厘米，那么梯形ABCD的面积是多少？答案: 51平方厘米【例 4】已知如图，求阴影部分的面积（π取3.14）44答案: 4.56【练习】求图中阴影部分的面积。
小升初真题专练：图形与几何-小学数学六年级下册人教版(有答案 有解析)
小升初真题特训：图形与几何-小学数学六年级下册人教版学校:___________姓名：___________班级：___________考号：___________一、选择题1．（2022·湖南株洲·统考小升初真题）一个边长为acm的正方形（a＞2），相邻的两个边中，一个边增加2cm，一个边减少2cm，那么（ ）。
A．周长和面积都不变B．周长不变，面积变小C．面积不变、周长变大D．面积不变、周长变小2．（2022·江苏宿迁·统考小升初真题）小东看到一瓶墨水的包装盒上印有“净含量：120ml”字样，这个“120ml”指（）A．包装盒的体积B．墨水瓶的体积C．瓶内所装墨水的体积D．瓶内所装墨水的质量3．（2016·全国·小升初真题）下列轴对称图形中，对称轴最多的是（）。
A．B．C．D．4．（2022·云南昆明·统考小升初真题）一个长方形的长是6厘米，宽是4厘米。
如下图所示，以长为轴旋转一周形成圆柱甲，以宽为轴旋转一周形成圆柱乙。
下面说法正确的是（）。
①甲的底面积比乙的底面积大②甲的侧面积和乙的侧面积相等③甲的表面积与乙的表面积相等④甲的体积比乙的体积小A．②③B．②④C．①②③D．②③④5．（2020春·上海·五年级小升初模拟）（）个同样大小的小正方体能拼成一个大正方体。
A．12B．16C．27D．816．（2022·河南洛阳·统考小升初真题）小学阶段学的很多数学知识之间有着密切联系。
下面不能正确表示他们之间关系的是（）。
A．B．C．D．个．( )%。
16．（2021·广东深圳·统考小升初真题）一个圆锥形帐篷的底面周长是12.56m ，高是3m ，它的占地面积是( )，体积是( )。
17．（2022·河南焦作·统考小升初真题）把一个边长为25.12cm 的正方形纸卷成一个最大的圆柱（接头处不计），再给这个圆柱配一个底面，底面的面积是( )cm 2。
小升初数学几何热点“求阴影部分面积”专项练习(含解答)
小升初数学几何热点“求阴影部分面积”专项练习求平面图形中阴影部分的面积，是每年小升初考试中的几何热点，思维能力要求高，学生失分率高。
由于阴影部分的图形常常不是以基本几何图形的形状出现，没法直接利用课本中的基本公式来计算，所以比较麻烦。
家长辅导孩子处理这类型的几何题，除了要让孩子熟练地掌握平面图形的概念和面积公式之外，关键还在于懂得如何“巧用方法、妙在变形”。
以下是小学阶段常见的求阴影面积的方法，家长可以让孩子边做边总结方法，逐一攻关，体验解题思维的乐趣。
一、几何图形计算公式1.正方形：周长＝边长×4 C=4a面积=边长×边长 S=a×a2.正方体：表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3.长方形：周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4.长方体：表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)体积=长×宽×高V=abh5.三角形：面积=底×高÷2 s=ah÷26.平行四边形：面积=底×高 s=ah7.梯形：面积=(上底+下底)×高÷2 s=(a+b)×h÷28.圆形：周长=直径×π=2×π×半径 C=πd=2πr面积=半径×半径×π9.圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10.圆锥体：体积=底面积×高÷3二、解题方法解题要点：1.观察图形的特点，根据图形特点选择合适的方法求解图形的面积。
2.能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
小升初专项训练—第02讲几何篇1—解析及答案
第二讲小升初专项训练几何篇⑴解析与答案一、小升初考试热点及命题方向几何问题是小升初考试的重要内容，分值一般在12-14分（包含1道大题和2道左右的小题）。
尤其重要的就是平面图形中的面积计算，几何从内容方面，可以简单的分为直线形面积（三角形四边形为主），圆的面积以及二者的综合。
其中直线形面积近年来考的比较多，值得我们重点学习。
从解题方法上来看，有割补法，代数法等，有的题目还会用到有关包含与排除的知识。
二、知识要点1、三角形的等积变形⑴两个三角形的底高相等，则它们面积相等。
两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；⑵推广到平行四边形。
2、等分点结论( 共角模型、鸟头模型或鸟头定理)⑴两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．⑵共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．3、蝴蝶定理⑴任意四边形中的比例关系S1∶S2 =S4∶S3或 S1×S3 = S2×S4上、下部分的面积之积等于左、右部分的面积之积⑵梯形中的比例关系⑶长方形或正方形中的比例关系4、相似三角形性质：金字塔模型和沙漏模型。
5、共边：燕尾模型（燕尾定理）和风筝模型6、中间桥梁及“差不变”三、典型例题解析1、等积变换在三角形中的运用首先我们来讨论一下和三角形面积有关的问题，大家都知道，三角形的面积=1/2×底×高因此我们有【结论1】等底的三角形面积之比等于对应高的比【结论2】等高的三角形面积之比等于对应底的比这2个结论看起来很显然，可大家小看它们，在许多和三角形面积比有关的题目中它们都能发挥巨大的作用，因为它们把三角形的面积比转化为了线段的比，我们来看下面的例题。
【例1】（★★）如图，四边形ABCD中，AC和BD相交于O点，三角形ADO的面积=5，三角形DOC的面积=4，三角形AOB的面积=15，求三角形BOC的面积是多少？分析：等高的三角形，底之比＝＿＿＿＿＿＿＿＿（面积之比）解：15：5＝a：4a=12【练习】如下图，某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方千米，△BOC面积为2平方千米，△COD的面积为3平方千米，公园陆地的面积是6.92平方千米，求人工湖的面积是多少平方千米？分析：等高的三角形，底之比＝＿＿＿＿＿＿＿＿（面积之比）解：1：2＝a：3a=1.5(1+2+3+1.5)-6.92=0.58平方千米【例2】（★★）将下图中的三角形纸片沿虚线折叠得到右图，其中的粗实线图形面积与原三角形面积之比为2:3。
小升初数学几何图形专题训练含参考答案(5篇)
小升初数学几何图形专题知识训练含答案一、单选题1．甲数和乙数的比是4∶7，甲数是乙数的（）A．47B．74C．342．甲数的14和乙数的34相等，那么甲数（）乙数。
A．大于B．小于C．等于D．不能比较3．在一张长8厘米，宽6厘米的长方形纸上，剪下一个最大的正方形，这个正方形的面积是（）。
A．36平方厘米B．48平方厘米C．64平方厘米4．下面图形都是由3个边长1厘米的小正方形组成的，其中周长最长的是（）。
A．B．C．5．旋转能得到（）A．圆柱B．圆锥C．一个空心的球6．如图，图中的物体从（）看到的形状是相同的．A．正面和上面B．正面和右面C．上面和右面7．下面运用“转化”思想方法的是（）。
A．①和②B．①和③C．②和③8．下列叙述正确的是（）A．两个数的最小公倍数是它们最大公因数的倍数。
B．三角形的底和高扩大2倍，它的面积也扩大2倍。
C．相邻两个非0的自然数，其中一定有一个是合数。
9．两个完全相同的长方形（如图），将图①和图②阴影部分的面积相比，（）A．图①大B．图②大C．图①和图②相等10．下列说法中正确的有（）。
①2厘米长的线段向上平移10厘米，线段的长还是2厘米。
②8080008000这个数只读出一个“零”。
③万级包括亿万、千万、百万、十万、万五个数位。
④三位数乘两位数，积不可能是六位数。
A．2个B．3个C．4个二、填空题11．在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆(如图).圆的直径为厘米，半径为厘米；一个圆的周长为厘米，面积为平方厘米；长方形的面积是平方厘米，阴影部分的面积是平方厘米．12．一个梯形的上底是5.8厘米，下底是6.2厘米，高是2.5厘米，它的面积是平方厘米。
13．是由几个拼成的。
；；。
14．在横线上填上“平移”或“旋转”。
汽车行驶中车轮的运动是现象；推拉门被推开是现象。
15．把一个棱长为6 cm的正方体木块削成一个最大的圆柱，圆柱的体积是，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是。
小升初数学专项训练-几何篇-答案
小升初专项训练——几何篇一、解答题2．从一个长为8厘米，宽为7厘米，高为6厘米的长方体中截下一个最大的正方体，剩下的几何体的表面积是220平方厘米．最大正方体的棱长为6厘米，根据切割方法可知：切割后剩下表面积就是少了两个面积为6×6的，所以现在的面积为（8×7+8×6+7×6）×2﹣6×6×2=220平方厘米．解：（8×7+8×6+7×6）×2﹣6×6×2=（56+48+42）×2﹣72=220（平方厘米）；答：剩下的几何体的表面积是220平方厘米．3．有一个棱长为1米的立方体，沿长、宽、高分别切二刀、三刀、四刀后，成为60个小长方体（如图）．这60个小长方体的表面积总和是24平方米．根据正方体的切割方法可得：每切一次就增加2个正方体的面，一共切了2+3+4=9次，所以一共增加了2×9=18个面，一个面的面积是1×1=1平方米，所以切割后的表面积总和=正方体原来的表面积+增加的9个面的面积之和．解：1×1×6+1×1×（2+3+4）×2=6+18=24（平方米）；答：60个小长方体的表面积总和是24平方米．5．1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是多少个？表面涂漆的小正方体都在大正方体的表面上，由此可以先求得内部没有涂色的小正方体的个数，再利用小正方体的总个数﹣没有涂色的即可解答．解：共有小正方体：10×10×10=1000（个），其中没有涂色的为：（10﹣2）×（10﹣2）×（10﹣2）=8×8×8=512（个），所以至少有一面被油漆漆过的小正方体为1000﹣512=488（个）．答：至少有一面被油漆漆过的小正方体为488个．涂色的小正方体都在大正方体的表面上．8．如图，两个四分之一圆弧的半径分别是2和4，求两个阴影部分的面积差．（1）只要看清楚阴影部分如何构成则不难求解．较大面积的阴影部分是图形1；小阴影部分是图形2；长方形中的不规则白色部分是图形3；（2）图形1+3的面积等于大扇形减去小扇形；而图形2+3的面积等于长方形的面积；所以图形1+3﹣（图形2+3）=图形1﹣图形2的面积=大扇形减去小扇形，再减去长方形．解：π（42﹣22）﹣4×2=×3.14×12﹣8=9.42﹣8=1.42（平方厘米），答：两个阴影部分的面积差是1.42平方厘米．10．如图，AB与CD是两条垂直的直径，圆O的半径为15厘米，是以C为圆心，AC 为半径的圆弧，求阴影部分的面积．由图意可知：如图所示，连接AC、BC，则阴影部分的面积=半径为15厘米的圆面积的﹣（半径为AC的圆的面积﹣三角形ABC的面积），又因AB=30厘米，OC=15厘米，从而可以依据三角形ABC的面积求出AC的长度，进而求得阴影部分的面积．解：因为三角形ABC的面积为：=，所以AC2=30×15；阴影部分的面积=﹣（πAC2×﹣30×15×）=﹣（﹣），=﹣（）=225=225（平方厘米）；答：阴影部分的面积是225平方厘米．15．一个高为30厘米，底面为边长是10厘米的正方形的长方体水桶，其中装有容积的水，现在向桶中投入边长为2厘米×2厘米×3厘米的长方体石块，问需要投入多少块这种石块才能使水面恰与桶高相齐？由题意可知：所装入石块的体积应等于桶的容积的一半，用水桶的体积的除以每块石块的体积，就是所投入的石块的块数．解：（10×10×30）×÷（2×2×3）=3000×÷12=1500÷12=125（块）．答：需要投入125块这种石块才能使水面恰与桶高相齐．所装入石块的体积应等于桶的容积的一半，用水桶的体积的除以每块石块的体积，就是所投入的石块的块数．16．如图是由22个小正方体组成的立体图形，其中共有多少个大大小小的正方体？由两个小正方体组成的长方体有多少个？解答此题，应注意分类解决．（1）在求共有多少个正方体时，分为两种情况，由1个小正方体构成的正方体；由8个小正方体构成的正方体．（2）在求由两个小正方体组成的长方体时，根据方向来推算，可分为上下位、左右位、前后位三种．解：（1）正方体只可能有两种：由1个小正方体构成的正方体，有22个；由8个小正方体构成的2×2×2的正方体，有4个．所以共有正方体：22+4=26（个）．答：共有26个大大小小的正方体．（2）由两个小正方体组成的长方体，可分为上下位、左右位、前后位三种，其中上下位有13个，左右位有13个，前后位有14个，共有13+13+14=40（个）．答：由两个小正方体组成的长方体有40个．17．有甲、乙、丙3种大小的正方体，棱长比是1：2：3．如果用这三种正方体拼成尽量小的一个正方体，且每种都至少用一个，则最少需要这三种正方体共多少？设甲的棱长为1，则乙的棱长为2，丙的棱长为3．显然，大正方体棱长不可能是4，否则无法放下乙和丙各一个．于是，大正方体的棱长至少是5．事实上，用甲、乙、丙三种木块可以拼成棱长为5的大正方体，其中丙种木块只能用1块；乙种木块至多用7块（使总的块数尽可能少）；甲种木块需用5×5×5﹣3×3×3﹣7×2×2×2=42（块）．因此，用甲、乙、丙三种木块拼成体积最小的大正方体，至少需要这三种木块一共1+7+42=50（块）．解：设甲的棱长为1，则乙的棱长为2，丙的棱长为3，则大正方体的棱长至少为5，用甲、乙、丙三种木块可以拼成棱长为5的大正方体，其中丙种木块只能用1块；乙种木块至多用7块（使总的块数尽可能少）；甲种木块需用5×5×5﹣3×3×3﹣7×2×2×2=125﹣27﹣56=42（块），所以，用甲、乙、丙三种木块拼成体积最小的大正方体，至少需要这三种木块一共：1+7+42=50（块）．答：至少需要三种木块50块．18．现有一个长，宽，高都为1cm的正方体，一个长，宽，为1cm，高为2cm的长方体，三个长，宽为1cm，高为3cm的长方体．下列图是把这五个立体图形合并成某一立体图形时，从上面，前面，侧面所看到的图形．试利用下面三个图形把合并成的立体图形如（例）的样子画出来，并求出其表面积．先根据三视图得到立体图形的形状如右图所示：再根据面积公式分别求得从上面和下面看到的形状面积，从两个侧面看到的形状面积，从前面和后面看到的形状面积和隐藏着的面积，相加即可求解．解：立体图形的形状如右图所示．从上面和下面看到的形状面积都是9cm2，共18cm2；从两个侧面看到的形状面积都为7cm2，共14cm2；从前面和后面看到的形状面积都为6cm2，共12cm2．隐藏着的面积有2cm2．一共有18+16+12+2=46（cm2）．19．有两种不同形状的纸板，一种是正方形的，另一种是长方形的，正方形纸板的总数与长方形纸板的总数之比是1：2．用这些纸板做成一些竖式和横式的无盖纸盒．正好将纸板用完．问在所做的纸盒中，竖式纸盒的总数与横式纸盒的总数之比是多少？竖式纸盒要用1个正方形纸板和4个长方形纸板，横式纸盒要用2个正方形纸板和3个长方形纸板，设竖式纸盒有x个，横式纸盒有y个，根据题意即可解决问题．．解：设竖式纸盒有x个，横式纸盒有y个，那么正方形纸板一共有（x+2y）个，长方形纸板一共有（4x+3y）个，根据题意可得：（x+2y）：（4x+3y）=1：2根据比例的基本性质和等式的性质解得：x：y=1：2答：坚式纸盒的总数与横式纸盒的总数之比是1：2．故答案为：1：2．．20．图1是一个正方体，四边形APQC表示用平面截正方体的截面．请在图2中的展开图中画出四边形APQC的四条边．把立体图形表面的线条画在平面展开图上，只要抓住四边形APQC四个顶点所在的位置这个关键，再进一步确定四边形的四条边所在的平面就可容易地画出．解：（1）考虑到展开图上有六个顶点没有标出，可想象将展开图折成立体形，并在顶点上标出对应的符号，见左下图．（2）根据四边形所在立体图形上的位置，确定其顶点所在的点和棱，以及四条边所在的平面：顶点：A﹣A，C﹣C，P在EF边上，Q在GF边上．边AC在ABCD面上，AP在ABFE面上，QC在BCGF面上，PQ在EFGH面上．（3）将上面确定的位置标在展开图上，并在对应平面上连线．需要注意的是，立体图上的A，C点在展开图上有三个，B，D点在展开图上有二个，所以在标点连线时必须注意连线所在的平面，连好线的图形如右上图．21．将一个正方体（图1）剪开可以展成一些不同的平面图形（图2）．其中的图2的（1），（2）都是“带状图”，好像是一条完整的削下来的苹果皮．仔细观察（1），（2）两个图可以发现，图中的每个小正方形都有两个边与其它的正方形“共用”，除了两头的两个正方形以外．再观察（3）和（4），由于这两个图中每个都有一个正方形（粉色）有两条以上的边（（3）有3条，（4）有4条）与周围的正方形“共用”．所以（3）和（4）都不是“带状图”．问题1：运用你的空间想象力或者动手将图2的四个图折成正方体．问题2：除了（1）和（2）以外还有两个正方体的平面展开图也是“带状图”，你能找出来吗？解：（1）如下图：①“1”为下底，“6”为上底，其余为侧面，并且“2”的对面是“4”，“3”的对面是“5”，折成正方体；②“3”为上底，“6”为下底，其余为侧面，并且“1”的对面是“4”，“2”的对面是“5”，折成正方体；③“3”为上底，“1”为下底，其余为侧面，并且“2”的对面是“5”，“4”的对面是“6”，折成正方体；④“6”为上底，“5”为下底，其余为侧面，并且“1”的对面是“3”，“2”的对面是“4”，折成正方体；（2）除了（1）和（2）以外还有两个正方体的平面展开图也是“带状图”，即图5、图6：23．如图所示，求阴影面积，图中是一个正六边形，面积为1040平方厘米，空白部分是6个半径为10厘米的小扇形．由图意可知：所要求的阴影面积是用正六边形的面积减去六个小扇形面积，正六边形的面积已知，现在关键是求小扇形的面积，由扇形面积公式S扇=可求得，为此需要知道半径和扇形弧的度数，由已知正六边形每边所对圆心角为60°，那么∠AOC=120°，又知四边形ABCD是平行四边形，所以∠ABC=120°，这样就能求出扇形的面积．从而可以求得阴影部分的面积．解：如图所示，因为正六边形每边所对圆心角为60°，那么∠AOC=120°，又知四边形ABCD是平行四边形，所以∠ABC=120°，则：阴影部分的面积=1040﹣6×=1040﹣628=412（平方厘米）；答：阴影部分的面积是412平方厘米．25．如图，两个半径相等的圆相交，两圆的圆心相距正好等于半径，AB弦约等于17厘米，半径为10厘米，求阴影部分的面积．（1）阴影部分由两个相等的弓形组成，我们只需要求出一个弓形面积，然后二倍就是要求的阴影面积了．由已知若分别连接AO1，AO2，BO1，BO2，O1O2，如图所示，就可以得到两个等边三角形（各边长等于半径），则∠AO2O1=∠BO2O1=60°，即∠AO2B=120°．这样就可以求出以O2为圆心的扇形AO1BO2的面积，（2）然后再减去三角形AO2B的面积，就得到弓形面积，三角形AO2B的面积就是二分之一底乘高，底是弦AB，高是O1O2的一半．解：分别连接AO1，AO2，BO1，BO2，O1O2，如图所示，就可以得到两个等边三角形（各边长等于半径），则∠AO2O1=∠BO2O1=60°，即∠AO2B=120°．120°÷360°=，×3.14×102﹣17×（10÷2）÷2=×3.14×100﹣17×5÷2≈104.67﹣42.5=62.17（平方厘米）；62.17×2=124.34（平方厘米）答：阴影部分的面积是124.34平方厘米．26．2100个边长为1米的正方体堆成一个实心的长方体．它的高是10米，长、宽都是大于10（米）的整数，问长方体长宽之和是几米？2100个边长为1米的正方体堆成一个实心的长方体．则这个长方体的体积就是：1×1×1×2100=2100立方米；高是10米，所以底面积就是2100÷10=210平方米，由此将210分解质因数，并写成两个数的积的形式，即可判断出长与宽的值，从而求得它们的和．解：长方体体积是2100立方米，高为10米，所以底面积为210平方米．210=1×210=2×105=3×70=5×42=6×35=7×30=10×21=14×15．因长、宽都是大于10（米）的整数，所以长为15米，宽为14米，则长宽之和是15+14=29（米）．答：长与宽之和是29米．27．有一个正方体，边长是5．如果它的左上方截去一个边长分别是5、3、2的长方体（如图），求它的表面积减少的百分比是少？（1）利用正方体的表面积公式先求得原来正方体的表面积；（2）减少部分的表面积是：3×2的两个长方形的面的面积，由此即可求得减少的百分比．解：原立方体的表面积=5×5×6=150，减少的表面积是两块3×2长方形面积：3×2×2=12，12÷150×100%=8%，答：它的表面积减少的百分比是8%．28．如图，在棱长为3的正方体中由上到下，由左到右，由前到后，有三个底面积是1的正方形高为3的长方体的洞，求所得形体的表面积是多少？先计算没打洞之前正方体表面积，再计算打洞后表面积减少的和增加的（洞的表面积）面积各是多少，原面积减去减少的加上增加的，就是所得形体的表面积．这三个洞在正方体中间有交叉连接，在正方体的中心的表面积为0，洞的表面积为6个棱长为1的正方体的4个面的面积．解：没打洞之前正方体表面积共：6×3×3=54，打洞后，表面积减少：1×1×6=6，增加的面积：4×1×1×6=24（洞的表面积），所得形体的表面积是：54﹣6+24=72．答：所得形体的表面积是72．29．现有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一只深是5厘米的长方体无盖铁皮盒（焊接处及铁皮厚度不计，容积越大越好），你做出铁皮盒容积是多少立方厘米？由题意可知：要做这样的铁皮盒，有以下三种方法，分别计算出其容积，即可比较出哪个铁盒的容积最大；方法一：4个角分别剪去1个边长为5厘米的正方形，如右图一所示；方法二：将长方形的两个角分别剪去1个边长为5厘米的正方形，再将剪下的正方形焊接在右边，如图二所示；方法三：从长方形的宽的两端分别剪去宽为5厘米，长为20厘米的1个长方形，再分别焊接在另外两边，如图三所示．解：如图，可有如下三种情况比较后可知：（1）30×10×5=300×5=1500（立方厘米）；（2）35×10×5=350×5=1750（立方厘米）；（3）（40﹣10﹣10）×20×5=20×20×5=400×5=2000（立方厘米）；最后一个容积最大．答：做出铁皮盒容积最大是2000立方厘米．。
小升初数学专项训练——几何图形及其面积(含详细解析)
小升初数学专项训练——几何图形及其面积一、单选题1.求这个图形的面积，可把它分为长方形和（）。
A. 梯形B. 三角形C. 平行四边形D. 正方形2.在下图中你可以找到（）种简单的基本图形。
A. 1B. 2C. 3D. 43.把一个圆分成若干等份，剪开后拼成近似的长方形，那么这两个图形的（）A. 面积、周长都相等B. 面积、周长都不相等C. 面积相等，周长不相等D. 面积不相等，周长相等4.如图中，阴影部分（甲）与空白部分（乙）的周长相比（）A. 甲长B. 乙长C. 一样长5.如图所示，图中三角形的个数为（）A. 9个B. 10个C. 7个D. 4个6.如图中共有（）个三角形．A. 5B. 20C. 157.一个5边形的三个内角是直角，另外两个角相等，那么这两个角的度数是（）。
A. 100°B. 120°C. 135°二、判断题8.105厘米＞1米．9.100厘米比1米长．10. 1米的线段比100厘米的线段长。
11.梯形的内角和是180°。
（）12.任意四边形的内角和都是360°．三、填空题13.如图，CD=15厘米，AE=16厘米．AB﹣BC=1厘米，则三角形ABC的面积是________ 平方厘米．14.把棱长为1分米的正方体表面涂上红色后，再把它分成棱长为1厘米的小正方体．小正方体中只有一面涂色的有________ 个．15.如图，已知三角形ABC中，BD：DC=3：2，E是AD的中点，阴影部分的面积是13.5平方分米，三角形ABC的面积是________ 平方分米16.把这个物体放到地面上，观察并填空。
是由________个小正方体拼成的。
如果把这个图形的表面涂上绿色，不涂色的有________个小正方体；一个面涂绿色的有________个小正方体；有2个面涂绿色的有________个小正方体；有3个面涂绿色的有________个小正方体；有4个面涂绿色的有________个小正方体；有5个面涂红色的有________个小正方体。
苏教版数学小升初图形与几何专项训练含答案
苏教版数学小升初图形与几何专项训练一、填空。
(每空3 分，共27 分)1．在同一平面内，如果直线b 和c都与直线a垂直，那么直线b和c的位置关系是( )。
2．一个圆形花坛的直径是6 米，现在沿花坛的外围铺上一条宽1 米的水泥路，水泥路的面积是( )平方米。
3．如右图所示，图中正方形的面积为3 平方厘米，涂色部分的面积为( )平方厘米。
4．【苏州市改编】聪聪有9 根x厘米长的小棒和6 根y 厘米长的小棒，他用其中的12 根搭成了一个长方体框架，这个长方体框架的棱长总和是( )厘米。
5．右图中三角形ABC的面积是30 平方厘米，平行四边形BCDE的面积是( )平方厘米。
6．【南京市江宁区】典典用一些体积为1 立方厘米的小正方体搭出一个立方图形，并且从不同的方向观察后画出如图三幅图。
典典搭这个立体图形用了( )个小正方体，搭出的立体图形的表面积是( )平方厘米。
7．有3 个同样大的正方形，在里面画圆，如下图所示。
第3 图中所有圆周长的和是第1图中圆周长的( )倍；第3 图中所有圆的面积之和( )(填“大于”“小于”或“等于”)第2 图中圆的面积。
二、选择。
(将正确答案的字母填在括号里)(每小题3 分，共18 分)1．一个等腰三角形的两条边分别是9 cm 和4 cm ，那么这个三角形的周长是( )。
A ．22 cm 或17 cmB ．22 cmC ．17 cmD ．13 cm2．【新角度】一辆行驶中的小汽车前轮压碎了一个苹果，在路上留下了几个印记(如下图)。
苹果与第一个印记之间的距离大约是2 米。
这个“2 米”表示( )。
A ．车轮的周长B ．小汽车的车长C ．前后车轮之间的距离3．把绕点O 顺时针旋转90°后得到的图形是( )。
4．圆柱的体积不变，如果底面半径扩大到原来的2 倍，高应该( )。
A ．扩大到原来的4 倍B ．缩小到原来的14C ．缩小到原来的12D ．不变5．如图，在直径是20 厘米的半圆形内，剪去一个直径是10 厘米的小圆，剩下涂色部分的面积( )。
人教版小学数学小升初《图形与几何》专项练习(含答案)
人教版小学数学小升初《图形与几何》专项练习（含答案）一、认真审题，填一填。
(第3小题4分，其余每小题3分，共28分)1.如图，同同将一些练习本叠在一起，再将它们均匀斜放。
侧面图形变化后与原来相比，面积( )。
(填“变大”“变小”或“不变”)2.有3 cm、8 cm的小棒各两根，选其中三根围成一个等腰三角形，则它的周长是( )cm。
3.如图，把“俄罗斯方块”插入虚线部分，应先向( )平移( )格，再向( )平移( )格。
4.一个立体图形，从正面看到的形状是，从左面看到的形状是，搭一个这样的立体图形至少要( )个小正方体，最多要( )个小正方体。
5.用图中的铁皮正好能做成一个圆柱且没有浪费，已知小圆的直径是1分米，那么圆柱的高是( )分米，体积是( )立方分米。
(第5题图) (第6题图) (第7题图)6.如图是由棱长为 1 cm的小正方体拼成的，表面积是( )cm2，至少还需要( )个这样的小正方体才能拼成一个大正方体。
7.六一儿童节时，爸爸送给天天一个圆锥形的玩具(如图)。
如果用一个长方体盒子包装它，这个盒子的容积至少是( )cm3。
8.一个梯形的下底是18 cm，如果下底缩短8 cm，就成为一个平行四边形，并且面积减少28 cm2，原梯形的高是( )cm。
9.我们经常用到“转化思想”来解决问题，比如圆柱的体积计算。
把一个高为10 cm的圆柱切成若干偶数等份，拼成一个近似的长方体(如图)，这个长方体的长是12.56 cm，那么圆柱的体积是( )cm3。
二、仔细推敲，选一选。
(将正确答案的序号填在括号里)(每小题3分，共15分)1.右图表示一张纸片被一个图钉固定在墙上，纸片可以绕图钉旋转。
如果将纸片绕图钉顺时针旋转90°，那么得到的是( )。
A. B. C. D.2.龙龙参加团体操表演，他的位置用数对表示是(3，7)，这时的方队是一个正方形，参加团体操表演的至少有( )人。
A.9B.21C.49D.1003.如图是一个长3 cm、宽与高都是2 cm的长方体。
(小升初高频考点)图形与几何(专项训练)2022-2023学年六年级下册数学人教版(含答案)
（小升初高频考点）图形与几何（专项训练）2022-2023学年六年级下册数学人教版（含答案）（小升初高频考点）图形与几何（专项训练）2022-2023学年六年级下册数学人教版一．选择题（共7小题）1．（2022 保定）下列说法正确的是（）A．一条射线长50米B．2022年2月有29天C．3和4是互质数，它们也都是12的质因数。
D．圆柱的底面半径扩大2倍，高同时也扩大2倍，这个圆柱的体积就扩大8倍。
2．（2022 虎林市）一个角的两条边是两条（）A．直线B．射线C．线段D．以上都对3．（2022 揭东区）钟面上，9：30分针与时针所夹的角是（）A．直角B．锐角C．钝角D．平角4．（2022 杭州）下面立体图形的截面一定不是四边形的是（）A．B．C．D．5．（2022 茌平区）下列说法正确的是（）A．一个平行四边形拉成长方形后，它的周长、面积都不变B．一个三角形最少有一个角是锐角C．用同样长的铁丝围成的长方形、正方形、三角形、和圆，正方形的面积最大D．只有一组对边平行的四边形是梯形6．（2022 邢台）如图，点A、B、C都在格点上，请在方格纸上找一点D（D在格点上），使四边形ABCD是梯形，这样的D点有（）个。
A．3 B．4 C．5 D．67．（2022 万州区）有5根小棒，长度分别为3，3，4，6，6，用其中的3根做等腰三角形的边，可以搭出（）种不同的等腰三角形。
A．5 B．4 C．3 D．2二．填空题（共7小题）8．（2022 嵩县）直线、射线、线段中，能量出长度的是。
9．（2022 讷河市）在钟面上，6时的时候，分针与时针所夹的角的度数是，是一个角。
10．（2022 未央区）在一个三角形中，至少有个锐角，最多只能有一个角或角。
11．（2022 大余县）在同一平面内两条直线的位置关系有和。
12．（2022 山阳区）数学知识之间会有很多密切的关系。
许多知识可以用如图来表示。
例如：若B是长方形，那么A可以是。
难点：总集篇-七种典型几何模型专项练习-2024年小升初数学(解析版)
难点：总集篇·七种典型几何模型专项练习一、填空题。
1倾斜正方形的顶点G 恰好落在水平正方形的BC 边上。
如果水平正方形的面积是16，阴影三角形的面积是1，那么倾斜正方形的面积是()。
【答案】18【分析】连接DG ，三角形ADG 的面积是正方形ABCD 面积的一半，也就是8，而三角形ADG 的面积与三角形DEF 的面积之和等于正方形AEFG 面积的一半，进而求出正方形AEFG 的面积。
【详解】如图所示：16÷2=88+1=99×2=18【点睛】本题考查的是一半模型，合理作辅助线是求解问题的关键。
2如右图，在三角形ABC 中，BD =5DC ,AM =MD 。
则AE :EC =()。
【答案】5∶6【分析】连接CM ，△ABE 和△BEC 是同高的三角形，则这两个三角形的面积比就是这两个三角形底的比，即AE EC =S ΔABE S ΔBEC ，同理△AME 和△CEM 也是同高的三角形，即AE EC =S ΔAEM S ΔCEM ，综上所述AE EC=S ΔABE S ΔBEC =S ΔAEM S ΔCEM =S ΔABE -S ΔAEM S ΔBEC -S ΔCEM =S ΔABM S ΔBMC。
△ABM 和△BMD 是同高的三角形，且AM =MD ，则这两个三角形等底等高，面积也相等。
△BMD和△MDC也是同高的三角形，且BD=5DC，则这两个三角形的面积比就是两个底的比，即SΔBMDSΔMDC=51，可以设△MDC的面积是1，则△BMD的面积就是5，即△ABM的面积也是5，△BMC的面积=△MDC的面积+△BMD的面积=6，AEEC =SΔABMSΔBMC=56【详解】设△MDC的面积是1因为BD=5DC则△BMD的面积就是5因为AM=MD则△ABM的面积是5△BMC的面积是5+1=6AE EC =SΔABESΔBEC=SΔAEMSΔCEM=SΔABE-SΔAEMSΔBEC-SΔCEM=SΔABMSΔBMC=56则AE:EC=5∶6【点睛】设有四个三角形的面积分别是S1、S2、S3、S4，当S1S2=ab、S3S4=ab，根据内项积=外项积，bS1=aS 2、bS3=aS4，bS1-bS3=aS2-aS4，b(S1-S3)=a(S2-S4)，则S1-S3S2-S4=ab，得出结论当S1S2=S3S4=ab，则S1-S3 S2-S4=ab。
2022年小升初名校奥数专题训练：几何(附答案解析)
2022年小升初名校奥数专题训练：几何一、填空题（共5小题）1．如图，ABCD是边长为10厘米的正方形，且AB是半圆的直径，则阴影部分的面积是平方厘米．（π取3.14）2．如图边长为4的正方形ABCD和边长为6的正方形BEFG并排放在一起，O1和O2分别是两个正方形的中心（正方形对角线的交点），则阴影部分的面积是．3．如图，正方形ABCD的边长是5厘米，点E、F分别是AB和BC的中点，EC与DF交于点G，则四边形BEGF的面积等于平方厘米．4．如图所示的四个正方形的边长都是1，图中的阴影部分的面积依次用S1，S2，S3，S4表示，则S1，S2，S3，S4从小到大排列依次是．5．手工课上，小红用一张直径是20cm的圆形纸片剪出如图所示的风车图案（空白部分），则被剪掉的纸片（阴影部分）的面积是cm2．（π取3.14）二、解答题（共16小题）6．A、B两点分别是长方形的长和宽的中点，那么，阴影部分（如图）占长方形面积的（填几分之几）．7．在如图的梯形中，A，M，N分别为所在线段的中点，阴影部分面积为15cm2，求梯形的面积．8．如图由两个相同的梯形重叠在一起，求图中阴影部分的面积．（单位：厘米）9．如图所示的大正方形的边长是10cm，求阴影部分的面积．10．如图是由直径分别为4cm，6cm和10cm的三个半圆所组成的图形，求图中阴影部分的面积．（π取3.14）11．将16个相同的小正方体拼成一个体积为16的长方体，表面涂上漆，然后分开，则3个面涂漆的小正方体最多有个，最少有个．12．如图，棱长分别为1cm，2cm，3cm，5cm的四个正方体紧贴在一起，则所得多面体的表面积是cm2．13．一个长方体的棱长之和是28厘米，而长方体的长、宽、高的长度各不相同，并且都是整数厘米，则长方体的体积等于立方厘米．14．一个深30厘米的圆柱形容器，外圆直径是22厘米，壁厚1厘米，已装深27.5厘米的水．现放入一个底面直径10厘米，高30厘米的圆锥形铁块，则将有立方厘米的水溢出．15．用若干棱长为1cm的小正方体码放成如图所示的立体，则这个立体的表面积（含下底面面积）等于cm2．16．如图一个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是．（填序号）17．将一个表面积为30cm2的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体，求大长方体的表面积．18．有30个边长为1米的正方体，在地面上摆成如图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．19．有大、中、小三个正方形水池，它们的内边长分别为4m，3m，2m，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4cm和11cm，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？20．有一个棱长4cm的正方体，从它的右上方截去一个棱长分别为4cm，2cm，1cm的长方体（如图），求剩下部分的表面积．21．求如图所示（单位：cm）的机器零件的体积．2022年小升初名校奥数专题训练：几何参考答案与试题解析一、填空题（共5小题）1．如图，ABCD是边长为10厘米的正方形，且AB是半圆的直径，则阴影部分的面积是17.875平方厘米．（π取3.14）【解答】解：连接BE，如图：半圆面积：3.14×（10÷2）2÷2＝39.25（平方厘米），三角形ABE面积：102÷2÷2＝25（平方厘米），月牙面积：（39.25﹣25）÷2＝7.125（平方厘米），阴影面积：25﹣7.125＝17.875（平方厘米）．故答案为：17.875．2．如图边长为4的正方形ABCD和边长为6的正方形BEFG并排放在一起，O1和O2分别是两个正方形的中心（正方形对角线的交点），则阴影部分的面积是6．【解答】解：因为O1和O2分别是两个正方形的中心，所以直角梯形的上底与下底分别是2和3，（2+3）×5÷2﹣2×2÷2﹣3×3÷2，＝12.5﹣2﹣4.5，＝6．故答案为：6．3．如图，正方形ABCD的边长是5厘米，点E、F分别是AB和BC的中点，EC与DF交于点G，则四边形BEGF的面积等于5平方厘米．【解答】解：因为，△CGF∽△CBE，所以，GC＝BC×CF CE，GF＝BE×CF CE，GF×GC＝BC×BE×(CFCE)2，＝5×2.5×2.52 2.52+52，＝2.5（厘米），S（BEGF）＝S△CEB﹣S△CGF=12（EB×BC﹣CG×GF）=12×（5×2.5﹣2.5）＝5（平方厘米），答：四边形BEGF的面积等于5平方厘米，故答案为：5．4．如图所示的四个正方形的边长都是1，图中的阴影部分的面积依次用S1，S2，S3，S4表示，则S1，S2，S3，S4从小到大排列依次是S2＜S4＜S3＜S1．【解答】解：图（1）阴影面积：S 1=12πr 2﹣1×1=12×3.14×12﹣1＝1.57﹣1＝0.57； 图（2）阴影面积：S 2＝1×1﹣3.14×（12）2＝1﹣3.14×14=0.215； 图（3）阴影面积：①叶形面积：12×3.14×（12）2−12×12=0.1425， ②阴影面积：3.14×（12）2﹣2×0.1425＝0.785﹣0.285＝0.5； 图（4）阴影面积：斜线部分的面积是0.215，刚好和第二个图形的面积相等，而黑色部分正好是第四个图形比第二个图形多出的那部分，所以 S 4面积大于S 2面积．综上，S 2＜S 4＜S 3＜S 1．故答案为：S 2＜S 4＜S 3＜S 1．5．手工课上，小红用一张直径是20cm 的圆形纸片剪出如图所示的风车图案（空白部分），则被剪掉的纸片（阴影部分）的面积是 157 cm 2．（π取3.14）【解答】解：大圆的半径为：20÷2＝10（厘米），小圆的半径为：10÷2＝5（厘米），3.14×102﹣2×3.14×52，＝314﹣175，＝157（平方厘米），答：阴影部分的面积为157平方厘米．二、解答题（共16小题）6．A 、B 两点分别是长方形的长和宽的中点，那么，阴影部分（如图）占长方形面积的38 （填几分之几）．【解答】解：根据题意设长方形的长和宽分别为a ，b ，则长方形的面积是ab ，小三角形的面积=12a ×12b ×12=18ab阴影部分面积=12ab −18ab =38ab ，阴影部分（如图）占长方形面积的38ab ÷ab =38． 故答案为38． 7．在如图的梯形中，A ，M ，N 分别为所在线段的中点，阴影部分面积为15cm 2，求梯形的面积．【解答】解：如图， ，因为M 是BE 的中点，N 是CD 的中点，所以MN ＝（ED +BC ）÷2，设梯形的高为h ，则S 梯形BCDE ＝（ED +BC ）×h ÷2＝MN ×h ，因为S △ABN =12MN ×12h ×12=18MN ×h ，所以S 梯形BCDE ＝8S △ABN ＝8×15＝120（cm 2）．答：梯形的面积是120cm 2．8．如图由两个相同的梯形重叠在一起，求图中阴影部分的面积．（单位：厘米）【解答】解：（10﹣3+10）×4÷2＝17×4÷2＝34（平方厘米）答：阴影部分的面积是34平方厘米．9．如图所示的大正方形的边长是10cm，求阴影部分的面积．【解答】解：如图，连接AB，则AB∥CD，，因为△ACD和△BCD等底等高，所以S△ACD＝S△BCD，即S阴影＝S△BCD=12S正方形BCED=12×10×10＝50（cm2）．答：阴影部分的面积是50cm2．10．如图是由直径分别为4cm，6cm和10cm的三个半圆所组成的图形，求图中阴影部分的面积．（π取3.14）【解答】解：（6+4）÷2＝5（厘米）4÷2＝2（厘米）π×52÷2+π×22÷2＝（25+4）×π÷2＝45.53（平方厘米）答：图中阴影部分的面积是45.53平方厘米．11．将16个相同的小正方体拼成一个体积为16的长方体，表面涂上漆，然后分开，则3个面涂漆的小正方体最多有12个，最少有0个．【解答】解：16＝1×1×16＝2×2×4＝1×2×8＝1×4×4当16＝1×2×8时，3个面涂漆的小正方体最多有2×（8﹣2）＝12个；当16＝1×1×16时，3个面涂漆的小正方体最少有0个；故答案为：12；0．12．如图，棱长分别为1cm，2cm，3cm，5cm的四个正方体紧贴在一起，则所得多面体的表面积是194cm2．【解答】解：5×5×6+3×3×4+2×2×2＝150+36+8＝194（平方厘米）故答案为：194．13．一个长方体的棱长之和是28厘米，而长方体的长、宽、高的长度各不相同，并且都是整数厘米，则长方体的体积等于8立方厘米．【解答】解：棱长之和：28÷4＝7（厘米）；且长宽高各不相同又都是整数，可能的情况有（长大于宽）：①长2厘米，宽1厘米，高4厘米；体积：2×1×4＝8（立方厘米）；②长4厘米，宽1厘米，高2厘米；体积：4×1×2＝8（立方厘米）；③长4厘米，宽2厘米，高1厘米；体积：4×2×1＝8（立方厘米）；故答案为：8．14．一个深30厘米的圆柱形容器，外圆直径是22厘米，壁厚1厘米，已装深27.5厘米的水．现放入一个底面直径10厘米，高30厘米的圆锥形铁块，则将有0立方厘米的水溢出．【解答】解：原来水的体积是：3.14×(202)2×27.5＝8635（立方厘米），放入圆锥形铁块后圆柱形容器内的水的体积是：3.14×(202)2×30−13×3.14×(102)2×30，＝9420﹣785，＝8635（立方厘米），所以溢出的水的体积是：8635﹣8635＝0（立方厘米），答：则有0立方厘米的水溢出．故答案为：0．15．用若干棱长为1cm的小正方体码放成如图所示的立体，则这个立体的表面积（含下底面面积）等于60cm2．【解答】解：根据题干分析可得：（11×4+8×2）×1×1＝60（平方厘米），答：这个立方体的表面积是60平方厘米．故答案为：60．16．如图一个图形都是由六个相同的正方形组成的，其中，折叠后不能围成正方体的是①．（填序号）【解答】解：第①幅图中，通过折叠，上面两个正方形会重叠．故选①17．将一个表面积为30cm2的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体，求大长方体的表面积．【解答】解：30÷6＝5（平方厘米）30+5＝35（平方厘米）答：这个大长方体的表面积是35平方厘米．18．有30个边长为1米的正方体，在地面上摆成如图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．【解答】解：4×4+（1+2+3+4）×4＝56（平方米）答：被涂成红色的表面积是56平方米．19．有大、中、小三个正方形水池，它们的内边长分别为4m，3m，2m，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4cm和11cm，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？【解答】解：4厘米＝0.04米11厘米＝0.11米（3×3×0.04+2×2×0.11）÷（4×4），＝0.8÷16，＝0.05（米），＝5（厘米）；答：大水池水面将升高5厘米．20．有一个棱长4cm的正方体，从它的右上方截去一个棱长分别为4cm，2cm，1cm的长方体（如图），求剩下部分的表面积．【解答】解：4×4×6﹣1×2×2＝96﹣4＝92（平方厘米）答：剩下部分的表面积是92平方厘米．21．求如图所示（单位：cm）的机器零件的体积．【解答】解：4×5×2﹣3×3×1＝40﹣9＝31（立方厘米）答：机器零件的体积是31立方厘米．。
六年级小升初毕业考试总复习——几何图形专项复习(附答案)
六年级小升初毕业考试——几何图形专项训练⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧→⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧→→圆锥圆柱正方体长方体立体图形扇形圆环圆梯形正方形长方形平行四边形四边形三角形平面图形几何图形 一、平面图形知识要点：1. 三角形（1）三角形具有稳定性。
（2）三角形的内角和是180°。
（3）三角形三边关系：在一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边。
（4）三角形的面积=底×高÷22.四边形（1）长方形的周长=(长+宽）×2 长方形的面积=长×宽 （2）正方形的周长=边长×4 正方形的面积=边长×边长 （3）平行四边形的面积=底×高 （4）梯形的面积=（上底+下底）×高÷23.圆（1）圆的周长:c=πd c=2πr 圆的面积：s=πr ²（2）圆环的面积=外圆面积-内圆面积 s=πR ²-πr ²或 s=π（R ²-r ²） （3）扇形的周长=半径×2+弧长 c=2r+2πr ×360n扇形的面积=圆面积×360n s=πr ²×360n28m 近似三角形了，真有意思 ！1.(西城2019年小学毕业数学测查卷)一个用草绳编织成的茶杯垫的上面是圆形，将它沿半径剪开，下面说法不正确．．．的是( ). A.近似三角形的底相当于圆的周长 B.近似三角形的高相当于圆的半径 C.近似三角形的面积相当于圆的面积 D.近似三角形的面积相当于圆面和的212.(西城2019年小学毕业数学测查卷)一个长方体，有两个相对的面是正方形。
它的长是8cm.宽是5cm.这个长方体的表面积最少是( )cm 2.A.130B. 200C.210D. 2883.(西城2019年小学毕业数学测查卷)如下图小圆贴着大圆的内侧从A 点开始按箭头所指方向滚动(大圆不动．．．．)。
冀教版小升初数学图形与几何专项训练含答案
冀教版小升初数学图形与几何专项训练一、填空。
(每空1 分，共21 分)1．3.05 公顷=( )平方米18.5 立方分米=( )升=( )立方厘米45 分=( )时20.5 升=( )升( )毫升2．如图是某市32 路公共汽车的某段行车路线图。
32 路公共汽车从中心广场向( )行驶到养老院，再向( )偏( )( )°方向行驶到人民医院。
(第2题图) (第3题图) (第4题图) 3．如图，时针从“1”绕点O顺时针旋转90°后指向( )；时针从“1”绕点O顺时针旋转180°后指向( )。
4．在直径是6 cm 的圆中画出一个等腰直角三角形(如图)，图中涂色部分的面积是( )cm2。
5．一个梯形的下底是15 cm，如果把它的下底缩短5 cm，那么它就变成一个平行四边形，且面积减少20 cm2。
原梯形的高是( )cm。
6．一个长方体相交于同一个顶点的三条棱的长度之比是3 ∶ 2 ∶ 1，这个长方体的棱长总和是96 cm，它的体积是( )cm3。
7．一种圆柱形罐头盒的底面半径是4 cm，高是6 cm，要在盒外面贴一圈高4 cm 的商标纸，这个罐头盒需要商标纸( )cm2，至少需要( )cm2铁皮才能做这个罐头盒，这个罐头盒的体积是( )cm3。
8．一个棱长为4 dm 的正方体容器(厚度忽略不计)里面装满了水，刚好能倒满等底等高的圆柱形和圆锥形两个容器，则圆柱形容器的容积是( )L，圆锥形容器的容积是( )L。
9．[石家庄市] 墙角处堆了一堆沙子(如图)，呈圆锥形，已知底面的弧长是6.28 m，沙堆的高是2 m。
如果每立方米沙子重1.5 吨，那么这堆沙子重( )吨。
二、选择。
(将正确答案的字母填在括号里)(每小题2 分，共16 分) 1．一张长方形彩纸，连续对折两次后展开，折痕所在直线( )。
A．互相平行B．互相垂直C．可能互相垂直，也可能互相平行D．不垂直也不平行2．如图，把一个面积为28.26 cm 2的圆剪拼成一个近似的梯形，这个梯形的周长是( )cm。
小学数学-有答案-北师大版小升初数学专项分类训练：几何计算
小学数学-有答案-北师大版小升初数学专项分类训练：几何计算一、解答题（共14小题，满分0分）1. 计算下面各图中阴影部分的面积。
（单位：厘米）2. 看图计算。
图中阴影部分的面积是37平方厘米，求长方形的周长。
（单位：厘米）3. 如图，长方形的面积是40平方米，求阴影部分的面积。
4. 如图的平行四边形中，空白部分的面积是10平方分米，求涂色部分的面积。
（单位：分米）5. 用篱笆靠墙围一个花圃（如右图所示），如果用这个篱笆改围成一个靠墙的最大正方形。
正方形的面积是________．6. 如图是一个长方体纸盒的表面展开图，这个纸盒的用料面积至少是多少平方厘米？（单位：厘米）7. 如图，计算图形的周长和面积。
（单位：厘米）8. 如图，求图形的面积。
（单位：厘米）9. 如图，长方形ABCD的面积是12平方分米，那么圆的面积是________平方分米。
10. 如图，半圆中三角形ABO的面积(S1)是11平方厘米，O为圆心，半径长5厘米，求阴影部分的面积。
11. 如图是一块土地的形状，可以分割成一个平行四边形和一个三角形。
这块土地的面积是多少公顷。
12. 求右图直圆锥的体积。
（单位：厘米）13. 如图：ACEG是梯形、BDFG是正方形，GE=30厘米，GB=24厘米，AC=39厘米。
求梯形ACEG的面积。
参考答案与试题解析小学数学-有答案-北师大版小升初数学专项分类训练：几何计算一、解答题（共14小题，满分0分）1.【答案】阴影部分的面积为45平方厘米。
(2)3×3÷2−2×2÷2−3×1÷2=4.5−2−1.5=1（平方厘米）答：阴影部分的面积为1平方厘米。
(3)(7+4)×4÷2−3.14×(4÷2)2=22−12.56=9.44（平方厘米）答：阴影部分的面积为9.44平方厘米。
(4)10×10÷2=100÷2=50（平方厘米）答：阴影部分的面积为50平方厘米。
小升初专项训练—第03讲几何篇2—解析及答案
第3讲小升初专项训练几何篇⑵解析与答案一、小升初考试热点及命题方向圆和立体几何近两年虽然不是考试热点，但在小升初考试中也会时常露面。
因为立体图形考察学生的空间想象能力，可以反映学生的本身潜能；而另一方面，初中很多知识点都是建立在空间问题上，所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
二、知识要点1、小学阶段，学习的简单的立体图形，如长方体、正方体（立方体）、直圆柱体，直圆锥体、球体等，并且知道了它们的体积、表面积的计算公式，归纳如下。
见下图。
2、一个长方体有8个角、12条棱、6个面，角上的8个小立方体三面涂有红色，在棱上而不在角上的小立方体两面涂有红色，在面上而不在棱上的小立方体一面涂有红色，不在面上的小立方体没有涂上红色。
3、题型分类：⑴与圆和扇形有关的题型。
⑵求不规则立体图形的表面积与体积。
⑶水位问题。
⑷计数问题。
⑸三维视图的问题。
三、典型例题解析1、与圆和扇形有关的题型【例1】（★★）如下图，等腰直角三角形ABC的腰为10厘米；以A为圆心，EF为圆弧，组成扇形AEF；阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
解：10×10÷2×（360÷45）＝40平方厘米【例2】（★★★）草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊（见左下图）。
问：这只羊能够活动的范围有多大？解：30×30×3.14×3÷4＋20×20×3.14÷4＋10×10×3.14÷4＝2512平方米【例3】（★★）在右图中，两个四分之一圆弧的半径分别是2和4，求两个阴影部分的面积差。
解：如图，两个阴影部分的面积差＝①－③＝（①+②+④）－（③+②+④））＝大圆弧－（小圆弧+长方形）＝3.14×4×4÷4 -（3.14×2×2÷4+2×4）＝1.42【例4】（★★★）如图，ABCD 是正方形，且FA=AD=DE=1，求阴影部分的面积。
人教版六年级数学小升初图形与几何专项训练含答案
人教版六年级数学小升初图形与几何专项训练一、填空。
(每空1分，共24分)1. 780 cm2＝() dm20. 8平方千米＝()公顷8 m360 dm3＝() m37. 5 L＝()cm32. 在括号里填上适当的单位名称。
(1)长江是世界上第三大河，全长约6300()。
(2)一瓶洗手液250()。
(3)天安门广场上升起的国旗面积是16. 5()。
3. 一个几何体，从左面看到的图形是，从上面看到的图形是，搭这样的立体图形，至少需要()个小正方体，最多需要()个小正方体。
4. 等边三角形至少绕其中心点旋转()°与原图形重合，长方形至少绕其中心点旋转()°与原图形重合，正六边形至少绕其中心点旋转()°与原图形重合。
5. 一个梯形的上底是10厘米，下底是12厘米，高是8厘米。
若以梯形的上、下底为一组对边，剪去一个最大的平行四边形，则这个平行四边形的面积是()平方厘米；若在这个梯形中剪去一个最大的三角形，则剩余部分的面积是()平方厘米。
6. 如右图，圆的面积与长方形的面积相等，如果圆的周长是6. 28 cm，那么长方形的周长是()cm。
7. 用4个棱长为2 cm的小正方体摆出一个长方体，该长方体的表面积可能是()cm2，也可能是()cm2。
8. 把1 L水倒入甲容器中水深8 cm，倒入乙容器中水深12 cm，则甲容器与乙容器的底面积比是()。
9. 把一个圆柱削成一个最大的圆锥，削去部分的体积是24立方分米，则圆柱的体积是( )立方分米，圆锥的体积是( )立方分米。
10. 如图所示，在这个正方体的表面涂了一层颜色。
一面涂色的有()块，两面涂色的有()块，三面涂色的有()块，没有涂色的有()块。
二、选择。
(把正确答案的字母填在括号里，每题2分，共16分)1. 用两个长是7 cm、宽是4 cm的长方形拼成一个大长方形，这个大长方形的周长最短是()cm。
A. 22B. 30C. 36D. 282. 毕达哥拉斯说过：“一切平面图形中最美的是圆。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
几何-答案小升初数学专线训练-小升初专项训练——几何篇一、解答题2．从一个长为8厘米，宽为7厘米，高为6厘米的长方体中截下一个最大的正方体，剩下的几何体的表面积是220平方厘米．最大正方体的棱长为6厘米，根据切割方法可知：切割后剩下表面积就是少了两个面积为6×6的，所以现在的面积为（8×7+8×6+7×6）×2﹣6×6×2=220平方厘米．3解：（8×7+8×6+7×6）×2﹣6×6×2=（56+48+42）×2﹣72=220（平方厘米）；答：剩下的几何体的表面积是220平方厘米．3．有一个棱长为1米的立方体，沿长、宽、高分别切二刀、三刀、四刀后，成为60个小长方体（如图）．这60个小长方体的表面积总和是24平方米．根据正方体的切割方法可得：每切一次就增加2个正方体的面，一共切了2+3+4=9次，所以一共增加了2×9=18个面，一个面的面积是1×1=1平方米，所以切割后的表面积总和=正方体原来的表面积+增加的9个面的面积之和．解：1×1×6+1×1×（2+3+4）×2=6+18=24（平方米）；答：60个小长方体的表面积总和是24平方米．5．1000个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是多少个？表面涂漆的小正方体都在大正方体的表面上，由此可以先求得内部没有涂色的小正方体的个数，再利用小正方体的总个数﹣没有涂色的即可解答．解：共有小正方体：10×10×10=1000（个），其中没有涂色的为：（10﹣2）×（10﹣2）×（10﹣2）=8×8×8=512（个），所以至少有一面被油漆漆过的小正方体为1000﹣512=488（个）．答：至少有一面被油漆漆过的小正方体为488个．涂色的小正方体都在大正方体的表面上．8．如图，两个四分之一圆弧的半径分别是2和4，求两个阴影部分的面积差．（1）只要看清楚阴影部分如何构成则不难求解．较大面积的阴影部分是图形1；小阴影部分是图形2；长方形中的不规则白色部分是图形3；（2）图形1+3的面积等于大扇形减去小扇形；而图形2+3的面积等于长方形的面积；所以图形1+3﹣（图形2+3）=图形1﹣图形2的面积=大扇形减去小扇形，再减去长方形．22）﹣4×2=×3.14×12﹣8=9.424π解：（﹣2﹣8=1.42（平方厘米），答：两个阴影部分的面积差是1.42平方厘米．小升初数学专线训练-几何-答案10．如图，AB与CD是两条垂直的直径，圆O的半径为15厘米，是以C为圆心，AC为半径的圆弧，求阴影部分的面积．，则阴影部分的面BC由图意可知：如图所示，连接AC、圆的面半径为15厘米的圆面积的AC的﹣（半径为积=厘厘米，OC=15ABC的面积），又因AB=30积﹣三角形的长度，的面积求出AC米，从而可以依据三角形ABC 进而求得阴影部分的面积．2；=30×=解：因为三角形ABC的面积为：，所以AC152），）阴影部分的面积×=15×=﹣（πAC﹣×﹣30﹣（（平方厘米）；﹣（=225=225）= 225平方厘米．答：阴影部分的面积是容积的水，10厘米的正方形的长方体水桶，其中装有15．一个高为30厘米，底面为边长是问需要投入多少块这种石块才能3厘米的长方体石块，×2厘米×现在向桶中投入边长为2厘米使水面恰与桶高相齐？由题意可知：所装入石块的体积应等于桶的容积的一半，用水桶的体积的除以每块石块的体积，就是所投入的石块的块数．．÷12=125（块）3）=3000×÷12=1500÷（（解：10×10×30）×2×2×答：需要投入125块这种石块才能使水面恰与桶高相齐．就是所投所装入石块的体积应等于桶的容积的一半，用水桶的体积的除以每块石块的体积，入的石块的块数．其中共有多少个大大小小的正方体？由两个小22个小正方体组成的立体图形，如图是由16．正方体组成的长方体有多少个？解答此题，应注意分类解决．个小正方体构成的正1（1）在求共有多少个正方体时，分为两种情况，由个小正方体构成的正方体．方体；由8）在求由两个小正方体组成的长方体时，根据方向来推算，可分为上下（2 位、左右位、前后位三种．解：（1）正方体只可能有两种：所个．×22的正方体，有4个小正方体构成的22由1个小正方体构成的正方体，有个；由82×22+4=26以共有正方体：（个）．答：共有26个大大小小的正方体．2）由两个小正方体组成的长方体，可分为上下位、左右位、前后位三种，其中上下位有（13个，左右位有13个，前后位有14个，共有13+13+14=40（个）．答：由两个小正方体组成的长方体有40个．2小升初数学专线训练-几何-答案17．有甲、乙、丙3种大小的正方体，棱长比是1：2：3．如果用这三种正方体拼成尽量小的一个正方体，且每种都至少用一个，则最少需要这三种正方体共多少？3．，则乙的棱长为2，丙的棱长为设甲的棱长为1否则无法放下乙和丙各4，显然，大正方体棱长不可能是5．一个．于是，大正方体的棱长至少是的大正丙三种木块可以拼成棱长为5事实上，用甲、乙、；甲种木块需7块（使总的块数尽可能少）方体，其中丙种木块只能用1块；乙种木块至多用．因此，用甲、乙、丙三种木块拼成体积最小的（块）2×2=423﹣7×2×用5×5×5﹣3×3×．大正方体，至少需要这三种木块一共1+7+42=50（块）2，丙的棱长为3，则大正方体的棱长至少为5解：设甲的棱长为1，则乙的棱长为，用甲、乙、丙三种木块可以拼成棱长为5的大正方体，其中丙种木块只能用1块；乙种木块至多用7块（使总的块数尽可能少）；甲种木块需用5×5×5﹣3×3×3﹣7×2×2×2=125﹣27﹣56=42（块），所以，用甲、乙、丙三种木块拼成体积最小的大正方体，至少需要这三种木块一共：1+7+42=50（块）．答：至少需要三种木块50块．18．现有一个长，宽，高都为1cm的正方体，一个长，宽，为1cm，高为2cm 的长方体，三个长，宽为1cm，高为3cm的长方体．下列图是把这五个立体图形合并成某一立体图形时，从上面，前面，侧面所看到的图形．试利用下面三个图形把合并成的立体图形如（例）的样子画出来，并求出其表面积．先根据三视图得到立体图形的形状如右图所示：再根据面积公式分别求得从上面和下面看到的形状面积，从两个侧面看到的形状面积，从前面和后面看到的形状面积和隐藏着的面积，相加即可求解．解：立体图形的形状如右图所示．222，7cm9cm；从两个侧面看到的形状面积都为，共18cm从上面和下面看到的形状面积都是222．12cm；从前面和后面看到的形状面积都为6cm 共14cm，共22）．（cm 隐藏着的面积有2cm．一共有18+16+12+2=4619．有两种不同形状的纸板，一种是正方形的，另一种是长方形的，正方形纸板的总数与长方形纸板的总数之比是1：2．用这些纸板做成一些竖式和横式的无盖纸盒．正好将纸板用完．问在所做的纸盒中，竖式纸盒的总数与横式纸盒的总数之比是多少？竖式纸盒要用1个正方形纸板和4个长方形纸板，横式纸盒要用2个正方形纸板和3个长方形纸板，设竖式纸盒有x个，横式纸盒有y个，根据题意即可解决问题．．解：设竖式纸盒有x个，横式纸盒有y个，那么正方形纸板一共有（x+2y）个，长方形纸板一共有 3小升初数学专线训练-几何-答案（4x+3y）个，根据题意可得：（x+2y）：（4x+3y）=1：2根据比例的基本性质和等式的性质解得：x：y=1：2答：坚式纸盒的总数与横式纸盒的总数之比是1：2．故答案为：1：2．．20．图1是一个正方体，四边形APQC表示用平面截正方体的截面．请在图2中的展开图中画出四边形APQC的四条边．把立体图形表面的线条画在平面展开图上，只要抓住四边形APQC四个顶点所在的位置这个关键，再进一步确定四边形的四条边所在的平面就可容易地画出．解：（1）考虑到展开图上有六个顶点没有标出，可想象将展开图折成立体形，并在顶点上标出对应的符号，见左下图．（2）根据四边形所在立体图形上的位置，确定其顶点所在的点和棱，以及四条边所在的平面：顶点：A﹣A，C﹣C，P在EF边上，Q在GF边上．边AC在ABCD面上，AP 在ABFE面上，QC在BCGF面上，PQ在EFGH面上．（3）将上面确定的位置标在展开图上，并在对应平面上连线．需要注意的是，立体图上的A，C点在展开图上有三个，B，D点在展开图上有二个，所以在标点连线时必须注意连线所在的平面，连好线的图形如右上图．21．将一个正方体（图1）剪开可以展成一些不同的平面图形（图2）．其中的图2的（1），（2）都是“带状图”，好像是一条完整的削下来的苹果皮．仔细观察（1），（2）两个图可以发现，图中的每个小正方形都有两个边与其它的正方形“共用”，除了两头的两个正方形以外．再观察（3）和（4），由于这两个图中每个都有一个正方形（粉色）有两条以上的边（（3）有3条，（4）有4条）与周围的正方形“共用”．所以（3）和（4）都不是“带状图”．问题1：运用你的空间想象力或者动手将图2的四个图折成正方体．问题2：除了（1）和（2）以外还有两个正方体的平面展开图也是“带状图”，你能找出来吗？解：（1）如下图：，4”2”的对面是“为下底，“6”为上底，其余为侧面，并且“①“1””，折成正方体；的对面是“5“3”，”的对面是“4为下底，其余为侧面，并且“1”6②“3”为上底，“”，折成正方体；5”的对面是“2”““1”为下底，其余为侧面，并且“2”③“3为上底，”的对面是“5”，“4”的对面是“6”，折成正方体；④“6”为上底，“5”为下底，其余为侧面，并且“1”的对面是“3”，“2”的对面是“4”，折成正方体；（2）除了（1）和（2）以外还有两个正方体的平面展开图也是“带状图”，即图5、图6：4小升初数学专线训练-几何-答案23．如图所示，求阴影面积，图中是一个正六边形，面积为1040平方厘米，空白部分是6个半径为10厘米的小扇形．由图意可知：所要求的阴影面积是用正六边形的面积减去六个小扇形面积，正六边形的面积已知，现在关键是求小扇形的面积，由扇形面积公式S扇=可求得，为此需要知道半径和扇形弧的度数，由已知正六边形每边所对圆心角为60°，那么∠AOC=120°，又知四边形ABCD是平行四边形，所以∠ABC=120°，这样就能求出扇形的面积．从而可以求得阴影部分的面积．°，解：如图所示，因为正六边形每边所对圆心角为60 °，那么∠AOC=120 °，是平行四边形，所以∠ABC=120又知四边形ABCD（平方厘﹣628=4126×=1040则：阴影部分的面积=1040﹣412平方厘米．米）；答：阴影部分的面积是厘米，17弦约等于25．如图，两个半径相等的圆相交，两圆的圆心相距正好等于半径，AB厘米，求阴影部分的面积．半径为10）阴影部分由两个相等的弓形组成，我们只需要求出一个弓形面积，然后二倍就是要求的（1，如图所示，就可以得到两个，OO，AO，BO，BO阴影面积了．由已知若分别连接AO221211．这样就可以求B=120°=60°，即∠AOAO等边三角形（各边长等于半径），则∠O=∠BOO21221 BO的面积，出以O为圆心的扇形AO212的面积就是二分之一BAO）然后再减去三角形B的面积，就得到弓形面积，三角形AO（222的一半．AB，高是OO底乘高，底是弦21，如图所示，就可以得到两个等边三角形（各边OBO，O解：分别连接AO，AO，BO，221112，=°÷360°=60∠BOO°，即∠AO°B=120．120O，则长等于半径）∠AO=212122；42.5=62.17≈104.67﹣（平方厘米）2173.14）（×10÷2÷2=××100﹣×5÷103.14××17﹣124.342=124.34（平方厘米）答：阴影部分的面积是平方厘米．62.17×米，长、宽都是大于10126．2100个边长为米的正方体堆成一个实心的长方体．它的高是10（米）的整数，问长方体长宽之和是几米？2100个边长为1米的正方体堆成一个实心的长方体．则这个长方体的体积就是：5小升初数学专线训练-几何-答案1×1×1×2100=2100立方米；高是10米，所以底面积就是2100÷10=210平方米，由此将210分解质因数，并写成两个数的积的形式，即可判断出长与宽的值，从而求得它们的和．解：长方体体积是2100立方米，高为10米，所以底面积为210平方米．210=1×210=2×105=3×70=5×42=6×35=7×30=10×21=14×15．因长、宽都是大于10（米）的整数，所以长为15米，宽为14米，则长宽之和是15+14=29（米）．答：长与宽之和是29米．27．有一个正方体，边长是5．如果它的左上方截去一个边长分别是5、3、2的长方体（如图），求它的表面积减少的百分比是少？（1）利用正方体的表面积公式先求得原来正方体的表面积；（2）减少部分的表面积是：3×2的两个长方形的面的面积，由此即可求得减少的百分比．解：原立方体的表面积=5×5×6=150，减少的表面积是两块3×2长方形面积：3×2×2=12，12÷150×100%=8%，答：它的表面积减少的百分比是8%．28．如图，在棱长为3的正方体中由上到下，由左到右，由前到后，有三个底面积是1的正方形高为3的长方体的洞，求所得形体的表面积是多少？先计算没打洞之前正方体表面积，再计算打洞后表面积减少的和增加的（洞的表面积）面积各是多少，原面积减去减少的加上增加的，就是所得形体的表面积．这三个洞在正方体中间有交叉连接，在正方体的中心的表面积为0，洞的表面积为6个棱长为1的正方体的4个面的面积．解：没打洞之前正方体表面积共：6×3×3=54，打洞后，表面积减少：1×1×6=6，增加的面积：4×1×1×6=24（洞的表面积），所得形体的表面积是：54﹣6+24=72．答：所得形体的表面积是72．29．现有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一只深是5厘米的长方体无盖铁皮盒（焊接处及铁皮厚度不计，容积越大越好），你做出铁皮盒容积是多少立方厘米？由题意可知：要做这样的铁皮盒，有以下三种方法，分别计算出其容积，即可比较出哪个铁盒的容积最大；方法一：4个角分别剪去1个边长为5厘米的正方形，如右图一所示；方法二：将长方形的两个角分别剪去1个边长为5厘米的正方形，再将剪下的正方形焊接在右边，如图二所示；方法三：从长方形的宽的两端分别剪去宽为5厘米，长为20厘米的1个长方形，再分别焊接在另外两边，如图三所示．解：如图，可有如下三种情况比较后可知：（1）30×10×5=300×5=1500（立方厘米）；（2）35×10×5=350×5=1750（立方厘米）；（3）（40﹣10﹣10）×20×5=20×20×5=400×5=2000（立方厘米）；最后一个容积最大．答：做出铁皮盒容积最大是2000立方厘米．6。