离散数学
离散数学

3、:N×NN,N是自然数集 (0∈N),(<x,y>)=|x2-y2|
解: 取<1,1>,<2,2>∈ N×N (<1,1>)=|12-12|=0 (<2,2>)=|22-22|=0 故不是单射. 又取2∈N, 因不存在自然数x,y∈N 满足: |x2-y2|=2 故不是满射. ∴ 既不是单射也不是满射.
2019/3/2
离散数学
9
§3.2 映射的运算
• 逆映射的概念
定义3.2.1 设:AB,定义关系RBA为: R={<y,x> | y∈B , x∈A,且(x)=y};如果R是B 到A的映射,则称R为的逆映射。记为– 1。
• 例如:设:N E,N 是自然数集合,E是 自然数中所有偶数的集合,(n) = 2n,n∈N。 则的逆映射-1为: -1 :E N,-1(m)=m/2,m∈E。
§3.1 基本概念
定义3.1.1: 设A,B是两个集合,是A到B的二 元关系,若对A中每个元素a,有唯一的 b∈B, 使得<a,b>∈ ,则称为A到B的映射,记为: : AB 或 A B
• 所谓从A到B的映射就是A中的每个人都向B中 的人射了一箭,并且都射中了B中的一个人。 既没有人偷懒不射,也没有人一箭双雕。 • 这时,B中的人,有的可能身中数箭,有的可 能一箭未中。当然也可能刚好每人中了一箭。
• 充分性:设是双射,考虑的逆关系,易知,对于B 中的每个元素y,都对应着A中唯一的一个在下以y 为映象的元素x,因此, 的逆关系是B到A的映射。
2019/3/2 离散数学 4
满射、单射和双射的例子
• 设:N N,N 是自然数集,(n)= 2n, n∈N。则是 单射,但不是满射。
离散数学简介

数理逻辑
非欧几何的产生和集合论的悖论的发现, 说明数学本身还存在许多问题,为了研 究数学系统的无矛盾性问题,产生了证 明论
数理逻辑
证明论(proof theory)
– 证明论是数学家D.希尔伯特于20世纪初期建立的,目的是要
证明公理系统的无矛盾性 – 1931年,K.哥德尔证明:一个包含公理化的算术的系统中不 能证明它自身的无矛盾性。这就是著名的哥德尔不完备性定 理 – 1936年,G.根岑证明了算术公理系统的无矛盾性 – 20世纪60年代以后,证明论不再局限于无矛盾性的证明
数理逻辑
现代数理逻辑可分为
– 命题逻辑演算 – 谓词逻辑演算 – 证明论 – 模型论
– 递归函数论
– 公理化集合论等
数理逻辑
命题逻辑和一阶谓词逻辑是数理逻辑中 最成熟的部分,在计算机科学中应用最 为广泛
– 命题逻辑是数理逻辑的最基础部分 – 谓词逻辑在命题逻辑的基础上发展起来
数理逻辑
在数理逻辑的历史上,哥德尔的工作起着承前 启后的作用 他的不完全性定理,把人们引向一种完全不同 的境界 第一不完全性定理:一个包括初等数论的形式 系统,如果是协调的,那就是不完全的。
欧氏几何
欧氏几何的五条公理是:
– 1、任意两个点可以通过一条直线连接。 – 2、任意线段能无限延伸成一条直线。 – 3、给定任意线段,可以以其一个端点作为圆心,该线段作为半径作
离散数学是后继课程的基础 离散数学是实际应用的基础工具 计算机科学和离散数学处理问题的方法、思维 方式有相似之处 离散数学可提供所需的思维训练,培养所需的 分析问题和解决问题的能力
简介
离散数学是学习数据结构与算法、数据库、编 译原理、算法设计与分析、计算机网络等课程 的主要基础,对开发大型软件、研究信息安全 和密码学、开展计算机理论研究以及开发新型 计算机都提供了不可缺少的基础知识
02324离散数学知识点

02324离散数学知识点
离散数学是研究离散对象和离散结构的数学分支,其知识点包括但不限于集合论、图论、逻辑学、组合数学等。
以下是其中一些重要的知识点:
1. 集合论:集合论是离散数学的基石,它研究集合、集合之间的关系和集合的性质。
2. 图论:图论是离散数学的重要组成部分,它研究图(由节点和边构成的结构)的性质和分类。
3. 逻辑学:逻辑学是离散数学的另一个重要组成部分,它研究推理的规则和形式。
在离散数学中,逻辑通常用于描述和证明一些结构或系统的性质。
4. 组合数学:组合数学是离散数学的一个分支,它研究计数、排列和组合问题。
5. 离散概率论:离散概率论是离散数学的另一个分支,它研究离散随机事件的数学模型。
6. 离散概率分布:离散概率分布是描述离散随机事件发生概率的数学模型。
7. 离散随机变量:离散随机变量是能够取到可数无穷多个值的随机变量。
8. 离散概率空间:离散概率空间是一个集合,它包含一个可数无穷多的元素,每个元素都有一个与之相关的概率值。
9. 离散随机过程:离散随机过程是离散随机事件在时间或空间上的序列。
这些知识点都是离散数学的重要组成部分,它们在计算机科学、数学、物理学等领域都有广泛的应用。
离散的数学定义

离散的数学定义
离散数学是数学的一个分支,主要研究离散对象和离散结构之间的关系,重点关注离散的整数值、集合和图论等。
以下是离散数学的一些主要概念和定义:
1. 集合论:
- 集合是离散数学中最基本的概念之一,表示一组独立对象的总体。
集合论研究集合之间的关系、运算和性质。
2. 逻辑:
- 逻辑是研究命题和推理的学科,离散数学中的逻辑主要包括命题逻辑和谓词逻辑,用于研究命题的真假和推理规则。
3. 图论:
- 图论是离散数学的一个重要分支,研究图(vertices 和edges组成的结构)之间的关系和性质,包括图的遍历、连通性、最短路径等问题。
4. 离散结构:
- 离散结构指的是离散对象之间的关系和结构,如排列组合、树、图等。
离散数学研究这些结构的性质和应用。
5. 组合数学:
- 组合数学是离散数学的一个重要分支,研究离散对象的排列组合方式,包括排列、组合、二项式定理等。
6. 概率论:
- 离散概率论研究离散随机变量的概率分布和性质,包
括概率空间、随机变量、概率分布等。
7. 离散数学的应用:
- 离散数学在计算机科学、信息技术、密码学、通信等领域有着广泛的应用,如算法设计、数据结构、网络设计等。
总的来说,离散数学是研究离散对象和结构的数学分支,涉及集合论、逻辑、图论、组合数学等内容,在计算机科学和信息技术等领域具有重要的理论和实际应用。
高三离散数学知识点归纳

高三离散数学知识点归纳离散数学是一门重要的数学学科,它针对离散对象及其相互关系展开研究,对于培养学生的逻辑思维能力和抽象思维能力具有重要作用。
在高三阶段,学生需要系统学习离散数学的知识点,为高考备战做好准备。
本文将对高三离散数学知识点进行归纳,包括集合论、命题逻辑、组合数学等内容。
一、集合论1. 集合的基本概念集合是由确定的、无序的、互异的对象组成的总体。
集合的元素可以是数字、字母、符号等。
2. 集合的运算交集、并集、差集和补集是集合的四种基本运算,它们分别表示两个集合的共有元素、所有元素和剩余元素。
3. 集合的关系包含关系、相等关系和互斥关系是集合之间的三种常见关系,它们描述了集合之间的包含、相等和互斥的关系。
二、命题逻辑1. 命题与命题联结词命题是陈述句,它可以为真或者为假。
命题联结词包括非、与、或、蕴含和等价等,用于描述命题之间的逻辑关系。
2. 命题的真值表和逻辑运算真值表是描述命题与命题联结词之间关系的表格,通过真值表可以确定复合命题的真假性。
3. 命题的等价和蕴含两个命题等价表示它们具有相同的真值,而一个命题蕴含另一个命题表示当前者为真时,后者一定为真。
三、组合数学1. 排列与组合排列是从一组元素中取出若干元素进行排序,组合是从一组元素中取出若干元素不考虑排序。
排列和组合分别具有不同的计算公式。
2. 二项式定理二项式定理描述了两个数的幂展开的结果,它在组合数学中有重要应用。
四、图论1. 图的基本概念图由顶点和边组成,可以分为有向图和无向图。
顶点之间的边表示两个顶点之间的联系。
2. 图的遍历算法深度优先搜索和广度优先搜索是两种常见的图的遍历算法,用于查找图中的特定路径或者寻找与某个顶点相关的其他顶点。
五、数理逻辑1. 数理逻辑的基本概念数理逻辑是研究逻辑的形式系统化的学科,主要包括语言、公式、推理规则等内容。
2. 形式系统和推导规则形式系统是由一组公理和一组推导规则组成的,通过推导规则可以从公理出发推导出其他命题。
离散数学知识点总结

离散数学知识点总结离散数学是数学的一个分支,主要研究离散的数学结构和离散的数学对象。
它包括了许多重要的概念和技术,是计算机科学、通信工程、数学和逻辑学等领域的基础。
本文将对离散数学的一些核心知识点进行总结,包括命题逻辑、一阶逻辑、图论、集合论和组合数学等内容。
1. 命题逻辑命题逻辑是离散数学的一个重要分支,研究命题之间的逻辑关系。
命题是一个陈述语句,要么为真,要么为假,而且不能同时为真和为假。
命题逻辑包括逻辑运算和逻辑推理等内容,是离散数学的基础之一。
1.1 逻辑运算逻辑运算包括与(∧)、或(∨)、非(¬)、蕴含(→)和双条件(↔)等运算。
与、或和非是三种基本的逻辑运算,蕴含和双条件则是基于这三种基本运算得到的复合运算。
1.2 逻辑等值式逻辑等值式是指在命题逻辑中具有相同真值的两个复合命题。
常见的逻辑等值式包括德摩根定律、双重否定定律、分配率等。
1.3 形式化证明形式化证明是命题逻辑的一个重要内容,研究如何利用逻辑规则和等值式来推导出给定命题的真值。
形式化证明包括直接证明、间接证明和反证法等方法,是离散数学中的常见技巧。
2. 一阶逻辑一阶逻辑是命题逻辑的延伸,研究命题中的量词和谓词等概念。
一阶逻辑包括量词、谓词逻辑和形式化证明等内容,是离散数学中的重要部分。
2.1 量词量词包括全称量词(∀)和存在量词(∃),用来对命题中的变量进行量化。
全称量词表示对所有元素都成立的命题,而存在量词表示至少存在一个元素使命题成立。
2.2 谓词逻辑谓词逻辑是一阶逻辑的核心内容,研究带有量词的语句和谓词的逻辑关系。
谓词是含有变量的函数,它可以表示一类对象的性质或关系。
2.3 形式化证明形式化证明在一阶逻辑中同样起着重要作用,通过逻辑规则和等值式来推导出给定命题的真值。
一阶逻辑的形式化证明和命题逻辑类似,但更复杂和抽象。
3. 图论图论是离散数学中的一个重要分支,研究图和图的性质。
图是由节点和边组成的数学对象,图论包括图的表示、图的遍历、最短路径、最小生成树等内容,是离散数学中的一大亮点。
离散数学知识点整理
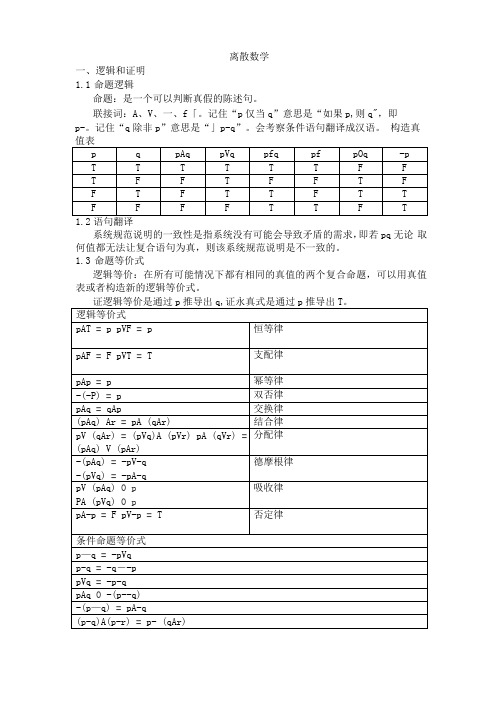
离散数学一、逻辑和证明1.1命题逻辑命题:是一个可以判断真假的陈述句。
联接词:A、V、一、f「。
记住“p仅当q”意思是“如果p,则q",即p-。
记住“q除非p”意思是“」p-q”。
会考察条件语句翻译成汉语。
构造真1.2语句翻译系统规范说明的一致性是指系统没有可能会导致矛盾的需求,即若pq无论取何值都无法让复合语句为真,则该系统规范说明是不一致的。
1.3命题等价式逻辑等价:在所有可能情况下都有相同的真值的两个复合命题,可以用真值表或者构造新的逻辑等价式。
证逻辑等价是通过p推导出q,证永真式是通过p推导出T。
(p—r)A(q-r) = (pVq)-r(p—q)V(p-r) = p—(qVr)(p—r)V(q-r) = (pAq)-r双条件命题等价式pf = (pfq) A (qfp)pf = -pfqpf Q (pAq) V(-pA-q)「(pf) = pfq1.4量词谓词+量词变成一个更详细的命题,量词要说明论域,否则没有意义,如果有约束条件就直接放在量词后面,如V x>0P(x)。
当论域中的元素可以一一列举,那么V xP(x)就等价于P(x1)AP(x2)...A P(xn)。
同理,3 xP(x)就等价于 P(x1)VP(x2)...VP(xn)。
两个语句是逻辑等价的,如果不论他们谓词是什么,也不论他们的论域是什么,他们总有相同的真值,如V x(P(x)AQ(x))和(V xP(x)) A (V xQ(x))。
量词表达式的否定:「V xP(x) Q 3 x-P(x),「3 xP(x) Q V x-P(x)。
1.5量词嵌套我们采用循环的思考方法。
量词顺序的不同会影响结果。
语句到嵌套量词语句的翻译,注意论域。
嵌套量词的否定就是连续使用德摩根定律,将否定词移入所有量词里。
1.6推理规则一个论证是有效的,如果它的所有前提为真且蕴含着结论为真。
但有效论证不代命题和量化命题的组合使用。
二、集合、函数、序列、与矩阵2.1集合£说的是元素与集合的关系,^说的是集合与集合的关系。
离散数学概述

1.计算学科的概念
攻关小组的结论是: 攻关小组的结论是:计算学科所研究的根本问 题是能行问题 什么能被(有效地)自动进行)。 能行问题( 题是能行问题(什么能被(有效地)自动进行)。 计算学科的基本原理已纳入理论、抽象和设计这3 计算学科的基本原理已纳入理论、抽象和设计这 个具有科学技术方法意义的过程中。 个具有科学技术方法意义的过程中。学科的各分支 领域正是通过这3个过程来实现它们各自的目标 个过程来实现它们各自的目标。 领域正是通过这 个过程来实现它们各自的目标。 而这3个过程要解决的都是计算过程中的 个过程要解决的都是计算过程中的“ 而这 个过程要解决的都是计算过程中的“能行性 有效性”问题。 ”和“有效性”问题。这两个问题渗透在包括硬件 和软件在内的理论、方法、 和软件在内的理论、方法、技术的研究和应用的研 究和开发之中, 究和开发之中,且学科的方法论的主要理论基础 ――以离散数学为代表的构造性数学与能行性问题 以离散数学为代表的构造性数学与能行性问题 形成了天然的一致。 形成了天然的一致。
1.计算学科的概念
计算学科作为现代技术的标志, 计算学科作为现代技术的标志,已成为世界 各国经济增长的主要动力。 各国经济增长的主要动力。但如何认识这门 学科,它究竟属于理科还是工科, 学科,它究竟属于理科还是工科,属于科学 还是属于工程的范畴, 还是属于工程的范畴,这是困扰国内外计算 机科学界很长时间且争论不休的问题。 机科学界很长时间且争论不休的问题。 计算学科诞生于20世纪 年代初, 世纪40年代初 计算学科诞生于 世纪 年代初,它的理论 基础可以说在这之前就已经建立起来了。 基础可以说在这之前就已经建立起来了。正 是电子数字计算机的问世才促进这一门学科 的发展。 的发展。
1.计算学科的概念
世人一般公认1946年2月14日研制成功 年 月 日研制成功 世人一般公认 的ENIAC(电子数字积分器和计算器, (电子数字积分器和计算器, Electronic Numerical Integrator and Calculator)是世界上第一台通用电子数字 ) 计算机(事实上,早在1943年,英国数学家 计算机(事实上,早在 年 图灵领导制造出了一台名叫“巨人” 图灵领导制造出了一台名叫“巨人”( Colossus)的电子计算机,它专门用于译 )的电子计算机, 由于英国政府的保密制度, 码。由于英国政府的保密制度,故人们对它 的成就了解甚少)。美国的普渡大学于1962 )。美国的普渡大学于 的成就了解甚少)。美国的普渡大学于 年开设了最早的计算机科学学位课程。 年开设了最早的计算机科学学位课程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1 命题和命题联结词
6.异或联结词 指的是排斥或,当且仅当p、q的真值相异时,p q为真。
由定义知 有如下性质: (1 p q等价于q p )
p F T
q F T F
p F T T
q
( 2) p q等价于( p q ) (p q ) F
T
例:今天第一节课上离散数学或数据结构。
p:王化的成绩很好。 q:王化的1 命题和命题联结词
3).析取词 命题p、q和 组成的复合命题记作p q, 读作“p或q”。
是自然语言中的“或” 、“或者”中的可兼或 的逻辑抽象。
p q
F T
p:开关坏了。 q:灯泡坏了。
开关坏了或灯泡坏了。 p∨q:
假 — 假命题
注意:此处不纠缠具体命题的真假问题,只是将其作为数学概念来处理。
3.命题和真值的符号化
命题 : 一般用p, q, r ,或pi , qi ,表示。
真值:真用T或1表示,假用F或0表示。
1.1 命题和命题联结词
原子命题:不能被分解为更简单的陈述句 复合命题:原子命题通过联结词联结而成
离散数学
离散数学
• • • • • 离散数学概述 第一部分 数理逻辑 第二部分 集合论 第三部分 图论 第四部分 抽象代数
第一部分 数理逻辑
• 寻找真理的人存在吗? • 上帝是万能的吗? • 你能获得会员资格吗?
桌子上摆着两个盒子:一个圆盒子,一个方盒子。 圆盒子上写着一句话:“申请不在盒中”。 方盒子上写着一句话:“这两句话中只有一句是真话”。 那么申请表在哪个盒子里呢?
1.1 命题和命题联结词
4、命题联结词
1).否定词 用命题p和“非”、“不”、“没有”等否定词组成的复合命题, 称作p的否命题,记作p, 读作“非p”。
是自然语言中的“非”、“不”和“没有”等的逻辑抽象。 如:p : 4是质数。 p: 4不是质数。
p
p
F
T
T
F
1.1 命题和命题联结词
1.1 命题和命题联结词
5).等价词 由命题p、q和 组成的复合命题记作p q, 读作“p当且仅当q”。 是自然语言中的“充要条件”,“当且仅当”的逻辑抽象。
p q的逻辑关系为p与q互为充要条件 p 例:1.3是有理数当且仅当加拿大位于亚洲。 2.两圆的面积相等,则他们的半径相等, 反之亦然。 F F T T q F T F T p q T F F T
p
F F
q
F T
T
T
F
T
T
T
1.1 命题和命题联结词
例:1.张晓婧爱唱歌或爱听音乐。 2.张晓婧是内蒙人或是陕西人。 3.张晓婧只能挑选202或203房间。
注意:当排斥或两边的情况实际根本不可能同时发生的时候,排斥或也 可抽象为∨。但为了方便起见一般不这样抽象。
1.1 命题和命题联结词
4).蕴涵词 由命题p、q和 组成的复合命题记作p q, 读作“如果p, 则q” 或“p条件q”。称为前件(前提),q称作后件(结论)。
第一部分 数理逻辑
一人在寻找真理,别人问他:“你真的不知道 真理是什么 吗?” 那个人说:“当然!” 别人又问:“你既然不知道真理是什么,当 你找到真理的时 候,你又如何辨别出来呢? 如果你辨别得出真理与否,那说明你已经知 道了真理是什 么,又何来寻找呢?”
第一部分 数理逻辑
上帝真的是万能的吗? 让我们来问提出一个问题:上帝是否能创造出一块连自 己都举不起来的石头? 如果上帝创造出了一块连他自己都举不起来的石头,那么上 帝就不是万能的,因为有一块石头他举不起来。 如果上帝不能创造出一块连他自己都举不起来的石头,那么 上帝也不是万能的,因为有一块石头他创造不出来。 所以无论上帝是否能创造出这么一块石头,他都不是万能的。
第一部分 数理逻辑
逻辑推理俱乐部门口贴着一张布告:“欢迎你加入推理俱乐部!只要你 通过推理取得一张申请表,就可以获得会员资格了!” 只见桌子上摆着两个盒子:一个圆盒子,一个方盒子。 圆盒子上写着一句话:“申请不在盒中”。 方盒子上写着一句话:“这两句话中只有一句是真话”。 那么申请表在哪个盒子里呢?
1.1 命题和命题联结词
1. 命题:能判断真假的陈述句。 包含两层意思:
自然语言中的陈述句 1)必须是陈述句 等式 不等式
2)能够确定(分辨)其真值。
注意:能否分辨真假与是否知道真假是不同的。 如:张校长的头发有一万根。
1.1 命题和命题联结词
2. 命题的真值:判断结果 真 — 真命题
是自然语言中的“如果 ,则 ”,“若 ,则 ” 的逻辑抽象。
有位父亲对儿子说:“如果我 去书店,就一定给你买电脑 报“。问:在什么情况下,
p F F T T
q F T F T
p T T F T
父亲算失信呢?
q
1.1 命题和命题联结词
注意:①“只要p,就q‘,’因为p,所以q”,“p仅 当q”, ‘只有q,才p“,”除非q才p“,”除非q,否则非 p“都可 抽象为p→q。 ②p,q可以没有任何内在联系。 例:1.如果3+3=6,那么雪是白的。 2.除非我能工作完成了,我才去看电影。 3.只要天下雨,我就回家。 4.我回家仅当天下雨。 p→q的逻辑关系为q是p的必要条件或p是q的充分条件。
1、设方盒子上写的话是真的,推出圆盒子上的话是假的,推出 申请表在圆盒子中。 2、设方盒子上的话是假的,推出圆盒子上的话也是假的,推出 申请表在圆盒子里。 3、或者方盒子上的话是真的,或者方盒子上的话是假的。总 之,申请表在圆盒子中。
第一部分 数理逻辑
数理逻辑: 是用数学方法研究逻辑或形式逻辑的学科。
1.1 命题和命题联结词
注意: ( )给定句子是否是命题 ,如:我和他是同学。 1 (2)要善于识别自然语言 中的联结词,如:狗急 跳墙。
例1.如果你和他不都是傻子 ,那么你们俩都不会去 自讨没趣。 2.如果你走路时看书,那 么你一定会成为近视眼 。 3.他虽有理论知识但无实 践经验。 4.选小陈或小周一人为代 表。 5.如果明天天气好,我们 去郊游,否则就不去。
推理:
是由一个或几个判断推出一个新判断的思维形式。 数学方法: 是指建立一套表意符号体系,对具体事物进行抽象的形 式研究的方法。
第一部分 数理逻辑
• 第一章 命题逻辑 • 第二章 一阶谓词逻辑
第一章 命题逻辑
• • • • • • 1.1 命题和命题联结词 1.2 命题公式及其赋值 1.3 等值演算与联结词完备集 1.4 析取范式与合取范式 1.5 推理的形式结构 1.6 自然推理系统P
T
F
1.1 命题和命题联结词
联结词的优先次序: (1 )由强到弱依次是:, , , , ,。 (2)按优先级书写,可以省略不必要的括号。 (3)同级的联结词,按从左往右的次序运算。
例:p:北京比天津人口多 q:2+2=4 r:乌鸦是黑色的
求以下命题的真值 ( )p q q r 1 (2)r q p q p
2).合取词 p、q是命题,由p、q和 组成的复合命题,记作p q, 读作“p与q”或“p合取q”。
是自然语言中的“并且”、 “既 又 ”、“不但 而且”、“虽然但是” 、“一面一面”等的逻辑抽象。
p F F T T q F T F T p q F F F T
