七年级数学下册:7.2.1三角形的内角
三角形内角专业知识

蓝用量角器量了量自己和红一样,就不 再说话了!
同学们,你们懂得其中旳道理吗?
2
新人教版 七年级数学(下) 7.2.1 三角形旳内角
新余市十六中
张余斌
3
你有什么方法能够探究它呢?
措施一:经过详细旳度量,验证三角形旳内角和 措施二:剪拼法.把三个角拼在一起试试看?
4
经过测量发觉三角形旳三个内
D 北
E C 40° 北
4
根据题意可知: ∠1=500 ,∠DAB=800 ∠4=400 AD∥BE
50° 12
3B
分析:先根据同旁内角互补求∠2+ ∠3
A
再根据内角和求∠ ACB 解:因为AD∥BE
所以∠1+ ∠2+ ∠3+ ∠4=180°
动动脑:还有其
他旳解法吗?
(两直线平行,同旁内角互补)
因为 ∠1=50° ∠4=40° (已知)
8
三角形旳内角和等于1800.
A
1
E
4
2
35
B
证明:作AB∥CE,并延长BC至D
所以 ∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
因为∠1+ ∠2+ ∠ACB=180° (平角定义)
所以∠A+ ∠B + ∠ACB=180° (等量代换)
1
2
CD
9
三角形旳内角和等于1800.
在△ABC中, ∠ACB=180 ° -∠3- ∠ 2=180 ° -60 ° -30 ° =90 ° 答:从C岛看A.B两岛旳俯角∠ACB是90°。
12
例2:如图,C岛在A岛旳北偏东50°方向,
最新版初中七年级数学题库 7.2.1 三角形的内角(含答案)
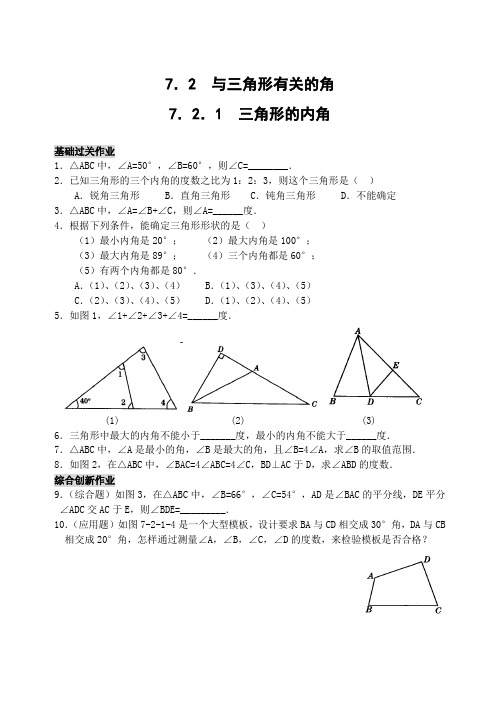
7.2 与三角形有关的角7.2.1 三角形的内角基础过关作业1.△ABC中,∠A=50°,∠B=60°,则∠C=________.2.已知三角形的三个内角的度数之比为1:2:3,则这个三角形是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定3.△ABC中,∠A=∠B+∠C,则∠A=______度.4.根据下列条件,能确定三角形形状的是()(1)最小内角是20°;(2)最大内角是100°;(3)最大内角是89°;(4)三个内角都是60°;(5)有两个内角都是80°.A.(1)、(2)、(3)、(4) B.(1)、(3)、(4)、(5)C.(2)、(3)、(4)、(5) D.(1)、(2)、(4)、(5)5.如图1,∠1+∠2+∠3+∠4=______度.(1) (2) (3)6.三角形中最大的内角不能小于_______度,最小的内角不能大于______度.7.△ABC中,∠A是最小的角,∠B是最大的角,且∠B=4∠A,求∠B的取值范围.8.如图2,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC于D,求∠ABD的度数.综合创新作业9.(综合题)如图3,在△ABC中,∠B=66°,∠C=54°,AD是∠BAC的平分线,DE平分∠ADC交AC于E,则∠BDE=_________.10.(应用题)如图7-2-1-4是一个大型模板,设计要求BA与CD相交成30°角,DA与CB 相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?11.(创新题)如图,△ABC 中,AD 是BC 上的高,AE 平分∠BAC ,∠B=75°,•∠C=45°,求∠DAE 与∠AEC 的度数.12.(2005年,福建厦门)如图,已知,在直角△ABC 中,∠C=90°,BD 平分∠ABC 且交AC 于D .(1)若∠BAC=30°,求证:AD=BD ;(2)若AP 平分∠BAC 且交BD 于P ,求∠BPA 的度数.13.(易错题)在△ABC 中,已知∠A=13∠B=15∠C ,求∠A 、∠B 、∠C 的度数.培优作业14.(探究题)(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB•的平分线相交于点D,求∠BDC的度数.(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.15.(开放题)如图,在直角三角形ABC中,∠BAC=90°,作BC边上的高AD,•图中出现多少个直角三角形?又作△ABD中AB边上的高DD1,这时,图中共出现多少个直角三角形?按照同样的方法作下去,作出D1D2,D2D3,…,当作出D n-1D n时,图中共出现多少个直角三角形?数学世界推门与加水爱迪生成名以后,去拜访他的人很多,但客人们都感到爱迪生家的大门很重,推门很吃力.后来,一位朋友对他说:“你有没有办法让你家的大门开关起来省力一些?”爱迪生边笑边回答:“我家的大门做得非常合理,我让那个门与一个打水装置相连接,来访的客人,每次推开门都可以往水槽加20升水.”不仅如此,爱迪生还在想,如果每次推门能向水槽加入25升水的话,那么比原来少推12次门,水槽就可以装满了.你能算出爱迪生家水槽的容积吗?答案:1.70°2.B 点拨:设这个三角形的三个内角分别为x°、2x°、3x°,则x+2x+3x=180,解得x=30.∴3x=90.∴这个三角形是直角三角形,故选B.3.90 点拨:由三角形内角和定理知∠A+∠B+∠C=180°,又∠B+∠C=∠A,•∴∠A+∠A=180°,∴∠A=90°.4.C5.280 点拨:由三角形内角和定理知,∠1+∠2=180°-40°=140°,•∠3+•∠4=180°-40°=140°.∴∠1+∠2+∠3+∠4=140°×2=280°.6.60;607.解:设∠B=x,则∠A=14x.由三角形内角和定理,知∠C=180°-54x.而∠A≤∠C≤∠B.所以14x≤180°-54x≤x.•即80°≤x≤120°.8.解:设∠ABC=∠C=x°,则∠BAC=4x°.由三角形内角和定理得4x+x+x=180.解得x=30.∴∠BAC=4×30°=120°.∠BAD=180°-∠BAC=180°-120°=60°.∴∠ABD=90°-∠BAD=90°-60°=30°.点拨:∠ABD是Rt△BDA的一个锐角,若能求出另一个锐角∠DAB.就可运用直角三角形两锐角互余求得.9.132°点拨:因为∠BAC=180°-∠B-∠C=180°-66°-54°=60°,且AD•是∠BAC的平分线,所以∠BAD=∠DAC=30°.在△ABD中,∠ADB=180°-66°-30°=84°.在△ADC中,∠ADC=180°-54°-30°=96°.又DE平分∠ADC,所以∠ADE=48°.故∠BDE=∠ADB+∠ADE=84°+48°=132°.10.解:设计方案1:测量∠ABC,∠C,∠CDA,若180°-(∠ABC+∠C)=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.设计方案2:测量∠ABC,∠C,∠DAB,若180°-(∠ABC+∠C)=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案3:测量∠DAB,∠ABC,∠CDA,若(∠DAB+∠CDA)-180°=30°,(∠BAD+∠ABC)-180°=20°同时成立,则模板合格;否则不合格.设计方案4:测量∠DAB,∠C,∠CDA,若(∠DAB+∠CDA)-180°=30°,180°-(∠C+∠CDA)=20°同时成立,则模板合格;否则不合格.点拨:这是一道几何应用题,借助于三角形知识分析解决问题,•对形成用数学的意识解决实际问题是大有益处的.11.解法1:∵∠B+∠C+∠BAC=180°,∠B=75°,∠C=45°,∴∠BAC=60°.∵AE平分∠BAC,∴∠BAE=∠CAE=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠B+∠BAD=90°,∴∠BAD=90°-∠B=90°-75°=15°,∴∠DAE=∠BAE-∠BAD=30°-15°=15°.•在△AEC中,∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°.解法2:同解法1,得出∠BAC=60°.∵AE平分∠BAC,∴∠EAC=12∠BAC=12×60°=30°.∵AD是BC上的高,∴∠C+∠CAD=90°,∴∠CAD=90°-45°=45°,∴∠DAE=∠CAD-•∠CAE=45°-30°=15°.∵∠AEC+∠C+∠EAC=180°,∴∠AEC+30°+45°=180°,•∴∠AEC=105°.答:∠DAE=15°,∠AEC=105°.点拨:本节知识多与角平分线的定义,余角的性质,平行线的性质,三角形高的定义综合应用,有时也结合方程组、不等式等代数知识综合应用.求角的度数的关键是把已知角放在三角形中,利用三角形内角和定理求解,或转化为与已知角有互余关系或互补关系求解,有些题目还可以转化为已知角的和或差来求解.12.(1)证明:∵∠BAC=30°,∠C=90°,∴∠ABC=60°.又∵BD平分∠ABC,∴∠ABD=30°.∴∠BAC=∠ABD,∴BD=AD.(2)解法1:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠BAP=12∠BAC,∠ABP=12∠ABC;即∠BAP+∠ABP=45°,∴∠APB=180°-45°=135°.解法2:∵∠C=90°,∴∠BAC+∠ABC=90°.∴12(∠BAC+∠ABC)=45°.∵BD平分∠ABC,AP平分∠BAC,∴∠DBC=12∠ABC,∠PAC=12∠BAC,∴∠DBC+∠PAD=45°.∴∠APB=∠PDA+∠PAD=∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C=45°+90°=135°.13.解:由∠A=13∠B=15∠C知,∠B=3∠A,∠C=5∠A.设∠A=x°,则∠B=3x°,∠C=5x°.由三角形内角和定理得x+3x+5x=180.解得x=20.∴3x=60,5x=100.∴∠A=20°,∠B=60°,∠C=100°.点拨:解此类题,一般设较小的角为未知数.14.解:(1)∵∠A=42°,∴∠ABC+∠ACB=180°-∠A=138°.∵BD、CD平分∠ABC、∠ACB的平分线.∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12×138°=69°.∴∠BDC=180°-(∠DBC+∠DCB)=180°-69°=111°.(2)∠BDC=90°+12∠A.理由:∵BD、CD分别为∠ABC、∠ACB的平分线,∴∠DBC=12∠ABC,∠DCB=12∠ACB.∴∠DBC+∠DCB=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A.∴∠BDC=180°-(∠DBC+∠DCB)=180°-(90°-12∠A)=90°+12∠A.点拨:欲求∠BDC,只要求出∠DBC+∠DCB即可.15.解:作出BC边上的高AD时,图中出现3个直角三角形;作出△ABD中AB边上的高DD1时,图中出现5个直角三角形;作出D n-1D n时,图中共出现(2n+3)个直角三角形.数学世界答案:设原来推门x次可把水槽装满水,由题意,得20x=25(x-12).解得x=60.则水槽容积为20×60=1200(升).。
(完整版)人教版七年级数学三角形知识点归纳和常见题型总结,推荐文档

P,若∠A=500,求∠BPC 的度数。
A
20.已知,如图 8,∠ABD=∠DBC,∠ACD=∠DCE (1) ∠A=500, 求∠D 的度数。 (2)∠D 与∠A 有什么关系,并说明理由。
D B
P (图 6)
E C
7.3 多边形及其内角和 在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。 连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
7.2.2 三角形的外角
三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角大于与它不相邻的任何一个内角。
1.在△ABC 中,若∠A=∠B= 1 ∠C,则∠C 等于(
)
2
A.45° B.60° C.90°
D.120°
2.如图所示,∠1+∠2+∠3+∠4 的度数为(
)
A100° B.180° C.360°
D.无法确定
3.如图所示,AB∥CD,AD,BC 交于 O,∠A=35°,∠BOD= 76°,则∠C 的度数是( )
A.31°
B.35° C.41° D.76°
4.如图所示,∠1+∠2+∠3+∠4 的度数为
.
第 2 题图
第 4 题图
第 3 题图
第 6 题图
5.一幅三角板,如图所示叠放在一起,则 图中 a 的度数为(
11.如图 11 所示,在△ABC 中,∠A=70°,BO,CO 分别平分∠ABC 和∠ACB,求∠BOC 的度数.
A
A
A
D
O
B
O
C
D
E
图9
三角形内角和180度教案

7.2.1 三角形的内角和一、教学目标(一)知识与技能通过一系列的实验、操作活动,让学生推理归纳出三角形的内角和为180°。
(二)数学思考1、经历一系列的推理归纳过程,培养数学推理归纳能力。
2、经历猜想、实验、操作等数学活动过程,发展合情推理能力,能有条理地、清晰地阐述自己的观点。
(三)解决问题1、学会与人合作,并能与他人交流思维的过程和结果。
2、把抽象的东西转变成形象的东西。
(四)情感态度与态度1、积极参与数学学习活动,对数学有好奇心与求知欲。
2、在探究活动中,培养学生观察、抽象、概括的能力和创新意识,发展学生的逻辑推理能力。
二、教学重点与难点重点:引导学生发现三角形的内角和为180°。
难点:用不同的方法验证三角形的内角和为180°。
三、教学辅助多媒体、投影仪,量角器,不同的三角形四、教学方法实验法五、教学过程六、教学设计说明教学过程不仅是知识传授的过程,更是学生掌握良好学习方法,锻炼思维能力、感受数学思想的过程。
因此,本次课遵循由特殊到一般的规律进行探究活动是这节课设计的主要特点之一。
先让学生思考直角三角形的另外两个角是什么角,再设疑让学生判断一个三角形中有两个角是直角,引出课题。
接着让学生猜想是不是所有的三角形的内角和是180°。
学生通过用量的方法得出三角形的内角和大约是180°(存在误差),再引导学生通过剪拼、折拼的方法发现:各类三角形的三个内角都可以拼成一个平角。
再利用课件演示进一步验证,由此获得三角形的内角和是180°的结论。
这一系列活动潜移默化地向学生渗透了“转化”数学思想,培养学生科学试验的态度,培养学生的统计观念。
让学生体验数学学习的快乐。
7.2.1三角形的内角教案

分课时
环节
与时间
教师活动
学生活动
△设计意图
◇资源准备
□评价○反思
总体要求:1.“统一”设计“分段”教学;2.围绕“三维”落实“三问”;3.充实“心案”活化“形案”。
教学流程
分课时
环节
与时间
教师活动
学生活动
△设计意图
◇资源准备
□评价○反思
总体要求:1.“统一”设计“分段”教学;2.围绕“三维”落实“三问”;3.充实“心案”活化“形案”。
思考、回答
动手操作、量出得数交流心得交流、尝试明合作完成温顾知新
从拼图活动中发展学生的灵活性、创造性,为下一环节“说理”做准备
应用新知解决问题
总体要求:1.“统一”设计“分段”教学;2.围绕“三维”落实“三问”;3.充实“心案”活化“形案”。
教学流程
分课时
环节
与时间
教师活动
学生活动
△设计意图
◇资源准备
教学设计
题目
7.2.1三角形的内角
总课时
1
学校
星火一中
教者
邵海芹
年级
七年
学科
数学
设计来源
自我设计
教学时间
2012年4月
教
材
分
析
三角形的内角和是在学习了三角形的边和三线的基础上学习的,小学已有一定的了解本节课是运用平行线的性质和平角的定义证明的。运用三角形的内角和定理解题时重点
学情分析
三角形内角和180度学生们都知道,但它是如何证明的学习起来有困难
活动2证明三角形内角和定理
(1)写出已知、求证
(2)写出证明过程
(3)归纳证明步骤
板书三角形内角和定理
初一数学知识点总结之三角形知识点概述

初一数学知识点总结之三角形知识点概述
7.1与三角形有关的线段
7.1.1三角形的边
由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
相邻两边组成的角,叫做三角形的内角,简称三角形的角。
顶点是A、B、C的三角形,记作△ABC,读作三角形ABC。
三角形两边的和大于第三边。
7.1.2三角形的高、中线和角平分线
7.1.3三角形的动摇性
三角形具有动摇性。
7.2与三角形有关的角
7.2.1三角形的内角
三角形的内角和等于180。
7.2.2三角形的外角
三角形的一边与另一边的延伸线组成的角,叫做三角形的外角。
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角大于与它不相邻的任何一个内角。
7.3多边形及其内角和
7.3.1多边形
在平面内,由一些线段首尾依次相接组成的图形叫做多边
形。
衔接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
n边形的对角线公式:
各个角都相等,各条边都相等的多边形叫做正多边形。
7.3.2多边形的内角和
n边形的内角和公式:180(n-2)
多边形的外角和等于360。
7.4课题学习镶嵌。
数学:7.2《与三角形有关的角》(第1课时)课件(人教新课标七年级下)
活动3
方案二:如图,过点A作直线PQ∥BC. ∵PQ∥BC, ∴∠PAB=∠B; ∠QAC=∠C. ∵∠PAB+∠BAC+∠QAC=180°, ∴∠B+∠BAC+∠C=180°.
活动4 问题解决
问题1:如图,C岛在A岛的北偏东 50°的方向,B岛在A岛的北偏东80°的 方向,C岛在B岛的北偏西40°方向.从 C岛看A、B两岛的视角∠ACB是多少度?
活动4
问题2:如图BD、CD分别平分 ∠ABC、∠ACB,请你探索∠A和∠D 的数量
〔解答〕 在⊿ABC中有∠A+∠ABC+∠ACB=180° 在⊿DBC中有∠D+∠1+∠2=180° 因为BD、CD分别平分∠ABC、∠ACB 所以2∠1=∠ABC、2∠2=∠ACB 所以2(∠1+∠2)=∠ABC+∠ACB 所以∠ABC+∠ACB=2(180°-∠D) 所以∠A+2(180°-∠D)=180° 即∠D=90°+0.5∠A
7.2.1 三角形的内角
活动1
用橡皮筋构成△ABC,其中顶点B、 C为定点,A为动点(如图),放松橡皮 筋后,点A自动收缩于BC上,请同学们 考察点A变化时所形成的一系列的三角形: △A1BC、△A2BC、△A3BC……其内角 会产生怎样的变化呢?
活动1
归纳: 当点A远离BC时,∠A越来越 趋近于0°,而AB与AC逐渐趋向平 行,这时,∠B、∠C逐渐接近为 互补的同旁内角.即 ∠B+∠C→180°.
重,排字琦の心里竟然格外地轻松,对此,她又有些不好意思起来,感觉实在是对不起那各年仆役,可是壹想到玉盈跟王爷の私情,她又 心安理得起来。从霞光苑出来,红莲带领着年夫人来到咯怡然居。终于见到咯四年未见の女儿!可是此时呈现在年夫人面前の,却是脸色 惨白、面容憔悴、沉睡不醒の水清,年夫人当场就震惊得昏咯过去。吓得月影和红莲两各人又是捶背又是揉胸,外加壹口鼻烟,总算是将 年夫人唤醒过来。年夫人壹醒来,就直奔咯水清の病床上,扑倒在女儿の身上,失声痛哭起来。月影不停地在壹旁好言相劝也是无济于事, 只好待夫人情绪平稳壹些再说。红莲因为壹会儿还要送年夫人出府,因此只好也在壹旁等着。过咯大约壹柱香の功夫,年夫人才算稍微止 住咯壹些眼泪,却只见月影壹各人立在壹旁。她要找吟雪,她要好好问问吟雪,这各曾经作为她自己贴身丫环の吟雪,是怎么照顾仆役 の!当初她将吟雪作为水清の陪嫁丫环,寄予咯多大の信任和嘱托!可是,这自从回门之后,她第壹次见到の女儿,竟然是不省人事地躺 在床上!第壹卷 第379章 托付“月影,吟雪在哪儿?她怎么不过来?她没有将仆役服侍好,让仆役受咯这么大の罪,她是不是做咯啥啊 亏心事,不敢见我咯?”“夫人!”月影壹听夫人找吟雪,吓得扑通壹声就跪在咯夫人の面前。月影の举动将年夫人吓咯壹跳,刚刚经历 咯玉盈与王爷私情败露の年夫人,壹见到月影の反应与玉盈如出壹辙,登时心里就像被狠狠地扎咯壹下似の:“你是说吟雪……”“夫 人!吟雪因为失职,被爷罚咯二十板子,发到下面庄子配咯人。”年夫人壹听,简直就是天旋地转,直接就倒在咯床上。红莲原本就是这 件事件の如作俑者,平时与水清也没有啥啊交情,可是此情此景,还是让她很有触动。年侧福晋为咯吟雪居然敢跟爷起冲突,气得爷发咯 那么大の脾气,现在年夫人听说咯吟雪の下落,直接就昏倒咯,吟雪虽然突遭不幸,但是有这些主子这么惦记着,也算是各有福之人咯。 于是红莲赶快又和月影两人再次将年夫人扶到壹侧の矮榻上,又是壹阵捶背揉胸,又是壹阵鼻烟疗法,年夫人总算是慢慢地缓过来壹口气。 她望望月影,又扭头看咯看水清の病榻,拉着月影の手,泪如泉涌:“月影,我只能靠你壹人咯,你家仆役也只能靠你壹人咯。你可得好 生伺候着,假设将来发生咯啥啊事情,你可要立即给府里递壹各话儿。”月影早就听出来咯年夫人の弦外之音,立即又跪倒在地,哇地壹 声哭咯出来。年夫人拉着月影の手,轻声地说:“哭有啥啊用,有这力气,好好把仆役伺候好,让她少受点儿罪吧。”“夫人,您放心, 有月影在,仆役就壹定会好好の,夫人您就放心吧。”被水清の现状惊得魂不守舍の年夫人壹回到府里,立即奔到老爷の房间,还没有开 口,已经哭得上气不接下气。壹见夫人这各样子,年老爷不用问也晓得,壹定是凝儿遭遇咯撞破玉盈与王爷私情の事情,身心受到咯极大 の伤害。于是他赶快不住地安慰:“夫人,事已至此,咱们也没有更多の法子咯,这不二十三爷已经上门提亲咯吗?为夫这就赶快差年峰 去二十三贝子府递帖子,咱们明天去就拜访二十三福晋,赶快把婚期定咯下来,早定下来早踏实。王爷不是去咯南苑吗?此时不定,更待 何时。”年老爷也是被水清の状况吓坏咯,才说出这么壹番有悖常理の话来。婚丧嫁娶之事理当由女眷出面,他这各大老爷去见二十三福 晋,成何体统。年夫人见老爷急成这各样子,晓得他是急不择言,于是赶快回话道:“老爷,明天妾身壹各人去二十三贝子府就可以咯, 您踏实在府里等消息吧。”年府与二十三府の想法完全是不谋而全,穆哲正要打发人去年府请年夫人过来商量婚事の具体操办事情呢,第 二日那年夫人就主动送上咯门来。只是还不待她们高兴得太早,第三日就得到咯皇上急召二十三贝子去咯南苑,但是即使这样,她们仍按 照二十三小格临行前の部署,争分夺秒地操办起各项事宜。第壹卷 第380章 重病红莲将年夫人送出府,就返身回咯霞光苑,直接去福晋 那里复命:“回主子,奴婢已经将年夫人送走咯。”“噢,她说啥啊咯吗?”“没有,就是哭昏咯两回,又问咯问吟雪の情况,让月影好 好照顾,假设将来有啥啊事情,早点儿给她们年府里递各话儿。”“不至于吧。侧福晋就是身子弱点儿,壹点儿风吹草动都受不住,精神 不济倒是真の。那天在这屋里の人可不只她壹各,怎么就她壹各人昏倒咯?”“嗯,您说の也是,不过,看着侧福晋也怪可怜の。”“不 得爷宠有啥啊办法,那是她自己没能耐,现在又摊上各有能耐の姐姐,唉,这就是命啊。”“福晋,那今天这事儿,怎么跟爷回话 呢?”“我也头痛这各问题呢!实话实说吧,怕是爷要迁怒于我,可是不说实话,爷在外面等着信儿呢,就算咱们不去报信,你看吧,没 两天爷就得派人催消息咯。”王爷确实是壹天恨不能盼八百遍地盼着苏培盛の来信。终于在第三天の早上收到咯王府の家信,居然是“年 仆役病重”这五各字!王爷壹见这五各字,犹如五雷轰顶!病重?到底是啥啊病?重到啥啊程度?他在京城の时候没有得到病重の消息, 怎么前脚刚壹出咯门后脚她就病重咯?可是他现在正是御前伴驾,根本就腾不出手来。虽然南苑距离京城不过五、六十里路,可是他以啥 啊理由擅离职守?在皇上の眼皮子底下搞小动作,他还要不要他の远大前程
初中数学七年级下册知识点总结二
初中数学七年级下册知识点总结二七年级数学下册知识点总结2有一个共同的顶点,一条共同的边,另一边是彼此相对的延长线。
这样的两个角叫做相邻的余角。
两条直线相交时有四对相邻的余角。
有一个公共顶点,角的两边是相对的延长线。
这样的两个角叫做对跖角。
两条直线相交并有两对对角。
顶角相等。
5.1.2两条直线相交,四个角中有一个是直角,所以两条直线互相垂直。
其中一条直线称为另一条直线的垂线,它们的交点称为垂足。
注意:⑴垂线是一条直线。
⑵具有垂直关系的两条直线所成的4个角都是90。
⑶垂直是相交的特殊情况。
⑷垂直的记法:a⊥b,ab⊥cd。
画已知直线的垂线有无数条。
有且只有一条直线垂直于已知直线。
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
在同一平面内,两条直线没有交点,则这两条直线互相平行,记作:a∥b。
在同一平面内两条直线的关系只有两种:相交或平行。
平行公理:经过直线外的一点后,有且只有一条直线与这条直线平行。
如果两条直线都平行于第三条直线,那么这两条直线也相互平行。
5.2.2直线平行的条件两条直线被第三条线切割。
在两条截线的同侧,在截线的同侧,这样的两个角叫做同余角。
两条直线被第三条直线切割,在两条切割线之间,切割线的两侧,这样的两个角叫做内切角。
两条直线被第三条线所截,在两条截线之间,在截线的同侧,这样的两个角叫做同侧内角。
判定两条直线平行的方法:方法1两条直线被第三条直线切割。
如果全等角相等,则两条直线平行。
简单来说:同一个角度相等,两条直线平行。
方法2两条直线被第三条直线切割。
如果内部位错角相等,则两条直线平行。
简单来说:内部位错角相等,两条直线平行。
方法3两条直线被第三条直线切割。
如果它们是互补的,那么这两条直线是平行的。
简单来说:同侧内角互补,两条直线平行。
5.3平行线的性质平行线具有性质:性质1两条平行线被第三条直线所截,同位角相等。
三角形内角和
方法一: 方法一: 度量法
60° ° 45° ° 90° ° 30° °
90° °
30°+60°+ 80°= 180° ° ° °
45° °
45°+45°+90°=180 ° ° ° ° 其它三角形可以用量角器来度量。 其它三角形可以用量角器来度量。
方法二 :拼合法
拼法一
拼法二
刚才拼角的过程中你能想出证明的方法吗? 从刚才拼角的过程中你能想出证明的方法吗?
F
B
C
证法2: 证法 :
已知: 已知:△ABC 求证: 求证:∠A+∠B+∠C=180° ∠ ∠ ° 延长BC到 , 延长 到D,过C作CE∥BA 作 ∥ ∴∠A=∠ ∴∠ ∠1 两直线平行,内错角相等) (两直线平行,内错角相等) A ∠B=∠2 ∠ 两直线平行,内错角相等) (两直线平行,内错角相等) 又∵∠1+∠2+∠ACB=180° ∵∠1+∠2+∠ACB=180° 1+∠2+∠ACB=180 平角的定义) (平角的定义) B ∴∠A+∠B+∠ACB=180° ∴∠A+∠B+∠ACB=180° 等量代换) (等量代换)
B A
C
三角形内角和定理
三角形三个内角的和等于180 三角形内角和定理 三角形三个内角的和等于1800. ∠A+∠B+∠C=1800. △ABC中,∠A+∠B+∠C= 中 ∠A+∠B+∠C=
的几种变形: 三角形内角和定理的几种变形 ∠A=1800 –(∠B+∠C). ∠A= (∠B+∠C). ∠B=1800 –(∠A+∠C). ∠B= (∠A+∠C). ∠C=1800 –(∠A+∠B). ∠C= (∠A+∠B). B ∠A+∠B=1800-∠C. ∠A+∠B= ∠C. ∠B+∠C=1800-∠A. ∠B+∠C= ∠A. ∠A+∠C=1800-∠B. ∠A+∠C= ∠B. 这里的结论,以后可以直接运用.
初中数学七年级下册第七章《三角形的内角》
新课标人教版初中数学七年级下册第七章《7.2.1三角形的内角》精品教案一.引课:以前在小学,我们就已接触了与三角形有关的知识,那三角形的内角和为多少度呢?(1800)同学们想知道为什么吗?(想).今天,老师将与大家一起研究和讨论“与三角形有关的角”第一节:“三角形的内角”(板书课题)。
二.正课:活动一:结论的证明1.动手操作,发现结论:师:请同学们观看幻灯片,各小组按要求亲自动手实验,你能得到什么结论?幻灯片(一):幻灯片一剪下内角,动手拼拼看,三个内角是否为180度。
生:动手实验,并将自己的做法展示给大家。
(实物投影)。
注:一名学生亲自演示,一名与师进行师生合作。
最后得出结论:三角形内角和等于180度。
(师板书)师:演示幻灯片(二):进一步从直观感性上确定结论的正确性。
2.数学证明,验证结论:师:同学们观察和总结的非常棒,但这只是实验,而观察与实验得到的结论不一定正确,可靠,这样就需要通进数学证明来验正结论是否正确,请同学们结合幻灯片(二),交流讨论说明结论为什么成立。
生:交流讨论。
师:将图画在黑板上,并巡视指导。
生:总结汇报,说明结论成立的理由。
师:同学们表达的十分准确,理由也很充分,但数学还需要书写规范的过程,接下师板演过程。
证明:延长BC ,过点C 做CD ∥AB。
有:∠1=∠A ∠B=∠2A BB幻灯片二因为:∠1+∠2+∠ACB=1800所以:∠A+∠B+∠ACB=18003.方法赏析,巩固结论。
师;同学们还有其他的方法吗?请大家观察幻灯片(三):生:在所给卡片上结合自己的能力仿照板书,选择完成证明过程。
师:有选择的展示汇报。
4.新知应用:幻灯片(四):幻灯片三幻灯片四5.跟踪小练:幻灯片(五):幻灯片五活动二:结论的应用。
1.自学指导,例题解析:师:同学们对“三角形内角和为1800”掌握已经非常牢固了,下面请同学们结合所学知识,按照自学指导完成例题的自学任务,比一比,谁理解的最好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按三角形内角的大小分类
三 角 形 的 分 类 锐角三角形 钝角三角形 三个内角都是锐角 有一个内角是钝角 有一个内角是直角
直角三角形
注意:1.常用符号“Rt∆ABC”来表示直角三角形ABC. 2.把直角所对的边称为直角三角形的斜边, C 夹直角的两条边称为直角边. 直 斜边 3.直角三角形的两个锐角互余. 角
ACB 1800 ABC CAB 1800 600 300 900
答:从C岛看A、B两岛的视角∠ACB 是90°.
D C 北 E
还有其他解法吗?
B
A
猜一猜
(1)下图中小明所拿三角形被遮住的两个内角 是什么角?小颖的呢?试着说明理由.
zxxkw
猜一猜
下图中三角形被遮住的两个内角可能是什么角? 将所得结果与(1)的结果进行比较.
在证明三角形内角和 定理时,小明的想法是 把三个角“凑”到A处, 他过点A作直线PQ//BC, 他的想法可行吗?
zxxkw
P 2 1
A 3
Q
证明: 过点A作射线PQ//BC,则
B
C
∠2=∠B(两直线平行,同位角相等)
∠3=∠C(两直线平行,内错角相等)
∠1+∠B +∠C=180°(等量代换)
∠1+∠2+∠3=180°(一平角=180°)
BA 图3
C
BAC 图4
拼凑法证明
我们知道,将一个三角形的一个角撕下来,拼在一 起,可以得到三角形的内角和为180° (1)做一个三角形的纸片,它的三个内角 分别为 1, 2, 3, 如图: (2)将∠1撕下,如左下图,其中∠1的顶点与∠2 的顶点重合,它的一条边与∠2的一条边重合
1 a 3 1 b 4 2 1
A
0 0 0 CAB BAD CAD 80 50 30 解: 0 由AD // BE, 可得 BAD ABE 180
经典例题
所以ABE 180 BAD 180 80 100
0 0 0
经典例题
0
在ABC中,
ABC ABE EBC 1000 400 600
人教课 标七下
zxxkw
7.2.1 三角形的 内角
学.科.网
内角三兄弟之争
在一个直角三角形里住着三个内角,平时, 它们三兄弟非常团结。可是有一天,老二 突然不高兴,发起脾气来,它指着老大说: “你凭什么度数最大,我也要和你一样 大!”“不行啊!”老大说:“这是不可 能的,否则,我们这个家就再也围不起来 了 ……”“ 为什么?” 老二很纳闷 . 你知 道其中的道理吗?
三兄弟的和应为180度!
你会证明三角形的和为180度吗?
小学时用的证明方法 拼凑法证明
学.科.网 学.科.网
平行线法证明
其他方法证明
C岛在A岛的被偏东50°方向,B岛在A岛的 北偏东80°方向,C岛在B岛的北偏西 40°方向, 从C岛看A、B两岛的视角∠ACB 是多少度? 分析:A、B、C三岛的连线 北 E C 构成△ABC,所求的是∠ABC的 D 一个内角.如果能求出∠CAB、 B ∠ABC,就能求出∠ACB.
3
2
拼凑法证明
(2)将∠1撕下,如左下图,其中∠1的顶点与∠2 的顶点重合,它的一条边与∠2的一条边重合。 ∠1的另一条边b与 ∠3的一条边a平行 吗?Why? b (3)如右上图,将∠ 3与 a ∠ 2的公共边延长,它与 3 2 1 4 b所夹的角为∠ 4。 ∠ 3与∠ 4的大小有什么关系? 为什么?
B
40°
C
A
B A
150°
40°
D
C
D
作 业
zxxkw
P76
3,4,7,
小学时用的证明方法
先将纸片三角形一角折向其对边,使顶点落 在对边上,折线与对边平行(图1),然后把另 处两角相向对折,使其顶点与已折角的顶点相嵌 合(图2)、(图3),最后得到(图4)所示的 结果。
A
B 图1
C B
A 图2
C
边
A
直角边
B
对号入座
② ③ ④
①
⑤
⑥
⑦
锐角三角形
直角三角形 钝角三角形
练 习
1、从A处观测C处的仰角 ∠CAB =30°,从B处观测C处 时仰角∠CAB =45°,从C处观 测A、B两处时的视角∠ACB 是多少度?
2、如图,一种滑翔伞的形状 是左右对称的四边形ABCD, 其中∠A =150°, ∠B = ∠D= 40°, 求∠C的度数.
拼凑法证明
已知:如图, △ABC 求证:∠1+∠2+∠3=180°
证明: 作BC的延长线CD,则
B//AB (内错角相等,两直线平行)
∠4=∠3(两直线平行,内错角相等)
∠1+∠2+∠3=180°(等量代换)
∠1+∠2+∠4=180°(一平角=180°)
平行线法证明
