随机过程-重庆邮电大学研究生院

合集下载

HSPA+系统中增强随机接入过程分析

引入的增强随机接八过程，包括上行同步、物理信 Байду номын сангаас 的处理以及无线资源的请求过
程。
关键词：上行同步增强随机接入签名码时间提前
园匿匿匡
周亮
重庆邮电大学通信与信息工程学院硕士研究生，主要从事ＴＳＤ— ＣＤＭＡ高层协
ＨＰ＋ＳＡ系统中增强随机接入过程分析
［亮】周
ｌ是何移信中本Ｄ机协描随致，但任个通统版ＴＣ过其原入和圜在一动系，的随入中的接程都些，是都及Ｄ议述理相存差即Ｒ会到接程基机过在别使４涉ＳＡ，本大同 —Ｍ
ＴＤＨＰ协议中描述的随机过程也是不相同的。本文主要介绍ＴＳＰ＋ＤＳＤＤＨＡ系统中
图１增强随机接入过程流程
由系统信息广播（省值为２或４子子帧）。在缺０ｍｓ个ＨＳＡ＋统中，每个小区可以配置多个ＦＡＣＨ道，其Ｐ系Ｐ信
园圈圈国
２上行同步的建立
ＴＤＨＰ系统是一个同步系统，对上行和下行同ＤＳＡ＋
在ＴＳＡ系统中，触发随机接入过程的原因很ＤＤＨＰ＋多，可以是来自网络的寻呼、终端的业务请求、ＭＭ层的
特殊过程以及ＲＲＣ需要和网络建立的联系。在进行这些过
４４
版本中的随机接入过程，ＨＡ＋强随机接入过程在建ＳＰ增立上行同步的部分变化不大，主要差别在于资源请求的相关内容。在该论文中，根据图１首先介绍上行同步的建将

重邮随机过程复习题

☆对于一个强度为的 Poisson 过程，在 t 时间内来 k 个顾客的概率为；
☆设 { X ( t ), t 0} 为具有参数＞0 的泊松过程，则 P{ X ( t h) X ( t ) 0} ；
☆ 设 { X ( t ), t 0} 是具有参数的泊松分布， Tn (n 1) 是对应的时间间隔序列，则随机变量； Tn (n 1,2,) 的概率密度函数为
2
☆设 X,Y 是两个具有二阶矩的随机变量， E( X 2 ) 则
, E(Y 2 ) 的乘积与 ( E ( XY ))2 的关系为
；
☆设随机变量 X 服从正态分布 N(0,4)，则其特征
函数 f X (t ) 为
；
n
☆若随机变量 X 的 n 阶矩 E( X
k
) 存在，则 X 的
(k )
特征函数 g(t)可微分 n 次，且当 k n 时， g 与 E( X ) 的关系为；
(n pij ) 用一 n 0,0 l n 和 i , j I ，步转移概率 n
步转移概率表达为
；
☆ 设 { X n , n T } 为马尔可夫链，则对任意 j I 和
n 1 ，绝对概率 p j (n) 用初始概率和 n 步转移概率
表达为
；
（17）首达概率可以用一步转移概率来表示：
所对应的随机变量的分布函数。（

e
j
2 e d 2 ） 1

☆、设 { X i , i 1,2,} 是一独立随机变量序列，且有相同的两点分布

基于随机过程分析的项目投资柔性决策

险评价方法。
在经济研究中，产品价格变动通常被假定为服从对数正
态扩散过程 [1]（或称布朗几何漂移运动），在这种情况下，可以
用如下偏微分方程来描述其随机波动过程：
d1nPt=μdt+σdz
(1)
或表达为：dPt=μPtdt+σPtdz
(2)
式中：Pt 为时间 t 时的产品价格；
决策参考
基于随机过程分析的项目投资柔性决策
向鹏成 1，向敏 2
（1.重庆大学建设管理与房地产学院，重庆 400045；2.重庆邮电大学自动化学院，重庆 400065）
摘要：文章分析了传统的项目决策与风险评估方法的缺陷，阐述了产品价格随机游走的特征
和随机过程模拟方法。提出了基于随机过程分析的项目投资决策与风险评估方法，并以一个金矿开
P(NPV<0) 29.1% 28.3% 40.8% 37.7% 43.8% 39.7%
E(NPV) 340.7 348.1 352.1 425.7 358.9 532.9
μ=1% S(NPV) 321.4 300.2 641.6 585 974.3 781.1
P(NPV<0) 14.8% 12.7% 31.6% 27.5% 39.1% 27.8%
dPt 为在某一短时间间隔内的价格增量；
dz 为在某一短时间间隔内的标准维纳过程增量；
μ 为价格漂移率；
σ 为价格波动率。
上述随机过程是一种连续的随机游走，偏微分方程中包
含了价格变动的一般趋势及其随机扰动两个因素，从而使它
更能反映出价格在时间序列上的动态特征。这一过程从性质
上来说属于马尔柯夫过程，这就意味着价格的所有未来值只

2014年重庆邮电大学硕士研究生招生专业一览表

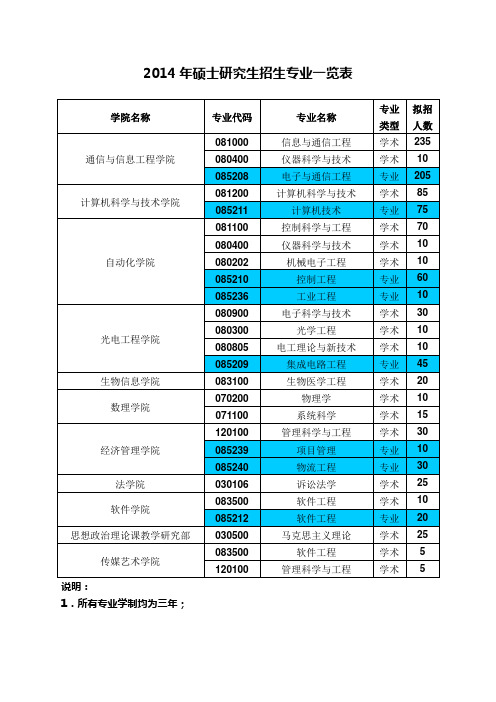
2014年硕士研究生招生专业一览表
学院名称
专业代码
专业名称
专业
类型
拟招
人数
通信与信息工程学院
081000
信息与通信工程
学术
235
080400
仪器科学与技术
学术
10
085208
电子与通信工程
专业
205
计算机科学与技术学院
081200
计算机科学与技术
学术
85
085211
计算机技术
专业
75
自动化学院
081100
控制科学与工程
学术
70
080400
仪器科学与技术
学术
10
080202
机械电子工程
学术
10
085210
控制工程
专业
60
085236
工业工程
专业
10
光电工程学院
080900
电子科学与技术
学术
30
080300
光学工程
学术
10
080805
电工理论与新技术
学术
10
085209
集成电路工程
专业
45
生物信息学院
083100
生物医学工程
学术
20
数理学院
070200
物理学学术10 Nhomakorabea071100
系统科学
学术
15
经济管理学院
120100
管理科学与工程
学术
30
085239
项目管理
专业
10
085240
物流工程
专业
30
法学院

随机过程讲义(中科院-孙应飞)

是常数， A ~ U [ 0, 1] 。试求：（1）画出 X (t ) 的样本函数；（2）确定过程的状态空间；（3）求 t = 0, π / 4ω , 3π / 4ω , π / ω , π / 2ω 时 X (t k ) 的密度函数。例 4：质点在直线上的随机游动，令 X n 为质点在 n 时刻时所处的位置，试考察其样本函数和状态空间。例 5：考察某“服务站”在 [0, t ] 时间内到达的“顾客”数，记为 N (t ) ，则
{N (t ), t ≥ 0} 是一随机过程，试考察其样本函数和状态空间。若记 S n 为第 n 个
“顾客”到达的时刻，则 {S n , n = 1,2,L} 为一随机序列，我们自然要关心
{S n , n = 1,2,L} 的情况以及它与随机过程 {N (t ), t ≥ 0} 的关系，这时要将两个随
为随机过程 { X (t ); t ∈ T } 的有限维特征函数族。数字特征之间的关系：
C X ( s, t ) = ˆ E{[ X ( s ) − µ X ( s )][ X (t ) − µ X (t )]} = E{ X ( s ) X (t )} − µ X ( s ) ⋅ µ X (t ) = R X ( s, t ) − µ X ( s ) ⋅ µ X (t )
µ X (t ) = ˆ m(t ) = E{ X (t )}
（b）方差函数：随机过程 { X (t ); t ∈ T } 的方差函数定义为：（假设存在）
2 σX (t ) = ˆ D X (t ) = E{[ X (t ) − µ X (t )]2 }
（ c）
（自）协方差函数：随机过程 { X (t ); t ∈ T } 的（自）协方差函数定

第3-4讲随机过程孙应飞

j

(i
,
1)

,
i 1 i0
其中为该周期内到达的顾客数。
记第 n 个周期开始的顾客数为 X n ，则 X n1 ( X n 1) n ，其中
a ˆ max{a,0}，根据马氏链的定义，可知{X n , n 0}是一马氏链。
由此推出：
P(m) P P (m1) (1) (P)m Pm
其中： P(1) P 由此可知：对于齐次马氏链，如果知道了它的初始分布 (0) 和一步转移矩
阵 P ，就可以求得 X (n) 的所有有限维概率分布。即有：
P{X (n1) i1, X (n2 ) i2 ,, X (nk ) ik }

m1

n

j 2

i
,
m2

n
j 2

i
中国科学院大学 2019～2020 第一学期随机过程讲稿孙应飞
n ji n ji n ji
C p q , (n)
2
2
2
n
p ij
0 ,
(n j i 是偶数) (n j i 是奇数)
p(n) ii

n
即上面式子的右边与时刻 n 无关，则称此马氏链为齐次（或时齐的）马氏链。对于齐次马氏链，我们记 P ( pi j ) ，称矩阵 P 为齐次马氏链的一步转移概
中国科学院大学 2019～2020 第一学期随机过程讲稿孙应飞
率矩阵，简称为转移矩阵。
注 3：对于马氏链{X (n); n 0} ，我们有： P{X (0) i0 , X (1) i1,, X (n) in} P{X (n) in X (0) i0 , X (1) i1,, X (n 1) in1}

重邮随机过程复习题-文档资料

☆对于一个强度为的 Poisson 过程，在 t 时间内来 k 个顾客的概率为；
☆设 { X ( t ), t 0} 为具有参数＞0 的泊松过程，则 P{ X ( t h) X ( t ) 0} ；
☆ 设 { X ( t ), t 0} 是具有参数的泊松分布， Tn (n 1) 是对应的时间间隔序列，则随机变量； Tn (n 1,2,) 的概率密度函数为
☆设随机变量 X 的特征函数为 g X (t ) (1 ait )1 ，则随机变量 X 的数学期望 E ( X ) 为；
☆设随机变量 X 与 Y 相互独立，且 X 特征函数为
g X (t ) e
it 3 t 2
，Y 特征函数为 gY ( t ) e ；
2 it t 2
2
☆设 X,Y 是两个具有二阶矩的随机变量，则 E( X 2 )
, E(Y 2 ) 的乘积与 ( E ( XY ))2 的关系为
；
☆设随机变量 X 服从正态分布 N(0,4)，则其特征
函数 f X (t ) 为
；
n
☆若随机变量 X 的 n 阶矩 E( X
) 存在，则 X 的
(k )
特征函数 g(t)可微分 n 次，且当 k n 时， g 与 E( X ) 的关系为
随机过程复习题
1、填空题
X ~ ☆设 X ~ N ( , ) ，则 2
2
；
；
☆随机变量 X 的特征函数 g (t ) 的定义是
☆ 设随机变量 X ~ N ( 0 ,的 1 )特征函数为
g X (t ) e

重邮随机过程复习题-文档资料共30页文档

ቤተ መጻሕፍቲ ባይዱ
66、节制使快乐增加并使享受加强。 ——德谟克利特 67、今天应做的事没有做，明天再早也是耽误了。——裴斯泰洛齐 68、决定一个人的一生，以及整个命运的，只是一瞬之间。 ——歌德 69、懒人无法享受休息之乐。——拉布克 70、浪费时间是一桩大罪过。——卢梭
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有久久不会退去的余香。
重邮随机过程复习题-文档资料 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮回里有你。

重邮研究生2015-2016学年第1学期课程表

[徐豪]
英语读写译10
[王强]
通信网理论与分析[李云]博士课程
中西人文经典对比阅读[代晓丽]
高级视听说3
[Gloria]
下
午
56
7
信号处理基础1
[周围]
线性系统理论2
[蔡林沁]
高等代数与矩阵分析1[王长有]
高等代数与矩阵分析2[鲜思东]
高级生物化学
[常平安]
晚上
9 10
11
现代通信系统2
[胡敏]
计算理论基础
星
期
四
上午
12
面向对象程序设计3
[张璞]
物联网导论
[王平]
激光原理
[郑培超]
稀土光谱理论
[马崇庚]
34
自然辩证法概论（1）
[李文清]]单周
自然辩证法概论（2）
[李文清]双周
自然辩证法概论（3）[冉启锋]单周
自然辩证法概论（4）[冉启锋]双周
自然辩证法概论（5）[王贵喜]单周
自然辩证法概论（6）[王贵喜]双周
自然辩证法概论（7）[马理]单周
自然辩证法概论（8）[马理]双周
信息安全理论
[陈龙罗文俊刘宴兵]博士课程
下
午
56
7
信号处理基础2
[张天骐]
运筹学
[卢安文]
随机过程及其应用2
[游晓黔]
图论及其应用4
[徐阳栋]
大数据分析与挖掘博士课程
[王国胤刘群]56节
高等量子力学
[朱家骥]
稳定性理论、方法和应用
[胡晓红]
[艾治琼]
英语读写译5
[陈民]
下
午
56
计算机图形学及三维建模

鲜思东重庆邮电学院400065概率论与随机过程讲义

2.
3.
随机试验
1、可以在相同的条件下重复地进行；
2、每次试验的可能结果不止一个，并且能事先明确试验的所有可能结果； 3、进行一次试验之前不能确定那一个结果会现。在概率论中，我们将具有上述三个特点的验称为随机试验。本书中以后提到的试验都是指随机试验。
样本空间
对于随机试验，尽管在每次试验之前不能预知试验的结果，但试验的所有可能结果组成的集合是已知的，我们将随机试验E的所有可能结果组成的集合称为E的样本空间，记为S。样本空间的元素，即E的每个结果，称为样本点。
古典概型的计算公式
设试验的样本空间为
包含 k 个基本事件，即
S = {e1 , e 2 , L , e n }, 事件 A
A=
∑ A ，且有
j =1
j
k
1 ≤ i1 < i 2 < L i k ≤ n ，则有
P(A = ∑P( ej )
j= 1 k
{ }
k A包的本件含基事数 )= = n S中本件总基事的数
例1·2·3 设A、B、C是S中的随机事件
事件“A与B发生，C不发生”可以表示成 “A、B、C中至少有二个发生”可以表示成 A、B、C中恰好发生二个”可以表示成 “A、B、C中有不多于一个事件发生”可以表示成
事件的运算
A 1、交换律： U B = B U A, AB = BA 、交换律：
2、结合律：A( BC ) 、结合律：
A= A
A U A = S, AA = Φ A ⊂ B ⇔ A − B = AB
8、子集的等价表示 A U B = B ⇔ AB = A 、 9、反演律（德·摩根律）、反演律（摩根律摩根律）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017 年重庆邮电大学博士研究生入学考试《随机过程》考试大纲
一．总体要求要求考生全面系统地掌握随机过程的有关理论，具备较强的分析问题与解决问题的能力，并能灵活运用。二．具体内容及要求 1．概率空间、随机变量及数字特征考试内容：概率空间的概念、随机变量及其分布函数、随机变量的数字特征、特征函数、母函数、n 维正态分布、条件期望。考试要求：（1）了解概率空间的概念。（2）理解随机变量的概念，掌握分布函数、密度函数的基本性质。（3）理解随机变量的期望、方差、协方差、特征函数、母函数概念，掌握其基本性质，会求随机变量的期望、方差、协方差、特征函数、母函数。（4）掌握 n 维正态分布的性质。（5）理解条件概率、条件分布函数、条件密度函数的概念，理解独立随机变量的概念，掌握条件随机变量的期望性质，会应用全数学期望公式。 2．随机过程的基本概念考试内容：随机过程的概念、随机过程的分布函数族、随机过程的数字特征、正交增量过程、独立增量过程、正态过程、维纳过程、复随机过程。考试要求：（1）理解随机过程的概念、随机过程的分布函数族，充分理解随机过程的存在性定理的数学及工程意义，会求随机过程的均值函数、方差函数、相关函数，协方差函数。
（2）理解正交增量过程、独立增量过程、平稳增量过程、平稳独立增量过程、正态过程、维纳过程的概念。
（3）理解复随机过程的概念。 3．泊松过程
考试内容：泊松过程的概念、泊松过程的数字特征、时间间隔与等待时间分布、到达时间的条件分布、非齐次泊松过程及数字特征、复合泊松过程及数字特征。考试要求：（1）理解泊松过程的概念、掌握两种定义。（2）掌握泊松过程的基本性质、会求泊松过程的数字特征、时间间隔与等待时间的分布、到达时间的条件分布。（3）理解非齐次泊松过程的概念、会求其数字特征。（4）理解复合泊松过程、会求其数字特征。 4．马尔可夫链考试内容：马尔可夫过程的概念、马尔可夫链的概念、马尔可夫链的转移概率、马尔可夫链的状态分类、常返性的判别及其性质、状态空间的分解、状态转移概率的渐近性质与平稳分布。考试要求：（1）了解马尔可夫过程的概念，马尔科夫性及工程意义，理解马尔可夫链的概念。（2）掌握马尔可夫链的状态转移概率性质、会根据状态转移概率描绘状态转移图、会确定实际马氏链的转移概率、转移矩阵。（3）理解状态的周期、常返概念，会求状态的周期、会判断状态的常返性、会分解状态空间。（4）掌握状态转移概率的渐近性质。（5）掌握其绝对概率分布、极限分布、平稳分布的概念及计算方法。
6．随机分析考试内容：随机过程的极限概念及基本性质、随机过程的均方连续及性质、随机过程的均方导数及性质、随机过程的均方积分及性质。考试要求：（1）了解随机序列的极限概念、理解随机序列的处处收敛、几乎处处收敛、依概率收敛、均方收敛概念及关系、掌握随机序列的均方收敛的基本性质。（2）理解二阶矩过程的均方收敛概念，掌握均方极限的运算性质，随机过程的均方连续的概念，掌握随机过程的均方连续与相关函数的关系。（3）理解随机过程的均方导数的概念，掌握随机过程的均方导数与相关函数的关系，掌握随机过程的均方导数基本性质。（4）理解随机过程的均方积分的概念，掌握随机过程的均方积分与相关函数的关系，掌握随机过程的均方积分基本性质。 7. 平稳随机过程考试内容：平稳随机过程的概念、联合平稳过程、平稳随机过程的相关函数的性质、平稳过程的遍历性、平稳过程的谱密度及性质、窄带过程及白噪声过程的谱密度、联合平稳过程的互谱密度。考试要求：（1）理解严平稳过程、宽平稳过程和联合平稳过程的数学定义及工程意义，掌握平稳随机过程的自（互）相关函数的性质。（2）理解平稳过程的遍历性概念、会求平稳过程的时间均值和时间相关函数、会判断平稳过程的遍历性。（3）理解平稳过程的谱密度的概念、掌握平稳过程的谱密度性质，掌握谱密度与相关函数的关系。（4）理解窄带过程及白噪声过程的概念、会根据其谱密度求相关函数。（5）理解联合平稳过程的互谱密度、掌握联合平稳过程的互谱密度性质，掌握联合平稳过程的互谱密度与互相关函数的关系。
三、参考书 1、《随机过程》（第四版），刘次华编著，华中科技大学出版社（2008） 2、《随机过程》，毛5．连续时间的马尔可夫链考试内容：连续时间的马尔可夫链的概念、状态转移速率、柯尔莫哥洛夫微分方程、生灭过程。考试要求：（1）理解连续时间的马尔可夫链的概念、掌握连续时间的马尔可夫链的基本性质、掌握连续时间的马尔可夫链与泊松过程的关系。
（2）理解状态转移速率的概念、理解柯尔莫哥洛夫微分方程、会根据该方程求状态转移概率。