电磁场习题讲解
电磁场例题讲解1
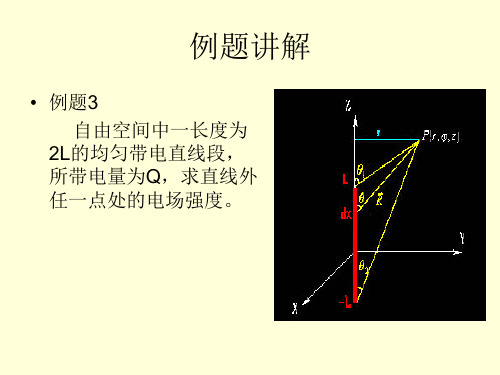
• 例题3 自由空间中一长度为 2L的均匀带电直线段, 所带电量为Q,求直线外 任一点处的电场强度。
分析
• 1、因为直导线的电场具有轴对称性,所以 选用圆柱坐标系。 • 2、 由于导线长度有限,虽然电场关于z轴对 称,但是沿z方向,电场是变化的,找不到 处处与电场垂直、而且电场幅度相等的简 单的闭合面。本题利用积分求和的方法求 解导线上各点的电荷在空间任一点所产生 的总电场。
• 设矢径R与Z轴间的夹角为 ,则
• 3.经积分求得整个线段在P点处产生的电场 强度
由图可知距离R与夹角
及坐标r之间的关系为
,
,
将这些关系式代入积分式中得
式中
和
分别为线段上下端点到场点的矢径与Z轴间的夹角。
讨 论
• 对上述结果有两点可进行讨论: • (1)如果线段的长度2L远远大于场点到Z 轴的距离r,则在直线段中部附近电场,应 与例1中得到的结果近似相等,因为如果线 段长度2L趋于无穷,即 时,
• 2.如果距离R远远大于直线段长度2L,则在 很远处电场的解为
利用二项式展开,取一次项近似得:
该结果与点电荷产生的电场相同
由此可以看出,尽管实际上不存在真正的点 电荷因为即使带电量最小的单个电子体积也并非 为零,也不可能存在真正的无限长的带电直线, 但这些理想情况的假设却有其实际背景的,利用 它们可使问题分析得到简化。
可见,静电场中旋度源处处为零。
例2由电场强度求空间电荷分布
• 已知自由空间球坐标系中电场分布:
求空间各处体电荷密度分布 由电场散度与电荷源的关系,可由已知电场分布确 定空间体电荷题3:证明:由点电荷q所产生的电场,其电场 强度 的旋度在空间处处为零。 证明:已知点电荷q的电场 在球坐标系中求旋度(见球坐标旋度表示式)。 因为点电荷的 ,且 所以
高考物理电磁场经典练习题(含答案详解)

高三物理第一轮专题复习——电磁场在以坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,如图所示。
一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿-x方向射入磁场,恰好从磁场边界与y轴的交点C处沿+y方向飞出。
(1)请判断该粒子带何种电荷,并求出其比荷q/m;(2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为B’,该粒子仍从A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了60°角,求磁感应强度B’多大?此次粒子在磁场中运动所用时间t是多少?电子自静止开始经M、N板间(两板间的电压A点垂直于磁场边界射入宽度为d的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.(已知电子的质量为m,电量为e)高考)如图所示,abcd为一正方形区域,正离子束从a点沿ad方向以=80m/s 的初速度射入,若在该区域中加上一个沿ab方向的匀强电场,电场强度为E,则离子束刚好从c点射出;若撒去电场,在该区域中加上一个垂直于abcd平面的匀强磁砀,磁感应强度为B,则离子束刚好从bc的中点e射出,忽略离子束中离子间的相互作用,不计离子的重力,试判断和计算:(1)所加磁场的方向如何?(2)E与B的比值BE/为多少?制D 型金属扁盒组成,两个D 形盒正中间开有一条窄缝。
两个D 型盒处在匀强磁场中并接有高频交变电压。
图乙为俯视图,在D 型盒上半面中心S 处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D 型盒中。
在磁场力的作用下运动半周,再经狭缝电压加速。
如此周而复始,最后到达D 型盒的边缘,获得最大速度,由导出装置导出。
已知正离子的电荷量为q ,质量为m ,加速时电极间电压大小为U ,磁场的磁感应强度为B ,D 型盒的半径为R 。
每次加速的时间很短,可以忽略不计。
正离子从离子源出发时的初速度为零。
高等电磁场理论习题解答(作业)

⾼等电磁场理论习题解答(作业)第⼀章基本电磁理论1-1 利⽤Fourier 变换, 由时域形式的Maxwell ⽅程导出其频域形式。
(作1-2—1-3)解:付⽒变换和付⽒逆变换分别为:dt e t f F t j ?∞∞-=ωω)()(ωωπωd e F t f tj ?∞∞--=)(21)( 麦⽒⽅程:t D J H ??+=??ρρρtB E ??-=??ρρ0=??B ρρ=??D ρ对第⼀个⽅程进⾏付⽒变换:),(),(),ωωωr H dt e t r H dt e t r H t j tj ρρρρρρ??=??=??=∞∞-∞∞-(左端),(),(),(),(]),(),[ωωωωωωωr D j r J dte t r D j r J dt e t t r D t r J t j tj ρρρρρρρρρρρρ+=+=??+=??∞∞-∞∞-(右端(时谐电磁场) =??∴),(ωr H ρρ),(),(ωωωr D j r J ρρρρ+同理可得:()()ωωω,,r B j r H ??ρρ-=??()0,=??ωr B ρ()()ωρω,,r r D ?ρ?=??上⾯四式即为麦式⽅程的频域形式。
1-2 设各向异性介质的介电常数为=300420270εε当外加电场强度为 (1) 01E x e E =;(2)02E y e E =;(3) 03E z e E =;(4) )2(04y x E e e E +=;(5))2(05y x E e e E +=求出产⽣的电通密度。
(作1-6)解:()),(,t r E t r D ?Θ?=ε=333231232221131211εεεεεεεεεz y x D D D 即z y x E E E 将E 分别代⼊,得:=??=??????????027003000420270000111E E D D D z y x εε )?2?7(001y x E D +=ε?=??=??????????042003000420270000322E E D D D z y x εε )?4?2(002y x E D +=ε? ????=??=??????????300003000420270000333E E D D D z y x εε z E D ?3003ε=? ??==010110230004202700000444E E E D D D z y x εε )?10?11(004y x E D +=ε? ==08160230004202700000555E E E D D D z y x εε )?8?16(005y x E D +=ε? 1-3 设各向异性介质的介电常数为=4222422240εε试求:(1) 当外加电场强度)(0z y x E e e e E ++=时,产⽣的电通密度D ;(2) 若要求产⽣的电通密度004E x εe D =,需要的外加电场强度E 。
电磁场理论习题及答案

电磁场理论习题及答案电磁场理论是电磁学的基础,它描述了电荷和电流产生的电磁场在空间中的分布和演化规律。
在学习电磁场理论时,习题是巩固和深化理解的重要方式。
本文将介绍一些电磁场理论的习题及其答案,帮助读者更好地掌握这一理论。
一、电场和电势1. 问题:一个均匀带电球体,半径为R,总电荷为Q。
求球心处的电场强度。
答案:根据库仑定律,电场强度E与电荷Q和距离r的关系为E = kQ/r^2,其中k为库仑常数。
对于球体内部的点,距离球心的距离r小于半径R,所以电场强度为E = kQ/r^2。
对于球体外部的点,距离球心的距离r大于半径R,所以电场强度为E = kQ/R^3 * r。
2. 问题:一个无限长的均匀带电线,线密度为λ。
求距离线上一点距离为r处的电势。
答案:根据电势公式V = kλ/r,其中k为库仑常数。
所以距离线上一点距离为r处的电势为V = kλ/r。
二、磁场和磁感应强度1. 问题:一根无限长的直导线,电流为I。
求距离导线距离为r处的磁感应强度。
答案:根据安培环路定理,磁感应强度B与电流I和距离r的关系为B =μ0I/2πr,其中μ0为真空中的磁导率。
所以距离导线距离为r处的磁感应强度为B = μ0I/2πr。
2. 问题:一根长为L的直导线,电流为I。
求距离导线距离为r处的磁场强度。
答案:根据比奥萨伐尔定律,磁场强度H与电流I和距离r的关系为H = I/2πr。
所以距离导线距离为r处的磁场强度为H = I/2πr。
三、电磁场的相互作用1. 问题:一个半径为R的导体球,带电量为Q。
求导体球表面的电荷密度。
答案:导体球表面的电荷密度σ等于导体球上的电荷总量Q除以导体球表面的面积A。
导体球表面的面积A等于球的表面积4πR^2。
所以导体球表面的电荷密度为σ = Q/4πR^2。
2. 问题:一个平行板电容器,两个平行金属板之间的距离为d,电介质的介电常数为ε。
一块电介质板插入到电容器中间,使得电容器的电容增加了n倍。
电磁场习题解2(上)

第二章习题解2-1.已知真空中有四个点电荷q C 11=,q C 22=,q C 34=,q C 48=,分别位于(1,0,0),(0,1,0),(-1,0,0,),(0,-1,0)点,求(0,0,1)点的电场强度。
解:设z r ˆ=,y r x r y r xr ˆ',ˆ',ˆ',ˆ'2321-=-=== z y r r R z x r r R z y r r R z xr r R ˆˆ';ˆˆ';ˆˆ';ˆˆ'44332211+=-=+=-=+-=-=+-=-=84ˆ15ˆ6ˆ3)ˆˆˆˆ(41024442333222221110πεπεz y x R R q R R q R R q R R q E ++=+++=2-2.已知线电荷密度为ρl 的均匀线电荷围成如图所示的几种形状,求P 点的电场强度。
(a) (b) (c)题2-2图解:(a) 由对称性04321=+++=E E E E E(b) 由对称性0321=++=E E E E(c) 两条半无限长线电荷产生的电场为ya y x y x a E E E ll a ˆ2)}ˆˆ()ˆˆ{(40021περπερ-=--+-=+= 半径为a 的半圆环线电荷产生的电场为y a E lb ˆ20περ=总电场为0=+=b a E E E2-3.真空中无限长的半径为a 的半边圆筒上电荷密度为ρs ,求轴线上的电场强度。
解:在无限长的半边圆筒上取宽度为ϕad 的窄条,此窄条可看作无限长的线电荷,电荷线密度为ϕρρad s l =,对ϕ积分,可得真空中无限长的半径为a 的半边圆筒在轴线上的电场强度为yd x yad r a E s ss ˆ)ˆc o s ˆs i n (22ˆ0000⎰⎰-=--==πππερϕϕϕπερπεϕρ题2-3图 题2-4图2-4.真空中无限长的宽度为a 的平板上电荷密度为ρs ,求空间任一点上的电场强度。
电磁场与电磁波习题讲解02

ax
109
5 4 4 107
sin(5z)
ax
1 sin(5z) 20
习题讲解四
例题 已知某无耗媒质中的电场强度瞬时值形式为
Ez,t ay 4 sin(109t) cos(5z), 且=0
,求相应的磁场强度的复数表达式
解:E z, t
ay
4
cos(109 t
EH
t
1 2
H
B
1 2
E
D
J
E
坡印廷定理的物理意义:单位时间内通过曲面S进入体积 V的电磁能量等于单位时间内体积V内所增加的电磁场能 量与损耗的能量之和
5.3 麦克斯韦方程及边界条件
坡印廷矢量
S EH
坡印廷矢量的物理意义:它表示单位时间内通过垂直于能 量传输方向的单位面积的电磁能量,其方向就是电磁能量 传输的方向
(3) E ax cos(t z) ay 2sin(t z)
解:E(
z,t)Βιβλιοθήκη axcos(t
z)
ay
2
cos(t
z
2
)
ax
Re[e
j(t z)
]
ay
2
Re[e
j (t
z 2
)
]
E(z) axe j z ay 2 je j z
ax
j2
e
j5z
ax
j2
e
j5z
r 0
电磁学第四版赵凯华习题解析
电磁学第四版赵凯华习题解析第一章电磁场的基本概念题1.1解析:该题主要考察对电磁场基本概念的理解。
根据定义,电场强度E是单位正电荷所受到的电力,磁场强度B是单位长度为1、电流为1的导线所受到的磁力。
因此,电场强度E与电势差V之间的关系为E=-dV/dx,磁场强度B与安培环路定律有关,即B=μ₀I/2πr。
答案:电场强度E与电势差V之间的关系为E=-dV/dx,磁场强度B与安培环路定律有关,即B=μ₀I/2πr。
题1.2解析:该题考查对电场线和磁场线的基本理解。
电场线从正电荷出发,指向负电荷;磁场线从磁南极指向磁北极。
在非均匀磁场中,电荷的运动轨迹会受到磁场的影响,当电荷的运动速度与磁场垂直时,洛伦兹力提供向心力,使电荷沿磁场线运动。
答案:电场线从正电荷出发,指向负电荷;磁场线从磁南极指向磁北极。
在非均匀磁场中,电荷的运动轨迹会受到磁场的影响,当电荷的运动速度与磁场垂直时,洛伦兹力提供向心力,使电荷沿磁场线运动。
第二章电磁场的基本方程题2.1解析:该题考查对高斯定律的理解。
根据高斯定律,闭合曲面所包围的电荷量与该曲面上的电通量成正比,即∮E·dA=Q/ε₀。
其中,E为电场强度,dA为曲面元素,Q为曲面内的电荷量,ε₀为真空电容率。
答案:根据高斯定律,闭合曲面所包围的电荷量与该曲面上的电通量成正比,即∮E·dA=Q/ε₀。
题2.2解析:该题考查对法拉第电磁感应定律的理解。
根据法拉第电磁感应定律,感应电动势E与磁通量变化率ΔΦ/Δt成正比,即E=ΔΦ/Δt。
其中,E为感应电动势,ΔΦ为磁通量的变化量,Δt为时间变化量。
答案:根据法拉第电磁感应定律,感应电动势E与磁通量变化率ΔΦ/Δt成正比,即E=ΔΦ/Δt。
第三章电磁波的传播题3.1解析:该题考查对电磁波的基本理解。
电磁波是由振荡的电场和磁场组成的横波,其传播速度为光速c,波长λ与频率f之间的关系为c=λf。
电磁波在真空中的传播不受阻碍,但在介质中传播时,其速度会发生变化。
电磁场理论课后习题1答案
电磁场理论课后习题1答案电磁场理论是物理学中的重要课程,它研究了电磁场的产生、传播和相互作用。
在学习这门课程时,课后习题是巩固知识、提高能力的重要途径。
本文将针对电磁场理论课后习题1给出详细的解答。
习题1:一个带电粒子在电磁场中运动,受到的洛伦兹力为F=q(E+v×B),其中q是粒子的电荷量,E是电场强度,v是粒子的速度,B是磁感应强度。
请证明:洛伦兹力对粒子所做的功率为P=qv·E。
解答:根据洛伦兹力的表达式F=q(E+v×B),我们可以将其展开为F=qE+qv×B。
其中第一项qE表示粒子在电场中受到的电力,第二项qv×B表示粒子在磁场中受到的磁力。
根据功率的定义,功率P等于力F对时间t的导数,即P=dW/dt,其中W表示对物体所做的功。
所以我们需要计算洛伦兹力对粒子所做的功。
根据力的功的定义,功W等于力F对位移的积分,即W=∫F·ds。
在这里,位移ds是粒子在运动过程中的微小位移。
将洛伦兹力F=qE+qv×B代入功的计算式中,得到W=∫(qE+qv×B)·ds。
由于电场强度E和磁感应强度B是空间中的矢量场,所以我们可以将其展开为E=E_xi+E_yj+E_zk和B=B_xi+B_yj+B_zk的形式。
对于微小位移ds,我们可以将其表示为ds=dx·i+dy·j+dz·k。
将上述表达式代入功的计算式中,得到W=∫(q(E_xi+E_yj+E_zk)+q(v_xi+v_yj+v_zk)×(B_xi+B_yj+B_zk))·(dx·i+dy·j+dz·k)。
根据矢量积的性质,可以得到v×B=(v_yB_z-v_zB_y)i-(v_xB_z-v_zB_x)j+(v_xB_y-v_yB_x)k。
将其代入功的计算式中,得到W=∫(q(E_xi+E_yj+E_zk)+q((v_yB_z-v_zB_y)i-(v_xB_z-v_zB_x)j+(v_xB_y-v_yB_x)k))·(dx·i+dy·j+dz·k)。
高二物理电磁场练习题讲解
高二物理电磁场练习题讲解电磁场是高中物理的重要内容之一,也是学生在学习物理过程中常常会遇到的难点之一。
为了帮助高二学生更好地理解和掌握电磁场的相关知识,以下是一些电磁场的练习题及其详细讲解。
1. 题目:一根长直导线通以电流I,求离导线距离为r处的磁感应强度B的表达式。
解析:根据比奥-萨伐尔定律,通过一条长直导线所产生的磁场大小与距离这条导线的距离成反比。
所以根据比奥-萨伐尔定律,可以得到以下的表达式:B = (μ₀I)/(2πr)其中,B为磁感应强度,μ₀为真空磁导率,I为电流强度,r为距离导线的距离。
2. 题目:两根平行的长直导线之间的间距为d,两根导线通以相反方向相等的电流,求两导线之间的磁感应强度B的表达式。
解析:根据比奥-萨伐尔定律,两根平行的长直导线之间的磁感应强度大小可以用以下公式来计算:B = (μ₀I)/(2πd)其中,B为磁感应强度,μ₀为真空磁导率,I为电流强度,d为两根导线之间的间隔距离。
3. 题目:一个长直导线与一个长方形回路(边长为a和b)垂直放置,长方形回路的一条边与长直导线平行。
长直导线通以电流I,求回路中的电动势ε。
解析:根据法拉第电磁感应定律,当导线中的磁场发生变化时,会在回路中产生感应电动势。
对于这个题目,长直导线中电流I的存在会产生一个磁场,而由于长方形回路边长与导线平行,所以回路中感应电动势的大小可以通过以下公式计算:ε = B * L其中,ε为感应电动势,B为磁感应强度,L为回路边的长度。
4. 题目:一根半径为R的无限长细导线通以电流I,求与导线距离为r处的磁感应强度B。
解析:这是一个经典的安培环路定律的应用题。
根据安培环路定律,可以推导出以下公式:B = (μ₀I)/(2R)其中,B为磁感应强度,μ₀为真空磁导率,I为电流强度,R为导线的半径。
通过对以上练习题的详细讲解,相信大家对电磁场的相关知识有了更深入的理解。
掌握了这些基本的公式和定律,对于后面的学习和解题将会起到很大的帮助。
电磁场例题分步骤解答PPT课件
Hale Waihona Puke v (C A)dv C v( A)dv
根据散度定理,上式左边等于:
s(C A) ds s( A ds ) C C s A ds
C
A ds
s
C v( A)dv
因为 C 是任意常矢量,故
( A)dv A ds
v
s
第5页/共34页
例1.4 求函数 u x2 y2 z2 在点M (1, 0, 1)处沿 l xˆ 2 yˆ 2zˆ 方向的 方向导数。
(1)求电场强度衰减为1uV/m处的水深。应选用哪个频率作潜水艇的水下 通信?
(2)求3KHz的电磁波从海平面下侧向海水中传播的平均功率流密度?
第23页/共34页
解:(1) f =3 kHz:
4
3105
2 3 103 80 1 109
36
此时海水为良导体,所以
2 3103 4 107 4 0.218
第10页/共34页
解:
由全电流连续性原理可知,传导电流应等于两平板间 的位移电流。
I
Id
AJd
A D t
其中
D E
E U d
I A U C U
d t
t
式中 C A
d
第11页/共34页
例2.3 试用麦克斯韦方程组推导 出 RLC 串 联 电 路 的 电 压 方 程 (电路全长远小于波长)。
xˆDx yˆDy zˆDz
Dx q [
x
] q r 2 3x2
x 4 x (x2 y 2 z 2 )3 4 r 5
D y q r 2 3 y 2
y 4
r5
Dz q r 2 3z 2
z 4 r 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一、单项选择题
1.全电流定律的微分方程为( )
A .▽×H=J C
B .▽×H=J+t
D ∂∂
C .▽×H=t
D ∂∂
D .▽×H=0 2.所谓点电荷是指可以忽略掉电荷本身的( )
A .质量
B .重量
C .体积
D .面积
3.静电场中两点电荷之间的作用力与它们之间的距离( )
A .成正比
B .平方成正比
C .平方成反比
D .成反比
4.真空中均匀平面波的波阻抗为( )
A .237Ω
B .277Ω
C .337Ω
D .377Ω
5.载流回路中的电流在建立过程中需要外源提供能量,故一部分能量将转化为( )
A.电场能量B.线圈能量C.磁场能量D.电流能量6.变压器电动势的产生条件是()A.电场恒定B.磁场恒定C.电场变化D.磁场变化7.已知两点电荷在同一处产生的电场分别为E1=-48.0e y+60.0e z v/m,
E2=74.9e x-124.9e z v/m,则该处的电场
强度为()
A.74.9e x-48.0e y v/m
B.-74.9e x+48.0e y-184.9e z v/m C.74.9e x+48.0e y-184.9e z v/m
D.74.9e x-48.0e y-64.9e z v/m
8.0ε是真空中的介电常数,其值为()
A.4π×10-7H/m B.4π×10-12F/m C.8.85×10-12F/m D.8.85×10-12F·m 9.已知平行板电容器中,电位函数2ax=ϕ,则电容器中的电场强度为()A.2axe x B.2aεxe x
C.2aεe x D.-2axe x
2
10.一个电量为1.6×10-19C的粒子,以83.5km/s的初速度进入B=5mT的磁场中,假设速度v和B是垂直的,则作用在此粒子上的力为()
A.6.68×10-20N B.6.68×10-17N C.6.68×10-14D.0N
11.电流密度的单位为()
A.安/米3B.安/米2
C.安/米D.安
12.如向量磁位A=5(x2+y2+z2)-1e x Wb/m,则B为()A.10(x2+y2+z2)-2ye z-10(x2+y2+z2)-2ze y( T)
B.5(x2+y2+z2)-1e z-5(x2+y2+z2)-1e y(T) C.10(x2+y2+z2)-1ye z-10(x2+y2+z2)-1ze y( T)
D.5(x2+y2+z2)-2e z-5(x2+y2+z2)-2e y(T) 13.在场源分布相同情况下,普通磁媒质中的磁感应强度是真空中磁感应强度的()
A.0μ倍B.rμ倍
3
C.μ倍D.mχ倍
14.在恒定磁场中,已知H=a(ye x-xe y),则电流密度J等于()
A.-2ae z B.-2ae y
C.2ae x D.2ae z
二、填空题
15.在正方形的四顶点上,各放一电量相等的同性点电荷,则几何中心处
的电场强度为。
16.不导电的自由空间电荷运动形成的电流称为运流电流。
17.在线性导电媒质中电流密度与电场强度成关系。
18.电磁感应定律的本质就是变化的磁场产生。
19.时变电磁场的频率越高,则透入深度,集肤效应越明显。
三、名词解释
20.恒定场
21.非线性导电媒质
4
22.动态位
23.自有静电能量
5。
