电磁场习题解读
电磁场例题讲解1
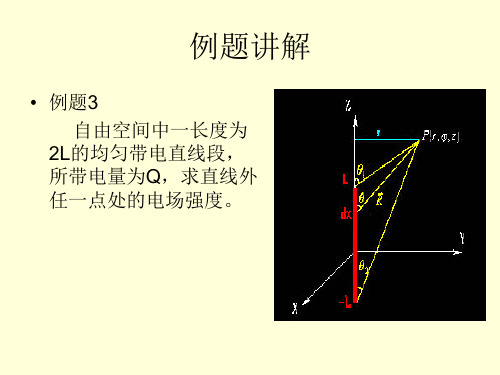
• 例题3 自由空间中一长度为 2L的均匀带电直线段, 所带电量为Q,求直线外 任一点处的电场强度。
分析
• 1、因为直导线的电场具有轴对称性,所以 选用圆柱坐标系。 • 2、 由于导线长度有限,虽然电场关于z轴对 称,但是沿z方向,电场是变化的,找不到 处处与电场垂直、而且电场幅度相等的简 单的闭合面。本题利用积分求和的方法求 解导线上各点的电荷在空间任一点所产生 的总电场。
• 设矢径R与Z轴间的夹角为 ,则
• 3.经积分求得整个线段在P点处产生的电场 强度
由图可知距离R与夹角
及坐标r之间的关系为
,
,
将这些关系式代入积分式中得
式中
和
分别为线段上下端点到场点的矢径与Z轴间的夹角。
讨 论
• 对上述结果有两点可进行讨论: • (1)如果线段的长度2L远远大于场点到Z 轴的距离r,则在直线段中部附近电场,应 与例1中得到的结果近似相等,因为如果线 段长度2L趋于无穷,即 时,
• 2.如果距离R远远大于直线段长度2L,则在 很远处电场的解为
利用二项式展开,取一次项近似得:
该结果与点电荷产生的电场相同
由此可以看出,尽管实际上不存在真正的点 电荷因为即使带电量最小的单个电子体积也并非 为零,也不可能存在真正的无限长的带电直线, 但这些理想情况的假设却有其实际背景的,利用 它们可使问题分析得到简化。
可见,静电场中旋度源处处为零。
例2由电场强度求空间电荷分布
• 已知自由空间球坐标系中电场分布:
求空间各处体电荷密度分布 由电场散度与电荷源的关系,可由已知电场分布确 定空间体电荷题3:证明:由点电荷q所产生的电场,其电场 强度 的旋度在空间处处为零。 证明:已知点电荷q的电场 在球坐标系中求旋度(见球坐标旋度表示式)。 因为点电荷的 ,且 所以
电磁场的典型练习题及解答

电磁场的典型练习题及解答电磁学是物理学中的重要分支,研究电荷和电流所产生的电场和磁场的相互作用规律。
在学习电磁学的过程中,练习题是检验我们对理论知识掌握的有效方法。
本文将介绍一些典型的电磁场练习题,并给出详细的解答,帮助读者加深对电磁场的理解。
1. 题目:一根无限长直导线产生的电场强度已知一根无限长直导线,导线上带有均匀分布的电荷线密度λ。
求导线距离d处的电场强度E。
解答:根据库仑定律可知,电场强度E与电荷线密度λ成正比,与距离d 成反比。
所以可以得出结论:电场强度E和d满足反比关系。
2. 题目:两个点电荷的叠加效应已知两个点电荷q1和q2,分别位于坐标原点和坐标轴上一点P(x,0)。
求点P处的电场强度E。
解答:根据叠加原理,点P处的电场强度E等于点电荷q1和q2分别在点P处产生的电场强度之和。
由库仑定律可知,点电荷产生的电场强度与电荷量成正比,与距离的平方成反比。
根据该性质,可以分别求出点电荷q1和q2在点P处产生的电场强度,再将两者相加得到点P处的总电场强度。
3. 题目:平行板电容器的电场强度已知一对平行板电容器,两平行板间距离为d,电容器的电容为C。
求平行板电容器中的电场强度E。
解答:根据平行板电容器的结构特点,可知平行板电容器中的电场强度E对于两平行板之间的距离d是均匀的,且大小与电容C的倒数成正比。
所以可以得出结论:电场强度E和d满足正比关系,与电容C成正比。
4. 题目:磁场的洛伦兹力已知带电粒子以速度v在磁场B中运动,其电荷量为q。
求带电粒子所受的洛伦兹力F。
解答:根据洛伦兹力的定义,带电粒子所受的洛伦兹力F等于其电荷量q与速度v以及磁场B的矢量积。
通过对矢量积的计算,可以得到带电粒子所受的洛伦兹力F的大小和方向。
5. 题目:安培环路定理的应用已知一安培环路中有多个电流元素,它们的电流分别为I1,I2,I3...In。
求安培环路中的磁场强度B。
解答:根据安培环路定理,安培环路中的磁场强度B与电流元素的电流之和成正比。
高中物理电磁场题解析

高中物理电磁场题解析电磁场是高中物理中一个重要的知识点,涉及到电荷、电场、磁场等概念和相互作用。
在考试中,电磁场题目往往涉及到电场强度、电势、电荷分布、电场线、磁感应强度等内容。
下面我将结合具体题目,分析解题思路和考点,并给出一些解题技巧。
一、电场强度和电势1. 题目:一均匀带电球面,半径为R,总电荷为Q。
在球面上某点A的电场强度为E,求球心的电场强度。
解析:这道题目考察了电场强度的叠加原理。
由于带电球面是均匀的,所以球面上任意一点的电场强度大小是相等的,即E。
根据叠加原理,球心的电场强度等于球面上各点电场强度的矢量和,即E。
2. 题目:在无限大平面上有一个均匀带电面,面电荷密度为σ。
求离平面距离为d处的电场强度。
解析:这道题目考察了电场强度的计算。
由于面电荷是均匀的,所以可以使用高斯定律。
取一个以平面为底面、高为d的长方体高斯面,根据高斯定律可知,电场强度的大小等于电通量除以高斯面积,即E = σ/2ε0,方向垂直于平面向上。
3. 题目:在电势为V的点电荷附近,距离为r处的电势是多少?解析:这道题目考察了电势的计算。
根据电势的定义,电势等于电场强度乘以距离,即V = kQ/r,其中k为比例常数。
根据题目给出的条件,可以直接计算出电势。
二、电荷分布和电场线1. 题目:一根无限长的直导线,线密度为λ,求距离导线r处的磁感应强度。
解析:这道题目考察了磁感应强度的计算。
根据比奥-萨伐尔定律,磁感应强度的大小等于电流元除以距离的平方乘以μ0,即 B = (λ/2πr)μ0,方向垂直于导线。
2. 题目:一根无限长的直导线,电流为I,求距离导线r处的磁感应强度。
解析:这道题目考察了磁感应强度的计算。
根据安培定理,磁感应强度的大小等于电流除以距离乘以μ0,即B = (I/2πr)μ0,方向按右手螺旋法确定。
三、电磁场的相互作用1. 题目:一根无限长的直导线,电流为I,与一根平行的无限长直导线,电流为2I,距离为d。
电磁学第四版赵凯华习题解析

电磁学第四版赵凯华习题解析第一章电磁场的基本概念题1.1解析:该题主要考察对电磁场基本概念的理解。
根据定义,电场强度E是单位正电荷所受到的电力,磁场强度B是单位长度为1、电流为1的导线所受到的磁力。
因此,电场强度E与电势差V之间的关系为E=-dV/dx,磁场强度B与安培环路定律有关,即B=μ₀I/2πr。
答案:电场强度E与电势差V之间的关系为E=-dV/dx,磁场强度B与安培环路定律有关,即B=μ₀I/2πr。
题1.2解析:该题考查对电场线和磁场线的基本理解。
电场线从正电荷出发,指向负电荷;磁场线从磁南极指向磁北极。
在非均匀磁场中,电荷的运动轨迹会受到磁场的影响,当电荷的运动速度与磁场垂直时,洛伦兹力提供向心力,使电荷沿磁场线运动。
答案:电场线从正电荷出发,指向负电荷;磁场线从磁南极指向磁北极。
在非均匀磁场中,电荷的运动轨迹会受到磁场的影响,当电荷的运动速度与磁场垂直时,洛伦兹力提供向心力,使电荷沿磁场线运动。
第二章电磁场的基本方程题2.1解析:该题考查对高斯定律的理解。
根据高斯定律,闭合曲面所包围的电荷量与该曲面上的电通量成正比,即∮E·dA=Q/ε₀。
其中,E为电场强度,dA为曲面元素,Q为曲面内的电荷量,ε₀为真空电容率。
答案:根据高斯定律,闭合曲面所包围的电荷量与该曲面上的电通量成正比,即∮E·dA=Q/ε₀。
题2.2解析:该题考查对法拉第电磁感应定律的理解。
根据法拉第电磁感应定律,感应电动势E与磁通量变化率ΔΦ/Δt成正比,即E=ΔΦ/Δt。
其中,E为感应电动势,ΔΦ为磁通量的变化量,Δt为时间变化量。
答案:根据法拉第电磁感应定律,感应电动势E与磁通量变化率ΔΦ/Δt成正比,即E=ΔΦ/Δt。
第三章电磁波的传播题3.1解析:该题考查对电磁波的基本理解。
电磁波是由振荡的电场和磁场组成的横波,其传播速度为光速c,波长λ与频率f之间的关系为c=λf。
电磁波在真空中的传播不受阻碍,但在介质中传播时,其速度会发生变化。
电磁场原理习题与解答(第5章)

第五章习题答案5-2 如题图所示,一半径为a 的金属圆盘,在垂直方向的均匀磁场B 中以等角速度ω旋转,其轴线与磁场平行。
在轴与圆盘边缘上分别接有一对电刷。
这一装置称为法拉第发电机。
试证明两电刷之间的电压为22ωBa 。
证明:,选圆柱坐标, ρφe vB e B e v B v E z ind=⨯=⨯=其中 φρωe v=22ωρρωρερρa B d B e d e v B l d E aal ind====⎰⎰⎰∙∙∴证毕 5-3解:5-4 一同轴圆柱形电容器,其内、外半径分别为cm r 11=、cm r 42=,长度cm l 5.0=,极板间介质的介电常数为04ε,极板间接交流电源,电压为V t 10026000u πsin =。
求s t 0.1=时极板间任意点的位移电流密度。
解法一:因电源频率较低,为缓变电磁场,可用求静电场方法求解。
忽略边沿效应,电容器中的场为均匀场,选用圆柱坐标,设单位长度上内导体的电荷为τ,外导体电荷为τ-,因题图5-2zvρ此有ρρπετe 2E 0=21r r <<ρ1200222121r r d dl E u r r r r lnπετρρπετ===⎰⎰∙1202r r u ln=∴πετ所以ρρer r u E 12 ln =, ρρεer r u D 12ln=2A/mρρππρερεe t 10010026000r r e tu r r tD J 1212dcos ln ln ⨯=∂∂=∂∂=当s t 1=时2512A/m10816100100260004108584ρρρππρe e J d--⨯=⨯⨯⨯⨯=.cos ln .解法二:用边值问题求解,即⎪⎩⎪⎨⎧=====∇401u 02ρϕρϕϕ 由圆柱坐标系有0)(1=∂∂∂∂ρϕρρρ(1)解式(1)得 21ln c c +=ρϕ由边界条件得: 4u c 1ln -= u c 2=u 4u +-=∴ρϕln ln所以 ρρπϕe 4t10026000Eln sin =-∇=ρρπεεe 4t 100260004E D 0ln sin ==ρπρπεe 1004t 100260004t D J 0D⨯=∂∂=ln cos当s t 1=时)(.25D mAe 10816J ρρ-⨯=5-5由圆形极板构成的平板电容器)(d a >>见题图所示,其中损耗介质的电导率为γ、介电系数为ε、磁导率为μ,外接直流电源并忽略连接线的电阻。
电磁场与电磁兼容习题答案与详解第2章

电磁场与电磁兼容习题答案与详解-第2章第2章:电磁场基础知识1.题目:电场强度的方向与电荷正负有关吗?答案:是的,电场强度的方向与电荷的正负有关。
正电荷的电场强度方向指向远离电荷的方向,负电荷的电场强度方向指向靠近电荷的方向。
详解:电场强度的方向由正电荷指向负电荷,这是由于电荷之间存在相互作用力。
根据库仑定律,同性电荷之间的相互作用力是斥力,异性电荷之间的相互作用力是吸引力。
电场强度的方向就是这种相互作用力的方向。
2.题目:什么是电场线?答案:电场线是描述电场强度方向的线条。
在电场中,电场线的方向与电场强度的方向一致,电场线之间不会相交。
详解:电场线是静电场中电场强度方向的图形表示。
它可以用来表示电场强度的大小和方向。
电场线的方向由正电荷指向负电荷,线的密度表示电场强度的大小。
电场线之间不会相交,这是因为在相交点上电场强度有多个值,与实际不符。
3.题目:什么是电场强度?答案:电场强度是描述电场对单位正电荷施加的力的大小和方向。
详解:电场强度是电场的物理量,它表示电场对单位正电荷施加的力的大小和方向。
电场强度的单位是牛顿/库仑。
电场强度的方向由正电荷指向负电荷。
4.题目:电场强度与电场线之间的关系是什么?答案:电场强度和电场线是相互对应的。
电场强度的方向与电场线的方向一致,电场线的密度表示电场强度的大小。
详解:电场强度和电场线是相互对应的。
电场强度的方向由正电荷指向负电荷,电场线的方向也是由正电荷指向负电荷。
电场线的密度表示电场强度的大小,密度越大,表示电场强度越大。
5.题目:电场强度的大小与电荷量有关吗?答案:是的,电场强度的大小与电荷量有关。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
详解:电场强度的大小与电荷量有关。
根据库仑定律,电场强度与电荷量成正比,与距离的平方成反比。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
电磁场习题解读

电磁场习题解读静电例1、三个点电荷q1、q2、q3沿一条直线分布,已知其中任一点电荷所受合力均为零,且q1=q3=Q ,求在固定q1、q3的情况下,将q2从o →∞,外力需作功A=?解:由已知q1所受静电力例2、有两个点电荷带电量为nq 和-q (n>1),相距d,证明电势为零的等势面为一球面。
证明:空间任一点电势整理可得:上式为球面方程:球心坐标球面半径例3、点电荷-q 位于圆心处,A 、B 、C 、D 位于同一圆周上的四点如图示。
将q0从A 移至B 、C 、D 点,电场力的功。
A=0 例4. 已知: 是闭合曲面的一部分,面内无净电荷电场线穿过该闭合面,穿过部分的电场通量1?Φ,求:通过其余部分的电场通量2?Φ。
解:由高斯定理∑=?=ΦSiie q S d E 0ε ,00=Φ∴=∑eii q,12120?Φ-=Φ∴=?Φ+Φ∴ 例5、长为L,线电荷密度λ的两根均匀带电细棒,沿同一直线放置,两棒近端相距 a ,求两棒间的静电力。
q 2x od n n 1(22- 、0、0) 04)2(420322031=+=a q q a q q f πεπε4412Q q q -=-=∴e A A -=∴)0(2--=o U q a Q q 0242πε-=a Q 028πε=qnq U U U -+=22202220)(44z y d x qz y x nq ++--+++=πεπε0=令 222222)(z y d x qz y x nq ++-=++∴[]2222222)(z y x z y d x n ++=++-22222221()1(-=++--n nd z y d n n x 12-=n nd R S ?S ?解:任意一根棒上一段电荷元在其延长线上一点产生场强dE: xl x dlE d ?)(420-=πελ,?-=∴Ll x dlE 020)(4πελLl x 00)(4-=πελ--=x L x 1140πελ则棒2受棒1静电力:?=f d f,其中df 是棒2上一段电荷元所受棒1的静电力E dq df ?=dx x L x λπελ--=1140 , dx x L x f aL aL--=?++114202πελ)2()(ln 4202a L a a L ++=πελ例6 .无限长共轴直圆筒,半径为R1,R2,均匀带正电,单位长度电量分别为λ1,λ2,设外筒电势为0,求各区域内的电势分布,以及两筒间的电势差。
电磁场原理习题与解答(第2章)

(4)长圆柱中,有体密度为的电荷,与它偏轴地放有一半 径为a的无限长圆柱空洞,两者轴线平行且距离为d,如图2-6所示,求 空洞内的电场强度。 x y o
b (b)0 x y o d ( c) 图2-6 (a) 解:由于空洞存在,电荷分布不具有对称性,由此产生的场亦无对称 性,因此不能用高斯定律求解。这是可把空洞看作也充满,使圆柱体内 无空洞,然后再令空洞中充满-,并单独作用,分别求出两种场的分布 后叠加即可。设空洞内的电场强度为。 第一步 单独作用,如图(b)所示, 由体密度为的电荷产生的电场强 度为,由高斯定理
将电位参考点设在外导体上,即 则 , , 即 ,所以,内,外
2-9 用双层电介质制成的同轴电缆如题图2-9所示,介电常数 , 内、外导 体单位长度上所带电荷分别为和 (1)求两种电介质中以及 和处的电场强度与电通密度;
(2)求两种电介质中的电极化强度; (3)问何处有极化电荷,并求其密度。 解: (1)由高斯定理可得:
因此
(3) 球内电场, (r<a)
球外电场,由高斯定理:
, (r>a) 或
2-8 具有两层同轴介质的圆柱形电容器,内导体的直径为2cm,内层介 质的相对介电常数,外层的相对介电常数,要使两层介质中的最大场强 相等,并且内层介质所承受的电压和外层介质相等,问两层介质的厚度 各为多少? 解:以圆柱心为坐标原点,径向为轴,设单位长度上带电荷为,由高斯 定理,。 ,,
2-32 空气中,相隔1cm的两块平行导电平板充电到100V后脱离电 源,然后将一厚度为1mm的绝缘导电片插入两极间,问:
(1)忽略边缘效应,导电片吸收了多少能量?这部分能量起到了什 么作用?两板间的电压和电荷的改变量各为多少?最后存储在其中的能 量多大?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电例1、三个点电荷q1、q2、q3沿一条直线分布,已知其中任一点电荷所受合力均为零,且 q1=q3=Q ,求在固定q1、q3的情况下,将q2从o →∞,外力需作功A= 解:由已知q1所受静电力例2、有两个点电荷带电量为nq 和-q (n>1),相距d,证明电势为零的等势面为一球面。
证明:空间任一点电势整理可得: 上式为球面方程:球心坐标 球面半径例3、点电荷-q 位于圆心处,A 、B 、C 、D 位于同一圆周上的四点如图示。
将q0从A 移至B 、C 、D 点,电场力的功。
A=0 例4. 已知: 是闭合曲面的一部分,面内无净电荷电场线穿过该闭合面,穿过 部分的电场通量1∆Φ,求:通过其余部分的电场通量2∆Φ。
解:由高斯定理⎰∑=⋅=ΦSiie q S d E 0ε ,00=Φ∴=∑eii q,12120∆Φ-=Φ∴=∆Φ+Φ∴ 例5、长为L,线电荷密度λ的两根均匀带电细棒,沿同一直线放置,两棒近端相距 a ,求两棒间的静电力。
q 2x od n n 1(22- 、0、0) 04)2(420322031=+=a q q a q q f πεπε4412Q q q -=-=∴e A A -=∴)0(2--=o U q a Q q 0242πε-=a Q 028πε=qnq U U U -+=22202220)(44z y d x qz y x nq ++--+++=πεπε0=令 222222)(z y d x qz y x nq ++-=++∴[]2222222)(z y x z y d x n ++=++-22222221()1(-=++--n nd z y d n n x 12-=n nd R S ∆S ∆解:任意一根棒上一段电荷元在其延长线上一点产生场强dE: xl x dlE d ˆ)(420-=πελ,⎰-=∴Ll x dlE 020)(4πελLl x 00)(4-=πελ⎪⎭⎫⎝⎛--=x L x 1140πελ则棒2受棒1静电力:⎰=f d f,其中df 是棒2上一段电荷元所受棒1的静电力E dq df ⋅=dx x L x λπελ⋅⎪⎭⎫⎝⎛--=1140 , dx x L x f aL aL ⎪⎭⎫⎝⎛--=⎰++114202πελ)2()(ln 4202a L a a L ++=πελ例6 .无限长共轴直圆筒,半径为R1,R2,均匀带正电,单位长度电量分别为λ1,λ2,设外筒电势为0,求各区域内的电势分布,以及两筒间的电势差。
解:电场具有对称性,利用叠加原理求场强: 当r<R1时,E1=0; 当R1 <r<R2时,rE 0122πελ=; 当r>R2时, rE 02122πελλ+=;然后用线积分求电势分布,当r<R1⎰⋅=21R Pl d E V ⎰⎰⋅+⋅=121R r R R l d E l d E ⎰+=210120R R rdr πελ1201ln 2R R πελ= 当R1 <r<R2时, ⎰⋅=22R pl d E V ⎰=2012R r rdr πελr R 201ln 2πελ= 当r>R2时,⎰⋅=22R pl d E V ⎰+-=r R r dr 20212πελλr R2021ln 2πελλ+=筒间电势差U ∆即r=R1处的电势1201ln 2R RU πελ=∆ 选做题1、半径为R 的均匀带电圆面,电荷的面密度为σe , (1)球轴线上离圆心的坐标为x 处的场强;(2)在保持σe 不变的情况下,当R 分别趋于0和∞时,结果各如何?(3)在保持总电荷Q=πR2不变的情况下,当R 分别趋于0和∞时,结果各如何? (4)求轴线上电势U (x )的分布,并画出U-x 关系曲线。
2、半径为R1的导体球带有电荷q ,球外有一个内外半径分别为R2、 R3的同心导体球壳,壳上带有电荷Q ,(1)求两球的电势U1和U2;(2)以导线把球和壳接在一起后, U1和U2分别是多少? (3)在(1)中,若外球接地,则U1和U2分别是多少? (4)设外球离地面很远,若内球接地,情况如何?[例题1 ] 设电偶极子的两电荷-q 和+q 间的距离为l ,求距离电偶极子远处的电势和场强的分布。
[解] ( 1 ) 电势分布设场点P 到q ±的距离分别为+r 和-r ,则q ±单独存在时P 点的电势为±±=r q U 041επ. 根据电势叠加原理,有-++=U U U )11(40-+-=r r q επ. 电偶极子的中点O 到场点P 的距离为r , 按题意l r >>,于是有:θcos 2lr r -≈+,θcos 2lr r +≈-;θcos l r r ≈-+-,2r r r ≈-+.将它们代入U 的表达式,可得200cos 44r p q r r r r q U θεεππ≈-=-++-04r q r p ⋅π=ε,电偶极子在远处的性质是由它的电偶极矩l p q =决定的。
( 2 ) 场强分布由于轴对称性,U 与方位角ϕ无关,采用平面极坐标系,其极轴沿电矩p ,原点O 位于电偶极子的中心。
场强E 的两个分量分别为: 30cos 241r p r U E r θεπ=∂∂-=,30sin 411r p U r E θεθθπ=∂∂-=,在电偶极子的延长线上,有:0=θE ,30241r p E E r επ==; 在电偶极子的中垂面上,2π=θ,有:0=r E ,3041r p E E εθπ==. [例题2] 一示波器中阳极A 和阴极K 之间的电压是3000 V ,试求阴极发射的电子到达阳极时的速度,设电子从阴极出发时初速为零。
[解] 电子带负电,C 1060.119e -⨯-=-=e q,所以它沿电势升高的方向加速运动,即从阴极 K 出发到达阳极 A. 于是,J )0003()1060.1(19KA KA -⨯⨯-=-=-U e AJ 1080.416-⨯=.电场力作功使电子动能增加,因此电子到达阳极时获得的动能为 J1080.42116KA 2e -⨯=-=U e v m .又,电子质量kg 1011.931e -⨯=m ,所以电子到达阳极时的速率为m/s1025.3m/s 1011.91080.42271316eKA⨯=⨯⨯⨯=-=--m U e v .元电荷C 1060.119-⨯=e 是电子和质子等微观粒子带电的基本单位。
任何一个带有电量e 的粒子,只要飞越一个电势差为1 V 的区间,电场力就对它作功J 1060.1J 11060.11919--⨯=⨯⨯=A ,从而该微观粒子本身就获得了这么多的能量。
在近代物理学中,常把这个能量称为1 eV (电子伏特),即J 1060.1eV 191-⨯=.[例题三]设想一厚度l 均匀的曲面薄壳,两面带有符号相反的面电荷e σ± ——电偶极层,如图,求P 点的电势和场强。
解:⎰='0''41)(S e r dS p U σπε⎰-+'0)(41S e r dS σπε⎰⎪⎭⎫⎝⎛-=Se dS r r 1'1410σπε从图中看:θθ,cos 'l r r +≈为矢径r 与d S 法线n 之间的夹角,于是有⎪⎭⎫ ⎝⎛-≈+=+≈r l r rr l r r θθθcos 11)1(1cos 1'122c o s1'1c o s 1r l r r r l r θθ-=-⇒-=,代入)(p U ⎰-=Se r dS l p U 2cos 41)(θσπε Ωd rdS=2cos θ 定义电偶极层强度:——单位面积上的电偶极矩l e e στ≡ΩΩ0044)(πετπετe S e d p U -=-=⎰P 点的电场强度Ω∇=-∇=04)(πετe p U E讨论: 1) 电偶极层的电势和场强只与对场点所张的立体角有关; 2)几何上决定,电偶极层两侧立体角有π4-的跃变:面元dS 在垂直于矢径r 方向的投影曲面S 对场点P所张的立体角负电荷一侧:0,0cos ,2/,cos 2>=∴><=⎰Sd rdS d ΩΩΩθπθθ ;正电荷一侧:0,0cos ,2/,cos <=∴<>=⎰Sd rdS d ΩΩΩθπθθ 具体考察图中两点-立体角+立体角ΩΩ−−→−−−→−-+P P ,当该两点趋于偶极层表面时,相对应的立体角之差:π4=+=-+-+-ΩΩΩΩ 电偶极层两侧的电势跃变: 00044)(4)()(ετππετπετee e p U pU =⨯=--=--+-+ΩΩ 稳恒磁场定理及定律:洛伦兹力公式:B v q E q f⨯+=安培定律 :B l Id F d⨯=毕—萨定理:2ˆ4rr l Id B d ⨯=πμ 几种典型电流的B 分布: 一段载流直导线:)sin (sin 4120ββπμ-=aIB 圆电流圈的圆心和轴线上:())(222/32200不必记轴线中心xR ISB R I B +==πμμ例题1、如图在半径为R 的圆周上,a 、b 、c 三点依次相隔90°,a 、c 两处有垂直纸面 向里的电流元。
求:b 点磁感应强度 解: 2024R Idl dB dB l Id l Id πμ==' ;2224220⋅⨯=R Idl dB πμ2024R Idl πμ=例题2、 无限长载流圆柱体,半径R ,通以电流I ,电流均匀分布在截面上,现在圆柱体挖去一半径为b 的小圆柱体,其轴线相互平行,且相距a(a+b<R),设挖去小圆柱体后,余下部分电流密度不变,p 点在o’o 的延长线上op=a 。
求:Bp=?解:电流均匀分布的无限长载流柱体的磁场分布为:⎪⎪⎩⎪⎪⎨⎧∞<≤<≤=r R r I Rr R Ir B πμπμ202020;此题相当于电流流向相反的大小两载流柱体产生磁场的叠加a I R Ia B 222020πμπμ'-=∴22R b I I ππ=')2(2220ab a R I -πμ 例题3、 载流方线圈边长2a,通电流I,求:中心o 处磁感应强度解:O 点B 为四段有限长直载流导线产生的磁感应强度的叠加,方向相同,所以104B B =]sin [sin 44120θθπμ-⨯=a I[])45sin(45sin 4400--⨯=o a I πμaI πμ02=方向: 例题4、无限长直电流I1在纸面内,无限长直电流I2与纸面垂直,并与I1相距d , P 点纸面内与I1I2的距离均为d 。
