图的深度遍历与广度遍历
第15讲图的遍历

V6
V8
V8
V7
V5 深度优先生成树
V8 V1
V2
V3
V4 V5 V6 V7
V8 广度优先生成树
27
例A
B
CD E
F
GH
I
K
J
L
M
A
D
G
LCF
KI E
H M
JB
深度优先生成森林
28
二、图的连通性问题
▪1、生成树和生成森林
▪ 说明
G
▪ 一个图可以有许多棵不同的生成树
KI
▪ 所有生成树具有以下共同特点:
g.NextAdjVex(v, w))
{
if (g.GetTag(w) == UNVISITED)
{
g.SetTag(w, VISITED);
g.GetElem(w, e);
Visit(e);
q.InQueue(w);
}
}}}
24
一、图的遍历 两种遍历的比较
V0
V1 V4
V0
V1 V4
V3
V2 V5
16
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
V3
V1
V4
V5 V6
V7
V8
遍历序列: V1
17
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
V3
V2 V3
V4
V5 V6
V7
V8
遍历序列: V1 V2 V3
18
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
第7章图的深度和广度优先搜索遍历算法
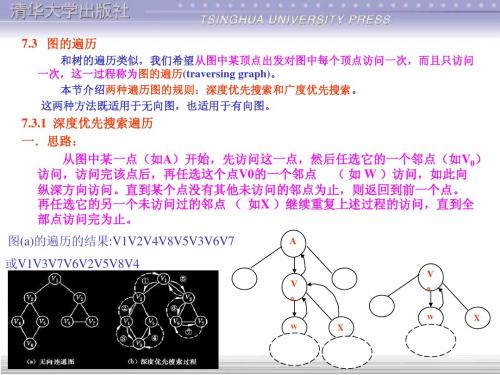
和树的遍历类似,我们希望从图中某顶点出发对图中每个顶点访问一次,而且只访问 一次,这一过程称为图的遍历(traversing graph)。 本节介绍两种遍历图的规则:深度优先搜索和广度优先搜索。 这两种方法既适用于无向图,也适用于有向图。
7.3.1 深度优先搜索遍历 一.思路: 从图中某一点(如A)开始,先访问这一点,然后任选它的一个邻点(如V0) 访问,访问完该点后,再任选这个点V0的一个邻点 ( 如 W )访问,如此向 纵深方向访问。直到某个点没有其他未访问的邻点为止,则返回到前一个点。 再任选它的另一个未访问过的邻点 ( 如X )继续重复上述过程的访问,直到全 部点访问完为止。 图(a)的遍历的结果:V1V2V4V8V5V3V6V7 或V1V3V7V6V2V5V8V4
p
v0 w x v 1
V
0
v 2
V
0
typedef struct {VEXNODE adjlist[MAXLEN]; // 邻接链表表头向量 int vexnum, arcnum; // 顶点数和边数 int kind; // 图的类型 }ADJGRAPH;
W W
X
X
7.3.2 广度优先搜索遍历 一.思路:
V
0
A V
0
W W
XXΒιβλιοθήκη 二.深度优先搜索算法的文字描述: 算法中设一数组visited,表示顶点是否访问过的标志。数组长度为 图的顶点数,初值均置为0,表示顶点均未被访问,当Vi被访问过,即 将visitsd对应分量置为1。将该数组设为全局变量。 { 确定从G中某一顶点V0出发,访问V0; visited[V0] = 1; 找出G中V0的第一个邻接顶点->w; while (w存在) do { if visited[w] == 0 继续进行深度优先搜索; 找出G中V0的下一个邻接顶点->w;} }
数据结构 第七章-图2

{DeQueue(Q,u); /*队头元素出队,并赋值给u*/
/*访问u所有未被访问的邻接点*/
for(w=0; w<G.vexnum; w++;)
if (G.arcs[u,w].adj && !visited[w])
{ visited[w]=1; Visit(w); EnQueue(Q,w); }
void DFS(Graph G, int v)
7.3 图的遍历
visited 0 0 10 20 30 40
……
{/* 从第v个顶点出发,递归地深度优先遍历图G*/
/* v是顶点在一维数组中的位置,假设G是非空图*/
visited[v] =1;
Visit(v); /*访问第v个顶点*/
for ( w=FirstAdjVex(G, v); w; w=NextAdjVex(G, v, w) )
效率。
2
7.3 图的遍历
7.3 图的遍历:从图的某顶点出发,访问图中所有顶点, 并且每个顶点仅访问一次。
图结构的遍历复杂性:
(1)在图结构中,没有一个“自然”的首结点,图中的任 意一个顶点都可以作为第一个被访问的结点
(2)在非连通图中,从一个顶点出发,只能访问它所在的 连通分量上的所有顶点,因此,还需考虑如何选取下一个出 发点以访问图中的其余连通分量
} }/*DFSAL*/
8
7.3 图的遍历
在遍历时,对图中每个顶点至多调用一次DFS函数,因为 一旦某个顶点被标志成已被访问,就不再从它出发进行搜索。 因此,遍历图的过程实质上是对每个顶点查找其邻接点的过 程。其耗费的时间则取决于所采用的存储结构。
用邻接矩阵做图的存储结构时,查找各个顶点的邻接点所 需的时间为O(n2),其中n为图中顶点数。当以邻接矩阵做存 储结构时,深度优先搜索遍历图的时间复杂度为O(n2+n)。
深度遍历和广度遍历例题

深度遍历和广度遍历例题深度遍历(Depth First Search, DFS)和广度遍历(Breadth First Search, BFS)是图遍历的两种常用方法。
在本文中,将介绍深度遍历和广度遍历的定义、原理、应用以及两种方法的例题。
一、深度遍历(DFS)深度遍历使用堆栈(Stack)实现,其基本思想是先访问根节点,然后再递归地访问其相邻节点,直到所有节点都被访问。
深度遍历能够搜索到最深层次的节点,但可能会陷入死循环。
1. 深度遍历的应用场景:深度遍历常用于解决图的连通性问题、拓扑排序、求解图中的环等。
另外,也可以应用于解决迷宫问题、数独等。
2. 深度遍历的基本过程:(1)首先访问初始节点,并标记为已访问。
(2)递归地访问初始节点的相邻节点,对于每一个相邻节点,若未被访问,则进行递归访问。
(3)重复步骤(2),直到所有节点都被访问。
3. 深度遍历的例题:假设有以下有向图:A -> B,A -> C,B -> D,B -> E,C -> F,D -> G,E -> H,F -> G,G -> E,H -> E现在要求从节点A开始进行深度遍历,从A到E的路径请写出所有可能的路径。
答案:A -> B -> D -> G -> E,A -> B -> E,A -> C -> F -> G -> E,A -> C -> F -> G -> E,A -> B -> D -> G -> E -> H -> E,A -> C -> F -> G -> E -> H -> E二、广度遍历(BFS)广度遍历使用队列(Queue)实现,其基本思想是先访问根节点,然后再按照层次逐层访问其相邻节点,直到所有节点都被访问。
广度优先和深度优先的例子

广度优先和深度优先的例子广度优先搜索(BFS)和深度优先搜索(DFS)是图遍历中常用的两种算法。
它们在解决许多问题时都能提供有效的解决方案。
本文将分别介绍广度优先搜索和深度优先搜索,并给出各自的应用例子。
一、广度优先搜索(BFS)广度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,逐层扩展,先访问起始节点的所有邻居节点,再依次访问其邻居节点的邻居节点,直到遍历完所有节点或找到目标节点。
例子1:迷宫问题假设有一个迷宫,迷宫中有多个房间,每个房间有四个相邻的房间:上、下、左、右。
现在我们需要找到从起始房间到目标房间的最短路径。
可以使用广度优先搜索算法来解决这个问题。
例子2:社交网络中的好友推荐在社交网络中,我们希望给用户推荐可能认识的新朋友。
可以使用广度优先搜索算法从用户的好友列表开始,逐层扩展,找到可能认识的新朋友。
例子3:网页爬虫网页爬虫是搜索引擎抓取网页的重要工具。
爬虫可以使用广度优先搜索算法从一个网页开始,逐层扩展,找到所有相关的网页并进行抓取。
例子4:图的最短路径在图中,我们希望找到两个节点之间的最短路径。
可以使用广度优先搜索算法从起始节点开始,逐层扩展,直到找到目标节点。
例子5:推荐系统在推荐系统中,我们希望给用户推荐可能感兴趣的物品。
可以使用广度优先搜索算法从用户喜欢的物品开始,逐层扩展,找到可能感兴趣的其他物品。
二、深度优先搜索(DFS)深度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,沿着一条路径一直走到底,直到不能再继续下去为止,然后回溯到上一个节点,继续探索其他路径。
例子1:二叉树的遍历在二叉树中,深度优先搜索算法可以用来实现前序遍历、中序遍历和后序遍历。
通过深度优先搜索算法,我们可以按照不同的遍历顺序找到二叉树中所有节点。
例子2:回溯算法回溯算法是一种通过深度优先搜索的方式,在问题的解空间中搜索所有可能的解的算法。
回溯算法常用于解决组合问题、排列问题和子集问题。
例子3:拓扑排序拓扑排序是一种对有向无环图(DAG)进行排序的算法。
数据结构课设——有向图的深度、广度优先遍历及拓扑排序
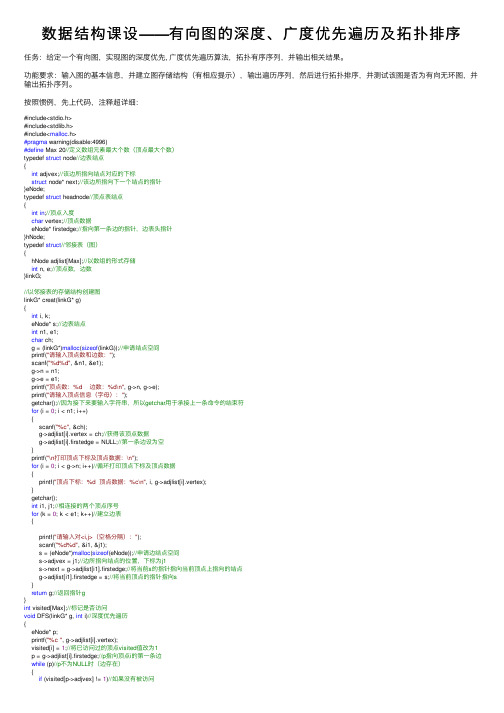
数据结构课设——有向图的深度、⼴度优先遍历及拓扑排序任务:给定⼀个有向图,实现图的深度优先, ⼴度优先遍历算法,拓扑有序序列,并输出相关结果。
功能要求:输⼊图的基本信息,并建⽴图存储结构(有相应提⽰),输出遍历序列,然后进⾏拓扑排序,并测试该图是否为有向⽆环图,并输出拓扑序列。
按照惯例,先上代码,注释超详细:#include<stdio.h>#include<stdlib.h>#include<malloc.h>#pragma warning(disable:4996)#define Max 20//定义数组元素最⼤个数(顶点最⼤个数)typedef struct node//边表结点{int adjvex;//该边所指向结点对应的下标struct node* next;//该边所指向下⼀个结点的指针}eNode;typedef struct headnode//顶点表结点{int in;//顶点⼊度char vertex;//顶点数据eNode* firstedge;//指向第⼀条边的指针,边表头指针}hNode;typedef struct//邻接表(图){hNode adjlist[Max];//以数组的形式存储int n, e;//顶点数,边数}linkG;//以邻接表的存储结构创建图linkG* creat(linkG* g){int i, k;eNode* s;//边表结点int n1, e1;char ch;g = (linkG*)malloc(sizeof(linkG));//申请结点空间printf("请输⼊顶点数和边数:");scanf("%d%d", &n1, &e1);g->n = n1;g->e = e1;printf("顶点数:%d 边数:%d\n", g->n, g->e);printf("请输⼊顶点信息(字母):");getchar();//因为接下来要输⼊字符串,所以getchar⽤于承接上⼀条命令的结束符for (i = 0; i < n1; i++){scanf("%c", &ch);g->adjlist[i].vertex = ch;//获得该顶点数据g->adjlist[i].firstedge = NULL;//第⼀条边设为空}printf("\n打印顶点下标及顶点数据:\n");for (i = 0; i < g->n; i++)//循环打印顶点下标及顶点数据{printf("顶点下标:%d 顶点数据:%c\n", i, g->adjlist[i].vertex);}getchar();int i1, j1;//相连接的两个顶点序号for (k = 0; k < e1; k++)//建⽴边表{printf("请输⼊对<i,j>(空格分隔):");scanf("%d%d", &i1, &j1);s = (eNode*)malloc(sizeof(eNode));//申请边结点空间s->adjvex = j1;//边所指向结点的位置,下标为j1s->next = g->adjlist[i1].firstedge;//将当前s的指针指向当前顶点上指向的结点g->adjlist[i1].firstedge = s;//将当前顶点的指针指向s}return g;//返回指针g}int visited[Max];//标记是否访问void DFS(linkG* g, int i)//深度优先遍历{eNode* p;printf("%c ", g->adjlist[i].vertex);visited[i] = 1;//将已访问过的顶点visited值改为1p = g->adjlist[i].firstedge;//p指向顶点i的第⼀条边while (p)//p不为NULL时(边存在){if (visited[p->adjvex] != 1)//如果没有被访问DFS(g, p->adjvex);//递归}p = p->next;//p指向下⼀个结点}}void DFSTravel(linkG* g)//遍历⾮连通图{int i;printf("深度优先遍历;\n");//printf("%d\n",g->n);for (i = 0; i < g->n; i++)//初始化为0{visited[i] = 0;}for (i = 0; i < g->n; i++)//对每个顶点做循环{if (!visited[i])//如果没有被访问{DFS(g, i);//调⽤DFS函数}}}void BFS(linkG* g, int i)//⼴度优先遍历{int j;eNode* p;int q[Max], front = 0, rear = 0;//建⽴顺序队列⽤来存储,并初始化printf("%c ", g->adjlist[i].vertex);visited[i] = 1;//将已经访问过的改成1rear = (rear + 1) % Max;//普通顺序队列的话,这⾥是rear++q[rear] = i;//当前顶点(下标)队尾进队while (front != rear)//队列⾮空{front = (front + 1) % Max;//循环队列,顶点出队j = q[front];p = g->adjlist[j].firstedge;//p指向出队顶点j的第⼀条边while (p != NULL){if (visited[p->adjvex] == 0)//如果未被访问{printf("%c ", g->adjlist[p->adjvex].vertex);visited[p->adjvex] = 1;//将该顶点标记数组值改为1rear = (rear + 1) % Max;//循环队列q[rear] = p->adjvex;//该顶点进队}p = p->next;//指向下⼀个结点}}}void BFSTravel(linkG* g)//遍历⾮连通图{int i;printf("⼴度优先遍历:\n");for (i = 0; i < g->n; i++)//初始化为0{visited[i] = 0;}for (i = 0; i < g->n; i++)//对每个顶点做循环{if (!visited[i])//如果没有被访问过{BFS(g, i);//调⽤BFS函数}}}//因为拓扑排序要求⼊度为0,所以需要先求出每个顶点的⼊度void inDegree(linkG* g)//求图顶点⼊度{eNode* p;int i;for (i = 0; i < g->n; i++)//循环将顶点⼊度初始化为0{g->adjlist[i].in = 0;}for (i = 0; i < g->n; i++)//循环每个顶点{p = g->adjlist[i].firstedge;//获取第i个链表第1个边结点指针while (p != NULL)///当p不为空(边存在){g->adjlist[p->adjvex].in++;//该边终点结点⼊度+1p = p->next;//p指向下⼀个边结点}printf("顶点%c的⼊度为:%d\n", g->adjlist[i].vertex, g->adjlist[i].in);}void topo_sort(linkG *g)//拓扑排序{eNode* p;int i, k, gettop;int top = 0;//⽤于栈指针的下标索引int count = 0;//⽤于统计输出顶点的个数int* stack=(int *)malloc(g->n*sizeof(int));//⽤于存储⼊度为0的顶点for (i=0;i<g->n;i++)//第⼀次搜索⼊度为0的顶点{if (g->adjlist[i].in==0){stack[++top] = i;//将⼊度为0的顶点进栈}}while (top!=0)//当栈不为空时{gettop = stack[top--];//出栈,并保存栈顶元素(下标)printf("%c ",g->adjlist[gettop].vertex);count++;//统计顶点//接下来是将邻接点的⼊度减⼀,并判断该点⼊度是否为0p = g->adjlist[gettop].firstedge;//p指向该顶点的第⼀条边的指针while (p)//当p不为空时{k = p->adjvex;//相连接的顶点(下标)g->adjlist[k].in--;//该顶点⼊度减⼀if (g->adjlist[k].in==0){stack[++top] = k;//如果⼊度为0,则进栈}p = p->next;//指向下⼀条边}}if (count<g->n)//如果输出的顶点数少于总顶点数,则表⽰有环{printf("\n有回路!\n");}free(stack);//释放空间}void menu()//菜单{system("cls");//清屏函数printf("************************************************\n");printf("* 1.建⽴图 *\n");printf("* 2.深度优先遍历 *\n");printf("* 3.⼴度优先遍历 *\n");printf("* 4.求出顶点⼊度 *\n");printf("* 5.拓扑排序 *\n");printf("* 6.退出 *\n");printf("************************************************\n");}int main(){linkG* g = NULL;int c;while (1){menu();printf("请选择:");scanf("%d", &c);switch (c){case1:g = creat(g); system("pause");break;case2:DFSTravel(g); system("pause");break;case3:BFSTravel(g); system("pause");break;case4:inDegree(g); system("pause");break;case5:topo_sort(g); system("pause");break;case6:exit(0);break;}}return0;}实验⽤图:运⾏结果:关于深度优先遍历 a.从图中某个顶点v 出发,访问v 。
图的各种算法(深度、广度等)

vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top
4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top 4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
c a g b h f d e
a
b h c d g f
e
在算法中需要用定量的描述替代定性的概念
没有前驱的顶点 入度为零的顶点 删除顶点及以它为尾的弧 弧头顶点的入度减1
算法实现
以邻接表作存储结构 把邻接表中所有入度为0的顶点进栈 栈非空时,输出栈顶元素Vj并退栈;在邻接表中查找 Vj的直接后继Vk,把Vk的入度减1;若Vk的入度为0 则进栈 重复上述操作直至栈空为止。若栈空时输出的顶点个 数不是n,则有向图有环;否则,拓扑排序完毕
^
4
^
top
输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^ p
^
4
^topBiblioteka 5输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
w2 w1 V w7 w6 w3
算法设计:深度优先遍历和广度优先遍历

算法设计:深度优先遍历和广度优先遍历实现深度优先遍历过程1、图的遍历和树的遍历类似,图的遍历也是从某个顶点出发,沿着某条搜索路径对图中每个顶点各做一次且仅做一次访问。
它是许多图的算法的基础。
深度优先遍历和广度优先遍历是最为重要的两种遍历图的方法。
它们对无向图和有向图均适用。
注意:以下假定遍历过程中访问顶点的操作是简单地输出顶点。
2、布尔向量visited[0..n-1]的设置图中任一顶点都可能和其它顶点相邻接。
在访问了某顶点之后,又可能顺着某条回路又回到了该顶点。
为了避免重复访问同一个顶点,必须记住每个已访问的顶点。
为此,可设一布尔向量visited[0..n-1],其初值为假,一旦访问了顶点Vi之后,便将visited[i]置为真。
--------------------------深度优先遍历(Depth-First Traversal)1.图的深度优先遍历的递归定义假设给定图G的初态是所有顶点均未曾访问过。
在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过;然后依次从v出发搜索v的每个邻接点w。
若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
图的深度优先遍历类似于树的前序遍历。
采用的搜索方法的特点是尽可能先对纵深方向进行搜索。
这种搜索方法称为深度优先搜索(Depth-First Search)。
相应地,用此方法遍历图就很自然地称之为图的深度优先遍历。
2、深度优先搜索的过程设x是当前被访问顶点,在对x做过访问标记后,选择一条从x出发的未检测过的边(x,y)。
若发现顶点y已访问过,则重新选择另一条从x出发的未检测过的边,否则沿边(x,y)到达未曾访问过的y,对y访问并将其标记为已访问过;然后从y开始搜索,直到搜索完从y出发的所有路径,即访问完所有从y出发可达的顶点之后,才回溯到顶点x,并且再选择一条从x出发的未检测过的边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图的深度遍历和广度遍历程序源代码如下:
#include"stdio.h"
#include"stdlib.h"
#define MAXQSIZE 100
#define MVNum 100
int visited[100];
typedef struct
{
char *base;
int front;
int rear;
}SqQueue;
int InitQueue(SqQueue &Q) //初始化队列
{
Q.base=new char[MAXQSIZE];
if(!Q.base)
exit(-1); //存储失败
Q.front=Q.rear=0; //队列为空
return 1;
}
int QueueEmpty(SqQueue &Q) //判断队非空
{
if(Q.front==Q.rear)
return 0;
return 1;
}
int EnQueue(SqQueue &Q,char e) //入队
{
if((Q.rear+1)%MAXQSIZE==Q.front) //队满
return 0;
Q.base[Q.rear]=e; //新元素插入队尾
Q.rear=(Q.rear+1)%MAXQSIZE; //队尾指针加1
return 1;
}
int DeQueue(SqQueue &Q,char &e) //出队
{
if(Q.front==Q.rear)
return 0; //队空
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXQSIZE;
return 1;
}
int GetHead(SqQueue Q) //取队头元素{
if(Q.front!=Q.rear)
return Q.base[Q.front];
}
typedef struct //定义图
{
char vexs[MVNum];
int arcs[MVNum][MVNum];
int vexnum,arcnum;
}AMGraph;
int LocateVex(AMGraph G,char u)
{
int i;
for(i=0;i<G.vexnum;++i)
if(u==G.vexs[i])
return i;
return -1;
}
int CreateUDN(AMGraph &G) //创建图{
int i,j,k;
char v1,v2;
printf("输入顶点个数和边的个数:\n");
scanf("%d%d",&G.vexnum,&G.arcnum);
getchar();
printf("请输入图:\n");
for(i=0;i<G.vexnum;++i)
scanf("%c",&G.vexs[i]);
getchar();
for(i=0;i<G.vexnum;++i)
for(j=0;j<G.vexnum;++j)
G.arcs[i][j]=0;
for(k=0;k<G.arcnum;++k)
{
scanf("%c%c",&v1,&v2);
getchar();
i=LocateVex(G,v1);
j=LocateVex(G,v2);
G.arcs[i][j]=1;
G.arcs[j][i]=G.arcs[i][j];
}
return 1;
}
void DFS(AMGraph G,int v) //深度遍历图{
int w;
printf("%c",G.vexs[v]);
visited[v]=1;
for(w=0;w<G.vexnum;w++)
if((G.arcs[v][w]!=0)&&(!visited[w]))
DFS(G,w);
}
void DFSTraverse(AMGraph G)
{
int v;
for(v=0;v<G.vexnum;++v)
visited[v]=0;
for(v=0;v<G.vexnum;++v)
if(!visited[v])
DFS(G,v);
}
void BFS(AMGraph G,int v) //广度遍历
{
int w;
SqQueue Q;
printf("%c",G.vexs[v]); //访问第v个顶点
visited[v]=1;
InitQueue(Q); //初始化队列,置空
EnQueue(Q,v); //v进队
char u=GetHead(Q);
while(!QueueEmpty(Q)) //队列非空
{
DeQueue(Q,u); //队头元素出队,置为u
for(w=0;w<G.vexs[v];w++)
if(visited[w])
{
scanf("%d",&w);
visited[w]=1;
EnQueue(Q,w); //w进队
}
}
}
void BFSTraverse(AMGraph G)
{
int v;
for(v=0;v<G.vexnum;++v)
visited[v]=0;
for(v=0;v<G.vexnum;++v)
if(!visited[v])
BFS(G,v);
}
main()
{
AMGraph G;
CreateUDN(G);
printf("深度遍历结果:\n");
DFSTraverse(G);
printf("\n广度遍历结果:\n");
BFSTraverse(G);
printf("\n");
}
深度遍历结果:abdecfg 广度遍历结果:abcdefg。
