15-云模型专题解析
高考化学复习专题检测—物质结构与性质(含解析)

高考化学复习专题检测—物质结构与性质(含解析)一、选择题(本题包括25小题,每小题2分,共50分,每小题只有一个选项符合题意)1.(2023·黑龙江省绥化市第九中学高三质检)已知在一定条件下,SO2也能体现其氧化性,例如:2H2S+SO2=3S+2H2O,下列化学用语使用正确的是()A.SO2的VSEPR模型:B.HS-电离的离子方程式:HS-+H2O H2S+OH-C.基态硫原子p x轨道的电子云轮廓图:D.基态氧原子最外层电子的轨道表示式:【答案】C【解析】A项,二氧化硫中心原子S的价层电子对数为3,有1对孤电子对,S杂化类型为sp2,VSEPR模型为平面三角形,A错误;B项,HS-电离的离子方程式HS-H++S2-,B错误;C项,基态硫原子P x轨道的电子云轮廓为哑铃型,C正确;D项,基态氧原子最外层电子的轨道表示式:,D错误;故选C。
2.(2023·江苏省南京市江宁区高三期中)尿素CO(NH2)2是一种高效化肥,也是一种化工原料。
反应CO2+2NH3CO(NH2)2+H2O可用于尿素的制备。
下列有关说法不正确...的是()A.NH3与CO(NH2)2均为极性分子B.N2H4分子的电子式为C.NH3的键角大于H2O的键角D.尿素分子σ键和π键的数目之比为6∶1【答案】D【解析】A项,NH3分子为三角锥形,为极性分子,CO(NH2)2中的N原子与NH3中的N成键方式相同,所以二者均为极性分子,A正确;B项,N原子的最外层电子数为5个,要达到稳定结构,N2H4的电子式为:,B正确;C项,NH3分子中有3个σ键,1对孤电子对,H2O分子中有2个σ键和2对孤电子对,孤电子对与成键电子对之间的排斥力大于成键电子对之间的排斥力,所以H2O的键角小于NH3中的键角,C正确;D项,1个单键1个σ键,1个双键1个σ键和1个π键,尿素中含有6个单键和1个双键,7个σ键和1个π键,尿素分子σ键和π键的数目之比为7∶1,D错误;故选D。
精品解析:2024年山东省济宁市中考地理真题(解析版)

C.沪昆线—京沪线—京哈线D.沪昆线—京包线—京哈线
【答案】16. C 17. A 18. C
【解析】
【16题详解】
哈尔滨举办冰雪节的自然条件是纬度较高,冬季寒冷漫长,河流冰层厚,冰雕原材料充足;积雪厚且雪期长,冰雕保存时间长,①③正确;举办冰雪节经验丰富、当地居民热情好客不是自然条件,②④错误。故选C。
【2题详解】
由题干知,相邻节气间隔约15天。立秋和立冬相隔6个节气,故大约经历了90天,故选C。
【3题详解】
白菜的生长期大约在8月初至11月初。8 - 11月温度是逐渐降低的过程,说明白菜具有喜温凉、耐寒的生长习性,故选B。
【点睛】二十四节气是我国古代人民通过观察太阳周年运动,以黄河中下游地区的天象、气温、降水和物候的时序变化规律为基准所形成的知识体系和社会实践,自秦汉至今指导着我国传统农业生产和日常生活。
2024年春节期间,家住兖州区李家湾小区的小亮一家从大安机场乘飞机外出旅游,用手机导航确定去机场的路线,屏幕显示如下图。完成下面小题。
4.去机场的路线中,在246省道上的行驶方向是()
A.从东南向西北B.从西北向东南C.从正西向正东D.从正东向正西
5.去机场途中,小亮帮开车的爸爸导航。小亮对电子地图进行“放大”或“缩小”操作,查询沿途更多信息。小亮的操作可以改变()
【15题详解】
欧洲西部地区属于温带海洋性气候,适合多汁牧草的生长,加上生产规模大,生产机械化水平高,畜牧业发达,A正确。欧洲西部是世界上工业最发的地区之一,工农业普遍实现了高度的机械化,自动化,信息化,B错误。欧洲西部有得天独厚的自然旅游资源和丰富的历史文化遗迹,C错误。欧洲西部是世界上较为稠密的地区之一,但也是人口老龄最化严重的地区之一,自然增长率较低,D错误。故选A。
BIM建筑模型练习题

BIM技术旳解析应用单项选择题:1、BIM是以建筑工程项目旳(A. 各项有关信息数据)作为模型旳基础,进行建筑模型旳建立,通过数字信息仿真模拟建筑物所具有旳真实信息。
2、如下有关BIM旳概念旳表述,对旳旳是(D. BIM是一种处理方案旳集合)。
3、BIM最大旳意义在于(D. 全生命周期应用)。
4、BIM让人们将以往旳线条式旳构件形成一种三维旳立体实物图形展示在人们旳面前,这体现了BIM旳( A. 可视化)特点。
5、最早有关 BIM 旳概念是(B.1975.0)年提出旳。
6、(C. 《2023-2023 年建筑业信息化发展纲要》)旳颁布,标志着 BIM 技术真正成为我国建筑信息化旳主线,也成为我国旳“BIM 元年”。
7、BIM 技术最先从(B. 美国)发展开来。
8、BIM在施工阶段应加入旳信息有(D. 材料)。
9、全生命周期旳广义定义是(C.涵盖并服务于建筑乃至都市旳全生命周期)。
10、实现BIM全生命周期旳关键在于BIM模型旳(B.信息传递)。
11、(A.施工建设)中旳风险属于显性风险。
12、如下不属于BIM应用产生旳收益和效果旳是(C.协议价格提高)。
13、BIM原则化研究工作旳实行主体是(A. 企业级)。
14、BIM 构件分类以(A. 企业属性)为基础构建管理体系。
15、以矩形截面型钢构造框架梁为例进行面分法分类时,可按(C. 功能、材质、形状)进行。
16、如下不是企业级 BIM 原则化政策实行路线旳内容旳是(B. 全面把握)。
17、建筑工业化和(C. 建筑业信息化)是建筑业可持续发展旳两大构成部分。
18、BIM 旳一种基本前提是(A. 项目全寿命期内不一样阶段不一样利益有关方旳协同)。
19、(B. 建筑信息模型)是指全寿命期工程项目或其构成部分物理特性、功能特性及管理要素旳共享数字化体现。
20、工程项目全寿命期可划分为(B. 筹划与规划、勘察与设计、施工与监理、运行与维护、改造与拆除)五个阶段。
专题1.2 梯子滑动模型(强化)(解析版)
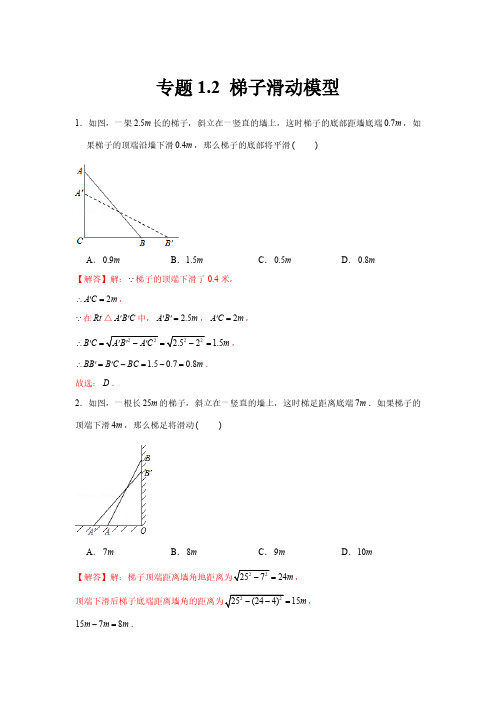
专题1.2 梯子滑动模型1.如图,一架2.5m长的梯子,斜立在一竖直的墙上,这时梯子的底部距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯子的底部将平滑( )A.0.9m B.1.5m C.0.5m D.0.8m【解答】解:Q梯子的顶端下滑了0.4米,A C m\¢=,2Q在Rt△A B CA C m¢=,¢¢=,2A B m¢¢中, 2.5\¢===,B C m1.5BB B C BC m\¢=¢-=-=.1.50.70.8故选:D.2.如图,一根长25m的梯子,斜立在一竖直的墙上,这时梯足距离底端7m.如果梯子的顶端下滑4m,那么梯足将滑动( )A.7m B.8m C.9m D.10m=,24m=,15m-=.m m m1578故选:B .3.一架2.5米长的梯子靠在一座高10米的建筑物上,此时梯子底部离建筑物墙面0.7米.若梯子的顶部滑下0.4米,则梯子的底部向外滑出距离为( )A .1米B .0.8米C .0.6米D .0.4米【解答】解:在Rt AOB D 中,根据勾股定理222AB AO OB =+,可以求得:2.4OA =(米),现梯子的顶部滑下0.4米,即 2.40.42OC =-=(米),且 2.5CD AB ==米,所以在Rt COD D 中,222DO CD CO =-,即 1.5DO ==(米),所以梯子的底部向外滑出的距离为1.50.70.8-=(米).答:梯子的底部向外滑出的距离为0.8米,故选:B .4.要登上12m 高的建筑物,为了安全需使梯子底端离建筑物5m ,则梯子的长度至少为( )【解答】解:如图所示:12AC m =Q ,5BC m =,\在Rt ABC D 中,13()AB m ==,故选:A .5.如图,一根长25m 的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底端7m .如果梯子的顶端下滑4m ,那么梯子的底端将向右滑动( )A .15mB .9mC .7mD .8m24()m =,15()m =,1578()m -=.故选:D .6.如图,一个梯子斜靠在一竖直的墙AO 上,测得4AO m =,若梯子的顶端沿墙下滑1m ,这时梯子的底端也下滑1m ,则梯子AB 的长度为( )【解答】解:设BO x =m ,由题意得:1AC m =,1BD m =,4AO m =,在Rt AOB D 中,根据勾股定理得:222224AB AO OB x =+=+,在Rt COD D 中,根据勾股定理得:22222(41)(1)CD CO OD x =+=-++,22224(41)(1)x x \+=-++,解得:3x =,5()AB m \===,即梯子AB 的长为5m ,故选:A .7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )A .2.2米B .2.3米C .2.4米D .2.5米【解答】解:在Rt ACB D 中,90ACB Ð=°Q ,0.7BC =米, 2.4AC =米,2220.7 2.4 6.25AB \=+=.在Rt △A BD ¢中,90A DB Т=°Q ,2A D ¢=米,222BD A D A B +¢=¢,222 6.25BD \+=,2 2.25BD \=,0BD >Q ,1.5BD \=米,0.7 1.5 2.2CD BC BD \=+=+=米.故选:A .二.填空题(共6小题)8.如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,1AD=米,则BE= 1 米.AC===(米【解答】解:在Rt ABCD中,根据勾股定理,可得:4),\=-=-=(米),DC AC AD413CE===(米),在Rt DCED中,4\=-=-=(米),431BE CE BC故答案为:1.9.如图,一架10米长的梯子斜靠在墙上,梯顶A刚好抵达8米高的路灯.当师傅沿梯上去修路灯时,梯顶A下滑到A¢处,前后梯脚B、B¢间的距离为2米,则下滑后梯顶离路灯 2 米.【解答】解:在直角三角形AOB中,根据勾股定理,得:==,6()OB m根据题意,得:628()OB m ¢=+=,又Q 梯子的长度不变,\在Rt △A OB ¢¢中,根据勾股定理,得:6()OA m ¢==.则862()AA m ¢=-=.答:梯顶离路灯2米.故答案为:2.10.如图,有互相垂直的两面墙OM ,ON ,梯子6AB m =,两端点A ,B 分别在两面墙上滑动(AB 长度不变),P 为AB 的中点,柱子4CD m =,底端C 到墙角O 的距离为6m .在此滑动过程中,点D 到点P 的距离的最小值为 3)- m .【解答】解:Q 木棍的中点为P ,AOB D 为直角三角形,132OP AB m \==,即点P 到点O 的距离为3m ,\点P 的轨迹为以O 为圆心,3m 为半径的弧上,如图,连接OD 交O e 于P ,则D 到P 的距离最小.在弧上任取一点P ¢,连接OP ¢,DP ¢,OP DP OD OP DP ¢+¢>=+Q ,OP OP =¢,DP DP \¢>,DP \为最小值,在Rt OCD D 中,6OC =,4CD =,OD \===,3)()PD OD OP m \=-=-,故答案为:3)-.11.如图,“人字梯”放在水平的地面上,AB AC =,当梯子的一边与地面所夹的锐角a 为60°时,两梯角之间的距离BC 的长为2m .周日亮亮帮助妈妈整理换季衣服,先使a 为60°,后又调整a 为45°,则梯子顶端A 离地面的高度下降了 - m .【解答】解:如图1所示:过点A 作AD BC ^于点D ,由题意可得:60B C Ð=Ð=°,则ABC D 是等边三角形,故2BC AB AC m ===,则2sin 60AD =°=,如图2所示:过点A 作AE BC ^于点E ,由题意可得:60B C Ð=Ð=°,则ABC D 是等腰直角三角形,AC AB =,则12AE BC ==,故梯子顶端离地面的高度AD 下降了m .故答案为:.12.如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m当梯子的顶端A沿墙向下滑的距离AC与梯子底端B向外移的距离BD相等时,AC的长是 1.4 m.【解答】解:90AB=, 2.4Q, 2.6OA=,Ð=°O\===,OB1设AC BD x==,OD x=+,\=-,1OC x2.4222\=+,CD OC OD222\=-++,2.6(2.4)(1)x x解得: 1.4x=,\=.1.4AC故答案为:1.4.13.如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为0.7米,梯子滑动后停在DE的位置上,测得BD长为1.3米,则梯子顶端A下滑了 0.9 米.【解答】解:在Rt ABC D 中, 2.5AB =米, 1.5BC =米,2.4AC \===米,在Rt ECD D 中, 2.5AB DE ==米, 1.30.72CD =+=米,1.5EC \===米,2.4 1.50.9AE AC CE \=-=-=米.故答案为:0.9.三.解答题(共7小题)14.如图,一架长5m 的梯子AB 斜靠在墙AC 上,90C Ð=°,此时,梯子的底端B 离墙底C 的距离BC 为3m .(1)求此时梯子的顶端A 距地面的高度AC ;(2)如果梯子的顶端A 下滑了2m ,那么梯子的顶端B 在水平方向上向右滑动了多远?【解答】解:(1)90C Ð=°Q ,5AB m =,3BC m =,4()AC m \===,答:此时梯顶A 距地面的高度AC 是4m ;(2)Q 梯子的顶端A 下滑了2m 至点A ¢,422()A C AC A A m \¢=-¢=-=,在Rt △A CB ¢¢中,由勾股定理得:222A C B C A B ¢+¢=¢¢,即22225B C +¢=,)B C m \¢=,3)()BB CB BC m \¢=¢-=-,答:梯子的底端B 在水平方向滑动了3)m -.15.如图,一架梯子AB斜靠在某个走廊竖直的左墙上,顶端在点A处,底端在水平地面的点B处.保持梯子底端B的位置不变,将梯子斜靠在竖直的右墙上,此时梯子的顶端在点E 处.(1)如图1,若顶端A距离地面的高度AC为2.4米,BC为0.7米.①则梯子的长为 2.5 米;②若顶端E距离地面的高度EF比AC少0.4米,求走廊的宽是多少米?(2)如图2,G是线段AE上中点左侧一点,若2×=,则梯子的长为 BG=,AG GE米.【解答】解:(1)①在Rt ABCD中,AB===(米),2.5故答案为:2.5;②Q梯子的长度不变,\==,BE AB2.5Q顶端E距离地面的高度EF比AC少0.4米,EF\=-=,2.40.42在Rt BEFD中,BF===,1.50.7 1.5 2.2CF BC BF \=+=+=(米),答:走廊的宽是2.2米;(2)如图,设AE 的中点为H ,连结BH ,设AG x =米,AG GE ×=Q,GE \米,设梯子的长为y 米,AB BE =Q ,AE 的中点为HBH AE \^,在Rt ABH D 中,22222BH AB AH y =-=-,在Rt BGH D 中,222222)BH BG GH x =-=-,22222)yx \-=--,化简得:24y =+1y \=.\梯子的长为1)+米,故答案为:1)+.16.某校秉承“学会生活,学会学习,学会做人”的办学理念,将本校的办学理念做成宣传牌()AB ,放置在教室的黑板上面(如图所示).在三月雷锋活动中小明搬来一架梯子(5AE =米)靠在宣传牌()AB A 处,底端落在地板E 处,然后移动的梯子使顶端落在宣传牌()AB 的B处,而底端E 向外移到了1米到C 处(1CE =米).测量得4BM =米.求宣传牌()AB 的高度(结果用根号表示).【解答】解:由题意可得:5AE BC ==米,4BM =米,1EC =米,在Rt MBC D 中,3MC ==(米),则312EM =-=(米),在Rt AEM D 中,AM =),故4)AB AM BM =-=-米,答:宣传牌()AB 的高度为4)-米.17.在一次消防演习中,消防员架起一架25米长的云梯,斜靠在一面墙上;梯子底端C 离墙20米,如图.(1)求这个梯子的顶端A 距地面有多高?(2)如果消防员接到命令,要求梯子的顶端上升4米(云梯长度不变),那么云梯底部在水平方向应滑动多少米?【解答】解:(1)由题意得:25AC =米,20BC =米,则15AB ===(米).答:这个梯子的顶端距地面有15米;(2)由题意得:4EA =米,则19BE =米,BD ===),20BC =Q 米,(20CD \=-米,答:云梯的底部在水平方向应滑动(20-米.18.一梯子AC 长2.5m ,如图那样斜靠在一面墙上,梯子底端离墙0.7m .(1)这架梯子的顶端离地面有多高?(2)设梯子顶端到水平地面的距离为m ,底端到垂直墙面的距离为n ,若m a n=,根据经验可知:当2.7 5.6a <<时,梯子最稳定,使用时最安全.若梯子的顶端下滑了0.4m ,请问这时使用是否安全.【解答】解:(1)由题意可知,90B Ð=°, 2.5AC m =,0.7BC m =,2.4()AB m \===,答:这架梯子的顶端离地面有2.4m 高;(2)这时使用不安全,理由如下:由题意得:0.4AA m ¢=,在Rt △A BC ¢¢中, 2.40.42()A B AB AA m ¢¢=-=-=, 2.5A C m ¢¢=,1.5()BC m ¢\===,\242.71.53m n ==<,\这时使用不安全.19.生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的13,则梯子比较稳定,如图,AB 为一长度为6米的梯子.(1)当梯子稳定摆放时,它的顶端能达到5.7米高的墙头吗?1.414)»(2)如图2,若梯子底端向左滑动使OD=留1位小数)【解答】解:(1)由题意可得,6AB m=,123OB AB m==,在Rt AOBD中,由勾股定理可得,5.656AO===»,5.656 5.7<Q,\梯子的顶端不能到达5.7米高的墙头;(2)在Rt DOCD中,由勾股定理可得,OC===米,1.4AC OA OC\=-==»米.\梯子的顶端将下滑动1.4米.20.如图,一个梯子AB斜靠在一面墙上,梯子底端为A,梯子的顶端B距地面的垂直距离为BC的长.(1)若梯子的长度是10m,梯子的顶端B距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端A向外滑动多少米?(2)设AB c=,BC a=,AC b=,且a b>,请思考,梯子在滑动的过程中,是否一定存在顶端下滑的距离与底端向外滑动的距离相等的情况?若存在,请求出这个距离;若不存在,说明理由.【解答】解:(1)由题意知:10AB m =,8BC m =,由勾股定理得:6()AC m ==,当梯子的顶端下滑1m 时,如图,7CB m ¢\=,由勾股定理得)A C m ¢==,6)AA A C AC m ¢¢\=-=-,\梯子的底端A 向外滑动6)m -;(2)存在顶端下滑的距离与底端向外滑动的距离相等的情况,设梯子底端向外滑动x 米,则222()()a x b x c -++=,解得1x a b =-,20x =(舍),x a b \=-,即梯子底端向外滑动()a b -米.。
八年级上期末物理试题精选专题及解析---机械运动

八年级上期末物理试题精选专题及解析---机械运动1.(2022·黑龙江哈尔滨·八年级期末)南朝诗人萧绎在《早发龙巢》有诗句“不疑行船动,唯看远树来”,其中“唯看远树来”的参照物可能的是()A.河岸B.行船C.岸边的房屋D.远处的树2.(2022·黑龙江齐齐哈尔·八年级期末)《吕氏春秋·察今篇》记载了刻舟求剑的故事,当中有这样的文句:“舟已行矣,而剑不行,求剑若此,不亦惑乎!”文中对舟和剑运动状态的描述,可选择的共同参照物是()A.舟中人B.舟C.剑D.江岸3.(2022·黑龙江七台河·八年级期末)下列运动中,不属于机械运动的是A.月球绕着地球转B.公路上行驶的汽车C.空气的流动 D.洒在水里的糖使水变甜4.(2022·黑龙江哈尔滨·八年级期末)2020年6月30日,随着最后一颗组网卫星成功定点于地球同步轨道,中国建成世界领先的“北斗”导航系统。
这里的“同步”是指卫星()A.相对太阳静止B.相对火星静止C.相对地球静止D.相对月球静止5.(2022·黑龙江哈尔滨·八年级期末)小红和小华站在公交站台等公交车,小红对小华说自己是运动的,她选择的参照物是()A.公交站台B.小华C.路边的树木D.行驶过来的公交车6.(2022·黑龙江省八五七农场第一中学八年级期末)甲、乙两列火车在两条平行的铁轨上匀速行驶,两车交汇时,甲车座位上的乘客从车窗看到地面上的树木向北运动,看到乙车向南运动.由此可判断A.甲、乙两车都向南运动B.甲、乙两车都向北运动C.甲车向南运动,乙车向北运动D.甲车向北运动,乙车向南运动7.(2022·黑龙江鹤岗·八年级期末)如图所示,是穿行在餐厅的机器人端着托盘送餐时的情景.若认为托盘是静止的,则所选择的参照物可能是A.地面B.机器人C.餐桌D.墙壁8.(2022·黑龙江大庆·八年级期末)如图所示的四个图像中,物体的运动速度相同的是()A.甲、乙B.乙、丙C.丙、丁D.甲、丁9.(2022·黑龙江牡丹江·八年级期末)这是宋代诗人陈与义的一首诗:“飞花两岸照船红,百里榆堤半日风,卧看满天云不动,不知云与我俱东”,在诗人看来云是不动的,他选择的参照物是()A.岸边的江堤B.江边的树C.树上的飞花D.诗人的小船10.(2022·黑龙江鸡西·八年级期末)行驶中列车行李架上的物品相对于下列哪个物体是静止的()A.树木B.房屋C.车厢的座椅D.车厢内走过的列车员11.(2022·黑龙江哈尔滨·八年级期末)一物体在运动过程中的路程随时间的变化关系如图所示,由图象可知A.物体在2~4 s内做匀速直线运动B.物体在4~6 s内运动的速度是10 m/sC.物体在0~2 s内比在4~6 s内运动的慢D.物体在0~6 s内运动的路程是10 m12.(2022·黑龙江哈尔滨·八年级期末)如图所示,小明利用学生刻度尺测量了一个物体的长度,记录的测量结果正确的是()A.2.15cm B.1.15cm C.2.2cm D.1.3cm 13.(2022·黑龙江·肇东市第十中学八年级期末)下列成绩记录符合实际的是()A.立定跳远成绩为5m B.投掷实心球,成绩为6.5mC.女子800m长跑成绩为40s D.男子1000m长跑成绩为50s 14.(2022·黑龙江·虎林市实验中学八年级期末)用图象可以表示物体的运动规律,图中可以用来表示物体做匀速直线运动的是()A.①和②B.③和④C.①和③D.②和④15.(2022·黑龙江哈尔滨·八年级期末)平直轨道上行驶的火车中,放在车厢内小桌上的苹果相对于下列哪个物体是运动的()A.坐在车厢椅子上的乘客B.这列火车的机车C.关着的车门D.从旁边走过的列车员16.(2022·黑龙江·虎林市实验中学八年级期末)小华家距学校2.5 km,他骑自行车的平均速度是10 km/h,学校要求早上7点准时到校,小华从家中出发的时间一般不能晚于早上()A.6︰45 B.6︰30 C.6︰20 D.6︰50 17.(2022·黑龙江哈尔滨·八年级期末)在新型汽车的研制中,将汽车模型放在风洞中固定不动,让风(高速流动的空气)迎面吹来,可模拟汽车在高速行驶的情况.在此情境中下列说法正确的是()A.汽车模型相对于地面是运动的B.汽车模型相对于空气是运动的C.空气相对于地面是静止的D.空气相对于汽车模型是静止的18.(2022·黑龙江·大庆市北湖学校八年级期末)雷达是现代战争重要的军事装备。
专题12 物质结构与性质综合(题型突破)(测试)-2024年高考化学二轮复习讲练测(新(0002)

专题12 物质结构与性质综合(题型突破)(考试时间:75分钟试卷满分:100分)一、选择题(本题共15小题,每小题3分,共45分。
每小题只有一项是符合题目要求的)1.含有N3-、N5+的材料Pb(N3)2、N5AsF6可以用于炸药。
下列说法正确的是( )A.Pb属于d区元素B.基态As原子的d轨道与p轨道上的电子数之比为3:2C.N3-的空间构型为直线形D.基态F原子中,核外电子的空间运动状态有9种【答案】C【解析】A项,铅元素的原子序数为82,价电子排布式为6s26p2,处于元素周期表的p区,故A错误;B项,砷元素的原子序数为33,电子排布式为1s22s22p63s23p63d104s24p3,则原子的d轨道与p轨道上的电子数之比为10:15=2:3,故B错误;C项,等电子体具有相同的空间构型,N3-离子与二氧化碳分子的原子个数都为3、价电子数都为16,互为等电子体,二氧化碳的空间构型为直线形,则N3-离子的空间构型为直线形,故C正确;D项,核外电子的空间运动状态与原子轨道的数目相同,氟元素的原子序数为9,电子排布式为1s22s22p5,氟原子的原子轨道数目为5,则核外电子的空间运动状态有5种,故D错误;故选C。
2.(2024·江苏苏州高三期中)Na、Mg、Al均为第三周期元素。
下列说法正确的是( )A.离子半径:r(Na+)<r(Mg2+)<r(Al3+) B.第一电离能:I1(Na)> I1(Mg)> I1(Al)C.还原性:Na>Mg>Al D.碱性:NaOH<Mg(OH)2<Al(OH)3【答案】C【解析】A项,三种离子核外电子排布相同半径随核电荷数增大而减小,故A错误;B项,同周期元素第一电离能总体趋势:核电荷数越大,第一电离能越大,故B错误;C项,同周期元素,核电荷数越大金属性越弱,对应单质还原性越弱,故C正确;D项,金属性Na>Mg>Al,其对应最高价氧化物水化物碱性越弱,碱性:NaOH>Mg(OH)2>Al(OH)3,故D错误;故选C。
警务云深度解析

42
43
目录
一、建设历程 二、总体介绍 三、功能演示 四、建设探讨
警务云建设问题
双轨 并存
44
云计算架构 传统架构
公安部业务应用 山东警务云计算
45
警务云—省与市 全省一片云
主 体
标
主
准 五统一 干
安
应
全
用
运 行
六开放
个 人
安
数
全
据
数
开
据
发
总体规划
省厅
顶层设计
开发应用
各地
云端集成
支持各地应用创新
建设历程 共赴公安部汇报警务云建设情况
14
建设历程 建设警务云机房
山东警务云计算机房落户浪潮
15
建设历程 实施计划表
云安全 27%
云基础 20%
云应用 10%
云数据 16%
云平台 27%
16
建设历程 系统上线-警务千度开通
17
建设历程 系统上线-警务千度开通
18
建设历程 系统上线-警务千度开通
云主体
服务中心 警务千度 人像识别
多点碰撞
32
山东警务云一期简介
应用服务中心 开发服务中心 个人服务中心 数据服务中心
33
山东警务云一期简介
运维中心
34
山东警务云
打破了部 门警种的业务应
用壁垒
现代警务 工作与云计算 技术紧密融合
山东 警务云计算
实现了公 安大数据的深
度挖掘
推动了合 成应用和高端应 用再上新台阶
警务云深度解析
-山东警务云实践
政法行业部 英杰 2014年5月
2024届北京市西城区高三一模语文试题(含答案与解析)_9110

2024届北京市西城区高三一模试题语文本试卷共10页,共150分。
考试时长150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、本大题共5小题,共18分。
阅读下面材料,完成小题。
材料一今日世界之复杂、变化之迅捷,已远超我们的想象,看似遥不可及的未来正变得触手可及。
如今,百度Apollo(阿波罗)开放平台可以引导百余辆自动驾驶汽车在港珠澳大桥上奔驰,可穿戴技术能让你的衣服监控心率,广东省东莞市长安镇诞生了首个无人工厂……人工智能机器正大举进入全球制造业,代替人类在做许多工作。
从基因测序到纳米技术,从可再生能源到量子计算,各领域的技术突破风起云涌,新技术不断催生着更新、更强大的技术,并不断交叉迭代,融合应用到各个领域,推动各行各业转型升级,快速向数字化、智能化迈进。
人类已跨入第四次工业革命时代(即利用信息化技术促进产业变革的智能化时代),信息爆炸、大裂变式的脑力增长正以全新的、强有力的且令人惊诧的方式,挑战和重塑着社会根基,改变着我们的生活、工作和学习方式。
世界变化太快了,引起了人们对“乌卡时代”(VUCA)的共鸣。
所谓“乌卡时代”,即指具有易变性(volatile)、不确定性(uncertain)、复杂性(complex)、模糊性(ambiguous)的时代。
“易变性”指事情变化非常快,“不确定性”指不知道下一步的方向在哪儿,“复杂性”指每件事会牵连影响到另外一些事情,“模糊性”指关系不明确。
这意味着,秉持单一知识类型、技术手段,应对单一社会生活情境的时代一去不返。
苹果公司现任CEO蒂姆·库克说:“我不担心机器会像人一样思考,我担心的是人会像机器一样思考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云的基本定义
设U是一个用精确数值表示的定量论域, T是U空间上的定性概念,若元素x(x∈X)对T的隶属的确 定度CT(x)∈[0,1]是一有稳定倾向的随机数(式F1.1), 则概念T从论域U到区间[0,1]的映射在数域空间的分布, 称为云(Cloud)。
13
这个定义还可以推广到N维云。即若U是N维论域,X∈U, 则N维元素x=(x1,x2,…,xn) (x∈X)对T的隶属的确定度 CT(x)∈[0,1]也是一有稳定倾向的随机数(式F1.1)。由此, 如果在给定论域的数域空间中,x为(xl,x2,…,xn),那 么一个云滴的严格表达,应为一个由自变量的论域空间坐标 及其对概念的确定度的数值对,即:
空间数据挖掘专题
云模型方法
洪金益 中南大学地学院 zxlhong@
1
主要参考文献
• 王树良:基于数据场与云模型的空间数据挖掘和 知识发现,博士论文;
• 邸凯昌 空间数据发掘和知识发现的理论与方法, 博士论文;
• 李德仁、王树良、李德毅:空间数据挖掘理论与 方法,科学出版社,2006.
x2(1,:)=[7.0,6.4,6.9,5.5,6.5,5.7,6.3,4.9,6.6,5.2,5.0,5.9,6.0,6.1,5.6,6.7,5.6,5]; x2(2,:)=[3.2,3.2,3.1,2.3,2.8,2.8,2.3,2.4,2.9,2.7,2.0,3.0,2.2,2.9,2.9,3.1,3.0,2]; x2(3,:)=[4.7,4.5,4.9,4.0,4.6,4.5,4.7,3.3,4.6,3.9,3.5,4.2,4.0,4.7,3.6,4.4,4.5,4]; x2(4,:)=[1.4,1.5,1.5,1.3,1.5,1.3,1.6,1.0,1.3,1.4,1.0,1.5,1.0,1.4,1.3,1.4,1.5,1];
15
这种一个定量数值属于一个定性概念语言的不确定变化,
在每个云滴表现出来时,也许不会剧烈影响到云的整体特征。
即某一个特定的云滴可能无足轻重。但是,一定数量的云滴
的整体分布特性就体现了云映射的模糊性和随机性,也就是
说,云的整体形状反映了在用定量数值表示定性概念时的不
确定特性。例如,“滑坡体向南位移20毫米左右”就是一个
4
Matlab部分云模型程序
逆向云子程序: function [b_Ex,b_En,b_He]=back_cloud(x)
b_Ex=mean(x); b_En=mean(abs(xb_Ex))*sqrt(pi/2); b_He=sqrt(var(x)-b_En^2);
5
经过Matlab处理
6
得ቤተ መጻሕፍቲ ባይዱ的部分结果
7
8
9
10
11
1 云的定义和特性
云是用语言值表示的某个定性概念与其定量 表示之间的不确定性转换模型。它主要反映客观世 界中事物或人类知识中概念的两种不确定性:模糊 性(边界的亦此亦彼性)和随机性(发生的概率),并 把二者完全集成在一起,构成定性和定量相互间的 映射。因为在数域空间中,云既不是一个确定的概 率密度函数,也不是一条明晰的隶属曲线,而是一 朵可伸缩、无边沿、有弹性、近视无边、远观像云 的一对多的数学映射图象,与自然现象中的云有着 相似的不确定性质,所以借用“云”来命名这个数 据——概念之间的数学转换理论。
2
主要内容
0 应用实例 1 云的定义和特性 2 云模型的类型 3 云发生器 4 虚拟云 5 云变换 6 基于云模型的不确定推理
3
应用实例
一组(4*100*3)数据:
x1(1,:)=[5.1,4.9,4.7,4.6,5.0,5.4,4.6,5.0,4.4,4.9,5.4,4.8,4.8,4.3,5.8,5.7,5.4,5]; x1(2,:)=[3.5,3.0,3.2,3.1,3.6,3.9,3.4,3.4,2.9,3.1,3.7,3.4,3.0,3.0,4.0,4.4,3.9,3]; x1(3,:)=[1.4,1.4,1.3,1.5,1.4,1.7,1.4,1.5,1.4,1.5,1.5,1.6,1.4,1.1,1.2,1.5,1.3,1]; x1(4,:)=[0.2,0.2,0.2,0.2,0.2,0.4,0.3,0.2,0.2,0.1,0.2,0.2,0.1,0.1,0.2,0.4,0.4,0];
x3(1,:)=[6.3,5.8,7.1,6.3,6.5,7.6,4.9,7.3,6.7,7.2,6.5,6.4,6.8,5.7,5.8,6.4,6.5,7]; x3(2,:)=[3.3,2.7,3.0,2.9,3.0,3.0,2.5,2.9,2.5,3.6,3.2,2.7,3.0,2.5,2.8,3.2,3.0,3]; x3(3,:)=[6.0,5.1,5.9,5.6,5.8,6.6,4.5,6.3,5.8,6.1,5.1,5.3,5.5,5.0,5.1,5.3,5.5,5]; x3(4,:)=[2.5,1.9,2.1,1.8,2.2,2.1,1.7,1.8,1.8,2.5,2.0,1.9,2.1,2.0,2.4,2.3,1.8,1];
坡体向南位移20毫米左右”这个概念。
空间概念,而“滑坡体向南位移20毫米”就是一个空间数据,
是该定性概念在论域中的一次具体定量实现,经过云映射,
这个云滴代表该定性概念的确定程度是1。可是,这种实现
也可能是“滑坡体向南位移19毫米”等数据,代表该定性概
念的确定程度也可能是0.9等。所有的这些实现积累到一定
数量,经过云映射,在论域空间中就形成一朵云,表达“滑
14
从云的基本定义中可以看出,论域U上的概念T从论域U到区间[0,1]的映射 是一对多的关系。即论域中某一元素与它对概念T的隶属度之间的映射是一对多 的转换,而不是传统的模糊隶属函数中的一对一关系。表达概念T的云由许许多 多的云滴组成,每个云滴均是这个定性概念映射到数域空间的一个点,即定性概 念的语言值在数量上的一次具体样例实现。这种实现带有不确定性,模型同时给 出这个点能够代表该定性概念的确定程度。每个云滴都是随机产生的,而且每个 云滴代表该定性概念的确定程度也是模糊的,始终在细微变化着。
