【2018年数学高考】河南省信阳市普通2018届高中高三第二次教学质量检测 数学文
2018年河南省信阳市高考数学二模试卷(理科)(解析版)

2018年河南省信阳市高考数学二模试卷(理科)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合M={x|x<2},N={x|x2﹣x<0},则下列关系中正确的是()A.M∪N=R B.M∪(∁R N)=R C.N∪(∁R M)=R D.M∩N=M 2.(5分)《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为()A.钱B.钱C.钱D.钱3.(5分)下面是关于复数z=的四个命题:p1:|z|=2;p2:z2=2i;p3:z的共轭复数为1+i;p4:z的虚部为﹣1.其中的真命题为()A.p1,p2B.p2,p4C.p2,p3D.p3,p44.(5分)已知定义在R上的函数f(x)=ax3+x2+ax+1有三个不同的单调区间,则实数a的取值范围是()A.(﹣∞,﹣1)∪(1,+∞)B.[﹣1,0)∪(0,1]C.(﹣1,1)D.(﹣1,0)∪(0,1)5.(5分)若偶函数f(x)在区间(﹣∞,0]上单调递减,且f(3)=0,则不等式(x﹣1)f(x)>0的解集是()A.(﹣3,1)∪(3,+∞)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣∞,﹣3)∪(3,+∞)D.(﹣∞,﹣1)∪(3,+∞)6.(5分)的展开式的常数项是()A.5B.﹣10C.﹣32D.﹣427.(5分)某校高三年级10个班参加合唱比赛得分的茎叶图如图所示,若这组数据的平均数是20,则+的最小值为()A.1B.C.2D.8.(5分)若输出的S的值等于22,那么在程序框图中的判断框内应填写的条件是()A.i>5B.i>6C.i>7D.i>89.(5分)要得到函数的图象,只需将函数的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度10.(5分)过抛物线y2=4x的焦点F作直线l交抛物线于A,B两点,若=,则直线l的倾斜角θ(0<θ<)等于()A.B.C.D.11.(5分)设x,y,z为正实数,且log2x=log3y=log5z>0,则的大小关系不可能是()A.B.==C.D.12.(5分)如图,将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状,下底AB是半圆的直径,上底CD的端点在圆周上,则所得梯形面积的最大值为()A.3B.3C.5D.5二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.(5分)已知向量,的夹角为60°,||=1,|2﹣|=,则||=.14.(5分)某化肥厂生产甲、乙两种肥料,生产一车皮甲种肥料需要磷酸盐4吨、硝酸盐18吨;生产一车皮乙种肥料需要磷酸盐1吨、硝酸盐15吨.已知生产一车皮甲种肥料产生的利润是10万元,生产一车皮乙种肥料产生的利润是5万元.现库存磷酸盐10吨、硝酸盐66吨.如果该厂合理安排生产计划,则可以获得的最大利润是.15.(5分)过双曲线的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为.16.(5分)在平面四边形ABCD中,∠A=∠B=60°,AB=1,∠D=150°,则四边形ABCD 面积的取值范围是.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(12分)已知a,b,c分别是△ABC内角A,B,C的对边,且满足:(a+b+c)(sin B+sin C ﹣sin A)=b sin C.(Ⅰ)求角A的大小;(Ⅱ)设a=,S为△ABC的面积,求S+cos B cos C的最大值.18.(12分)为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?(2)求这80位师范类毕业生从事与教育有关工作的频率;(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).参考公式:k2=(n=a+b+c+d).附表:19.(12分)已知数列{a n}的前n项和为S n,且a 1=2,2S n=(n+1)2a n ﹣n2a n+1,数列{b n}满足b1=a1,nb n+1=a n b n.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)若数列{c n}满足c n=a n+b n(n∈N*),求数列{c n}的前n项和T n.20.(12分)已知直线l与椭圆C:+=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,又=(ax1,by1),=(ax2,by2),若⊥且椭圆的离心率e=,又椭圆经过点(,1),O为坐标原点.(Ⅰ)求椭圆的方程;(Ⅱ)试问△AOB的面积是否为定值?21.(12分)已知函数f(x)=4x2+﹣a,g(x)=f(x)+b,其中a,b为常数.(1)若x=1是函数y=xf(x)的一个极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若函数f(x)有2个零点,f(g(x))有6个零点,求a+b的取值范围.选考题:共10分.请考生从第22、23题中任选一题作答,并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,按本选考题的首题进行评分.[选修4-4:坐标系与参数方程]22.(10分)已知直线l的参数方程为(其中t为参数),曲线C1:ρ2cos2θ+3ρ2sin2θ﹣3=0,以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,两种坐标系中取相同长度单位.(Ⅰ)求直线l的普通方程及曲线C1的直角坐标方程;(Ⅱ)在曲线C1上是否存在一点P,使点P到直线l的距离最大?若存在,求出距离的最大值及点P的直角坐标;若不存在,请说明理由.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣5|﹣|x﹣2|.(Ⅰ)若∃x∈R,使得f(x)≤m成立,求实数m的取值范围;(Ⅱ)解不等式x2﹣8x+15+f(x)≤0.2018年河南省信阳市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合M={x|x<2},N={x|x2﹣x<0},则下列关系中正确的是()A.M∪N=R B.M∪(∁R N)=R C.N∪(∁R M)=R D.M∩N=M【解答】解:N={x|0<x<1};∴M∪N={x|x<2},∁R N={x|x≤0,或x≥1},M∪(∁R N}=R.故选:B.2.(5分)《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为()A.钱B.钱C.钱D.钱【解答】解:依题意设甲、乙、丙、丁、戊所得钱分别为a﹣2d,a﹣d,a,a+d,a+2d,则由题意可知,a﹣2d+a﹣d=a+a+d+a+2d,即a=﹣6d,又a﹣2d+a﹣d+a+a+d+a+2d=5a=5,∴a=1,则a﹣2d=a﹣2×=.故选:B.3.(5分)下面是关于复数z=的四个命题:p1:|z|=2;p2:z2=2i;p3:z的共轭复数为1+i;p4:z的虚部为﹣1.其中的真命题为()A.p1,p2B.p2,p4C.p2,p3D.p3,p4【解答】解:复数z===﹣1﹣i.∴|z|=,z2=2i,=﹣1+i,z的虚部为﹣1.因此只有p2,p4是真命题.故选:B.4.(5分)已知定义在R上的函数f(x)=ax3+x2+ax+1有三个不同的单调区间,则实数a的取值范围是()A.(﹣∞,﹣1)∪(1,+∞)B.[﹣1,0)∪(0,1]C.(﹣1,1)D.(﹣1,0)∪(0,1)【解答】解:根据题意,函数f(x)=ax3+x2+ax+1,其导数f′(x)=ax2+2x+a,若函数f(x)=ax3+x2+ax+1有三个不同的单调区间,则f′(x)=ax2+2x+a=0有2个零点,则有△=4﹣4a2>0,且a≠0,解可得:﹣1<a<1,且a≠0,即实数a的取值范围是(﹣1,0,(0,1);故选:D.5.(5分)若偶函数f(x)在区间(﹣∞,0]上单调递减,且f(3)=0,则不等式(x﹣1)f(x)>0的解集是()A.(﹣3,1)∪(3,+∞)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣∞,﹣3)∪(3,+∞)D.(﹣∞,﹣1)∪(3,+∞)【解答】,解:根据题意,偶函数f(x)在区间(﹣∞,0]上单调递减,则其在[0,+∞)上为增函数,又由f(3)=0,则f(﹣3)=0,由图象知当x<﹣3或x>3时,f(x)>0;当﹣3<x<3时,f(x)<0,(x﹣1)f(x)>0等价为或,即或,得x>3或﹣3<x<1综合可得:不等式(x﹣1)f(x)>0的解集是(﹣3,1)∪(3,+∞);故选:A.6.(5分)的展开式的常数项是()A.5B.﹣10C.﹣32D.﹣42【解答】解:由于的通项为,故的展开式的常数项是+(﹣2)5=﹣42,故选:D.7.(5分)某校高三年级10个班参加合唱比赛得分的茎叶图如图所示,若这组数据的平均数是20,则+的最小值为()A.1B.C.2D.【解答】解:根据茎叶图知,这组数据的平均数是[12+13+15+19+17+23+(20+a)+25+28+(20+b)]=20,∴a+b=8,∴+=(+)(a+b)=(1+9++)≥(10+2)=2,当且仅当b=3a=6时取“=”,∴+的最小值为2.故选:C.8.(5分)若输出的S的值等于22,那么在程序框图中的判断框内应填写的条件是()A.i>5B.i>6C.i>7D.i>8【解答】解:S=1+1=2,i=2,不满足条件,执行循环;S=2+2=4,i=3,不满足条件,执行循环;S=4+3=7,i=4,不满足条件,执行循环;S=7+4=11,i=5,不满足条件,执行循环;S=11+5=16,i=6,不满足条件,执行循环;S=16+6=22,i=7,满足条件,退出循环体,输出S=22故判定框中应填i>6或i≥7故选:B.9.(5分)要得到函数的图象,只需将函数的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【解答】解:=,故把的图象向左平移个单位,即得函数的图象,即得到函数的图象.故选:C.10.(5分)过抛物线y2=4x的焦点F作直线l交抛物线于A,B两点,若=,则直线l的倾斜角θ(0<θ<)等于()A.B.C.D.【解答】解:方法一:由题意可得直线AB的斜率k存在设A(x1,y1)B(x2,y2),F(1,0)则可得直线AB的方程为y=k(x﹣1)联立方程,整理可得k2x2﹣2(k2+2)x+k2=0∴x1+x2=,x1x2=1∴x2﹣x1==,∵=﹣===,∴解得:k=或k=﹣,∵0<θ<,∴k=,∴θ=,故选B.方法二:由抛物线的焦点弦性质,+==1,由=,解得:|AF|=,|BF|=4,∴|AB|=|AF|+|BF|===,解得:sinα=,∵θ=,故选:B.11.(5分)设x,y,z为正实数,且log2x=log3y=log5z>0,则的大小关系不可能是()A.B.==C.D.【解答】解:x,y,z为正实数,且log2x=log3y=log5z=k>0,可得:x=2k>1,y=3k>1,z=5k>1.∴=2k﹣1,=3k﹣1,=5k﹣1,①若0<k<1,则函数f(x)=x k﹣1单调递减,∴>>;②若k=1,则函数f(x)=x k﹣1=1,∴==;③若1<k,则函数f(x)=x k﹣1单调递增,∴<<.∴的大小关系不可能是D.因此A,B,C,正确;D错误.故选:D.12.(5分)如图,将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状,下底AB是半圆的直径,上底CD的端点在圆周上,则所得梯形面积的最大值为()A.3B.3C.5D.5【解答】解:连接OD,过C,D分别作DE⊥AB于E,CF⊥AB,垂足分别为E,F.设∠AOD=θ,θ∈.OE=2cosθ,DE=2sinθ.可得CD=2OE=4cosθ,∴梯形ABCD的面积S=(4+4cosθ)•2sinθ=4sinθ(1+cosθ),S′=4(cosθ+cos2θ﹣sin2θ)=4(2cos2θ+cosθ﹣1)=4(2cosθ﹣1)(cosθ+1).∵θ∈.∴cosθ∈(0,1).∴当cosθ=即θ=时,S取得最大值,S=3.故选:A.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.(5分)已知向量,的夹角为60°,||=1,|2﹣|=,则||=1.【解答】解:∵向量,的夹角为60°,||=1,|2﹣|=,∴|2﹣|2==3,解得:=1.故答案为:114.(5分)某化肥厂生产甲、乙两种肥料,生产一车皮甲种肥料需要磷酸盐4吨、硝酸盐18吨;生产一车皮乙种肥料需要磷酸盐1吨、硝酸盐15吨.已知生产一车皮甲种肥料产生的利润是10万元,生产一车皮乙种肥料产生的利润是5万元.现库存磷酸盐10吨、硝酸盐66吨.如果该厂合理安排生产计划,则可以获得的最大利润是30万元.【解答】解:设x、y分别为计划生产甲、乙两种混合肥料的车皮数,于是满足以下条件:再设分别生产甲、乙两种肥料各x、y车皮产生的利润为z=10000x+5000y=5000(2x+y),由得两直线的交点M(2,2).令t=2x+y,当直线L:y=﹣2x+t经过点M(2,2)时,它在y轴上的截距有最大值为6,此时z=30000.故分别生产甲、乙两种肥料各2车皮时产生的利润最大为30万元.故答案为:30万元.15.(5分)过双曲线的左焦点F(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,若E为线段FP的中点,则双曲线的离心率为.【解答】解:设双曲线的右焦点为F',则F'的坐标为(c,0)因为抛物线为y2=4cx,所以F'为抛物线的焦点O为FF'的中点,E为FP的中点所以OE为△PFF'的中位线,那么OE∥PF'因为OE=a那么PF'=2a又PF'⊥PF,FF'=2c所以PF=2b设P(x,y)x+c=2ax=2a﹣c过点F作x轴的垂线,点P到该垂线的距离为2a由勾股定理y2+4a2=4b24c(2a﹣c)+4a2=4(c2﹣a2)得e=.故答案为:.16.(5分)在平面四边形ABCD中,∠A=∠B=60°,AB=1,∠D=150°,则四边形ABCD面积的取值范围是(,).【解答】解:平面四边形ABCD中,∠A=∠B=60°,∠D=150°,∴∠C=90°;延长AD、BC相交于点O,则△OAB为等边三角形,如图(1)所示;此时△AOB的面积为×1×1×sin60°=;当A,D重合时,AC⊥BC,∠B=60°,如图(2)所示;此时△ABC的面积为×1××sin60°=;∴平面四边形ABCD的面积S满足<S<.故答案为:(,).三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(12分)已知a,b,c分别是△ABC内角A,B,C的对边,且满足:(a+b+c)(sin B+sin C ﹣sin A)=b sin C.(Ⅰ)求角A的大小;(Ⅱ)设a=,S为△ABC的面积,求S+cos B cos C的最大值.【解答】解:(Ⅰ)(a+b+c)(sin B+sin C﹣sin A)=b sin C,由正弦定理可得(a+b+c)(b+c﹣a)=bc,即(b+c)2﹣a2=bc,即为b 2+c 2﹣a 2=﹣bc , 由余弦定理可得cos A ==﹣,由0<A <π,可得A =;(Ⅱ)a =,由正弦定理可得:====2,可得b =2sin B ,c =2sin C , 则S =bc sin A =sin B sin C , S +cos B cos C =sin B sin C +cos B cos C=cos (B ﹣C ),当B =C =时,S +cos B cos C 的最大值为.18.(12分)为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?(2)求这80位师范类毕业生从事与教育有关工作的频率;(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X ,求X 的数学期望E (X ). 参考公式:k 2=(n =a +b +c +d ).附表:【解答】解:(1)根据列联表计算观测值K2=≈2.0513,因为K2<3.841,所以在犯错误的概率不超过5%的前提下,不能认为“师范类毕业生从事与教育有关的工作与性别有关”;(2)由图表知这80位师范类毕业生从事与教育有关工作的频率为P==;(3)由题意知X服从B(4,),则E(X)=np=4×=.19.(12分)已知数列{a n}的前n项和为S n,且a1=2,2S n=(n+1)2a n﹣n2a n+1,数列{b n}满足b1=a1,nb n+1=a n b n.(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)若数列{c n}满足c n=a n+b n(n∈N*),求数列{c n}的前n项和T n.【解答】解:(I)由2S n=(n+1)2a n﹣n2a n+1,可得:2S n+1=(n+2)2a n+1﹣(n+1)2a n+2,两式相减可得:2a n+1=(n+2)2a n+1﹣(n+1)2a n+2﹣(n+1)2a n+n2a n+1,∴2a n+1=a n+2+a n,∴数列{a n}是等差数列,2S1=22a1﹣a2,a1=2,解得a2=4.∴d=4﹣2=2.∴a n=2+2(n﹣1)=2n.由b1=a1=2,nb n+1=a n b n.∴b n+1=2b n,∴数列{b n}是等比数列,首项与公比都为2.∴b n=2n.(II)c n=a n+b n=2n+2n,∴数列{c n}的前n项和T n=+=2n+1+n2+n﹣2.20.(12分)已知直线l与椭圆C:+=1(a>b>0)交于A(x1,y1),B(x2,y2)两点,又=(ax1,by1),=(ax2,by2),若⊥且椭圆的离心率e=,又椭圆经过点(,1),O为坐标原点.(Ⅰ)求椭圆的方程;(Ⅱ)试问△AOB的面积是否为定值?【解答】解:(Ⅰ)由题意的离心率e===,则a=2b,将(,1)代入,即,解得:b=1,则a=2,∴椭圆的标准方程为:;(Ⅱ)由⊥,则•=0,即4x1x2+y1y2=0,由于A(x1,y1),B(x2,y2)在椭圆上,则,两式相乘,(y12+4x12)(y22+4x22)=(y1y2)2+16(x1x2)2+4(x12y22+x22y12),=(4x1x2+y1y2)2+4(x1y2﹣x2y1)2=4(x1y2﹣x2y1)2=16,∴(x1y2﹣x2y1)2=4,∴△AOB的面积S△AOB=|x1y2﹣x2y1|=1,△AOB的面积为定值1.注S△AOB=||或过A,B分别作y轴的垂线转化为直角梯形,与直角三角形的面积问题即可.21.(12分)已知函数f(x)=4x2+﹣a,g(x)=f(x)+b,其中a,b为常数.(1)若x=1是函数y=xf(x)的一个极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若函数f(x)有2个零点,f(g(x))有6个零点,求a+b的取值范围.【解答】解:(1)函数f(x)=4x2+﹣a,则y=xf(x)=4x3+1﹣ax的导数为y′=12x2﹣a,由题意可得12﹣a=0,解得a=12,即有f(x)=4x2+﹣12,f′(x)=8x﹣,可得曲线在点(1,f(1))处的切线斜率为7,切点为(1,﹣7),即有曲线y=f(x)在点(1,f(1))处的切线方程为y+7=7(x﹣1),即为y=7x﹣14;(2)由f(x)=4x2+﹣a,导数f′(x)=8x﹣,当x>时,f′(x)>0,f(x)递增;当x<0或0<x<时,f′(x)<0,f(x)递减.可得x=处取得极小值,且为3﹣a,由f(x)有两个零点,可得3﹣a=0,即a=3,零点分别为﹣1,.令t=g(x),即有f(t)=0,可得t=﹣1或,则f(x)=﹣1﹣b或f(x)=﹣b,由题意可得f(x)=﹣1﹣b或f(x)=﹣b都有3个实数解,则﹣1﹣b>0,且﹣b>0,即b<﹣1且b<,可得b<﹣1,即有a+b<2.则a+b的范围是(﹣∞,2).选考题:共10分.请考生从第22、23题中任选一题作答,并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,按本选考题的首题进行评分.[选修4-4:坐标系与参数方程]22.(10分)已知直线l的参数方程为(其中t为参数),曲线C1:ρ2cos2θ+3ρ2sin2θ﹣3=0,以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,两种坐标系中取相同长度单位.(Ⅰ)求直线l的普通方程及曲线C1的直角坐标方程;(Ⅱ)在曲线C1上是否存在一点P,使点P到直线l的距离最大?若存在,求出距离的最大值及点P的直角坐标;若不存在,请说明理由.【解答】解:(Ⅰ)直线l的参数方程为(其中t为参数),转化为直角坐标方程为:x﹣y+1=0.曲线C1:ρ2cos2θ+3ρ2sin2θ﹣3=0,转化为直角坐标方程为:.(Ⅱ)由(Ⅰ)知:C1的参数方程为:(θ为参数).所以:点P到直线l的距离d==,则:,此时:cos()=1,解得:(k∈Z).所以:,故P()到直线l的距离最大.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣5|﹣|x﹣2|.(Ⅰ)若∃x∈R,使得f(x)≤m成立,求实数m的取值范围;(Ⅱ)解不等式x2﹣8x+15+f(x)≤0.【解答】解:(Ⅰ)f(x)=|x﹣5|﹣|x﹣2|=,当2<x<5时,﹣3<7﹣2x<3,所以﹣3≤f(x)≤3,∴m≥﹣3;(Ⅱ)不等式x2﹣8x+15+f(x)≤0,即﹣f(x)≥x2﹣8x+15由(1)可知,当x≤2时,﹣f(x)≥x2﹣8x+15的解集为空集;当2<x<5时,﹣f(x)≥x2﹣8x+15,即x2﹣10x+22≤0,∴5﹣≤x<5;当x≥5时,﹣f(x)≥x2﹣8x+15,即x2﹣8x+12≤0,∴5≤x≤6;综上,原不等式的解集为{x|5﹣≤x≤6}.。
2018年高三最新 河南省信阳市2018学年高三第二次调研
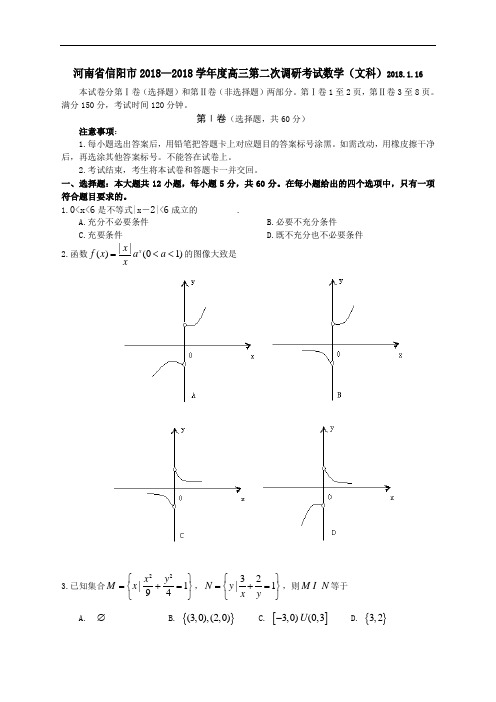
河南省信阳市2018—2018学年度高三第二次调研考试数学(文科)2018.1.16本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至8页。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
2.考试结束,考生将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项符合题目要求的。
1.0<x<6是不等式|x-2|<6成立的 .A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.函数||()(01)xxf x a ax=<<的图像大致是3.已知集合22|194x yM x⎧⎫=+=⎨⎬⎩⎭,32|1N yx y⎧⎫=+=⎨⎬⎩⎭,则M N等于A.∅B.{}(3,0),(2,0) C.[]3,0)(0,3- D.{}3,24.把函数c o s 2in 2y x x =-的图像按向量平移后得到的图象关于y 轴对称,则||m 的最小值为A.12πB.6πC.3πD.512π5.已知函数3()42f x x x =-且''()()f x f a >成立,则实数a 的取值范围是A. (,1)-∞B. (1,)+∞C. (,1)(1,)U -∞-∞D. (1,1)- 6.已知向量(1,2)a =,(1,)b x x =+-,且a b ⊥,则x =A.2B.23C.1D.07.设函数,22,232(){xx xx x f x <≥+=若()1f a >,则a 的取值范围是A. (0,2)(3,)U +∞B. (3,)+∞C. (0,1)(2,)U +∞D. (0,2) 8.等差数列中有两项1m a k=,1k a m=则该数列前mK 项之和为A.12m k + B.2m k k + C.2m k m+ D.2k m +9.设椭圆221xym n +=的一个焦点与抛物线28xy =的焦点相同,离心率为12,则此椭圆方程为A.2211612xy+= B.2216448xy+= C.2214864xy+= D.2211216xy+=10.已知,x y 满足1032602x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩,则22x y +的最小值是A.1B.13C.3613D.13411.某人射击8次,有3次命中目标,其中恰有2次连续命中目标的情形有A.15种B.30种C.48种D.60种 12.若函数()()y f x x R =∈满足(2)()f x f x +=,且(1,1]x ∈-时,()f x x =,则函数()y f x =的图像与函数4lo g y x =的图像的交点个数为A.3B.4C.6D.8第Ⅱ卷(非选择题,共90分)注意事项:1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试卷上。
河南省2018届高三第二次统一考试

河南省2018届高三第二次统一考试数学试卷(文科) 第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知复数z 满足()11z i i -=-,则z =2i +2.已知集合{}21|log 1,|1A x x B x x ⎧⎫=≤=>⎨⎬⎩⎭,则()R A C B =A. (],2-∞B. (]0,1C. []1,2 D.()2,+∞ 3.已知()()2,,1,2a m b ==-,若()//2a a b +,则m 的值是 A. 4- B. 4 C. 0 D.2-4.已知直线()1y k x =+与不等式组40300,0x y x y x y +-≤⎧⎪-≥⎨⎪>>⎩表示的平面区域有公共点,则k 的取值范围是A.[)0,+∞B. 30,2⎡⎤⎢⎥⎣⎦C. 30,2⎛⎤ ⎥⎝⎦ D. 3,2⎛⎫+∞ ⎪⎝⎭5.执行如图所示的程序,则输出的结果是A. 513B. 1023C. 1025D. 20476.平面内凸四边形有2条对角线凸五边形有5条对角线,依次类推,凸13边形的对角线条数为A. 42B. 65C. 143D. 169 7.刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居中,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为1:2,这个比是不变的.下图是一个阳马的三视图,则其表面积为A. 2B. 2338.已知()sin 4f x a x =+,若()lg33f =,则1lg 3f ⎛⎫= ⎪⎝⎭A. B. C. D.9.已知函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><的部分图象如图所示,则下列说法错误的是A. ωπ=B. 4πϕ=C. ()f x 的单调递减区间是132,2,44k k k z ⎛⎫-+∈ ⎪⎝⎭D. ()f x 的对称中心为1,0,4k k z ⎛⎫+∈ ⎪⎝⎭10.设函数()()0sin fx x =,定义()()()()()()()()1021,,,f x f f x f x f f x ⎡⎤⎡⎤''==⎣⎦⎣⎦()()()()1,n n f x f f x -⎡⎤'=⎣⎦则()()()()()()122017000151515f f f +++的值是11.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱最大体积为 A.27π B. 827π C. 3π D.29π 12.已知(),P x y (其中0x ≠)为双曲线2214y x -=上的任一点,过P 点向双曲线的两条渐近线分别作垂线,垂足分别为A,B ,则PAB ∆的面积为 A.25 B. 45 C.825D.与P 点位置有关第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知实数,x y 满足11y xx y y ≥⎧⎪+≤⎨⎪≥-⎩,则目标函数2z x y =-的最大值是 .14.已知1,2,()3a b a b b ==+⋅= ,设a 与b 的夹角为θ,则θ等于 . 15已知圆C 的圆心时直线20x y -+=与x 轴的交点,且圆C 与圆22(2)(3)9x y -+-=相外切,若过点(1,1)P -的直线l 与圆C 交于两点,当最小时,直线l 的方程为. .16.设n S 为数列{}n a 的前n 项和,且113,222n n n a a S +==-,则5a = . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 如图,已知扇形的圆心角23AOB π∠=,半径为C 是AB 上一动点(不与点,A B 重合).(1)若弦1)BC =,求BC 的长; (2)求四边形OACB 面积的最大值.18. 已知四棱锥P ABCD -的底面是平行四边形,PA ⊥平面,4,ABCD PA AB AC AB AC ===⊥,点,E F 分别在线段,AB PD 上. (1)证明:平面PDC ⊥平面PAC ; (2)若三棱锥E DCF -的体积为4,求FDPD的值.19.已知药用昆虫的产卵数y 与一定范围内的温度x 有关,现收集了该中药用昆虫的6组观测数据如表:经计算得:6666211111126,33,()()557,()84,66i i i i i i i i i x x y y x x y y x x ========--=-=∑∑∑∑621()3930ii y y =-=∑,线性回归模型的残差平方和为62 6.00661ˆ()236.64,3167i i y ye =-=≈∑,分别为观察数据中温度和产卵数1,2,3,4,5,6i =,(1)若用线性回归模型,求y 关于x 的回归方程ˆˆˆy bx a =+(精确到0.1 );(2)若用非线性回归模型求得y 关于x 的回归方程0.2103ˆ0.06x y e =,且相关指数20.9952R =,试与(1)中的回归模型相比.①用2R 说明哪种模型的拟合效果更好;②用拟合效果更好的模型预测温度为035C 时该中药用昆虫的产卵数(结果取整数). 附:一组数据1122(,),(,),,(,)n n x y x y x y ,其回归直线ˆˆˆybx a =+的斜率和截距的最小二乘估计分为121()()ˆˆˆ,()niii nii x x y y bay bx x x ==--==--∑∑,相关指数22121ˆ()()ni i nii y yR y y ==-=-∑∑20. 在直角坐标xOy 中,已知椭圆E 中心在原点,长轴长为8,椭圆E 的一个焦点为圆22:420C x y x +-+=的圆心.(1)求椭圆E 的标准方程;(2)设P 是椭圆E 上y 轴左侧的一点,过P 作两条斜率之积为12的直线12,l l ,当直线12,l l 都与圆C 相切时,求P 的坐标. 21.已知函数()ln ()f x x ax a R =-∈.(1)若曲线()y f x =与直线1ln 20x y ---=相切,求实数a 的值; (2)若不等式(1)()ln xx f x x e+≤-在定义域内恒成立,求实数a 的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.已知极坐标的极点在平面直角坐标系的原点O 处,极轴与x 轴的正半轴重合,且长度单位相同,曲线C的方程是)4πρθ=-,直线l 的参数方程为1cos (2sin x t t y t αα=+⎧⎨=+⎩为参数,0απ≤<),设(1,2)P ,直线l 与曲线C 交于,A B 两点.(1)当0α=时,求AB 的长度; (2)求22PA PB +的取值范围.23.已知函数()1(0)2f x x a a a=-+≠. (1)若不等式()()1f x f x m -+≤恒成立,求实数m 的最大值; (2)当12a <时,函数()()21g x f x x =+-有零点,求实数a 的取值范围.一、选择题:DCACD BBCBA BC。
2018年河南省信阳高中高考数学二模试卷和答案(理科)

=1,则 f(
)的值为
.
16.(5 分)设 an 表示正整数 n 的所有因数中最大的奇数与最小的奇数的等差中项,数列{an}
的前 n 项和为 Sn,那么 S63 的值为
.
三、解答题:本大题共 5 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.(12 分)在△ABC 中,D∈BC,
x
1.6
1.7
1.74
1.8
10
y
4.953
5.474
5.697
6.050
22026
lnx
0.470
0.531
0.554
0.588
2.303
请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分.[选修 4-4:坐标 系与参数方程]
第 4 页(共 18 页)
22.(10 分)在平面直角坐标系 xOy 中,直线 l 的参数方程为
=
=λ.
(1)求证:AD 平分∠BAC;
(2)当
时,若 AD=1,DC= ,求 BD 和 AC 的长.
18.(12 分)国家放开计划生育政策,鼓励一对夫妇生育 2 个孩子.在某地区的 100000 对 已经生育了一胎夫妇中,进行大数据统计得,有 100 对第一胎生育的是双胞胎或多胞胎, 其余的均为单胞胎.在这 99900 对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩 的有 50000 对,男方愿意生育二孩女方不愿意生育二孩的有 x1 对,男方不愿意生育二孩 女方愿意生育二孩的有 x2 对,其余情形有 x3 对,且 x1:x2:x3=300:100:99.现用样 本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出 x1,x2,x3 的值;
河南省信阳市普通2018届高中高三第二次教学质量检测 数学理

信阳市2017—2018学年普通高中高三第二次教学质量检测数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并帖好条形码。
请认真核准条形码的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
第Ⅰ卷 (满分60分)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M ={x |x <2},N ={x |2x -x <0},则下列关系中正确的是A .M ∪N =RB .M ∪(C R N )=R C .N ∪(CR M )=R D .M ∩N =M2.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何”其意思为:“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为 A .54钱 B .53钱 C .32钱 D .43钱 3.下面是关于复数z =21i i --的四个命题:p 1:|z |=2;p 2:z 2=2i ;p 3:z 的共轭复数为1+i ;p 4:z 的虚部为-1.其中的真命题为A .p 1,p 2B .p 2,p 4C .p 2,p 3D .p 3,p 44.已知定义在R 上的函数f (x )=313ax +2x +ax +1有三个不同的单调区间,则实数a 的取值范围是A .(-∞,-1)∪(1,+∞)B .[-1,0)∪(0,1]C .(-1,1)D .(-1,0)∪(0,1)5.若偶函数f (x )在区间(-∞,0]上单调递减,且f (3)=0,则不等式(x -1)f (x )>0的解集是A .(-3,1)∪(3,+∞)B .(-∞,-1)∪(1,+∞)C .(-∞,-3)∪(3,+∞)D .(-∞,-1)∪(3,+∞)6.25(2)x+1的展开式的常数项为 A .5 B .-10 C .-32D .-427.某校高三年级10个班参加合唱比赛得分的茎叶图如图1所示,若这组数据的平均数是20,则1a +9b的最小值为 A .1 B .32C .2D .52 8.若输出的S 的值等于22,那么在如图2所示的程序框图中的判断框内应填写的条件是A .i >5B .i >6C .i >7D .i >89.要得到函数f (x )=cos (2x +3π)的图象,只需将函数g (x )= sin (2x +3π)的图象 A .向左平移2π个单位长度 B .向右平移2π个单位长度 C .向左平移4π个单位长度 D .向右平移4π个单位长度 10.过抛物线2y =4x 的焦点F 作直线l 交抛物线于A 、B 两点,若1AF -1BF =12,则 直线l 的倾斜角θ(0<θ<2π)等于 A .2π B .3π C .4π D .6π 11.设x ,y ,z 为正实数,且2log x =3log y =5log z >0,则2x ,3y ,5z 的大小关系不可是 A .2x <3y <5z B .2x =3y =5z C .3y <2x <5z D .5z <3y <2x12.如图3,将一半径为2的半圆形纸板裁剪成等腰梯形ABCD 的形状,下底AB 是半圆的直径,上底CD 的端点在圆周上,则所得梯形面积的最大值为A .5B .3C .5D .3第Ⅱ卷(满分90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.已知向量a,b的夹角为60°,且|a|=1,|2a-b b|=__________.14.某化肥厂生产甲、乙两种肥料,生产一车皮甲肥料需要磷酸盐4吨、硝酸盐18吨;生产一车皮乙种肥料需要磷酸盐1吨、硝酸盐15吨.已知生产一车皮甲种肥料产生的利润是10万元,生产一车皮乙种肥料产生的利润是5万元.现库存磷酸盐10吨、硝酸盐66吨,如果该厂合理安排生产计划,则可以获得的最大利润是____________万元.15.过双曲线22221x ya b-=(a>0,b>0)的左焦点F(-c,0)作圆222x y a+=的切线,切点为E,延长FE交抛物线2y=4cx于点P,O为坐标原点,若E为PF的中点,则双曲线的离心率为_____________.16.在平面四边形ABCD中,∠A=∠B=60°,AB=1,∠D=150°,则四边形ABCD面积的取值范围是_____________.三、解答题:本大题共6小题,共70分。
河南省六市2018届高三第二次联考(二模)数学(理)试题答案

(Ⅱ )当a<12时 ,g(x)=f(x)+|2x-1|=|x-a|+|2x-1|+21a
ìïï-3x+a+21a+1,x<a, = íïïï-x-a+21a+1,a≤x≤12,…………………………………………………… 7分
îïïï3x-a+21a-1,x>1 2,
∴g(x)min=g(12)=12
15.15
11-12 CA
16.Sn
=
(n2-n+1)·3n+1 2
17.解:(Ⅰ )依题设:sinA=
1-cos2A =
1-
(3)2 4
=
7, 4
sinC=
1-cos2C =
1-
(1)2 8
=387,故
cosB
=cos[π
﹣
(A
+C)]
=-cos(A+C)=-(cosAcosC-sinAsinC)=-(332-2312 )=196.……… 4分
令平面 ABC 的一个法向量为n=(x,y,z)
{ { 则有
n·AB→=0 n·AC→=0
即 -y+ 3z=0 - 3-y=0
令z=1,则x=-1,y= 3
……… 8分
∴n=(-1,3,1)
令 AB1 与平面 ABC 所成的角为θ
则sinθ=|cos<n,AB→1>|=
n·AB→1 |n||AB→1|
(Ⅱ )由 (Ⅰ )知 :sinB =
1-cos2B =
1=
(9 )2 16
57 = 16
,
再由正弦定理易得:a4=b5=c6,…………………………………………………… 6分
2018届高三第二次质量检测文科数学答案
2018届高三第二次质量检测卷文科数学参考答案第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项符合要求.第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.3; 14. [3,)+∞; 15.1(,1)2; 16.2π3+ 三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知三个集合:{}22log (58)1A x x x =∈-+=R ,{}22821R x x B x +-=∈=,{}22190R C x x ax a =∈-+->.(I )求A B ;(II )已知,A C B C ≠∅=∅,求实数a 的取值范围.解:(Ⅰ){}{}25822,3R A x x x =∈-+==, ………………………........................2分 {}{}22802,4R B x x x =∈+-==-, ……………………….....................4分{}2,3,4.A B ∴=- ……………………....................…5分(Ⅱ),A C B C ≠∅=∅,2,4,3.C C C ∴∉-∉∈ …………………….................…6分{}22190,R C x x ax a =∈-+->22222222190,(4)4190,33190.a a a a a a ⎧-+-≤⎪∴-++-≤⎨⎪-+->⎩…………………….................…10分即35,222 5.a a a a -≤≤⎧⎪--≤≤-⎨⎪<->⎩或解得3 2.a -≤<-……………………….................11分 所以实数a 的取值范围是[3,2).--.................................................................................12分 18. (本小题满分12分)已知函数()()sin f x a x b ωθ=+-()x ∈R 的部分图象如图所示,其中,a b 分别是ABC ∆的角,A B 所对的边, ππ0,[,]22ωθ>∈-.(I )求,,,a b ωθ的值;(II )若cos ()+12CC f =,求ABC ∆的面积S .解:(Ⅰ)0,0a ω>>及图象特征知: ①()f x 的最小正周期2π3ππ2[()]π,88ω=--=2.ω=……………………….......................................................................................................2分②当()sin 1x ωθ+=-时,min ()1f x a b =--=; 当()sin 1x ωθ+=时,max ()1f x a b =-=.解得 1.a b ==………………………..................................................................................4分③ππ()))1188f θ-=-+-=,得ππ2π,42k θ-+=-π2π,4k θ=-.k ∈Z由ππ[,]22θ∈-得π.4θ=- 所以π2,, 1.4a b ωθ==-==…………………….....................................................…6分(II )由π()214f x x ⎛⎫=-- ⎪⎝⎭及cos ()+12C C f =得,πsin c s os o 4c C C C C ⎛⎫-=- ⎪⎝⎭=,即C C sin 21cos = ……………….............…..........................................................................8分又22sin cos 1C C +=,得552sin ,54sin 2±==C C …………………………...........…10分由0πC <<得,sin C =1sin 2S ab C ==……………………...........……12分 19.(本小题满分12分)中国移动通信公司早前推出“全球通”移动电话资费“个性化套餐”,具体方案如下:(I )写出“套餐”中方案1的月话费y (元)与月通话量t (分钟)(月通话量是指一个月内每次通话用时之和)的函数关系式;(II )学生甲选用方案1,学生乙选用方案2,某月甲乙两人的电话资费相同,通话量也相同,求该月学生甲的电话资费;(III )某用户的月通话量平均为320分钟,则在表中所列出的七种方案中,选择哪种方案更合算,说明理由.解: (Ⅰ) 30, 048,300.6(48) , 48.t y t t ≤≤⎧=⎨+⨯->⎩, ……………………..............……3分即:30, 048,0.6 1.2 , 48.t y t t ≤≤⎧=⎨->⎩………………………...........…4分(Ⅱ)设该月甲乙两人的电话资费均为a 元,通话量均为b 分钟.当048b ≤≤时, 甲乙两人的电话资费分别为30元, 98元,不相等;…….........5分 当170b >时, 甲乙两人的电话资费分别为1300.6(48)y b =+-(元),2980.6(170)y b =+-元, 21 5.20y y -=-<,21y y <; ……………......…6分当48170b <≤时, 甲乙两人的电话资费分别为300.6(48)a b =+-(元),98a =(元), 解得484.3b =所以该月学生甲的电话资费98元. …………….................................…8分(Ⅲ)月通话量平均为320分钟,方案1的月话费为:30+0.6×(320-48)=193.2(元); ……………….........9分方案2的月话费为:98+0.6×(320-170)=188(元); ……………..........…10分 方案3的月话费为168元. 其它方案的月话费至少为268元. …………….........…11分 经比较, 选择方案3更合算. ……………........…12分 20.(本小题满分12分)已知函数32()f x ax x b =++的图象在点1x =处的切线方程为13y =,其中实数,a b 为常数.(I )求,a b 的值;(II )设命题p 为“对任意1(2,)x ∈+∞,都存在2(1,)x ∈+∞,使得12()()1f x f x =”,问命题p 是否为真命题?证明你的结论.解: (I )32(),f x ax x b =++ 2()32.f x ax x '∴=+……………......................…1分(1)1,(1)32,f a b f a '=++=+∴函数()f x 的图象在点1x =处的切线方程为(1)(32)(1)y a b a x -++=+-, 即(32)21y a x b a =++-- ………………4分该切线方程为13y =, ∴1320,21,3a b a +=--=…………....................……5分 即2,0.3a b =-= ………….....................……6分(II )命题p 为真命题. ……………................…7分证明如下: 322(),3f x x x =-+ 2()222(1).f x x x x x '=-+=-- 当1x >时, ()0f x '<,()f x 在区间(1,)+∞单调递减,集合{}1()1,(,(1))(,).3R A f x x x f =>∈=-∞=-∞ ……………..................…9分当2x >时, ()f x 的取值范围是4(,(2))(,).3f -∞=-∞-集合132,(,0).()4R B x x f x ⎧⎫=>∈=-⎨⎬⎩⎭…………….................…11分从而.B A ⊆所以对任意1(2,)x ∈+∞,都存在2(1,)x ∈+∞,使得211(),()f x f x =即12()() 1.f x f x = ……………..................…12分21.(本小题满分12分) 已知函数1()ln ,1xf x a x x-=++其中实数a 为常数且0a >. (I )求函数()f x 的单调区间;(II )若函数()f x 既有极大值,又有极小值,求实数a 的取值范围及所有极值之和; (III )在(II )的条件下,记12,x x 分别为函数()f x 的极大值点和极小值点,求证:1212()()()22x x f x f x f ++<. 解:(Ⅰ) 函数2()ln 11f x a x x=+-+的定义域为∞(0,+),22222(1)()(1)(1)a ax a x af x x x x x +-+'=-=++, …………...........……1分 设222()2(1)4(1)44(12).g x ax a x a a a a =+-+∆=--=-,① 当12a ≥时, 0∆≤,()0,g x ≥()0f x '≥,函数()f x 在∞(0,+)内单调递增; …………..........……2分② 当102a <<时, 0∆>,方程()0g x =有两个不等实根:12x x ==,且1201.x x <<< 1()0()00,f x g x x x '>⇔>⇔<<或2.x x >12()0()0.f x g x x x x '<⇔<⇔<< .............................................3分综上所述,当12a ≥时, ()f x 的单调递增区间为∞(0,+),无单调递减区间;当102a <<时,()f x 的单调递增区间为1a a -(0,, 1a a -+∞(),单调递减区间.............................................................4分(II )由(I )的解答过程可知,当12a ≥时,函数()f x 没有极值. ......................................5分 当102a <<时,函数()f x 有极大值1()f x 与极小值2()f x ,121212(1), 1.x x x x a+=-=12()()f x f x ∴+=121211*********(1)(ln )(ln )ln()0.11(1)(1)x x x x a x a x a x x x x x x ---+++=+=++++ .....................................7分故实数a 的取值范围为1(0,)2,所有极值之和为0. ……………................8分 (III )由(II )知102a <<,且1211()(1)ln(1)212x x f f a a a a+=-=-+-, 12()()02f x f x +=.…………9分原不等式等价于证明当102a <<时,1ln(1)210a a a-+-<,即11ln(1)2a a-<-. ………………......................................10分设函数()ln 1h x x x =-+,则(1)0,h =当1x >时,1()10h x x'=-<. 函数()h x 在区间[1,)+∞单调递减,由102a <<知111a ->,1(1)(1)0h h a -<= ……………….....................................11分 . 即11ln(1)2a a-<-. 从而原不等式得证. ………………....................................12分22.[选修4−4:坐标系与参数方程] (本小题满分10分)在平面直角坐标系中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知直线l的参数方程为122(2x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数);曲线1C的极坐标方程为2cos ρθθ=+;曲线2C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数) (Ⅰ)求直线l 的直角坐标方程、曲线1C 的直角坐标方程和曲线2C 的普通方程;(Ⅱ)若直线l 与曲线1C 曲线2C 在第一象限的交点分别为,M N ,求,M N 之间的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信阳市2017—2018学年普通高中高三第二次教学质量检测
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并帖好条形码。
请认真核准条形码的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
第Ⅰ卷 (满分60分)
一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.复数z =3i i
+7的实部与虚部分别为 A .7,-3 B .7,-3i C .-7,3 D .-7,3i 2.已知全集U =R ,集合A ={x |x <-
12,或x >1},B ={x |-1≤x ≤2,x ∈Z},则图1
所示的阴影部分表示的集合等于
A .{-1,2}
B .{-1,0}
C .{1,2}
D .{0,1}
3.已知命题p :x ∃∈R ,x
e -x -1≤0,则p ⌝为
A .x ∀∉R ,x e -x -1>0
B .x ∀∈R ,x e -x -1≥0
C .x ∀∈R ,x e -x -1>0
D .x ∃∈R ,x e -x -1>0
4.已知双曲线22
221x y a b
-=(a >0,b >0)的一条渐近线经过点(3,则双曲线的离心率为
A B .2 C 2 D 2 5.某同学先后投掷一枚骰子两次,第一次向上的点数记为x ,第二次向上的点数记为y .在直角坐标系xOy 中,以(x ,y )为坐标的点落在直线2x -y =1上的概率为
A .19
B .112
C .536
D .16 6.如果f (x )是定义在R 上的奇函数,那么下列函数中,一定为偶函数的是 A .y =x +f (x ) B .y =2x +f (x ) C .y =xf (x ) D .y =2x f (x )
7.已知等比数列{n a }的前n 项和为n S ,a 1+a 3=
52,且a 2+a 4=54,则n n S a 等于 A .n 2-1 B .1n -2 C .1n -4
D .1n 4- 8.执行图2所示的程序框图,若输出的y 的值为5,则判断框
中可以填入的条件是
A .i <6?
B .i <5?
C .i <4?
D .i <3?
9.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、
丁的供词如下:甲说:“罪犯在乙、丙、丁三人之中”;乙
说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一
人是小偷”;丁说:“乙说的是事实”.经过调查核实,四人
中有两人说的是真话,另外两人说的是假话,并且这四人
中只有一人是罪犯,由此可判断罪犯是
A .甲
B .乙
C .丙
D .丁
10.在△ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c .
若asinBcosC +csinBcosA =
12
b ,且a >b ,则B 等于 A .56π B .3π C .23π D .6π 11.已知x =-
8π与0x 分别是函数f (x )=Asin (ωx +ϕ)(A >0,ω>0,|ϕ|<2
π)的一条对称轴和零点,且|0x +8π|min =4
π,则ϕ等于 A .-8π B .-4π C .8π D .4
π 12.已知函数f (x )(x ∈R )满足f (-x )=8-f (4+x ),函数g (x )=432x x +-,若函数 f (x )与g (x )的图象共有168个交点,记作P i (x i ,y i )(i =1,2,…,168),则
(x 1+y 1)+(x 2+y 2)+…+(x 168+y 168)的值为
A .2018
B .2017
C .2016
D .1008
第Ⅱ卷(满分90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.设向量a =(1,-2),a +b =(0,2),则|a -2b |=________________.
14.已知椭圆C :221x my +=的焦点在y 轴上,长轴长是短轴长的两倍,则m =_______________.
15.直线ax +by +c =0与圆C :22
240x x y y -++=相交于A ,B 两点,且|AB uu u r
则CA uu r ·CB uu r =_______________。
16.某化肥厂生产甲、乙两种肥料,生产一车皮甲肥料需要磷酸盐4吨、硝酸盐18吨;生产一车皮
乙种肥料需要磷酸盐1吨、硝酸盐15吨.已知生产一车皮甲种肥料产生的利润是10万元,生产一车皮乙种肥料产生的利润是5万元.现库存磷酸盐10吨、硝酸盐66吨,如果该厂合理安排生产计划,则可以获得的最大利润是____________万元.
三、解答题:本大题共6小题,共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21
题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
17.(本小题满分12分)
已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c +bsinA =0.
(Ⅰ)求角B 的大小;
(Ⅱ)若a +c =4,b ABC 的面积.
18.(本小题满分12分)
已知等差数列{n a }的前n 和为n S ,且S 5=45,S 6=60.
(Ⅰ)求数列{n a }的通项公式n a ;
(Ⅱ)若数列{n b }满足1n b +-n b =n a (n ∈N ﹡),且b 1=3,求数列{1n
b }的前n 和为n T .
19.(本小题满分12分)
二手车经销商小王对其所经营的某一型号二手汽车的使用年数x (0<x ≤10)与销售价格y (单
(Ⅰ)试求y 关于x 的回归直线方程;
(Ⅱ)已知每辆该型号汽车的收购价格为ω=0.052
x -1.75x +17.2(单位:万元),根据(Ⅰ)
中所求的回归方程,预测x 为何值时,小王销售一辆该型号汽车所获得的利润z (单位:万元)最大?
20.(本小题满分12分)
已知抛物线C :2x =2py (p >0)的焦点为F ,过点F 的直线l 交C 于A ,B 两点,且以AB 为
直径的圆M 与直线y =-1相切于点N .
(Ⅰ)求抛物线C 的方程;。
