非齐次方程的冲量定理法求解
数学物理方程复习

一、填空题1、物理规律反映同一类物理现象的共同规律,称为___________。
2、在给定条件下求解数学物理方程,叫作____________________。
3、方程20tt xx u a u -=称为_________方程4、方程20t xx u a u -=称为_________方程5、静电场的电场强度E是无旋的,可用数学表示为_____________。
6、方程0j Ñ×=称为_____________的连续性方程。
7、第二类边界条件,就是______________________________________。
8、第一类边界条件,就是______________________________________。
9、00(0,)(0,)x x u x t u x t -=+称为所研究物理量u 的_____________。
10、00(0,)(0,)u x t u x t -=+称为所研究物理量u 的_____________。
11、对于两个自变量的偏微分方程,可分为双曲型、________和椭圆型。
12、对于两个自变量的偏微分方程,可分为双曲型、抛物线型和________。
13、分离变数过程中所引入的常数l 不能为_____________。
14、方程中,特定的数值l 叫作本征值,相应的解叫作_____________。
15、分离变数法的关键是________________________代入微分方程。
16、非齐次振动方程可采用______________和冲量定理法求解。
17、处理非齐次边界条件时,处理非齐次边界条件时,可利用叠加原理,可利用叠加原理,可利用叠加原理,把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
18、处理非齐次边界条件时,处理非齐次边界条件时,可利用叠加原理,可利用叠加原理,可利用叠加原理,把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
数学物理方法-8.2非齐次方程-文档资料
T1 ' ' (t )
(
a
l
) 2 T1 (t )
A a at a 2 [ sin ( ) sin t ] 2 (a / l ) l l l
2
T1 ' ' (t ) (
A a at A a at a 2 2 [ sin sin t ] [ sin ( ) sin t ] l 2 (a / l ) 2 l l 2 (a / l ) 2 l l l A a 2 [ 2 sin t ( ) 2 sin t ] A sin t 2 (a / l ) l ) 2 T1 (t )
sincossinsinsinsinsinsinsinsinsincossinsinsincossinsinxxtt解的分解iixxiittii这是普通道具有齐次边界条件的齐次方程初始值零点非齐次方程可用冲量定理法物理思想时刻t单位长弦受力xxtt数学检验
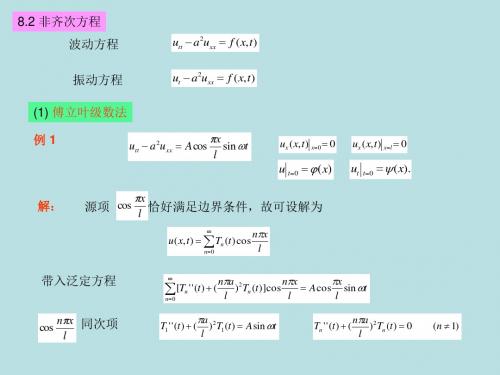
8.2 非齐次方程 波动方程 振动方程 (1) 傅立叶级数法 例1
T1 (t ) Al 1 at a at l at ( sin sin t ) cos sin 1 1 a 2 (a / l ) 2 l l l a l
a
u ( x, t )
Al 1 at a ax ( sin sin t ) cos 0 0t a 2 (a / l ) 2 l l l ( n cos
d (t ) (t ) g ( t ; ) d g ( t ; ) d g [ t ; ( t )] g [ t ; ( t )] dt t t (t ) ( t ) t
非齐次方程的冲量定理法求解

而
0
u
0
t
( x, t ; ) lim
0
v( x, t ; )d
0
例:用冲量法求定解问题: 泛定方程 边界 条件
utt a u xx A cos
2
x
l
sin t
u x ( x, t ) x0 0 u x ( x, t ) xl 0
Tn (0) 0 T0 (0) 0
n0 n0
n a 2 Tn ' (t ) ( ) Tn (t ) 0 l
T0 ' (t ) A sin t
n0
T0 ' (t ) A sin t T0 (0) 0
n a 2 Tn ' (t ) ( ) Tn (t ) 0 l
t
初始 条件
u( x, t ) t 0 0 ut ( x, t ) t 0 0
(0 x l t 0)
解: 用冲量法,上述定解问题变为 v 的定解问题vtt a vxx 0
2
v x x 0 0 v x x l 0
x vt t A cos sin l (0 x l t d )
vtt a vxx 0
2
( )
(0 x l t )
v x 0 0 (t ) v x l 0
u ( x, t ) lim
t
v t 0 vt
( )
(0 x l )
t
f ( x, )
v( x, t ; )
0 t
另一方法:考虑线性叠加法 令 有
I tt 2 I xx
u u u
冲量定理 (2)

冲量定理简介冲量定理是力学中的一个重要定理,它描述了非弹性碰撞过程中的物体运动规律。
冲量定理给出了物体的冲量与物体速度变化的关系,是力学中的基本定律之一。
冲量的定义冲量是一个矢量量,表示力作用在物体上的效果。
冲量可以用力在时间上的积分来计算,即:$$ \\vec{I} = \\int \\vec{F} dt $$其中,$\\vec{I}$表示冲量,$\\vec{F}$表示力,dd表示时间的微元。
冲量定理的表述冲量定理告诉我们,力的冲量等于物体的动量变化。
这个定理可以用以下数学公式表示:$$ \\vec{I} = \\Delta \\vec{p} $$其中,$\\vec{I}$表示冲量,$\\Delta \\vec{p}$表示物体的动量变化。
应用示例为了更好地理解冲量定理的应用,我们来看一个具体的示例。
示例问题一个质量为2 kg的物体以4 m/s的速度向右运动,受到一个6 N的恒力作用,持续时间为3 s。
求物体在力作用下的冲量和速度变化量。
解决方法首先,我们需要计算力的冲量。
根据冲量的定义,可以得到:$$ \\vec{I} = \\int \\vec{F} dt = \\vec{F} \\cdot \\Delta t $$代入具体数值,得到:$$ \\vec{I} = 6 \\, \\text{N} \\cdot 3 \\, \\text{s} = 18 \\, \\text{Ns} $$接下来,我们需要计算物体的动量变化量。
根据动量的定义,可以得到:$$ \\Delta \\vec{p} = m \\cdot \\Delta \\vec{v} $$代入具体数值,得到:$$ \\Delta \\vec{p} = 2 \\, \\text{kg} \\cdot \\Delta\\vec{v} $$由于物体最初的速度为4 m/s,受到恒力作用后速度会变化,假设变化量为$\\Delta v$,则有:$$ \\Delta v = v_f - v_i = \\Delta \\vec{v} $$其中,d d表示物体最终的速度,d d表示物体最初的速度。
高考物理考点必背:冲量与动量公式

2019 年高考物理考点必背:冲量与动量公式下边是编写老师整理的2019 年高考物理考点必背:冲量与动量公式,希望对您提升学习效率有所帮助.1.动量: p=mv {p :动量 (kg/s),m:质量 (kg),v:速度 (m/s),方向与速度方向同样}2.冲量: I=Ft {I :冲量 (N s),F:恒力 (N),t:力的作用时间 (s),方向由F决定}3.动量定理: I=p 或 Ft=mvtmvo {p :动量变化 p=mvtmvo,是矢量式 }4.动量守恒定律: p 前总 =p 后总或 p=p 也能够是m1v1+m2v2=m1v1+m2v25.弹性碰撞: Ek=0 { 即系统的动量和动能均守恒}6.非弹性碰撞 0EKEKm {EK :损失的动能, EKm :损失的最大动能 }7.完整非弹性碰撞EK=EKm { 碰后连在一同成一整体 }8.物体 m1 以 v1 初速度与静止的物体m2 发生弹性正碰:v1=(m1-m2)v1/(m1+m2) v2=2m1v1/(m1+m2)9.由 8 得的推论等质量弹性正碰时两者互换速度(动能守恒、动量守恒)10.子弹 m 水平速度 vo 射入静止置于水平圆滑地面的长木块M,并嵌入此中一同运动时的机械能损失。
E 损=mvo2/2-(M+m)vt2/2=fs 相对 {vt :共同速度, f:阻力,s 相对子弹相对长木块的位移 }注:(1)正碰又叫对心碰撞,速度方向在它们中心的连线上;(2)以上表达式除动能外均为矢量运算,在一维状况下可取正方向化为代数运算 ;(3)系统动量守恒的条件:合外力为零或系统不受外力,则系统动量守恒 (碰撞问题、爆炸问题、反冲问题等);(4)碰撞过程 (时间极短,发生碰撞的物体组成的系统)视为动量守恒,原子核衰变时动量守恒;(5)爆炸过程视为动量守恒,这时化学能转变为动能,动能增添;(6)其余有关内容:反冲运动、火箭、航天技术的发展和宇宙航行。
冲量法与齐次化原理

冲量法与齐次化原理
吴长泰
【期刊名称】《大学数学》
【年(卷),期】1989(000)001
【摘要】§1 引言本文运用冲量法把强迫振动的问题化为自由振动的问题并进行了详细的推导和论证,这有益于理解这些内容、搞好教学工作。
【总页数】3页(P16-18)
【作者】吴长泰
【作者单位】华侨大学应用数学系
【正文语种】中文
【中图分类】O1
【相关文献】
1.冲量定理法在求解非齐次波动方程中的应用 [J], 张梦梨
2.常微分方程中的齐次化原理与Green函数 [J], 阿布力米提·阿布都热衣木
3.利用齐次化原理求解常系数非齐次线性方程初值问题 [J], 樊龙;李高
4.冲量定理在解非齐次线性常微分方程中的应用 [J], 丁禄保
5.用齐次化原理解线性非齐次微分方程 [J], 盛佩君
因版权原因,仅展示原文概要,查看原文内容请购买。
山东大学工科研究生数学物理方法class14第2节非齐次振动方程和输运方程.ppt
na(t
l
)
cos
nx
l
系数 An ( ), Bn ( ) 由初始条件确定,把上式代入初始条件:
A0 (
)
n1
An (
) cos
nx
l
0
17
B0 (
)
n1
Bn (
)
nx
l
cos
nx
l
A cos
nx
l
s in x
右边的 Acos nx sinx 也是傅里叶余弦级数,只有一个单项n=1
l
两边比较系数可得:
系数,上述两边都是傅立叶余弦级数,由于基本函数族 cos nx
l 的正交性,等式两边对应于同一基本函数的傅立叶系数必相等:
T0 (0) 0
1 l
l
( )d
0
T0(0) 0
1 l
l
( )d
0
Tn (0) n
Tn(0) n
2 l
2 l
l ( ) cos n
0
l
l
(
)
cos
n
0
l
d
同时,量纲分析也可以侧面证明此法是正确的!
(2)冲量定理法的数学验证 即要验证通过积分得到的解u(x,t)是原非齐次振动方程定
解问题的解。
首先来验证边界条件:v |x0 0, v |xl 0 故有:
t
t
u |x0 0 v |x0 d 0, u |xl 0 v |xl d 0
边界条件
初始位移: u |t0
t
0 f (x, ) (t )d
其中 F(x, ) (t )d 为作用在很短的时间区间 ( , d ) 9
数学物理方法中无界区域的定解问题
无界区域的定解问题前言:对于定义在整个空间或半空间的偏微分方程的定解问题,原则上可以用分离变量法求解,另外还有一些专门的方法来解决这类问题,本章就讨论这些解法。
含两个自变量x 和y 的二阶线性偏微分方程的一般形式为:),(22122222122211y x f cu y ub x u b yu a y x u a x u a =+∂∂+∂∂+∂∂+∂∂∂+∂∂其中11a ,12a ,22a ,1b ,2b 和c 都只是x 和y 的函数。
根据判别式2211212a a a -=∆符号的不同可如下来划分偏微分方程的类型⎪⎩⎪⎨⎧<-=∆=-=∆>-=∆椭圆型,抛物型,双曲型,000221121222112122211212a a a a a a a a a 定解问题: ⎪⎪⎩⎪⎪⎨⎧>>∞<<-∞=∂∂==∂∂-∂∂==)0,0,(,)(),(),(),(00022222a t x x t x u t x t x u x u a t u t t ψϕ由于111=a ,012=a ,222a a -=,则0)(222211212>=-->-=∆a a a a a 。
令at x t x +=),(ζ,at x t x -=),(η,),(),(ηζv t x u =,可化为:02=∂∂∂ηζv通解为:)()(),(21ηζηζf f v +=,其中)(1ζf ,)(2ηf 为任意函数。
通解为:)()(),(21at x f at x f t x u -++= 代入初始条件可得:⎪⎩⎪⎨⎧-+=-⇒='-'⇒=∂∂=+⇒=⎰==)()()(1)()()()()()(),()()()()(),(0201212102100x f x f d a x f x f x x f a x f a x t x u tx x f x f x t x u x x t t ζζψψψϕϕ由上式可推出:⎪⎩⎪⎨⎧---=-++=⎰⎰)]()([21)(21)(21)()]()([21)(21)(21)(020*******00x f x f d a x x f x f x f d a x x f x x x x ζζψϕζζψϕ 特解: ⎰+-+-++=atx at x d aat x at x t x u ζζψϕϕ)(21)]()([21),(达朗贝尔公式的物理意义: 初位移)(x ϕ分成两半,各为2)(x ϕ,经过时间t 分别向左移动at 变成2)(at x +ϕ,向右移动at 变成2)(at x -ϕ,移动的速度均为a ,弦的总位移),(t x u 为2)(at x +ϕ和2)(at x -ϕ的叠加。
用常数变易法求解非齐次线性偏微分方程
的解,得特征值问题,
( ) + ( ) = 0, 0 < < (0) = ( ) = 0
(10)2018.8(下) 知识 237知识 第 16 期
求解特征值为
( )=
22
= 2 ( = 1,2,3 … ) , 特 征 函 数 为
( = 1,2,3 … ) 。利用常数变易法,设
原模型有解形如 常微分方程初值问题, 求解得,
( )+ 2 ( )=
(0) = , (0) =
其中, , , 是 ( ), ( ), ( , ) 关于 ( ) 的傅
里叶系数。利用拉普拉斯变换法或常数变易法,求解该常微分
方程得,
( )=
+1
故(6),(2),(7)的解为,
+1
()
0
(−)
∞
( , )= [
+1
=1
3 总结与举例
+1
()
0
(− ) ] ()
变易法,设原模型有解形如
∞
( , )=
()
(2 + 1) 2
。
=1
代入得到常微分方程初值问题, 得,
(
,
)
=
32
3
1
−2
∞ (−1) +1 (2 + 1)3
=1
−(2
+1)2 42
2
2
(2 + 1) 2
(作者单位:中国地质大学(北京)数理学院)
. All Rights Reserved.
。代入得到
( )=
+
+
()
0
故固定的有界弦强迫振动模型的形式解为:
冲量定理法
§37.1 冲量定理法
定解问题2000(,)||0||0tt xx x x l t t t u a u f x t u u u u ====⎧-=⎪==⎨⎪==⎩
(,)(,)/f x t F x t ρ= 作用于弦上单位长度单位质量上的力。
力(,)f x t 持续作用于整个系统,对(,)u x t 的影响是0—t 时刻的作用的累加,注意到: 0(,)(,)()t
f x t f x t d τδττ=-⎰。
考虑到泛定方程和定解条件的线性性,则方程的解应是由瞬时力引起的振动的累加。
即0(,)(,,)t
u x t v x t d ττ=⎰(这里要求初始条件为零,因为我们只考虑了时刻t=0之后的瞬时力的作用)其中:
22(,)()00t 00000(,)()(,)()||0||0||0||0tt xx tt xx f x t x x l x x l t t t t t t v a v f x t v a v f x t v v v v v v v v τδτττττδττδτ-=====-===-=-⎧⎧-=--=-⎪⎪==⇒==⎨⎨⎪⎪====⎩⎩
由于直到时刻仍未起作用对泛定方程从00ττ-→+积分有2000||(,,)0(,)2
t t xx v v a v x f x τττττ+---+⨯=即 0|(,)t t v f x ττ=+=考虑到(,)()f x t t δτ-从0t τ=+开始不再起作用,因此
若将初始时刻取0t τ=+,则有()
2000000,,tt xx x x l t t t a f x ττυυυυυυτ===+=+⎧-=⎪⎪==⎨⎪==⎪⎩ 求出该自由振动的(),,x t υτ,然后再进行叠加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于是
lA π a(t −τ ) nπ v= sin ωτ sin cos x l l πa
于是
u = ∫ v(x, t;τ )dτ
0
t
lA π a(t −τ ) nπ =∫ sin ωτ sin cos x dτ 0π a l l π at π a ω sin − sin ω t lA nπ l l cos x = 2 2 π a πa l 2 ω − 2 l
Tn ' (0) = 0
nπ a 2 Tn"(t) + ( ) Tn (t) = fn (t) l Tn (0) = 0 2 l nπξ fn (t) = ∫ f (ξ , t) sin dξ Tn ' (0) = 0 l 0 l
nπ a Tn (t) = ∫0 fn (τ )sin l (t −τ ) dτ nπ a l
t
T0 ' (t) = Asin ω t
n=0
T0 ' (t) = Asin ω t T0 (0) = 0
nπ a 2 Tn ' (t) + ( ) Tn (t) = 0 l
n≠0
Tn (0) = 0
T0 (t) = A
ω
(1− cosω t)
u(x, t) =
Tn (t) = 0
A
ω
(1− cosω t)
τ τ +∆τ t
t
f(x,t)
τ τ +∆τ t
u
(τ ) tt (τ )
t
−a u
x=0 x=l t =τ
2 (τ ) xx
=0
u
=0 =0
u u
(τ )
(τ )
=0
= f (x,τ )∆τ (τ ) (τ ) (0 < x < l τ < t < τ + dτ ) 显然 u = u (x, t,τ , ∆τ ) u
t
nπ a nπ u(x, t) = ∑[ ∫0 fn (τ )sin l (t −τ ) dτ ]sin l x n=1 nπ a
∞
l
t
例:求定解问题: 求定解问题: 泛定方程
ut − a uxx = Asin ω t
2
边界条件
ux (x, t) x=0 = 0 ux (x, t) x=l = 0
∞
初始
vt
t =τ
= Acos
πx
l
sin ωτ
A0 = 0
∞
A =0 n
vt
有
t =τ
nπ a nπ πx = B0 + ∑Bn cos x = Acos sin ωτ l l l n=1 lA B0 = 0 B1 = sin ωτ πa Bn = 0 (n = 2,3,L) lA π a(t −τ ) nπ v= sin ωτ sin cos x l l πa
令
u (x, t,τ , ∆τ ) = v(x, t,τ )∆τ
vtt − a vxx = 0
2
(τ )
(0 < x < l t > τ )
v x=0 = 0 (t > τ ) v x=l = 0
u(x, t) = lim
t
v t =τ = 0 vt
(τ )
(0 < x < l)
t =τ
= f (x,τ )
∞
nπ u(x, t) = ∑Tn (t) cos x 将 l n=0 代入初始条件 u(x, t) t =0 = 0 ∞ nπ 有 ∑Tn (0) cos l x = 0 n=1
∞
Tn (0) = 0 T0 (0) = 0
n=0 n≠0
nπ a 2 ) Tn (t) = 0 Tn ' (t) + ( l
I
u (x, t) t =0 = ϕ(x) I ut (x, t) t =0 =ψ (x)
I
u − a u = f (x, t)
II tt 2 II xx
u (x, t) x=0 = 0 II u (x, t) x=l = 0
II
u (x, t) t =0 = 0 II ut (x, t) t =0 = 0
考虑定解问题: 考虑定解问题:
utt − a uxx = f (x, t)
2
u(x, t) x=0 = 0 u(x, t) x=l = 0
∞
u(x, t) t =0 = ϕ(x) ut (x, t) t =0 =ψ (x)
nπ u(x, t) = ∑Tn (t) sin x l n=1 nπ a 2 Tn"(t) + ( ) Tn (t) = fn (t) l
X "+λ X = 0 X (0) = 0 X (l) = 0
nπ Xn = Cn sin x l
2、Tn(t) 的解 、
nπ Xn = Cn sin x l
nπ u(x, t) = ∑Tn (t) sin x l n=1
∞
仿照常数变易法, 仿照常数变易法,令
2
泛定方程
utt − a uxx = f (x, t)
2 l nπ ξ Tn (0) = ∫ ϕ(ξ ) sin dξ l 0 l
2 l nπ ξ Tn ' (0) = ∫ ψ (ξ ) sin dξ l 0 l
另一方法:考虑线性叠加法 另一方法: 令 有
I tt 2 I xx
u = u +u
I
II
u −a u = 0
u (x, t) x=0 = 0 I u (x, t) x=l = 0
初始 条件
u(x, t) t =0 = 0 ut (x, t) t =0 = 0
(0 < x < l t > 0)
解: 用冲量法, 用冲量法,上述定解问题变为 v 的定解问题
vtt − a vxx = 0
2
vx x=0 = 0 vx x=l = 0
v t =τ = 0
vt t =τ = Acos sin ωτ l (0 < x < l τ < t < τ + dτ )
f(x,t)
u(x, t) t =0 = 0 ut (x, t) t =0 = 0
f(x,t)表示单位长度、 f(x,t)表示单位长度、 表示单位长度 单位质量作用力
1
ρ
F(x, t)
f(x, τ)∆τ 表示 ∆τ 内的冲量
这个冲量使得系统的速度有 一定的增量,即 f(x, τ) ∆τ , 一定的增量,
∞
将
∞
nπ u(x, t) = ∑Tn (t) sin x l n=1
代入泛定方程
nπ a 2 nπ ∑[Tn"(t) + ( l ) Tn (t)]sin l x = f (x, t) n=1
nπ a 2 nπ ∑[Tn"(t) + ( l ) Tn (t)]sin l x = f (x, t) n=1
∞
nπ a 2 ) Tn (t) = fn (t) Tn"(t) + ( l
其中
2 l nπξ fn (t) = ∫ f (ξ , t) sin dξ l 0 l
将
2 l nπξ fn (t) = ∫ f (ξ , t) sin dξ l 0 l ∞ nπ u(x, t) = ∑Tn (t) sin x 代入初始条件 l n=1 ∞ nπ u(x, t) t =0 = 0 ∑Tn (0) sin l x = 0 n=1 ut (x, t) = 0 ∞ nπ ∑Tn ' (0) sin l x = 0 n=1 Tn (0) = 0
(τ ) t t =τ
现在,我们把在时间∆τ 现在, 内得到的速度增量看成 内得到的速度增量看成 速度 是 t= τ 瞬时集中得到 的,而在∆τ 的其余时 间里没有冲量的作用, 间里没有冲量的作用, 即认为在这段时间内没 有力的作用,故方程是 有力的作用, 齐次的。 t= τ 时的集 齐次的。 中速度可置于 “初始 ” 条件中, 得到的关于瞬 条件中, 时力引起的振动的定解 方程为: 方程为:
II
(二)、冲量定理法 (T2 sin α2 −T sin α1 + Fdx = ρ dxutt ) )、冲量定理法 1 考虑强迫弦振动定解问题: 考虑强迫弦振动定解问题:
utt − a uxx = f (x, t)
2
u(x, t) x=0 = 0 u(x, t) x=l = 0
f (x, t) =
弦两端固定
初始条件
用式
u(x, t) = X (x)T (t)
代入方程,不能分离变量 代入方程,
一、Fourier级数法 Fourier级数法 1、齐次解
2
对应齐次方程为
泛定方程
utt − a uxx = 0
u(x, t) x=0 = 0 边界条件 u(x, t) x=l = 0 分离变量得本征方程 u(x, t) = X (x)T (t)
§8.2 非齐次振动方程和输运方程(齐次边界条件) 8.2 非齐次振动方程和输运方程(齐次边界条件) 考虑定解问题: 考虑定解问题: 泛定方程 边界条件
utt − a uxx = f (x, t)
2
u(x, t) x=0 = 0 u(x, t) x=l = 0 u(x, t) t =0 = 0 ut (x, t) t =0 = 0
u(x, t) t =0 = 0 nπ 解: Xn = Cn cos x l ∞ nπ u(x, t) = ∑Tn (t) cos x 代入泛定方程有 l n=0 ∞ nπ a 2 nπ ∑[Tn ' (t) + ( l ) Tn (t)]cos l x = Asin ω t n=0
