纯剪切切应力互等定理剪切胡克定律
合集下载
切应力互等定理ShearingStressTheorem
Ip
2dA
A
Wt
IP
max
（1）实心圆截面 (Solid circular section) d
dA 2π(d )
Ip
2dA
A
d
2 2π 3d
πd 4
0
32
Wt
Ip
max
（2）空心圆截面
πd 4 / 32 πd 3 d / 2 16
(Hollow circular
D section)
A
22 kN·m
64.84MPa [ ]
+
2max
T2 Wt 2
T2 πd23 / 16
14 103 π(0.13 ) / 16
B
C
_
14 kN·m
71.3MPa [ ]
因此，该轴满足强度要求.
(Torsion)
例题4 实心圆轴１和空心圆轴２（图a、b）材料、扭转力偶矩 m
和长度 l 均相等，最大切应力也相等.若空心圆轴的内外径之比
在 AD 段内
B1 C
T3 Me4 6370 N m Me2 T1
注意：若假设扭矩为正值，则
Me1 3 Me4
A 3D
T3
Me4
扭矩的实际符号与计算符号相同. 作出扭矩图 从图可见，最大扭矩
在 CA段内.
6370 N·m
+ _
Tmax 9560 N m
4780 N·m 9560 N·m
(Torsion)
切应变为 2
切应变为 0
(Torsion)
§3-4 圆轴扭转的应力
变
观察变形
形
提出假设
几
何
关
13-2广义胡克定律与变形能-材料力学
1 m 形状改变
3 m
②形状改变比能：
证明在：
' 1
1
m
,
' 2
2
m
,
' 3
3
m
作用下，体积没有变化 。
3(1
2)
1'
' 2
' 3
E
3
1 2
E
(1'
' 2
' 3
)
1 2
E
[(1
m
)
(
2
1
该单元体所储存的应变
能为：
3
U
1 2
(
1e1
2
e
2
3e
3
)dxdydz
②比能：
u
U V
1 2
(
1e1
2e2
3e
3
)
③代入虎克定律：
u
1 2E
[12
2 2
2 3
2
(1
2
2
3
31
)]
（二）、体积改变比能 ut 与形状改变比能 u x
1.有关概念：
三、复杂应力状态下的变形比能 （一）、总应变比能
1.有关概念： ①应变能(变形能)：伴随弹性体的变 形而储存在弹性体的能量。用U表示；
材料力学第三章 扭转
n
250
横截面上的最大切应力为
max
T Wt
T (D4 d 4)
16D
16 0.55573000 Pa 19.2MPa [ ] 50MPa (0.554 0.34 )
满足强度要求。
跟踪训练 7.机车变速箱第II轴如图所示，轴所传递的功率为
p 5.5KW,转速n 200r / min，材料为45钢，
（3）主动轮放在两从动轮之间可使最大扭矩取最小值
B
A
C
Me2
Nm
M e1
Me3
4220
2810
本章小结
1.外力偶矩的计算 内力的计算——扭矩图
P M e 9549 n (N m)
2.圆轴扭转切应力公式的建立
τρ
Tρ Ip
强度条件的应用
max
Tmax Wt
[ ]
刚度条件的应用
' max
T
180 [']
（3）主动轮和从动轮应如何安排才比较合理。
再根据平衡条件，可得 Me1 Me2 Me3 (2810 4220)N m 7030N m
所作扭矩图如右图
（1）试确定AB段的直径d1和BC段的直径d2。
根据强度条件确定AB直径d1
AB
TAB Wt
16TAB
d12
[ ]
根据刚度条件确定AB直径d1
mB
(a)
1
350 2
C
1
2
T1
11463
446
A
D
3
mB
(b)
(c) mB
mC
T2
mC
mA T3
mD
T1 350N m 350 1 350 2
工程力学第六章杆件的应力
DB
D
t´
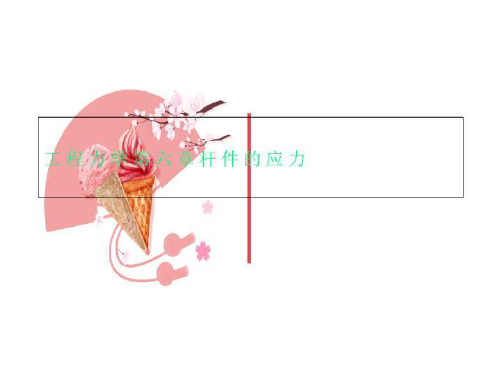
上述变形现象表明：微体ABCD既无轴向正应变，也无横 向正应变，只是相邻横截面ab与cd之间发生相对错动，即产生 剪切变形；而且，沿圆周方向所有的剪切变形相同。由于管壁 很薄，故可近似认为管的内外变形相同，则可认为仅存在的垂
直于半径方向的切应力t沿圆周大小不变。
26
剪应力在截面上均匀分布，方向垂直于半径 与周线相切
5
B A su
A s B
平均线应变：
e u
s
线应变:
e lim u
s0 s
6
dy
dx
角应变 g
7
练习
8
一 拉压胡克定律
实验表明，在比例极限范围内，正应力与 正应变成正比，即
引入比例系数E，则
胡克定律 比例系数E称为弹性模量
9
二 剪切胡克定律
g
在纯剪状态下，单元体 相对两侧面将发生微小 的相对错动，原来互相 垂直的两个棱边的夹角 改变了一个微量g。
t dx
t t
29
• 剪应力互等定理 : 在相互垂直的两个平面上, 剪应力一定成对出现，其数值相等，方向同 时指向或背离两平面的交线。
30
6-5 圆轴扭转时横截面上的应力
一、扭转切应力的一般公式
从三方面考虑：变形几何关系 物理关系 静力学关系
31
1.变形几何关系
观察到下列现象:
(1)各圆周线的形状、大小以及两圆周线间的距离没有 变化
一 基本假设
用较易变形的材料制成的矩形截面等直梁作纯弯曲试验:
纯弯曲：梁横截面上 只有弯矩而无剪力时 的弯曲。
46
• 观察到以下变形现象: • (1)aa、bb弯成弧线，aa缩短，bb伸长
工程力学C-第9章 扭转
T 1000 0.04 3 Wp (1 0.54 )
max
84.88MPa
16
min max
10 42.44MPa 20
§9-6 圆轴扭转破坏与强度条件
一、圆轴扭转时的破坏现象
脆性材料扭转破坏
沿450螺旋曲面被拉断
塑性材料扭转破坏
沿横截面被剪断
二、圆轴扭转的强度条件
D 1.192 得： d1
2
D2
A空 A实 4
(1 0.8 )
d1
4
2
0.512
例6 传动轴AB传递的功率为 P =7.5kW， 转速n=360r/min。轴的 AC 段为实心圆轴， CB 段为空心圆轴。已知：D =30mm，d =20mm。试计算AC段的最大剪应力，CB 段横截面上内、外缘处的剪应力。 解： （1）计算外力偶矩和扭矩 P AC段最大剪应力： m 9549 198.9N m n Tmax D 1max 37.5 10 6 Pa 37.5MPa T m 198.9N m I P1 2 （2）计算极惯性矩 CB段上内外缘的剪应力： D 4 T d 8 4 AC段：I P1 7.95 10 m 2内 I P2 2 32 D 4 4 31.2 10 6 Pa 31.2MPa (1 ) CB段：I P 2 T D 32 2外 8 4 6.38 10 m I P2 2 46.8 10 6 Pa 46.8MPa （3）计算应力
A
ρτ
ρ
dA T
d 2 G ρ dA T dx A
令：
ρ dA I P
2 A
极惯性矩
d G IP T dx
max
84.88MPa
16
min max
10 42.44MPa 20
§9-6 圆轴扭转破坏与强度条件
一、圆轴扭转时的破坏现象
脆性材料扭转破坏
沿450螺旋曲面被拉断
塑性材料扭转破坏
沿横截面被剪断
二、圆轴扭转的强度条件
D 1.192 得： d1
2
D2
A空 A实 4
(1 0.8 )
d1
4
2
0.512
例6 传动轴AB传递的功率为 P =7.5kW， 转速n=360r/min。轴的 AC 段为实心圆轴， CB 段为空心圆轴。已知：D =30mm，d =20mm。试计算AC段的最大剪应力，CB 段横截面上内、外缘处的剪应力。 解： （1）计算外力偶矩和扭矩 P AC段最大剪应力： m 9549 198.9N m n Tmax D 1max 37.5 10 6 Pa 37.5MPa T m 198.9N m I P1 2 （2）计算极惯性矩 CB段上内外缘的剪应力： D 4 T d 8 4 AC段：I P1 7.95 10 m 2内 I P2 2 32 D 4 4 31.2 10 6 Pa 31.2MPa (1 ) CB段：I P 2 T D 32 2外 8 4 6.38 10 m I P2 2 46.8 10 6 Pa 46.8MPa （3）计算应力
A
ρτ
ρ
dA T
d 2 G ρ dA T dx A
令：
ρ dA I P
2 A
极惯性矩
d G IP T dx
材料力学复习笔记
材料力学（一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。
为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。
【重点、难点】重点考察基本概念，掌握截面法求轴力、作轴力图的方法，截面上应力的计算。
【内容讲解】一、基本概念强度—-构件在外力作用下，抵抗破坏的能力，以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形.刚度-—构件在外力作用下，抵抗变形的能力，以保证在规定的使用条件下不会产生过分的变形。
稳定性--构件在外力作用下，保持原有平衡形式的能力，以保证在规定的使用条件下,不会产生失稳现象。
杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件，称为杆件或简称杆。
根据轴线与横截面的特征，杆件可分为直杆与曲杆，等截面杆与变截面杆。
二、材料力学的基本假设工程实际中的构件所用的材料多种多样，为便于理论分析，根据它们的主要性质对其作如下假设。
(一）连续性假设-—假设在构件所占有的空间内均毫无空隙地充满了物质，即认为是密实的。
这样，构件内的一些几何量，力学量(如应力、位移）均可用坐标的连续函数表示,并可采用无限小的数学分析方法。
（二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。
按此假设通过试样所测得的材料性能，可用于构件内的任何部位（包括单元体).(三)各向同性假设——沿各个方向均具有相同力学性能。
具有该性质的材料，称为各向同性材料。
综上所述，在材料力学中,一般将实际材料构件，看作是连续、均匀和各向同性的可变形固体。
三、外力内力与截面法（一）外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力，例如载荷与约束力.外力可分为:表面力与体积力;分布力与集中力；静载荷与动载荷等.当构件（杆件)承受一般载荷作用时，可将载荷向三个坐标平面（三个平面均通过杆的轴线，其中两个平面为形心主惯性平面）内分解，使之变为两个平面载荷和一个扭转力偶作用情况.在小变形的情况下，三个坐标平面内的力互相独立，即一个坐标平面的载荷只引起这一坐标平面内的内力分量,而不会引起另一坐标平面内的内力分量。
工程力学(静力学与材料力学)第二篇第九章扭转
P = Mω
2πn P ×10 = M × 60
3
M N⋅m = 9549
P kW nr / min
例: P＝5 kW, n=1450 r/min, 则 ＝
5 kW M＝9549× (N⋅m) = 32.9 N⋅m 1450r/min
单辉祖:材料力学教程 8
扭矩与扭矩图
扭矩
扭矩定义－矢量方向垂直于横截面的内力偶矩， 扭矩定义－矢量方向垂直于横截面的内力偶矩， 并用 T 表示 符号规定－按右手螺旋法则将扭矩用矢量表示， 符号规定－按右手螺旋法则将扭矩用矢量表示， 矢量方向与横截面外法线方向一致 的扭矩为正， 的扭矩为正，反之为负
极惯性矩与抗扭截面系数
空心圆截面
dA=2πρdρ
Ip = ρ dA =
2
∫A
∫
D/ 2
d/2
ρ2 ⋅ 2πρ dρ
πD4 α= d Ip = 1−α4 D 32 Ip πD3 W= = 1−α4 p D 16 2
(
)
(
)
实心圆截面
πd4 Ip = 32
单辉祖:材料力学教程
πd 3 W= p 16
24
γ ≈tanγ =1.0×10−3rad
τ = Gγ
τ = (80×109 Pa)(1.0×10−3 rad) = 80 MPa
注意： 虽很小， 很大， 注意：γ 虽很小，但 G 很大，切应力 τ 不小
单辉祖:材料力学教程 18
例 3-2 一薄壁圆管，平均半径为 0，壁厚为δ，长度为 ， 一薄壁圆管，平均半径为R 长度为l， 横截面上的扭矩为T，切变模量为G， 横截面上的扭矩为 ，切变模量为 ，试求扭转角ϕ。
解：1. 扭矩分析
材料力学(第五版)扭转切应力
(
)
d 2 = 0.8D2=43 mm π 2 d1 A1 452 4 = = =1.95 2 2 A2 π D2 1 α2 53.7 1 0.8 2 4
(
)
(
)
空心圆轴能比实心圆轴更充分的使用材料。 空心圆轴能比实心圆轴更充分的使用材料。
理由？ 理由？
空心圆轴能比实心圆轴更充分的使用材料的原因： 空心圆轴能比实心圆轴更充分的使用材料的原因：
(
)
五、圆轴扭转时的强度条件 圆轴扭转时的最大切应力不能超过 材料的许用切应力
τmax
T ax m = ≤ [τ] W p
例题 d2
A
B
C
d1 mA mB mC
已知： 已知：阶梯轴尺寸如图 mA = 22 kN m, mB = 36 kN m, mC =14 kN m
[τ]= 80 MPa
d1 =120 m , d2 =100m m m
对于钢材: 对于钢材:
200 G= = 80GPa 2(1+ 0.25)
§3-4 圆轴扭转时的应力
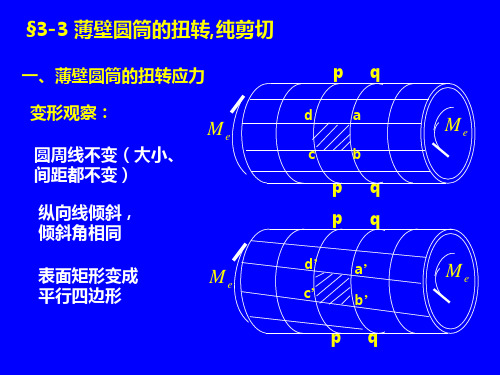
一、变形几何条件 1、变形观察： 变形观察：
圆周线不变（大小、 圆周线不变（大小、 间距都不变） 间距都不变） 纵向线倾斜， 纵向线倾斜， 倾斜角相同 表面矩形变成 平行四边形
薄壁圆筒由于壁很薄， 薄壁圆筒由于壁很薄，表 面变形即为内部变形。 面变形即为内部变形。
圆轴内部任意一点的切应力 圆轴内部任意一点的切应力 τ ρ 与该点到圆心的距离ρ 与该点到圆心的距离ρ成正比
d τ ρ = Gρ dx
(c)
ρ =0
τρ = 0
ρ=R
τ ρ =τ max
d = GR dx
三、静力关系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
料相同，试校核其强度。
解：1.板的拉伸强度
2.板的剪切强度
Fs F 50103 A 4a 4 0.08 0.01
15.7106 15.7MPa [ ]
FN F A (b 2d )
50 103
(0.15 2 0.017) 0.01
43.1106 43.1MPa [ ]
15
§3-1 连接件的强度计算
d
b
a
3.铆钉的剪切强度
Fs A
4F 2πd 2
2F πd 2
2 50103 π 0.0172
110106 110MPa [ ]
4.板和铆钉的挤压强度
bs
Fbs Abs
F
2d
9
§3-1 连接件的强度计算
Fs F
A lb
bs
Fbs Abs
F cb
10
§3-1 连接件的强度计算
4F
d 2
F 2
dh
Fs A
4F
d 2
bs
Fbs Abs
F dh
2
为充分利用材
料切应力和挤压应
力均达到最大值。
27
§3-2 纯剪切 切应力互等定理 剪切胡克定律
三.剪切胡克定律
G
其中，比例常数G 称为切变模量。常用单位GPa
28
§3-2 纯剪切 切应力互等定理 剪切胡克定律
对各向同性材料可以证明，弹性常数E、G、 μ存在关系
G E
2(1 )
表明3个常数间相互不独立的
29
§3-3 剪切应变能
第三章 剪 切
§3-1 连接件的强度计算 §3-2 纯剪切 切应力互等定理
剪切胡克定律 §3-3 剪切应变能
1
§3-1 连接件的强度计算
1.剪切的工程实例
2
§3-1 连接件的强度计算
3
§3-1 连接件的强度计算
4
§3-1 连接件的强度计算
铆钉连接
螺栓连接
销轴连接
5
§3-1 连接件的强度计算
50103 2 0.017 0.01
147106 147MPa [ bs ]
结论：强度足够。
16
§3-1 连接件的强度计算
17
§3-1 连接件的强度计算
18
§3-1 连接件的强度计算
19
§3-1 连接件的强度计算
20
§3-1 连接件的强度计算
2 2 F2 80 50 40
Me
外力功：W
1 2
M e
Me
φ
φ
Me 所作功全部转变为剪切应变能Vs 存储在薄壁圆管内
Vs
W
1 2
M e
单位体积应变能称为应变能密度：
vs
Vs V
M e / 2 2 r l
1 2
M er 2 r 2 l
进一步简化得：vs
1
2
2
2G
30
F2
50 2
kN
21
§3-1 连接件的强度计算
22
§3-1 连接件的强度计算
4.其它连接件的实用计算方法 焊缝剪切计算
有效剪切面
23
§3-1 连接件的强度计算
4.其它连接件的实用计算方法
胶粘缝的计算
F
F
不同的粘接方式
F
F
[ ] [ ]
24
§3-2 纯剪切 切应力互等定理 剪切胡克定律
A
常由实验方法确定
7
§3-1 连接件的强度计算
3.挤压的实用计算
F
Fbs
假设应力在挤压面上应力是均
匀分布的
F
得实用挤压应力公式
bs
Fbs Abs
*注意挤压面面积的计算
Fbs
Abs d
挤压强度条件：
bs
Fbs Abs
bs
bs 常由实验方法确定
8
§3-1 连接件的强度计算
平键连接
焊接连接
榫连接
6
§3-1 连接件的强度计算
2.剪切的实用计算
F
剪切受力特点：作用在构件两侧 面上的外力合力大小相等、方向 F 相反且作用线很近。
变形特点：位于两力之间的截面 发生相对错动。
假设切应力在剪切面（m-m 截面）上是均匀分布的
得切应力计算公式： Fs
A
切应力强度条件： Fs
即：
4F
d 2
F 2dh
d 8h
11
§3-1 连接件的强度计算
1.要使被冲钢板冲断；
F
d
b
d F
b
2.同时要使冲头强度足够。
4F
d2
d
4F
4F
d
F
b
12
§3-1 连接件的强度计算
4.连接件失效形式
剪断 (连接件与连接板) 挤压破坏 连接板拉断
切应力强度条件： Fs
A
挤压强度条件：
bs
Fbs Abs
bs
塑性材料： 0.5 0.7 bs 1.5 2.5
脆性材料： 0.8 1.0 bs 0.9 1.5
13
§3-1 连接件的强度计算
l
F
F
F
F
F
F
d
(a)
(b)
F
F
(c)
(d)
(e)
14
§3-1 连接件的强度计算
d
b
a
图示接头，受轴向力F 作 用。已知F =50kN，b=150mm， δ=10mm，d=17mm，a=80mm， [σ]=160MPa，[τ]=120MPa， [σbs]=320MPa，铆钉和板的材
一、纯剪切
r
M
2 r 2
Me
A
rdA
2 0
r rd 2
r 2
l
r
l
r
纯剪切：单元体截面上只有切应力
而无正应力作用，这种应力状态叫
做纯剪切应力状态。
25
§3-2 纯剪切 切应力互等定理 剪切胡克定律
二.切应力互等定理
26
§3-2 纯剪切 切应力互等定理 剪切胡克定律
解：1.板的拉伸强度
2.板的剪切强度
Fs F 50103 A 4a 4 0.08 0.01
15.7106 15.7MPa [ ]
FN F A (b 2d )
50 103
(0.15 2 0.017) 0.01
43.1106 43.1MPa [ ]
15
§3-1 连接件的强度计算
d
b
a
3.铆钉的剪切强度
Fs A
4F 2πd 2
2F πd 2
2 50103 π 0.0172
110106 110MPa [ ]
4.板和铆钉的挤压强度
bs
Fbs Abs
F
2d
9
§3-1 连接件的强度计算
Fs F
A lb
bs
Fbs Abs
F cb
10
§3-1 连接件的强度计算
4F
d 2
F 2
dh
Fs A
4F
d 2
bs
Fbs Abs
F dh
2
为充分利用材
料切应力和挤压应
力均达到最大值。
27
§3-2 纯剪切 切应力互等定理 剪切胡克定律
三.剪切胡克定律
G
其中，比例常数G 称为切变模量。常用单位GPa
28
§3-2 纯剪切 切应力互等定理 剪切胡克定律
对各向同性材料可以证明，弹性常数E、G、 μ存在关系
G E
2(1 )
表明3个常数间相互不独立的
29
§3-3 剪切应变能
第三章 剪 切
§3-1 连接件的强度计算 §3-2 纯剪切 切应力互等定理
剪切胡克定律 §3-3 剪切应变能
1
§3-1 连接件的强度计算
1.剪切的工程实例
2
§3-1 连接件的强度计算
3
§3-1 连接件的强度计算
4
§3-1 连接件的强度计算
铆钉连接
螺栓连接
销轴连接
5
§3-1 连接件的强度计算
50103 2 0.017 0.01
147106 147MPa [ bs ]
结论：强度足够。
16
§3-1 连接件的强度计算
17
§3-1 连接件的强度计算
18
§3-1 连接件的强度计算
19
§3-1 连接件的强度计算
20
§3-1 连接件的强度计算
2 2 F2 80 50 40
Me
外力功：W
1 2
M e
Me
φ
φ
Me 所作功全部转变为剪切应变能Vs 存储在薄壁圆管内
Vs
W
1 2
M e
单位体积应变能称为应变能密度：
vs
Vs V
M e / 2 2 r l
1 2
M er 2 r 2 l
进一步简化得：vs
1
2
2
2G
30
F2
50 2
kN
21
§3-1 连接件的强度计算
22
§3-1 连接件的强度计算
4.其它连接件的实用计算方法 焊缝剪切计算
有效剪切面
23
§3-1 连接件的强度计算
4.其它连接件的实用计算方法
胶粘缝的计算
F
F
不同的粘接方式
F
F
[ ] [ ]
24
§3-2 纯剪切 切应力互等定理 剪切胡克定律
A
常由实验方法确定
7
§3-1 连接件的强度计算
3.挤压的实用计算
F
Fbs
假设应力在挤压面上应力是均
匀分布的
F
得实用挤压应力公式
bs
Fbs Abs
*注意挤压面面积的计算
Fbs
Abs d
挤压强度条件：
bs
Fbs Abs
bs
bs 常由实验方法确定
8
§3-1 连接件的强度计算
平键连接
焊接连接
榫连接
6
§3-1 连接件的强度计算
2.剪切的实用计算
F
剪切受力特点：作用在构件两侧 面上的外力合力大小相等、方向 F 相反且作用线很近。
变形特点：位于两力之间的截面 发生相对错动。
假设切应力在剪切面（m-m 截面）上是均匀分布的
得切应力计算公式： Fs
A
切应力强度条件： Fs
即：
4F
d 2
F 2dh
d 8h
11
§3-1 连接件的强度计算
1.要使被冲钢板冲断；
F
d
b
d F
b
2.同时要使冲头强度足够。
4F
d2
d
4F
4F
d
F
b
12
§3-1 连接件的强度计算
4.连接件失效形式
剪断 (连接件与连接板) 挤压破坏 连接板拉断
切应力强度条件： Fs
A
挤压强度条件：
bs
Fbs Abs
bs
塑性材料： 0.5 0.7 bs 1.5 2.5
脆性材料： 0.8 1.0 bs 0.9 1.5
13
§3-1 连接件的强度计算
l
F
F
F
F
F
F
d
(a)
(b)
F
F
(c)
(d)
(e)
14
§3-1 连接件的强度计算
d
b
a
图示接头，受轴向力F 作 用。已知F =50kN，b=150mm， δ=10mm，d=17mm，a=80mm， [σ]=160MPa，[τ]=120MPa， [σbs]=320MPa，铆钉和板的材
一、纯剪切
r
M
2 r 2
Me
A
rdA
2 0
r rd 2
r 2
l
r
l
r
纯剪切：单元体截面上只有切应力
而无正应力作用，这种应力状态叫
做纯剪切应力状态。
25
§3-2 纯剪切 切应力互等定理 剪切胡克定律
二.切应力互等定理
26
§3-2 纯剪切 切应力互等定理 剪切胡克定律