《线段的垂直平分线》典型例题
线段的垂直平分线经典习题及答(精.选)

线段的垂直平分线一、选择题(共8小题)1、如图,在△ABC 中,分别以点A 和点B 为圆心,大于的21AB 的长为半径画孤,两弧相交于点M ,N ,作直线MN , 交BC 于点D ,连接AD .若△ADC 的周长为10,AB=7,则△ABC 的周长为( ) A 、7 B 、 14 C 、17 D 、20第1题 第2题 第3题2、如图,在Rt △ACB 中,∠C=90°,BE 平分∠ABC ,ED 垂直平分AB 于D .若AC=9,则AE 的值是( )A 、6B 、4C 、6D 、43、如图,直线CD 是线段AB 的垂直平分线,P 为直线CD 上的一点,已知线段PA=5,则线段PB 的长度为( )A 、6B 、5C 、4D 、34、如图,等腰△ABC 中,AB=AC ,∠A=20°.线段AB 的垂直平分线交AB 于D ,交AC 于E ,连接BE ,则∠CBE 等于( )A 、80°B 、70°C 、60°D 、50°第4题 第 5题 第6题 5、如图,直线CP 是AB 的中垂线且交AB 于P ,其中AP=2CP .甲、乙两人想在AB 上取两点D 、E ,使得AD=DC=CE=EB ,其作法如下:(甲)作∠ACP 、∠BCP 之角平分线,分别交AB 于D 、E ,则D 、E 即为所求;(乙)作AC 、BC 之中垂线,分别交AB 于D 、E ,则D 、E 即为所求.对于甲、乙两人的作法,下列判断何者正确( )A 、两人都正确B 、两人都错误C 、甲正确,乙错误D 、甲错误,乙正确6、如图,在Rt △ABC 中,∠C=90°,∠B=30°.AB 的垂直平分线DE 交AB 于点D ,交BC 于点E ,则下列结论不正确的是( )A 、AE=BEB 、AC=BEC 、CE=DED 、∠CAE=∠B7、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )A 、△ABC 的三条中线的交点B 、△ABC 三边的中垂线的交点 C 、△ABC 三条角平分线的交点D 、△ABC 三条高所在直线的交点第7题 第8题8、如图,AC=AD ,BC=BD ,则有( ) A 、AB 垂直平分CD B 、CD 垂直平分AB C 、AB 与CD 互相垂直平分 D 、CD 平分∠ACB二、填空题(共12小题)9、如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3.则CE长为_________.第9题第10题第11题10、如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=_________度.11如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为_________°.12、如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC 的周长之差为12,则线段DE的长为_________.第12题第13题第14题第15题13、如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB=_________度.14、如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC=_________度.15、如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是_________度.16、如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有_________个不同的四边形.第16题第17题第18题17已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________.18、如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=1/2∠DAC;④△ABC是正三角形.请写出正确结论的序号_________(把你认为正确结论的序号都填上)19、如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为_________cm.20、在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是_________°.三、解答题(共6小题)21、如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.22、如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.1、如图,在△ABC中,分别以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为()A、7B、14C、17D、20考点:线段垂直平分线的性质。
线段的垂直平分线典型例题
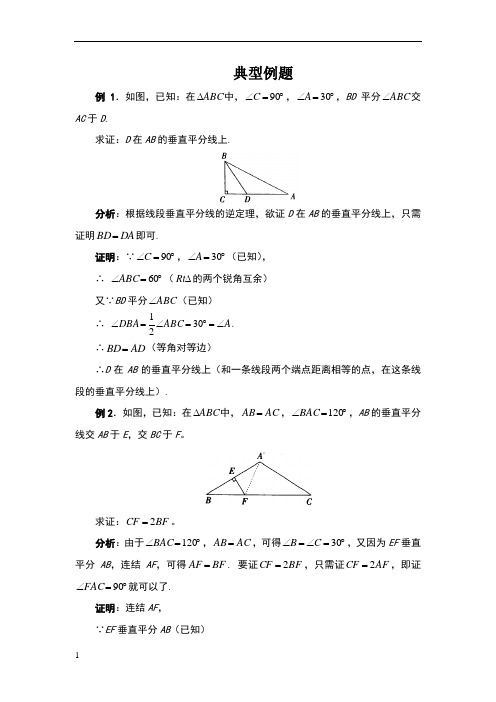
典型例题例1.如图,已知:在ABC ∆中,︒=∠90C ,︒=∠30A ,BD 平分ABC ∠交AC 于D .求证:D 在AB 的垂直平分线上.分析:根据线段垂直平分线的逆定理,欲证D 在AB 的垂直平分线上,只需证明DA BD =即可.证明:∵︒=∠90C ,︒=∠30A (已知),∴ ︒=∠60ABC (∆Rt 的两个锐角互余)又∵BD 平分ABC ∠(已知)∴ A ABC DBA ∠=︒=∠=∠3021. ∴AD BD =(等角对等边)∴D 在AB 的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上).例2.如图,已知:在ABC ∆中,AC AB =,︒=∠120BAC ,AB 的垂直平分线交AB 于E ,交BC 于F 。
求证:BF CF 2=。
分析:由于︒=∠120BAC ,AC AB =,可得︒=∠=∠30C B ,又因为EF 垂直平分AB ,连结AF ,可得BF AF =. 要证BF CF 2=,只需证AF CF 2=,即证︒=∠90FAC 就可以了.证明:连结AF ,∵EF 垂直平分AB (已知)∴FB FA =(线段垂直平分线上的点和这条线段两端点的距离相等)∴B FAB ∠=∠(等边对等角)∵AC AB =(已知),∴C B ∠=∠(等边对等角)又∵︒=∠120BAC (已知),∴︒=∠=∠30C B (三角形内角和定理)∴︒=∠30BAF∴︒=∠90FAC∴FA FC 2=(直角三角形中,︒30角所对的直角边等于斜边的一半)∴FB FC 2=说明:线段的垂直平分线的定理与逆定理都由三角形的全等证得,初学者往往不习惯直接使用绝无仅有垂直平分线的定理与逆定理,容易舍近求远,由三角形全等来证题.例3.如图,已知:AD 平分BAC ∠,EF 垂直平分AD ,交BC 延长线于F ,连结AF 。
求证:CAF B ∠=∠。
分析:B ∠与CAF ∠不在同一个三角形中,又B ∠,CAF ∠所在的两个三角形不全等,所以欲证CAF B ∠=∠,不能利用等腰三角形或全等三角形的性质. 那么注意到EF 垂直平分AD ,可得FD FA =,因此ADF FAD ∠=∠,又因为CAD FAD CAF ∠-∠=∠,BAD ADF B ∠-∠=∠,而BAD CAD ∠=∠,所以可证明B CAF ∠=∠.证明:∵EF 垂直平分AD (已知),∴FDFA=(线段垂直平分线上的点和这条线段的两端点的距离相等).∴ADF∠(等边对等角)=FAD∠∵BAD=∠(三角形的一个外角等于和它不相邻的两个内角的∠ADFB∠-和),=∠∠,FADCADCAF∠-又CADBAD∠∠(角平分线定义),=∴CAF∠B∠=说明:运用线段的垂直平分线的定理或逆定理,能使问题简化,如本例题中,EF垂直平分AD,可以直接有结论FDFA=,不必再去证明两个三角形全等.例4.如图,已知直线l和点A,点B,在直线l上求作一点P,使PBPA=.分析:假设P点已经作出,则由PBPA=,那么根据“到线段两端点距离相等的点在这条线段的垂直平分线上”可知,点P在线段AB的垂直平分线上. 而点P又在直线l上,则点P应是AB的垂直平分线与垂线l的交点。
专题1.5 线段的垂直平分线-重难点题型(举一反三)(北师大版)(解析版)

专题1.5 线段的垂直平分线-重难点题型【北师大版】【题型1 利用线段垂直平分线的性质求线段】【例1】(2021春•莱阳市期末)如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC 的延长线于点E,若BF=6,CF=2,则AC的长为 .【分析】根据线段垂直平分线的性质得到AF=BF=6,结合图形计算即可.【解答】解:∵ED垂直平分AB,BF=6,∴AF=BF=6,∵CF=2,∴AC=AF+CF=6+2=8,故答案为:8.【变式1-1】(2020秋•长宁区期末)如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.△ABC的周长为19,△ACE的周长为13,则AB的长为( )A.3B.6C.12D.16【分析】根据线段垂直平分线的性质和等腰三角形的性质即可得到结论.【解答】解:∵AB的垂直平分线交AB于点D,∴AE=BE,∵△ACE的周长=AC+AE+CE=AC+BC=13,△ABC的周长=AC+BC+AB=19,∴AB=△ABC的周长﹣△ACE的周长=19﹣13=6,故选:B.【变式1-2】(2021春•高新区期末)如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE、AF,若△AEF的周长为2,则BC的长是( )A.2B.3C.4D.无法确定【分析】根据线段的垂直平分线的性质得到EA=EB,FA=FC,根据三角形的周长公式即可求出BC.【解答】解:∵AB的垂直平分线交BC于点E,∴EA=EB,∵AC的垂直平分线交BC于点F.∴FA=FC,∴BC=BE+EF+FC=AE+EF+FC=△AEF的周长=2.故选:A.【变式1-3】(2021春•乾县期末)如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )A.13B.14C.15D.16【分析】利用线段的垂直平分线的性质以及线段的和差关系即可解决问题.【解答】解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,∴EB=EA,GB=GC,∵△BEG周长为16,∴EB+GB+EG=16,∴EA+GC+EG=16,∴GA+EG+EG+EG+EC=16,∴AC+2EG=16,∵EG=1,∴AC=14,故选:B.【题型2 利用线段垂直平分线的性质求角度】【例2】(2021•越秀区模拟)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )A.70°B.75°C.80°D.85°【分析】设∠CAD=2x°,∠BAD=5x°,根据线段垂直平分线的性质得出BD=AD,求出∠BAD=∠B =5x°,根据直角三角形的性质得出∠CAB+∠B=90°,求出x,再求出∠B和∠BAD,根据三角形的外角性质求出答案即可.【解答】解:设∠CAD=2x°,∠BAD=5x°,∵AB 的垂直平分线是DE ,∴BD =AD ,∴∠BAD =∠B ,即∠B =5x °,∵∠C =90°,∴∠CAB +∠B =90°,∴2x +5x +5x =90,解得:x =152,即∠B =∠BAD =(752)°,∴∠ADC =∠B +∠BAD =(752)°+(752)°=75°,故选:B .【变式2-1】(2021春•建平县期末)如图,已知△ABC 中,∠B =50°,P 为△ABC 内一点,过点P 的直线MN 分别交AB ,BC 于点M 、N .若M 在PA 的中垂线上,N 在PC 的中垂线上,则∠APC 的度数为( )A .100°B .105°C .115°D .120°【分析】根据三角形的内角和得到∠BAC +∠ACB =130°,根据线段的垂直平分线的性质得到AM =PM ,PN =CN ,由等腰三角形的性质得到∠MAP =∠APM ,∠CPN =∠PCN ,进而得出∠MAP +∠PCN =∠PAC +∠ACP =12×130°=65°,根据三角形内角和定理计算即可.【解答】解:∵∠ABC =50°,∴∠BAC+∠ACB=130°,∵M在PA的中垂线上,N在PC的中垂线上,∴AM=PM,PN=CN,∴∠MAP=∠APM,∠CPN=∠PCN,∵∠APC=180°﹣∠APM﹣∠CPN=180°﹣∠PAC﹣∠ACP,∴∠MAP+∠PCN=∠PAC+∠ACP=12×130°=65°,∴∠APC=115°,故选:C.【变式2-2】(2021•市南区一模)如图,在△ABC中,点O是边AB和AC的垂直平分线OD、OE的交点,若∠BOC=100°,则这两条垂直平分线相交所成锐角α的度数为( )A.40°B.45°C.50°D.80°【分析】连接OA,根据线段垂直平分线的性质得出OA=OB=OC,根据等腰三角形的性质得出∠BAO=∠ABO,∠OBC=∠OCB,∠CAO=∠ACO,求出∠BAC,再根据四边形的内角和等于360°求出答案即可.【解答】解:连接OA,∵点O是边AB和AC的垂直平分线OD、OE的交点,∴OA=OB,OB=OC,∴OA=OB=OC,∴∠BAO=∠ABO,∠OBC=∠OCB,∠CAO=∠ACO,∵∠BOC=100°,∴∠OBC+∠OCB=180°﹣100°=80°,∴∠ABO+∠BAO+∠OCA+∠OAC=180°﹣(∠OBC+∠OCB)=100°,∴2(∠BAO+∠CAO)=100°,即∠BAC=50°,∵点O是边AB和AC的垂直平分线OD、OE的交点,∴∠ODA=∠OEA=90°,∴∠DOE=360°﹣90°﹣90°﹣50°=130°,∴∠α=180°﹣130°=50°,故选:C.【变式2-3】(2021春•安国市期末)如图,在△ABC中,I是三角形角平分线的交点,O是三边垂直平分线的交点,连接AI,BI,AO,BO,若∠AOB=140°,则∠AIB的大小为( )A.160°B.140°C.130°D.125°【分析】连接CO,根据三角形内角和定理求出∠OAB+∠OBA,根据线段垂直平分线的性质得到OA=OC,OB=OC,进而得到∠OCA=∠OAC,∠OCB=∠OBC,求出∠CAB+∠CBA,根据角平分线的定义、三角形内角和定理计算,得到答案.【解答】解:连接CO,∵∠AOB=140°,∴∠OAB+∠OBA=180°﹣140°=40°,∴∠OCA+∠OAC+∠OCB+∠OBC=180°﹣40°=140°,∵O是三边垂直平分线的交点,∴OA=OC,OB=OC,∴∠OCA=∠OAC,∠OCB=∠OBC,∴∠OCA+∠OCB=70°,∴∠CAB+∠CBA=180°﹣70°=110°,∵AI平分∠BAC,BI平分∠ABC,∴∠IAB=12∠CAB,∠IBA=12∠CBA,∴∠IAB+∠IBA=12(∠CAB+∠CBA)=55°,∴∠AIB=180°﹣55°=125°,故选:D.【题型3 线段垂直平分线的性质的应用】【例3】(2020秋•甘井子区期末)如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )A.A处B.B处C.C处D.D处【分析】根据线段垂直平分线的性质得出即可.【解答】解:根据作图可知:EF是线段MN的垂直平分线,所以EF上的点到M、N的距离相等,即发射塔应该建在C处,故选:C.【变式3-1】(2020秋•偃师市期末)元旦联欢会上,同学们玩抢凳子游戏,在与A、B、C三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将A、B、C三名同学所在位置看作△ABC的三个顶点,那么凳子应该放在△ABC的( )A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边垂直平分线的交点【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边垂直平分线的交点上.【解答】解:∵三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,∴凳子应放在△ABC的三条垂直平分线的交点最合适.故选:D.【变式3-2】(2021春•宁阳县期末)如图,若记北京为A地,莫斯科为B地,雅典为C地,若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )A.三边垂直平分线的交点B.三边中线的交点C.三条角平分线的交点D.三边上高的交点【分析】根据线段的垂直平分线的性质解答即可.【解答】解:∵中转仓到A、B两地的距离相等,∴中转仓的位置应选在边AB的垂直平分线上,同理,中转仓的位置应选在边AC、BC的垂直平分线上,∵中转仓到A、B、C三地的距离相等,∴中转仓的位置应选在三边垂直平分线的交点上,故选:A.【变式3-3】(2021春•惠来县期末)《中共中央国务院关于促进农民增加收入若干政策的意见》中提出“进一步精简乡镇机构和财政供养人员,积极稳妥地调整乡镇建制,有条件的可实行并村”.《中共中央国务院关于积极发展现代农业扎实推进社会主义新农村建设的若干意见》中明确提出“治理农村人居环境,搞好村庄治理规划和试点,节约农村建设用地”.以上两个政策出台后,山东陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )A.三条边的垂直平分线的交点处B.三个角的平分线的交点处C.三角形三条高线的交点处D.三角形三条中线的交点处【分析】根据性的垂直平分线的性质解答即可.【解答】解:∵电动车充电桩到三个出口的距离都相等,∴充电桩应该在三条边的垂直平分线的交点处,故选:A.【题型4 线段垂直平分线的性质综合】【例4】(2021春•平顶山期中)如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN 交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:(1)AE=DE;(2)EM=EC.【分析】(1)根据线段垂直平分线的性质得到DA=DB,得到∠DAB=∠B=22.5°,根据三角形的外角性质得到∠ADE=∠DAB+∠B=45°,根据等腰三角形的性质证明;(2)证明△MDE≌△CAE,根据全等三角形的性质证明结论.【解答】证明:(1)∵DN是AB的垂直平分线,∴DA=DB,∴∠DAB=∠B=22.5°,∴∠ADE=∠DAB+∠B=45°,∵AE⊥BC,∴∠AED=90°,∴∠DAE=∠ADE=45°,∴AE=DE;(2)∵DF⊥AC,AE⊥BC,∴∠MDE=∠CAE,在△MDE和△CAE中,∠MDE=∠CAEDE=AE,∠DEM=∠AEC∴△MDE≌△CAE(ASA),∴EM=EC.【变式4-1】(2021春•高州市期末)如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A 作BC的平行线AF交CD于F,延长AB、DC交于点E.求证:(1)AC平分∠EAF;(2)∠FAD=∠E.【分析】(1)根据线段垂直平分线的性质得到BA=BC,根据等腰三角形的性质得到∠BAC=∠BCA,根据平行线的性质得到∠CAF=∠BCA,等量代换证明结论;(2)根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质得到∠DAC=∠DCA,再根据三角形的外角性质证明即可.【解答】证明:(1)∵BD所在的直线垂直平分线段AC,∴BA=BC,∴∠BAC=∠BCA,∵BC∥AF,∴∠CAF=∠BCA,∴∠CAF=∠BAC,即AC平分∠EAF;(2)∵BD所在的直线垂直平分线段AC,∴DA=DC,∴∠DAC=∠DCA,∵∠DCA是△ACE的一个外角,∴∠DCA=∠E+∠EAC,∴∠E+∠EAC=∠FAD+∠CAF,∵∠CAF=∠EAC,∴∠FAD=∠E.【变式4-2】(2021春•莲湖区期末)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.(1)若△ABC的周长为18,△DEC的周长为6,求AB的长.(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.【分析】(1)根据线段垂直平分线的性质得到AB=BE,AD=DE,根据三角形的周长公式计算,得到答案;(2)根据三角形内角和定理求出∠BAC,证明△BAD≌△BED,根据全等三角形的性质得到∠BED=∠BAC=105°,根据三角形的外角性质计算即可.【解答】解:(1)∵BD是线段AE的垂直平分线,∴AB=BE,AD=DE,∵△ABC的周长为18,△DEC的周长为6,∴AB+BE+EC+CD+AD=18,CD+EC+DE=CD+CE+AD=6,∴AB+BE=18﹣6=12,∴AB=6;(2)∵∠ABC=30°,∠C=45°,∴∠BAC=180°﹣30°﹣45°=105°,在△BAD和△BED中,BA=BEBD=BD,DA=DE∴△BAD≌△BED(SSS),∴∠BED=∠BAC=105°,∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.【变式4-3】(2020秋•渑池县期末)在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.(1)AD与BD的数量关系为 .(2)求BC的长.(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.【分析】(1)根据线段的垂直平分线上的点到线段的两个端点的距离相等解答;(2)根据线段垂直平分线的性质得到EA=EC,根据三角形的周长公式计算即可;(3)根据线段垂直平分线的性质得到OB=OC,根据三角形的周长公式计算,得到答案.【解答】解:(1)∵l1是线段AB的垂直平分线,∴AD=BD,故答案为:AD=BD;(2)∵l2是线段AC的垂直平分线,∴EA=EC,∵△ADE的周长为6,∴AD+DE+AE=6,∴BD+DE+EC=6,即BC=6;(3)∵l1是线段AB的垂直平分线,∴OA=OB,∵l2是线段AC的垂直平分线,OA=OC,∴OB=OC,∵△OBC的周长为16,BC=6,∴OB+OC=10,∴OA=OB=OC=5.【题型5 线段垂直平分线的判定】【例5】(2021秋•仪征市月考)如图.AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.【分析】由AB=AC,MB=MC,根据线段垂直平分线的判定定理,可得点A在BC的垂直平分线上,点M在BC的垂直平分线上,又由两点确定一条直线,可得直线AM是线段BC的垂直平分线.【解答】证明:∵AB=AC,∴点A在BC的垂直平分线上,∵BM=CM,∴点M在BC的垂直平分线上,∴直线AM是BC的垂直平分线.【变式5-1】(2021•沭阳县校级开学)如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.【分析】根据全等三角形的判定定理证明△BQP≌△CRQ,得到QP=QR,根据线段的垂直平分线的判定证明结论.【解答】证明:连接PQ,在△BQP和△CRQ中,PB=QC∠B=∠C,QB=RC∴△BQP≌△CRQ,∴QP=QR,∴点Q在PR的垂直平分线上.【变式5-2】(2021秋•博白县期末)如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.(1)若∠BAC=50°,求∠EDA的度数;(2)求证:直线AD是线段CE的垂直平分线.【分析】(1)在Rt△ADE中,求出∠EAD即可解决问题;(2)只要证明AE=AC,利用等腰三角形的性质即可证明;【解答】(1)解:∵∠BAC=50°,AD平分∠BAC,∴∠EAD=12∠BAC=25°,∵DE⊥AB,∴∠AED=90°,∴∠EDA=90°﹣25°=65°.(2)证明∵DE⊥AB,∴∠AED=90°=∠ACB,又∵AD平分∠BAC,∴∠DAE=∠DAC,∵AD=AD,∴△AED≌△ACD,∴AE=AC,∵AD平分∠BAC,∴AD⊥CE,AD平分线段EC,即直线AD是线段CE的垂直平分线.【变式5-3】(2020秋•雁塔区校级期末)如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.求证:线段BF垂直平分线段AD.【分析】根据三角形内角和定理求出∠C=∠BAM,根据角平分线的定义求出∠DAM=∠CAD,求出∠BAD=∠ADB,得出△ABD是等腰三角形,根据等腰三角形的性质得出即可.【解答】证明:∵∠BAC=90°,∴∠ABC+∠C=90°,∵AM⊥BC,∴∠AMB=90°,∴∠ABC+∠BAM=90°,∴∠C=∠BAM,∵AD平分∠MAC,∴∠MAD=∠CAD,∴∠BAM+∠MAD=∠C+∠CAD,∵∠ADB=∠C+∠CAD,∴∠BAD=∠ADB,∴AB=BD,∵BE平分∠ABC,∴BF⊥AD,AF=FD,即线段BF垂直平分线段AD.【题型6 线段垂直平分线的作法】【例6】(2020秋•盘龙区期末)如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于12 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE 的面积比△CDB的面积小5,则△ADE的面积为( )A.5B.4C.3D.2【分析】根据题意得到MN是线段AB的垂直平分线,进而得到点D是AB的中点,根据三角形的面积公式计算,得到答案.【解答】解:由尺规作图可知,MN是线段AB的垂直平分线,∴点D是AB的中点,∴S△ADC =S△BDC,∵S△BDC ﹣S△CDE=5,∴S△ADC ﹣S△CDE=5,即△ADE的面积为5,故选:A.【变式6-1】(2021春•碑林区校级期中)在△ABC中,∠C>∠B、请用尺规作图法,在AB上找一点P,使∠PCB=∠B.(保留作图痕迹,不写作法.)【分析】作线段BC的垂直平分线交AB于点P,点P即为所求作.【解答】解:如图,点P即为所求作.【变式6-2】(2021•碑林区校级模拟)尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)【分析】作线段BC的垂直平分线交AC于点D,连接BD即可.【解答】解:如图,点D即为所求作.【变式6-3】(2021春•长安区期末)尺规作图(保留作图痕迹,不写作法):如图,直线m表示一条公路,A、B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.(1)请用尺规在图上找出点P;(2)请说明你作图的依据.【分析】(1)作线段AB的垂直平分线MN交直线m于点P,连接PA,PB.(2)根据线段的垂直平分线的性质解决问题即可.【解答】解:(1)如图,点P即为所求.(2)∵MN垂直平分线段AB,∴PA=PB(线段的垂直平分线上的点到线段的两个端点的距离相等).。
线段的垂直平分线、角平分线经典习题及答案

3.线段的垂直平分线4.角平分线例1: (1)在厶ABC中,AB= AC, AB的垂直平分线交AB于N,交BC的延长线于M / A= 40°, 求/ NMB的大小(2) 如果将(1)中/ A的度数改为70°,其余条件不变,再求/ NMB的大小(3) 你发现有什么样的规律性?试证明之•(4) 将(1)中的/ A改为钝角,对这个问题规律性的认识是否需要加以修改ANC例2:在厶ABC中,AB的中垂线DE交AC于F,垂足为D,若AC=6 BC=4求厶BCF的周长。
例3:如图所示,AC=AD BC=BD AB与CD相交于点巳求证:直线AB是线段CD的垂直平分线。
例4 :如图所示,在△ ABC中,AB=AC / BAC=12°, D F分别为AB AC的中点,,E、G 在BC上, BC=15cm 求EG的长度。
例5::如图所示,Rt△ ABC中,,D是AB上一点,BD=BC过D作AB的垂线交AC于点E,CD交BE于点F。
求证:BE垂直平分CD例6::在"ABC中,点O是AC边上一动点,过点O作直线MIN/ BC与/ACB的角平分线交于点E,与/ ACB的外角平分线交于点F,求证:OE=OFA例7、如图所示,AB>AC的平分线与BC的垂直平分线相交于D,自D作于E,,求证:BE=CF答案如下:例1:解:(1)vZ B= 1/2 (180° - / A) =70°,二/ M=20 ;(2)同理得,/ M=35 ;(3)规律是:/ M的大小为/ A大小的一半,即:AB的垂直平分线与底边BC所夹的锐角等于/ A的一半.证明:设/ A=a,则有/ B= 1/2 (180° - a), / M=90 - 1/2 (180° - a) = 1/2 a.( 4)改为钝角后规律成立.上述规律为:等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半.例2:解:连接BF,由线段的垂直平分线的性质可得,FB= FA又因为AOAF+CF =6,所以BF+C M6A BCF的周长=BC+CF+*4+6= 10例3:证明:因为AC=AD所以A在线段CD的垂直平分线上又因为BC=BD所以B在线段CD的垂直平分线上所以直线AB是线段CD的垂直平分线例4:解:作AF U BC于H, HC=15/2•••等腰•••/ ACB=/ ABC=30••• AC=2EC根号3EC=5根号3••• F为AC中点••• FC=5/2根号3••• FGL AC••• CG=5同理, BE=5••• EG=5例5:证明:v DEL AB,/ ACB= 90•••/ BDE=Z ACB= 90••• BD= BC, BE^ BE•••△BCE^A BDE (HL)•••/ CBE=Z DBE••• BF= BF•••△BCF^A BDF (SAS •••/ BFC=Z BFD CF= DF vZ BFC+Z BFD= 180 •••/ BFC=Z BFD= 90••• BE! CD••• BE垂直平分CD例6:解:v MN/ BC,•Z OEC=Z BCE,Z OFC=Z GCF,又已知CE平分Z BCO CF平分Z GCO •Z OCE Z BCE Z OC F^Z GCF•Z OCE=Z OEC Z OCF=Z OFC•EO=COFO=CO•EO=FO.例7 :证明:连接DC DBv点D在BC的垂直平分线上•DB=DCv D在Z BAC的平分线上•DE=DFvZ DFC=Z DEB•△DCF^A DEB•CF=BE。
《垂直平分线》练习题(含答案)
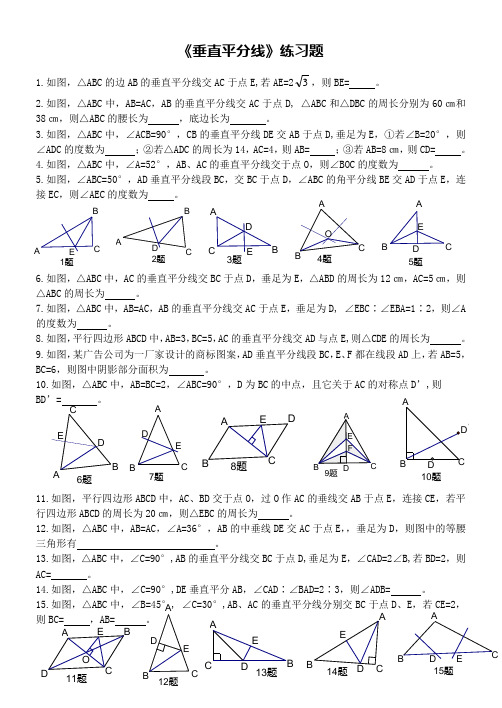
1题A B E C 2题D A B C 3题D AB EC 4题A B C O 5题D A BE C 11题D A B E C O 12题D A B E C 13题D A B E C 14题D A B E C 15题D A B E C6题D A BE C 8题D A B E C 7题D A B E C 10题'9题《垂直平分线》练习题1.如图,△ABC 的边AB 的垂直平分线交AC 于点E,若AE=23,则BE= 。
2.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点D, △ABC 和△DBC 的周长分别为60㎝和38㎝,则△ABC 的腰长为 ,底边长为 。
3.如图,△ABC 中,∠ACB=90°,CB 的垂直平分线DE 交AB 于点D,垂足为E ,①若∠B=20°,则∠ADC 的度数为 ;②若△ADC 的周长为14,AC=4,则AB= ;③若AB=8㎝,则CD= 。
4.如图,△ABC 中,∠A=52°,AB 、AC 的垂直平分线交于点O ,则∠BOC 的度数为 。
5.如图,∠ABC=50°,AD 垂直平分线段BC ,交BC 于点D ,∠ABC 的角平分线BE 交AD 于点E ,连接EC ,则∠AEC 的度数为 。
6.如图,△ABC 中,AC 的垂直平分线交BC 于点D ,垂足为E ,△ABD 的周长为12㎝,AC=5㎝,则△ABC 的周长为 。
7.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点E ,垂足为D, ∠EBC ∶∠EBA=1∶2,则∠A 的度数为 。
8.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 与点E,则△CDE 的周长为 。
9.如图,某广告公司为一厂家设计的商标图案,AD 垂直平分线段BC ,E 、F 都在线段AD 上,若AB=5,BC=6,则图中阴影部分面积为 。
10.如图,△ABC 中,AB=BC=2,∠ABC=90°,D 为BC 的中点,且它关于AC 的对称点D ’,则 BD ’= 。
专题04 线段的垂直平分线(七大题型+跟踪训练)(解析版)
专题04线段的垂直平分线(七大题型+跟踪训练)A.13A .31︒B .62︒【答案】C 【分析】根据线段垂直平分线的性质得到角平分线的定义、三角形内角和定理计算即可.【解析】解:∵在ABC 中,∠∴,BD DC BE CE ==,在DBE 和DCE △中,BD CD BE CE DE DE =⎧⎪=⎨⎪=⎩∴()DBE DCE SSS ≌,∴31DBE C ∠=∠=︒,∴223162ABC DBE ∠=∠=⨯︒=︒,∴180180316287A C ABC ∠=︒-∠-∠=︒-︒-︒=︒.故选:C【点睛】本题考查的是线段的垂直平分线的性质和全等三角形的性质和判定,掌握线段的垂直平分线上的点到线段的两个端点的距离相等.4.如图,在ABC 中,AB 的垂直平分线交AB 于点E ,交AC 于点D .若10cm AC =,7cm BD =,求CD 的长.【答案】3cm【分析】根据垂直平分线的性质得到BD AD =,再做差即可.【解析】DE 垂直平分线AB ,AD BD ∴=,CD AC AD AC BD ∴=-=-,又10cm AC = ,7cm BD =,1073cm CD ∴=-=.【点睛】本题考查利用垂直平分线性质进行边长计算,须注意线段位置,正确的计算是解题的关键.5.如图,ABC 中,=AB AC ,=50A ∠︒,AB 的垂直平分线DE 分别交AC 、AB 于点D 、E .求CBD ∠的度数.【答案】15︒【分析】根据等腰三角形的性质求出==65ABC C ∠∠︒,根据线段垂直平分线的性质得到AD BD =,得到答案.【解析】解: =AB AC ,=50A ∠︒,∴==65ABC C ∠∠︒,DE 垂直平分AB ,∴AD BD =,∴==50ABD A ∠∠︒,∴==6550=15CBD ABC ABD ∠∠-∠︒-︒︒【点睛】本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.题型2:线段垂直平分线的性质的应用6.如图,A ,B ,C 表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在()A .AC ,BC 两边高线的交点处B .AC ,BC 两边中线的交点处C .AC ,BC 两边垂直平分线的交点处D .∠A ,∠B 两内角平分线的交点处【答案】C 【分析】要求到三个小区的距离相等,首先思考到A 小区、C 小区距离相等,根据线段垂直平分线定理的逆定理知满足条件的点在线段AC 的垂直平分线上,同理到B 小区、C 小区的距离相等的点在线段BC 的垂直平分线上,于是到三个小区的距离相等的点应是其交点,答案可得.【解析】解:A ,B ,C 表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在AC ,BC 两边垂直平分线的交点处.故选:C .【点睛】本题主要考查线段的垂直平分线定理的逆定理:到一条线段的两端距离相等的点在这条线段的垂直平分线上,掌握线段垂直平分线的性质与判定是解题的关键.7.如图,DE 是△ABC 中AC 边上的垂直平分线,如果BC =8cm ,AB =10cm ,则△EBC 的周长为()A .16cmB .18cmC .26cmD .28cm【答案】B 【分析】由DE 是△ABC 中AC 边上的垂直平分线,可得AE =CE ,继而可得△EBC 的周长=BC +AB .【解析】解:∵DE 是△ABC 中AC 边上的垂直平分线,∴AE =CE ,∵BC =8cm ,AB =10cm ,∴△EBC 的周长为:BC +BE +CE =BC +BE +AE =BC +AB =8+10=18(cm ).故选:B .【点睛】本题考查了线段垂直平分线的性质.注意掌握数形结合思想与转化思想的应用.8.如图,在ABC 中,PM 、QN 分别是线段AB 、AC 的垂直平分线,若100BC =,则APQ △的周长是()A .120B .50C .100D .90【答案】C 【分析】利用垂直平分线的性质得PA PB =,QA QC =,等量代换即可求解.【解析】解:∵PM 、QN 分别是线段AB 、AC 的垂直平分线,∴PA PB =,QA QC =,∴APQ △的周长100PQ QA PA PQ QC PB BC =++=++==.故选C .【点睛】本题考查垂直平分线的性质,解题的关键是掌握线段垂直平分线上的点到线段两端的距离相等.9.如图,DE 为ABC 中AC 边的中垂线,8,10BC AB ==,则EBC 的周长是()A .16B .【答案】B 【分析】利用线垂直平分线的性质得【解析】∵DE 是ABC ∆中∴10AE BE CE BE +=+=∴EBC ∆的周长BE CE =+故选:B .【点睛】本题主要考查了线段垂直平分线的性质;利用线段进行等量代换,把线段进行等效转移是正确解答本题的关键.题型3:线段垂直平分线—尺规作图10.如图,在ABC 中,分别以点MN ,交BC 于点D ,交AB 的长等于()A .3B .∴△ACD 的周长=CD +AD +AC =4+10=14,故选:D .【点睛】此题主要考查了线段垂直平分线的性质和作法,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.12.小明在纸上画出线段AB 及它的中点O ,再过点O 画出与AB 垂直的直线CD ,沿直线CD 将纸对折.发现OA 与OB 重合,则直线CD 称为线段AB 的__________.【答案】垂直平分线/中垂线【分析】根据线段垂直平分线的定义,即可得到直线CD 称为线段AB 的垂直平分线.【解析】解:∵沿直线CD 将纸对折.发现OA 与OB 重合∴OA OB=∵点O 画出与AB 垂直的直线CD∴AB CD⊥∴直线CD 称为线段AB 的垂直平分线故答案为:垂直平分线【点睛】本题考查了线段垂直平分线定义,理解线段垂直平分线的定义是解题的关键.题型4:线段垂直平分线的判定13.在ABC 中,AB AC =,OB OC =,点A 到BC 的距离是6,O 到BC 的距离是4,则AO 等于__________.【答案】2或10【分析】根据AB AC OB OC ==,可判断点A O 、都在BC 的垂直平分线上,然后分两种情况讨论:①当点O 在ABC 的内部时,②当点O 在ABC 的外部时,分别计算AO 即可.【解析】解:∵AB AC OB OC ==,,∴点A O 、都在BC 的垂直平分线上,由题意知,分两种情况:①当点O 在ABC 的内部时,642AO =-=;②当点O 在ABC 的外部时,6410AO =+=;故答案为:2或10.【点睛】本题主要考查了垂直平分线的基本性质.解本题的关键在于分类讨论.14.如图,在ABC 中,BD AC ⊥,垂足为D ,PQ 是BC 边的垂直平分线,交BC 于点Q ,交AC 于点P ,AD PD =.若ABC 的周长是28cm ,6cm CQ =,则+AB AD 的长是_______.【答案】8cm /8厘米【分析】先根据垂直平分线的性质得到AB PB =,CP PB =,212cm BC CQ ==,再求出=16cm AB AC +,=16cm AB AP BP ++,即可求出=8cm AB AD +.【解析】解:∵BD AC ⊥,AD PD =,∴BD 是线段AP 的垂直平分线,∴AB PB =,∵PQ 是BC 边的垂直平分线,∴CP PB =,212cm BC CQ ==,∴=AB PB PC =,∵ABC 的周长是28cm ,∴28cm AB AC BC ++=,∴=2812=16cm AB AC +-,即==16cm AB AP PC AB AP BP ++++,∵AB PB =,AD PD =,∴=8cm AB AD +.故答案为:8cm【点睛】本题考查了线段垂直平分线的定义和性质,熟知线段垂直平分线的性质和定义,结合题意进行线段的转化是解题关键.15.如图,ABC 中,90ACB ∠=︒,AD 平分BAC ∠,DE AB ⊥于E .A .AB 垂直平分CDB .CD 垂直平分ABC .AB 与CD 互相垂直平分D .CD 平分∠ACB【答案】A 【分析】由AC =AD ,BC =BD ,可得点A 在CD 的垂直平分线上,点B 在CD 的垂直平分线上,又由两点确定一条直线,可得AB 是CD 的垂直平分线.【解析】解:∵AC =AD ,BC =BD ,∴点A 在CD 的垂直平分线上,点B 在CD 的垂直平分线上,∴AB 是CD 的垂直平分线.即AB 垂直平分CD .故选:A【点睛】本题考查了垂直平分线的判定定理,熟悉垂直平分线的判定定理是解题的关键.17.已知:如图,AB AC =,DB DC =,点E 在AD 上.求证:EB EC =.【答案】见解析【分析】先根据线段垂直平分线的判定定理说明AE 是线段BC 的垂直平分线,再根据线段垂直平分线的性质定理得出答案.【解析】证明:如图,连接BC ,∵AB AC =,∴点A 是线段BC 垂直平分线上的点.∵DB DC =,∴点D 是线段BC 垂直平分线上的点,∴AE 是线段BC 垂直平分线,∴EB EC =.【点睛】本题主要考查了线段垂直平分线的性质定理和逆定理,灵活的应用定理是解题的关键.18.如图,如图,AD 为三角形ABC 的角平分线,DE AB ⊥于点E ,DF AC ⊥于点F ,连接EF 交AD 于点O .(1)若BE DE =,60BAC ∠=︒,求CDF ∠的度数;(2)写出AD 与EF 的关系,并说明理由.【答案】(1)15︒(2)AD EF ⊥.理由如下【分析】(1)根据三角形内角和可得,C ∠再利用内角和即可得出CDF ∠;(2)证得点A 、D 在线段EF 的垂直平分线上.【解析】(1)解:∵DE AB⊥90BED ∴∠=︒∵BE DE=45B ∴∠=︒∵60BAC ∠=︒180456075C ∴∠=︒-︒-︒=︒∵DF AC⊥90DFC ∴∠=︒∴15CDF ∠=︒(2)解:AD EF ⊥.理由如下:AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,DE DF ∴=.D ∴在线段EF 的垂直平分线上.DE AB ∵⊥,DF AC ⊥,90AED AFD ∴∠=∠=︒,在Rt ADE 和Rt ADF 中,AD AD DE DF=⎧⎨=⎩,()Rt Rt HL ADE ADF ∴ ≌.AE AF ∴=.又EAD FAD ∠=∠ ,AO AO =,AEO AFO ∴ ≌,EO FO ∴=,90AOE AOF ∠=∠=︒,AD ∴是线段EF 的垂直平分线.EF AD ∴⊥.【点睛】本题考查了全等三角形的证明,角平分线的性质.找到Rt AED 和Rt ADF ,通过两个三角形全等,找到各量之间的关系,即可证明.题型6:轴对称中的光线反射问题19.如图,光线自点P 射入,经镜面EF 反射后经过的点是()A.A点B.B点C.C点D.D点【答案】B【分析】利用轴对称变换的性质判断即可.【解析】解:如图,过点P,点B的射线交于一点O,故选:B.【点睛】本题考查轴对称变换的性质,解题的关键是理解题意,灵活运用所学知识解决问题.20.如图,两平面镜α、β的夹角θ∠,入射光线AO平行于β,入射到α上,经两次反射后的出射光线CB ∠等于()平行于α,则θA.30︒B.45︒C.60︒D.90︒【答案】C【分析】利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角,再利用平行的性质把相应的角转移到一个三角形中求解.【解析】如图,由题意得,∠1=∠θ=∠3,由镜面成像原理可知,∠1=∠2,∠3=∠4,∴∠2=∠θ=∠4,∴∠θ=60°,故选C.【点睛】本题考查了镜面对称问题,需注意利用反射的性质、平行的性质把相应的角转移到一个三角形中求解是正确解答本题的关键.21.光线以如图所示的角度α照射到平面镜工上,然后在平面镜I ,Ⅱ之间来回反射.若50α∠=︒,60β∠=︒,则γ∠等于()A .80︒B .70︒C .60︒D .50︒【答案】B 【分析】根据入射光线与水平线的夹角等于反射光线与水平线的夹角将已知转化到三角形中,利用三角形的内角和是180︒求解.【解析】解:如图:由反射规律可知:1α∠=∠,3γ∠=∠,21802β∠=︒-∠,又∵123180∠+∠+∠=︒∴1802180βαγ︒-∠+∠+∠=︒,2βαγ∴∠=∠+∠即26050γ⨯︒=︒+∠1205070γ∴∠=︒-︒=︒.故选:B .【点睛】本题主要考查了三角形内角和定理,掌握入射光线与水平线的夹角等于反射光线与水平线的夹角是解题关键,注意隐含的180︒的关系的使用.题型7:线段的垂直平分线的性质与判定的综合解答题22.如图,在ABC ∆中,111ACB ∠=︒,AC 边上的垂直平分线交AB 于点D ,交AC 边于点E ,连接CD .(1)若15AB =,8BC =,求BCD ∆的周长;(2)若AD BC =,试求A ∠的度数.【答案】(1)23(2)23°【分析】(1)根据线段垂直平分线的性质,可得CD AD =,根据三角形的周长公式,可得答案;(2)根据线段垂直平分线的性质,可得CD AD =,根据等腰三角形的性质,可得B ∠与CDB ∠的关系,根据三角形外角的性质,可得CDB ∠与A ∠的关系,根据三角形内角和定理,可得答案.【解析】(1)解:DE 是AC 的垂直平分线,AD CD ∴=.BCD C BC BD CD BC BD AD BC AB ∆=++=++=+ ,又15AB = ,8BC =,23BCD C ∆∴=;(2)解:AD CD= A ACD ∴∠=∠,设A x ∠=,AD CB = ,CD CB ∴=,CDB CBD ∴∠=∠.CDB ∠ 是ACD ∆的外角,2CDB A ACD x ∴∠=∠+∠=,A ∠、B ∠、ACB ∠是三角形的内角,180A B ACB ∠+∠+∠=︒ ,2111180x x ∴++︒=︒,解得23x =︒23A ∴∠=︒.【点睛】本题考查了线段垂直平分线的性质,(1)利用线段垂直平分线的性质得出DC 与AD 的关系,把三角形的周长转化成AB BC +是解题关键,(2)利用等腰三角形的性质,三角形外角的性质得出B ∠与A∠的关系是解题关键.23.如图,在ABC 中,DE 垂直平分线段BC ,ACD 的周长为18,且4AB AC -=,求AB 、AC 的长各为多少?【答案】11AB =;7AC =【分析】利用中垂线的性质得到ACD 的周长AC AB =+,再结合4AB AC -=,即可得解.【解析】解:∵DE 垂直平分线段BC ,∴DB DC =,又∵ACD 的周长为18,∴18AD DC CA ++=,∴18AD DB CA ++=,即:18AB AC +=,又∵4AB AC -=,∴4AB AC =+,∴418AC AC ++=,∴7AC =,∴7411=+=AB .【点睛】本题考查中垂线的性质.熟练掌握中垂线上的点到线段两端点的距离相等是解题的关键.24.如图在ABC 中,12AB AC ==,15BC =,AC 的垂直平分线交BC 于点D ,垂足为E .(1)求ABD △的周长;(2)若35B ∠=︒,求BAD ∠的度数.【答案】(1)27;(2)75BAD ∠=︒.【分析】(1)根据线段垂直平分线的性质易得到△ABD 的周长=AB +BC ;(2)根据等腰三角形的性质得到35C B CAD ∠=∠=∠=︒,根据三角形外角的性质求出ADB ∠,然后由三角形内角和定理求得BAD ∠的度数.【解析】(1)解:∵DE 是AC 的垂直平分线,∴AD CD =,∵12AB AC ==,15BC =,∴ABD △的周长是:121527AB BD AD AB BD CD AB BC ++=++=+=+=;(2)解:如图,∵35AB AC B =∠=︒,,∴35B C ∠=∠=︒,又∵AD CD =,∴35DAC C ∠=∠=︒,∴353570ADB DAC C ∠=∠+∠=︒+︒=︒,∴180180357075BAD B ADB ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形外角的性质以及三角形内角和定理,熟练掌握线段垂直平分线上的点到线段两端点的距离相等是解题关键.25.如图,在△ABC 中,AB=AC ,AB 的垂直平分线交AB 于N ,交AC 于M .(1)若∠B =65°,则∠NMA 的度数是______;(2)连接MB ,若AB =6cm ,△MBC 的周长是10cm.①求BC 的长;②在直线MN 上是否存在点D ,使由B 、C 、D 三点构成的△DBC 的周长值最小?若存在,标出点D 的位置并求△DBC 的周长最小值;若不存在,说明理由.【答案】(1)40°(2)①BC 的长为4cm ;②存在,标出点D 的位置见解析,△DBC 的周长最小值为10cm【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A 的度数,根据直角三角形两锐角的关系,可得答案;(2)①根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;②根据两点之间线段最短,可得D点与M点的关系,可得DB+DC与AC的关系.(1)解:∵AB=AC,∴∠B=∠C,∴∠A=180°−2∠B,又∵MN垂直平分AB,∴∠NMA=90°−∠A=90°−(180°−2∠B)=2∠B−90°=40°,故答案为:40°;(2)如图:①∵MN垂直平分AB,∴MB=MA,又∵△MBC的周长是10cm,∴AC+BC=10cm,∴BC=4cm.②当点D与点M重合时,△DBC的周长最小,最小值是10cm.【点睛】本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等得出DB=DA.一、单选题AC ,则BC的长为()1.如图所示,线段AB的垂直平分线CD与AB相交于点D,已知3A.4B.3C.2D.1....3.如图,在ABC 中,DE 是AC 的垂直平分线,3cm AE =,ABD △的周长为13cm ,则ABC 的周长是().A .13cmB .16cmC .19cmD .22cm【答案】C 【分析】由已知条件,利用线段的垂直平分线的性质,得到AD =CD ,AC =2AE ,结合周长,进行线段的等量代换可得答案.【解析】解:∵DE 是AC 的垂直平分线,∴AD =CD ,AC =2AE =6cm ,又∵△ABD 的周长=AB +BD +AD =13cm ,∴AB +BD +CD =13cm ,即AB +BC =13cm ,∴△ABC 的周长=AB +BC +AC =13+6=19cm .故选C .【点睛】本题考查线段垂直平分线的性质(垂直平分线上任意一点,到线段两端点的距离相等),进行线段的等量代换是正确解题关键.4.如图所示,直线l 是一条河的河岸,P ,Q 是河同侧的水产的生产基地,现从河岸某点M 处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是()A .B .C .D .【答案】B【分析】根据“将军饮马”模型求最短路线题型,作点P 关于直线l 的对称点P ',连接Q P '交直线l 于点M ,作图即可.【解析】根据“将军饮马”模型求最短路线题型,作点P 关于直线l 的对称点P ',连接Q P '交直线l 于点M ,利用两点之间线段最短和线段垂直平分线的性质作图即可,故选:B .【点睛】本题考查了“将军饮马”模型求最短路线题型,掌握两点之间线段最短和线段垂直平分线的性质作图方法.5.如图,在四边形ABCD 中,AC 垂直平分BD ,垂足为点E ,下列结论不一定成立的是()A .AB AD=B .BCE DCE ∠=∠C .BEC DEC △≌△D .AB BD=【答案】D 【分析】先根据线段垂直平分线的性质得出AB =AD ,BC =BD ,再对各选项进行逐一分析即可.【解析】解:∵AC 垂直平分BD ,∴,,AB AD BC CD BE DE ===,故A 正确,该选项不符合题意;在BEC 和DEC 中,,,,BC DC CE CE BE DE =⎧⎪=⎨⎪=⎩∴()BEC DEC SSS ≌,故C 正确,该选项不符合题意,;∴BCE DCE ∠=∠,故B 正确,该选项不符合题意;;AB 不一定等于BD ,故D 错误,符合题意;故选:D .【点睛】本题考查的是线段垂直平分线的性质和全等三角形的性质和判定,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.6.如图,有A 、B 、C 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在().A .在AC 、BC 两边高线的交点处B .在AC 、BC 两边垂直平分线的交点处C .在AC 、BC 两边中线的交点处D .在∠A 、∠B 两内角平分线的交点处【答案】B 【分析】根据线段垂直平分线的性质即可得出答案.【解析】根据线段垂直平分线上的点到线段两个端点的距离相等,可知超市应建在AC 、BC 两边垂直平分线的交点处,故选:B .【点睛】本题考查线段垂直平分线性质:线段垂直平分线上的点到线段两个端点的距离相等,熟练掌握其性质是解题的关键.7.如图,AD BE ⊥,BD DE =,点E 在线段AC 的垂直平分线上,若6cm AB =,3cm BD =,则DC 的长为()A .3cmB .6cmC .9cmD .12cm【答案】C 【分析】根据线段垂直平分线的性质得到6AE AB ==,EA EC =,结合图形计算,得到答案.【解析】解:AD BE ⊥ ,BD DE =,6AE AB ∴==,点E 在线段AC 的垂直平分线上,EA EC ∴=,9()DC DE EC AB BD cm ∴=+=+=,故选:C .【点睛】本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.A.只有①此时BE +EF 最小.∵AD 是△ABC 的角平分线,∠BAC =50°,∴∠BAD =∠B ′AD =25°,∵BB ′⊥AD ,∴∠AGB =∠AGB ′=90°,在△ABG 和△AB ′G 中,BAG B AG AG AG AGB AGB ∠=∠⎧⎪=⎨⎪∠'=∠⎩',∴△ABG ≌△AB ′G (ASA ),∴BG =B ′G ,AB =AB ′,∴AD 垂直平分BB ′,∴BE =BE ′,在△ABE ′和△AB ′E ′中,BE BE AE AE AB AB ''''⎧⎪=⎨⎪=⎩=,∴△ABE ′≌△AB ′E ′(SSS ),∴∠AE ′B =AE ′B ′,∵AE ′B ′=∠BAD +AF ′E ′=25°+90°=115°,∴∠AE ′B =115°.即当BE +EF 的值最小时,∠AEB 的度数为115°.故选B .【点睛】本题考查垂直平分线的判定与性质,全等三角形的判定与性质,角平分线的定义,三角形外角的性质,三角形三边关系等知识点,解题的关键是找出BE +EF 取最小值时点E 的位置.二、填空题【答案】6【分析】本题考查了线段垂直平分线的性质:线段垂直平分线上的点到这条线短两个端点的距离相等,熟练掌握线段垂直平分线的性质是解题的关键.【解析】解:∵DE 垂直平分∴4DB DA ==,又∵3BC CD =,∴334622BC BD ==⨯=,故答案为:6.12.如图,在ABC 中,【答案】22【分析】先根据垂直平分线的性质可得长等于+AB AC 即可解答.本题主要考查了垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解答本题的关键.【解析】解:∵DE 垂直平分∴BD DC =,∴ABD △的周长等于AB BD +故答案为:22.【答案】8【分析】先作辅助线HD HB=外角的性质及等腰三角形的性质和判定,可以得到【解析】解:如图,在线段BC则1==,HD HB,AH BC⊥∴垂直平分BD,AH∴==,ABC ADB6AB ADÐ=Ð,∠=∠ABC ACB2ADB ACB∴∠=∠,2,∠=∠+∠ADB CAD ACDCAD ACD ACD∴∠+∠=∠,2∴∠=∠,CAD ACDAD CD∴==,6∴=++=++BC HB HD CD11故答案为:8.【点睛】本题考查了线段垂直平分线的判定与性质,等腰三角形的性质和判定,三角形外角的性质,作出【答案】5【分析】由三角形的周长求出出AB CE =,由此求出AB 【解析】解:∵ABC 周长为∴16610cm AB BC +=-=,∵AD BC BD DE ⊥=,,∴AD 是BE 的垂直平分线,∴AB AE=∵EF 垂直平分AC ,∴AE CE=∴AB CE=【答案】6【答案】5 4【分析】连接BD交AC于点O,作可得出四边形ABCD的面积,然后求出即可得出答案.【解析】连接BD交AC于点O,过点∵2AB AD ==,CB CD ==∴点A ,C 在BD 的垂直平分线上,即∵90DAB ∠=︒,∴222BD AB AD =+=,ABD S ∴1AO DO BO ===,∴222CO BC OB =-=,∴11222BCD S BD OC =⋅=⨯⨯ ∴四边形ABCD 的面积123+=.∵122BCD S BC DM =⋅= ,∴4455DM BC ==,∴22164BM BD DM =-=-∵线段DE 平分四边形ABCD 的面积,∴32CDE S =△,12BDE S = ,【答案】24EF <<【分析】延长ED 到M ,使DM ED =,连接,FM CM ,利用SAS 证明BED CMD ≌ ,得到6BE CM ==,再根据三线合一的逆定理得出EF FM =,最后根据三角形三边关系即可得解.【解析】解:延长ED 到M ,使DM ED =,连接,FM CM ,∵D 为BC 中点,∴BD CD =,在BED 和CMD △中,ED DM BDE CDM BD CD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BED CMD ≌ ,∴1BE CM ==,DM ED =,∵DE DF ⊥,∴90FDE FDM ∠=∠=︒,又∵DM ED =,∴FE FM =,在CFM △中,1,3CM CF ==,∴CF CM FM CM CF -<<+,即24FM <<,∴24EF <<,故答案为:24EF <<.【答案】①④⑤【分析】由BD 是角平分线及BAF BFA ∠=∠,由AE FE =计算出45CDF ∠=︒,则可判定②错误;可判定①正确;由CG AB ∥AN 、AM ,过A 作AH BC ⊥合时,AM 最小,且最小值为故答案为:①④⑤.【点睛】本题考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,等腰三角形的判定与性质,线段垂直平分线的判定与性质,垂线段最短等知识,注意灵活运用这些知识.三、解答题19.如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【答案】见解析【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【解析】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.20.如图,AD是△ADC中∠A的平分线,DE⊥AB于E,DF⊥AC于F,联结EF.求证:AD⊥EF【答案】见解析【分析】由角平分线的性质可知ED FD =,再利用三角形全等证明AE AF =,根据线段垂直平分线的判定定理可得结论.【解析】解:∵AD 是ADC ∆中A ∠的平分线,DE AB ⊥,DF AC⊥∴BAD CAD ∠=∠,ED FD=∵90AED AFD ∠=∠= ,AD AD =,ED FD=∴AED AFD∆≅∆AE AF∴=∴点A 、D 都在EF 的垂直平分线上∴AD EF⊥【点睛】本题综合考查了角平分线及线段的垂直平分线,熟练掌握角平分线的性质定理及线段垂直平分线的判定定理是解题的关键.21.如图,已知AB AC =,DB DC =,P 是AD 上一点.求证:ABP ACP ∠=∠.【答案】证明见解析.【分析】连接BC ,根据线段垂直平分线性质得出AD 是线段BC 的垂直平分线,根据线段垂直平分线性质得出PB=PC ,再利用SSS 证明△ABP 与△ACP 全等,进而得出.【解析】证明:连接BCAB AC= ∴点A 在BC 的垂直平分线上,同理,点D 也在BC 的垂直平分线上,∵两点确定一条直线,∴直线AD 是线段BC 的垂直平分线,P 是AD 上一点,PB PC∴=又AB AC = ,AP AP =,ABP ACP∴∆≅∆ABP ACP ∴∠=∠.【点睛】本题考查全等三角形的判定和性质,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.22.如图,在四边形ABCD 中,AD BC ∥,E 为CD 的中点,连接AE 、BE ,BE AE ⊥,延长AE 交BC 的延长线于点F .(1)请判断FC 与AD 的数量关系,并说明理由;(2)若AB =6,AD =2,求BC 的长度.【答案】(1)FC =AD ,理由见解析(2)4【分析】(1)根据AD ∥BC 可知∠ADC =∠ECF ,再根据E 是CD 的中点可求出△ADE ≌△FCE ,根据全等三角形的性质即可解答;(2)根据全等三角形的性质、线段垂直平分线的性质判断出AB =BF ,据此求解即可.【解析】(1)解:FC =AD ,理由如下:∵AD ∥BC (已知),∴∠ADC =∠ECF (两直线平行,内错角相等),∵E 是CD 的中点(已知),∴DE =EC (中点的定义).在△ADE 与△FCE 中,ADC ECF DE EC AED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADE ≌△FCE (ASA ),∴FC =AD (全等三角形的性质);(2)解:∵△ADE ≌△FCE ,∴AE =EF ,AD =CF (全等三角形的对应边相等),∵BE ⊥AE ,∴BE 是线段AF 的垂直平分线,∴AB =BF =BC +CF ,∴AB =BC +AD ,∵AB =6,AD =2,∴BC =4.【点睛】本题考查了全等三角形的判定和性质,线段垂直平分线的判定和性质,证明三角形全等是解题的关键.23.如图,ABC 中,AB AC =,120BAC ∠=︒.(1)尺规作图:在线段BC 上找一点D ,使得DB DA =;(保留作图痕迹,不写作法)(2)证明:如图所示,连接∵AB AC =,120BAC ∠=︒,∴1801802BAC B C ︒-∠∠=∠==∵DE 垂直平分AB ,∴DB DA =,∴30DAB B ∠=∠=︒,∴120CAD BAC DAB ∠=∠-∠=∴2CD AD =,∴2CD BD =.24.如图,AB AC ⊥,AD AE ⊥(1)求证:AM AN =;(2)连接EC ,AO ,求证:AO 垂直平分EC .【答案】(1)见解析(2)见解析【分析】(1)先证得△≌△Rt ABC Rt ADE ,可得B D ∠=∠.再由AB AC ⊥,AD AE ⊥,.可证得ABM ADN △≌△,即可求证;(2)由(1)可知,AC AE =,ACB AED ∠=∠.可得BCE DEC ∠=∠,从而得到OE OC =,进而得到点O 在EC 的垂直平分线上.再由AE AC =,点A 也在EC 的垂直平分线上,即可求证.【解析】(1)证明:在Rt ABC 和Rt ADE △中,∵AB AD =,BC DE =,∴()Rt ABC Rt ADE HL ≌△△,∴B D ∠=∠.∵AB AC ⊥,AD AE ⊥,∴90BAM EAC DAN ∠=︒-∠=∠,∵AB AD =,∴()ABM ADN ASA ≌△△,∴AM AN =;(2)证明∶如图,由(1)可知,AC AE =,ACB AED ∠=∠.∴ACE AEC ∠=∠,∴ACE ACB AEC AED ∠-∠=∠-∠,即BCE DEC ∠=∠,∴OE OC =,∴点O 在EC 的垂直平分线上.又∵AE AC =,∴点A 也在EC 的垂直平分线上,∴AO 垂直平分EC .【点睛】本题主要考查了全等三角形的判定和性质,线段垂直平分线的判定,熟练掌握全等三角形的判定和性质,线段垂直平分线的判定是解题的关键.25.如图,等腰直角ABC 中,90CAB ∠=︒,AC AB =,点E 为BC 上一点,BD AE ⊥于点M ,交AC 于点D ,AH CB ⊥于点H ,交BD 于点G ,连接DE ,MH .(1)若BE BA =,求证:BD 垂直平分AE ;(2)若点E 在线段CH 上运动.①请判断CE 与AG 的数量关系,并说明理由;②求证:MH 平分EMB ∠.∴C BAG ∠=∠,在ACE △和BAG △中,EAD ABG AC BA C BAG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA ACE BAG ≌,∴CE AG =;②作HN HM ⊥交BD 于点N ,∴90AHB MHN ∠=∠=︒,∴45∠=∠,∵790AGM ∠+∠=︒,690BGH ∠+∠=︒,且AGM BGH ∠=∠,∴67∠=∠,∵等腰直角ABC 中,AC AB =,AH CB ⊥,∴BH AH =,在AMH 和BNH 中,6754BH AH ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA AMH BNH ≌,∴HM HN =,即MHN 是等腰直角三角形,∴45HMN ∠=︒,∵90BME ∠=︒∴MH 平分EMB ∠.26.如图,平面直角坐标系中,直线:AB y x b =-+交y 轴于点()0,4A ,交x 轴于点B .(1)求直线AB 的表达式和点B 的坐标;(2)直线l 垂直平分OB 交AB 于点D ,交x 轴于点E ,点P 是直线上一动点,且在点D 的上方,设点P 的纵坐标为n ,①用含n 的代数式表示ABP 的面积,并求当8ABP S = 时,点P 的坐标;②在①的条件下,在坐标轴上,是否存在一点Q ,使得ABQ 与ABP 面积相等?若存在,请求出点Q 的坐标;若不存在,请说明理由.【答案】(1)直线AB 的表达式为4y x =-+,点B 的坐标为()4,0;(2)①24n -,点()2,6P ;②存在一点Q ,使得ABQ 与ABP 面积相等,且点Q 的坐标为()0,0或()8,0或()0,8.【分析】(1)利用待定系数法即可求解;(2)①由OB 的长度结合直线l 的垂直平分OB ,可求出OE ,BE 的长度,利用一次函数解析式求出点D 坐标,进而用含n 的式子表示点P 坐标,再利用面积公式即可求解;②分点Q 在x 轴和y 轴两种情况考虑,利用三角形面积即可求出点Q 坐标;本题考查了一次函数的图象及性质,垂直平分线的性质等,熟练掌握一次函数的图象及性质,垂直平分线的性质及其应用是解题的关键.【解析】(1)∵直线AB :y x b =-+交y 轴于点()0,4A ,∴4b =,∴直线AB 的表达式为4y x =-+,当0y =时,4x =,∴点B 的坐标为()4,0,(1)如图1,当点D 是BC 的中点时,求证:BD CE =;(2)如图2,当点D 在线段BC 上移动时,过点D 作DF 终保持全等?若全等,请证明,若不全等,请说明你的理由.(3)若等边ABC 的边长为4,当BD a =时,求AE 的长.【答案】(1)见解析(2)全等,证明见解析(3)4AE a=+【分析】本题主要考查等边三角形的性质,全等三角形的判定与性质,线段垂直平分线的判定与性质等知识:(1)由D 是等边三角形BC 边的中点可得BD CD =,再证明论;(2)由DF AC ∥可得60,BFD BAC BDF ∠=∠=︒∠=∠60,B BFD BDF ∠=∠=∠=︒,BD DF BF ==得出AF DC =知,AFD DCE ∠=∠再证明FAD CDE ∠=∠,进而再利用(3)由(2)知 ≌AFD DCE 得CE FD =,由DF BD =【解析】(1)证明:∵D 是等边三角形BC 边的中点,∴BD CD =,∵ABC 是等边三角形,∴603030,CDE BCA CED ∠=∠-∠=︒-︒=︒∴,CDE CED ∠=∠∴,CD CE =∵,BD CD =∴BD CE =;(2)全等,证明如下:∵ABC 是等边三角形,∴60,BAC BCA B ∠=∠=∠=︒,AB BC AC ==∵DF AC ∥,∴60,60,BFD BAC BDF BCA ∠=∠=︒∠=∠=︒∴60,B BFD BDF ∠=∠=∠=︒∴,BD DF BF ==120,AFD ∠=︒∴,AF DC =∵60ACB ∠=︒,∴120,DCE ∠=︒∴120,AFD DCE ∠=∠=︒∵,AH HE =且,DH AE ⊥∴,AD DE =∴,DAE DEA ∠=∠又60,60,CDE CED FAD CAD ∠+∠=︒∠+∠=︒∵,CED CAD ∠=∠∴,FAD CDE ∠=∠在AFD △和DCE △中,AF DC AFD DCE FAD CDE =⎧⎪∠=∠⎨⎪∠=∠⎩,∴()ASA AFD DCE ≌;(3)解:由(2)知,,DF BD a ==且 ≌AFD DCE ,CE DF a ==,∴4AE AC CE a =+=+.。
线段垂直平分线的练习题

一、填空题1、如图,MN 是线段AB 的垂直平分线,P 为MN 上一点,则PA,PB 的大小关系是________。
2、如图,∠C=90°,DE 垂直平分AB ,∠1:∠2=2:3,则∠CAB=________。
3、如图,点O 为△ABC 三边垂直平分线的交点,点O 到顶点A 的距离为5㎝,则AO+BO+CO=________㎝。
4、如图,在△ABC 中,∠C=90°,DE 是斜边AB 的垂直平分线,分别交AB ,AC 于D 、E 两点,∠BEC=60°,EC=1,则AE=______。
5、如图,在△ABC 中,AC=BC=2,∠ACB=90°,D 是BC 边的中点,E 是AB 边上一动点,则EC+ED 的最小值是______。
(1)POABN M (3)OCBA(4)DE BCA (5)ED BC A二、选择题1、给出下列命题:①如果等腰三角形内有一点到底边的两个端点的距离相等,那么这个点与顶点的连线必垂直平分底边;②等腰三角形底边的高上任意一点到底边两端点的距离相等;③M 点在线段AB 外,MB=MA ,则过M 点所作直线l 是AB 的垂直平分线;④三角形三边的垂直平分线必相交于一点。
其中正确的命题有( )个A 、1B 、2C 、3D 、 42、等腰三角形的顶角为100°,两腰的垂直平分线交于点P ,则( ) A 、点P 在三角形内; B 、点P 在三角形底边上;C 、点P 在三角形外D 、点P 的位置与三角形的边长有关 3、如图,△ABC 中,MD 垂直平分AB 于M ,交BC 于D ,NE 垂直平分AC 于N ,交交BC 于E ,若∠BAC=120°,则∠DAE=( ) A 、50° B 、60° C 、70° D 、80°4、如图,在Rt △ABC 中,∠ACB=90°,BC 边上的垂直平分线交AB 于D ,AB=12,AC=6,,则图中等于6的线段共有( )条A 、2B 、3C 、4D 、 55、下列命题中,是假命题的是( )A 、斜边和一锐角对应相等的两个直角三角形全等B 、两条直角边对应相等的两个直角三角形全等C 、两个锐角对应相等的两个直角三角形全等D 、一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等 三、如图 ,△ABC 中,AB=AC=16,D 为AB 的中点,且DE⊥AB 交AC 于E ,△BCE 的周长为26 求BC 的长EDCB AADE BC N M ED CB A。
线段的垂直平分线

线段的垂直平分线[知识要点]1.垂直平分线的基本性质:线段垂直平分线上任意一点到线段两端点的距离相等2.到线段两端点距离相等的点在该线段的垂直平分线上3.线段的垂直平分线等腰三角形[典型例题]例1.如图,△ABC是等边三角形,BD是中线,延长BC于E,使CE=CD.求证:点D在线段BE的垂直平分线上.例2.如图,AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC•的延长线于点E,连接AE、DF,求证:(1)DF∥AC;(2)∠B=∠EAC.例3.如图,在△ABC中,AE⊥BC于E,∠B=22.5°,AB的中垂线DN交BC于D,DF•⊥AC于F,交AE于M.求证:EM=EC.例4.如图,在△ABC中,BD,CF分别是高,M为BC的中点,N为DF的中点.求证:•MN⊥DF.例5.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于M,∠A=40°(1)求∠NMB的大小.(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小;(3)你发现有什么样的规律性?试证明之;(4)将(1)中的∠A改为钝角,对这个问题规律性的认识是否需要加以修改?[经典练习]一、选择题1.三角形中,一条边的垂直平分线恰好经过三角形的另一个顶点,那么这个三角形一定是().A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形2.已知直线a是线段AB的垂直平分线,C,D是直线a上的两点,则∠CAD与∠CBD•的关系是().A.∠CAD>∠CBD B.∠CAD<∠CBD C.∠CAD与∠CBD互补 D.∠CAD=∠CBD3.如图,Rt△ABC的斜边AB的中点为E,ED⊥AB,且∠CAD:∠BAD=•1:•7,则∠BAC=().A.70° B.60° C.48° D.45°4.在同一平面内,到平面上三点A、B、C距离相等的是().A.只有一个 B.有两个 C.有三个或三个以上 D.有一个或没有5.由下列条件可以作出等腰三角形的是().A.已知等腰三角形的两腰 B.已知一腰和一腰上的高C.已知底角的度数和顶角的度数 D.已知底边长和底边上的中线的长6.已知线段AB和点C,D,且CA=CB,DA=DB,那么直线CD是线段AB的().A.垂线 B.平行线 C.垂直平分线 D.过中点的直线二、填空题1.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所成的锐角为50°,则∠B的大小为_______.(第2题图) (第3题图)(第4题图)2.如图,△ABC中,∠BAC=100°,DE,FG分别为AB,AC的垂直平分线,•如果BC=16cm,那么△AEG的周长为_______,∠EAG=_______.3.如图,在△ABC中,AB=AC,∠C=65°,MN垂直平分AB,则∠NBC=•______,•∠BNC=______.4.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB•于E,DB=10,则CD=________.三、解答题在一条公路旁有A,B两个工厂,要在公路旁修一个汽车站,•请分别按如下要求确定汽车站M的位置:①要求车站M到A,B两厂的距离相等;②要求车站M到A,B•两厂的距离之和AM+BM最短.(1)如图,当A,B两厂在公路的同侧时(2)如图,当A,B两厂在公路的两侧时.[课后作业]1.如图,在△ABC中,AB=BC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EAC•的周长为25cm,则AC长为_______cm.(第1题图) (第3 题图)2.△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,则AD:DB=_______.3.如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,•交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=________,∠EFC=_______.4.△ABC中,边AB的垂直平分线交AC于E,△ABC和△BEC的周长分别是24和14,•则AB=________.5.在Rt△ABC中,∠ACB=90°,∠A=60°,D是斜边AB的中点,将△ABC沿某条直线翻折,使点C落在D上,折痕与AC,BC的交点分别为M,N,求∠CND的大小.6.三角形三条边的垂直平分线相交于一点,这一点称为三角形的外心.•一个三角形的外心一定在三角形的内部吗?画几个三角形试一试,并将你的猜想写出来.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型例题
例1.如图,已知:在ABC ∆中,︒=∠90C ,︒=∠30A ,BD 平分ABC ∠交AC 于D .
求证:D 在AB 的垂直平分线上.
分析:根据线段垂直平分线的逆定理,欲证D 在AB 的垂直平分线上,只需证明DA BD =即可.
证明:∵︒=∠90C ,︒=∠30A (已知),
∴ ︒=∠60ABC (∆Rt 的两个锐角互余)
又∵BD 平分ABC ∠(已知)
∴ A ABC DBA ∠=︒=∠=∠302
1. ∴AD BD =(等角对等边)
∴D 在AB 的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
例2.如图,已知:在ABC ∆中,AC AB =,︒=∠120BAC ,AB 的垂直平分线交AB 于E ,交BC 于F 。
求证:BF CF 2=。
分析:由于︒=∠120BAC ,AC AB =,可得︒=∠=∠30C B ,又因为EF 垂直平分AB ,连结AF ,可得BF AF =. 要证BF CF 2=,只需证AF CF 2=,即证︒=∠90FAC 就可以了.
证明:连结AF ,
∵EF 垂直平分AB (已知)
∴FB FA =(线段垂直平分线上的点和这条线段两端点的距离相等) ∴B FAB ∠=∠(等边对等角)
∵AC AB =(已知),
∴C B ∠=∠(等边对等角)
又∵︒=∠120BAC (已知),
∴︒=∠=∠30C B (三角形内角和定理)
∴︒=∠30BAF
∴︒=∠90FAC
∴FA FC 2=(直角三角形中,︒30角所对的直角边等于斜边的一半) ∴FB FC 2=
说明:线段的垂直平分线的定理与逆定理都由三角形的全等证得,初学者往往不习惯直接使用绝无仅有垂直平分线的定理与逆定理,容易舍近求远,由三角形全等来证题.
例3.如图,已知:AD 平分BAC ∠,EF 垂直平分AD ,交BC 延长线于F ,连结AF 。
求证:CAF B ∠=∠。
分析:B ∠与CAF ∠不在同一个三角形中,又B ∠,CAF ∠所在的两个三角形不全等,所以欲证CAF B ∠=∠,不能利用等腰三角形或全等三角形的性质. 那么注意到EF 垂直平分AD ,可得FD FA =,因此ADF FAD ∠=∠,又因为CAD FAD CAF ∠-∠=∠,BAD ADF B ∠-∠=∠,而BAD CAD ∠=∠,所以可证明B CAF ∠=∠.
证明:∵EF 垂直平分AD (已知),
∴FD FA =(线段垂直平分线上的点和这条线段的两端点的距离相等). ∴ADF FAD ∠=∠(等边对等角)
∵BAD ADF B ∠-∠=∠(三角形的一个外角等于和它不相邻的两个内角的和),
CAD FAD CAF ∠-∠=∠,
又CAD
∠(角平分线定义),
=
BAD∠
∴CAF
∠
B∠
=
说明:运用线段的垂直平分线的定理或逆定理,能使问题简化,如本例题中,EF垂直平分AD,可以直接有结论FD
FA=,不必再去证明两个三角形全等.
例4.如图,已知直线l和点A,点B,在直线l上求作一点P,使PB
PA=.
分析:假设P点已经作出,则由PB
PA=,那么根据“到线段两端点距离相等的点在这条线段的垂直平分线上”可知,点P在线段AB的垂直平分线上. 而点P又在直线l上,则点P应是AB的垂直平分线与垂线l的交点。
作法:1.连结AB.
2.作线段AB的垂直平分线,交直线l于点P.
则P即为所求的点.
说明:在求作一个点时,要考虑该点具备什么样的特点,如它到一条线段的两个端点距离相等,它就在连结这两点的线段的垂直平分线上,如果它到一个角的两边的距离相等,它就在这个角的平分线上.。
