SOR迭代_C语言代码
6.4超松弛迭代法

表6.3 Gauss-Seidel迭代法与SOR迭代法比较
Gauss-Seidel迭代法
SOR迭代法(ω=1.25)
k
x1
0
1.0000000
x2 1.0000000
x3 1.0000000
x1 1.0000000
x2 1.0000000
x3 1.0000000
1
5.2500000
3.1825000
第六章 线性方程组迭代解法
§ 6.4 超松弛迭代法(SOR)
§ 6.4超松弛迭代法(SOR)
SOR(Successive Over-Relaxation)法, 即超松弛迭代法,是目前解大型线性方程 组的一种最常用的方法,是Gauss-Seidel迭 代法的一种加速方法。
一、SOR法迭代公式
例6.6 用SOR法求解线性方程组
前面我们看到,SOR法收敛与否或收敛速度都 与松弛因子ω 有关,关于ω 的范围,有如下定理。
SOR法收敛与收敛速度有关定理
定理6.5 设A∈Rnn,满足a ii≠0 (i=1,2,,n),则有 ρ(Bω)≥ |1-ω| 。
推论 解线性方程组,SOR法收敛的必要条件是 |1-ω| <1 ,即 0<ω <2。
4.0009262
-4.9982822
7 3.0134110
3.9888241
-5.0027940
3.0000498
4.0002586
-5.0003486
迭代法若要精确到七位小数, Gauss-Seidel迭代法需要34次迭代; 而用SOR迭代法(ω=1.25),只需要14次迭代。
可见,若选好参数ω,SOR迭代法收敛速度会很 快。
西工大-计算流体力学大作业
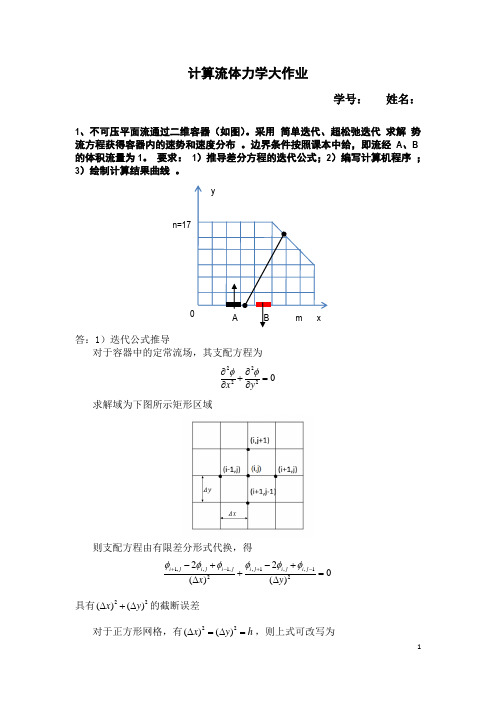
计算流体力学大作业学号: 姓名:1、不可压平面流通过二维容器(如图)。
采用 简单迭代、超松弛迭代 求解 势流方程获得容器内的速势和速度分布 。
边界条件按照课本中给,即流经 A 、B 的体积流量为1。
要求: 1)推导差分方程的迭代公式;2)编写计算机程序 ; 3)绘制计算结果曲线 。
答:1)迭代公式推导对于容器中的定常流场,其支配方程为22220x yφφ∂∂+=∂∂ 求解域为下图所示矩形区域则支配方程由有限差分形式代换,得1,,1,,1,,122220()()i j i j i ji j i j i j x y φφφφφφ+-+--+-++=∆∆具有22()()x y ∆+∆的截断误差对于正方形网格,有22()()x y h ∆=∆=,则上式可改写为n=17,1,1,,1,11()4i j i j i j i j i j φφφφφ+-+-=+++若采用简单迭代公式,即Liebmann 公式,则有(1)()(1)()(1),1,1,,1,11()4n n n n n i j i j i j i j i j φφφφφ++++-+-=+++若采用超松弛迭代,即SOR 公式,则有(1)()()(1)()(1),,1,1,,1,1(1)()4n n n n n n i j i j i j i j i j i j ωφωφφφφφ++++-+-=-++++其中松弛因子12ω<<。
ω最佳值opt ω为opt ω=式中cos(/)cos(/)m n αππ=+,m ,n 分别表示在网格系统中垂直线和水平线的总数。
2)计算机程序本程序采用C 语言编写。
程序源代码如下: #include<stdio.h> #include<math.h> void main() { int m=25,n=17,ilast[17],jlast[25]; int step1,step2; double h=0.25; double psi_j[25][17],psiprv_j,vel_j[25][17],velx_j[25][17],vely_j[25][17]; double psi_c[25][17],psiprv_c,vel_c[25][17],velx_c[25][17],vely_c[25][17]; double Pi,Alpha,Omega,Error; int i,j; for(i=0;i<17;i++) jlast[i]=17; for(i=17;i<m;i++) jlast[i]=17-(i-16); for(j=0;j<9;j++) ilast[j]=25; for(j=9;j<n;j++) ilast[j]=25-(j-8); //数据初始化 for(j=0;j<n;j++) { psi_j[0][j]=1.0; psi_c[0][j]=1.0;}for(i=1;i<m;i++){psi_j[i][jlast[i]-1]=1.0;psi_c[i][jlast[i]-1]=1.0; }for(j=0;j<8;j++){psi_j[m-1][j]=1.0;psi_c[m-1][j]=1.0;}for(i=1;i<m-1;i++){if(i>6 && i<21){psi_j[i][0]=0.0;psi_c[i][0]=0.0;}else{psi_j[i][0]=1.0;psi_c[i][0]=1.0;}}for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psi_j[i][j]=0.5;psi_c[i][j]=0.5;}}//处理右上角数据for(i=0;i<m;i++){for(j=0;j<n;j++){if(j>jlast[i]-1){psi_j[i][j]=0;vel_j[i][j]=3;psi_c[i][j]=0;vel_c[i][j]=3;}}}Pi=4.0*atan(1.0);Alpha=cos(Pi/m)+cos(Pi/n);Omega=(8.0-4*sqrt(4-pow(Alpha,2)))/pow(Alpha,2);//计算速势step1=0;step2=0;//简单迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_j=psi_j[i][j];psi_j[i][j]=(psi_j[i-1][j]+psi_j[i+1][j]+psi_j[i][j-1]+psi_j[i][j+1])/4.0;Error=Error+fabs(psi_j[i][j]-psiprv_j);}}step1++;if(step1>1000)break;if(Error<=0.001)break;}//超松弛迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_c=psi_c[i][j];psi_c[i][j]=(1-Omega)*psi_c[i][j]+Omega*(psi_c[i-1][j]+psi_c[i+1][j]+psi_c[i][j-1]+psi_c[i][j+1])/4.0;Error=Error+fabs(psi_c[i][j]-psiprv_c);}}step2++;if(step2>1000)break;if(Error<=0.001)break;}//计算速度for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){if(j==0){vely_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i][j+1]-psi_j[i][j+2])/2/h;vely_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i][j+1]-psi_c[i][j+2])/2/h;}else if(j==jlast[i]-1){vely_j[i][j]=(psi_j[i][j-2]-4*psi_j[i][j-1]+3*psi_j[i][j])/2/h;vely_c[i][j]=(psi_c[i][j-2]-4*psi_c[i][j-1]+3*psi_c[i][j])/2/h;}else{vely_j[i][j]=(psi_j[i][j+1]-psi_j[i][j-1])/2/h;vely_c[i][j]=(psi_c[i][j+1]-psi_c[i][j-1])/2/h;}}}for(j=0;j<n;j++){for(i=0;i<ilast[j];i++){if(i==0){velx_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i+1][j]-psi_j[i+2][j])/2/h;velx_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i+1][j]-psi_c[i+2][j])/2/h;}else if(i==ilast[j]-1){velx_j[i][j]=(psi_j[i-2][j]-4*psi_j[i-1][j]+3*psi_j[i][j])/2/h;velx_c[i][j]=(psi_c[i-2][j]-4*psi_c[i-1][j]+3*psi_c[i][j])/2/h;}else{velx_j[i][j]=(psi_j[i+1][j]-psi_j[i-1][j])/2/h;velx_c[i][j]=(psi_c[i+1][j]-psi_c[i-1][j])/2/h;}}}for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){vel_j[i][j]=sqrt(pow(velx_j[i][j],2)+pow(vely_j[i][j],2));vel_c[i][j]=sqrt(pow(velx_c[i][j],2)+pow(vely_c[i][j],2));}}//输出结果分布FILE *fp;fp=fopen("f:\\ESL\\YFresult.txt","w");fprintf(fp,"简单迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_j[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_j[i][j]);}}fprintf(fp,"超松弛迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_c[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_c[i][j]);}}fclose(fp);//输出tecplot数据FILE *fp1;fp1=fopen("f:\\ESL\\TECPLOT-result.txt","w");fprintf(fp1,"title=erwei grid\n");fprintf(fp1,"variables=x, y, psi_easy, velocity_easy, psi_SOR\n, velocity_SOR\n");fprintf(fp1,"zone t=grid,i=25,j=17,f=point\n");for(j=0;j<n;j++){for(i=0;i<m;i++){fprintf(fp1,"%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f\n",i*h,j*h,psi_j[i][j],vel_j[i][j],p si_c[i][j],vel_c[i][j]);}}fclose(fp1);}3)计算结果采用简单迭代,容器内的速势和速度分布速势分布(简单迭代)速度分布(简单迭代)采用超松弛迭代,容器内的速势和速度分布速势分布(SOR ) 速度分布(SOR )2、用点源(汇)分布在对称轴的源汇模拟流体绕过NACA0012旋称体的二维轴对称势流解。
SOR迭代法

SOR迭代法常以这种形式进行计算。
格式(3.4)的矩阵形式为
X (k1) (1 ) X k D1 b LX k UX (k) ,
3.5
其中
a11
D
a22
O
0
0
,
ann
0 a12 L
U
0O
O
0
a1n
an1,n
0
显然,A D L U.
0
0
L
a21
O
OO
上述定理说明,对于任何系数矩阵 A,若要 SOR
法收敛,必须选取松弛因子 0,2 , 然而,当松
弛因子满足条件 0 2 时,并不是对所有系数矩 阵 A 来说,SOR 法都是收敛的。但是,对一些特殊矩 阵来说,这一条件是充分的。
定理7 如果矩阵 A 是对称正定的,则 SOR 法 对于0 2 是收敛的。
ω
0.6 0.8 1 1.1 1.15 1.25 1.3 1.5 1.8
迭代次数 16 10 8 7 8 11 15 15 15
近似解与 5 5 5 5 5 5 5 4 1 准确解重 复合位数
使 SOR 法收敛最快的松弛因子通常称为最 优 松
弛因子。目前,只有少数特殊类型的矩阵,才有确定 的最优松弛因子的理论公式,但实际使用时也有一定 困难。通常的办法,是选不同的 进行试算,以确定
其 Gauss Seidel 迭 代 格 式 可写为 (aii 0) :
x(k1) i
x(k) i
1 aii
bi
a x(k1) i1 1
L
a x(k1) i,i1, i1
aii xi(k)
L
ain xn(k)
x(k) i
第一次迭代解法之SOR

种相容范数都有 ρ(A)≤||A||
(6.2)
2021/6/17
13
另一个更深刻的结果,对于任意的ε>0,必存在一种相
容的矩阵范数,使
|| A ||≤ ρ(A) +ε
(6.3)
式(6.2)和(6.3)表明,矩阵A的谱半径是它所有相 容范数的下确界。
定义6.4 设有n×n矩阵序列 A(k) (ai(jk) ), k 1, 2, 方阵A=(aij), 如果
多大算病态没有标准。如果主元很小或者元素数量级相差大,可能是病态
cond ( A) A A1 AA1 1
2021/6/17
18
§2 迭代解法与收敛性
一、迭代解法
设有线性方程组
Ax=b
(1)
A∈Rn×n, b∈Rn .
对A 进行分裂, A=A1+A2 , 其中 A1 可逆,
则 (A1+A2)x=b A1x = - A2x+b x = - A1-1 A2 x + A1-1 b
再由 Ax =b,得到 || b||= || Ax || ≤||A || ||x||
2021/6/17
16
于是,由 || △x ||≤||A-1 || ||△b||
及 ||b || ≤||A || ||x|| 1 A
x
b
得到解的相对误差为
x A
A1
b
x
b
令 Cond(A)=||A || ||A-1 || ,并称其为矩阵A的条件数。
14 20
则它的特征方程为:
I AT A 10 14
2 30 4 0
14
20
2021/6/17
10
此方程的根为矩阵ATA的特征值,解得
C语言迭代部分的代码编写

C语⾔迭代部分的代码编写
C语⾔代码学习
迭代部分
迭代要⽤到函数部分的知识,⼀开始我写了计算n!的计算,代码和运⾏结果如下:
结果只能单⼀的计算出整数内的值,如果输⼊负值则结果为返回值1,显然是不对的,根据查书学习以后,知道⾃⼰的代码是不健壮的,不能应对异常结果,所以我将代码进⾏了修改,增加了对函数⼊⼝参数的合法性检验。
代码和结果如下:
图中运⾏的结构好像还不对,-10的结果还是返回值的结果,后来发现主函数没有对函数Fact()返回值的代表异常情况发⽣的特殊值进⾏处理,修改代码以后如下:
迭代循环部分代码编写
编写代码的过程中⼀定要保证代码的完整性,⼀定要能处理⽤户输⼊的任何情况。
!。
sor迭代法

SOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/A(i,i);endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);end常微分方程的数值解法实验目的:熟悉在Matlab平台上直接求解常微分方程初值问题试验方法1、利用改进欧拉法解方程:程序内容为:fun=@(x,y)x^(-2)-y/x;h=0.05;X=1:h:2;Y(1)=1;for i=2:21Y(i)=Y(i-1)+h/2*(fun(X(i-1),Y(i-1))+fun(X(i),Y(i-1))+h*fun(X(i-1),Y(i-1))); end;Y运行结果为:Y =Columns 1 through 91.0000 0.9989 0.9957 0.9909 0.9848 0.9778 0.9701 0.9618 0.9530Columns 10 through 180.9440 0.9348 0.9254 0.9160 0.9065 0.8971 0.8876 0.8783 0.8690Columns 19 through 210.8598 0.8508 0.8418真实解的求法为:x=1:0.05:2;y=1./x.*(log(x)+1)y =Columns 1 through 81.0000 0.9988 0.9957 0.9911 0.9853 0.9785 0.9710 0.9630Columns 9 through 160.9546 0.9459 0.9370 0.9279 0.9188 0.9096 0.9004 0.8912Columns 17 through 210.8821 0.8731 0.8641 0.8553 0.8466用四阶R-K算法解常微分方程的程序为:fun=@(x,y)x^(-2)-y/x;h=0.1;X=1:h:2;Y(1)=1;for n=2:11k1=fun(x(n-1),Y(n-1));k2=fun(x(n-1)+h/2,Y(n-1)+h/2*k1);k3=fun(x(n-1)+h/2,Y(n-1)+h/2*k2);k4=fun(x(n-1)+h,Y(n-1)+h*k3);Y(n)=Y(n-1)+h/6*(k1+2*k2+2*k3+k4)end;Y运行后了结果为:Y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466真实解的求法为:x=1:0.1:2;y=1./x.*(log(x)+1)y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466可见其精确度至少已达到0.0012、MATLAB中数值解法“ode45”为:[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],y0);符号解法“dsolve”求解为:dsolve('Dy=x^(-2)-y/x','y(1) = 1','x')ans =(log(x)+1)/x画出两种算法的图形位:[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],1);fplot('(log(x)+1)/x',[1,2]);hold on, plot(x1,y1,'ro');数值算法同解析算法几乎完全吻合。
数学实验“线性方程组的j迭代,gs迭代,sor迭代解法”实验报告(内含matlab程序代码)【最新精

西京学院数学软件实验任务书实验四实验报告一、实验名称:线性方程组的J-迭代,GS-迭代,SOR-迭代。
二、实验目的:熟悉线性方程组的J-迭代,GS-迭代,SOR-迭代,SSOR-迭代方法,编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组12123123521064182514x x x x x x x x +=⎧⎪++=⎨⎪++=-⎩的根,提高matlab 编程能力。
三、实验要求:已知线性方程矩阵,利用迭代思想编程求解线性方程组的解。
四、实验原理:1、雅可比迭代法(J-迭代法):线性方程组b X A =*,可以转变为:迭代公式(0)(1)()k 0,1,2,....k k J XXB X f +⎧⎪⎨=+=⎪⎩ 其中b M f U L M A M I B J 111),(---=+=-=,称J B 为求解b X A =*的雅可比迭代法的迭代矩阵。
以下给出雅可比迭代的分量计算公式,令),....,()()(2)(1)(k n k k k X X X X =,由雅可比迭代公式有b XU L MXk k ++=+)()1()(,既有i ni j k i iji j k iij k iij b X aXa X a +--=∑∑+=-=+1)(11)()1(,于是,解b X A =*的雅可比迭代法的计算公式为⎪⎩⎪⎨⎧--==∑∑-=+=+)(1),....,(111)()()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 2、 高斯-赛德尔迭代法(GS-迭代法):GS-迭代法可以看作是雅可比迭代法的一种改进,给出了迭代公式:⎪⎩⎪⎨⎧--==∑∑-=+=+++)(1),....,(111)1()1()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 其余部分与雅克比迭代类似。
C语言复习---迭代法,牛顿迭代法,二分法求根

C语⾔复习---迭代法,⽜顿迭代法,⼆分法求根⼀:⽤迭代法求 x=√a。
求平⽅根的迭代公式为:X(n+1)= (Xn+a/Xn) /2。
#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆:⽤求⽅程在1.5附近的根(2x3-4x2+3x-6=0)例:⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三:⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0(这是前提,选取的区间必须满⾜这个条件),给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代码运行可用
# include <stdio.h>
# include <math.h>
#include<stdlib.h>
float **a; /*存放 A 矩阵*/
float *b; /*存放 b 矩阵*/
float *x; /*存放 x 矩阵*/
float p; float w; int n; int c;
for(i=1;i<n+1;i++)
{
t=0.0;
tt=0.0;
for(j=1;j<i;j++)
t=t+a[i][j]*xl[j];
for(j=i;j<n+1;j++)
tt=tt+a[i][j]*xk[j];
xl[i]=xk[i]+w*(b[i]-t-tt)/a[i][i];
}
t=0.0; for(i=1;i<n+1;i++) {
printf("%f\n",x[i]); }
tt=fabs(xl[i]-xk[i]); tt=tt*tt; t+=tt; } t=sqrt(t);
for(i=1;i<n+1;i++) xk[i]=xl[i];
if(k+1<=c&&t>p)
{ k++; SOR(xk);
} } void main() {
int i,j; printf("输入矩阵维数 N:\n"); scanf("%d",&n); a=(float **)malloc(sizeof(float)*(n+1)); for(i=0;i<n+1;i++)
a[i]=(float*)malloc(sizeof(float)*(n+1)); printf("输入矩阵 A:\n"); for(i=1;i<n+1;i++)
for(j=1;j<n+1;j++) scanf("%f",&a[i][j]); for(i=1;i<n+1;i++) for(j=1;j<n;j++) if(a[i][j]==0) printf("a[%d][%d]不能为 0\n",i,j); b=(float *)malloc(sizeof(float)*(n+1)); printf("输入矩阵 b:\n"); for(i=1;i<n+1;i++) scanf("%f",&b[i]); x=(float *)malloc(sizeof(float)*(n+1));
printf("输入矩阵 x:\n"); for(i=1;i<n+1;i++)
scanf("%f",&x[i]); printf("输入精确值:\n"); scanf("%f",&p); printf("输入最大迭代次数:\n"); scanf("%d",&c); printf("输入松弛因子 w(0<w<2):\n"); scanf("%f",&w); SOR(x); for(i=1;i<n+1;i++)
/*精确度*/ /*松弛因子*/ /*未知数个数*/ /*最大迭数*/
void SOR(float xk[])
{
int i,j;
float t=0.0;
float tt=0.0;
float *xl;
xl=(float *)malloc(sizeof(float)*(n+1));
