冷却塔热力计算书1
章— 冷却塔热力计算基本方程

三、冷却塔的性能
(1)热力性能 (2)空气阻力特性 (定一 :)填料公的式容:积散质系数βXV及特性数N′的求
βxvV Cw t1 dt
Q K t2 ii
左侧: N xvV
Q
βxvV—蒸发水量。 Q—总水量。 N′—是两者的比值 。
填料的容积散质系数:βxV 是填料散热能力的综合参数,取决于材料、构 造、尺寸、布置、高度:
水的散热 K 1CwQdt空气吸 G热 di 即: di 1 Q
Cwdt K G
令: G (气水比)
Q
di 1 tg Cwdt K
表示di与dt成直线关系,斜率为:
1 K
积分下式:边界条件用塔底空气焓i1和水温t2 。
Gdi
1 K
CwQdt
G(i2
i1)
Cw K
Q(t1
t2
)
i2 i1 (t1 K t2 )Q G C w i1 (t1 K t2 )C w (k/k J)g
iijj1列 入CKwjd表t 第λ—5列气。水比
G Q
(7)求
1 i
j
倒数,列入表第六列。
(8)求N i : 用抛物线法,把(2)视为
抛物线,取两格,由三个点,
如:
1i0,t0,1i1,t1,1i2,t2
这三点视为抛物线(不是
抛物) 。所围面积:
3t1i0
4 i1
1 i2
N C K w t t 2 1 i d i 3 C t K w 1 i 0 4 i 1 2 i 2 4 i 3 2 i 4 4 i 5 i 2 n 2 i 4 n 1 1 i n
(Csh=Cg+Cqx=1+1.84x) (近似值)(实验)
冷却塔的热力计算之欧阳家百创编

冷却塔的热力计算欧阳家百(2021.03.07)冷却塔的任务是将一定水量Q,从水温t1冷却到t2,或者冷却△t=t1-t2。
因此,要设计出规格合适的冷却塔,或核算已有冷却塔的冷却能力,我们必须做冷却塔的热力计算。
为了便于计算,我们对冷却塔中的热力过程作如下简化假设:(1)散热系数,散质系数,以及湿空气的比热,在整个冷却过程被看作是常量,不随空气温度及水温变化。
(2) 在冷却塔内由于水蒸气的分压力很小,对塔内压力变化影响也很小,所以计算中压力取平均大气压力值。
(3)认为水膜或水滴的表面温度与内部温度一致,也就是不考虑水侧的热阻。
(4) 在热平衡计算中,由于蒸发水量不大,也可以将蒸发水量忽略不计。
(5) 在水温变化不大的范围内,可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。
冷却塔的热力计算方法有焓差法、湿差法和压差法等,其中最常用的是麦克尔提出的焓差法,以下简要介绍冷却塔的焓差法热力计算。
麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式,统一为一个以焓差为动力的传热公式。
在方程式中,麦克尔引进入刘易斯关系式,导出了以焓差为动力的散热方程式。
(1)式中:——水散出热量;——以含湿差为基准的容积散质系数;——温度为水温t时饱和空气比焓 ();——空气比焓 ()。
将式(1)代入冷却塔内热平衡方程:(2)式中:——水散出热量;——水的比热;——冷却水量 ();——蒸发水量 ()——水温度(℃)并引入系数K:式中——塔内平均汽化热()经整理,并积分后,可得冷却塔热力计算的基本方程式:(3)上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力,它与淋水填料的特性、构造、几何尺寸、冷却水量有关,称冷却塔的特性数,以符号愿表示,即:(3)式的右端表示冷却任务的大小,与气象条件有关,而与冷却塔的构造无关,称为冷却数(或交换数),以符号表示,也即:由于水温不是空气焓的直接函数,直接积分有困难,所以,在求解冷却数的时候,一般均采用近似积分方法。
10章—4冷却塔热力计算基本方程

(8)求N i : 用抛物线法,把(2)视为 抛物线,取两格,由三个点, 如: 1 1 1
i , t1 , i , t 2 i , t 0 , 0 1 2
这三点视为抛物线(不是 抛物) 。所围面积:
xv
Q
dV
Cwdt K i i
t1
xv
Cw V Q K
dt t2 i i
在Merkel方程基础上建立的冷却塔基本计算方 程(以焓差为推动力) xv Cw t dt
Q V K
1
t2
i i
冷却塔所具有 的散热能力
冷却任务的大小, 对冷却塔的要求。
由式:
1 C wQdt 空气吸热 Gdi 水的散热 K
即: 令:
di 1Q Cwdt K G
G (气水比) Q
di 1 tg Cwdt K
1 K
表示di与dt成直线关系,斜率为: 积分下式:边界条件用塔底空气焓i1和水温t2 。
1 Gdi K CwQdt Cw G(i2 i1 ) Q(t1 t2 ) K (t1 t2 ) Q (t1 t2 ) i2 i1 Cw i1 Cw (kJ / kg ) K G K
xv
K imV
可知:V可越小(填料、塔体均可小)
(3)t2越小(t2-τ)值越小→△i也越小, 冷却困难;V增大。 一般要求t2-τ≮3~5℃
G (4) 的变化,使操作线斜率变化 Q
λ↗ → 斜率 λ ↗ →风量G↗ → 电耗↗
设计时λ应在最佳范围。
1 K↘→△im↗
→有利冷却
冷却塔的热力计算

冷却塔的热力计算冷却塔的任务是将一定水量Q ,从水温t 1冷却到t 2,或者冷却△t =t 1-t 2。
因此,要设计出规格合适的冷却塔,或核算已有冷却塔的冷却能力,我们必须做冷却塔的热力计算。
为了便于计算,我们对冷却塔中的热力过程作如下简化假设:(1)散热系数α,散质系数v β,以及湿空气的比热c ,在整个冷却过程被看作是常量,不随空气温度及水温变化。
(2) 在冷却塔内由于水蒸气的分压力很小,对塔内压力变化影响也很小,所以计算中压力取平均大气压力值。
(3)认为水膜或水滴的表面温度与内部温度一致,也就是不考虑水侧的热阻。
(4) 在热平衡计算中,由于蒸发水量不大,也可以将蒸发水量忽略不计。
(5) 在水温变化不大的范围内,可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。
冷却塔的热力计算方法有焓差法、湿差法和压差法等,其中最常用的是麦克尔提出的焓差法,以下简要介绍冷却塔的焓差法热力计算。
麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式,统一为一个以焓差为动力的传热公式。
在方程式中,麦克尔引进入刘易斯关系式,导出了以焓差为动力的散热方程式。
()dV h h dH t xv q 0"-=β (1) 式中:q dH —— 水散出热量;xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ;"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /); 0h —— 空气比焓 (kg kJ /)。
将式(1)代入冷却塔内热平衡方程:n w w q tdQ c Qdt c dH += (2)式中:q dH —— 水散出热量;w c —— 水的比热()[]C /J o ⋅kg k ;Q —— 冷却水量 (s /g k );u Q —— 蒸发水量 (s /g k )t —— 水温度 (℃) 并引入系数K :式中 m r ——塔内平均汽化热(kg kJ /)经整理,并积分后,可得冷却塔热力计算的基本方程式:⎰-=120"t t t w xv h h dt c Q v K β (3) 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力,它与淋水填料的特性、构造、几何尺寸、冷却水量有关,称冷却塔的特性数,以符号愿'Ω表示,即:(3)式的右端表示冷却任务的大小,与气象条件有关,而与冷却塔的构造无关,称为冷却数(或交换数),以符号'Ω表示,也即:由于水温不是空气焓的直接函数,直接积分有困难,所以,在求解冷却数的时候,一般均采用近似积分方法。
冷却塔逆流闭式热交换器热力计算

冷却塔逆流闭式热交换器热力计算冷却塔逆流闭式热交换器是一种常用的设备,用于在不同介质之间进行热量传递。
本文将介绍如何进行冷却塔逆流闭式热交换器的热力计算。
1. 热力计算的基本原理在冷却塔逆流闭式热交换器中,热量的传递是通过传热面积、传热系数和温度差来实现的。
传热面积是指两种介质接触的面积,传热系数是介质之间传热的效率,温度差是指介质之间的温度差异。
2. 热力计算的步骤进行冷却塔逆流闭式热交换器的热力计算,需要以下步骤:步骤1:计算传热面积传热面积可以通过以下公式计算:\[A = \frac{Q}{U \cdot \Delta T_{lm}}\]其中,A为传热面积,Q为传热量,U为传热系数,\(\Delta T_{lm}\)为对数平均温差。
步骤2:确定传热系数传热系数是介质之间传热效率的一个参数,可以通过实验或者参考相关文献来确定。
步骤3:计算对数平均温差对数平均温差可以通过以下公式计算:\[\Delta T_{lm} = \frac{\Delta T_1 - \Delta T_2}{\ln(\frac{\Delta T_1}{\Delta T_2})}\]其中,\(\Delta T_1\)和\(\Delta T_2\)分别为两种介质的温度差。
步骤4:计算传热量传热量可以通过以下公式计算:\[Q = U \cdot A \cdot \Delta T_{lm}\]其中,Q为传热量。
3. 示例举个例子来说明热力计算的过程。
假设冷却塔逆流闭式热交换器的传热系数为10 W/ (m2·°C),传热面积为50 m2,两种介质的温度差为20°C。
首先,我们可以通过步骤1计算出对数平均温差:\[\Delta T_{lm} = \frac{20 - 0}{\ln(\frac{20}{0})} =\frac{20}{\ln(\infty)} = 20\]然后,根据步骤4计算传热量:\[Q = 10 \cdot 50 \cdot 20 = \]所以,该冷却塔逆流闭式热交换器的传热量为 W。
空调系统中的冷却塔应用手册

冷却塔是水与空气进行热交换的一种设备,它主要由风机、电机、填料、播水系统、塔身、水盘等组成,而进行热交换主要由在风机作用下比较低温空气与填料中的水进行热交换而降低水温。
冷却塔的降温及耗水量分析:在冷却塔的水气热交换中,水蒸发吸收潜热、湿空气升温吸收显热,是冷却水温度降低的原因。
据热平衡原理有:Q= r×I+ C×C L×ΔT,Kcal/h ⑴或Q=L O×(t1-t2),Kcal/h ⑵式中,Q:冷却水释放的热量,即是冷却水塔的热负荷或制冷量;r:水的蒸发潜热,Kcal/h;I:水的蒸发量 Kg/h;C:空气的比热Kcal/kg.℃;C L:空气的质量流量Kg/hΔT= T2-T1:空气通过水塔的温升,℃;L O:冷却水的质量流量,Kg/h;t1-t2:冷却水进出塔的温差,℃。
众所周知:水的蒸发潜热是很大的(约 2427.9KJ/KG或 580Kcal/KG)而空气的比热则是很小的(0.2Kcal/kg℃),所以两种热量传递方式中,尤其是在气候温度比较高时,水的蒸发吸收的热量是引起冷却水降温的主要原因,而水、气之间的温差传递则是次要的,二者比值将随着气候条件而变化。
通常,可设水蒸发吸热占总散热量的 75~80%,温差传热占 20~25%,并以此比值估计水塔的空气用量,但是实际上则不然,许多资料表明,实测数据亦证实,水蒸发吸收的热量随气候条件变化是很明显的,高可达 95%以上,低则小于 75%,了解冷却水塔的工作原理,就不难进行耗水量分析,如不考虑冷却水系统的漏损,则冷却水的消耗包括如下三部分:①冷却水的部分蒸发:部分水蒸发引起冷却水消耗是正常的、必须的,其消耗量不仅同冷却水本身的质量、流量、降温幅度(即热负荷)有关,同时还和入塔空气的温度(包括干球温度和湿球温度)和质量流量有关,为了向用户提供较可信的蒸发数据,在收集并分析有关数据的基础上,用试验方法验证,测得数据用如下公式计算的:e=G(X2-X1)/L×100%式中:e:水的百分蒸发量,%;G:空气的质量流量 kg/h或kg/min;L:冷却水的质量流量,kg/h或 L/min;X2-X1:空气在出塔和入塔时的含湿量 kg/kg;下表列出收集的文献数据及的实测数据,不难看出文献值的平均值与实测值是极其接近的。
冷却塔热力计算书1

YNZT 型玻璃钢双曲线自然通风冷却塔三、计算方热力计算书冷却为图表求一、已知条件1、试差法1、气象参数:干 球 温 度(θ1 ℃湿 球 温 度(大 气 压 力(P0)最大相对湿度(Φ2、工况条件: 试差法计循 环 水 量(Q) m³/h进 水 温 度(t1)出 水 温 度(t2)工况水温降(Δt ℃3、所用冷却塔的基本参数:1淋水面积(F1)m22出风口处有效面积(F T)m23进 风 口 高 度 (H1)m4有 效 高 度 (H0)5进风口 平均直径 (Dz)6淋水密度(q)3/m2h74、所用淋水填料的特性参数:8该冷却塔采用PVC淋水填料,波形为Z形波,淋水填料的有效高度 1米。
9a、淋水填料的特征数 N’N’=1.76λ0.5810b、淋水填料的阻力特性 ΔP△P/ρ= A V m1112二、设计计算采用试差法1、热力计算的目的:通过热力计算求证 实际出水温度 t2≤32℃2、初始参数: 2、图表法a、干球温度θ时的进塔空气密度 ρ1 kg/ m³b、进 塔 空 气 焓 h1KJ/kgc、进水温度 t1 时的饱和空气焓 h1〃KJ/kg3、所用计算公式:a、冷却塔热力计算基本公式:N =∫Cdt/h″-hN值的计算采用幸普逊两段积分法,公式如下:N =[(Δt/k6)C m[1/(h2〃-h1)+4/(h m〃-h m)+1/h1〃-h2)]h1 — 为进塔空气焓KJ/kgh2 — 为进塔空气焓KJ/kg第 1 页h m — 为平均空气焓KJ/kg四、结t m — 平均进水温度t m=(t1+t2)/2 ℃h1〃 — 进塔水温t1时的饱和空气焓KJ/kgh2〃 — 进塔水温t2时的饱和空气焓KJ/kgh m〃 — 进塔水温t m时的饱和空气焓KJ/kgb、所需参数的计算公式: ⑴、进塔空气相对湿度的计算公式:Φ=[(Pτ〃-AP0(θ1-τ)]/Pθ1〃 ⑵、进塔干空气密度:ρ1=[(P0-ΦPθ1〃)×1000]/[287.14(273+θ1)] ⑶、饱和空气的水蒸汽分压在0~100℃时的计算公式:lg Pt〃=2.0057173-3.142305(1000/T-1000/373.16)+8.2lg(373.16/T)-0.0024804(373.16-T) ⑷、气水比的计算公式:λ=3600ρ1V m/1000q ⑸、进塔空气焓的计算公式:h1=1.006θ1+(2500+1.858θ1)×[ΦPθ1〃/(P0-ΦPθ1〃)] ⑹、温度为 t 时的饱和空气焓计算公式:h t〃=1.006t+(2500+1.858t)×[P t〃/(P0-P t〃)] ⑺、出塔空气焓的计算公式:h2=h1+(CΔt/kλ) ⑻、塔内空气的平均焓计算公式:h m=(h2+h1)/2 ⑼、出塔空气干球温度的计算公式:θ2=θ1+(t m-θ1)×(h2-h1)/(h m-h1) ⑽、出塔干空气密度的计算公式: (设Φ=1)ρ2=[(P0-Pθ2〃)×1000]/[287.14(273+θ2)] ⑾、平均空气密度的计算公式:ρm=(ρ2+ρ1)/2 c、冷却塔抽力的计算公式:Z=H0g(ρ1-ρ2)d、冷却塔阻力的计算公式:ΔP=ξρm V m2 /2 公式中:k=1-t2/[586-0.56(t2-20)]C — 水的比热,C=4.187KJ/Kg℃第 2 页⑴、假定风速,求t2~V m关系曲线假定风速为:0.8、1.0、1.2、1.4 m/s附图风 速 V m(m/s)出水温度t2(℃)⑵、假定风速,求Z~V m关系曲线冷却塔抽力计算的结果如下:风 速 V m(m/s)抽力Z (KPa)⑶、假定风速,求ΔP~V m关系曲线风 速 V m(m/s)阻力ΔP(KPa)⑷、用求出的 t2~V m Z~V m ΔP~V m三条关系曲线作图,见附图。
冷却塔模拟计算方法1
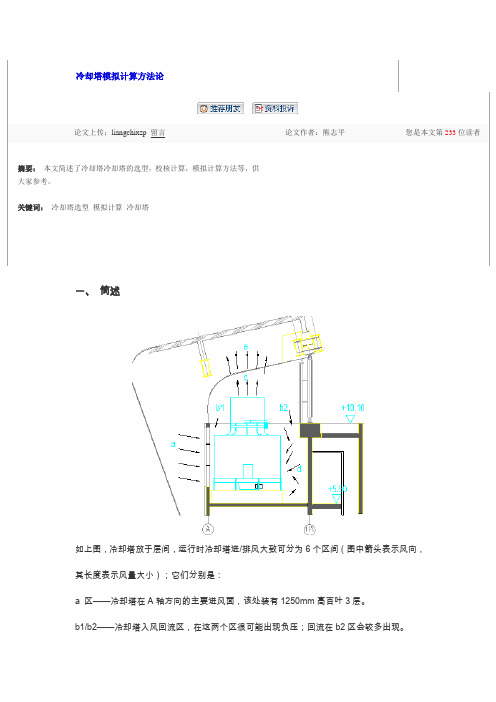
一、简述如上图,冷却塔放于层间,运行时冷却塔进/排风大致可分为6个区间(图中箭头表示风向,其长度表示风量大小);它们分别是:a 区——冷却塔在A轴方向的主要进风面,该处装有1250mm高百叶3层。
b1/b2——冷却塔入风回流区,在这两个区很可能出现负压;回流在b2区会较多出现。
c 区——冷却塔高速排风区。
d 区——冷却塔在1/A轴方向通风区,该区为负压区,风速较a区高,且以乱流出现居多。
e 区——热风扩散区;冷却塔排风经过一段距离(冷却塔排风口到建筑顶部百叶约4000m m)后,动压明显下降,静压上升,该区属正压区,其间大部分热风经建筑顶部百叶排入大气,少部分弥散后排风受阻会滞留一段时间,但,由于上下(e 区~b区)空间随机存在着压差,使得部分e区弥散的热风回流。
二、冷却塔的选型1、设计条件温度:38℃进水,32℃出水,27.9℃湿球;水量:1430M³/H;水质:自来水;耗电比:≤60Kw/台,≤0.04Kw/M³·h,场地:23750mm×5750mm;通风状况:一般。
2、冷却塔选型符合以上条件的冷却塔为:LRCM-H-200SC8×1台。
(冷却塔[设计基准]37-32-28℃,此条件下冷却塔处理水量为名义处理水量)其中,LRC表示良机方形低噪声冷却塔,M表示大陆性气候适用,H表示加高型,200表示冷却塔单元名义处理水量200M³/H,S表示该机型区别于一般冷却塔,C8表示该塔共由8个单元并联组合而成,即名义处理总水量为1600M³/H。
冷却塔的外观尺寸为:22630×3980×4130。
冷却塔配电功率:7.5Kw×8=60Kw,耗电比为60÷1600=0.0375Kw/M³·h。
三、校核计算1、已知条件:冷却塔LRCM-H-200SC8在37-32-28℃温度条件下单元名义处理水量L=200 M³/H;冷却塔风量G=1690M³/min。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
YNZT 型玻璃钢双曲线自然通风冷却塔三、计算方
热力计算书冷却
为图表求一、已知条件1、试差法
1、气象参数:干 球 温 度(θ1 ℃
湿 球 温 度(
大 气 压 力(P0)
最大相对湿度(Φ
2、工况条件: 试差法计
循 环 水 量(Q) m³/h
进 水 温 度(t1)
出 水 温 度(t2)工况
水温降(Δt ℃
3、所用冷却塔的基本参数:1
淋水面积(F1)m22
出风口处有效面积(F T)m23
进 风 口 高 度 (H1)m4
有 效 高 度 (H0)5
进风口 平均直径 (Dz)6
淋水密度(q)3/m2h7
4、所用淋水填料的特性参数:8
该冷却塔采用PVC淋水填料,波形为Z形波,淋水填料的有效高度 1米。
9
a、淋水填料的特征数 N’N’=1.76λ0.5810
b、淋水填料的阻力特性 ΔP△P/ρ= A V m11
12
二、设计计算采用试差法
1、热力计算的目的:
通过热力计算求证 实际出水温度 t2≤32℃
2、初始参数: 2、图表法
a、干球温度θ时的进塔空气密度 ρ1 kg/ m³
b、进 塔 空 气 焓 h1KJ/kg
c、进水温度 t1 时的饱和空气焓 h1〃KJ/kg
3、所用计算公式:
a、冷却塔热力计算基本公式:
N =∫Cdt/h″-h
N值的计算采用幸普逊两段积分法,公式如下:
N =[(Δt/k6)C m[1/(h2〃-h1)+4/(h m〃-h m)+1/h1〃-h2)]
h1 — 为进塔空气焓KJ/kg
h2 — 为进塔空气焓KJ/kg
第 1 页
h m — 为平均空气焓KJ/kg四、结
t m — 平均进水温度t m=(t1+t2)/2 ℃
h1〃 — 进塔水温t1时的饱和空气焓KJ/kg
h2〃 — 进塔水温t2时的饱和空气焓KJ/kg
h m〃 — 进塔水温t m时的饱和空气焓KJ/kg
b、所需参数的计算公式:
⑴、进塔空气相对湿度的计算公式:
Φ=[(Pτ〃-AP0(θ1-τ)]/Pθ1〃
⑵、进塔干空气密度:
ρ1=[(P0-ΦPθ1〃)×1000]/[287.14(273+θ1)]
⑶、饱和空气的水蒸汽分压在0~100℃时的计算公式:
lg Pt〃=2.0057173-3.142305(1000/T-1000/373.16)
+8.2lg(373.16/T)-0.0024804(373.16-T)
⑷、气水比的计算公式:
λ=3600ρ1V m/1000q
⑸、进塔空气焓的计算公式:
h1=1.006θ1+(2500+1.858θ1)×[ΦPθ1〃/(P0-ΦPθ1〃)]
⑹、温度为 t 时的饱和空气焓计算公式:
h t〃=1.006t+(2500+1.858t)×[P t〃/(P0-P t〃)]
⑺、出塔空气焓的计算公式:
h2=h1+(CΔt/kλ)
⑻、塔内空气的平均焓计算公式:
h m=(h2+h1)/2
⑼、出塔空气干球温度的计算公式:
θ2=θ1+(t m-θ1)×(h2-h1)/(h m-h1)
⑽、出塔干空气密度的计算公式: (设Φ=1)
ρ2=[(P0-Pθ2〃)×1000]/[287.14(273+θ2)]
⑾、平均空气密度的计算公式:
ρm=(ρ2+ρ1)/2
c、冷却塔抽力的计算公式:
Z=H0g(ρ1-ρ2)
d、冷却塔阻力的计算公式:
ΔP=ξρm V m2 /2
公式中:
k=1-t2/[586-0.56(t2-20)]
C — 水的比热,C=4.187KJ/Kg℃
第 2 页
⑴、假定风速,求t2~V m关系曲线
假定风速为:0.8、1.0、1.2、1.4 m/s
附图
风 速 V m(m/s)
出水温度t2(℃)
⑵、假定风速,求Z~V m关系曲线
冷却塔抽力计算的结果如下:
风 速 V m(m/s)
抽力Z (KPa)
⑶、假定风速,求ΔP~V m关系曲线
风 速 V m(m/s)
阻力ΔP(KPa)
⑷、用求出的 t2~V m Z~V m ΔP~V m三条关系曲线作图,见附图。
⑸、采用图表法计算的结果如下:
a、出水温度 t2 =31.753℃
b、填料处风速 V m=1.0634 m/s
第 4 页
三、计算方法
冷却塔的热力计算采用两种计算方法,第一种方法为试差法,第二种方法为图表求解法。
1、试差法
试差法的求解主要是应用了冷却塔热力计算中的两个等式,即:
⑴、填料的特性数 N'等于热工的交换数 N 即 N'-N = 0
⑵、冷却塔的抽力 Z 等于冷却塔的阻力 ΔP 即 Z -ΔP = 0
在两个等式中有两个变量即出水温度 t2和填料横截面的风速 V
试差法计算的所用的公式全部编入计算机的程序,并列出数次试差的记录,其记录的数据列入下表:
⑴、出水温度 t2 =32.75℃, (N'-N)/N'<1.0‰
⑵、填料处风速 V m=1.063m/s (Z-ΔP)/ Z <1.0‰
2、图表法
图表法的求解做出三条关系曲线:
a、出水温度 t2 与风速 V m的关系曲线,即 t2~V m关系曲线。
b、冷却塔抽力 Z 与风速 V m的关系曲线,即 Z~V m关系曲线。
c、冷却塔阻力 ΔP 与风速 V m的关系曲线,即 ΔP~V m关系曲线。
求出三条关系曲线后,以风速V m为横坐标将三条关系曲线画在坐标图上。
由 Z~V m曲线和ΔP~V m曲线的交点做直线与t2~V m曲线相交求出冷却塔的
出水温度 t2 和相的应风速 V m。
计算步骤:
a、应用填料的特性数 N'等于热工的交换数 N,即 N'-N=0的关系式
假定风速,用试差法求出t2~V m关系曲线。
b、假定风速,进行冷却塔抽力的计算,求出 Z~V m关系曲线。
c、假定风速,进行冷却塔阻力的计算,求出 ΔP~V m关系曲线。
第 3 页
四、结论
根据当地的气象参数及技术条件,本工程选用一座YNZT 600平方米的
玻璃钢双曲线自然通风冷却塔。
实际出水温度 t2 = 31.32℃
五、 其他因素的影响
1、 在干球温度 26.8℃, 湿球温度 24℃, 相对湿度80%的条件下
进水温度℃40414243
出水温度℃31.0331.1931.3231.45
水 温 降Δt8.979.8110.6811.55
从上述数据中可以看出:在同等的气象条件下,随着进水温度的提高,出水 温度的变化不大,而水温降随着进水温度的提高而增大.
2、 在进水温度 42℃, 相对湿度80%的条件下
湿球温度℃24252627
出水温度℃31.3231.8832.4533.03
水 温 降Δt10.6810.129.558.97
从上述数据中可以看出:在进水温度和相对湿度一定的条件下,随着湿球 温度的提高,出水温度随着升高,而水温降随着进水温度的提高而降小.
第 5 页
附图
第 6 页。
