数学模型-市场经济中的蜘蛛网模型

1
18
(9)、(10)与蛛网模型的(3)、(4)式是 一致的。
19
方程模型
在P0点附近用直线近似曲线
yk f ( xk )
yk y0 ( xk x0 ) ( 0) xk 1 x0 ( yk y0 ) ( 0)
xk 1 h( yk )
k x x ( ) ( x1 x0 ) xk 1 x0 ( xk x0 ) k 1 0
2
趋向平稳，有的则振幅越来越大导致经 济崩溃。当然政府会对后者采取干预手 段。
这一节我们先用图形方法建立所谓 “蛛网模型”，对上述现象进行分析， 讨论市场经济趋于稳定的条件。用分差 方程建模，对结果进行解释，并适当推 广。
3
7.1 市场经济中的蛛网模型
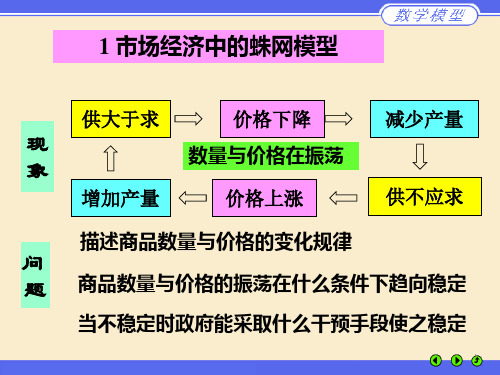
供大于求 价格下降
数量与价格在振荡 增加产量 价格上涨 供不应求
13
等因素有关。
一旦需求曲线和供应曲线被确 定下来，如何判断它们的交点—平 衡点P0得稳定性呢？从图8-1和图8-2 不难看出，当市场经济偏离P0点不大 (|x1 – x0|较小)时，P0点得稳定取决于f 和 g 在P0的斜率。 记f 在P0点斜率的绝对值（因为 它是下降的）为Kf ， g 在P0点的斜率
(14)
31
当αβ > 8时显然有
( ) 2 8 2 4

4
从而，|λ2| > 2, λ2在单位圆外。下面设α
β < 8,可以算出
1, 2

2
（15）
32
由|λ2| < 1得到P0点稳定的条件为
αβ < 2
（16）
与原有模型中P0点稳定的条件（9） 式相比，保持经济稳定的参数α 、β 的范围放大了（α、β得含义未变）。 可以想到，这是生产经营者的生产 管理水平提高，对市场经济稳定起 着有利影响的必然结果。
减少产量
现 象
问 题
描述商品数量与价格的变化规律 商品数量与价格的振荡在什么条件下趋向稳定
当不稳定时政府能采取什么干预手段使之稳定
4
蛛网模型 记第k时段商品的数量为xk, k = 1,2,… 。这里我们把时间离散化为时段， 一个时段相当于商品的一个生产周期，如 蔬菜、水果可以是1年，肉类则是一个饲养 周期。 同一时段商品的价格yk取决于数量xk ,设
yk y0 ( xk x0 )
~ 商品数量减少1单位, 价格上涨幅度
xk 1 x0 ( yk y0 )
~ 价格上涨1单位, (下时段)供应的增量 ~ 消费者对需求的敏感程度 ~ 生产者对价格的敏感程度 小, 有利于经济稳定 小, 有利于经济稳定
（13）是二阶线性差分方程，为了寻求 k∞时xk x0 ，即P0点稳定的条件， 不必解方程（13），只须利用判断稳定
30
条件—防城特征根均在单位圆内（见 8.6节(9)式）。
因为方程（13）的特征方程
2 0
2
容易算出其特征根为
( ) 2 8 1, 2 4
供应曲线变为竖直
靠经济实力控制数量不变
0 x0
x
28
模型的推广 如果生产者的管理水平更高一些，他们 在决定商品生产数量xk+1时，不是仅根据前一时期的 价格yk ，而是更具前两个时期的价格 yk和yk-1 。为了 简单起见不妨设取二者的平 均值(yk+yk-1) /2，
于是供应函数(2)式表示为
yk yk 1 xk 1 g ( ) 2
P0是不稳定平衡点
y P3 f P0 P1 x0 x
f
P3 P2
g P4 P0
曲线斜率
K f Kg
P1 x1
g
P4
y0 0
P2
K f Kg
12
x2
x0 x3
x
图8-1和图8-2中折线P1P2P3P4…形 似蛛网，于是，这种需求曲线和供 应曲线分析市场经济稳定性的图示 法在经济学上称为蛛网模型。实际 上，需求曲线f 和供应曲线 g 的具体 形式通常是根据各个阶段商品数量 和价格的一些列统计资料x1, y1 ,x2 ,y2 , …得到的。一般地说，f 取 决于消费者对这种商品的需求程度 和他们的消费水平，g 则与生产者的 生产能力、经营水平
市场经济中的蜘蛛网模型
在自由贸易市场上你注意过这样的现 象吗：一个时期由于猪肉的上市量远大 于需求，销售不畅导致价格下降，农民 觉得养猪赔钱，于是转而经营其他农副 产品。过一段时间后猪肉上市量大减， 供不应求导致物价上涨。原来的饲养户 看到有利可图，有重操旧业。这样下一 个时期会出重现供大于求，价格下降的
1
局面。在没有外面干预的情况下，这种现 象将如此循环下去。在完全自由竞争的市 场经济中上述现象通常是不可避免的。因 为商品的价格是由消费者的需求关系决定 的。商品数量越多价格越低。而下一时期 商品的数量由生产者的供求关系决定，商 品价格越低生产的数量就越少。这样的需 求和供应关系决定了市场经济中商品的价 格和数量必然是震荡的。在现实世界里这 样的震荡出现不同的形式，有的振幅渐小
xk+1 = (-αβ)kx1+(1 - (-
(8)
17
由此可得，当k∞时xk x0 ,使得 P0稳定的条件是
αβ < 1 或 α <1
而k∞时，xk∞, 即P0点不是稳定 点的条件是
1
αβ < 1 或 α < 1
注意到(5)、(6)式中α、β的定义， 1 有Kf = α，kg= ，所以条件
23
即α固定时，β越小，供应曲线越陡， 表明生产者对价格的敏感程度越小(使 (9)式成立),越利于经济稳定。 反之，当α、β较大，表明消费者 对商品的需求和生产者对商品的价格 都很敏感，则会导致经济不稳定。
24
结果解释 结果解释
考察 , 的含义
xk~第k时段商品数量；yk~第k时段商品价格
9
函数由图8-2的曲线所示，则类似的分 析发现，市场经济将按照P1, P2, P3, P4，… 的规律变化而远离P0，即P0不 是稳定的平衡点，市场经济趋向不稳 定。
10
图8-2 P0是不稳定的平衡点
11
P P P P P P P P0 1 2 3 1 2 3 0
14
为Kg ，则当
Kf < K g
(3)
时P0是稳定点的（图8-1），而当
Kf < Kg
(4)
时P0点是不稳定的（图8-2）。由此可 见，需求曲线越平，供应线越陡，越 有利于经济稳定。在对这种现象作出
15
解释之前，我们先利用差分方程将蜘 蛛网模型的结果用公式表示出来。
差分方程形式 在P0点附近取函数 f 和h的线性近似，设（1）、（2）式 分别近似为
xk 1 x0
（11）
在P0点附近取线性近似时（6）式表示为

2( yk ຫໍສະໝຸດ yk 1 2 y0 )（12）
29
β含义不变。又设需求函数仍为（1）、 （5）式表示。则由（5）、（12）式 得到
2 xk 2 xk 1 xk (1 ) x0 , (k 1,2,) （13）
22
上涨立即大量增加生产，那么β值会比 较大；反之，若他们素质较高，有长 远的计划，则β较小。 根据α、β的意义很容易对商场经 济稳定与否的条件(9)、(10)做出解释。 当供应函数g ,即β固定式，α越小，需 求曲线越平，表明消费者对商品需求 的敏感程度越小（使(9)式 成立），越 利于经济稳定。当需求函数f ，
yk – y0 =α(xk – x0) , α > 0 (5)
xk+1 – x0 = β(yk – y0 ), β >0 (6)
16
消去yk , (5) , (6)可合并为
xk+1 = (-αβ)kxk+(1- (-αβ)k)x0
（k =1,2 ，…） (7)
（7）是一阶线性差分方程，对k递推
不难得到
P0是稳定平衡点
y y2 y0 y3 y1 0
蛛 网 模 型 yk f ( xk ) xk 1 h( yk ) yk g ( xk 1 ) x1 y1 x2 y2 x3 设x1偏离x0 xk x0 , yk y0 xk x0 , yk y0
yk = f (xk)
(1)
它反映消费者对这种商品的需求关系，称 为需求函数。因为商品的数量越多价格越
5
低，所以在图8-1中用一条下降曲线 f 表 示它，f 为需求曲线。
下意识段商品的数量xk+1由上一时段价 格yk 决定，设
xk+1 = h (yk) , 或 yk = g (xk+1) (2)
它反映生产者的供应关系，称供应函数。 因为价格越高生产产量才越大，所以在 图中供应曲线是一条上升曲线。
1 ( 1 / )
xk x0 xk
P0稳定 K f K g P0不稳定 K f K g
1 ( 1 / )
方程模型与蛛网模型的一致
Kf
1/ K g
20
模型解释 首先考察α 、β得含义。需求函数f 的斜率 α（取绝对值）表示商品供应量减少1 个单位时价格的上涨幅度；供应函数h的斜率 β 表示价格上涨1个单位时（下一时期）商品 供应的增加量。
6
图中两个曲线相交于P0(x0 , y0)点。P0 是平衡点，因为一段对某个 k 有 x k = x0， 则由(1)、(2)可知 yk =y0 ，xk+1 = x0 , yk+1 = y0 , … ， 即商品的数量和价格将永远保 持在p0(x0 , y0 ) 点。但在实际生活中的种 种干扰使得 x , y不可能停止在P0点，不妨 设x1偏离x0(如图8-1）。我们分析随着k的 增加xk , yk的变化。