最优装载
贪心算法之最优装载问题
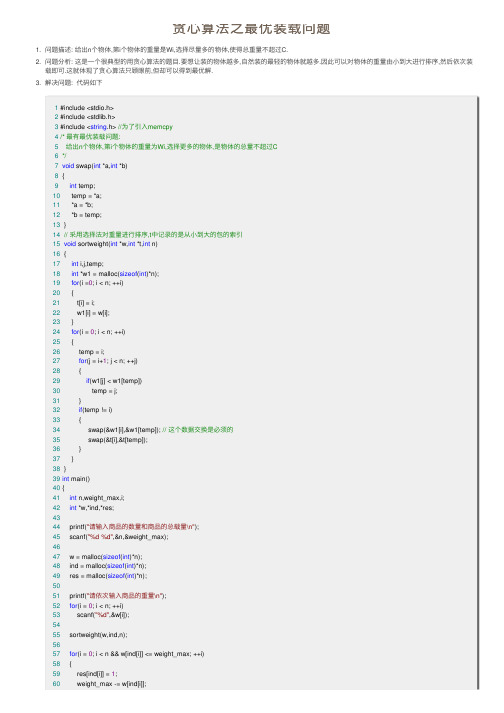
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。
最优装载问题

3基于背包和装载数量限制分类类
4基于所装物品的依赖性分类
001 基于背包的限制条件分类
···
002 基于待选择装载物品的数量分类
···
003 基于背包和装载数量限制分类
···
004 基于所装物品的依赖性分类
···
根据所装物品的依赖性,可将最优装载问题分为“分组的最优转载 问题”和“有依赖的最优装载问题”
必需品编号
1
2
3
4
5
6
7
体积(升)
4
3
1.5
2.5
4.5
7.6
1.9
1 可选带物品编号
2
3
4
5
6
7
8
体积(升) 2.5 4
5.5
4.8
3.7
1.6
7.5
4.5
价格(元) 20 50 105
75
55
80
200 100
最优装载问题的数学抽象就是著名的背包问题
案例 2
货轮装载问题:有一艘货轮分为前、中、后三个舱位,其容积与最大允
“分组的最优装载问题”就是把待装物品分为若干组,每组中至多 选一件装载;
“有依赖的最优装载问题”就是选择某一待装载物品,必须选择另 一个物品装载。
小结 最优装载问题不同类型之间的组合情况
···
分组问题 二维费用问题
0-1问题 完全装载 多重装载
分组问题
二维费用问题
0-1问题 完全装载 多重装载
分组问题
3 最优装载问题的MATLAB求解
···
3 最优装载问题的MATLAB求解
···
标题4 案 例 模型
1
铁路平板车包装箱的最优化装载模型new(2)

铁路平板车包装箱最优化装载模型小组成员:张建栋 蔡艺鑫 杨榕榕铁路平板车包装箱的最优化装载模型目录大纲摘要 (2)关键词 (2)一、问题的提出 (2)二、基本假设和符号规定 (2)三、分析与建立模型 (3)模型一:个体最优化 (3)模型二、整体最优化Ⅰ (5)整体最优化Ⅱ (6)四、结果分析 (7)五、模型优化 (8)六、参考文献 (8)七、附件(lingo代码) (8)铁路平板车包装箱的最优化装载模型摘要 本论文根据铁路平板车的装载要求以及包装箱的限制条件,将包装箱的最优化装载方案转化为整数线性规划中的最值求解问题。
模型一采用单个分析法,先求出第一辆车的最优装载方式。
模型二则采用整体最优规划方案,通过分枝定界法和lingo 软件求解确定最优化整数值。
关键词 整数线性规划ILP 个体最优 整体最优 分枝定界法 一、问题的提出7种规格的包装箱要象面包片那样装到两辆铁路平板车上去,包装箱的宽和高相同,但厚度(t ,以cm 计)和重量(w,以kg 计)不同,每种包装箱的厚度, 重量和数量在表一中列示。
限制条件为每辆车包装物的总厚度不得超过10.2m ,每辆车包装物的总重量不得超过40吨,567C C C 、、规格的包装箱所占的空间(厚度)不能超过302.7cm 。
试把包装箱装到两辆平板车上去(图1),使得浪费的空间最小,即求装载包装物所占空间的最大值。
二、基本假设和符号规定1、基本假设:1)两个包装物摆放时都紧密贴合,无缝隙。
2)包装箱的厚度, 重量和数量在表一中列示,没有误差。
2、符号规定:i C 表示1—7种规格的包装物 ti C 表示第i 种规格的包装物的厚度i x 表示在第一辆车上装载i C 种包装箱的个数。
1y 表示在第二辆车上装载i C 种包装物的个数三、分析与建立模型 模型一:个体最优化分析过程:设想先将第一量车在约束条件下装载最大货物,再将剩下的货物有选择地装载在第二量车上,使得第二量车装载量达到最大值。
贪心算法之最优装载问题

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船,其中集装箱i的重量为W i。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略,可产⽣该问题的最优解。
2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序,(x1,x2,…,x n)是其最优解,x i={0,1},设x k是第⼀个等于1的。
(1) 如k=1,则满⾜贪⼼选择性质(2) 如k≠1,⽤x1替换x k,构造的新解同原解最优值相同,故也是最优解,满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解(满⾜贪⼼策略)。
此⽅法对⼦问题同样有效,因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。
如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质,设1⾄n个集装箱装上船的最⼤数量为T(1,n,w),则T(1,n,w)=1+T(2,n,w−w1);因T(1,n,w)是最优值,则T(2,n,w−w i)⼀定是最优值,反证法证明之反证法:如果T(2,n,w−w1)不是该问题的最优解,则存在最优值T′(2,n,w−w1)>T(2,n,w−w1),则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w),这与⼤前提T(1,n,w)是最优值相⽭盾,故T(2,n,w−w1)⼀定是最优值。
最优装载问题

for(int j=n-1;j>0;j--)
r[j]=r[j+1]+w[j+1];
int i=1;
bbnode *E=0;
int Ew=0;
b->Lchild=ch; //cout<<"b->Lchild"<<b->Lchild<<endl;
HeapNode N;
N.uweight=wt;
N.level=lev;
};
//template <class int>
class MaxHeap{
friend void AddLiveNode(MaxHeap&,bbnode *,int,int,int );
friend int Maxloading(int*,int,int,int*);
// template<class int>
int MaxLoading(int w[],int c,int n,int bestw[])
{
MaxHeap H(20);
int *r=new int[n+1];
return N;
}
};
////////////////////////////////////////////////////////////////////
// template<class int> //将活节点加入到最大堆H中
}
AddLiveNode(H,E,Ew+r[i],0,i+1); // 右儿子节点
HeapNode N;
英语 算法 -回复

英语算法-回复如何使用贪心算法(Greedy Algorithm)解决最优装载问题(Knapsack Problem)。
【引言】贪心算法是一种基于局部最优选择的算法思想,可用于解决最优装载问题,即在给定容量的背包中,如何选择物品使其总价值最大。
本文将介绍如何使用贪心算法逐步解决最优装载问题,帮助读者更好地理解和应用贪心算法。
【步骤一:问题描述】首先,让我们明确最优装载问题的具体要求。
给定一个背包的容量C和N 个物品,每个物品有自己的重量w和价值v。
我们的目标是在不超过背包容量的情况下,选择物品放入背包,使得放入背包的物品的总价值最大。
【步骤二:贪心选择策略】贪心算法的核心思想是进行局部最优选择,以期望最终得到整体最优解。
对于最优装载问题,我们可以采用“单位重量价值最大”的贪心选择策略。
即优先选择单位重量价值最大的物品放入背包中,直至背包无法再放入物品。
【步骤三:算法实现】基于贪心选择策略,我们可以使用如下步骤实现算法:1. 根据物品的重量w和价值v,计算每个物品的单位重量价值vu = v / w。
2. 按照单位重量价值vu从大到小对物品进行排序。
3. 初始化当前背包的总价值val = 0和当前背包的剩余容量rc = C。
4. 逐个遍历排序后的物品列表:a. 如果当前物品的重量小于等于当前背包的剩余容量,则将该物品放入背包中,更新当前背包的总价值val和剩余容量rc。
b. 如果当前物品的重量大于当前背包的剩余容量,则放弃该物品,继续遍历下一个物品。
5. 返回最终的背包总价值val作为最优装载问题的解。
【步骤四:算法示例】接下来,我们通过一个简单的例子演示如何使用贪心算法解决最优装载问题。
假设背包容量C为10,有以下4个物品可供选择:物品1:重量w1 = 2,价值v1 = 5物品2:重量w2 = 3,价值v2 = 8物品3:重量w3 = 4,价值v3 = 9物品4:重量w4 = 5,价值v4 = 10按照贪心选择策略,首先计算每个物品的单位重量价值vu:物品1:vu1 = v1 / w1 = 5 / 2 = 2.5物品2:vu2 = v2 / w2 = 8 / 3 ≈2.67物品3:vu3 = v3 / w3 = 9 / 4 = 2.25物品4:vu4 = v4 / w4 = 10 / 5 = 2.0然后,按照单位重量价值vu从大到小对物品进行排序:物品2 > 物品1 > 物品3 > 物品4接下来,我们按照步骤三中的算法实现进行装载:初始化当前背包的总价值val = 0和剩余容量rc = 10。
贪心算法5

1
学习要点
理解贪心算法的概念。掌握贪心算法的基本要素。
(1)求解最优结构问题 (2)贪心选择性质
理解贪心算法与动态规划算法的差异;理解贪心算法的 一般理论;通过应用范例学习贪心设计策略。
(1)活动安排问题; (2)最优装载问题; (3)哈夫曼编码; (4)单源最短路径; (5)最小生成树; (6)多机调度问题。
算法huffmanTree用最小堆实现优先队列Q。初 始化优先队列需要O(n)计算时间,由于最小堆的 removeMin和put运算均需O(logn)时间,n-1次的 合并总共需要O(nlogn)计算时间。因此,关于n个字 符的哈夫曼算法的计算时间为O(nlogn) 。
26
4.4 哈夫曼编码
3、哈夫曼算法的正确性
实际上也是如此,动态规划算法的确可以有效地解01背包问题。
19
4.3 最优装载
有一批集装箱要装上一艘载重量为c的轮船。其中 集装箱i的重量为Wi。最优装载问题要求确定在装载体 积不受限制的情况下,将尽可能多的集装箱装上轮船。
1、算法描述
最优装载问题可用贪心算法求解。采用重量最轻者 先装的贪心选择策略,可产生最优装载问题的最优解。 具体算法描述如下页。
1、前缀码
对每一个字符规定一个0,1串作为其代码,并要求 任一字符的代码都不是其它字符代码的前缀。这种编码 称为前缀码。
23
4.4 哈夫曼编码
编码的前缀性质可以使译码方法非常简单。 表示最优前缀码的二叉树总是一棵完全二叉树,即 树中任一结点都有2个儿子结点。 平均码长定义为:
B(T ) f (c)dT (c) cC
3
4.1 活动安排问题
活动安排问题就是要在所给的活动集合中选出最 大的相容活动子集合,是可以用贪心算法有效求解的很 好例子。该问题要求高效地安排一系列争用某一公共资 源的活动。贪心算法提供了一个简单、漂亮的方法使得 尽可能多的活动能兼容地使用公共资源。
【数据结构】--C++实现箱子装箱问题

【数据结构】--C++实现箱⼦装箱问题⼀、问题描述①在箱⼦装载问题中,有若⼲个容量为c的箱⼦和n个待装载⼊箱⼦中的物品。
物品i需占是s[i]个单元(0<s[i]<=c)。
所谓成功装载(feasible packing),是指能把所有物品都装⼊箱⼦⽽不溢出,⽽最优装载(optimal packing)是指使⽤了最少箱⼦的成功装载。
对于箱⼦装载问题,有4种流⾏的求解算法。
②基本要求:->n依次取100,200,500,1000,⽐较以上四种⽅法(在时间上和所⽤箱⼦的数量上)的性能。
->FF,FFD⽅法使⽤竞赛树结构,BF,BFD使⽤⼆叉搜索树结构。
⼆、需求描述1.4种流⾏的求解算法:<1>最先匹配法(FF):物品按1,2...,n的顺序装⼊箱⼦。
假设箱⼦从左⾄右排列,每⼀物品i放⼊可盛载它的最左箱⼦。
<2>最先匹配递减法(FFD):⽅法与FF类似,区别在于各物品⾸先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].<3>最优匹配法(BF):设c[j]为箱⼦j的可⽤容量,初始时,所有箱⼦的可负载容量为c。
物品i放⼊具有最⼩c且容量⼤于s[i]的箱⼦中。
<4>最优匹配递减法(BFD):⽅法与BF相似,区别在于各物品⾸先按容量递减的次序排列,即对于1<=i<n,有s[i]>=s[i+1].2.输⼊要求:①第⼀种输⼊⽅式:n在程序中固定读⼊100,200,500,1000个数,这些数预先在⽂本中⼿动输⼊为固定的⽆序正整数。
②第⼆种输⼊⽅式:n为程序运⾏后,⼈为输⼊的数n,并且⽣成n个随机数,⽤作程序所需要测试的物品⼤⼩数。
3.输出要求:输出的要求为:直观的分析排列出在不同的箱⼦数量、不同的物品数量以及不同的物品⼤⼩的情况下,上述四种⽅法在时间上和所⽤的箱⼦的数量上的不同。
⽐较四种⽅法的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优装载
一、问题描述:
有一批集装箱要装上一艘载重量为c的轮船。
其中集装箱i的重量为Wi。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
二、输入:
表格一:物品的重量
三、输出:
图一:放入轮船的物品
四、算法描述:
定义存放的重量w[]、总容量为c、定义一个新数组数组内的序号定义为0,首先把数组的序号和数值打印出来,进行冒泡排序,把排序好的数组内的值打印一遍,开始往船上放物品,每放入一个物品,把这个物品的下标定义为1,并且用总容量c-w[i],当c大于0,就一直存放,直到不能放入为止。
五、算法设计:
使用贪心算法
首先要明白贪心算法,贪心算法以贪心为主,要达到每一步都是最优解。
于是,我先对物品的重量进行排序,在问题描述中已经得知,要将尽可能多的集装箱装上轮船,所以我按照从小到大的顺序物品排序完毕后,开始往轮船上放;在每一次放入后,刷新剩余的总容量,并将放入物品的下表定义为1,就这样依次装入,直到物品不能放入为止。
六、举例:
表格二:排序后的物品重量
因为轮船的容量为100,当第一个物品放入后当前背背包的容量为90,并且下标为1.
表格三:第一个物品放入后
当第一个物品放入后容量已经变为90,开始放入第二个物品,放入后当前总量为78,并让第二个物品下标为1。
表格四:第二个物品放入后
第二个物品放入后容量由原来的90变为现在的78,准备放入第三个物品,并让第三个下标为1。
表格五:第三个物品放入后
第三个物品放入后容量由原来的78变为现在的64,准备放入第四个物品,并让第四个下标为1。
表格六:第四个物品放入后
第四个物品放入后容量由原来的64变为现在的49,准备放入第五个物品,并让第五个下标为1。
表格七:第五个物品放入后
第五个物品放入后容量由原来的49变为现在的34,准备放入第六个物品,并让第六个下标为1。
表格八:第六个物品放入后
第六个物品放入后容量由原来的34变为现在的18,准备放入第七物品,并让第七个下标为1。
表格九:第七个物品放入后
第七个物品放入后容量由原来的18变为现在的2,准备放入第八个物品,发现第八个物品无法放入,循环结束。
七、附录:
#include <stdio.h>
#include <iostream>
#include <iomanip>
using namespace std;
void maopao(int b[],int t)
{
for (int i=t-1;i>0;i--)
{
for(int j=0;j<i;j++)
{
if(b[j]>b[j+1])
{
int temp=b[j];
b[j]=b[j+1];
b[j+1]=temp;
}
}
}
}
void printf1(int b[])
{
for(int i=0;i<5;i++)
{
cout<<setw(8)<<b[i];
}
cout<<endl;
}
void loading(int *a,int *r,int w,int n) {
r[0]=1;
w-=a[0];
for (int i=1;i<n;i++)
{
if(w-a[i]>=0)
{
w-=a[i];
r[i]=1;
}
}
}
void printf2(int *r,int len){
for (int i=0;i<len;i++)
{
cout<<setw(8)<<r[i];
}
printf("\n");
}
int main()
{
int w[5]={5,6,7,8,9}; //w数组中存放重量,x数组存放要放入的物体的序号/* int w[20];
for(int i=1;i<=10;i++)
{
cin>>w[i];
}*/
int x[5];
int dinyi[5]={0};
int c=20;
for(int j = 0;j<5;j++)
{
x[j]=j;
cout<<setw(8)<<x[j];
}
cout<<endl;
printf1(w);
maopao(w,5);
printf1(w);
loading(w,dinyi,c,5);
printf2(dinyi,5);
return 0;
}。
