实验四Matlab神经网络及应用于近红外光谱的汽油辛烷值预测
汽油组分及汽油辛烷值预测方法研究进展_仇爱波

关键词:辛烷值;汽油;汽油组分;拓扑指数法;基团贡献法
中 图 分 类 号 :TE62
文 献 标 识 码 :A
文 章 编 号 :1001-9219(2014)02-62-05
辛烷值是在内燃机的燃烧室中未燃混合气受已 燃气压缩和热传递时汽油抑制过早燃烧的表现数 值,是汽油性能最重要的指标之一,过早燃烧不仅过 度消耗了汽油资源, 还可能会在发动机工作时产生 爆炸性威胁,并且对发动机有所损害。汽油辛烷值是 用 ASTM-CFR 内 燃 机 在 相 同 测 试 条 件 下 与 测 试 汽 油达到相同爆震强度时异辛烷和正庚烷混合物的异 辛烷的体积分数表示的, 根据发动机的转速及进气 温 度 分 为 研 究 法 辛 烷 值 (RON) 和 马 达 法 辛 烷 值 (MON)。 随着汽车发动机压缩比的增加,对汽油辛 烷值的要求也越来越高, 如对每一个可能提高辛烷 值的物质进行合成, 再利用仪器对其辛烷值进行测 定, 这不仅花费大量的时间, 更花费大量的研究经 费, 因此通过各种算法来建立辛烷值的预测模型受 到广泛的关注,在早期一些文献[1]只报道了辛烷值与 化合物结构之间的一些定性关系, 随着各种计算软 件的研究开发,各种定量计算的方法才逐步被提出。
的含氧类化合物对辛烷值有所提高,并认为在整个 燃烧过程中自由基的形成来源于羰基结构,在燃烧 过程中影响着整个自由基的传递和终止, 确定了 α 位的 C-H 键对产生自由基起着决定性的作用。 通过 对影响分子键强度的现象分析,确定烯醇-酮的互变 异构的气象常数和形成最稳定的烯醇二聚物时烯 丙基氢的数量对自由基的传递起着决定性的作用。 基团贡献法的适用范围较广,主要注重分子结构的 拆解,要想拥有较高的相关性,则更要保证拆解的 正确性, 不过利用该方法获得的标准偏差相对较 大。 1.3 仪器分析法
汽油辛烷值神经网络预测模型的设计

汽油辛烷值神经网络预测模型的设计
秦秀娟;陈宗海
【期刊名称】《控制与决策》
【年(卷),期】1999(14)2
【摘要】针对催化重整工艺仿真数学模型中遇到的汽油辛烷值预测方面的困难,
提出一种将定量计算与神经网络计算相结合的催化重整工艺汽油辛烷值的预测模型。
此预测模型综合考虑了反应器温度。
【总页数】5页(P151-155)
【关键词】汽油;辛烷值;神经网络;预测模型;设计
【作者】秦秀娟;陈宗海
【作者单位】中国科学技术大学自动化系
【正文语种】中文
【中图分类】TE626.21
【相关文献】
1.汽油精制过程中的辛烷值损失预测模型 [J], 杜明洋;张甜甜;薄其高;许文文
2.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
3.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
4.基于改进PCA-RFR算法的汽油辛烷值损失预测模型的构建与分析 [J], 蒋伟;佟
国香
5.基于汽油催化裂化过程实时数据的辛烷值损失预测模型 [J], 韩庆珏;邹敏;霍皓灵
因版权原因,仅展示原文概要,查看原文内容请购买。
基于数据挖掘的汽油精制过程辛烷值损失预测模型
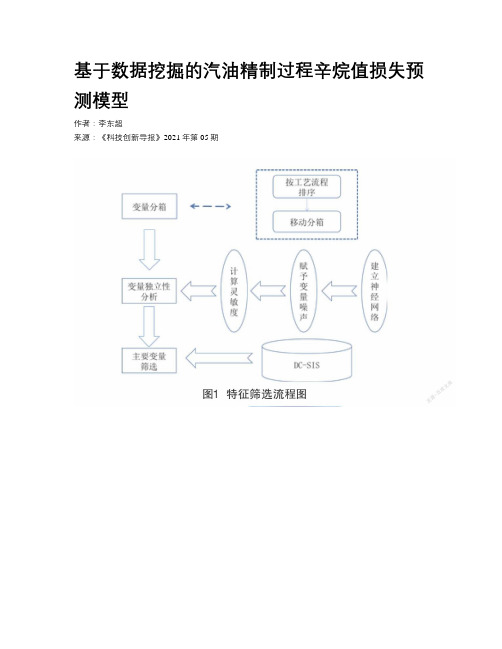
基于数据挖掘的汽油精制过程辛烷值损失预测模型作者:***来源:《科技创新导报》2021年第05期摘要:汽油精制过程中造成的辛烷值损失会降低汽油的燃烧效率,如何降低汽油精制过程中辛烷值的损失量是目前相关企业面临的一个重要课题。
本文利用我国某石化企业在催化裂化汽油精制过程中积累的数据,建立基于神经网络、测量误差模型以及DC-SIS数据降维方法的两阶段特征筛选模型,选择出对辛烷值影响比较大的因素。
设计了一种基于XGBoost和神经网络的辛烷值预测模型,可以实现对不同原材料和不同操作下精制后辛烷值的预测,经验证,模型的均方误差为0.06876,所设计模型在处理辛烷值预测问题时可以达到比较好的预测效果。
关键词:辛烷值高维降维测量误差模型神经网络 XGBoost中图分类号:TP274 文獻标识码:A 文章编号:1674-098X(2021)02(b)-0092-05Prediction Model of Octane Number Loss in Gasoline Refining Process Based on Data Mining LI Dongchao(School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing, Jiangsu Province, 210044 China)Abstract: The loss of octane number in the process of gasoline refining will reduce the combustion efficiency of gasoline. How to reduce the loss of octane number in the process of gasoline refining is an important issue facing related enterprises. This paper uses the data accumulated by a petrochemical enterprise during the refining process of catalytic cracking gasoline to establish a two-stage feature screening model based on neural network, measurement error model and DC-SIS data dimensionality reduction method, and select the one that has a greater impact on the octane number factor. An octane number prediction model based on XGBoost and neural network is designed,which can predict the octane number after refining under different raw materials and different operations. After verification, the mean square error of the model is 0.06876. A better prediction effect can be achieved in the alkane number prediction problem.Key Words: Octane number; High dimensionality reduction; Neural networks; XGBoost汽油是小型车辆的主要燃料,汽油燃烧产生的尾气排放对大气环境有重要影响。
数学建模实验四:Matlab神经网络以及应用于汽油辛烷值预测

实验四:Matlab 神经网络以及应用于汽油辛烷值预测专业年级: 2014级信息与计算科学1班姓名: 黄志锐 学号:201430120110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据,将数据存贮在data.mat 文件中(下载后拷贝到Matlab 当前目录),其中input 是函数输入数据,output 是函数输出数据。
从输入输出数据中随机选取1900中数据作为网络训练数据,100组作为网络测试数据,并对数据进行归一化处理。
第二步 建立和训练BP 神经网络构建BP 神经网络,用训练数据训练,使网络对非线性函数输出具有预测能力。
第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。
第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。
详细MATLAB代码如下:27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']);%% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下:MATLAB代码运行结果如下所示:图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。
近红外光谱预测汽油辛烷值

前言烃加工工业中,连续在线监测关键石油物流的性质,是强化过程控制和炼厂信息系统集成的重要环节,为表征石油物流这一高度复杂的烃类混合物,引入了一系列测试手段和标准指标,总的来说,这些指标测试费用高、重复性差、试样用量大,在线实现时维护代价高,响应速度慢。
七十年代以来,近红外光谱(NIR)技术在分析机理、仪器制造、数据处理方面有了很大发展,与传统分析仪器相比,近红外分析仪有显著优势:光纤远程信号传输,可实现非接触式测量;一谱多用,只要建立模型,可同时测量多个指标;预处理简单,分析中不需化学试剂;响应速度快;易于制成小型紧凑的过程分析仪,在农作物分析等方面已建立实用标准[47]。
八十年代末,西雅图华盛顿大学过程分析化学中心(CPAC)进行了将近红外技术用于石油化学领域的研究,最重要的工作是测量汽油辛烷值,族组成和其它几个关键指标,随后在世界范围内的众多试验室和炼厂开展了这方面的研究工作,例如位于法国的BP拉菲尔炼厂将近红外技术大量用于过程控制,效益显著:在调合工艺中,一套近红外分析仪可替代两台辛烷机和一套雷德蒸汽压测试仪和其它蒸馏测试装置,月维护时间减小到数小时,光学仪器发生故障的平均时间间隔能够提高到几百小时,辛烷值测量范围增宽,重复性偏差小于0.1,该厂借助于近红外分析系统对乙烯蒸汽裂解炉的进料进行高频监测和优化,年收益百万美元,分析设备的投资可很快回收,还有利于下游分馏塔的稳定操作尽管NIR预测的重复性很好,在数学模型的设计上仍要谨慎从事。
因为近红外技术用于石油物流性质的预测是基于ASTM系列测定的二次方法,NIR模型只有在其适用范围内,才能获得与ASTM测试一样的准确性,当对象物流由于进料、工艺等原因偏离原模型的适用范围时,NIR模型必须重新标定。
如何提取NIR光谱和目标性质的统计关系是这门技术软件方面的关键。
一些典型的数学方法有主因子分析(PCA)、偏最小二乘法(PLS)、多元线性回归(MLR)、判别分析(DA)、聚类分析和人工神经网络(ANN)等,这些基本属于计量化学问题。
近红外光谱法测定成品汽油中的芳烃和烯烃含量

近红外光谱法测定成品汽油中的芳烃和烯烃含量肖学喜【摘要】介绍了近红外光谱测定90#汽油及93#汽油中芳烃和烯烃含量.选择1100~1 300 nm的近红外光谱域,在荧光指示剂吸附法的基础上,采用偏最小二乘法建立了适合测定90#汽油及93#汽油中芳烃和烯烃含量的分析模型,通过大量试验对所建分析模型的可靠性进行了验证.近红外光谱法的测定结果与荧光指示剂吸附法的测定结果具有很好的一致性.与荧光指示剂吸附法相比,近红外光谱法可以提高分析效率,降低分析成本,具有较高的分析精密度.【期刊名称】《化学分析计量》【年(卷),期】2008(017)005【总页数】4页(P21-24)【关键词】近红外光谱法;汽油;芳烃;烯烃【作者】肖学喜【作者单位】宁波北仑环境保护监测站,宁波,315800【正文语种】中文随着我国经济的持续快速发展,汽车保有量迅速增加。
汽车在为人们生活工作带来诸多便捷的同时也带来了较为严重的环境污染,目前汽车尾气污染已越来越受到人们的普遍关注。
汽车尾气污染除与发动机性能有关外,还与发动机燃料的质量密切相关,芳烃和烯烃含量就是车用汽油的重要环保质量指标,由国家质量监督检验检疫总局、国家标准化管理委员会发布的《GB 17930-2006 车用汽油》和原国家环保总局发布的《GWKB1-1999 车用汽油有害物质控制标准》均对车用汽油的芳烃和烯烃含量做了明确规定。
目前测定汽油中芳烃和烯烃含量的标准方法主要有荧光指示剂吸附法[1]、多维气相色谱法[2]等。
荧光指示剂吸附法的分析周期较长,分析成本较高,分析精密度范围较宽且受人为操作因素影响较大。
多维气相色谱法的仪器投入较大,仪器维护操作复杂,对操作人员的技术要求较高。
而近红外光谱法作为一种二次分析方法,由于其具有投资少、产出多、操作技术要求低、分析速度快等优点,近年来发展较快,已广泛应用于油品性质的测定[3-8];同时该分析方法不破坏样品、不用试剂、不污染环境,既可以用于样品的定性分析也可以得到准确度较高的定量结果。
用近红外光谱分析法测定汽油辛烷值

用近红外光谱分析法测定汽油辛烷值
曹动;谭吉春;陈哲;胡永明;韩素芳
【期刊名称】《光谱学与光谱分析》
【年(卷),期】1999(19)3
【摘要】用近红外光谱技术测定汽油辛烷值,在高精度分光光度计上测得12个汽油标准样品和4个未知样品的近红外区(700~2500nm)吸收光谱,建立多元统计分析模型,用逐步回归法和偏最小二乘法对模型进行校准,并将其用于未知样品的预估分析,辛烷值的分析精度达到≤±1.0。
【总页数】4页(P314-317)
【关键词】汽油;测定;近红外光谱;辛烷值
【作者】曹动;谭吉春;陈哲;胡永明;韩素芳
【作者单位】国防科技大学应用物理系光电技术教研室
【正文语种】中文
【中图分类】TE626.21
【相关文献】
1.近红外光谱法测定汽油辛烷值和辛烷值仪的研制 [J], 王宗明;华伟英
2.近红外光谱法测定汽油辛烷值 [J], 康蕴天;李敬清
3.近红外光谱预测汽油辛烷值和辛烷值仪的研制 [J], 王宗明;华伟英;韦占凯;张弧弘;武惠忠
4.化学计量学方法在近红外光谱分析中的应用--近红外光谱法测定汽油辛烷值 [J],
陈锴;张岩
5.小波去噪-微分法用于近红外光谱分析汽油辛烷值 [J], 田高友;袁洪福;褚小立;刘慧颖;陆婉珍
因版权原因,仅展示原文概要,查看原文内容请购买。
6-有导师学习神经网络的回归拟合

基础理论
神经网络的学习规则又称神经网络的训练算法,用来计算
更新神经网络的权值和阈值。学习规则有两大类别:有导师学
习和无导师学习。在有导师学习中,需要为学习规则提供一系 列正确的网络输入/输出对(即训练样本),当网络输入时,将 网络输出与相对应的期望值进行比较,然后应用学习规则调整
RBF具体步骤
(1)确定隐含层神经元径向基函数中心
C P'
(2)确定隐含层神经元阈值
b1 [b11 , b12 ,, b1Q ]'
其中, b11 b12 b1Q
0.8326 spread
spread为径向基函数的扩展速度。 (3)确定隐含层与输出层间权值和阈值
ai exp( C pi bi )
油样品近红外光谱与辛烷值间的数学模型,并对模型进行评价。
的,即网络的输出是隐含层神经元输出的线性加权和。
权值和阈值由线性方程组直接解出。
典型的RBF神经网络结构如图所示
IW1,1 dist
a1
LW1,2
a2
*
b2
+
b1
a1 radbas ( IW1,1 p b1 )
输入层 隐含层
a 2 purelin( LW 2,1a1 b2 )
输出层
n n l m 2
BP网络函数命令
(1) BP神经网络创建
net =
newff(P,T,[S1 S2 … S(N-1)],{TF1 TF2 …TFN1}, …
BTF,BLF,PF,IPF,OPF,DDF)
(2) BP神经网络训练函数
[net,tr,Y,E,Pf,Af] = train (net,P,T,Pi,Ai)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四Matlab神经网络以及应用于汽油辛烷值预测一、实验目的1. 掌握MATLAB创建BP神经网络并应用于拟合非线性函数2. 掌握MATLAB创建REF神经网络并应用于拟合非线性函数3. 掌握MATLAB创建BP神经网络和REF神经网络解决实际问题4. 了解MATLAB神经网络并行运算二、实验原理2.1 BP神经网络2.1.1 BP神经网络概述BP神经网络Rumelhard和McClelland于1986年提出。
从结构上将,它是一种典型的多层前向型神经网络,具有一个输入层、一个或多个隐含层和一个输出层。
层与层之间采用权连接的方式,同一层的神经元之间不存在相互连接。
理论上已经证明,具有一个隐含层的三层网络可以逼近任意非线性函数。
隐含层中的神经元多采用S型传递函数,输出层的神经元多采用线性传递函数。
图1所示为一个典型的BP神经网络。
该网络具有一个隐含层,输入层神经元数据为R,隐含层神经元数目为S1,输出层神经元数据为S2,隐含层采用S型传递函数tansig,输出层传递函数为purelin。
图1含一个隐含层的BP网络结构2.1.2 BP神经网络学习规则BP网络是一种多层前馈神经网络,其神经元的传递函数为S型函数,因此输出量为0到1之间的连续量,它可以实现从输入到输出的任意的非线性映射。
由于其权值的调整是利用实际输出与期望输出之差,对网络的各层连接权由后向前逐层进行校正的计算方法,故而称为反向传播(Back-Propogation )学习算法,简称为BP 算法。
BP 算法主要是利用输入、输出样本集进行相应训练,使网络达到给定的输入输出映射函数关系。
算法常分为两个阶段:第一阶段(正向计算过程)由样本选取信息从输入层经隐含层逐层计算各单元的输出值;第二阶段(误差反向传播过程)由输出层计算误差并逐层向前算出隐含层各单元的误差,并以此修正前一层权值。
BP 网络的学习过程主要由以下四部分组成: 1)输入样本顺传播输入样本传播也就是样本由输入层经中间层向输出层传播计算。
这一过程主要是 输入样本求出它所对应的实际输出。
① 隐含层中第i 个神经元的输出为111111,,2,1s i b p w f a R j i jij i② 输出层中第k 个神经元的输出为:2211222,2,1,1s i b a w f a k S i iki k其中f 1(·), f 2 (·)分别为隐含层和输出层的传递函数。
2)输出误差逆传播在第一步的样本顺传播计算中我们得到了网络的实际输出值,当这些实际的输出值与期望输出值不一样时,或者说其误差大于所限定的数值时,就要对网络进行校正。
首先,定义误差函数E (w ,b )=221)(212k k s k a t其次,给出权值的变化 ① 输出层的权值变化从第i 个输入到第k 个输出的权值为:i ki kiki a w Ew 122其中:'2f e k ki , k k k a l e 2② 隐含层的权值变化从第j 个输入到第i 个输出的权值为:101jij ijij p w Ew (η为学习系数)其中:'1f e i ijki ki s k i w e 212由此可以看出:①调整是与误差成正比,即误差越大调整的幅度就越大。
②调整量与输入值大小成比例,在这次学习过程中就显得越活跃,所以与其相连的权值的调整幅度就应该越大,③调整是与学习系数成正比。
通常学习系数在0.1~0.8之间,为使整个学习过程加快,又不会引起振荡,可采用变学习率的方法,即在学习初期取较大的学习系数随着学习过程的进行逐渐减小其值。
最后,将输出误差由输出层经中间层传向输入层,逐层进行校正。
2.1.3 BP神经网络的训练对BP网络进行训练时,首先要提供一组训练样本,其中每个样本由输入样本和输出对组成。
当网络的所有实际输出与其期望输出小于指定误差时,训练结束。
否则,通过修正权值,使网络的实际输出与期望输出接近一致(图2)。
实际上针对不同具体情况,BP网络的训练有相应的学习规则,即不同的最优化算法,沿减少期望输出与实际输出之间误差的原则,实现BP网络的函数逼近、向量分类和模式识别。
图2 神经网络的训练2.2 RBF神经网络2.2.1 RBF神经网络概述1985年,Powell提出了多变量插值的径向基函数(Radical Basis Function, RBF)方法。
1988年,Moody和Darken提出了一种神经网络结构,即RBF 神经网络,属于前向神经网络类型,它能够以任意精度逼近任意连续函数,特别适合于解决分类问题。
RBF网络的结构与多层前向网络类似,它是一种三层前向网络。
输入层由信号源节点组成;第二层为隐含层,隐单元数视所描述问题的需要而定,隐单元的变换函数RBF()是对中心点径向对称且衰减的非负非线性函数;第三层为输出层,它对输入模式的作用作出响应。
从输入空间到隐含层空间的变换是非线性的,而从隐含层空间的输出层空间变换是线性的。
RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入向量直接(即不需要通过权接)映射到隐空间。
当RBF的中心点确定以后,这种映射关系也就确定了。
而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和。
此处的权即为网络可调参数。
由此可见,从总体上看,网络由输入到输出的映射是非线性的,而网络输出对可调参数而言却又是线性的。
这样网络的权就可由线性方程直接解出,从而大大加快学习速度并避免局部极小问题。
径向基神经网络的神经元结构如图3所示。
径向基神经网络的激活函数采用径向基函数,通常定义为空间任一点到某一中心之间欧氏距离的单调函数。
由图3所示的径向基神经元结构可以看出,径向基神经网络的激活函数是以输入向量和权值向量之间的距离dist作为自变量的。
径向基神经网络的激活函数(高斯函数)的一般表达式为2dist disteRdist1xmx2x1h2hihbny图3 径向基神经元模型随着权值和输入向量之间距离的减少,网络输出是递增的,当输入向量和权值向量一致时,神经元输出1。
在图3中的b为阈值,用于调整神经元的灵敏度。
利用径向基神经元和线性神经元可以建立广义回归神经网络,该种神经网络适用于函数逼近方面的应用;径向基神经元和竞争神经元可以组建概率神经网络,此种神经网络适用于解决分类问题。
由输入层、隐含层和输出层构成的一般径向基神经网络结构如图4所示。
图4 径向基神经网络结构2.2.2 RBF神经网络的学习算法径向基函数网络是由输入层,隐含层和输出层构成的三层前向网络(以单个输出神经元为例),隐含层采用径向基函数作为激活函数,该径向基函数一般为高斯函数,隐含层每个神经元与输入层相连的权值向量1iW和输入矢量qX(表示第q个输入向量)之间的距离乘上阈值1ib,作为本身的输入(图5)。
1qxxqmx11iw1miw1qiW X1ibqikqir图5 径向基神经网络神经元的输入与输出由此可得隐含层的第i个神经元的输入为:111q qii i i k W Xb b输出为:22exp(())exp((11))q q q i i i i r k W X b径向基函数的阈值1b 可以调节函数的灵敏度,但实际工作中更常用另一参数C (称为扩展常数)。
1b 和C 的关系有多种确定方法,在MATLAB 神经网络工具箱中,1b 和C 的关系为10.8326/i i b C ,此时隐含层神经元的输出变为:20.8326exp((1))q q i i ig W X C在MATLAB 神经网络工具箱中,C 值用参数spread 表示,由此可见,spread 值的大小实际上反映了输出对输入的响应宽度。
spread 值 越大,隐含层神经元对输入向量的响应范围将越大,且神经元间的平滑度也较好。
输出层的输入为各隐含层神经元输出的加权求和。
由于激活函数为纯线性函数,因此输出为:12nqq i i i y r wRBF 网络的训练过程分为两步:第一步为无教师式学习,确定训练输入层与隐含层间的权值1W ;第二步为有教师式学习,确定训练隐含层与输出层间的权值2W .在训练以前需要提供输入向量X 、对应的目标向量T 和径向基函数的扩展常数C 。
训练的目的是求取两层的最终权值1W ,2W 和阈值1b ,2b 。
在RBF 网络训练中,隐含层神经元数量的确定是一个关键问题,简便的做法是使其与输入向量的个数相等(称为精确(exact) RBF )。
显然,在输入向量个数很多时,过多的隐含层单元数是难以让人接受的。
其改进方法是从1个神经元开始训练,通过检查输出误差使网络自动增加神经元。
每次循环使用,使网络产生的最大误差所对应的输入向量作为权值向量,产生一个新的隐含层神经元,然后检查新网络的误差,重复此过程直到达到误差要求或最大隐含层神经元数为止(称为近似(approximate ) RBF )。
2.3 RBF 神经网络与BP 神经网络的比较在理论上,RBF 网络和BP 网络一样能以任意精度逼近任何非线性函数。
但由于它们使用的激活函数不同,其逼近性能也不相同。
Poggio 和Girosi 已经证明,RBF 网络是连续函数的最佳逼近,而BP 网络不是。
BP 网络使用的Sigmoid 函数具有全局特性,它在输入值的很大范围内每个节点都对输出值产生影响,并且激活函数在输入值的很大范围内相互重叠,因而相互影响,因此BP 网络训练过程很长。
此外,由于BP 算法的固有特性,BP 网络容易陷入局部极小的问题不可能从根本上避免,并且BP 网络隐层节点数目的确定依赖于经验和试凑,很难得到最优网络。
采用局部激活函数的RBF 网络在很大程度上克服了上述缺点,RBF 不仅有良好的泛化能力,而且对于每个输入值,只有很少几个节点具有非零激活值,因此只需很少部分节点及权值改变。
学习速度可以比通常的BP 算法提高上千倍, 容易适应新数据,其隐含层节点的数目也在训练过程中确定,并且其收敛性也较BP 网络易于保证,因此可以得到最优解。
2.4 BP神经网络与RBF神经网络的MATLAB实现2.4.1 BP神经网络的相关函数(1) newff: BP神经网络参数设置函数函数功能:构建一个BP神经网络函数形式:net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)P: 输入数据矩阵(训练集的输入向量作为列构成的矩阵)T: 输出数据矩阵(训练集的期望向量作为列构成的矩阵)S:隐合层节点数TF: 节点传递函数,包括硬限幅传递函数hardlim,对称硬限幅传递函数hardlims,线性传递函数purelin,正切S型传递函数tansig,对数S型传递函数logsig.BTF:训练函数,包括梯度下降BP算法训练函数traingd,动量反传的梯度下降BP算法训练函数traingdm.动态自适应学习率的梯度下降BP算法训练函数traingda,动量反传和动态自适应学习率的梯度下降BP算法训练函数traingdx、Levenberg-_Marquardt的BP算法训练函数trainlm。
