多元函数微分学及应用
《高等数学B》第八章 多元函数微分学 第三节 全微分及其应用
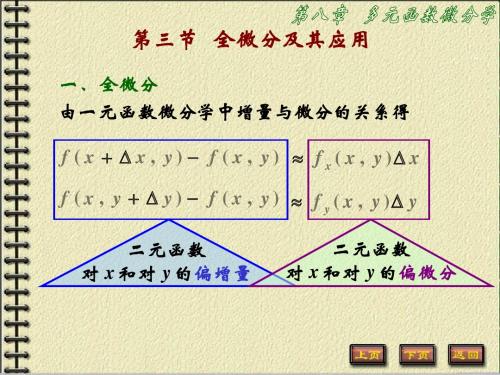
∆ z = A∆ x + B∆ y + o( ρ ) 总成立 ,
上式仍成立, 当 ∆ y = 0 时,上式仍成立,此时 ρ = | ∆ x | ,
f ( x + ∆ x , y ) − f ( x , y ) = A ⋅ ∆ x + o(| ∆ x |) ,
所求全微分 dz = e 2dx + 2e 2dy .
y yz 例2 计算函数 u = x + sin + e 的全微分 . 2
y ∂u 1 ∂u ∂u yz yz 解 = ye , =1, = cos + ze , ∂y 2 2 ∂z ∂x
所求全微分
1 y yz yz du = dx + ( cos + ze )dy + ye dz . 2 2
例4 试证函数
1 , ( x , y ) ≠ ( 0 , 0) , xy sin 2 2 x +y f ( x , y) = 0, ( x , y ) = ( 0 , 0) .
在点 (0 , 0) 连续且偏导数存在,但偏导数在点 (0 , 0) , 0) 可微 . 不连续, (证明略) 证明略)
∂u ∂u ∂u du = dx + dy + dz . ∂x ∂y ∂z
例1 计算函数 z = e x y在点 ( 2 , 1) 处的全微分 . 解
∂z = ye xy , ∂x
∂z = e2 , ∂x ( 2 , 1 )
∂z = xe xy , ∂y
∂z = 2e 2 , ∂y ( 2 , 1 )
∆ z ≈ dz = f x ( x , y )∆ x + f y ( x , y )∆ y .
多元函数微分学的应用

多元函数微分学的应用一、极值问题多元函数微分学最重要的应用之一是求解极值问题。
通过求取函数的偏导数,我们可以找到函数的极值点。
这对于经济学家、物理学家和其他相关领域的研究者来说是非常重要的。
例如,在经济学中,我们可以使用多元函数微分学来确定产品的最优产量和价格,以使利润最大化。
在物理学中,我们可以使用多元函数微分学来优化力学系统的能量和动量。
二、方向导数与梯度方向导数是一个重要概念,它描述了函数在其中一点沿着一些方向的变化率。
梯度是一个向量,它指向函数值增加最快的方向,并且梯度的模表示函数在其中一点的最大变化率。
方向导数和梯度在工程技术中的应用非常广泛。
例如,在机器学习中,我们可以使用梯度下降算法来优化模型的参数,以最小化损失函数。
三、偏微分方程偏微分方程是描述自然现象的重要数学工具,包括热传导、扩散、波动等。
多元函数微分学为解偏微分方程提供了重要的数学基础。
通过偏微分方程的分析解或数值解,我们可以深入了解自然现象的行为和性质。
例如,在工程技术中,我们可以使用多元函数微分学来解决电磁场、弹性力学和流体力学等方面的问题。
四、约束优化约束优化是指在满足一定条件下找到使目标函数最大或最小的参数的问题。
多元函数微分学是解决约束优化问题的重要工具。
通过拉格朗日乘数法,我们可以将约束优化问题转化为无约束优化问题,并应用多元函数微分学的方法求解。
约束优化问题在经济学、运筹学和供应链管理等领域有着广泛的应用。
例如,在经济学中,我们可以使用约束优化来确定消费者的最优选择。
五、多元函数积分学多元函数微分学与多元函数积分学是紧密相关的。
多元函数微分学提供了计算多元函数导数的方法,而多元函数积分学则通过对函数的积分来研究函数的整体性质。
应用多元函数积分学,我们可以计算多元函数在其中一区域上的平均值、总值和概率密度等。
多元函数积分学在统计学、物理学和金融工程学等领域有广泛的应用。
例如,在统计学中,我们可以使用多元函数积分学来计算多维随机变量的期望和方差。
3.3 全微分

多元函数微分学及其应用
注意:一元函数中,可微与可导是等价的。但在二元函数 中,偏导数存在是可微的必要条件,而非充分条件,即
可微
可导。
z z 当偏导数存在时可得表达式 x y ,但它不一定 x y z z 是全微分 dz,必须加上“ z [ x y ] 是比 高阶 x y
第章
多元函数微分学及其应用 2
证明: ( 1)当 x 2 y 2 0 时,有 1 2x 1 f x ( x , y ) 2 x sin 2 2 cos 2 , 2 2 2 x y x y x y
1 2y 1 f y ( x , y ) 2 y sin 2 2 cos 2 , 2 2 2 x y x y x y
当 y 0 时, x ,
z f ( x x, y) f ( x, y) Ax o x ,
o x f ( x x , y ) f ( x , y ) lim lim( A ) A, x 0 x 0 x x
f x ( x, y ) A .
lim
011 ,
第五章
多元函数微分学及其应用
z [ f x ( x, y) ]x [ f y ( x, y) ]y
f x ( x, y)x f y ( x, y)y x y
x y x y 而0 2 2 2 2 x y x y
( x, y) (0,0)
即 f x ( x 1x, y y) f x ( x, y ) ,其中
( x , y ) (0,0)
lim
0,
同理 f y ( x, y 2 y) f y ( x, y) ,其中
多元函数微分学的基本原理及其在实际问题中的应用

多元函数微分学的基本原理及其在实际问题中的应用多元函数微分学是微积分的一个分支,主要研究多元函数在某点处的变化率及其相关性质。
在实际问题中,多元函数微分学有广泛的应用,可以帮助我们理解和解决各种实际问题。
一、多元函数微分学的基本原理1. 偏导数:对于多元函数,偏导数是指将其他所有自变量固定,只对一个自变量求导的过程。
偏导数可以表示函数在某一方向上的变化率。
2. 全微分:给定一个多元函数,如果函数在某一点可导,则存在一个线性映射,将各个自变量的变化与函数值的变化联系起来。
这个线性映射称为全微分,表示函数在某一点的变化。
3. 方向导数:方向导数表示函数在给定方向上的变化率。
对于足够光滑的函数,在某一点处的方向导数可以通过对该点处的梯度与方向向量取内积得到。
4. 雅可比矩阵:雅可比矩阵是偏导数的推广,用于描述多元函数的变化率。
它是一个 m×n 的矩阵,其中 m 表示函数的输出维度,n 表示函数的输入维度。
二、多元函数微分学在实际问题中的应用1. 最优化问题:多元函数微分学可以帮助我们解决最优化问题。
通过求解多元函数的导数以及方程组,我们可以找到函数的最值点。
这在经济学、工程学和物理学等领域中有广泛的应用,如最大化收益、最小化成本、优化产品设计等。
2. 凸优化问题:凸优化问题在机器学习和数据分析中起着重要的作用。
多元函数微分学可以帮助我们判断一个函数是否是凸函数,并且通过求解函数的导数和二阶导数,可以找到函数的凸区域和凸包络。
这对于解决凸优化问题和设计高效算法至关重要。
3. 方程组求解:多元函数微分学可以应用于求解多元方程组。
通过对方程组中的各个方程进行偏导数运算,并联立求解方程组,我们可以求得方程组的根。
这在工程学和科学研究中经常用到,如电路分析、物理问题求解等。
4. 曲面拟合:多元函数微分学可以帮助我们对实际观测的数据进行曲面拟合。
通过求解多元函数的一阶导数和二阶导数,我们可以确定曲面的局部特性,并找到最适合观测数据的拟合曲面。
第8章 多元函数微分学及其应用

第8章 多元函数微分学及其应用上册中我们所讨论的函数都只有一个自变量,这种函数称为一元函数.而在实际问题中,还会遇到多于一个自变量的函数,这就是本章将要讨论的多元函数.多元函数是一元函数的推广.它的一些基本概念及研究问题的思想方法与一元函数有许多类似之处,但是由于自变量个数的增加,它与一元函数又存在着某些区别,这些区别之处在学习中要加以注意.对于多元函数,我们将着重讨论二元函数.在掌握了二元函数的有关理论与研究方法之后,我们可以把它推广到一般的多元函数中去.§1 多元函数的极限与连续一、平面点集与n 维空间一元函数的定义域是实数轴上的点集,而二元函数的定义域是坐标平面上的点集.因此,在讨论二元函数之前,有必要先了解有关平面点集的一些基本概念.1.平面点集由平面解析几何知道,当在平面上确定了一个直角坐标系后,平面上的点P 与二元有序实数组(,)x y 之间就建立了一一对应.于是,我们常把二元有序实数组(,)x y 与平面上的点P 看作是等同的.这种建立了坐标系的平面称为坐标平面.二元有序实数组(,)x y 的全体,即2{(,),}R x y x y R =∈就表示坐标平面.坐标平面上满足某种条件C 的点的集合,称为平面点集,记作{(,)(,)E x y x y =满足条件}C .例如,平面上以原点为中心,r 为半径的圆内所有点的集合是222{(,)}E x y x y r =+<.现在,我们引入平面中邻域的概念.设000(,)P x y 是平面上一点,δ是一正数.与点000(,)P x y 距离小于δ的点(,)P x y 的全体,称为点0P 的δ邻域,记为0(,)U P δ或0()U P ,即00(,){ }{(,}U P P P P x y δδδ=<=<.不包含点0P 在内的邻域称为点0P 的空心δ邻域,记为0(,)UP δ 或0()U P ,即00(,){ 0<}{(,)0}U P P P P x y δδδ=<=<< . 在几何上,邻域0(,)U P δ就是平面上以点000(,)Px y 为中心,δ为半径的圆的内部的点(,)P x y 的全体.下面利用邻域来描述点和点集之间的关系.任意一点2P R ∈与任意一个点集2E R ⊂之间必有以下三种关系之一:(1)内点:若存在点P 的某个邻域()U P ,使得()U P E ⊂,则称点P 是点集E 的内点(见图8-1).(2)外点:如果存在点P 的某个邻域()U P ,使得()U P E =∅ ,则称点P 是点集E 的外点(见图8-2).(3)边界点:如果在点P 的任何邻域内既含有属于E 的点,又含有不属于E 的点,则称点P 是点集E 的边界点(见图8-3).E 的边界点的全体称为E 的边界,记作E ∂.E 的内点必定属于E ;E 的外点必定不属于E ;E 的边界点可能属于E ,也可能不属于E .点和点集还有另外一种关系,这就是下面定义的聚点.聚点:若点P 的任何空心邻域0()U P 内总有E 中的点,则称P 为点集E 的聚点.聚点本身可能属于E 也可能不属于E .显然,E 的内点一定是E 的聚点,E 的外点一定不是E 的聚点.例如,点集22{(,)14}D x y x y =≤+<,满足2214x y <+<的一切点是D 的内点;满足221x y +=的一切点是D 的边界点,它们都属于D ;满足224x y +=的点也是D 的边界点,但它们不属于D ;点集D 连同它的外圆边界上的点都是D 的聚点.根据点集的特征,我们再来定义一些重要的平面点集.开集:如果点集E 的点都是E 的内点,则称E 为开集.闭集:如果点集E 的所有聚点都属于E ,则称E 为闭集. 例如,集合22{(,)14}x y x y <+<是开集;集合22{(,)14}x y x y ≤+≤是闭集;而集合22{(,)14}x y x y ≤+<既非开集,也非闭集.此外,还约定全平面2R 和空集∅既是开集又是闭集.连通集:若点集E 中任意两点都可以用完全含于E 的有限条直线段所组成的折线相连接,则称E 是连通集.区域(开区域):连通的开集称为区域或开区域.闭区域:开区域连同它的边界一起组成的集合,称为闭区域. 例如,22{(,)14}x y x y <+<是区域;22{(,)14}x y x y ≤+≤是闭区域.有界集:对于点集E ,如果能包含在以原点为中心的某个圆内,则称E 是有界点集.否则称为无界点集. 例如22{(,)1}x y x y +≤是有界闭区域,而22{(,)1}x y x y +>是无界的开区域.2.n 维空间称n 元有序实数组12(,,)n x x x 的全体为n 维空间,记为12{(,,,),1,2,,}n n i R x x x x R i n =∈= .n R 中的每个元素12(,,,)n x x x 称为n 维空间中的一个点,i x 称为该点的第i 个坐标.设点12(,,,)n M x x x ,12(,,,)n N y y y 为nR 中的两点,我们规定M ,N 两点间的距离为MN =显然,当1,2,3n =时,上式就是解析几何中在直线、平面、空间中两点间的距离公式.有了两点间的距离规定之后,就可以把平面点集中的邻域的概念推广到n R 中去.设0n P R ∈,δ是一正数,那么nR 中的点集 00(,){ ,}n U P P P P P R δδ=<∈就称为点0P 的δ邻域.有了邻域之后,就可以把平面点集中的内点、外点、边界点、聚点、开集、闭集、区域等概念推广到n 维空间去.二、二元函数的概念1.二元函数的概念在很多自然现象以及实际问题中,经常会遇到一个变量依赖于多个变量的关系,下面先看几个例子.例1 正圆锥体的体积V 和它的高h 及底面半径r 之间有关系213V r h π=.当r 和h 在集合{(,)0,0}r h r h >>内取定一组数时,通过关系式213V r h π=,V 有唯一确定的值与之对应. 例 2 一定量的理想气体的压强P 、体积V 和绝对温度T 之间有关系RT PV =,其中R 为常数.当V 、T 在集合{(,)0,0}V T V T >>内取定一组数时,通过关系式RT P V=,P 有唯一确定的值与之对应. 上面两个例子,虽然来自不同的实际问题,但都说明,在一定的条件下三个变量之间存在着一种依赖关系,这种关系给出了一个变量与另外两个变量之间的对应法则,依照这个法则,当两个变量在允许的范围内取定一组数时,另一个变量有唯一确定的值与之对应.由这些共性便可得到以下二元函数的定义.定义1 设D 是平面上的一个点集,如果对于D 内任意一点(,)P x y ,变量z 按照某一对应法则f 总有唯一确定的值与之对应,则称z 是变量x 、y 的二元函数(或称z 是点P 的函数),记作(,),(,)z f x y x y D =∈或(),z f P P D =∈.其中点集D 称为函数的定义域,x ,y 称为自变量,z 也称为因变量,数集{(,),z z f x y = (,)}x y D ∈称为该函数的值域.z 是x ,y 的函数也可记为(,)z z x y =.按照定义,在例1和例2中,V 是h 和r 的函数,P 是V 和T 的函数,它们的定义域由实际问题来确定.当二元函数仅用算式表示而未注明定义域时,约定其定义域为使算式有意义的点的集合.例3 求下列函数的定义域.(1)ln()z x y =+; (2)22arcsin()z x y =+.解 (1)要使ln()x y +有意义,必须有0x y +>,所以定义域为 {(,)0}x y x y +>.(见图8-4),这是一个无界开区域.(2)要使22arcsin()x y +有意义,必须有221x y +≤,所以定义域为22{(,)1}x y x y +≤.(见图8-5),这是一个有界闭区域.设二元函数(,)z f x y =的定义域为D ,对任一点(,)x y D ∈,必有唯一的(,)z f x y =与之对应.这样,以x 为横坐标,y 为纵坐标,(,)z f x y =为竖坐标在空间就确定一个点(,,)P x y z .当(,)x y 取遍D 上一切点时,相应地得到一个空间点集{(,,)(,),(,)}x y z z f x y x y D =∈,这个点集称为二元函数(,)z f x y =的图形(见图8-6).通常(,)z f x y =的图形是一张曲面,函数(,)f x y 的定义域D 便是该曲面在xOy 面上的投影.例如,由空间解析几何知道,25zx y =+的图形是一张平面,而函数22z x y =+的图形是旋转抛物面.2.n 元函数的概念定义2 设E 是nR 中的一个点集,如果对于E 中任意一点12(,,,)n P x x x ,变量u 按照某一对应法则f 总有唯一确定的值与之对应,则称u 是定义在E 上的n 元函数,记作 1212(,,,),(,,,)n n u f x x x x x x E =∈ ,或(),u f P P E =∈.点集E 称为函数的定义域,数集1212{(,,,),(,,,)}n n u u f x x x x x x E =∈ 称为该函数的值域.在定义2中,分别令2n =和3n =,便得到二元函数和三元函数的定义,二元及二元以上的函数统称为多元函数.三、二元函数的极限设二元函数(,)z f x y =定义在平面点集D 上,000(,)P x y 为点集D 的聚点,我们来讨论当点000(,)(,)P x y P x y →,即点0x x →,0y y →时函数(,)z f x y =的极限.这里000(,)(,)P x y P x y →是指点P 以任意的方式趋于0P ,亦即两点P 与0P 之间的距离趋于零,也就是00P P =→.与一元函数的极限概念类似,如果在000(,)(,)P x y P x y →的过程中,(,)P x y 所对应的函数值(,)f x y 无限接近于一个常数A ,则称当000(,)(,)P x y P x y →时,函数(,)z f x y =以A 为极限.下面用“εδ-”语言来描述这个极限的概念.定义3 设二元函数(,)z f x y =的定义域为D ,000(,)P x y 是D 的聚点,A 是一个常数.如果对于任意给定的正数ε,总存在正数δ,使得当0(,)(,)P x y UP D δ∈ 时,恒有 ()(,)f P A f x y A ε-=-<成立,则称当000(,)(,)P x y P x y →时函数(,)z f x y =以A 为极限,记为 00(,)(,)lim (,)x y x y f x y A →=或00lim (,)x x y y f x y A →→=, 也记作0lim ()P P f P A →=.二元函数的极限也称为二重极限.例4设(,)f x y =(,)(0,0)lim (,)0x y f x y →=.证 这里函数(,)f x y 的定义域是2D R =,点(0,0)O 显然为D 的聚点.由于(,)0sin 0f x y -=≤可见,对任意给定的0ε>,取δε=,则当0δ<<,即(,)(,)P x y U O D δ∈ 时,恒有(,)0f x y ε-≤<,成立,根据二元函数极限的定义,证得(,)(0,0)lim (,)0x y f x y →=.我们必须注意,所谓二重极限存在,是指(,)P x y 以任何方式趋于000(,)P x y 时,函数(,)f x y 都无限接近于同一个常数A .因此,当P 以某种特殊方式趋近于0P ,即使函数(,)f x y 无限接近于某一常数,也不能断定二重极限存在.但当P 以某种特殊方式趋近于0P 时,函数(,)f x y 的极限不存在,或者当P 沿两个特殊方式趋近于0P 时,函数(,)f x y 分别无限接近于两个不同的常数,则可以断定二重极限不存在. 例5 讨论22(,)xy f x y x y=+当(,)(0,0)x y →时是否存在极限. 解 当点(,)x y 沿着直线ykx =趋于(0,0)时,有2222222(,)(0,0) 0 lim lim 1x y x y kxxy kx k x y x k x k →→===+++. 其值因k 而异,这与极限定义中当(,)P x y 以任何方式趋于000(,)P x y 时,函数(,)f x y 都无限接近于同一个常数A 的要求相违背,因此当(,)(0,0)x y →时,22(,)xy f x y x y =+的极限不存在.以上关于二元函数极限的有关描述,可相应地推广到一般的n 元函数()u f P =即12(,,,)n u f x x x = 上去.多元函数极限的性质和运算法则与一元函数相仿,这里不再重复.例6 求22(,)(0,0)1lim ()sin x y x y x y→++. 解 因为(,)(0,0)lim ()0x y x y →+=,而221sin 1x y ≤+,利用有界函数与无穷小的乘积是无穷小,即知22(,)(0,0)1lim ()sin 0x y x y x y→+=+. 例7 2222(,)(0,0)sin()lim x y x y x y→++. 解 利用变量替换.令22u x y =+,当(,)(0,0)x y →时,有0u →,因此2222(,)(0,0)0sin()sin lim lim 1x y u x y u x y u→→+==+. 例8 求222(,)(0,0)lim x y x y x y →+. 解 利用极坐标变换.令co s x r θ=,sin y r θ=,当(,)(0,)x y →时,有0r →,因此2322222(,)(0,0)00cos sin lim lim lim cos sin 0x y r r x y r r x y rθθθθ→→→===+. 四、二元函数的连续有了二元函数极限的概念,仿照一元函数连续性的定义,不难得出二元函数连续性的定义.定义4 设二元函数(,)z f x y =的定义域为D ,000(,)P x y 是D 的聚点,且0P D ∈,如果0000(,)(,)lim (,)(,)x y x y f x y f x y →= (1) 则称二元函数(,)z f x y =在0P 点连续.若记0x x x ∆=-,0y y y ∆=-,则称0000(,)(,)z f x x y y f x y ∆=+∆+∆-为函数(,)f x y 在点000(,)P x y 的全增量.和一元函数一样,可用增量的形式来描述连续性,即当 0000(,)(0,0)(,)(0,0)lim lim (,)(,)0x y x y z f x x y y f x y ∆∆→∆∆→∆=+∆+∆-= 时,(,)f x y 在点000(,)P x y 连续.若函数(,)f x y 在D 上每一点都连续,则称(,)f x y 在D 上连续,或称(,)f x y 是D 上的连续函数.若(,)f x y 在0P 点不连续,则称0P 是函数(,)f x y 的间断点.当函数(,)f x y 在0P 点没有定义;或虽有定义,但当0P P→时函数(,)f x y 的极限不存在;或极限虽存在,但极限值不等于该点处的函数值,则0P 都是函数(,)f x y 的间断点.例如,考察函数22 ()(00)() 0 ()(00).xy x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,,,,,,,,例5中已说明,22(,)(0,0)limx y xy x y →+不存在,所以点(00),是函数()f x y ,的间断点. 再如函数2()x y f x y x y -=-,在曲线2x y =上每一点处都没有定义,所以曲线2x y =上每一点都是该函数的间断点.根据极限的运算法则和多元函数连续性的定义,不难证明多元连续函数的和、差、积、商(分母不等于零)也都是连续函数.多元连续函数的复合函数也是连续函数.与一元初等函数类似,多元初等函数是指可用一个式子表示的多元函数,这个式子是由常数及具有不同自变量的一元基本初等函数经过有限次的四则运算和复合运算得到的.例如22sin()x y +,ln()x y +都是多元初等函数.根据连续函数的和、差、积、商的连续性以及连续函数的复合函数的连续性,再利用基本初等函数的连续性,我们进一步可以得出如下结论:多元初等函数在其定义区域内是连续的.所谓定义区域是指包含在定义域内的区域或闭区域.由多元初等函数的连续性,如果需求极限0lim()P P f P →,而0P 正是初等函数()f P 定义区域内的一点,则00lim ()()P P f P f P →=.例9 求(,)(1,2)lim ln()x y x y →+.解 函数ln()x y +是多元初等函数,它的定义域{(,)0}D x y x y =+>是一个区域,而点(1,2)D ∈,所以(,)(1,2)lim ln()ln(12)ln3x y x y →+=+=.例10求(,)lim x y → 解(,)((,)(0,0)l i m l i x y x y →→=(,)(l i m 1 2.x y →=+=1+在点(0,0)的连续性.类似于闭区间上一元连续函数的性质,在有界闭区域上的多元连续函数具有以下几个重要性质:性质1(最大值、最小值定理) 在有界闭区域上连续的多元函数,在该区域上有最大值与最小值;性质2(有界性定理) 在有界闭区域上连续的多元函数,在该区域上有界;性质3(介值定理) 在有界闭区域上连续的多元函数,必能取得介于最大值与最小值之间的任何值.习题 8-11.判断下列平面点集中哪些是开集、闭集、区域、闭区域、有界集、无界集,并指出它们的边界和聚点. (1){(,)0,0}D x y x y =≠≠;(2)2{(,)}D x y y x =>; (3){(,)1}D x y x y =+≤.2.求下列函数的定义域,并作出定义域的草图:(1)2222x y z x y+=-; (2)ln ln z x y =+; (3)22z=(4)z=3.求下列各极限: (1)2222(,)(0,0)1lim ()sinx y x y x y→++; (2)(,)(0,2)sin()lim x y xy x →; (3)22(,)limx y →; (4)(,)limy x y →.4.证明下列极限不存在: (1)22(,)(0,0)limx y xy x y →+; (2)(,)(0,0)limx y x yx y →+-. 5.求下列函数的间断点:(1)1sinx y+; (2)22tan()x y +. §2 偏导数与全微分一、偏导数1.偏导数定义及其计算在一元函数中,我们通过函数的增量与自变量增量之比的极限引出了导数的概念,这个比值的极限刻画了函数对于自变量的变化率.对于多元函数同样需要讨论它的变化率,由于多元函数的自变量多于一个,使得变化率问题变得较为复杂.在这一节里,我们首先考虑多元函数关于其中一个自变量的变化率,即讨论只有一个自变量变化,而其余自变量固定不变(视为常量)时函数的变化率.定义1 设函数(,)z f x y =在点00(,)x y 的某邻域内有定义,当y 固定在0y ,而x 在0x 处有增量x ∆时(点(00,x x y +∆)仍在该邻域中),相应地函数有增量 0000(,)(,)f x x y f x y +∆-. 如果极限00000(,)(,)limx f x x y f x y x∆→+∆-∆存在,则称此极限为函数(,)z f x y =在点00(,)x y 处对x 的偏导数,记作00(,)x y zx ∂∂,00(,)x y fx ∂∂,00(,)x z x y 或00(,)x f x y ①,即0000000(,)(,)(,)limx x f x x y f x y f x y x∆→+∆-=∆. (1)类似地,函数(,)z f x y =在点00(,)x y 处对y 的偏导数定义为00000(,)(,)limy f x y y f x y y∆→+∆-∆, (2)记作00(,)x y z y∂∂,00(,)x y f y∂∂,00(,)y z x y 或00(,)y f x y .①偏导数记号x z ,x f 也常记作x z ',x f '.由偏导数的定义可知,二元函数(,)z f x y =在点00(,)x y 处对x 的偏导数00(,)x f x y , 实际上就是把y 固定在0y 时,一元函数0(,)f x y 在0x 点的导数0d (,)d x x f x y x =;00(,)y f x y 就是一元函数0(,)f x y 在0y 点的导数0d (,)dyy y f x y =.如果函数(,)z f x y =在区域D 内每一点(,)x y 处对x 的偏导数都存在,那么这个偏导数就是x ,y 的函数,称它为函数(,)z f x y =对自变量x 的偏导函数,记作z x ∂∂,fx∂∂ x z 或(,)x f x y .类似地,可以定义函数(,)z f x y =对自变量y 的偏导函数,记作z y ∂∂,f y∂∂,y z 或(,)y f x y .偏导函数也简称为偏导数.显然函数(,)z f x y =在点00(,)x y 处对x 的偏导数00(,)x f x y 就是偏导函数(,)x f x y 在点00(,)x y 处的函数值;00(,)y f x y 就是偏导函数(,)y f x y 在点00(,)x y 处的函数值.至于实际求(,)z f x y =的偏导数,并不需要用新的方法,因为偏导数的实质就是把一个自变量固定,而将二元函数(,)z f x y =看成是另一个自变量的一元函数的导数.计算f x ∂∂时,只要把y 看作常数,而对x 求导数;类似地,计算f y∂∂时,只要把x 看作常数,而 对y 求导数.二元以上的函数的偏导数可类似定义.例如三元函数(,,)u f x y z =在点(,,)x y z 处对x 的偏导数可定义为(,,)(,,)(,,)limx x f x x y z f x y z f x y z x∆→+∆-=∆其中(,,)x y z 是函数(,,)u f x y z =的定义域的内点.求二元以上函数对某个自变量的偏导数也只需把其余自变量都看作常数而对该自变量求导即可.例1 求二元函数arctanyz x=的偏导数. 解 对x 求偏导数时,把y 看作常数,则222211z y y xx x y y x ∂⎛⎫=⋅-=- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭; 对y 求偏导数时,把x 看作常数,则222111z xyx x yy x ∂=⋅=∂+⎛⎫+ ⎪⎝⎭. 例2 设323(,)2f x y x x y y =+-,求(1,3)x f ,(1,3)y f .解 方法一:先求出偏导函数(,)x f x y 和(,)y f x y ,再求偏导函数在点(1,3)的函数值.2(,)34x f x y x xy =+,22(,)23y f x y x y =-,所以 (1,3)15x f =,(1,3)25y f =-.方法二:将(1,3)x f 转化为当3y =时,计算一元函数(,3)f x 在1x =处的导数,32(,3)627f x x x =+-,所以 211d (,3)(1,3)(312)15d x x x f x f x x x ====+=.将(1,3)y f 转化为当1x =时,计算一元函数(1,)f y 在3y =处的导数,3(1,)12f y y y =+-,所以 233d (1,)(1,3)(23)25dyy y y f y f y ====-=-.例3已知函数r =2221r r r x y z ⎛⎫∂∂∂⎛⎫⎛⎫++= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭.证 求rx∂∂时,把y 和z 看作常数,则r x x r∂==∂,由于所给函数关于自变量对称①,所以r y y r∂=∂,r z z r ∂=∂,从而有22222221r r r x y z x y z r ⎛⎫∂∂∂++⎛⎫⎛⎫++== ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭. 例4 已知理想气体的状态方程是PV RT =(R 是常数),求证1P V TV T P∂∂∂⋅⋅=-∂∂∂. 证2P R T R TV V V V ∂∂⎛⎫==- ⎪∂∂⎝⎭, V RT RT T P P ∂∂⎛⎫== ⎪∂∂⎝⎭, T PV V P P RR∂∂⎛⎫== ⎪∂∂⎝⎭, 故21P V T RT R V RT V T P V P R PV∂∂∂⋅⋅=-⋅⋅=-=-∂∂∂. 从例4不难说明偏导数的记号P V ∂∂,V T ∂∂,TP∂∂是一个整体记号,不能像一元函数的导数d d y x那样看成分子与分母之商,否则将导致1P V TV T P ∂∂∂⋅⋅=∂∂∂的错误结论. 2.偏导数的几何意义在空间直角坐标系中,二元函数(,)z f x y =的图像是一个空间曲面S .根据偏导数的定义,00(,)x f x y 就是把y 固定在0y ,一元函数0(,)f x y 在0x 点的导数.而在几何上,一元函数0(,)z f x y =表示曲面S 与平面0y y =的交线10(,):z f x y C y y =⎧⎨=⎩,则由一元函数导数的几何意义知,00(,)x f x y 就是曲线1C 在点00000(,,(,))P x y f x y 处的切线0x PT 对x 轴的斜率,即0x PT 与x 轴正向所成倾角的正切tan α(见图8-7). 同理,00(,)y f x y 就是曲面S 与平面0x x =的交线20(,):z f x y C x x =⎧⎨=⎩在点0P 处的切线①若函数表达式中任意两个自变量对调后,仍表示原来的函数,则称函数关于这两个自变量对称.0y PT 对y 轴的斜率tan β(见图8-8).3.偏导数与连续的关系我们知道,若一元函数()y f x =在点0x 处可导,则()f x 必在点0x 处连续.但对于 二元函数(,)z f x y =来讲,即使在点00(,)x y 处的两个偏导数都存在,也不能保证函数(,)f x y 在点00(,)x y 处连续.这是因为偏导数00(,)x f x y ,00(,)y f x y 存在只能保证一元函数0(,)z f x y =和0(,)z f x y =分别在0x 和0y 处连续,但不能保证(,)x y 以任何方式趋于00(,)x y 时,函数(,)f x y 都趋于00(,)f x y . 例5 求二元函数22()(00)() 0 ()(00)xyx y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,,,,,,,,,在点(0,0)处的偏导数,并讨论它在点(0,0)处的连续性.解 点(0,0)是函数(,)f x y 的分界点,类似于一元函数,分段函数分界点处的偏导数 要用定义去求.0(0,0)(0,0)00(0,0)limlim 0x x x f x f f xx ∆→∆→+∆--===∆∆, 又由于函数关于自变量x ,y 是对称的,故(0,0)0y f =.我们在第一节已经知道(,)f x y 在点(0,0)处不连续.当然,(,)z f x y =在点00(,)x y 处连续也不能保证(,)f x y 在点00(,)x y 的偏导数存在. 例6讨论函数(,)f x y =(0,0)处的偏导数与连续性.图8-7 图8-8解 因为(,)f x y =2R 是一个区域,而2(0,0)R ∈,因此(,f x (0,0)处连续.但00(0,0)(0,0)(0,0)limlim x x x x f x f f x x∆→∆→∆+∆-==∆∆不存在.由函数关于自变量的对称性知,(0,0)y f 也不存在.4.高阶偏导数设函数(,)z f x y =在区域D 内具有偏导数(,)x zf x y x ∂=∂,(,)y z f x y y∂=∂, 一般来讲,在D 内(,)x f x y ,(,)y f x y 仍然是x ,y 的函数,如果(,)x f x y ,(,)y f x y 关于x ,y 的偏导数也存在,则称(,)x f x y ,(,)y f x y 的偏导数是函数(,)z f x y =的二阶偏导 数.按照对两个自变量求导次序不同,二元函数(,)z f x y =的二阶偏导数有如下四种情形:对x 的二阶偏导数:2222(,)xx z z ff x y x x x x ∂∂∂∂⎛⎫=== ⎪∂∂∂∂⎝⎭, 先对x 后对y 的二阶偏导数:22(,)xy z z ff x y y x x y x y∂∂∂∂⎛⎫=== ⎪∂∂∂∂∂∂⎝⎭, 先对y 后对x 的二阶偏导数:22(,)yx z z ff x y x y y x y x ⎛⎫∂∂∂∂=== ⎪∂∂∂∂∂∂⎝⎭, 对y 的二阶偏导数:2222(,)yy z z f f x y y y y y⎛⎫∂∂∂∂=== ⎪∂∂∂∂⎝⎭①.如果二阶偏导数的偏导数存在,就称它们是函数(,)f x y 的三阶偏导数,例如2323z z x x x ⎛⎫∂∂∂= ⎪∂∂∂⎝⎭,2322z zy x x y⎛⎫∂∂∂= ⎪∂∂∂∂⎝⎭等.类似地,我们可以定义四阶,五阶,…,n 阶偏导数.二阶及二阶以上的偏导数统称为高阶偏导数.如果高阶偏导数中既有对x 也有对①二阶偏导数记号xx f ,xy f ,yx f ,yy f 也常记作xxf '', xy f '', yx f '', yy f ''.y 的偏导数,则此高阶偏导数称为混合偏导数,例如2z x y ∂∂∂,2zy x∂∂∂.例7 求函数2x yz e +=的所有二阶偏导数.解 由于2x y z e x +∂=∂,22x y ze y+∂=∂, 因此有 2222()x y x yz z e e x x x x++∂∂∂∂⎛⎫=== ⎪∂∂∂∂⎝⎭, 222()2x y x y z z e e x y y x y++∂∂∂∂⎛⎫=== ⎪∂∂∂∂∂⎝⎭, 2222222(2)2(2)4.x y x y x y x yz z e e y x x y xz z e e y y y y++++⎛⎫∂∂∂∂=== ⎪∂∂∂∂∂⎝⎭⎛⎫∂∂∂∂=== ⎪∂∂∂∂⎝⎭,在此例中,两个二阶混合偏导数相等,即22z zx y y x∂∂=∂∂∂∂,但这个结论并非对任何函数 成立,只有在满足一定条件时,二阶混合偏导数才与求偏导的次序无关.对此,我们不加证明地给出下面的定理.定理1 如果函数(,)z f x y =的两个二阶混合偏导数2z x y ∂∂∂及2zy x∂∂∂在区域D 内连续,那么在该区域内这两个二阶混合偏导数相等.换句话说,两个二阶混合偏导数在偏导数连续的条件下与求偏导的次序无关.对于二元以上的函数,我们也可以类似地定义高阶偏导数.而且高阶混合偏导数在偏导数连续的条件下也与求偏导的次序无关.例8验证函数ln z =满足拉普拉斯(Laplace )方程22220z zx y∂∂+=∂∂.证因为221lnln()2z x y ==+,所以2222222222222222()2()()()z x x x yz z x x y x x y xx x x x x y x y x y ∂=∂+∂∂∂∂+-⋅-⎛⎫==== ⎪∂∂∂∂+++⎝⎭,,利用函数关于自变量的对称性,在22zx∂∂的结果中,将x 与y 互换,便得到2222222()z x y y x y ∂-=∂+, 因此 222222222222220()()z z y x x y x y x y x y ∂∂--+=+=∂∂++.二、全微分1.全微分的定义我们知道一元函数()y f x =在点0x 可微是指:如果当自变量x 在0x 处有增量x ∆时,函数增量y ∆可表示为00()()()y f x x f x A x o x ∆=+∆-=∆+∆,其中A 与x ∆无关,()o x ∆是当0x ∆→时较x ∆高阶的无穷小量,则称()y f x =在点0x 可微,并称A x ∆为()f x 在点0x 处的微分,记为d y A x =∆.对于二元函数,我们也用类似的方法来定义可微性及全微分.定义2 设函数(,)z f x y =在点00(,)x y 的某邻域内有定义,点00(,)x x y y +∆+∆为该邻域内任意一点,若函数在点00(,)x y 处的全增量0000(,)(,)z f x x y y f x y ∆=+∆+∆-可表示为 ()z A x B y o ρ∆=∆+∆+, (3)其中A ,B 仅与点00(,)x y 有关,而与x ∆,y ∆无关,ρ=()o ρ是当0ρ→时较ρ高阶的无穷小量,即0()lim0o ρρρ→=,则称函数(,)z f x y =在点00(,)x y 处是可微的,并称A x B y ∆+∆为函数(,)z f x y =在点00(,)x y 处的全微分,记作00(,)d xy z ,即(,)d x y z A x B y =∆+∆. (4)2.可微性条件定理2(可微的必要条件) 若(,)z f x y =在点00(,)x y 处可微,则 (1)(,)f x y 在点00(,)x y 处连续;(2)(,)f x y 在点00(,)x y 处的偏导数存在,且00(,)x A f x y =,00(,)y B f x y =.证(1) 设(,)z f x y =在点00(,)x y 处可微,根据可微的定义有0000(,)(,)()z f x x y y f x y A x B y o ρ∆=+∆+∆-=∆+∆+,当(,)(0,0)x y ∆∆→时,有0ρ=,于是()0o ρ→,从而有0000(,)(0,0)(,)(0,0)lim lim(,)(,)x y x y z f x x y y f x y ∆∆→∆∆→∆=+∆+∆- (,)(0,0)lim()0x y A x B y o ρ∆∆→=∆+∆+=,所以(,)f x y 在点00(,)x y 处连续.(2)因为(,)z f x y =在点00(,)x y 处可微,则有0000(,)(,)()z f x x y y f x y A x B y o ρ∆=+∆+∆-=∆+∆+,上式对任意的x ∆,y ∆都成立,特别地,当0y ∆=时,x ρ=∆,则有0000(,)(,)()f x x y f x y A x o x +∆-=∆+∆,等式两边同除以x ∆,再令0x ∆→,得000000()(,)(,)limlim x x A x o x f x x y f x y A x x∆→∆→∆+∆+∆-==∆∆, 即(,)f x y 在点00(,)x y 处对x 的偏导数存在,且00(,)x f x y A =.同理可证(,)f x y 在点00(,)x y 处对y 的偏导数也存在,且00(,)y f x y B =.证毕.根据此定理,(,)z f x y =在点00(,)x y 处的全微分可以写成0000(,)d (,)(,)x y x y z f x y x f x y y =∆+∆.与一元函数的情形一样,由于自变量的增量等于自变量的微分,即d x x ∆=,d y y ∆=,所以(,)z f x y =在点00(,)x y 处的全微分又可以写成0000(,)d (,)d (,)d x y x y z f x y x f x y y =+. (5)如果函数(,)z f x y =在区域D 上每一点都可微,则称函数在区域D 上可微,且(,)z f x y =在D 上全微分为d d d z zz x y x y∂∂=+∂∂. (6) 在一元函数中,函数在某点可导与可微是等价的,但对于多元函数来说,情形就不同了,函数的偏导数存在,不一定能保证函数可微.当偏导数存在时虽然在形式上能写出0000(,)(,)x y f x y x f x y y ∆+∆,但它与z ∆的差不一定是当0ρ→时较ρ高阶的无穷小量,62只有当0000[(,)(,)]()x y z f x y x f x y y o ρ∆-∆+∆=时,即00000[(,)(,)]limx y z f x y x f x y y ρρ→∆-∆+∆=时,才能说函数在该点可微.例如本节例5中所讨论的函数22()(00)() 0 ()(00)xyx y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,,,,,,,,,在点(0,0)处有(0,0)0x f =,(0,0)0y f =,所以3222[(0,0)(0,0)](0,0)(0,0)[(0,0)(0,0)][()()]x y z f x f y f x y f f x f y x y x y ρ∆-∆+∆+∆+∆--∆+∆=∆∆=∆+∆,如果考虑点(,)x y ∆∆按照y x ∆=∆的方式趋向于点(0,0),这时有233(,)(0,0)022322()limlim[()()]2()x y x y xx y x x y x ∆∆→∆→∆=∆∆∆∆==∞∆+∆∆,即0[(0,0)(0,0)]limx y z f x f y ρρ→∆-∆+∆不存在,则由可微性定义有(,)f x y 在点(0,0)处不可微.当然由本节例5可知,函数(,)f x y 在点(0,0)处不连续,由定理2知不连续则不可微,因此(,)f x y 在点(0,0)处的不可微.此例题说明偏导数存在只是可微的必要条件而不是充分条件.但是如果将可偏导的条件加强为偏导数连续,则函数就可微了.定理3(可微的充分条件) 若函数(,)z f x y =的偏导数在点00(,)x y 的某邻域内存 在,且(,)x f x y 与(,)y f x y 在点00(,)x y 处连续,则函数(,)f x y 在点00(,)x y 处可微.证 函数(,)f x y 的全增量z ∆可以表示为000000000000(,)(,)[(,)(,)][(,)(,)],z f x x y y f x y f x x y y f x y y f x y y f x y ∆=+∆+∆-=+∆+∆-+∆++∆-63在第一个方括号中,变量0y y +∆保持不变,因此可以把方括号中的表达式看作是关于x 的一元函数0(,)f x y y +∆的增量;在第二个方括号中,变量0x 保持不变,因此可以把方括号中的表达式看作是关于y 的一元函数0(,)f x y 的增量.对它们分别应用一元函数的拉格朗日中值定理得010002(,)(,)x y z f x x y y x f x y y y θθ∆=+∆+∆∆++∆∆,(10θ<,21θ<). 由于(,)x f x y 与(,)y f x y 在点00(,)x y 处连续,因此有01000(,)(0,0)lim(,)(,)x x x y f x x y y f x y θ∆∆→+∆+∆=, 00200(,)(0,0)lim(,)(,)y y x y f x y y f x y θ∆∆→+∆=,即 01000(,)(,)x x f x x y y f x y θα+∆+∆=+,00200(,)(,)y y f x y y f x y θβ+∆=+,其中当0x ∆→,0y ∆→时,0α→,0β→.从而0000(,)(,)x y z f x y x f x y y x y αβ∆=∆+∆+∆+∆.而20)x y αβρ∆+∆≤0αβ≤+→,(0x ∆→,0)y ∆→所以(,)(0,0)lim0x y x yαβρ∆∆→∆+∆=,又由于0x ∆→,00y ρ∆→⇔→①,所以0lim0x yραβρ→∆+∆=,即当0ρ→时,有()x y o αβρ∆+∆=.①由于,x yx yρ∆∆≤=∆+∆,所以有0x ∆→,00y ρ∆→⇔→.64于是证明了(,)f x y 在点00(,)x y 处可微.证毕.注意偏导数连续只是函数可微的充分条件,不是必要条件.例9 证明22221(sin ()(00)(,) 0 ()(00)x y x y x y f x y x y ⎧+≠⎪+=⎨⎪=⎩),,,,,,,,在点(0,0)处可微,但在点(0,0)处偏导数不连续.证 20(0,0)(0,0)1(0,0)limlim sin 0()x x x f x f f x x x ∆→∆→+∆-==∆=∆∆, 由于函数关于自变量是对称的,则(0,0)0y f =.于是[(0,0)(0,0)]limx y z f x f y ρρ→∆-∆+∆22220(0,0)(0,0)[(0,0)(0,0)]lim1[()()]sin[()()]lim x y f x y f f x f y x y x y ρρρρ→→+∆+∆--∆+∆=∆+∆∆+∆=221sinlim0ρρρρ→==,所以函数(,)f x y 在点(0,0)处可微.当(,)(0,0)x y ≠时,由22221(,)(sinf x y x y x y =++)有222222121(,)2sincos x x f x y x x y x y x y=-+++, 222222(,)(0,0)(,)(0,0)121lim(,)lim 2sin cos x x y x y x f x y x x y x y x y →→⎛⎫=- ⎪+++⎝⎭, 当点(,)x y 沿x 轴趋于(0,0)时,由于222(,)(0,0)0 011lim 2sinlim2sin 0x y x y x x x y x →→===+,6522222(,)(0,0)0 02121limcos lim cos x y x y x x y x y x x →→==++不存在,所以(,)(0,0)lim (,)x x y f x y →不存在,即(,)x f x y 在点(0,0)处不连续,同理(,)y f x y 在点(0,0)处也不连续.根据前面的讨论,函数(,)f x y 连续,偏导数存在,可微的关系可用下图表示:偏导数连续连续以上关于全微分的定义及可微的必要条件和充分条件可以完全类似地推广到三元及三元以上的函数.例如,若三元函数(,,)u f x y z =的三个偏导数都存在且连续,则它的全微分存在,并有d d d d u u uu x y z x y z∂∂∂=++∂∂∂. 例10 求函数222z x y xy =+在点(1,2)处的全微分.解24z xy y x ∂=+∂,2(1,2)(1,2)(4)12zxy y x ∂=+=∂,222z x xy y ∂=+∂,2(1,2)(1,2)(22)6zx xy y ∂=+=∂,由于z x ∂∂,zy∂∂在点(1,2)处连续,所以函数222z x y xy =+在点(1,2)处可微,且有 (1,2)(1,2)(1,2)d d d 12d 6d z zz x y x y x y ∂∂=+=+∂∂. 例11 求函数2xyzu exy z =++的全微分.解xyz u yze y x ∂=+∂,xyz uxze x y∂=+∂,2xyz u xye z z ∂=+∂ 由于u x ∂∂,u y ∂∂,u z∂∂连续,所以函数2xyz u e xy z =++可微,且有 d ()d ()d (2)d xyz xyz xyz u yze y x xze x y xye z z =+++++.66例12 求函数22z x y =在点(2,1)-处,当0.02x ∆=,0.01y ∆=-时的全微分d z 和全增量z ∆.解22z xy x ∂=∂,2(2,1)(2,1)24z xy x --∂==∂,22z x y y ∂=∂,2(2,1)(2,1)28zx y y --∂==-∂,由于z x ∂∂,zy∂∂在点(2,1)-处连续,所以函数22z x y =在点(2,1)-处可微,且 (2,1)(2,1)(2,1)d 4(0.02)(8)(0.01)0.16z zz x y x y ---∂∂=∆+∆=⨯+-⨯-=∂∂,2222(20.02)(10.01)2(1)0.1624z ∆=+⨯---⨯-=.此例中z ∆与d z 的差仅为0.0024.3.全微分在近似计算中的应用设函数(,)z f x y =在点00(,)x y 处可微,则它在点00(,)x y 处的全增量为00000000(,)(,)(,)(,)()x y z f x x y y f x y f x y x f x y y o ρ∆=+∆+∆-=∆+∆+,其中()o ρ是当0ρ→时较ρ高阶的无穷小量.因此,当x ∆,y ∆都很小时,有近似公 式 0000d (,)(,)x y z z f x y x f x y y ∆≈=∆+∆, 上式有时也写成00000000(,)(,)(,)(,)x y f x x y y f x y f x y x f x y y +∆+∆≈+∆+∆. (7)利用上面的近似公式(7)可以计算函数的近似值. 例13 计算 3.96(1.08)的近似值.解 把 3.96(1.08)看作是函数(,)yf x y x =在 1.08x =, 3.96y =时的函数值(1.08,3.96)f .取01x =,04y =,0.08x ∆=,0.04y ∆=-.由于1(,)y x f x y yx -=,(1,4)4x f =,(,)ln y y f x y x x =,(1,4)0y f =,67(1,4)1f =,应用近似公式(7)有3.96(1.08)(1,4)(1,4)0.08(1,4)(0.04) 140.080(0.04) 1.32.x y f f f ≈+⨯+⨯-=+⨯+⨯-=例14 金属圆锥体受热变形,底面半径由30cm 增加到30.1cm ,高由60cm 减少到59.5cm ,求圆锥体体积变化的近似值.解 设圆锥体的底面半径、高和体积依次为r 、h 和V ,则圆锥体体积为213V r h π=. 记r 、h 和V 的增量依次为r ∆、h ∆和V ∆.应用近似公式(7)有221d 33V V V V r h rh r r h r h ππ∂∂∆≈=∆+∆=∆+∆∂∂. 将30r =,60h =,0.1r ∆=,0.5h ∆=-代入上式,得圆锥体体积变化的近似值232130600.130(0.5)3330().V cm πππ∆≈⨯⨯⨯+⨯⨯-=- 即圆锥体的体积约减少了330cm π.习题 8-21.求下列函数的偏导数:(1)yz x =; (2)sin x z xe y =; (3)ln()z x x y =+; (4)z =(5)z = (6)ln(z x =+;(7)arctan1x yz xy +=-; (8)zx u y ⎛⎫= ⎪⎝⎭; (9)z yu x =; (10)zyu x =.2.设(,)(f x y x y =+-(,1)x f x .683.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩,,在点(2,4,5)处的切线与x 轴正向所成的倾角. 4.求下列函数的二阶偏导数:(1)44224z x y x y =+-; (2)xyz e =; (3)2sin (2)z x y =+; (4)arctan x z y=. 5.验证: (1)11x y z e⎛⎫-+ ⎪⎝⎭=满足方程222z z xy z x y∂∂+=∂∂; (2)ln()x yz e e =+满足方程2222220z z z x y x y ⎛⎫∂∂∂⋅-= ⎪∂∂∂∂⎝⎭;(3)r =2222222r r r x y z r∂∂∂++=∂∂∂;(4)1u r =满足方程2222220u u u x y z∂∂∂++=∂∂∂,其中r =6.设ln()z x xy =,求32z x y ∂∂∂,32zx y∂∂∂. 7.考察函数221sin ()(00)() 0 ()(00)y x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩,,,,,,,,,在点(0,0)处的偏导数是否存在.8.求下列函数的全微分: (1)y z x=; (2)yz x =; (3)xyz xe y =+; (4)222ln()u x y z =++. 9.求下列函数在指定点的全微分:(1)xyz e =,在点(2,1)处; (2)arctanyz x=,在点(1,1)处.6910.求函数z xy =,当10x =,8y =,0.2x ∆=,0.1y ∆=-时的全增量和全微分.11.证明函数222(,)(0,0)(,)0(,)(0,0)x yx y f x y x y x y ⎧≠⎪=+⎨⎪=⎩, , 在点(0,0)处连续,且偏导数存在,但在点(0,0)处不可微.12.求下列各式的近似值:(1) 1.98(1.03); (2.13.金属圆柱体受热变形,半径由20cm 增加到20.02cm ,高由30cm 增长到30.03cm ,求圆柱体体积变化的近似值.§3 多元函数微分法一、复合函数微分法1.复合函数微分法在一元函数中,我们介绍了复合函数的求导法则:如果函数()u x ϕ=在点x 处可导 而()y f u =在对应点u (())u x ϕ=处可导,则复合函数(())y f x ϕ=在点x 处可导,且有d d d ()()d d d y y u f u x x u xϕ''=⋅=⋅. 现在将这一微分法则推广到多元复合函数的情形,并按照多元复合函数的不同的复合情形,分三种情况讨论.(1)复合函数的中间变量均为一元函数的情形定理1 设函数()u t ϕ=,()v t ψ=在点t 处可导,函数(,)z f u v =在对应点(,)u v 处可微,则复合函数[(),()]z f t t ϕψ=在点t 处可导,并且有d d d d d d z z u z v t u t v t∂∂=+∂∂. (1) 证 给t 以增量t ∆,相应地()()u t v t ϕψ==,有增量u ∆和v ∆,从而函数(,)z f u v = 有增量z ∆.因为函数(,)z f u v =在点(,)u v 可微,故有()z z z u v o u vρ∂∂∆=∆+∆+∂∂,其中ρ=()o ρ是当0ρ→时较ρ高阶的无穷小量.上式两端同时除以t ∆,得()z z u z v o t u t v t tρ∆∂∆∂∆=++∆∂∆∂∆∆,。
多元函数微分法及其应用

第九章多元函数微分法及其应用一、基本要求及重点、难点1. 基本要求(1)理解二元函数的概念,了解多元函数的概念。
(2)了解二元函数的极限、连续性概念,有界闭域上连续函数的性质。
(3)理解偏导数和全微分的概念,熟练掌握偏导数的计算,了解全微分存在的必要条件和充分条件。
(4)了解方向导数与梯度的概念及其计算方法。
(5)掌握复合函数一阶偏导数的求法,会求复合函数的二阶偏导数。
(6)会求隐函数(包括由方程组确定的隐函数)的偏导数(主要是一阶)。
(7)了解曲线的切线和法平面及曲面的切平面与法线、并会求出它们的方程。
(8)理解多元函数极值和条件极值的概念,会求二元函数的极值。
了解求条件极值的拉格朗日乘数法,会求解一些较简单的最大值和最小值的应用问题。
2. 重点及难点(1)重点:多元函数概念,偏导数与全微分概念,偏导数计算,微分在几何上的应用,多元函数的极值的计算。
(2)难点:二重极限的定义与计算,多元函数连续;偏导数存在与可微之间的关系;复合函数的高阶偏导数;方向导数、偏导数、梯度之间的关系。
二、内容概述多元函数微分学是一元函数微分学的推广,因此两者之间有许多相似之处,但是要特别注意它们之间的一些本质差别。
1.多元函数的极限和连续(1)基本概念1)点集和区域。
2)多元函数的定义、定义域。
3)二元函数的极限、连续。
(2)基本定理1)多元初等函数在其定义域内是连续的。
2)多元连续函数在有界闭区域上一定有最大值M、最小值m;且必取到最大值M和最小值m之间的任何值。
2.多元函数微分法(1)基本概念偏导数、全微分、高阶偏导数的定义。
(2) 计算方法1) 偏导数:),(y x f z =在),(00y x 处对x 的偏导数x x xz =∂∂,就是一元函数),(0y x f z =在0x x =处的导数;对y 的偏导数x x xz =∂∂(同理)。
2) `全微分:),(y x f z =的全微分dy yzdx x z dz ∂∂+∂∂=3) 复合函数求导法则:画出函数到自变量的路经,然后利用链式迭加法则:即同条路经的偏导数相乘,不同路经的偏导数相加,求出所要的偏导数。
多元函数微分法及其应用

第九章 多元函数微分法及其应用§8 1 多元函数的基本概念一、平面点集n 维空间1.平面点集二元的序实数组x y 的全体 即R 2RR {x y |x y R }就表示坐标平面坐标平面上具有某种性质P 的点的集合 称为平面点集 记作E {x y | x y 具有性质P } 例如 平面上以原点为中心、r 为半径的圆内所有点的集合是C {x y | x 2y 2r 2} 如果我们以点P 表示x y 以|OP |表示点P 到原点O 的距离 那么集合C 可表成C {P | |OP |r }邻域设P 0x 0 y 0是xOy 平面上的一个点 是某一正数 与点P 0x 0 y 0距离小于的点P x y 的全体 称为点P 0的邻域 记为U P 0 即}|| |{),(00δδ<=PP P P U 或} )()( |) ,{(),(20200δδ<-+-=y y x x y x P U 邻域的几何意义 U P 0 表示xOy 平面上以点P 0x 0 y 0为中心、 >0为半径的圆的内部的点P x y 的全体 点P 0的去心邻域 记作) ,(0δP U即}||0 |{) ,(00δδ<<=P P P P U注 如果不需要强调邻域的半径 则用U P 0表示点P 0的某个邻域 点P 0的去心邻域记作)(0P U点与点集之间的关系任意一点P R 2与任意一个点集E R 2之间必有以下三种关系中的一种1内点 如果存在点P 的某一邻域UP 使得UPE 则称P 为E 的内点2外点 如果存在点P 的某个邻域UP 使得UPE 则称P 为E 的外点3边界点 如果点P 的任一邻域内既有属于E 的点 也有不属于E 的点 则称P 点为E 的边点E 的边界点的全体 称为E 的边界 记作EE 的内点必属于E E 的外点必定不属于E 而E 的边界点可能属于E 也可能不属于E 聚点如果对于任意给定的0 点P 的去心邻域),( P U内总有E 中的点 则称P 是E 的聚点由聚点的定义可知 点集E 的聚点P 本身 可以属于E 也可能不属于E例如 设平面点集E {x y |1x 2y 22}满足1x 2y 22的一切点x y 都是E 的内点 满足x 2y 21的一切点x y 都是E 的边界点 它们都不属于E 满足x 2y 22的一切点x y 也是E 的边界点 它们都属于E 点集E 以及它的界边E 上的一切点都是E 的聚点开集 如果点集E 的点都是内点 则称E 为开集闭集 如果点集的余集E c为开集 则称E 为闭集开集的例子 E {x y |1<x 2y 2<2}闭集的例子 E {x y |1x 2y 22}集合{x y |1x 2y 22}既非开集 也非闭集连通性 如果点集E 内任何两点 都可用折线连结起来 且该折线上的点都属于E 则称E 为连通集区域或开区域 连通的开集称为区域或开区域 例如E {x y |1x 2y 22}闭区域 开区域连同它的边界一起所构成的点集称为闭区域 例如E {x y |1x 2y 22}有界集 对于平面点集E 如果存在某一正数r 使得 EUO r其中O 是坐标原点 则称E 为有界点集无界集 一个集合如果不是有界集 就称这集合为无界集例如 集合{x y |1x 2y 22}是有界闭区域 集合{x y | xy 1}是无界开区域集合{x y | xy 1}是无界闭区域 2 n 维空间设n 为取定的一个自然数 我们用R n表示n 元有序数组x 1 x 2 x n 的全体所构成的集合 即R nRRR {x 1 x 2 x n | x i R i 1 2 n } R n中的元素x 1 x 2 x n 有时也用单个字母x 来表示 即x x 1 x 2 x n 当所有的x i i 1 2 n 都为零时 称这样的元素为R n 中的零元 记为0或O 在解析几何中 通过直角坐标 R 2或R 3中的元素分别与平面或空间中的点或向量建立一一对应 因而R n中的元素x x 1 x 2 x n 也称为R n 中的一个点或一个n 维向量 x i称为点x 的第i 个坐标或n 维向量x 的第i 个分量 特别地 Rn中的零元0称为R n中的坐标原点或n 维零向量为了在集合R n 中的元素之间建立联系 在R n中定义线性运算如下 设x x 1 x 2 x n y y 1 y 2 y n 为R n 中任意两个元素 R 规定xy x 1 y 1 x 2 y 2 x n y n x x 1 x 2 x n这样定义了线性运算的集合R n称为n 维空间R n中点x x 1 x 2 x n 和点 y y 1 y 2 y n 间的距离 记作x y 规定2222211)( )()(),(n n y x y x y x -+⋅⋅⋅+-+-=y x ρ显然 n 1 2 3时 上术规定与数轴上、直角坐标系下平面及空间中两点间的距离一至R n中元素x x 1 x 2 x n 与零元0之间的距离x 0记作||x ||在R 1、R 2、R 3中 通常将||x ||记作|x | 即22221 ||||n x x x ⋅⋅⋅++=x采用这一记号 结合向量的线性运算 便得),()( )()(||||2222211y x y x ρ=-+⋅⋅⋅+-+-=-n n y x y x y x 在n 维空间R n 中定义了距离以后 就可以定义R n中变元的极限设x x 1 x 2 x n a a 1 a 2 a n R n如果||xa ||0则称变元x 在R n中趋于固定元a 记作xa 显然xa x 1a 1 x 2a 2 x n a n在R n中线性运算和距离的引入 使得前面讨论过的有关平面点集的一系列概念 可以方便地引入到nn 3维空间中来 例如设a a 1 a 2 a n R n是某一正数 则n 维空间内的点集U a {x | x R nx a }就定义为R n中点a 的邻域 以邻域为基础 可以定义点集的内点、外点、边界点和聚点 以及开集、闭集、区域等一系列概念二 多元函数概念例1 圆柱体的体积V 和它的底半径r 、高h 之间具有关系V r 2h这里 当r 、h 在集合{r h | r >0 h >0}内取定一对值r h 时 V 对应的值就随之确定例2 一定量的理想气体的压强p 、体积V 和绝对温度T 之间具有关系V RTp =其中R 为常数 这里 当V 、T 在集合{V T | V >0 T >0}内取定一对值V T 时 p 的对应值就随之确定 例3 设R 是电阻R 1、R 2并联后的总电阻 由电学知道 它们之间具有关系2121R R R R R +=这里 当R 1、R 2在集合{ R 1 R 2 | R 1>0 R 2>0}内取定一对值 R 1 R 2时 R 的对应值就随之确定定义1 设D 是R 2的一个非空子集 称映射f D R 为定义在D上的二元函数通常记为zfx y x yD或zfP PD其中点集D称为该函数的定义域x y称为自变量z称为因变量上述定义中与自变量x、y的一对值x y相对应的因变量z的值也称为f在点x y处的函数值记作fx y即zfx y 值域fD{z| zfx y x yD}函数的其它符号zzx y zgx y等类似地可定义三元函数ufx y z x y zD以及三元以上的函数一般地把定义1中的平面点集D换成n维空间R n内的点集D映射f D R就称为定义在D上的n元函数通常记为ufx1x2x n x1x2x n D或简记为uf x x x1x2x n D也可记为ufP Px1x2x n D函数定义域的约定在一般地讨论用算式表达的多元函数uf x时就以使这个算式有意义的变元x的值所组成的点集为这个多元函数的自然定义域因而对这类函数它的定义域不再特别标出例如函数z ln xy的定义域为{x y|xy>0}无界开区域函数z arcsin x2y2的定义域为{x y|x2y21}有界闭区域二元函数的图形点集{x y z|zfx y x yD}称为二元函数zfx y的图形二元函数的图形是一张曲面例如zaxbyc是一张平面而函数z=x2+y2的图形是旋转抛物面三多元函数的极限与一元函数的极限概念类似如果在Px yP0x0y0的过程中对应的函数值fx y无限接近于一个确定的常数A则称A 是函数fx y当x yx0y0时的极限定义2设二元函数fPfx y 的定义域为D P 0x 0 y 0是D 的聚点 如果存在常数A 对于任意给定的正数总存在正数 使得当),(),(0δP U D y x P⋂∈时 都有|fPA ||fx yA |成立 则称常数A 为函数fx y 当x yx 0 y 0时的极限 记为 Ay x f y x y x =→),(lim ),(),(0或fx yA x yx 0 y 0也记作AP f P P =→)(lim 0或fPAPP 0上述定义的极限也称为二重极限例4. 设22221sin)(),(y x y x y x f ++= 求证0),(lim )0,0(),(=→y x f y x证 因为2222222222 |1sin ||| |01sin)(||0),(|y x y x y x y x y x y x f +≤+⋅+=-++=-可见 >0 取εδ=则当δ<-+-<22)0()0(0y x即),(),(δO U D y x P⋂∈时 总有|fx y 0|因此0),(lim )0,0(),(=→y x f y x 必须注意1二重极限存在 是指P 以任何方式趋于P 0时 函数都无限接近于A2如果当P 以两种不同方式趋于P 0时 函数趋于不同的值 则函数的极限不存在 讨论函数⎪⎩⎪⎨⎧=+≠++=0 00 ),(222222y x y x y x xy y x f 在点0 0有无极限 提示 当点Px y 沿x 轴趋于点0 0时0lim )0 ,(lim ),(lim00)0,0(),(===→→→x x y x x f y x f 当点Px y 沿y 轴趋于点0 0时0lim ) ,0(lim ),(lim 0)0,0(),(===→→→y y y x y f y x f当点P x y 沿直线ykx 有22222022 )0,0(),(1lim lim kk x k x kx y x xy x kx y y x +=+=+→=→ 因此 函数fx y 在0 0处无极限极限概念的推广 多元函数的极限多元函数的极限运算法则 与一元函数的情况类似 例5 求x xy y x )sin(lim)2,0(),(→解 y xy xy xxy y x y x ⋅=→→)sin(lim )sin(lim)2,0(),()2,0(),(y xy xy y x y x )2,0(),()2,0(),(lim )sin(lim→→⋅=122 四 多元函数的连续性定义3 设二元函数fPf x y 的定义域为D P 0x 0 y 0为D的聚点 且P 0D 如果),(),(lim00),(),(00y x f y x f y x y x =→ 则称函数f x y 在点P 0x 0 y 0连续如果函数f x y 在D 的每一点都连续 那么就称函数f x y 在D 上连续 或者称f x y 是D 上的连续函数二元函数的连续性概念可相应地推广到n 元函数fP 上去例6设fx ,y sin x 证明fx y 是R 2上的连续函数证 设P 0x 0 y 0 R 20 由于sin x 在x 0处连续 故0 当|xx 0|时 有|sin x sin x 0|以上述作P 0的邻域UP 0 则当Px yUP 0 时 显然 |fx yfx 0 y 0||sin x sin x 0|即fx y sin x 在点P 0x 0 y 0 连续 由P 0的任意性知 sin x 作为x y 的二元函数在R 2上连续证 对于任意的P 0x 0 y 0R 2因为),(sin sin lim),(lim 000),(),(),(),(0000y x f x x y x f y x y x y x y x ===→→ 所以函数fx ,y sin x 在点P 0x 0 y 0连续 由P 0的任意性知 sin x作为x y 的二元函数在R 2上连续类似的讨论可知 一元基本初等函数看成二元函数或二元以上的多元函数时 它们在各自的定义域内都是连续的 定义4设函数fx y 的定义域为D P 0x 0 y 0是D 的聚点 如果函数fx y 在点P 0x 0 y 0不连续 则称P 0x 0 y 0为函数fx y 的间断点 例如 函数⎪⎩⎪⎨⎧=+≠++=0 00 ),(222222y x y x y x xy y x f其定义域D R 2O 0 0是D 的聚点 fx y 当x y 0 0时的极限不存在 所以点O 0 0是该函数的一个间断点又如 函数11sin22-+=y x z 其定义域为D {x y |x 2y 21} 圆周C {x y |x 2y 21}上的点都是D 的聚点 而fx y 在C 上没有定义 当然fx y 在C 上各点都不连续 所以圆周C 上各点都是该函数的间断点注 间断点可能是孤立点也可能是曲线上的点可以证明 多元连续函数的和、差、积仍为连续函数 连续函数的商在分母不为零处仍连续 多元连续函数的复合函数也是连续函数多元初等函数 与一元初等函数类似 多元初等函数是指可用一个式子所表示的多元函数 这个式子是由常数及具有不同自变量的一元基本初等函数经过有限次的四则运算和复合运算而得到的例如2221y y x x +-+ sin xy 222z y xe ++都是多元初等函数一切多元初等函数在其定义区域内是连续的 所谓定义区域是指包含在定义域内的区域或闭区域由多元连续函数的连续性 如果要求多元连续函数fP 在点P 0处的极限 而该点又在此函数的定义区域内 则 )()(lim 00P f P f p p =→例7 求xy y x y x +→)2,1(),(lim解 函数xy yx y x f +=),(是初等函数 它的定义域为D {x y |x 0 y 0}P 01 2为D 的内点 故存在P 0的某一邻域UP 0D 而任何邻域都是区域 所以UP 0是fx y 的一个定义区域 因此23)2,1(),(lim)2,1(),(==→f y x f y x 一般地 求)(lim 0P f P P →时 如果fP 是初等函数 且P 0是fP 的定义域的内点 则fP 在点P 0处连续 于是)()(lim 00P f P f P P =→例8 求xy xy y x 11lim)0 ,0(),(-+→解)11()11)(11(lim11lim)0 ,0(),()0 ,0(),(++++-+=-+→→xy xy xy xy xy xy y x y x 21111lim )0 ,0(),(=++=→xy y x多元连续函数的性质性质1 有界性与最大值最小值定理在有界闭区域D 上的多元连续函数 必定在D 上有界 且能取得它的最大值和最小值性质1就是说 若fP 在有界闭区域D 上连续 则必定存在常数M 0 使得对一切PD 有|fP |M 且存在P 1、P 2D 使得 fP 1max{fP |PD } fP 2min{fP |PD }性质2 介值定理 在有界闭区域D 上的多元连续函数必取得介于最大值和最小值之间的任何值§8 2 偏导数一、偏导数的定义及其计算法对于二元函数zfx y 如果只有自变量x 变化 而自变量y 固定 这时它就是x 的一元函数 这函数对x 的导数 就称为二元函数zfx y 对于x 的偏导数定义 设函数zfx y 在点x 0 y 0的某一邻域内有定义 当y 固定在y 0而x 在x 0处有增量x 时 相应地函数有增量fx 0x y 0fx 0 y 0如果极限x y x f y x x f x ∆-∆+→∆),(),(lim00000存在 则称此极限为函数zfx y 在点x 0 y 0处对x 的偏导数 记作0y y x x x z==∂∂ 00y y x x x f ==∂∂0y y x x xz == 或),(00y x f x例如x y x f y x x f y x f x x ∆-∆+=→∆),(),(lim),(0000000类似地 函数zfx y 在点x 0 y 0处对y 的偏导数定义为y y x f y y x f y ∆-∆+→∆),(),(lim00000记作y y x x y z==∂∂y y x x y f==∂∂y y x x yz == 或f y x 0 y 0偏导函数 如果函数zfx y 在区域D 内每一点x y 处对x 的偏导数都存在 那么这个偏导数就是x 、y 的函数 它就称为函数zfx y 对自变量x 的偏导函数 记作x z ∂∂ xf ∂∂ x z 或),(y x f x偏导函数的定义式x y x f y x x f y x f x x ∆-∆+=→∆),(),(lim),(0类似地 可定义函数zfx y 对y 的偏导函数 记为y z ∂∂ yf∂∂ z y 或),(y x f y偏导函数的定义式y y x f y y x f y x f y y ∆-∆+=→∆),(),(lim),(0求xf∂∂时 只要把y 暂时看作常量而对x求导数 求yf∂∂时只要把x 暂时看作常量而对y 求导数讨论 下列求偏导数的方法是否正确),(),(00y y x x x x y x f y x f ===),(),(00y y x x y y y x f y x f ===0]),([),(000x x x y x f dx d y x f == 0]),([),(000y y y y x f dy dy x f ==偏导数的概念还可推广到二元以上的函数例如三元函数ufx y z 在点x y z 处对x 的偏导数定义为x z y x f z y x x f z y x f x x ∆-∆+=→∆),,(),,(lim),,(0其中x y z 是函数ufx y z 的定义域的内点 它们的求法也仍旧是一元函数的微分法问题例1 求zx 23xyy 2在点1 2处的偏导数解 y x x z 32+=∂∂ yx y z 23+=∂∂ 8231221=⋅+⋅=∂∂==y x xz7221321=⋅+⋅=∂∂==y x yz例2 求zx 2sin 2y 的偏导数解 y x x z 2sin 2=∂∂ yx y z 2cos 22=∂∂例3 设)1,0(≠>=x x xz y求证zy z x x z y x 2ln 1=∂∂+∂∂证 1-=∂∂y yx x z xx y z y ln =∂∂zx x x x x yx y x y z x x z y x y y y y 2ln ln 1ln 11=+=+=∂∂+∂∂-例4 求222z y x r ++=的偏导数解 r x z y x x x r =++=∂∂222 r y z y x y y r =++=∂∂222例5 已知理想气体的状态方程为pV =RTR 为常数求证 1-=∂∂⋅∂∂⋅∂∂p T T V V p证 因为V RTp = 2V RT V p-=∂∂p RT V = p RT V =∂∂RpV T =R Vp T =∂∂所以12-=-=⋅⋅-=∂∂⋅∂∂⋅∂∂pV RT R V p R V RT p T T V V p例 5 说明的问题 偏导数的记号是一个整体记号 不能看作分子分母之商二元函数zfx y 在点x 0 y 0的偏导数的几何意义f x x 0 y 0fx y 0x 是截线zfx y 0在点M 0处切线T x 对x 轴的斜率f y x 0 y 0 fx 0 y y 是截线zfx 0 y 在点M 0处切线T y 对y 轴的斜率偏导数与连续性 对于多元函数来说 即使各偏导数在某点都存在 也不能保证函数在该点连续 例如⎪⎩⎪⎨⎧=+≠++=0 00),(222222y x y x y x xy y x f在点0 0有 f x 0 00 f y 0 00 但函数在点0 0并不连续提示0)0 ,(=x f 0) ,0(=y f0)]0 ,([)0 ,0(==x f dx d f x 0)] ,0([)0 ,0(==y f dy df y当点Px y 沿x 轴趋于点0 0时 有0lim )0 ,(lim ),(lim00)0,0(),(===→→→x x y x x f y x f当点Px y 沿直线ykx 趋于点0 0时 有22222022 )0,0(),(1lim lim kk x k x kx y x xy x kx y y x +=+=+→=→因此),(lim )0,0(),(y x f y x →不存在 故函数fx y 在0 0处不连续类似地 可定义函数zfx y 对y 的偏导函数 记为y z ∂∂ yf∂∂ z y 或),(y x f y偏导函数的定义式y y x f y y x f y x f y y ∆-∆+=→∆),(),(lim),(0二 高阶偏导数设函数zfx y 在区域D 内具有偏导数),(y x f x z x =∂∂ ),(y x f y z y=∂∂那么在D 内f x x y 、f y x y 都是x y 的函数 如果这两个函数的偏导数也存在 则称它们是函数zfx y 的二偏导数 按照对变量求导次序的为同有下列四个二阶偏导数如果函数zfx y 在区域D 内的偏导数f x x y 、f y x y 也具有偏导数则它们的偏导数称为函数zfx y 的二阶偏导数 按照对变量求导次序的不同有下列四个二阶偏导数),()(22y x f x z x z x xx =∂∂=∂∂∂∂ ),()(2y x f y x z x z y xy=∂∂∂=∂∂∂∂),()(2y x f x y z y z x yx =∂∂∂=∂∂∂∂ ),()(22y x f y z y z y yy =∂∂=∂∂∂∂其中),()(2y x f y x z x z y xy =∂∂∂=∂∂∂∂ ),()(2y x f x y z y z x yx=∂∂∂=∂∂∂∂称为混合偏导数22)(x z x z x ∂∂=∂∂∂∂ yx z x z y ∂∂∂=∂∂∂∂2)( x y z y z x ∂∂∂=∂∂∂∂2)( 22)(y zy z y ∂∂=∂∂∂∂同样可得三阶、四阶、以及n 阶偏导数二阶及二阶以上的偏导数统称为高阶偏导数例6 设zx 3y 23xy 3xy 1 求22x z ∂∂、33x z∂∂、x y z ∂∂∂2和y x z∂∂∂2解 y y y x x z --=∂∂32233 xxy y x y z --=∂∂23922226xy x z =∂∂ 2336y x z =∂∂196222--=∂∂∂y y x y x z 196222--=∂∂∂y y x x y z由例6观察到的问题 y x zx y z ∂∂∂=∂∂∂22定理 如果函数zfx y 的两个二阶混合偏导数x y z ∂∂∂2及yx z∂∂∂2在区域D 内连续 那么在该区域内这两个二阶混合偏导数必相等类似地可定义二元以上函数的高阶偏导数例7 验证函数22ln y x z +=满足方程02222=∂∂+∂∂y z x z证 因为)ln(21ln 2222y x y x z +=+= 所以22y x xx z +=∂∂22y x y y z +=∂∂222222222222)()(2)(y x x y y x x x y x xz +-=+⋅-+=∂∂222222222222)()(2)(y x y x y x y y y x yz +-=+⋅-+=∂∂因此 0)()(22222222222222=+-++-=∂∂+∂∂y x x y y x y x y z x z例8.证明函数r u 1=满足方程0222222=∂∂+∂∂+∂∂z u y u x u其中222z y x r ++=证 32211r xr x r x r r x u -=⋅-=∂∂⋅-=∂∂52343223131r x r x r r x r x u +-=∂∂⋅+-=∂∂同理5232231r y r y u +-=∂∂ 5232231r z r z u +-=∂∂因此)31()31()31(523523523222222r z r r y r r x r zu y u x u +-++-++-=∂∂+∂∂+∂∂33)(3352352223=+-=+++-=r r r r z y x r提示 6236333223)()(r x rr x r r r x x r rx x x u ∂∂⋅--=∂∂⋅--=-∂∂=∂∂§8 3全微分及其应用 一、全微分的定义根据一元函数微分学中增量与微分的关系有 偏增量与偏微分fxx yfx yf x x yxfxx yfx y 为函数对x 的偏增量 f x x yx 为函数对x 的偏微分fx yyfx yf y x yyfx yyfx y 为函数对y 的偏增量 f y x yy 为函数对y 的偏微分全增量 z fxx yyfx y计算全增量比较复杂 我们希望用x 、y 的线性函数来近似代替之定义 如果函数zfx y 在点x y 的全增量 z fxx yyfx y 可表示为) )()(( )(22y x o y B x A z ∆+∆=+∆+∆=∆ρρ 其中A 、B 不依赖于x 、y 而仅与x 、y 有关 则称函数zfx y 在点x y 可微分 而称AxBy 为函数zfx y 在点x y 的全微分 记作dz 即dzAxBy如果函数在区域D 内各点处都可微分 那么称这函数在D 内可微分可微与连续 可微必连续 但偏导数存在不一定连续 这是因为 如果zfx y 在点x y 可微则 z fxx yyfx yAxByo 于是 0lim 0=∆→z ρ从而),(]),([lim ),(lim)0,0(),(y x f z y x f y y x x f y x =∆+=∆+∆+→→∆∆ρ因此函数zfx y 在点x y 处连续 可微条件定理1必要条件如果函数zfx y 在点x y 可微分 则函数在该点的偏导数x z∂∂、y z ∂∂必定存在 且函数zfx y 在点x y 的全微分为yy z x xz dz ∆∂∂+∆∂∂= 证 设函数zfx y 在点Px y 可微分 于是 对于点P 的某个邻域内的任意一点P xx yy 有zAxByo 特别当y 0时有f xx yfx yAxo |x |上式两边各除以x 再令x 0而取极限 就得Ax y x f y x x f x =∆-∆+→∆),(),(lim从而偏导数x z ∂∂存在 且Ax z =∂∂同理可证偏导数y z ∂∂存在 且B y z =∂∂所以yy z x xz dz ∆∂∂+∆∂∂= 简要证明设函数zfx y 在点x y 可微分 于是有zAxByo 特别当y 0时有f xx yfx yAxo |x |上式两边各除以x 再令x 0而取极限 就得Ax x o A x y x f y x x f x x =∆∆+=∆-∆+→∆→∆]|)(|[lim ),(),(lim00从而x z ∂∂存在 且A x z =∂∂同理y z ∂∂存在 且B y z =∂∂ 所以yy z x xz dz ∆∂∂+∆∂∂= 偏导数x z∂∂、y z ∂∂存在是可微分的必要条件 但不是充分条件例如函数⎪⎩⎪⎨⎧=+≠++=0 00 ),(222222y x y x y x xy y x f 在点00处虽然有f x 0 00及f y 0 00但函数在00不可微分即zf x 0 0xf y 0 0y 不是较高阶的无穷小这是因为当x y 沿直线yx 趋于0 0时ρ])0 ,0()0 ,0([y f x f z y x ∆⋅+∆⋅-∆021)()()()(2222≠=∆+∆∆⋅∆=∆+∆∆⋅∆=x x x x y x y x定理2充分条件 如果函数zfx y 的偏导数x z∂∂、y z ∂∂在点x y 连续 则函数在该点可微分定理1和定理2的结论可推广到三元及三元以上函数 按着习惯x 、y 分别记作dx 、dy 并分别称为自变量的微分则函数zfx y 的全微分可写作dyy z dx x z dz ∂∂+∂∂=二元函数的全微分等于它的两个偏微分之和这件事称为二元函数的微分符合叠加原理 叠加原理也适用于二元以上的函数 例如函数uf x y z 的全微分为dzz u dy y u dx x u du ∂∂+∂∂+∂∂= 例1 计算函数zx 2y y 2的全微分解 因为xy x z 2=∂∂ yx y z 22+=∂∂所以dz 2xydxx 22ydy例2 计算函数ze xy在点2 1处的全微分解 因为xy ye x z =∂∂ xyxe y z =∂∂ 212e x z y x =∂∂== 2122ey z y x =∂∂==所以 dze 2dx 2e 2dy 例3 计算函数yze yx u ++=2sin 的全微分解 因为1=∂∂x u yz ze y y u +=∂∂2cos 21 yzye z u =∂∂ 所以 dzye dy ze ydx du yz yz +++=)2cos 21(二、全微分在近似计算中的应用当二元函数zf x y 在点P x y 的两个偏导数f x x y fyx y 连续 并且|x | |y |都较小时 有近似等式z dz f x x yxf y x yy即 f xx yy fx yf x x yxf y x yy我们可以利用上述近似等式对二元函数作近似计算 例4 有一圆柱体 受压后发生形变 它的半径由20cm 增大到20 05cm 高度由100cu 减少到99cm 求此圆柱体体积变化的近似值解 设圆柱体的半径、高和体积依次为r 、h 和V 则有V r 2h已知r 20 h 100 r 0 05 h 1 根据近似公式 有VdVV r rV h h 2rhrr 2h2201000 052021200 cm 3即此圆柱体在受压后体积约减少了200 cm 3例5 计算1 04202的近似值解 设函数f x yx y显然 要计算的值就是函数在x 104y 202时的函数值f 104 202 取x 1 y 2 x 004 y 002 由于f xx yy fx yf x x yxf y x yyx y yx y 1xx yln x y所以10420212212100412ln1002108例6 利用单摆摆动测定重力加速度g 的公式是224T lg π=现测得单摆摆长l 与振动周期T 分别为l =100±、T =2±.问由于测定l 与T 的误差而引起g 的绝对误差和相对误差各为多少解 如果把测量l 与T 所产生的误差当作|Δl |与|ΔT |,则利用上述计算公式所产生的误差就是二元函数224T lg π=的全增量的绝对值|Δg |.由于|Δl ||ΔT |都很小因此我们可以用dg 来近似地代替Δg 这样就得到g 的误差为||||||T T g l l g dg g ∆∂∂+∆∂∂=≈∆T l T g l g δδ⋅∂∂+⋅∂∂≤||||)21(4322Tl T l T δδπ+=其中l 与T 为l 与T 的绝对误差 把l =100 T =2, l =, δT =代入上式 得g 的绝对误差约为)004.02100221.0(4322⨯⨯+=πδg)/(93.45.022s cm ==π.02225.0210045.0=⨯=ππδg g从上面的例子可以看到对于一般的二元函数z =fx, y , 如果自变量x 、y 的绝对误差分别为x 、y , 即|Δx |x , |Δy |y , 则z 的误差||||||y y z x x z dz z ∆∂∂+∆∂∂=≈∆ ||||||||y y z x x z ∆⋅∂∂+∆⋅∂∂≤ y x y z x z δδ⋅∂∂+⋅∂∂≤||||从而得到z 的绝对误差约为yx z yz xz δδδ⋅∂∂+⋅∂∂=||||z 的相对误差约为yx z z y z z x zz δδδ∂∂+∂∂=||§8 4 多元复合函数的求导法则 设zfu v 而ut vt 如何求dt dz设zfu v 而ux y vx y 如何求x z∂∂和y z ∂∂1 复合函数的中间变量均为一元函数的情形定理1 如果函数ut 及vt 都在点t 可导 函数zfu v 在对应点u v 具有连续偏导数 则复合函数zft t 在点t 可导 且有dt dv v z dt du u z dt dz ⋅∂∂+⋅∂∂=简要证明1 因为zfu v 具有连续的偏导数 所以它是可微的 即有dvv z du uz dz ∂∂+∂∂=又因为ut 及vt 都可导 因而可微 即有dt dt du du = dtdt dv dv = 代入上式得dt dtdv v z dt dt du u z dz ⋅∂∂+⋅∂∂=dtdt dv v z dt du u z )(⋅∂∂+⋅∂∂= 从而 dt dvv z dt du u z dt dz ⋅∂∂+⋅∂∂=简要证明2 当t 取得增量t 时 u 、v 及z 相应地也取得增量u 、v 及z 由zfu v 、ut 及vt 的可微性 有)(ρo v v z u u z z +∆∂∂+∆∂∂=∆)()]([)]([ρo t o t dt dv v z t o t dt du u z +∆+∆∂∂+∆+∆∂∂=)()()()(ρo t o v z u z t dt dv v z dt du u z +∆∂∂+∂∂+∆⋅∂∂+⋅∂∂= t o t t o v z u z dt dv v z dt du u z t z ∆+∆∆∂∂+∂∂+⋅∂∂+⋅∂∂=∆∆)()()(ρ令t 0 上式两边取极限 即得dt dvv z dt du u z dt dz ⋅∂∂+⋅∂∂=注0)()(0)()()(lim )(lim 222200=+⋅=∆∆+∆⋅=∆→∆→∆dt dv dt du t v u o t o t t ρρρ推广 设zf u v w u t vt wt 则zf t t t 对t 的导数为dt dww z dt dv v z dt du u z dt dz ∂∂+∂∂+∂∂=上述dt dz称为全导数2 复合函数的中间变量均为多元函数的情形定理2 如果函数ux y vx y 都在点x y 具有对x 及y 的偏导数 函数zfu v 在对应点u v 具有连续偏导数 则复合函数zf x y x y 在点x y 的两个偏导数存在 且有x v v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂ y vv z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂推广 设zfu v w ux y vx y wx y 则x w w z x v v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂=∂∂ y ww z y v v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂=∂∂讨论 1设zfu v ux y vy 则=∂∂x z =∂∂y z提示 x u u z x z ∂∂⋅∂∂=∂∂ dy dvv z y u u z y z ⋅∂∂+∂∂⋅∂∂=∂∂2设zfu x y 且ux y 则=∂∂x z =∂∂y z提示 x f x u u f x z ∂∂+∂∂∂∂=∂∂ y fy u u f y z ∂∂+∂∂∂∂=∂∂ 这里x z∂∂与xf ∂∂是不同的 x z∂∂是把复合函数zfx y x y 中的y 看作不变而对x 的偏导数 xf∂∂是把fu x y 中的u 及y 看作不变而 对x 的偏导数 y z∂∂与yf ∂∂也有类似的区别3.复合函数的中间变量既有一元函数 又有多元函数的情形定理3 如果函数ux y 在点x y 具有对x 及对y 的偏导数 函数vy 在点y 可导 函数zfu v 在对应点u v 具有连续偏导数 则复合函数zfx y y 在点x y 的两个偏导数存在 且有x u u z x z ∂∂⋅∂∂=∂∂ dy dvv z y u u z y z ⋅∂∂+∂∂⋅∂∂=∂∂例1 设ze u sin v uxy vxy 求x z∂∂和y z ∂∂解 x vv z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂e u sin vye ucos v 1 e x yy sin xy cos xyy vv z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂e u sin vxe ucos v 1 e xyx sin xy cos xy 例2 设222),,(z y x ez y x f u ++== 而y x z sin 2= 求x u∂∂和y u ∂∂解 x zz f x f x u ∂∂⋅∂∂+∂∂=∂∂y x ze xez y xz y xsin 222222222⋅+=++++yx y xey x x 2422sin 22)sin 21(2++++=y zz f y f y u ∂∂⋅∂∂+∂∂=∂∂y x ze yez y xz y xcos 222222222⋅+=++++yx y xey y x y 2422sin 4)cos sin (2+++=例3 设zuv sin t 而uetv cos t 求全导数dt dz解 t zdt dv v z dt du u z dt dz ∂∂+⋅∂∂+⋅∂∂=ve tu sin t cos t e tcos te tsin t cos t e t cos t sin t cos t 例4 设wfxyz xyz f具有二阶连续偏导数 求x w∂∂及z x w ∂∂∂2解 令uxyz vxyz 则wfu v 引入记号u v u f f ∂∂='),(1 v u v u f f ∂∂∂='),(12同理有2f '11f ''22f ''等 21f yz f x v v f x u u f x w '+'=∂∂⋅∂∂+∂∂⋅∂∂=∂∂z f yz f y z f f yz f z z x w ∂'∂+'+∂'∂='+'∂∂=∂∂∂221212)(2222121211f z xy f yz f y f xy f ''+''+'+''+''= 22221211)(f z xy f y f z x y f ''+'+''++''= 注 1211111f xy f z v v f z u u f z f ''+''=∂∂⋅∂'∂+∂∂⋅∂'∂=∂'∂ 2221222f xy f z v v f z u u f z f ''+''=∂∂⋅∂'∂+∂∂⋅∂'∂=∂'∂例5 设ufx y 的所有二阶偏导数连续 把下列表达式转换成极坐标系中的形式122)()(y u xu ∂∂+∂∂ 22222y u x u ∂∂+∂∂ 解 由直角坐标与极坐标间的关系式得 ufx yf cos θ sin θF θ 其中x cos θ y sin θ 22yx +=ρx yarctan=θ应用复合函数求导法则 得x u x u x u ∂∂∂∂+∂∂∂∂=∂∂θθρρ2ρθρρy u x u ∂∂-∂∂=ρθθθρsin cos y u u ∂∂-∂∂=y u y u y u ∂∂∂∂+∂∂∂∂=∂∂θθρρ2ρθρρx u y u ∂∂+∂∂=ρθθθρcos sin ∂∂+∂∂=u u两式平方后相加 得22222)(1)()()(θρρ∂∂+∂∂=∂∂+∂∂u u yu x u 再求二阶偏导数 得x x u x x u x u ∂∂⋅∂∂∂∂+∂∂⋅∂∂∂∂=∂∂θθρρ)()(22θρθθθρρcos )sin cos (⋅∂∂-∂∂∂∂=u u ρθρθθθρθsin )sin cos (⋅∂∂-∂∂∂∂-u u 22222222sin cos sin 2cos ρθθρθθθρθρ∂∂+∂∂∂-∂∂=u u u ρθρρθθθ22sin cos sin 2∂∂+∂∂+u u同理可得2222222222cos cos sin 2sin ρθθρθθθρθρ∂∂+∂∂∂+∂∂=∂∂u u u y u ρθρρθθθ22cos cos sin 2∂∂+∂∂-u u两式相加 得22222222211θρρρρ∂∂++∂∂=∂∂+∂∂u u y u x u])([1222θρρρρρ∂∂+∂∂∂∂=u u全微分形式不变性 设zfu v 具有连续偏导数 则有全微分dvv z du uz dz ∂∂+∂∂= 如果zfu v 具有连续偏导数 而ux y vx y 也具有连续偏导数 则dyy z dx x z dz ∂∂+∂∂=dyy v v z y u u z dx x v v z x u u z )()(∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂=)()(dy y v dx x v v z dy y u dx x u u z ∂∂+∂∂∂∂+∂∂+∂∂∂∂= dv v z du uz ∂∂+∂∂= 由此可见 无论z 是自变量u 、v 的函数或中间变量u 、v 的函数 它的全微分形式是一样的 这个性质叫做全微分形式不变性例6 设ze usin v ux y vxy 利用全微分形式不变性求全微分解 dv v z du uz dz ∂∂+∂∂= e u sin vdu e ucos v dv e u sin vy dxx dy e u cos vdxdy ye u sin v e u cos vdxxe u sin v e ucos v dye xy y sin xy cos xydx e xyx sin xy cos xydy§8 5 隐函数的求导法则一、一个方程的情形 隐函数存在定理1设函数Fx y 在点Px 0 y 0的某一邻域内具有连续偏导数Fx 0 y 00 F y x 0 y 00 则方程Fx y 0在点x 0 y 0的某一邻域内恒能唯一确定一个连续且具有连续导数的函数yfx 它满足条件y 0fx 0 并有yx F F dx dy-= 求导公式证明 将yfx 代入Fx y 0 得恒等式 Fx fx 0 等式两边对x 求导得=⋅∂∂+∂∂dx dy y F x F由于F y 连续 且F y x 0 y 00 所以存在x 0 y 0的一个邻域 在这个邻域同F y 0 于是得yx F F dx dy-=例1 验证方程x 2y 210在点0 1的某一邻域内能唯一确定一个有连续导数、当x 0时y 1的隐函数yfx 并求这函数的一阶与二阶导数在x 0的值解 设Fx yx 2y 21 则F x 2x F y 2y F 0 10 F y 0 120 因此由定理1可知 方程x 2y 210在点0 1的某一邻域内能唯一确定一个有连续导数、当x 0时y 1的隐函数yfx yx F F dx dyy x -=-= 00==x dx dy332222221)(y y x y y y x x y y y x y dx y d -=+-=---='--=1022-==x dx yd隐函数存在定理还可以推广到多元函数 一个二元方程Fx y 0可以确定一个一元隐函数 一个三元方程Fx y z 0可以确定一个二元隐函数 隐函数存在定理2设函数Fx y z 在点Px 0 y 0 z 0的某一邻域内具有连续的偏导数 且Fx 0 y 0 z 00 F z x 0 y 0 z 00 则方程Fx y z 0在点x 0 y 0z 0的某一邻域内恒能唯一确定一个连续且具有连续偏导数的函数zfx y 它满足条件z 0fx 0 y 0 并有zxF F x z -=∂∂ zyF F y z -=∂∂公式的证明 将zfx y 代入Fx y z 0 得Fx y fx y 0 将上式两端分别对x 和y 求导 得0=∂∂⋅+x z F F z x 0=∂∂⋅+y zF F z y因为F z 连续且F z x 0 y 0 z 00 所以存在点x 0 y 0 z 0的一个邻域 使F z 0 于是得zx F F x z -=∂∂ zy F F y z -=∂∂例2. 设x 2y 2z 24z 0 求22x z∂∂解 设Fx y z x 2y 2z 24z 则F x 2x F y 2z 4 z x z x F F x z z x -=--=-=∂∂24223222222)2()2()2()2()2()2()2(z x x z z x x x z x z x x x z -+-=--+-=-∂∂+-=∂∂二、方程组的情形在一定条件下 由个方程组Fx y u v 0 Gx y u v 0可以确定一对二元函数uux y vvx y 例如方程xuyv 0和yuxv 1可以确定两个二元函数22y x y u +=22y x x v +=事实上 xuyv 0 u yx v =1=⋅+u y x x yu 22y x yu += 2222yx x y x yy x v +=+⋅=如何根据原方程组求u v 的偏导数 隐函数存在定理3 隐函数存在定理3设Fx y u v 、Gx y u v 在点Px 0 y 0 u 0 v 0的某一邻域内具有对各个变量的连续偏导数 又Fx 0 y 0 u 0 v 00 Gx 0 y 0 u 0 v 00 且偏导数所组成的函数行列式v G u Gv Fu Fv u G F J ∂∂∂∂∂∂∂∂=∂∂=),(),(在点Px 0 y 0 u 0 v 0不等于零 则方程组Fx y u v 0 Gx y u v 0在点Px 0 y 0 u 0 v 0的某一邻域内恒能唯一确定一组连续且具有连续偏导数的函数uux y vvx y 它们满足条件u 0ux 0 y 0 v 0vx 0y 0 并有v uv uv x v xG G F F G G F F v x G F J x u -=∂∂-=∂∂),(),(1vuv ux u x uG G F F G G F F x u G F J x v -=∂∂-=∂∂),(),(1vu vu vy v y G G F F G G F F v y G F J y u -=∂∂-=∂∂),(),(1vu vu yu y u G G F F G G F F y u G F J y v -=∂∂-=∂∂),(),(1隐函数的偏导数:设方程组Fx y u v 0 Gx y u v 0确定一对具有连续偏导数的二元函数uux y vvx y 则偏导数x u ∂∂ x v ∂∂由方程组⎪⎩⎪⎨⎧=∂∂+∂∂+=∂∂+∂∂+.0,0x v G x u G G x v F x u F F v u x v u x 确定偏导数y u ∂∂ y v ∂∂由方程组⎪⎩⎪⎨⎧=∂∂+∂∂+=∂∂+∂∂+.0,0y v G y u G G y v F y u F F v u y v u y 确定例3 设xuyv 0 yuxv 1 求x u ∂∂ x v ∂∂ y u∂∂和y v ∂∂解 两个方程两边分别对x 求偏导 得x u ∂∂和x v∂∂的方程组⎪⎩⎪⎨⎧=∂∂++∂∂=∂∂-∂∂+00x v x v x u y x v y x u x u当x 2y 2时 解之得22y x yv xu x u ++-=∂∂ 22y x xvyu x v +-=∂∂两个方程两边分别对x 求偏导 得y u∂∂和y v∂∂的方程组⎪⎩⎪⎨⎧=∂∂+∂∂+=∂∂--∂∂00y v x y u y u y v y v y u x 当x 2y 2时 解之得22y x yu xv y u +-=∂∂ 22y x yvxu y v ++-=∂∂另解 将两个方程的两边微分得⎩⎨⎧=+++=--+00xdv vdx ydu udy ydv vdy xdu udx 即⎩⎨⎧--=+-=-vdx udy xdv ydu udxvdy ydv xdu解之得dy y x yuxv dx y x yv xu du 2222+-+++-=dy y x yvxu dx y x xv yu dv 2222++-+-=于是 22y x yv xu x u ++-=∂∂ 22yx yu xv y u +-=∂∂22y x xv yu x v +-=∂∂ 22y x yv xu y v ++-=∂∂例 设函数xxu v yyu v 在点u v 的某一领域内连续且有连续偏导数 又0),(),(≠∂∂v u y x1证明方程组⎩⎨⎧==),(),(v u y y v u x x在点x y u v 的某一领域内唯一确定一组单值连续且有连续偏导数的反函数uux y vvx y2求反函数uux y vvx y 对x y 的偏导数 解 1将方程组改写成下面的形式⎩⎨⎧=-≡=-≡0),(),,,(0),(),,,(v u y y v u y x G v u x x v u y x F则按假设.0),(),(),(),(≠∂∂=∂∂=v u y x v u G F J由隐函数存在定理3 即得所要证的结论2将方程组7所确定的反函数uux yvvx y 代入7 即得⎩⎨⎧≡≡)],(),,([)],(),,([y x v y x u y y y x v y x u x x将上述恒等式两边分别对x 求偏导数得⎪⎩⎪⎨⎧∂∂⋅∂∂+∂∂⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂=x v v y x u u y x vv x x u u x 01由于J 0 故可解得v y J x u ∂∂=∂∂1 u yJ x v ∂∂-=∂∂1同理 可得v x J y u ∂∂-=∂∂1 u xJ y v ∂∂=∂∂1§8 6多元函数微分学的几何应用一 空间曲线的切线与法平面 设空间曲线的参数方程为 xt yt zt 这里假定t t t 都在 上可导在曲线上取对应于tt 0的一点M 0x 0 y 0 z 0及对应于tt 0t 的邻近一点Mx 0+x y 0+y z 0+z 作曲线的割线MM 0 其方程为z z z y y y x x x ∆-=∆-=∆-000当点M 沿着趋于点M 0时割线MM 0的极限位置就是曲线在点M 0处的切线 考虑t z z z ty y y t x x x ∆∆-=∆∆-=∆∆-000 当MM 0 即t 0时 得曲线在点M 0处的切线方程为)()()(000000t z z t y y t x x ωψϕ'-='-='- 曲线的切向量 切线的方向向量称为曲线的切向量 向量T t 0 t 0 t 0就是曲线在点M 0处的一个切向量法平面 通过点M 0而与切线垂直的平面称为曲线在点M 0 处的法平面 其法平面方程为 t 0xx 0t 0yy 0t 0zz 00例1 求曲线xt yt 2zt 3在点1 1 1处的切线及法平面方程解 因为x t 1 y t 2t z t 3t 2而点1 1 1所对应的参数t 1 所以T 1 2 3 于是 切线方程为 312111-=-=-z y x法平面方程为x 12y 13z 10 即x 2y 3z 6讨论1 若曲线的方程为 yx zx问其切线和法平面方程是什么形式提示 曲线方程可看作参数方程 xx yx zx 切向量为T 1 x x2 若曲线的方程为Fx y z 0 Gx y z 0 问其切线和法平面方程又是什么形式提示 两方程确定了两个隐函数 yx zx 曲线的参数方程为xx yx zx由方程组⎪⎩⎪⎨⎧=++=++00dx dz G dx dy G G dxdz F dx dy F F z y x z y x 可解得dx dy 和dx dz 切向量为) ,,1(dx dz dx dy =T例2 求曲线x 2y 2z 26 xyz 0在点1 2 1处的切线及法平面方程解 为求切向量 将所给方程的两边对x 求导数 得⎪⎩⎪⎨⎧=++=++010222dx dz dx dydxdz z dx dy y x解方程组得z y xz dx dy --= z y yx dx dz --=在点1 2 1处 0=dx dy 1-=dx dz从而T 1 0 1 所求切线方程为 110211--=+=-z y x法平面方程为x 10y 2z 10 即xz 0解 为求切向量 将所给方程的两边对x 求导数 得⎪⎩⎪⎨⎧=++=++010222dx dz dx dydx dz z dx dy y x方程组在点1 2 1处化为⎪⎩⎪⎨⎧-=+=-112dx dz dx dydx dz dx dy 解方程组得0=dx dy 1-=dx dz从而T 1 0 1 所求切线方程为 110211--=+=-z y x法平面方程为x 10y 2z 10 即xz 0。
多元函数的微分学的应用

多元函数的微分学的应用
多元函数的微分学在实际生活中有多种应用。
以下是其中几个常见的应用:
1. 最值问题:多元函数的微分学可以用来解决最值问题,例如优化问题,找到函数的最大值或最小值。
这种应用广泛用于物流、金融和工程等领域,其中包括确定最小成本生产和最大利润等问题。
2. 等高线图:多元函数的微分学也可以用来绘制等高线图。
等高线图常常用于表示地形,如山地,海底地形,或者用于表示等值线,如等压线,等温线和等高线等。
3. 导航系统:对于导航系统而言,通过多元函数微分学,不仅能够实时计算用户之间的距离,还能推断用户的行车方向,从而更好地指引用户前进方向。
4. 工程应用:对于工程师而言,他们会使用多元函数的微分学去计算关键参数,例如建筑物的结构支持力量、材料的伸缩性,以及各种形态的机器件等。
5. 统计分析:多元函数的微分学也可以帮助人们进行数据建模、数据预测,诸如对群体的群体大小计算以及分析等等。
在这种场合下,多元函数的微分学可帮助人们发现数据之间的关联以执行信息预测等任务。
总之,多元函数的微分学在实践中具有广泛应用,并为许多领域提供了重要的工
具和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课:多元函数求偏导,多元函数微分的应用多元复合函数、隐函数的求导法?(1) 多元复合函数设二元函数),(v u f z =在点),(00v u 处偏导数连续,二元函数),(),,(y x v v y x u u ==在点),(00y x 处偏导数连续, 并且),(),,(000000y x v v y x u u ==, 则复合函数)),(),,((y x v y x u f z = 在点),(00y x 处可微,且()()()()xy x v v v u f x y x u u v u f xz y x ∂∂⋅∂∂+∂∂⋅∂∂=00000000),(,,,,00∂∂()()()()yy x v v v u f y y x u u v u f yz y x ∂∂⋅∂∂+∂∂⋅∂∂=00000000),(,,,,00∂∂多元函数微分形式的不变性:设),(),,(),,(y x v v y x u u v u f z ===,均为连续可微,则将z 看成y x ,的函数,有dy yz dx x z dz ∂∂+∂∂=计算yvv f y u u f y z xvv f x u u f x z ∂∂∂∂+∂∂∂∂=∂∂∂∂∂∂+∂∂∂∂=∂∂,,代人, dv vf du u f dy y v dx x v v f dy y u dx x u u f dy y v v f y u u f dx x v v f x u u f dy y z dx x z dz ∂∂+∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+⎪⎭⎫⎝⎛∂∂∂∂+∂∂∂∂=∂∂+∂∂=我们将dv vf du u f dy y z dx x z dz ∂∂+∂∂=∂∂+∂∂=叫做微分形式不变性。
例1 设⎪⎭⎫ ⎝⎛=x y xy f x z ,3,求yzx z ∂∂∂∂,。
解:⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛'+'+=+⋅=x y d f xy d f x fdx x df x dx x f dz 213232)(33 ⎥⎦⎤⎢⎣⎡-'++'+=22132(3x ydx xdy f ydx xdy f x fdx xdy f x f x dx xyf yf x f x ⎪⎭⎫ ⎝⎛'+'+⎪⎭⎫ ⎝⎛'-'+=221421323由微分形式不变性, dy f x f x dx xyf yf x f x dy yz dx x z dz ⎪⎭⎫ ⎝⎛'+'+⎪⎭⎫ ⎝⎛'-'+=∂∂+∂∂=221421323 故 ⎪⎭⎫ ⎝⎛'+'=∂∂⎪⎭⎫ ⎝⎛'-'+=∂∂22142132,3f x f x yz xyf yf x f x xz 。
例2 已知 )1(1xy x-=,求dy dx.解 考虑二元函数 vu y =, u x v x==-11,,应用推论得.dx dvv y dx du u y dx dy ∂∂∂∂+=).ln 1(11)(ln 112221x x x u u x vu xv v -⎪⎭⎫ ⎝⎛=+---(2)隐函数 若函数()x y y =, 由方程()0,=y x F 确定,求导之函数?按隐函数定义有恒等式:()()0,≡x y x F ⇒()()0,=x y x F dxd, ⇒()()()()()0,,='⋅'+'x y x y x F x y x F y x ⇒()()()()()x y x F x y x F x y y x ,,''-='。
从这是可见:函数()x y y =可导有一个必要条件是,()0,≠'y x F y .例3 已知函数y f x =()由方程(), , 22b a y x f by ax +=+是常数,求导函数。
解:方程()22y x f by ax +=+两边对x 求导,⎪⎭⎫ ⎝⎛++'=+dx dy y x y x f dx dy ba 22)(22 )(2)(22222y x f y b ay x f x dx dy +'--+'=一般来说,若函数()x y y ρ=, 由方程()0,=y x F ρ确定,求导之函数? 将y 看作是n x x ,...,1的函数()),...,(1n x x y x y y ==ρ,对于方程0)),...,(,,...,(11=n n x x y x x F两端分别关于i x 求偏导数得到,并解i x f ∂∂,可得到公式 :()()y x F y x F x y y x i i,,ρρ''-=∂∂例4设函数y(z)y z x x == ),(由方程组⎩⎨⎧=--+=-++01201222222z y x z y x 确定, 求dzdy dz dx ,. 解 121222222⎪⎩⎪⎨⎧+=++-=+z y x z y x ⎪⎪⎩⎪⎪⎨⎧=+-=+⇒zdy dz y dxdz x z dy dz y dx dzx 242222解方程得: ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡dz dy dz dx =⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡---xz yz xy z z x x y y xy 8124122222441 由此得到 yz dz dyx z dz dx 2,3-==.例5 已知函数()y x z z ,=由参数方程:⎪⎩⎪⎨⎧===uvz v u y vu x sin cos ,给定,试求y z x z ∂∂∂∂,.解 这个问题涉及到复合函数微分法与隐函数微分法. y x ,是自变量,v u ,是中间变量(v u ,是y x ,的函数), 先由 z uv = 得到x vu x u v x v v z x u u z x z ∂∂∂∂∂∂∂∂∂∂∂∂∂∂+=+= yvu y u v y v v z y u u z y z ∂∂∂∂∂∂∂∂∂∂∂∂∂∂+=+= u v , 是由方程⎩⎨⎧==),(),(y x v v y x u u 的x y ,的隐函数,在这两个等式两端分别关于x y ,求偏导数,得⎪⎩⎪⎨⎧∂∂+∂∂=∂∂-∂∂=x v v u x u v x vv u x u v cos sin 0sin cos 1, ⎪⎩⎪⎨⎧∂∂+∂∂=∂∂-∂∂=y v vu y u v y v v u y u v cos sin 1sin cos 0 得到 uv x v v y u u u x v v x u cos ,sin ,sin ,cos =∂∂=∂∂-=∂∂=∂∂ 将这个结果代入前面的式子, 得到v v v x vu x u v x z sin cos -=-=∂∂∂∂∂∂ 与 v v v yvu y u v y z cos sin +=+=∂∂∂∂∂∂(3) 隐函数函数),(y x u u =由方程⎪⎩⎪⎨⎧===0),(0),,(),,,(t z h t z y g t z y x f u 确定,求y u x u ∂∂∂∂, 解: 函数关系分析: 5 (变量) ? 3 (方程)=2(自变量); 一函 (u ), 二自( x, y ), 二中( z, t )x f x u ∂∂=∂∂, yt t f y z z f y f y u ∂∂∂∂+∂∂∂∂+∂∂=∂∂ ⎪⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂-∂∂-∂∂⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂-0),(),(1t g z g z h t g t h t z h g y t y z , z h t g t h z g y g t h z f z h t f y f y u ∂∂∂∂-∂∂∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂∂∂-∂∂∂∂+∂∂=∂∂.二阶偏导数:一阶导函数的偏导数例6 ),(y x z z =由2222a z y x =++决定,求yx z∂∂∂2.解:022=∂∂+xzz x ,022=∂∂+y z z y zy y z z x x z -=∂∂-=∂∂, =∂∂⋅=∂∂∂x z z y y x z 223zxy-例7 设()()()22,,x x x f x g ϕ=,其中函数f 于ϕ的二阶偏导数连续,求()22dxx g d 例8 设z f xy x y =(,),f 二阶连续可微,求22xz∂∂. 解 记 yxv xy u ==,; v f f u f f ∂∂='∂∂='21,, 22222211,vf f u f f ∂∂=''∂∂='',u v ff v u f f ∂∂∂=''∂∂∂=''221212, 则211f yf y x v v f x u u f x z '+'=∂∂⋅∂∂+∂∂⋅∂∂=∂∂, x f y x f y x z x xz ∂'∂+∂'∂=⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂21221 因为 vff u f f ∂∂∂∂='='21,都是以u v ,为中间变量,以y x ,为自变量的函数,所以 x v f x u f x f ∂∂''+∂∂''='12111∂∂12111f y f y ''+''= x v f x u f x f ∂∂''+∂∂''='22212∂∂22211f yf y ''+''= 将以上两式代入前式得: f yf f y x z ''+''+''= 222121122212∂∂.例9 设),(y x z z =二阶连续可微,并且满足方程0222222=+∂+yz C y x z B x z A ∂∂∂∂∂∂ 若令,⎩⎨⎧+=+=y x v y x u βα 试确定βα,为何值时能变原方程为 02=∂∂∂v u z.解 将y x ,看成自变量,v u ,看成中间变量,利用链式法则得z v u v z u z x v v z x u u z x z ⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂ z v u v z u z y v v z y u u z y z ⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂βαβα z v u v z v u z u z v z u z x x z 222222222⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂=∂∂ 2222222222v z v u z u z v z u z y y z ∂∂+∂∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂=∂∂βαβαβαz v u2⎪⎭⎫ ⎝⎛∂∂+∂∂=βα ()222222vzv u z u z v z u z x y x z ∂∂+∂∂∂++∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂=∂∂∂ββααβα =z v uv u ⎪⎭⎫ ⎝⎛∂∂+∂∂⎪⎭⎫⎝⎛∂∂+∂∂βα 由此可得, 2222220y zCy x z B x z A ∂∂∂∂∂∂+∂+== =()()()+∂∂∂++++∂∂++v u z C B A u z C B A 222222αββααα()2222vz C B A ∂∂++ββ=0 只要选取βα,使得 ⎪⎩⎪⎨⎧=++=++020222ββααC B A C B A , 可得02=∂∂∂v u z . 问题成为方程022=++t C t B A 有两不同实根,即要求: 02>-C A B .令AC B B -+-=2α,AC B B ---=2β,即可。
