(完整word版)初一数学平行线证明题
(完整版)平行线及其判定(证明应用题)

授课教案学员姓名:________________ 学员年级:________________ 授课教师:_________________ 所授科目:_________ 上课时间:______年____月____日(~);共_____课时(以上信息请老师用正楷字手写)平行线及其判定(证明应用题)一.解答题(共11小题)1.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.2.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.3.如图,△ABC中,AB=AC,D是CA延长线上的一点,且∠B=∠DAM.求证:AM∥BC.4.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.5.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.6.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.7.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.8.已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.9.如图,CA⊥AD,垂足为A,∠C=50°,∠BAD=40°,求证:AB∥CD.10.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.11.如图所示,已知直线a、b、c、d、e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?2015年03月05日752444625的初中数学组卷参考答案与试题解析一.解答题(共11小题)1.(2014•槐荫区二模)已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.考点:平行线的判定.专题:证明题.分析:由∠A=∠F,根据内错角相等,两直线平行,即可求得AC∥DF,即可得∠C=∠FEC,又由∠C=∠D,则可根据同位角相等,两直线平行,证得BD∥CE.解答:证明:∵∠A=∠F,∴AC∥DF,∴∠C=∠FEC,∵∠C=∠D,∴∠D=∠FEC,∴BD∥CE.点评:此题考查了平行线的判定与性质.注意内错角相等,两直线平行与同位角相等,两直线平行.2.(2013•邵阳)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.考点:平行线的判定;角平分线的定义;三角形内角和定理.专题:证明题.分析:(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;(2)利用三角形内角和定理进行计算即可.解答:(1)证明:∵CF平分∠DCE,∴∠1=∠2=∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF(内错角相等,两直线平行);(2)∵∠D=30°,∠1=45°,∴∠DFC=180°﹣30°﹣45°=105°.点评:此题主要考查了平行线的判定,以及三角形内角和定理,关键是掌握内错角相等,两直线平行.3.(2010•江宁区一模)如图,△ABC中,AB=AC,D是CA延长线上的一点,且∠B=∠DAM.求证:AM∥BC.考点:平行线的判定.专题:证明题.分析:判别两条直线平行的方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.要证明AM∥BC,只要转化为证明∠C=∠DAM即可.解答:证明:∵AB=AC,∴∠B=∠C,∵∠B=∠DAM,∴∠C=∠DAM,∴AM∥BC.点评:本题主要考查了平行线的判定,注意等量代换的应用.4.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.考点:平行线的判定.专题:探究型.分析:因为DF∥AC,由内错角相等证明∠C=∠FEC,又因为∠C=∠D,则∠D=∠FEC,故CE∥BD.解答:解:CE∥BD.理由:∵DF∥AC(已知),∴∠C=∠FEC(两直线平行,内错角相等),又∵∠C=∠D(已知),∴∠D=∠FEC(等量代换),∴CE∥BD(同位角相等,两直线平行).点评:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题能有效地培养“执果索图”的思维方式与能力.5.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.考点:平行线的判定.专题:探究型.分析:设AB与DE相交于H,若判断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.解答:解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,又∵∠5=∠6,∴∠BAF=∠6,∴AB∥CD,∴∠2=∠EHA,又∵∠1=∠2,即∠1=∠EHA,∴BF∥DE.另解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,∵∠5=∠6,∴∠BAF=∠6,∵△BFA、△DEC的内角和都是180°∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6∵∠1=∠2;∠BAF=∠6∴∠BFA=∠4,∴BF∥DE.点评:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.6.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.考点:平行线的判定.专题:证明题.分析:先由已知证明AD∥EF,再证明1∠1=∠4,∠2=∠4,等量代换得出∠1=∠2.解答:证明:∵AD⊥BC,EF⊥BC(已知),∴AD∥EF(垂直于同一条直线的两直线平行),∴∠1=∠4(两直线平行,同位角相等),又∵∠3=∠C(已知),∴AC∥DG(同位角相等,两直线平行),∴∠2=∠4(两直线平行,内错角相等),∴∠1=∠2(等量代换).点评:此题的关键是理解平行线的性质及判定.①两直线平行,同位角相等.②两直线平行,内错角相等.③同位角相等,两直线平行.④内错角相等,两直线平行.7.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.考点:平行线的判定.专题:推理填空题.分析:由∠A=∠F,根据内错角相等,得两条直线平行,即AC∥DF;根据平行线的性质,得∠C=∠CEF,借助等量代换可以证明∠D=∠CEF,从而根据同位角相等,证明BD∥CE.解答:解:∵∠A=∠F(已知),∴AC∥DF(内错角相等,两直线平行),∴∠C=∠CEF(两直线平行,内错角相等),∵∠C=∠D(已知),∴∠D=∠CEF(等量代换),∴BD∥CE(同位角相等,两直线平行).点评:此题综合运用了平行线的判定及性质,比较简单.8.已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.考点:平行线的判定.专题:证明题.分析:首先根据角平分线的性质可得∠BAC=2∠DAC,再根据三角形外角与内角的关系可得∠G+∠GFA=∠BAC,又∠AFG=∠G.进而得到∠BAC=2∠G,从而得到∠DAC=∠G,即可判定出GE∥AD.解答:证明:∵AD是△ABC的平分线,∴∠BAC=2∠DAC,∵∠G+∠GFA=∠BAC,∠AFG=∠G.∴∠BAC=2∠G,∴∠DAC=∠G,∴AD∥GE.点评:此题主要考查了平行线的判定,关键是掌握三角形内角与外角的关系,以及平行线的判定定理.9.如图,CA⊥AD,垂足为A,∠C=50°,∠BAD=40°,求证:AB∥CD.考点:平行线的判定.专题:证明题.分析:利用直角三角形中两锐角互余得出∠D=40°,再利用内错角相等,两直线平行的判定证明即可.解答:证明:∵CA⊥AD,∴∠C+∠D=90°,∴∠C=50°,∴∠D=40°,∵∠BAD=40°,∴∠D=∠BAD,∴AB∥CD.点评:本题主要考查了平行线的判定和直角三角形中两锐角互余,比较简单.10.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.考点:平行线的判定;角平分线的定义.专题:证明题.分析:运用角平分线的定义,结合图形可知∠ABD=2∠1,∠BDC=2∠2,又已知∠1+∠2=90°,可得同旁内角∠ABD和∠BDC互补,从而证得AB∥CD.解答:证明:∵BE平分∠ABD,DE平分∠BDC(已知),∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义).∵∠1+∠2=90°,∴∠ABD+∠BDC=2(∠1+∠2)=180°.∴AB∥CD(同旁内角互补,两直线平行).点评:灵活运用角平分线的定义和角的和差的关系是解决本题的关键,注意正确识别“三线八角”中的同位角、内错角、同旁内角.11.如图所示,已知直线a、b、c、d、e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?考点:平行线的判定;平行公理及推论.专题:探究型.分析:根据内错角相等,两直线平行可知a∥b,由同旁内角互补,两直线平行可知b∥c,根据如果两条直线都与第三条直线平行那么这两条直线平行得出结论.解答:解:平行.理由如下:∵∠1=∠2,∴a∥b(内错角相等,两直线平行),∵∠3+∠4=180°,∴b∥c(同旁内角互补,两直线平行),∴a∥c(平行于同一直线的两直线平行).点评:本题很简单,考查的是平行线的判定定理和平行公理的推论.内错角相等,两直线平行;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行那么这两条直线平行.。
(完整版)平行线证明(填理由)
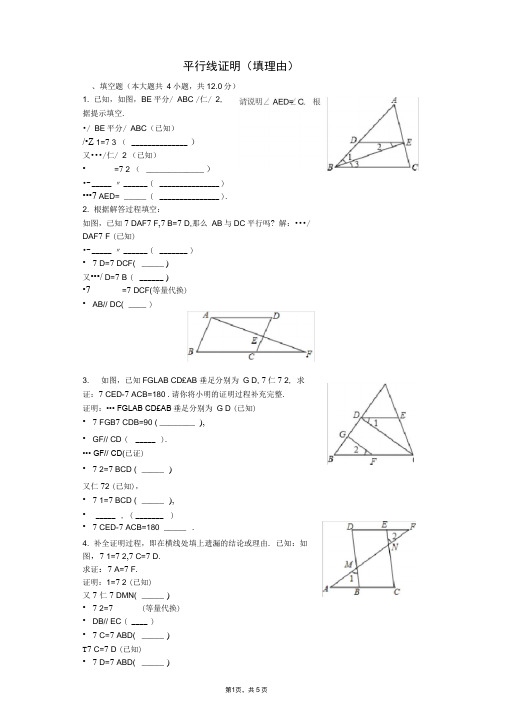
平行线证明(填理由)、填空题(本大题共4小题,共12.0分)1. 已知,如图,BE平分/ ABC /仁/ 2,据提示填空.•/ BE平分/ ABC(已知)/•Z 1=7 3 (______________ )又•••/仁/ 2 (已知)•- _____ =7 2 (_____________ )•- _____ 〃______ ( _______________ )•••7 AED= _____ ( _______________ ).2. 根据解答过程填空:如图,已知7 DAF7 F,7 B=7 D,那么AB与DC平行吗? 解:•••/ DAF7 F (已知)•- _____ 〃______ ( _______ )•7 D=7 DCF( _____ )又•••/ D=7 B ( ______ )•7______ =7 DCF(等量代换)•AB// DC( ____ )3. 如图,已知FGLAB CD£AB 垂足分别为G D, 7仁7 2, 求证:7 CED-7 ACB=180 .请你将小明的证明过程补充完整.证明:••• FGLAB CD£AB垂足分别为G D (已知)•7 FGB7 CDB=90 ( ________ ),•GF// CD ( _____ ).••• GF// CD(已证)•7 2=7 BCD ( _____ )又仁72 (已知),•7 1=7 BCD ( _____ ),• _____ , ( _______ )•7 CED-7 ACB=180 _____ .4. 补全证明过程,即在横线处填上遗漏的结论或理由. 已知:如图,7 1=7 2,7 C=7 D.求证:7 A=7 F.证明:1=7 2 (已知)又7 仁7 DMN( _____ )•7 2=7 _____ (等量代换)•DB// EC ( ____ )•7 C=7 ABD( _____ )T7 C=7 D (已知)•7 D=7 ABD( _____ )• _____ (内错角相等,两直线平行)/•Z A=Z F ( _____ )二、解答题(本大题共 12小题,共96.0分)5. (1)问题发现:如图①,直线 AB//CD E 是AB 与AD 之间的一点,连接 BE CE 可 以发现 Z B+Z C=Z BEC请把下面的证明过程补充完整:证明:过点E 作EF// AB••• AB// DC (已知),EF// AB (辅助线的作法)./• EF// DC( _____ ).•••Z C=Z CEF( ____ )•/ EF// AB /Z B=Z BEF (同理).•Z B+Z C= ______ (等量代换)即 Z B+Z C=Z BEC(2) 拓展探究:如果点 E 运动到图②所示的位置,其他条件不变,进一步探究发现: Z B+Z C=360 - Z BEC 请说明理由.(3)解决问题:如图③,AB// DC Z C=12C ° , Z AEC=80,请直接写出ZA 的度数.6. 阅读下列推理过程,在括号中填写理由.已知:如图,点D E 分别在线段 AB BC 上, AC// DE DF// AE 交BC 于点F, AE 平分Z BAC 求 证:DF 平分Z BDE证明:••• AE 平分Z BAC(已知)• Z 1=Z2 ( ______________________________ )•/ AC// DE(已知)• Z 1=Z 3 () 故Z 2=Z 3 () •••DF// AE(已知)• Z 2=Z 5 () • Z 3=Z 4 ( )圉①••• DF平分/ BDE( _________________________ )7. 如图(1), AB// CD猜想/ BPD与/ B/D的关系,说出理由.解:猜想/ BPD/ B+/ D=360理由:过点P作EF// AB•/ B+/ BPE=180 (两直线平行,同旁内角互补)•/ AB// CD EF// AB•EF/ CD (如果两条直线都和第三条直线平行,那么这两条直线也互相平行. )•/ EPD/ D=180 (两直线平行,同旁内角互补)•••/ B+/ BPE/ EPD/ D=360•••/ B+/ BPD/ D=360(1)依照上面的解题方法,观察图(2),已知AB// CD猜想图中的/ BPD与/ B/D 的关系,并说明理由.(2)观察图(3)和(4),已知AB// CD猜想图中的/ BPD与/ B/D的关系,不需要说明理由.A ------------ BC—P (4)8.如图,已知,CD// EF, /仁/ 2,求证:/ 3=/ ACB请补全证明过程.证明:••• CD// EF,( _____ )•/ 2=/ DCB (两直线平行,同位角相等)•••/仁/ 2, ( _____ )•/ 仁/ DCB ( _______ )•GD/ CB ( _______ )•/ 3=/ ACB ( _______ )9.在横线上填写理由,完成下面的证明.如图,已知/ 1+/2=180°, / B=/ 3,求证/ C=/证明:T/ 1+/2=180°(已知),/ 1+/ DFE=180AED•/ 2=/ DFE( ______ )• AB// EF ( _____ )•/ 3=/ ADE( _____ )又•••/ B=/ 3 (已知)•/ B=/ ADE( _____ )•DE// BC ( _____ ))•••/ C=Z AED( ______ )10. 阅读下面的证明过程,在每步后的横线上填写该步推理的依据. 如图,/ E=Z 1,Z 3+Z ABC=180 , BE是/ ABC的角平分线,求证:DF// AB.证明:••• BE是/ ABC的角平分线•••/ 1=Z 2 ( ___________ )又•••/ E=Z1/•Z E=Z 2 ( ____________ )•AE// BC ( ____________ )•Z A+Z ABC=180 ( ____________ )又T Z 3+Z ABC=180•Z A=Z 3 ( ____________ )•DF// AB ( ____________ ).11. 填空:如图,已知DE// AC Z A=Z DEF试说明AB// EF. 解:••• DE// AC _____________ _•Z A=Z BDE ___T Z A=Z DEF _____•Z BDE Z DEF ___ .•AB// EF ______12. 完成下面的证明:已知:如图,AB// DE 求证:Z D+Z BCD - Z B=180°, 证明:过点C作CF// AB.T AB// CF (已知),•Z B= _____ ( ______ ).T AB// DE CF// AB( 已知 ),•CF// DE ( ______ )•Z 2+ ____ =180 ( ______ )T Z 2=Z BCD- Z 1,•Z D+Z BCD- Z B=180°( _____ ).13. 完成下面推理过程.如图:在四边形ABCD中, Z A=106 - a,Z ABC=74+a,BDLDC于点D, EF±DC于点F,求证:Z仁Z2证明:T Z A=106 - a,Z ABC=74 + a(已知)•Z A+Z ABC=180•AD// ____ ( _____________ )•••/1= ______ ( _______________ )•/ BDL DC EF± DC(已知)•••/ BDF2 EFC=90 ( ________ )• BD// ______ ( _____________ )2= _____ ( _______________ )•••/ 仁/ 2 ( _______ )14. 完成下面的证明(在括号中填写推理理由) 如图,已知/ A=Z F,Z C=Z D,求证:BD// CE 证明:因为/ A=Z F,所以AC// DF ( ______ ),所以/ C+Z _____ =180 ( ________ ).因为/ C=Z D,所以Z D+Z _____ =180 ( ________ ),所以BD// CE ( ______ ).15. 如图AB// CD Z 仁Z 2,Z 3=Z 4,试说明AD// BE 解:••• AB// CD (已知)•Z 4=Z ______ ( _______ )•••Z 3=Z 4 (已知)•Z 3=Z ______ ( _______ )•Z仁Z 2 (已知)•Z 1+Z CAF Z 2+Z CAF( _____ )即Z _____ = Z_______ ( ______ )•Z 3=Z _____•AD// BE ( ____ )16. 如图,已知EF// AD Z 仁Z 2,Z BAC=70,求Z AGD(请填空)解:• EF// AD•Z 2= _____ ( ______又T Z 1=Z2•Z 1=Z 3 ( ______ )•AB// _____ ( _____ )•Z BAC+ ____ =180 ( ________ )•Z BAC=70 ( ______ )•Z AGD= ____ ( ______ )。
平行线证明题及答案

平行线证明题及答案【篇一:七年级数学平行线经典证明题】、选择题:1.如图,能与??构成同旁内角的角有() a. 5个b.4个c. 3个d. 2个16.如图,op∥qr∥st,则下列各式中正确的是()二、填空题:8.把一副三角板按如图方式放置,则两条斜边所形成的钝角??_______度.9.求图中未知角的度数,x=_______,y=_______.dec=________.三、计算证明题:17.已知:如图23,ad平分∠bac,点f在bd上,fe∥ad交ab于g,交ca的延长线于e,求证:∠age=∠e。
18. 如图,ab∥de,∠1=∠acb,∠cab=1∠bad,试说明:ad∥bc. 221.如图,已知:e、f分别是ab和cd上的点,de、af分别交bc于g、h,?a=?d,?1=?2,求证:?b=?c.22.已知:如图8,ab∥cd,求证:∠bed=∠b-∠d。
23.已知:∠1=∠2,∠3=∠4,∠5=∠6.求证:ad∥bc.25.如图所示,已知ab∥cd,分别探索下列四个图形中∠p与∠a,∠c的关系,?请你从所得的四个关系中任选一个加以说明.d c f图③图①求证:cd∥be。
求证:gh∥mn。
29、如图11,直线ab、cd被ef所截,∠1 =∠2,∠cnf =∠bme。
求证:ab∥cd,mp∥nq.e b a pc d q f图11【篇二:平行线的证明测试题】txt>一、填空题(每题4分,共32分)1.在△abc中,∠c=2(∠a+∠b),则∠c=________.2.如图,ab∥cd,直线ef分别交ab、cd于e、f,eg平分∠bef,若∠1=72o ,则∠2=;3.在△abc中,∠bac=90o,ad⊥bc于d,则∠b与∠dac的大小关系是________ aebcf12gd4.写出“同位角相等,两直线平行”的题设为_______,结论为_______.第2题5.如图,已知ab∥cd,bc∥de,那么∠b +∠d =__________.a b ec d b e 第7题第5题第6题6.如图,∠1=27o,∠2=95o,∠3=38o,则∠4=_______7.如图,写出两个能推出直线ab∥cd的条件________________________.8.满足一个外角等于和它相邻的一个内角的△abc是_____________二、选择题(每小题4分,共24分)9.下列语句是命题的是【】(a)延长线段ab(b)你吃过午饭了吗? (c)直角都相等 (d)连接a,b 两点10.如图,已知∠1+∠2=180o,∠3=75o,那么∠4的度数是【】(a)75o(b)45o(c)105o(d)135o11.以下四个例子中,不能作为反例说明“一个角的余角大于这个角”是假命题是【】12.若三角形的一个内角等于另外两个内角之差,则这个三角形是【】(a)锐角三角形 (b)直角三角形 (c)钝角三角形 (d)不能确定则∠dec等于【】(a)锐角三角形(b)钝角三角形 (c)直角三角形(d)无法确定三、(每小题10分,共20分)15.如图,ad=cd,ac平分∠dab,求证dc∥ab.的度数.四、(每小题12分,共24分)17.如图,be,cd相交于点a,∠dea、∠bca的平分线相交于f.(1)探求:∠f与∠b、∠d有何等量关系?(2)当∠b︰∠d︰∠f=2︰4︰x时,x为多少?18.如图,已知点a在直线l外,点b、c在直线l上.(1)点p是△abc内一点,求证:∠p∠a;(2)试判断:在△abc外又和点a在直线l同侧,是否存在一点q,使∠bqc∠a?试证明你的结论.c参考答案13、d;14、b;15、ad?cd??1??2????2??cab?dc平行ab;16、100o; ac平分?dab??1??cab?17、(1)连ce,记∠aec=∠1,∠ace=∠2,则∠d+∠2+∠1+∠dea=180o,∠b+∠1+∠2+∠bca=180o,∠f+∠1+∠2+11∠dea+∠bcd=180o. 2260o, 111(∠d+∠b)+∠1+∠2+∠bca+∠dea=180o, 222111∴∠1+∠2+∠bca+∠dea=180o-(∠d+∠b), 22211即∠f+180o-(∠d+∠b)=180o,∴∠f=(∠b+∠d); 22又∠b︰∠d︰∠f=2︰4︰x,∴x=3.18、(1)延长bp交ac于d,则∠bpc∠bdc,∠bdc∠a故∠bpc∠a;(2)在直线l同侧,且在△abc外,存在点q,使得∠bqc∠a成立.此时,只需在ab外,靠近ab中点处取点q,则∠bqc∠a(证明略).【篇三:平行线经典练习题-条件】xt>基础:cd3*.如图,∠1和∠d互余,ce⊥de,那么ab和cd平行吗?试说明理由.中等:10、如图,直线ef和ab、cd分别相交于k、h,且eg⊥ab,∠chf=60o,∠e=30o,试说明ab∥cd.(书)13.13.如图,直线ab、cd与ef相交于点g、h,且∠egb=∠ehd.(1)说明: ab∥cd(2)若gm是∠egb的平分线,fn是∠ehd的平分线,则gm与hn平行吗?说明理由11、如图,∠cda=∠cba,de平分∠cda,bf平分∠cba,且∠ade=∠aed.试说明de∥fb.规律20.(本题12分)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且?1=38o,则?2=_______o,?3_______o.(2)在(1)中,若?1=55o,则?3_______o;若?1=40o,则?3=_______o.(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角?3_______o时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?答案:(1)76,90 (2)90,90 (3)90。
(2021年整理)七年级数学平行线经典证明题(2)

(完整)七年级数学平行线经典证明题(2)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)七年级数学平行线经典证明题(2))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)七年级数学平行线经典证明题(2)的全部内容。
平行线经典证明题一、选择题:1.如图,能与∠α构成同旁内角的角有( ) A . 5个B .4个C . 3个D . 2个α2。
如图,AB ∥CD ,直线MN 与AB 、CD 分别交于点E 和点F ,GE ⊥MN,∠1=130°,则∠2等于 ( )A .50°B .40°C .30°D .65°3.如图,DE ∥AB ,∠CAE=31∠CAB ,∠CDE=75°,∠B=65°则∠AEB 是 ( )A .70°B .65°C .60°D .55° 4.如图,如果AB ∥CD ,则α∠、β∠、γ∠之间的关系是( ) A 、0180=∠+∠+∠γβα B 、0180=∠+∠-∠γβα C 、0180=∠-∠+∠γβα D 、0270=∠+∠+∠γβα 5.如图所示,AB ∥CD ,则∠A+∠E+∠F+∠C 等于( )A 。
180°B 。
360°C 。
540° D.720°6。
如图,OP ∥QR ∥ST,则下列各式中正确的是( )A 、∠1+∠2+∠3=180°B 、∠1+∠2-∠3=90°C 、∠1-∠2+∠3=90°D 、∠2+∠3-∠1=180°7.如图,AB∥DE,那么∠BCD于( )A、∠2-∠1B、∠1+∠2C、180°+∠1-∠2D、180°+∠2-2∠1二、填空题:8.把一副三角板按如图方式放置,则两条斜边所形成的钝角α=_______度.45°α30°9.求图中未知角的度数,X=_______,y=_______.(2)∠AFC=________。
(word版)七年级数学平行线性质与判定证明练习题及答案

.平行线的性质与判定的证明练习题温故而知新可以为师以:重点1.平行线的性质〔1〕两直线平行,同位角相等;〔2〕两直线平行,内错角相等;〔3〕两直线平行,同旁内角互补.2.平行线的判定〔1〕同位角相等,两直线平行;〔2〕内错角相等,两直线平行;〔3〕同旁内角互补,两直线平行互补.例1如图2-2,AB∥CD∥EF,点M,N,P分别在AB,CD,EF上,NQ平分∠MNP.〔1〕假设∠AMN=60°,∠EPN=80°,分别求∠MNP,∠DNQ的度数;〔2〕探求∠DNQ与∠AMN,∠EPN的数量关系.解析:根据两直线平行,内错角相等及角平分线定义求解 . Word资料〔标注∠MND=∠AMN,∠DNP=∠EPN〕答案:〔标注∠MND=∠AMN=60°,∠DNP=∠EPN=80°〕解:〔1〕∵AB∥CD∥EF,∴∠MND=∠AMN=60°,∠DNP=∠EPN=80°,∴∠MNP=∠MND+∠DNP=60°+80°=140°,又NQ平分∠MNP,∴∠MNQ=1∠MNP=1×140°=70°,22∴∠DNQ=∠MNQ-∠MND=70°-60°=10°,∴∠MNP,∠DNQ的度数分别为140°,10°.(下一步)〔2〕〔标注∠MND=∠AMN,∠DNP=∠EPN〕由〔1〕得∠MNP=∠MND+∠DNP=∠AMN+∠EPN,∴∠MNQ=1∠MNP=1〔∠AMN+∠EPN〕,=22=∴∠DNQ=∠MNQ-∠MND=1〔∠AMN+∠EPN〕-∠AMN 2=1〔∠EPN-∠AMN〕,2即2∠DNQ=∠EPN-∠AMN.小结:在我们完成涉及平行线性质的相关问题时,注意实现同位角、内错角、同旁内角之间的角度转Word资料换,即同位角相等,内错角相等,同旁内角互补.例2如图,∠AGD=∠ACB,CD⊥AB,EF⊥AB,证明:∠1=∠2.解析:〔标注:∠1=∠2=∠DCB,DG∥BC,CD∥EF〕答案:〔标注:∠1=∠2=∠DCB〕证明:因为∠AGD=∠ACB,所以DG∥BC,所以∠1=∠DCB,又因为CD⊥AB,EF⊥AB,所以CD∥EF,所以∠2=∠DCB,所以∠1=∠2.小结:在完成证明的问题时,我们可以由角的关系可以得到直线之间的关系,由直线之间的关系也可得到角的关系.例3〔1〕:如图2-4①,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD;〔2〕当点C位于如图2-4②所示时,∠ABC,∠CDE与∠BCD存在什么等量关系?并证明.Word资料〔1〕解析:动画过点C作CF∥AB由平行线性质找到角的关系.(标注∠1=∠ABC,∠2=∠CDE)答案:证明:如图,过点C作CF∥AB,∵直线AB∥ED,∴AB∥CF∥DE,∴∠1=∠ABC,∠2=∠CDE.∵∠BCD=∠1+∠2,∴∠ABC+∠CDE=∠BCD;2〕解析:动画过点C作CF∥AB,由平行线性质找到角的关系.〔标注∠ABC+∠1=180°,∠2+∠CDE=180°〕Word资料答案:∠ABC+∠BCD+∠CDE=360°.证明:如图,过点C作CF∥AB,∵直线AB∥ED,∴AB∥CF∥DE,∴∠ABC+∠1=180°,∠2+∠CDE=180°.∵∠BCD=∠1+∠2,∴∠ABC+∠BCD+∠CDE=360°.小结:在运用平行线性质时,有时需要作平行线,取到桥梁的作用,实现条件的转化.例4如图2-5,一条公路修到湖边时,需绕道,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C应为多少度?解析:动画过点B作BD∥AE,Word资料.答案:解:过点B作BD∥AE,∵AE∥CF,∴AE∥BD∥CF,∴∠A=∠1,∠2+∠C=180°∵∠A=120°,∠1+∠2=∠ABC=150°,∴∠2=30°,∴∠C=180°-30°=150°.小结:把关于角度的问题转化为平行线问题,利用平行线的性质与判定予以解答.举一反三:1.如图2-9,FG∥HI,那么∠x的度数为〔〕° B.72° C.90° D.100°Word资料∵.∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵解析:∠AEG=180°-120°=60°,由外凸角和等于内凹角和有60°+30°+30°=x+48°,解得x=72°.∵答案:B.∵∵∵∵∵∵∵如下图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF 的度数.∵∵∵∵∵∵∵∵∵∵解析:∵解:∵AB∥EF∥CD,∵∴∠B=∠BEF,∠DEF=∠D.∵∵∠B+∠BED+∠D=192°,∵即∠B+∠BEF+∠DEF+∠D=192°,∵2(∠B+∠D)=192°,∵即∠B+∠D=96°.∵∵∠B-∠D=24°,∵∴∠B=60°,∵即∠BEF=60°.∵EG平分∠BEF,Word资料.1∴∠GEF=∠BEF=30°.23.:如图2-10,AB∥EF,BC∥ED,AB,DE交于点G.求证:∠B=∠E.解析:标注AB∥EF,BC∥ED答案:证明:∵AB∥EF,∴∠E=∠AGD.∵BC∥ED,∴∠B=∠AGD,∴∠B=∠E.Word资料.例5如图2-6,AB∥CD,试再添上一个条件,使∠1=∠2成立,并说明理由.解析:标注AB∥CD,∠1=∠2答案:方法一:〔标注CF∥BE〕解:需添加的条件为CF∥BE,理由:∵AB∥CD,∴∠DCB=∠ABC.∵CF∥BE,∴∠FCB=∠EBC,∴∠1=∠2;方法二:〔标注CF,BE,∠1=∠2=∠DCF=∠ABE〕解:添加的条件为CF,BE分别为∠BCD,∠CBA的平分线.理由:∵AB∥CD,∴∠DCB=∠ABC.∵CF,BE分别为∠BCD,∠CBA的平分线,∴∠1=∠2.Word资料.小结:解决此类条件开放性问题需要从结果出发,找出结果成立所需要的条件,由果溯因.例6如图1-7,直线l1Pl2,且l3和l1、l2分别交于A、两点,点P在AB上,l4和l1、l2分别交于C、D两点,连接PC、PD。
平行线的证明试题总集含答案

平行线的证明试题总集含答案(共79页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《平行线的证明》单元测试题一、 填空题1.在△ABC 中,∠C =2(∠A +∠B ),则∠C =________.2.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF ,若∠1=72º ,则∠2= ;3.在△ABC 中,∠BAC =90º,AD ⊥BC 于D ,则∠B 与∠DAC 的大小关系是________4.写出“同位角相等,两直线平行”的题设为_______,结论为_______.5.如图,已知AB ∥CD ,BC ∥DE ,那么∠B +∠D =__________.6.如图,∠1=27º,∠2=95º,∠3=38º,则∠4=_______7.如图,写出两个能推出直线AB ∥CD 的条件________________________.8.满足一个外角等于和它相邻的一个内角的△ABC 是_____________ 二、 选择题9.下列语句是命题的是 【 】(A)延长线段AB (B)你吃过午饭了吗 (C)直角都相等 (D)连接A ,B 两点 10.如图,已知∠1+∠2=180º,∠3=75º,那么∠4的度数是 【 】 (A)75º (B)45º (C)105º (D)135º11.以下四个例子中,不能作为反例说明“一个角的余角大于这个角” 是假命题是 【 】(A)设这个角是30º,它的余角是60°,但30°<60°(B)设这个角是45°,它的余角是45°,但45°=45°(C)设这个角是60°,它的余角是30°,但30°<60° (D)设这个角是50°,它的余角是40°,但40°<50°12.若三角形的一个内角等于另外两个内角之差,则这个三角形是 【 】 (A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)不能确定 13.如图,△ABC 中,∠B =55°,∠C =63°,DE ∥AB , 则∠DEC 等于【 】 (A )63° (B) 118° (C) 55°(D )62°14.三角形的一个外角是锐角,则此三角形的形状是 【 】C A BDE E C D B A 1 3 24 第5题第6题 第7题A BC D E F G 12DABCE第10题(A)锐角三角形 (B)钝角三角形(C)直角三角形(D)无法确定三、解答证明题15.如图,AD=CD,AC平分∠DAB,求证DC∥AB.16.如图,已知∠1=20°,∠2=25°,∠A=55°,求∠BDC的度数.17.如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F.(1)探求:∠F与∠B、∠D有何等量关系?(2)当∠B︰∠D︰∠F=2︰4︰x时,x为多少?C ABD1218.如图,已知点A在直线l外,点B、C在直线l上.(1)点P是△ABC内一点,求证:∠P>∠A;(2)试判断:在△ABC外又和点A在直线l同侧,是否存在一点Q,使∠BQC>∠A试证明你的结论.19、如图,已知∠B=142°,∠BFE=38°,∠EFD=40°,∠D=140°,求证:AB∥C D.20、已知:如图,∠BAF、∠CBD、∠ACE是△ABC的三个外角.求证:∠BAF+∠CBD+∠ACE=360°.21、如图,已知BE、CE分别是△ABC的内角、外角的平分线,∠A=40°,求∠E的度数.22、已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论。
七年级数学平行线经典证明题--打印

平行线经典证明题二、填空题:??_______把一副三角板按如图方式放置,则两条斜边所形成的钝角度.8.45°α30°,则∠AEF的度数等于13.如图,把长方形ABCD沿EF对折,若∠1=500=____ °,则∠α1=100°,∠2=120如图,已知AB∥CD,∠14. 三、计算证明题:,求证∠FCD于D,EF⊥+ABC=76°∠2,BD⊥CD于ABCD15.如图,在四边形中,∠A=104°-∠2,∠2,试说明理由.1=∠有怎样的位置关系,为什与ABEFB=130°,问直线EF°,∠CD∥AB,∠DCB=70°,∠CBF=20如图,16.. 么?,的延长线于ECA交AB于G,交FEAD已知:如图23,平分∠BAC,点F在BD上,∥AD17. 。
=∠E求证:∠AGE1BC. AD∥∠BAD,试说明:DE,AB∥∠1=∠ACB,∠CAB=18. 如图,2AB. 2=90°,求证:DA⊥∠,,CB⊥ABCE平分∠BCDDE平分∠CDA,1+∠,已知:如图19.2220.如图,已知∠D = 90°,∠1 = ∠2,EF⊥CD,问:∠B与∠AEF是否相等?若相等,请说明理由。
1????,,于G、H,1=A=2D、、21.如图,已知:EF分别是AB和CD上的点,DEAF分别交BC?? B=.C 求证:。
B-∠D,AB∥CD,求证:∠BED=∠22.已知:如图8BC.求证:AD∥4,∠5=∠6.∠23.已知:∠1=∠2,∠3=∠γ,,且∠PAC=∠α,∠PBC=BP相交于点C,∠C=∠β,AP、交于点Pm24.如图,直线l与∠β++∠γ.求证:∠APB=αDMH。
AHM,MN平分∠平分∠=已知:如图:∠25AHF+∠FMD180°,GH E ∥MN。
求证:GH MB A 1PN DC2QF11 图2。
(word完整版)初中数学平行线练习

4、命题:1、知识点: 1、平行线的性质:性质1:两条直线被第三条直线所截,如果两条直线平行,那么同位角相等。
简单说成:两直线平行,同位角相等。
几何语言:•/ AB//CD••• / PMA=/ MNC性质2:两条直线被第三条直线所截,如果两条直线平行,那么内错角相等。
简单说成:两直线平行,内错角相等。
几何语言:•/ AB//CD• / BMN M CNM性质3:两条直线被第三条直线所截,如果两条直线平行,那么同旁内角互补。
简单说成: 两直线平行,同旁内角互补。
几何语言:•/ AB//CD • / AMN # CNM=1802、平行线的判定:几何符号语言:(1 )•••/ 3 =Z 2• AB // CD (同位角相等,两直线平行)(2 )•••/ 1 = Z 2• AB // CD (内错角相等,两直线平行)(3)•••/ 4 +Z 2 = 180°• AB // CD (同旁内角互补,两直线平行)3、两条平行线的距离如图,直线 AB // CD , EF 丄AB 于E , EF 丄CD 于F ,则称线段 EF 的长度为两平行线 AB 与CD 间的距离。
注意:直线 AB // CD ,在直线AB 上任取一点 G ,过点G 作CD 的垂线段GH ,则垂线段 GH 的长度也就是 直线AB 与CD 间的距离。
A_G E C 1 HFB⑴命题的概念:判断一件事情的语句,叫做命题。
⑵命题的组成每个命题都是 题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如 果……,那么……”的形式。
具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部 分是结论。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。
对于这样的命题,要经过分析才 能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分, 有时也可用“求证……”或“则……”等形式表述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线证明题
1.如图所示,已知下列条件不能判断l 1 ∥l 2的是( ) A .∠1=∠2 B .∠3=∠4 C .∠1=∠4 D .∠4+∠5=180°
5432
1
l 2
l 1
第1题图
2.如图所示,已知DE ⊥AC 于点E ,BC ⊥AC 于点C ,FG ⊥AB 于点G ,∠BFG=∠EDC ,求证:CD ⊥AB 。
G 6
54
3
2
1
F
E D C
B
A
3.如图所示,点B 在DC 上,BE 平分∠ABD ,∠DBE=∠A ,则BE 与AC 有何种位置关系?为什么?
第3题图
E
D
C
B A
4.如图所示,直线AB 、CD 被直线EF 所截,∠1=∠2,∠CNF=∠BME ,那么AB ∥CD ,MP ∥NQ ,请说明理由。
Q
P
N M
2
1
F
第4题图
E D C
B A
5.如图所示,已知∠1 =85,∠2 =85,∠3 = 125,求∠4与∠5的度数.
6如图所示,∠ABC=∠ACB,BD 平分∠ABC ,CE 平分∠ACB ,∠DBF=∠F ,问CE 与DF 平行吗?请给出理由。
F
E D C
A
A
C
D F
B
E
1
2 7、如图, 填空:
(1)∵ ∠2=∠B
∴ AB ∥______( )
(2)∵ ∠1=∠A
∴ _____∥_____( )
(3)∵_____∥_____
∴ ∠1=∠D ( )
(4)∵ AC ∥DF
∴ _______+∠F=180°( )
8、完成推理过程并填写推理理由:
已知:如图BE//CF ,BE 、CF 分别平分∠ABC 和∠BCD 。
求证:AB//CD.
证明:∵ BE 、CF 分别平分∠ABC 和∠BCD
∴∠1=
21∠ ∠2=2
1
∠ ( ) ∵BE//CF (已知)∴∠1=∠2( ) ∴
21∠ABC=2
1
∠BCD ( ) 即∠ABC=∠BCD ∴AB//CD ( )
9、如图,AB ∥CD,AD ∥BC,∠A=3∠B.求∠A 、∠B 、∠C 、∠D 的度数.
10、如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系?并证明。
11、如图,已知:AD ⊥BC ,EF ⊥BC ,∠1=∠2.求证:∠3 =∠B .
A D
C
B
12、如图,直线AB、CD相交于点O,OB平分∠EOD,∠COE=100°,求∠AOD和∠AOC的度数.
13、如图,已知∠1=∠3,∠P=∠T。
求证:∠M=∠R.
14已知∠B=∠BGD,∠DGF=∠F,求证:∠B +∠F =180°。
15、如图8,AB∥DE,∠1=∠ACB,AC平分∠BAD,(1) 试说明: AD∥BC.(2) 若∠B=80°,求:∠ADE的度数。
16、如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
17、如图,已知∠1=60°,∠2=120°,∠BAC=50°,求∠C的度数。
18、如图所示,直线AB 、CD 、EF 交于点O,OG 平分∠BOF,且CD ⊥EF,∠AOE=64°,•求∠AOF 、∠DOG 的度数.
19、如图EF ∥AD ,∠1=∠2,∠BAC=75 o 。
(1)求证:AB ∥DG ;(2)求∠AGD 。
20、(10分)如图,已知直线 1l ∥2l ,且 3l
和1l 、2l 分别交于A 、B 两点,点P 在AB 上。
(1)试找出∠1、∠2、∠3之间的关系并说出理由;
(2)如果点P 在A 、B 两点之间运动时,问 ∠1、∠2、∠3 之间的关系是否发生变化?(3)如果点P 在A 、B 两点外侧运动时,试探究 ∠1、∠2、∠3 之间的关系(点P 和A 、B 不重合).
A P
B
1
l 2
l 3
l 1 2
3
G O
F E
D
C
B
A。
