长方体和正方体总结
长方体和正方体的公式总结

长方体和正方体的公式总结在我们的数学世界里,长方体和正方体就像是两个性格各异但又相互关联的小伙伴。
它们有着自己独特的特点和公式,今天咱们就来好好聊聊这俩“小家伙”。
先来说说长方体,它就像是一个长长的盒子,有长、宽、高三个不同的尺寸。
计算长方体的表面积,公式就是 2×(长×宽 + 长×高 + 宽×高)。
比如说,有一个长方体的盒子,长是 5 厘米,宽是 3 厘米,高是 4 厘米。
那它的表面积就是 2×(5×3 + 5×4 + 3×4) = 2×(15 + 20 + 12) = 2×47 = 94 平方厘米。
这就好像是给这个长方体盒子穿上一件“衣服”,要知道这件“衣服”需要多大的布料,就得用这个公式来算。
还有长方体的体积公式,是长×宽×高。
还是刚才那个盒子,体积就是 5×3×4 = 60 立方厘米。
想象一下,这个盒子能装多少东西,就看它的体积有多大。
再看看正方体,它就像是一个特别规整的“小方块”,每条边都一样长。
正方体的表面积公式是6×边长×边长。
假如有一个正方体的积木,边长是 6 厘米,那它的表面积就是 6×6×6 = 216 平方厘米。
正方体的体积公式呢,就是边长×边长×边长。
这个积木的体积就是6×6×6 = 216 立方厘米。
记得有一次,我帮小侄子做数学作业,就碰到了关于长方体和正方体的题目。
那道题是让计算一个长方体形状的鱼缸能装多少水。
小侄子一脸迷茫地看着我,我就告诉他,咱们得先算出鱼缸的体积,也就是长×宽×高。
然后一步一步地带着他测量鱼缸的长、宽、高,最后算出了结果。
看着小侄子恍然大悟的样子,我心里可高兴了。
在实际生活中,长方体和正方体的应用可多啦。
像家里的冰箱、衣柜是长方体,魔方就是正方体。
长方体与正方体的计算与性质知识点总结

长方体与正方体的计算与性质知识点总结长方体和正方体是立体几何中常见的形状,它们具有一些共同的计算和性质知识点。
本文将对长方体和正方体的计算和性质进行总结。
一、长方体的计算与性质1. 表面积:长方体的表面积可以通过计算各个面的面积之和得到。
一个长方体有六个面,其中有两对相等的面,分别为底面和顶面、前后两个侧面和左右两个侧面。
由于长方体的前后两个侧面以及左右两个侧面的形状相同,所以可以将一个侧面的面积乘以2,再加上底面和顶面的面积,即可得到长方体的表面积。
2. 体积:长方体的体积可以通过计算底面积与高度之积得到。
即底面积乘以高度,就是长方体的体积。
3. 对角线长度:长方体的对角线可以通过利用勾股定理计算得到。
对角线的长度等于长方体的三个边长的平方和的平方根。
4. 切面形状:当切割一个长方体时,切面的形状可以是正方形、长方形或平行四边形,具体形状取决于切面与长方体的相对位置和角度。
二、正方体的计算与性质1. 表面积:正方体的表面积可以通过计算一个面的面积乘以6得到,因为正方体的六个面都是相等的。
2. 体积:正方体的体积可以通过计算一个边长的立方得到,即边长的三次方。
3. 对角线长度:正方体的对角线长度等于边长的平方根再乘以√3。
4. 切面形状:正方体的切面形状仍然是正方形,不会出现其他形状。
三、长方体与正方体的性质对比1. 表面积比较:长方体的表面积一般来说要大于正方体的表面积,因为长方体的三个边长不相等,而正方体的边长都相等。
2. 体积比较:正方体的体积一般来说要大于长方体的体积,因为正方体的边长相等,而长方体的三个边长不相等。
3. 对角线长度比较:正方体的对角线长度要大于长方体的对角线长度,因为正方体的边长比长方体的边长要大。
4. 切面形状比较:正方体的切面仍然是正方形,而长方体的切面形状可以是正方形、长方形或平行四边形。
综上所述,长方体与正方体在计算和性质上有一些共同点和差异。
对于两者的计算,我们可以根据其特点来选择相应的计算公式进行求解,而对于性质比较,我们可以根据实际情况选用适合的几何概念和公式进行分析和判断。
长方体与正方体知识点总结

长方体与正方体知识点总结一、长方体和正方体的认识1、长方体定义:长方体是由六个长方形(特殊情况下有两个相对的面是正方形)围成的立体图形。
特征:长方体有 6 个面,相对的两个面完全相同。
长方体有 12 条棱,相对的棱长度相等。
长方体有 8 个顶点。
长方体的棱长总和=(长+宽+高)× 42、正方体定义:正方体是用六个完全相同的正方形围成的立体图形。
特征:正方体有 6 个面,6 个面完全相同。
正方体有 12 条棱,12 条棱长度都相等。
正方体有 8 个顶点。
正方体的棱长总和=棱长×12二、表面积1、长方体的表面积定义:长方体 6 个面的总面积叫做它的表面积。
计算公式:长方体的表面积=(长×宽+长×高+宽×高)× 22、正方体的表面积定义:正方体 6 个面的总面积叫做它的表面积。
计算公式:正方体的表面积=棱长×棱长× 6三、体积1、长方体的体积定义:物体所占空间的大小叫做物体的体积。
计算公式:长方体的体积=长×宽×高用字母表示:V = abh (其中 a 表示长,b 表示宽,h 表示高)2、正方体的体积计算公式:正方体的体积=棱长×棱长×棱长用字母表示:V = a³(其中 a 表示棱长)四、容积1、定义:箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
2、单位:计量容积,一般就用体积单位。
计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成 L 和 mL。
3、换算:1 升= 1 立方分米,1 毫升= 1 立方厘米,1 升= 1000 毫升五、体积和容积的区别1、意义不同:体积是指物体所占空间的大小;容积是指容器所能容纳物体的体积。
2、测量方法不同:体积是从物体的外部测量长、宽、高;容积是从物体的内部测量长、宽、高。
3、单位名称不完全相同:体积单位一般用立方米、立方分米、立方厘米;容积单位一般用升、毫升。
(完整版)长方体和正方体知识点汇总(最新整理)
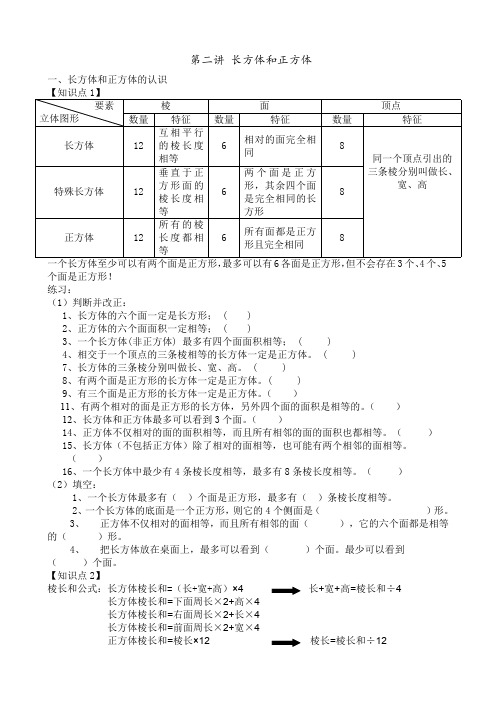
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形,其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( ) 14、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( ) 15、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )16、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
长方体与正方体的体积与表面积知识点总结

长方体与正方体的体积与表面积知识点总结长方体和正方体是几何学中常见的三维形体,它们的体积和表面积是两个重要的几何属性。
本文将对长方体和正方体的体积与表面积进行详细的知识点总结。
一、长方体的体积和表面积1. 长方体的定义与特征长方体是指六个面都是矩形的立体图形。
它具有以下特征:- 六个面都是矩形,相邻两面的边长相等;- 相对的两个面平行,且相等;- 其中的四个顶点本质上相等,八个角也都是直角。
2. 长方体的体积公式长方体的体积是指其所占的三维空间的大小。
计算长方体的体积可以使用以下公式:体积 = 长 ×宽 ×高其中,长、宽和高分别表示长方体的三条边的长度。
3. 长方体的表面积公式长方体的表面积是指其六个面的总面积。
计算长方体的表面积可以使用以下公式:表面积 = 2 × (长 ×宽 + 长 ×高 + 宽 ×高)其中,长、宽和高分别表示长方体的三条边的长度。
二、正方体的体积和表面积1. 正方体的定义与特征正方体是指六个面都是正方形的立体图形。
它具有以下特征:- 六个面都是正方形,相邻两面的边长相等;- 相对的两个面平行,且相等;- 其中的所有顶点和角都相等,均为直角。
2. 正方体的体积公式正方体的体积计算方法与长方体相同,即:体积 = 边长 ×边长 ×边长其中,边长表示正方体的边的长度。
3. 正方体的表面积公式正方体的表面积计算方法与长方体有所不同,可以使用以下公式:表面积 = 6 ×边长 ×边长其中,边长表示正方体的边的长度。
三、应用举例1. 长方体的应用场景长方体广泛应用于日常生活和工程领域中,例如:- 盒子、柜子等物品常常具有长方体的形状,计算其体积可以确定所需的空间大小;- 房间的长方体形状可以通过计算体积来确定其面积和容积等信息。
2. 正方体的应用场景正方体也有很多实际应用,以下是一些例子:- 骰子是常见的正方体,其每个面上的数字代表了一种随机结果;- 有些建筑物的结构采用正方体形状,计算其体积和表面积可以帮助规划和设计。
长方体与正方体知识点总结

长方体与正方体知识点总结长方体和正方体是我们在几何学中经常遇到的两种立体图形。
它们具有一些特殊的性质和特点,下面对长方体和正方体的知识点进行总结。
一、长方体的定义和性质长方体是一种具有六个矩形面的立体图形,其中相对的面是相等的。
长方体的八个顶点以及十二条棱都组成了它的全体边。
长方体的性质如下:1. 全面角:长方体的全面角为360度,即所有的面的面角之和为360度。
2. 对角线:长方体的对角线共有四条,每一条对角线都是两个不相邻顶点之间的直线段。
3. 面对角线:长方体的面对角线是指连接一个面上两个对角的线段。
长方体共有四对面对角线,长度相等。
4. 体对角线:长方体的体对角线是指连接两个相对顶点的线段。
体对角线的长度可以通过应用勾股定理得到。
5. 相邻棱:长方体的相邻棱是指共享同一个顶点的两条棱,共有12对相邻棱。
二、正方体的定义和性质正方体是一种具有六个正方形面的立体图形,每个面都相等且互相平行。
正方体的八个顶点以及十二条棱都组成了它的全体边。
正方体的性质如下:1. 全面角:正方体的全面角为360度,即所有的面的面角之和为360度。
2. 对角线:正方体的对角线共有四条,每一条对角线都是两个不相邻顶点之间的直线段。
3. 面对角线:正方体的面对角线是指连接一个面上两个对角的线段。
正方体共有四对面对角线,长度相等。
4. 体对角线:正方体的体对角线是指连接两个相对顶点的线段。
体对角线的长度可以通过应用勾股定理得到。
5. 相邻棱:正方体的相邻棱是指共享同一个顶点的两条棱,共有12对相邻棱。
三、长方体和正方体的区别与联系长方体和正方体在几何形状上的不同之处在于它们所拥有的面不同,长方体的面是矩形,而正方体的面是正方形。
此外,它们的边长也不同,长方体可以是边长各不相等的矩形,而正方体的边长相等。
然而,长方体和正方体也有很多相似之处。
它们都是由六个面组成的立体图形,全面角和对角线的性质都相同。
在计算体积和表面积时,长方体和正方体的公式也非常相似。
正方体与长方体知识点总结

正方体与长方体知识点总结一、正方体1、正方体有8个顶点、12条棱、6个面。
2、公式: 棱长总和=棱长×12棱长=棱长总和÷12正方体表面积=棱长×棱长×6正方体体积=棱长×棱长×棱长(V=a·a·a=a³)二、长方体1、长方体有8个顶点、12条棱、6个面。
2、公式: 棱长总和=(长+宽+高)×4长=棱长总和÷4-宽-高宽=棱长总和÷4-长-高高=棱长总和÷4-长-宽长方体表面积=(长×宽+长×高+宽×高)×2前面/后面:长×高左边/右面:宽×高上面/下面:长×宽长方体体积=长×宽×高=底面积×高=横截面面积×长长=体积÷宽÷高宽=体积÷长÷高高=体积÷长÷宽三、常用知识点总结1、正方体的棱长扩大n倍,棱长总和也扩大(n)倍,表面积扩大(n×n)倍,体积扩大(n×n×n)倍。
2、面积与体积无法比较,因为它们的意义不同。
3、占地面积=底面积=长×宽长方体体积公式可改写为:长方体体积=底面积×高高=体积÷底面积4、将一个物体投入水中,物体的体积=水面上升部分的体积。
5、将一个正方体模型熔化变成长方体模型,解题关键在于变化前后的体积不变。
6、单位换算口诀:大变小~乘进率~小数点向右移动小变大~除以进率~小数点向左移动。
7、几个同样大小的小正方体,搭成一个长方体,如何摆放长方体的表面积最大?(一条龙一样的摆放)如何摆放表面积最小?(形状越接近于正方体,表面积越小)。
四、关于涂色的正方体的一些规律正方体棱等分的份数三面涂色的个数(在顶点处)两面涂色的个数(在棱中间)一面涂色的个数(在面中间)没有涂色的正方体个数2 8个0 0 03 8个4 8个n 8个12x(3-2)=1212x(4-2)=2412x(n-2)6 x(3-2)²6 x(4-2)²6 x(n-2)²(3-2)³(4-2)³(n-2)³。
长方体与正方体的认识与性质总结与解析

长方体与正方体的认识与性质总结与解析长方体和正方体是我们在几何学中经常遇到的两种三维几何体。
它们在形状和性质上有着一些共同点,但也存在一些显著的差异。
本文将对长方体和正方体进行认识与性质的总结与解析,以帮助读者更好地理解这两种几何体的特点。
一、长方体长方体是一种具有六个矩形面的几何体。
它的六个面可以被划分为两组相等的平行面,每组有三个面。
其中,相对的面是相等的,并且每个面都是矩形。
长方体的六个面都是平面,并且相邻的面之间的角度是直角。
这使得长方体具有一些独特的性质。
1.1 面的性质长方体的面积可以通过计算各面的面积之和得出。
具体地说,长方体的总表面积等于6个面的面积之和。
另外,如果长方体的长、宽和高分别为L、W和H,则长方体的体积等于L×W×H。
1.2 对角线的性质长方体的对角线是连接相对顶点的线段。
根据长方体的性质,长方体的对角线可以划分为两组相等的对角线,每组有四条对角线。
其中,相对的对角线相等。
此外,长方体的对角线还满足勾股定理,即任意两条相交对角线的平方和等于第三条相交对角线的平方和。
二、正方体正方体是一种特殊的长方体,它有六个完全相等的正方形面。
正方体的六个面都是平面,并且相邻的面之间的角度是直角。
正方体的性质与长方体有一些相似之处,但也有一些独特之处。
2.1 面的性质正方体的面积可以通过计算一个面的面积,然后乘以6得出。
具体来说,正方体的总表面积等于一个面的面积乘以6。
正方体的体积可以通过计算一个面的面积,然后再乘以正方体的边长得出。
2.2 对角线的性质正方体的对角线是连接相对顶点的线段。
与长方体类似,正方体的对角线可以划分为两组相等的对角线,每组有四条对角线。
相对的对角线相等,并且任意两条相交对角线的平方和等于第三条相交对角线的平方和。
三、长方体与正方体的差异长方体和正方体在形状和性质上存在一些明显的差异。
首先,长方体的六个面可以是不相等的矩形,而正方体的六个面都是相等的正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形
棱
(面和面相交的线
段)
顶点
(棱和棱相交的点)
棱长和
(12条棱长的和)
表面积
(6个面的总面
积)
底面积
(底面的面积,用字母
S表示)
体积
(物体所站空间的大小,用字母V表示)长方体和正方体知识总结
6个(相对的面完全相同:前
面和后面一样、左面和右面一样、上面和下面一样) 12条(长、宽、高,相对的棱长度相等)
8个
4(长+宽+咼)
=4×长+4×宽+ 4×高
=4(a + b+h)=4a+4b+4h
2(长×宽+长×高+宽×高) =
长×宽× 2+长×高× 2+宽
×高×2
=2(ab+ah+bh) =2ab+2ah+2bh 长×宽
=a×b
=ab
长×宽×高
=底面积×高
=abh=Sh
1. 至少要8个小正方体才能拼成一个稍大的正方体。
2. 长方体最多有两个面是正方形。
正方体(特殊的长方体)
6个(都一样,都是正方形)
12条(都相
等)
12 ×棱
长
=12a
棱长×棱长
×6
=6× a×a
=6a2
棱长×棱长
=a×a
2
=a
棱长×棱长×棱长
=底面积×棱长
3
=a× a×a =a
=Sa
(2) “231 ”型:二三紧连错一个,三一相连一任意。
例如:
特点:相对的面不能相连
(3) 凹字”:
长方体和正方体的展开 (3) “ 33”
型:
(40 “ 222”
型:
常见的错误类型: (1) “田字”: (2) “L ”
容积和容积单位:仓库、箱子、油桶等所能容纳物体的体积,通常叫做容积。
单
位:升(L)、毫升(mL),IL=IOOOmL 单位换算:
1m = 10dm = 100cm 1 Cm = 0.1dm = 0.01m
2 2 2
1m = 100dm = 10000cm
3 3 3
1m = 1000d m = 1000000cm
3 3
1L = 1dm = 1000mL = 1000Cm
截面问题:长方体或正方体每截断一次会增加两个截面。
长方体或正方体的长、宽、高同时扩大几倍,棱长和就会扩大相同的倍数,表面积会扩大倍数的平方倍,体积会扩大倍数的立方倍。
不规则物体的体积:
(1)改变物体的形状使之成为规则物体(比长方体、正方体)在计算体积。
(2)排水法:
①容器的底面积×上升那部分水的高度
②放入物体后的体积一原来水的体积
探索图形
规律总结:
(1)三面涂色的小正方体:都在大正方体的顶点的位置,为8个。
(2)两面涂色的在正方体:棱上除去两端的位置,(每条棱上小正方体个数-2) × 12 个。
(3)一面涂色的在正方体:每个面除去一周边一圈的位置,(每条棱上小正方体个数-2 )的平方× 6个。
(4)没有涂色的在正方体:里面除去表面一层的位置,(每条棱上小正方体块数-2 )的立方个。
数正方体的个数
2 层:1+(1+2)=4 或1 × 2+2× 仁4
3 层:1+(1+2)+(1+2+3)= 10 或1 × 3+2× 2+3× 1=10
4 层:1+(1+2)+(1+2+3)+ (1+2+3+4)=20 或1 × 4+2× 3+3× 2+4× 1=20。
