多边形面积经典试题及答案
人教版苏科版小学数学—多边形的面积(经典例题含答案)

班级小组姓名成绩(满分120)一、比较图形的面积(一)平面图形面积大小的比较方法(共4小题,每题3分,共计12分)例1.比一比,看谁的面积大。
(在括号里填“>”“<”或“=”)例1.变式1.下面图形中,图(②⑤⑥⑦⑧)的面积与图①一样大。
例1.变式2.比较图中阴影部分Ⅰ和阴影部分Ⅱ的大小。
3×1×12=323×2×12=32×1×12=11×1×12=12图I 和图II 一样大.31+ + 1= 3222 3 = 66 - 3 = 3例1.变式3.比较图形的面积。
(在○中填写“+”或“=”)(二)平面图形面积大小的比较方法(共4小题,每题3分,共计12分)例2.选择。
一个平行四边形少了一块,如图,,下面(②)号图形补上去就可以使这个图形完整。
例2.变式1.如图,,一个长方形少了一块,下面(③)号图形补上去就能使这个长方形完整。
例2.变式2.图形是由下面的(②)号图形和(⑤)号图形拼成的。
例2.变式3.如图,正方形ABCD 的边长是10cm,长方形EFGH 的长为8cm,宽为5cm,阴影部分甲与阴影部分乙面积差是多少平方厘米?10×10-5×8=60(平方厘米)答:阴影部分甲与阴影部分乙面积是60平方厘米.二、认识底和高(三)用三角尺画高(共4小题,每题3分,共计12分)例3.画出下面各图形给定底边上的高。
例3.变式1.下面所作图形的高对吗?(对的画“√”,错的画“×”)例3.变式2.用一条虚线把图形分割成两个不同的图形。
×××√例3.变式3.你知道在三角形DHB中,DH边上的高是哪条边吗?边上的高是BA.三、平行四边形的面积(共4小题,每题3分,共计12分)(四)推导平行四边形的面积公式例4.填一填。
把一个平行四边形沿着底边上的(高)剪下来,拼成一个长方形,拼成的长方形与原来的平行四边形的面积(相等),长方形的(长)相当于平行四边形的(底),长方形的(宽)相当于平行四边形的(高),因为长方形的面积=(长×宽),所以平行四边形的面积=(底×高)。
多边形面积练习题及答案

多边形面积练习题及答案练习题一:矩形的面积计算1. 已知一个矩形的长度为12cm,宽度为8cm,求其面积。
解答:矩形的面积等于长度乘以宽度。
根据题目给出的数据,我们可以计算矩形的面积:面积 = 长度 ×宽度 = 12cm × 8cm = 96cm²练习题二:三角形的面积计算2. 已知一个三角形的底边长为5cm,高为6cm,求其面积。
解答:三角形的面积等于底边乘以高再除以2。
根据题目给出的数据,我们可以计算三角形的面积:面积 = 1/2 ×底边 ×高 = 1/2 × 5cm × 6cm = 15cm²练习题三:平行四边形的面积计算3. 已知一个平行四边形的底边长为9cm,高为4cm,求其面积。
解答:平行四边形的面积等于底边乘以高。
根据题目给出的数据,我们可以计算平行四边形的面积:面积 = 底边 ×高 = 9cm × 4cm = 36cm²练习题四:梯形的面积计算4. 已知一个梯形的上底长为6cm,下底长为10cm,高为8cm,求其面积。
解答:梯形的面积等于上底加下底再乘以高再除以2。
根据题目给出的数据,我们可以计算梯形的面积:面积 = 1/2 × (上底 + 下底) ×高 = 1/2 × (6cm + 10cm) × 8cm = 64cm²练习题五:菱形的面积计算5. 已知一个菱形的对角线1长为7cm,对角线2长为4cm,求其面积。
解答:菱形的面积等于对角线1乘以对角线2再除以2。
根据题目给出的数据,我们可以计算菱形的面积:面积 = 1/2 ×对角线1 ×对角线2 = 1/2 × 7cm × 4cm = 14cm²练习题六:不规则多边形的面积计算6. 已知一个不规则四边形的边长依次为5cm、6cm、8cm和7cm,求其面积。
人教版苏科版小学数学多边形的面积(百分卷含答案)
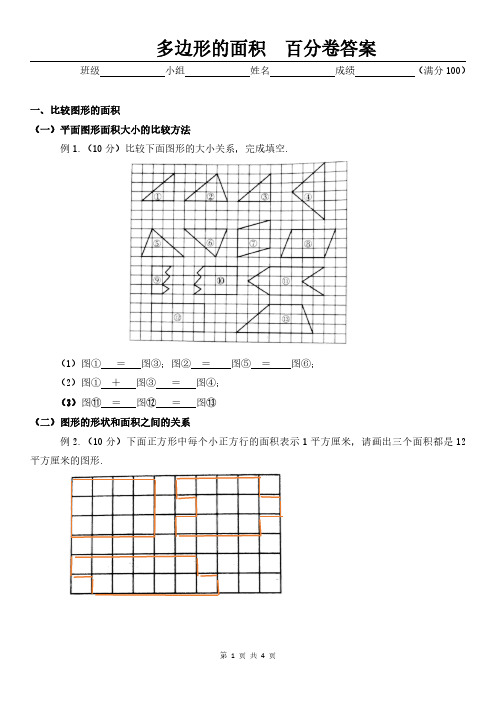
班级小组姓名成绩(满分100)一、比较图形的面积(一)平面图形面积大小的比较方法例1.(10分)比较下面图形的大小关系,完成填空.(1)图①=图③;图②=图⑤=图⑥;(2)图①+图③=图④;(3)图⑪=图⑫=图⑬(二)图形的形状和面积之间的关系例2.(10分)下面正方形中每个小正方行的面积表示1平方厘米,请画出三个面积都是12平方厘米的图形.二、认识底和高(三)找平行四边形的底所对应的高的方法例3.(5分)判断:平行四边形只有4条高.(×)(四)找三角形、梯形的底所对应的高的方法例4.(5分)画出下面梯形的高.(五)画平面图形高的方法例5.(10分)画出下面三角形底边上的高.500三、探索活动:平行四边形的面积(六)平行四边形面积计算公式的推导及应用例6.(10分)求下面平行四边形的面积.16×25=400(m²)18×10=180(dm²)(七)平行四边形的面积与它的底和高之间的关系例7.(10分)分别计算图中每个平行四边形的面积,你发现了什么?(单位:cm)2×5=10(cm)我发现平行四边形的面积与它的底和高之间的关系.(A.等底等高的平行四边形面积也相等,面积相等的两个平行四边形,他们的底和高不一定相等。
B.一个平行四边形,它的底(或高)不变,高(或底)扩大(或缩小)几倍,面积就扩大(或缩小)相同的倍数.四、三角形的面积(八)三角形面积计算公式的推导及应用例8.(10分)已知三角形的底和高如下图所示,求它的面积.6.4×1.9÷2=12.16÷2=6.08(m²)(九)三角形的面积与它的底和高之间的关系例9.(10分)计算下列三角形的面积,你发现了什么?(单位:cm)2×5÷2=10÷2=5(cm²)五、梯形的面积(十)梯形面积计算公式的推导及应用例10.(10分)计算下列梯形的面积.(5+17)×7÷2=22×7÷2=154÷2=77(dm²)(十一)梯形的面积与它的上、下底及高之间的关系例11.(10分)计算下列梯形的面积,你发现了什么?(单位:cm)(3+6)×7÷2=9×7÷2=63÷2=31.5(cm²)。
多边形的面积练习题及答案

多边形的面积练习题及答案一、选择题1. 下列哪个图形是不规则多边形?A. 正方形B. 三角形C. 长方形D. 梯形2. 以下哪个公式可用于计算正方形的面积?A. S = a * bB. S = 1/2 * a * bC. S = a^2D. S = (a + b) * h3. 如图所示,一块田地被修建成了如下图形,哪个图形的面积最大?A. 正方形B. 正三角形C. 圆形D. 正五边形二、计算题1. 计算下列多边形的面积:a) 一个正方形的边长为5cm;b) 一个边长为6cm的正三角形;c) 一个边长分别为4cm和6cm,高为3cm的梯形;d) 一个有6个边,每个边长为4cm的正六边形。
2. 计算下述图形的面积,保留两位小数:a) 一个边长为9cm的正方形的周长为36cm;b) 一个边长为6cm的正三角形的外接圆半径为10cm。
三、解答题1. 如图所示,一个边长为6cm的正方形被切割成4个等边三角形和1个小正方形,请计算小正方形的面积。
[示意图]2. 已知一个正方形的面积为36cm²,求其边长。
[解答]四、答案1. 选择题1. B2. C3. C2. 计算题1.a) 正方形的面积为 S = a^2 = 5^2 = 25cm²b) 正三角形的面积为 S = (sqrt(3) / 4) * a^2 = (sqrt(3) / 4) * 6^2 =9sqrt(3) cm² (约为 15.59cm²)c) 梯形的面积为 S = (a + b) * h / 2 = (4 + 6) * 3 / 2 = 15cm²d) 正六边形的面积为 S = (3 * sqrt(3) / 2) * a^2 = (3 * sqrt(3) / 2) * 4^2 = 24sqrt(3) cm² (约为 41.57cm²)2.a) 正方形的边长为 9cm / 4 = 2.25cm,面积为 2.25^2 = 5.06cm²b) 正三角形的外接圆半径为 a / (2sqrt(3)) = 6 / (2sqrt(3)) = 1.73cm,面积为(sqrt(3) / 4) * (2.66)^2 ≈ 6cm²三、解答题1. 小正方形的边长等于等边三角形的边长,即6cm,所以小正方形的面积为 6^2 = 36cm².2. 已知正方形的面积为36cm²,设其边长为 a,则 a^2 = 36,解得 a = 6cm,所以正方形的边长为6cm。
(完整版)多边形面积经典试题及答案

五年级数学上册第二单元多边形面积的计算一、基础知识测试。
1、把一个平行四边形转化成一个长方形,它的面积与原来平行四边形的面积( 相等),这个长方形的长等于原平行四边形的( 底),这个长方形的宽等于原平行四边形的( 高)。
长方形的面积等于长乘宽,所以平行四边形的面积等于( 底)乘( 高),用字母表示的公式为( S=A*H )。
2、一个平行四边形的底为15分米,高为18分米,面积为( 270 )平方分米。
如果一个平行四边形底为12分米,面积为180平方分米,则高为( 15 )分米。
3、一个平行四边形的底扩大4倍,高缩小2倍,则面积( 扩大两倍);如果它的底缩小3倍,高扩大3倍,则面积( 不变)。
4、一个梯形的面积是42平方米,它的上下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四边形的面积是( 84 )平方米。
5、一个梯形的面积是22平方分米,上、下底之和为11分米,它的高是( 4 )分米。
6、一个梯形的面积是24平方分米,下底是5分米,高是4分米,上底是( 7 )分米。
7、一个平行四边形的面积为64平方厘米,高为8厘米,底为( 8 )厘米。
8、一块直角三角形的地,两条直角边的长分别是36米、27米,这块地的面积是( 486 )平方米。
9、一个三角形,它的面积为36平方分米,高为8分米,则它的底为( 9 )分米。
10、一块直角梯形的地,它的下底是40米,如果上底增加38米,这块地就变成了正方形,原梯形的面积是( 4602 )平方米。
11、一个长方形木框,长10dm,宽8dm,将它拉成一个平行四边形,面积变( 小),这个平行四边形的周长为( 36 )dm。
12、三角形有一条边的长为9厘米,这条边上的高为4厘米,另一条边长6厘米,这条边上的高是( 6 )厘米。
13、一个三角形的面积为10平方分米,若底扩大2倍,高缩小4倍,则现在的面积为( 5 )平方分米。
14、一个三角形的面积比与它等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是( 24)平方分米,三角形的面积为( 12 )平方分米。
多边形面积练习及答案 6页

一、单选题1.把一个平行四边形拉成一个长方形,周长不变,面积()。
A. 变小了B. 变大了C. 不变D. 不确定2.( )的两个梯形一定能拼成一个平行四边形。
A. 面积相等B. 周长相等C. 完全相同D. 任意3.如图,从两张完全相同的梯形纸上剪下一个平行四边形和一个长方形,剪下的图形的面积()A. 平行四边形的大B. 长方形的大C. 一样大D. 无法判断4.一个梯形的上底增加2厘米,下底减少2厘米,高不变,这时的面积与原来的面积相比( )。
A. 变大了B. 变小了C. 不变D. 不知道高,所以无法比较二、判断题5.两个面积相等的梯形可以拼成一个平行四边形.()6.一个梯形的上、下底和高都扩大到原来的2倍,这个梯形的面积扩大到原来的8倍。
()7.面积相等的两个平行四边形的形状一定一样。
()8.两个完全一样的梯形可以拼成一个平行四边形.()三、填空题9.下面平行四边形的面积________.10.一个梯形,上底是2.4分米,下底是3.6分米,高是1.5分米,这个梯形的面积是________平方分米11.求图中阴影部分的面积为________ (结果保留π).12.如图,一个平行四边形被分成了四个小平行四边形,其中三个的面积分别是5平方厘米、8平方厘米、10平方厘米,第四个小平行四边形的面积是________平方厘米.四、解答题13.如果现在有个三年级小朋友请教你:为什么梯形的面积S=(a+b)×h÷2。
你会怎样做一个小老师,帮助他推导出梯形的面积计算公式呢?请你以下面直角梯形为例写出两种不同角度的三角形面积推导过程。
14.计算图形的面积五、应用题15.求下图阴影面积.(单位:分米)参考答案一、单选题1.【答案】B【解析】【解答】把一个平行四边形拉成一个长方形,周长不变,面积变大了.故答案为:B.【分析】把一个平行四边形拉成一个长方形,拉伸后底不变,高变大,根据公式S=ah,所以面积变大,据此解答.2.【答案】C【解析】【解答】完全相同的两个梯形一定能拼成一个平行四边形.故答案为:C.【分析】根据梯形面积公式可知,两个完全一样的梯形,将其中一个倒置,就可以拼成一个平行四边形,据此解答.3.【答案】C【解析】【解答】解:剪下的图形的面积相等。
人教版五年级上册数学《多边形的面积》专项练习(含答案)

人教版五年级上册数学《多边形的面积》专项练习(含答案)1.填空题。
(1)用两个完全一样的梯形拼成一个底是5.4cm,高是2.5cm的平行四边形,每个梯形上、下底的和是()cm,面积是()cm2。
(2)一个三角形的面积是18.2cm2,底是5.2cm,它的高是()cm。
(3)如图,平行四边形的面积与三角形的面积相等。
如果AB=6cm,那么CD=()cm。
(4)一个三角形的面积比和它等底等高的平行四边形的面积少 3.8dm2,这个平行四边形的面积是()dm2。
(5)把一个长、宽分别是15cm和10cm的长方形,拉成一个高是12cm的平行四边形,它的面积是()cm2。
2.计算下列各图形的面积。
(单位:dm)3.判断题。
(1)三角形的底和高都扩大到原来的2倍,它的面积就扩大到原来的4倍。
()(2)拼成一个平行四边形的两个梯形一定完全相同。
()(3)下面面积相等的平行四边形、长方形和等腰三角形中,阴影部分面积相等。
()(4)面积相等的长方形和平行四边形,长方形的周长长一些。
()4.填空题。
(1)如图,梯形的下底是上底的2倍,把这个梯形分成一个平行四边形和一个三角形。
如果这个梯形的面积是18cm2,那么平行四边形的面积是()cm2,三角形的面积是()cm2。
(2)如图,正方形的周长是80dm,那么阴影部分平行四边形的面积是()dm2。
5.选择题。
(1)如图,梯形ABCD中,D共有8个三角形,其中面积相等的三角形有()对。
A.1B.2C.3D.4(2)在下列各图形中,每个小正方形的边长都是1cm,则图中阴影部分面积最大的是()。
(3)一个直角梯形上、下底之和是20分米,两腰分别长6分米和10分米。
求这个梯形面积,正确列式是()。
A.20×6÷2B.20×10÷2C.(6+10)×20÷26.小红家有一块三角形麦田,底是600米,高是240米,今年她家共收获小麦48.6吨,平均每公顷收小麦多少吨?7.如图,已知阴影部分的面积是35cm2,求图中三角形的面积。
多边形面积练习题及答案

多边形面积练习题及答案多边形面积练习题及答案多边形是几何学中常见的图形,它由多条线段组成,每条线段称为边。
多边形的面积是一个重要的几何概念,它可以通过不同的方法计算。
本文将介绍一些多边形面积的练习题及其解答。
一、三角形的面积计算三角形是最简单的多边形,其面积计算公式为:面积 = 底边长度× 高÷ 2。
假设有一个底边长度为6cm,高为4cm的三角形,其面积可以计算为:6 × 4 ÷ 2 = 12 cm²。
二、矩形的面积计算矩形是一种特殊的四边形,其相邻两边相等且相互垂直。
矩形的面积计算公式为:面积 = 长× 宽。
例如,一个长为5cm,宽为3cm的矩形,其面积为:5 ×3 = 15 cm²。
三、正方形的面积计算正方形是一种特殊的矩形,其四条边相等且相互垂直。
正方形的面积计算公式同样为:面积 = 边长× 边长。
举例来说,一个边长为4cm的正方形,其面积为:4 × 4 = 16 cm²。
四、梯形的面积计算梯形是一种具有两条平行边的四边形,其面积计算公式为:面积 = (上底 + 下底)× 高÷ 2。
假设一个梯形的上底长为5cm,下底长为8cm,高为3cm,其面积可以计算为:(5 + 8)× 3 ÷ 2 = 19.5 cm²。
五、菱形的面积计算菱形是一种具有四条边相等的四边形,其面积计算公式为:面积 = 对角线1 × 对角线2 ÷ 2。
例如,一个菱形的对角线1长为6cm,对角线2长为8cm,其面积为:6 × 8 ÷ 2 = 24 cm²。
六、多边形的面积计算对于不规则的多边形,我们可以将其分割成多个三角形或梯形,然后分别计算每个部分的面积,最后将它们相加。
假设一个不规则多边形可以分割成两个三角形,其面积分别为10 cm²和15 cm²,那么整个多边形的面积为:10 + 15 =25 cm²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学上册第二单元多边形面积的计算
一、基础知识测试。
1、把一个平行四边形转化成一个长方形,它的面积与原来平行四边形的面积( 相等),这个长方形的长等于原平行四边形的(底),这个长方形的宽等于原平行四边形的( 高)。
长方形的面积等于长乘宽,所以平行四边形的面积等于( 底)乘( 高),用字母表示的公式为( S=A*H )。
2、一个平行四边形的底为15分米,高为18分米,面积为( 270 )平方分米。
如果一个平行四边形底为12分米,面积为180平方分米,则高为( 15 )分米。
3、一个平行四边形的底扩大4倍,高缩小2倍,则面积( 扩大两倍);如果它的底缩小3倍,高扩大3倍,则面积( 不变)。
4、一个梯形的面积是42平方米,它的上下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四边形的面积是( 84 )平方米。
5、一个梯形的面积是22平方分米,上、下底之和为11分米,它的高是( 4 )分米。
6、一个梯形的面积是24平方分米,下底是5分米,高是4分米,上底是( 7 )分米。
7、一个平行四边形的面积为64平方厘米,高为8厘米,底为( 8 )厘米。
8、一块直角三角形的地,两条直角边的长分别是36米、27米,这块地的面积是( 486 )平方米。
9、一个三角形,它的面积为36平方分米,高为8分米,则它的底为( 9 )分米。
10、一块直角梯形的地,它的下底是40米,如果上底增加38米,这块地就变成了正方形,原梯形的面积是( 4602 )平方米。
11、一个长方形木框,长10dm,宽8dm,将它拉成一个平行四边形,面积变( 小),这个平行四边形的周长为( 36 )dm。
12、三角形有一条边的长为9厘米,这条边上的高为4厘米,另一条边长6厘米,这条边上的高是( 6 )厘米。
13、一个三角形的面积为10平方分米,若底扩大2倍,高缩小4倍,则现在的面积为( 5 )平方分米。
14、一个三角形的面积比与它等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是( 24)平方分米,三角形的面积为( 12 )平方分米。
15、一个三角形与一个平行四边形的面积相等,高也相等,如果三角形的高是8米,那么平行四边形的高是( 8 )米;如果平行四边形的高是8米,那么三角形的高是( 8 )米。
16、一个梯形的高是6厘米,下底10厘米,如果上底增加7厘米,它就变成了一个平行四边形,这个梯形的面积是( 39 )平方厘米。
17、把一个长8厘米,宽4厘米的长方形框架拉成一个平行四边形,这时面积减少8平方厘米,平行四边形的面积为(24 )平方厘米,这时平行四边形的高为(3 )厘米。
二、基础选择。
1、下面的四个平行四边形,根据已知条件( 1 )的面积可以算出。
① ② ③ ④
2、将一个平行四边形拼成一个长方形,面积( 3 ),周长( 2 );将一个平行四边形拉成一个长方形,面积( 1 ),周长( 3 )。
①变大 ②变小 ③不变 ④无法比较
3、能拼成一个平行四边形的两个三角形必须具备( 3 )。
①面积相等 ②形状相同 ③完全一样 ④任意两个均可 4、周长相等的一个正方形,一个长方形,一个平行四边形,( 1 )面积最大。
①正方形 ②长方形
③平行四边形
④无法比较
5、梯形ABCD 中,三角形AOD 和三角形BOC 的面积相比,( 3 )
大。
①三角形AOD ②三角形BOC
③同样多 ④无法比较 6、把一个平行四边形任意分割成两个梯形,这两个梯形的( 1 )总是相等的。
①高
②面积
③上、下底的和 ④无法确定 7、一个三角形和一个平行四边形底相等,面积也相等,如果平行四边形的高是6厘米,那么三角形的高是( 3 )厘米。
①6
②3
③12
④18
8、一个样形的上底长36dm ,如果补上一块底为64dm ,面积为64dm 2的三角形,就变成了一个平行四边形,这个梯形的面积是( 2 )。
①20dm 2 ②136dm 2 ③272dm 2 ④68dm 2
③A 、B ④B 、C
三、判断题(对的打“√”,错的打“×”)。
1、周长相等的两个平行四边形面积相等。
( 2 ) 2、面积相等的两个梯形能拼成一个平行四边形。
( 2 )
3、平行四边形的底扩大到它的2倍,高缩小到它的2
1
,则面积不变。
( 1 ) 4、等底等高的两个三角形,形状不一定相同,但面积一定相等。
( 1 ) 5、把一个长方形拉成一个平行四边形后,它的面积没有改变。
( 2 )
6、三角形的面积大小只与它的底和对应的高有关,与它的形状和位置无关。
( 1 )
7、在一个长方形内画一个最大的三角形,这个三角形的面积一定等于长方形面积的一半。
(1 ) 8、两个完全重合的三角形,一定可以拼成一个长方形。
( 2 ) 9、梯形的面积比平行四边形面积小。
( 2 ) 10、一个长方形可以划分成两个完全一样的梯形。
( 1 )
D
C
A
B O
六、看图计算下列图形的面积。
① ②
③
④
七、求下列阴影部分的面积。
① ②已知S 平=48dm 2,求S 阴。
③已知:阴影部分的面积为24 ④求S 阴。
平方厘米,求梯形的面积。
七、解决问题。
1、一个平行四边形的停车场,底是65米,高是24米。
平均每辆车占地15平方米,这个停车场可停车多少辆?
玫 瑰
每棵占地1m 2
每棵6元
358
21
32
26
34
34
10
7c
8c
8c
1316
8d
3d
12
7c
4d
8d
牡丹每棵占地
2m2
每棵
10元
①玫瑰园占地多少平方米?种玫瑰一共需要多少钱?
3、梯形菜园的面积是多少?
4、计算下面每个平行四边形的面积,你能发现什么?
5、竹篱笆全长84米。
这个花园面积有多大?
6、小明家一面外墙墙皮脱落,要重新粉刷,每平方米需要用0.5千克涂料。
如果涂料的价格是每千克10元,粉刷这面墙需要多少元?
7、小明用红纸做直角三角形形状的小红旗,已知红纸长12分米,宽8分米,小
红旗的两条直角边分别是2分米和3分米,一张红纸可做多少面小红旗?
9、①这堆钢管一共有多少根?
②这根钢管在使用前,最上面一层只有1根,而且下一层总比上一层多1根,使用前,这堆钢管一共有多少根?。
