3-4高阶系统的时域分析
合集下载
自动控制理论稳态误差

稳
3
3.5 线性系统的稳定性分析
线性定常系统稳定的充分必要条件
jω
s平面
稳定区域 稳定区域
不稳定区域
σ
不稳定区域
临界稳定 /临界不稳定 不稳定
根在复平面的位置
4
上节课要点复习
3.5 线性系统的稳定性分析
劳斯(Routh)稳定判据
S控制系统稳定的必要条件是:控制系统特征方程式的 所有系数符号相同且不为零(不缺项)。
K
−
K
+1 t
(1 − e T )
K +1
ess
=1−
K K +1
=
1 K +1
开环、闭环传递函数?!! 17
3.3 二阶系统的时域分析(例子)
二阶系统的单位阶跃响应
R(s)
E(s)
ω
2 n
Y (s)
R(s)
ω
2 n
Y (s)
s(s + 2ζωn )
s2
+
2ζω n s
+
ω
2 n
a)
b)
G(s)H (s) =
E(s)
K
Ts
Y (s)
R(s)
K Y(s)
Ts + K
a)
b)
Ⅰ型系统 K p = ∞
−Kt
y(t) = 1− e T
R(s)
E(s)
K
Y (s)
R(s)
K
Y (s)
Ts +1
Ts + K +1
K P = limG(s)H (s) s→0
ess
=1 1+ Kp
3
3.5 线性系统的稳定性分析
线性定常系统稳定的充分必要条件
jω
s平面
稳定区域 稳定区域
不稳定区域
σ
不稳定区域
临界稳定 /临界不稳定 不稳定
根在复平面的位置
4
上节课要点复习
3.5 线性系统的稳定性分析
劳斯(Routh)稳定判据
S控制系统稳定的必要条件是:控制系统特征方程式的 所有系数符号相同且不为零(不缺项)。
K
−
K
+1 t
(1 − e T )
K +1
ess
=1−
K K +1
=
1 K +1
开环、闭环传递函数?!! 17
3.3 二阶系统的时域分析(例子)
二阶系统的单位阶跃响应
R(s)
E(s)
ω
2 n
Y (s)
R(s)
ω
2 n
Y (s)
s(s + 2ζωn )
s2
+
2ζω n s
+
ω
2 n
a)
b)
G(s)H (s) =
E(s)
K
Ts
Y (s)
R(s)
K Y(s)
Ts + K
a)
b)
Ⅰ型系统 K p = ∞
−Kt
y(t) = 1− e T
R(s)
E(s)
K
Y (s)
R(s)
K
Y (s)
Ts +1
Ts + K +1
K P = limG(s)H (s) s→0
ess
=1 1+ Kp
第三章 线性系统的时域分析法(第三四五讲)
若变号系统不稳定!
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
自动控制原理第三章

5
3-2 一阶系统的时域分析
用一阶微分方程描述的控制系统
3-2-1 一阶系统数学描述 RC电路 其微分方程为: 电路, 例如 RC电路,其微分方程为:
R + r(t) _ I
1 Cs
+ C c(t) _ C(s)
ɺ T c+c = r
其中:c(t) 为电路输出电压, 其中: 为电路输出电压, R(s) UR r(t) 为电路输入电压, 为电路输入电压, T=RC为时间常数 为时间常数 由原理图得系统结构图。 由原理图得系统结构图。 R(s) 当初始条件为零时,其传递函数为: 当初始条件为零时,其传递函数为 C ( s) 1 = Φ ( s) = 一阶惯性环节 R(s) Ts + 1
t − 1 2 c (t ) = t − Tt + T 2 1 − e T 2
误差: 误差:
(t ≥ 0)
t − e (t ) = r (t ) − c (t ) = Tt − T 1 − e T 2
(t ≥ 0)
跟踪误差随时间推移而增大,直至无限大。 跟踪误差随时间推移而增大,直至无限大。 因此,一阶系统不能跟踪加速度输入。 因此,一阶系统不能跟踪加速度输入。
1 R
-
1 Ts
C(s)
6
3-2-2 一阶系统单位阶跃响应 系统输入: 系统输入:R(s ) = 1 系统输出: 系统输出:C ( s ) = Φ ( s ) R( s ) = 1 ⋅ 1 Ts + 1 s 1 T = − s Ts + 1 变换, Λ−1变换,得:h( t ) = 1 − e ,t ≥ 0 阶跃响应的特点: 阶跃响应的特点: 1 1) 在 t=0 时的斜率最大,为: 时的斜率最大,
3-2 一阶系统的时域分析
用一阶微分方程描述的控制系统
3-2-1 一阶系统数学描述 RC电路 其微分方程为: 电路, 例如 RC电路,其微分方程为:
R + r(t) _ I
1 Cs
+ C c(t) _ C(s)
ɺ T c+c = r
其中:c(t) 为电路输出电压, 其中: 为电路输出电压, R(s) UR r(t) 为电路输入电压, 为电路输入电压, T=RC为时间常数 为时间常数 由原理图得系统结构图。 由原理图得系统结构图。 R(s) 当初始条件为零时,其传递函数为: 当初始条件为零时,其传递函数为 C ( s) 1 = Φ ( s) = 一阶惯性环节 R(s) Ts + 1
t − 1 2 c (t ) = t − Tt + T 2 1 − e T 2
误差: 误差:
(t ≥ 0)
t − e (t ) = r (t ) − c (t ) = Tt − T 1 − e T 2
(t ≥ 0)
跟踪误差随时间推移而增大,直至无限大。 跟踪误差随时间推移而增大,直至无限大。 因此,一阶系统不能跟踪加速度输入。 因此,一阶系统不能跟踪加速度输入。
1 R
-
1 Ts
C(s)
6
3-2-2 一阶系统单位阶跃响应 系统输入: 系统输入:R(s ) = 1 系统输出: 系统输出:C ( s ) = Φ ( s ) R( s ) = 1 ⋅ 1 Ts + 1 s 1 T = − s Ts + 1 变换, Λ−1变换,得:h( t ) = 1 − e ,t ≥ 0 阶跃响应的特点: 阶跃响应的特点: 1 1) 在 t=0 时的斜率最大,为: 时的斜率最大,
自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4<ζ<0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
3.3高阶系统的时域分析

j 1
k 1
式中,q+2r=n, q为实数极点的个数;r为共轭复数极点的对数。
部分分式展开,并设0<ζk<1,取拉氏反变换,并整理
q
r
h(t) A0
Ajesjt
B e kkt k
c os ( k
1
2 k
)t
j 1
k 1
r k 1
Ck
k
Bk kk
3、 调节时间的计算
ts
1
n
ln
2
n
si
m s1 zi
i2 n
i1 m
s1 si
zi
i2
i 1
结论:
(1)闭环零点越接近虚轴,峰值时间越小,超调量 和调节时间越大;
(2)闭环非主导极点的作用是增大峰值时间,但可 减小系统的超调量和调节时间。
高阶系统的增益常常调整到使系统具有一对闭环共轭 主导极点,这时可以用二阶系统的动态性能指标来估 算高阶系统的动态性能。
设单位反馈高阶系统具有一对共轭复数闭环主导极点: 系统单位阶跃响应的近似表达式:
s1,2 s jd , 0 1
C(s) M (s) 1 N(s) s
1
2 k
e kk t
s in( k
表明
1
2 k
)t,
t
0
(1)响应由一阶系统和二阶系统的时间响应函数项组成。当所 有闭环极点都位于左半s开平面时,系统是稳定的。
(2)零极点对系统性能的影响。
三、闭环主导极点
自控原理(3)
前 页 后 页
2003-09/10
<自动控制原理>(3-17)
3.4 高阶系统的时域分析 1、定义:能用三阶或三阶以上的微分方程描述的控 制系统。 2、分析方法:
1)定性分析; 2)主导极点法; 3)计算机分析 3 主导极点与偶极子问题 ① 主导极点: 在所有的闭环极点中,那些离虚轴最近、 且附近又没有其它零、极点,对系统动态性能影响起主 导的决定性作用的闭环极点,称之为主导极点。 主导极点法: 利用主导极点代替系统全部闭环极点来 估算系统性能的方法,称为主导极点法。 一般要求:
t
td tr tp ts b 单位阶跃信号作用下 反馈系统的过渡过程曲线
误差带△一般取0.02或0.05 ⑵ 动态性能指标: 延迟时间 td :指响应从0到第一次达到终值(稳态值)的一半 时所需要的时间;
上升时间 tr :指响应从0到第一次达到终值(稳态值)时所需要 的时间;
前 页 后 页
2003-09/10
j
S1 S2
j
0
0
t
② ξ = 1时,(临界阻尼) S1 ,S2 为一对相等的负实数根。
③ 0<ξ<1时,(欠阻尼) S1 ,S2 为一对具有负实部的共轭复根。
前 页 后 页
2003-09/10
<自动控制原理>(3-08)
④ 当ξ=0时,(无阻尼,零阻尼) S1 ,S2 为一对幅值相等的虚根。
⑤ 当ξ<0时,(负阻尼) S1 ,S2 为一对不等的负实数根。
结论分析: a) tr 、tp 、ts 、td 与ωn 的关系(反比关系);
b)
tp 、td与ξ的关系(正比关系);
ts与ξ的关系(反比关 系);
前 页 后 页
2003-09/10
<自动控制原理>(3-17)
3.4 高阶系统的时域分析 1、定义:能用三阶或三阶以上的微分方程描述的控 制系统。 2、分析方法:
1)定性分析; 2)主导极点法; 3)计算机分析 3 主导极点与偶极子问题 ① 主导极点: 在所有的闭环极点中,那些离虚轴最近、 且附近又没有其它零、极点,对系统动态性能影响起主 导的决定性作用的闭环极点,称之为主导极点。 主导极点法: 利用主导极点代替系统全部闭环极点来 估算系统性能的方法,称为主导极点法。 一般要求:
t
td tr tp ts b 单位阶跃信号作用下 反馈系统的过渡过程曲线
误差带△一般取0.02或0.05 ⑵ 动态性能指标: 延迟时间 td :指响应从0到第一次达到终值(稳态值)的一半 时所需要的时间;
上升时间 tr :指响应从0到第一次达到终值(稳态值)时所需要 的时间;
前 页 后 页
2003-09/10
j
S1 S2
j
0
0
t
② ξ = 1时,(临界阻尼) S1 ,S2 为一对相等的负实数根。
③ 0<ξ<1时,(欠阻尼) S1 ,S2 为一对具有负实部的共轭复根。
前 页 后 页
2003-09/10
<自动控制原理>(3-08)
④ 当ξ=0时,(无阻尼,零阻尼) S1 ,S2 为一对幅值相等的虚根。
⑤ 当ξ<0时,(负阻尼) S1 ,S2 为一对不等的负实数根。
结论分析: a) tr 、tp 、ts 、td 与ωn 的关系(反比关系);
b)
tp 、td与ξ的关系(正比关系);
ts与ξ的关系(反比关 系);
前 页 后 页
自动控制原理
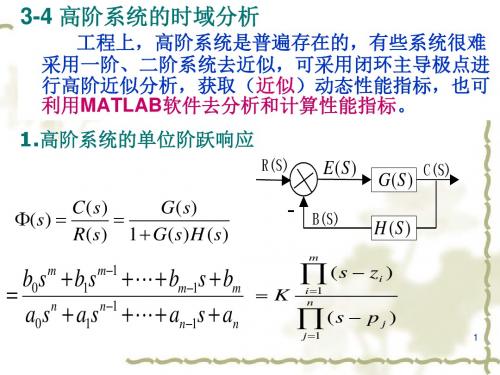
k ( t ) Ai e
i 1
i t
t
0
系统稳定的充要条件:系统所有闭环特征根均具有负的实部,
或所有闭环特征根均位于左半s平面。
系统稳定:充要条件 闭环特征方程的所有根均具有负实部 或系统闭环极点都位于S的左半平面 不稳定系统: 有一个或一个以上的正实部根。 临界稳定: 有一对纯虚根,而其余的特种根都有负 实部。 无阻尼系统 =0 。 12 工程上,临界稳定(线性系统不存在)为不稳定系统。
c1
b1a3 a1b2 b1 b a a1b3 c2 1 5 b1 b a a1b4 c3 1 7 b1
劳斯表第一列元素均大于零时系统稳定,否则系统不稳定 且第一列元素符号改变的次数就是特征方程中正实部根的个数
劳斯稳定判据
系统特征方程: a0 s
n
a1s an1s an 0
4
517 2.3 104
0 0
该表第一列系数符号不全为正,因而系统是不稳定的;且符 号变化了两次(+到-,-到+),所以该方程中有二个根在 S的右半平面。
18
例3.2 已知某调速系统的特征方程式为
S 3 41.5S 2 517S 1670 (1 K ) 0
求该系统稳定的K值范围。 解:列劳斯表
t
k ( t ) A1e
t
i t
A2 e
n i 1
2 t
i t
An e
0
n t
Ai e i t
i 1
n
limk ( t ) lim Ai e
t
i 0
i 1, 2, , n
n
充分性:
高阶系统的时域分析
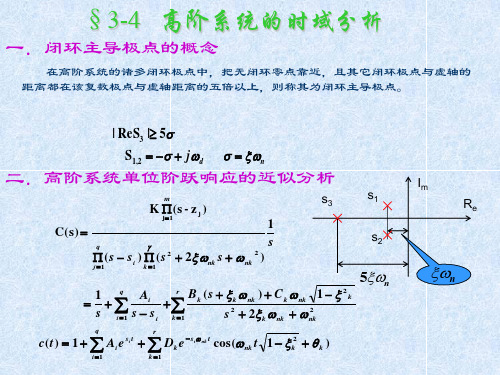
5n
n
c( t ) 1 Ai e
i 1
q
si t
Dk e si nk t cos( nk t 1 k2 k )
k 1
rn i 1
m
j
) ( s si ) s s
i
s ( s s i )
二.高阶系统单位阶跃响应的近似分析
C (s) ( s s i ) ( s 2 2 nk s nk )
2 j 1 k 1 q
1 s
r Bk ( s k nk ) C k nk 1 2 k 1 q Ai 2 s i 1 s s i k 1 s 2 2 k nk nk
§3-4 高阶系统的时域分析
一.闭环主导极点的概念
在高阶系统的诸多闭环极点中,把无闭环零点靠近,且其它闭环极点与虚轴的 距离都在该复数极点与虚轴距离的五倍以上,则称其为闭环主导极点。
| ReS3 | 5 S1,2 j d
K (s - z j )
j 1 m
n
s3 s1 s2 Im Re
k
k
由此可见高阶系统的暂态响应是一阶和二阶系统。
暂态响应分量的合成则有如下结论:
(1)各分量衰减的快慢由指数衰减系数 S i 及 k nk 决定。系统的极点在s平面左半部距虚轴愈远,相应的 暂态分量衰减愈快。 (2)系数 Ai 和 Dk 不仅与s平面中的极点位置有关, 并且与零点有关。
Ai 越小,对 c( t ) a.零极点相互靠近,且离虚轴较远, 影响越小;
b.零极点很靠近,对c(t ) 几乎没影响;
c.零极点重合(偶极子), 对 c(t ) 无任何影响;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h(t ) = 1 -
1
e - sot
bz 2(b - 2) + 1
-
e - zwn t
[bz 2(b -
bz 2(b - 2) + 1
2) cos wn
1- z 2t
bz (z 2(b - 2) + 1)
+
1- z2
sin wn
1- z2t]
由于
b 2 ( b 2 ) 1 2 ( b 1 ) 2 ( 1 2 ) 0 , b S 0 /w n
2、 超调量的计算
n
m
si
s% i3 n
s1 zi
i1
estp 10% 0
m
s1 si
zi
i3
i1
结论: (1)闭环零点会减小系统阻尼。 (2)闭环非主导极点会增大系统阻尼。 (3)若系统不存在闭环零点和非主导极点,则
s%e/ 12 10% 0
3、 调节时间的计算
s i为 D ( s ) 0 的 根 , 称 为 闭 环 极 点 。
当输入为单位阶跃函数时,
m
K (szi)
C (s)q
i 1 r
(ssj) (s22k
ksk 2)1 sA s0jq 1s A jsjkr 1s2 B 2 ksk k C skk 2
ts 1n ln2
n
si
i2 n
s1 si
m
s1 zi
i1 m
zi
i2
i1
结论:
(1)闭环零点越接近虚轴,峰值时间越小,超调量 和调节时间越大;
(2)闭环非主导极点的作用是增大峰值时间,但可 减小系统的超调量和调节时间。
(非主导极点实部的模比主导极点实部的模大三倍以上) 1、 峰值时间的计算
令 h´(t)=0,得
tp1 m (s1zi)n (s1si)
d i 1
i 3
结论:
(1)闭环零点越接近虚轴,峰值时间越小,系统响应速度越快; (2)闭环非主导极点的作用是增大峰值时间,使系统响应速度变缓; (3)若闭环零、极点彼此接近,则它们对系统响应速度的影响相互削弱; (4)若系统不存在闭环零点和非主导极点,则tp=π /ω d。
G (s)
R(s) 1 G (s)H (s)
M (s) D (s)
b0 s m b1 s m 1 a 0 s n a1s n1
bm 1s bm a n1s a n
m
K (s zi)
i 1 n
(s si )
i 1
式 中 , K b 0 /a 0 ; z i为 M ( s ) 0 的 根 , 称 为 闭 环 零 点 。
高阶系统的增益常常调整到使系统具有一对闭环共轭 主导极点,这时可以用二阶系统的动态性能指标来估 算高阶系统的动态性能。
设单位反馈高阶系统具有一对共轭复数闭环主导极点: 系统单位阶跃响应的近似表达式:
s1,2 sjd,01
C(s) M(s) 1 N(s) s
1 M(s) 1 1 M(s) 1 1
一、三阶系统的单位阶跃响应
三阶系统包括一对共扼极点和一个实极点
设闭环传递函数
(s)C R ((s s))(ss0)s(2 n 22 s 0 n sn 2)
当输入为单位阶跃函数时,
式中,s0>0,ζ<1
1A
B
C
C ( s )=+ +
+
ss + s 0 s + x w n -jw n1 -x 2 s + x w n + jw n1 -x 2
sin(k
1k2)t,t0
表明
(1)响应由一阶系统和二阶系统的时间响应函数项组成。当所 有闭环极点都位于左半s开平面时,系统是稳定的。
(2)零极点对系统性能的影响。
三、闭环主导极点
闭环主导极点:在所有的闭环极点中,距虚轴最近、 周围没有闭环零点、而又远离其它闭环极点的极点。 它所对应的响应分量在系统的响应过程中起主导作用。
s
D(s
D(s)
sss2
s s2
c(t)
1
2
M(s1) s1D(s1)
est
cosd
t
sM1D((ss11))
,t
0
上式中的振幅与相位已经考虑了闭环零点与非主导极点对 响应过程的影响
四、高阶系统的动态性能估算
取拉氏反变换,(且令b= s0/ζωn,)并整理得
h(t)=1-
1
e-sot
bz2(b-2)+1
-bz2(b e--zw 2 nt)+1轾 犏 犏 犏 臌 bz2(b-2)cosw n 1-z2t+bz(z2(1 b--z22 )+1)sinw n 1-z2t
(s)C R((s s))(ss0)(s2 n 22 s0nsn 2)
表明
(1)实数极点ss0 可使单位阶跃响应的超调量下降,并使调节时间增加。
(2)当系统阻尼比ζ不变时,随着b 值的下降,超调量不断下降、而峰值时间、 上升时间、和调节时间则不断加长。在b<1时,三阶系统将表现出明显的过阻 尼特性。
二、高阶系统的单位阶跃响应
其闭环传递函数
(s) C (s)
j 1
k 1
式中,q+2r=n, q为实数极点的个数;r为共轭复数极点的对数。
部分分式展开,并设0<ζ k<1,取拉氏反变换,并整理
q
r
h(t)A0
Ajesjt
Bekkt k
cosk(
1k2)t
j1
k1
r
Ck Bk
k
e k kkt
k1 k 1k2
3-4 高阶系统的时域分析
工程上的大部分系统是高阶系统,他们的动态性能 指标很难解析确定(但数值确定并不难),因此,在经 典控制理论的发展阶段,通过引入闭环主导极点的概念, 导出若干工程实用的动态性能指标估算公式。
一、三阶系统的单位阶跃响应
二、高阶系统的单位阶跃响应
三、闭环主导极点
四、高阶系统的动态性能估算
