轴向拉伸和压缩练习题
项目三 轴向拉伸与压缩试题

【开始】单选题(分值=2分;答案=C;难度=基本题)在其他条件不变时,若受轴向拉伸的杆件横截面面积增加一倍,则杆件横截面上的正应力()。
A、4倍B、2倍C、1/2倍D、1/4倍【结束】【开始】单选题(分值=2分;答案=C;难度=水平题)在其他条件不变时,若受轴向拉伸的杆件杆长增加一倍,则杆件纵向线应变()。
A、增大B、减小C、不变D、不能确定【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)弹性模量E与()有关。
A、应力和应变B、杆件的材料C、外力大小D、泊松比μ【结束】【开始】单选题(分值=2分;答案=B;难度=水平题)横截面面积不同的两根杆件,受到大小相同的轴向外力作用时,则()。
A、轴力相同,应力也相同B、轴力相同,应力不同C、轴力不同,应力也不同D、轴力不同,应力不同【结束】【开始】单选题(分值=2分;答案=A;难度=基本题)材料在轴向拉伸时,在比例极限内,线应变与()成正比。
A、正应力B、弹性模量EC、泊松比μD、都切应力【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)危险截面的确定,对于杆件对象的工程设计是非常重要的,若杆件的材料相同,轴向拉伸杆件危险截面发生在()的截面上。
A、轴力最大、横截面面积最大B、轴力最小、横截面面积最小C、轴力最小、横截面面积最大D、轴力最大、横截面面积最小【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)下列关于内力的说法中错误的是()。
A、由外力引起的杆件内各部分间的相互作用力B、内力随外力的改变而改变C、内力可由截面法求得D、内力不仅与外力有关,还与杆件的截面形状和尺寸有关【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)对于塑性材料取()作为材料的极限应力。
A、弹性极限B、屈服极限C、比例极限D、强度极限【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)轴向拉压杆的应力与杆件的()有关。
A、外力B、外力、截面面积和形状C、外力、截面面积和形状、材料D、外力、截面面积和形状、材料、杆长【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)轴向拉压杆的纵向线应变与杆件的()有关。
轴向拉伸与压缩和剪切挤压练习题

轴向拉伸压缩练习题一、判断题:1.在弹性范围内,杆件的正应力和正应变成正比。
(对)2.轴向拉压杆横截面上,只有一种内力,有两种应力。
(对)3.胡克定律仅适用于杆件的弹性变形范围(对)4.低碳钢受拉破坏时有屈服阶段,中碳钢和合金钢都没有屈服阶段。
(错)5.铸铁扭转破坏沿45度螺旋面断裂是因剪应力先达到极限所致。
(错)6.低碳钢扭转破坏沿轴横截面断裂是因剪应力先达到极限所致。
(对)7.低碳钢压缩实验曲线一直是上扬的,因此极限强度为无穷。
(错)8. 弹性极限是材料保持弹性的最大极限值,可以不保持线性。
(错)9.比例极限是材料能保持线性的最大值,必在材料的弹性范围内。
(错)10.构件内力的大小不但与外力大小有关,还与材料的截面形状有关(错)11.杆件的某横截面上,若各点的正应力均为零,则该截面上的轴力为零。
(对)12.两根材料、长度都相同的等直柱子,一根的横截面积为A1,另一根为A2,且A2>A1 如图所示。
两杆都受自重作用。
则两杆最大压应力相等,最大压缩量也相等。
(对)13. 受集中力轴向拉伸的等直杆,在变形中任意两个横截面一定保持平行。
所以纵向纤维的伸长量都相等,从而在横截面上的内力是均匀分布的。
(错)14. 若受力物体内某电测得x和y方向都有线应变εx和εy,则x和y方向肯定有正应力σx 和σy。
(错)二、选择题1 塑性材料冷作硬化后,材料的力学性能发生了变化。
试判断以下结论哪一个是正确的:__ (A) 屈服应力提高,弹性模量降低;(B) 屈服应力提高,塑性降低;(C) 屈服应力不变,弹性模量不变;(D) 屈服应力不变,塑性不变。
2 低碳钢材料在拉伸实验过程中,不发生明显的塑性变形时,承受的最大应力应当小于的数值,有以下4种答案,请判断哪一个是正确的:_B_ (A) 比例极限;(B) 屈服极限;(C) 强度极限;(D) 许用应力。
3.关于低碳钢试样拉伸至屈服时,有以下结论,请判断哪一个是正确的:__ _ (A) 应力和塑性变形很快增加,因而认为材料失效;(B) 应力和塑性变形虽然很快增加,但不意味着材料失效;(C) 应力不增加,塑性变形很快增加,因而认为材料失效;(D) 应力不增加,塑性变形很快增加,但不意味着材料失效。
工程力学轴向拉伸与压缩答案
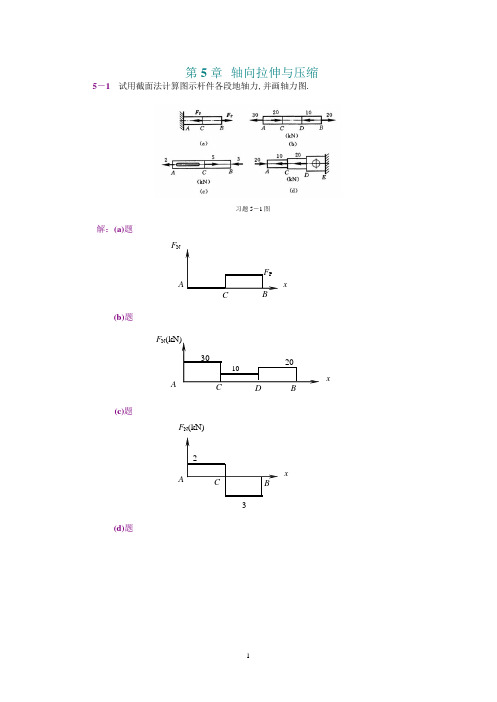
第5 章轴向拉伸与压缩5-1 试用截面法计算图示杆件各段地轴力,并画轴力图.习题5-1 图解:(a)题F Nx(b)题F NxA(c)题F N(kN)x-3(d)题F N-10x5-2 图示之等截面直杆由钢杆 ABC 与铜杆 CD 在 C 处粘接而成.直杆各部分地直径均为 d =36 mm ,受力如图所示.若不考虑杆地自重,试求 AC 段和 AD 段杆地轴向变形量 Δl AC和 Δl AD习题 5-2 图(F N ) l AB (F N ) l BC解: Δl AC =AB πd 2E s4+BC πd 2 E s 4 150 ×103 × 2000 +100 ×103 ×3000 4 = × = 2.947 mm(F N ) 200 ×103 l π ×362100 ×103 × 2500 × 4 Δl = Δl + CD CD = 2.947 + = 5.286 mm AD AC πd 2 E c4105 ×103 × π ×3625-3 长度 l =1.2 m 、横截面面积为 1.10×l0-3m 2 地铝制圆筒放置在固定地刚性块上;刚性板mC B −6 B 直径 d =15.0mm 地钢杆 BC 悬挂在铝筒顶端地刚性板上;铝制圆筒地轴线与钢杆地轴线重 合.若在钢杆地 C 端施加轴向拉力 F P ,且已知钢和铝地弹性模量分别为 E s =200GPa ,E a =70GPa ;轴向载荷 F P =60kN ,试求钢杆 C 端向下移动地距离.解:u A− u B −F l = P AB E a A a 3(其中 u A = 0)3∴ u =60 ×10 ×1.2 ×10= 0.935 mm B 70 ×10 3 ×1.10 ×10 −3 ×10 6钢杆 C 端地位移为F l60 ×103 × 2.1×103u = u + P BC = 0.935 + = 4.50 m m E s A s200 ×103 × π ×15245-4 螺旋压紧装置如图所示.现已知工件所受地压紧力为 F =4 kN .装置中旋紧螺栓 螺纹地内径 d 1=13.8 mm ;固定螺栓内径 d 2=17.3 mm .两根螺栓材料相同,其许用应力[σ ] =53.0 MPa .试校核各螺栓地强度是否安全.解:∑ M B = 0 ,F A = 2kN ∑ F y = 0 ,F B = 6kN习题 5-4 解图习题 5-4 图 σ = F A = 2000 = A π2000 × 42= 13.37 MPa < [σ ] ,安全. A A d 2 π ×13.8 ×104 σ = F B = 16000= 25.53 MPa <[σ ] ,安全. A B π ×17.32 ×10−645-5 现场施工所用起重机吊环由两根侧臂组成.每一侧臂 AB 和 BC 都由两根矩形截面 杆所组成,A 、B 、C 三处均为铰链连接,如图所示.已知起重载荷 F P =1200 kN ,每根矩形 杆截面尺寸比例 b/h =0.3,材料地许用应力[σ ]=78.5MPa .试设计矩形杆地截面尺寸 b 和 h .4⋅2FF N习题 5-5 图解:由对称性得受力图如习题 5-5 解图所示.∑ F y = 0 ,4F N cos α = F P 习题 5-5 解图F = F P = N 4 cos α 1200 ×103960 = 3.275 ×105 Nσ = F N A= F N 0.3h 2≤ [σ ]9602 + 42025h ≥ F N =0.3[σ ]3.275 ×100.3 × 78.5 ×106= 0.118m b = 0.3h ≥ 0.3 × 0.118 = 0.0354m = 35.4mmh = 118mm ,b = 35.4mm5-6 图示结构中 BC 和 AC 都是圆截面直杆,直径均为 d =20mm ,材料都是 Q235 钢, 其许用应力[σ ]=157MP .试求该结构地许用载荷.B习题 5-6 图习题 5-6 解图∑ F x = 0 , F B = 2F A (1)∑ F y= 0 ,2 F A + 23F B − F P = 0 2(2)1 + 3 F P = F B2(3)F ≤ [σ ] ⋅πd2B43 mdWs由式(1)、(2)得:F ≤ 1 + P2 = 1 + 23 ⋅π d 2 [σ ] 43 ⋅π × 202 ×10−4 ×157 ×106 = 67.4kN 4` (4)F P =2 (1 + 23 ) F A = 2 (1 + 2 3 ) ⋅[σ ]π 24= 90.28kN (5)比较(4)、(5)式,得 [F P ] = 67.4 kN5-7 图示地杆件结构中 1、2 杆为木制,3、4 杆为钢制.已知 1、2 杆地横截面面积A 1=A 2=4000 mm 2,3、4 杆地横截面面积 A 3=A 4=800 mm 2;1、2 杆地许用应力[σ]=20MPa , 3、4 杆地许用应力[σ ]=120 MPa .试求结构地许用载荷[F P ].习题 5-7 图P(a)3(b)解:1. 受力分析:由图(a )有5∑ F y = 0 , F 3 =F P 3 4 4由图(b )由∑ F x = 0 , F 1 = − 5 F 3 = − 3 F P∑ F x = 0 , F 4 = 4 F 3 = 5 43 F P2. 强度计算:5∑ F y = 0 , F 2= − 3F 3 = −F P| F 1 |>| F 2 || F 1 |≤ [σ w ] A 14 F ≤ A [σ ] 3P 1 w F ≤ 3 A [σ ] = 3 × 4000 ×10 −6 × 20 ×10 6 = 60 kN P 4 1 w4F 35F 3 > F 4 , ≤ [σ s ] , A 3F P ≤ [σ ]A 3 3F ≤3 [σ] A 3 ×120 ×10 6 × 800 ×10 −6= 57.6 kN[F P] = 57.6 kNa*5-8 由铝板和钢板组成地复合柱,通过刚性板承受纵向载 荷 F P =38 kN ,其作用线沿着复合柱地轴线方向.试确定:铝板和 钢板横截面上地正应力. 解:此为超静定问题.1. 平衡方程2. 变形协调方程:3. 物性关系方程:F Ns + F Na = F P Δl s = Δl a(1)(2)联立解得⎧F F Ns E s A sE s A s= FNaE a A a(3)习题 5-8 图⎪ Ns = E A E A F P ⎪ ⎨ ⎪F = s s + a E a A a a(压) F NaE A + E A P s s a aσ =F Ns =−E s F P = −E s F P s A E b h + E⋅ 2b h b hE + 2b hE s s 0 a 1 0 s 1 a9 3σ = − 200 ×10 ×385 ×10175MPa (压)= − s 0.03 × 0.05 × 200 ×109 + 2 × 0.02 × 0.05 × 70 ×109σa = F Na A = −b hE E a F P+ 2b hEa 0 s 1 aσ = −175E a E s = −17570 200= −61.25MPa (压)*5-9 铜芯与铝壳组成地复合棒材如图所示,轴向载荷通过两端刚性板加在棒材上. 现已知结构总长减少了 0.24 mm .试求:1.所加轴向载荷地大小; 2. 铜芯横截面上地正应力.习题 5-9 图F NcE A =F NaE A(1)E A E A σ aF = ΔlE c A c , F= ΔlE a A aF Nc + F Na = F P(2)Nc l NalF = F + F = ΔlE c A c + ΔlE a A aP Nc Nal l = Δl E A + E A( c c a a) l= 0.24 ×10−3 ⎧ π 2 =π ⎡ 2 2 ⎤⎫ = ⎨105 ×106 × ×(25 ×10−3 ) + 75 ×106 × × (60 ×10−3 ) − (25 ×10−3 ) ⎬ 30 ×10−3⎩ 4 4 ⎭ = 171 kNF =E c A cNc c c F P + E a A aF =E a A a Na c cF P + E a A a⎧ F Nc E c F P E c F P ⎪σ c = ⎪ A c ⎪ ∴ ⎨= E c A c + E a A a = E c ⋅ πd 2 4 + E a π 2 2 ⋅ (D− d ) 4 ⎪ = F Na ⎪ A a ⎪⎩ = πd 2E c 4E aF Pπ(D 2 − d 2 ) + E a 4 9 32. σ =4 ×105 ×10 ×171×1083.5MPa = c105 ×109 × π × 0.0252 + 70 ×109 × π × (0.062 − 0.025)2σa = σcE a = 83.5 × 70= 55.6MPa E c 105*5-10 图示组合柱由钢和铸铁制成,组合柱横截面为边长为 2b 地正方形,钢和铸铁 各占横截面地一半(b ×2b ).载荷 F P ,通过刚性板沿铅垂方向加在组合柱上.已知钢和铸铁 地弹性模量分别为 E s =196GPa ,E i =98.0GPa .今欲使刚性板保持水平位置,试求加力点地 位置 x =?解:∑ M 0 = 0 , (b ⋅ 2b σ 习题 5-10 图) ⋅( x − b ) = (b ⋅ 2b )σs i( 3 b − x )23∴σ σ s =iE sE i2 x − b = σ i3b − 2 x σ s(1)(2)代入(1)得σ i σ s4 x − 2b = 3b − 2 x5= 98 = 1196 2(2)∴ x = b 65-11 电线杆由钢缆通过旋紧张紧器螺杆稳固.已知钢缆地横截面面积为1×103 mm 2 ,E =200GPa ,[σ ] = 300MPa .欲使电杆有稳固力F R =100kN ,张紧器地螺杆需相对移动多少? 并校核此时钢缆地强度是否安全.F R习题 5-11 图解:(1)设钢缆所受拉力为 F N ,由平衡条件F N cos30°=F RF N =100/ cos30°=115.5kNΔl = F N l = 115.5 ×103 ×10 ×103= 6.67mm EA 200 ×103 ×103× 3 / 2张紧器地螺杆需相对移动 6.67mm .(2)钢缆地应力与强度σ = F N A = 115.5 ×10 103= 115.5MP a < [σ ]所以,强度安全.5-12 图示小车上作用着力 F P =15kN ,它可以在悬架地 AC 梁上移动,设小车对 AC梁地作用可简化为集中力.斜杆 AB 地横截面为圆形(直径 d =20mm),钢质,许用应力 [σ]=160MPa .试校核 AB 杆是否安全.3习题 5-12 图F N ABαF N ACF P习题 5-12 解图解:当小车开到 A 点时,AB 杆地受力最大,此时轴力为 F N A B .(1) 受力分析,确定 AB 杆地轴力 F N A B ,受力图如图 5-12 解图所示, 由平衡方程∑Fy= 0 ,F N AB sin α − F P = 0sin α =解得轴力大小为:0.8 0.82 +1.92F N AB = 38.7kN(2)计算应力σ = F N AB = F N AB = 4 × 38.7 ×10 =123 ×106Pa = 123MPa < [σ ] AB强度安全.A AB πd 2 4π × 202 ×10−65-13 桁架受力及尺寸如图所示.F P =30kN ,材料地抗拉许用应力[σ]+=120MPa , 抗压许用应力[σ]-=60MPa .试设计AC 及AD 杆所需之等边角钢钢号.(提示:利用附录B 型钢表.)F N AC45DAF N ADF PF RA习题 5-13 图习题 5-13 解图解:(1)受力分析,确定 AC 杆和 AD 杆地轴力 F N AC 、 F N AD ,对整体受力分析可得, F R A= F R B = F P 2= 15kN再取节点 A ,受力分析,受力图如图 5-13 解图所示,建立平衡方程D D 3 3 2 4 ∑F y = 0 , − F N AC sin 45 + F R A = 0解得 AC 杆轴力大小为:F N AC = 21.2kN(压)∑ F x = 0 , − F N AC cos 45 + F N AD = 0解得 AD 杆轴力大小为: F N AD = 15kN(拉)(2)强度条件拉杆:A AD = F N AD [σ ]+ = 15 ×10 120 = 125mm 2 压杆:(3)选择钢号A AC = F N AC [σ ]− = 21.2 ×10 60 = 353.3mm 2 拉杆: 20 × 20 × 4压杆: 40 × 40 × 55-14 蒸汽机地气缸如图所示.气缸内径D =560mm ,内压强p =2.5MPa ,活塞杆直径 d =100mm .所有材料地屈服极限σs =300MPa . (1)试求活塞杆地正应力及工作安全系数.(2)若连接气缸和气缸盖地螺栓直径为30mm ,其许用应力[σ]=60MPa ,求连接每个气缸盖 所需地螺栓数.习题 5-14 图解:(1)活塞杆受到地轴力为:⎡π (D 2 F = pA = p − d 2 ) ⎤ = 2.5⎡π (560 −1002 ) ⎤ = 596.12kN N ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ 4 ⎦活塞杆地正应力:σ =F N A 杆596.12 ×103 ) = = 75.9MPa π ×102 / 4 工作安全系数: (2)螺栓数mn = σ s σ= 300 = 3.95 75.93x 3 x y xm = F N = 596.12 ×10 = 14.1 个 A 栓 [σ ]栓 π × 302 / 4 × 60由于圆对称,取m =16个.5-15 图示为硬铝试件,h =200mm ,b =20mm .试验段长度l 0=70mm .在轴向拉力 F P =6kN 作用下,测得试验段伸长Δl 0=0.15mm ,板宽缩短Δb =0.014mm .试计算硬铝地弹 性模量E 和泊松比ν .习题 5-15 图解:(1)计算弹性模量Eε = Δl 0 l 0= 0.15 = 2.143 ×10−3 70σ = F P = 6 ×10 = 150MPa AE = σ = 20 × 2 150 ×106 = 70GPa ε 2.143 ×10−3 (2) 计算泊松比νε = Δb 0 b 0= − 0.014 = −7 ×10−4 20ε ν = y = − 7 ×10−4 = 0.327 ε 2.143 ×10−3上一章返回总目录下一章。
轴向拉伸与压缩练习题

轴向拉伸与压缩练习题在材料力学中,轴向拉伸与压缩是一种常见的载荷方式,它们用于研究材料的强度、刚度和变形特性。
这些练习题旨在帮助学生加深对轴向拉伸与压缩的理解,并提供实践应用的机会。
以下是一些典型的练习题,通过解答这些问题,我们可以更好地理解这一领域的概念和原理。
1. 假设一根钢杆的长度为L,直径为D,已知拉伸载荷为F,求该杆的应力和应变。
2. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,它的徐变模量为E,求该体的应变。
3. 如果一根杆材受到的拉伸载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?4. 如果一根杆材受到的压缩载荷逐渐增加,最终达到其屈服强度,该杆材会发生什么样的变形?5. 如果一根杆材同时受到轴向拉伸和压缩两种载荷,该杆材会如何变形?6. 一根弹性体的长度为L,横截面积为A,已知施加在该体上的拉伸载荷为F,计算该体的应力。
7. 一块材料在受到拉伸载荷时,其应力与应变之间的关系可以通过应力-应变曲线来表示,请描述应力-应变曲线的特点。
8. 如果一根杆材在受到轴向拉伸时断裂,这可能是由于哪些原因导致的?9. 一根杆材经过轴向拉伸后恢复原状的能力被称为什么?10. 在材料力学中,有一种称为胶黏剪切的变形模式,你了解它吗?请简要描述一下。
以上是一些典型的轴向拉伸与压缩练习题,通过解答这些问题,我们可以更好地理解轴向拉伸与压缩的基本概念和应用。
在解答问题的过程中,我们也可以运用公式和原理来计算并分析材料的应力、应变和变形等性质。
同时,通过这些练习题,我们可以培养应用知识解决实际问题的能力。
要提醒的是,在进行轴向拉伸与压缩练习题时,我们应该注意准确的计算和合理的分析。
在解答问题时,可以尝试用不同的方法和途径来验证答案,以加深对知识的理解和掌握。
同时,在实践中,我们也可以通过学习和研究更多的相关材料,来进一步拓展和深化对轴向拉伸与压缩的理解。
通过轴向拉伸与压缩练习题的学习与实践,我们可以更好地掌握这一领域的知识和技能。
第一章轴向拉伸和压缩习题

第一章轴向拉伸和压缩习题一、单项选择题1、构件具有足够的抵抗破坏的能力,我们就说构件具有足够的A、刚度,B、稳定性,C、硬度,D、强度。
2、构件具有足够的抵抗变形的能力,我们就说构件具有足够的A、强度,B、稳定性,C、刚度,D、硬度。
3、单位面积上的内力称之为A、正应力,B、应力,C、拉应力,D、压应力。
4、与截面垂直的应力称之为A、正应力,B、拉应力,C、压应力,D、切应力。
5、轴向拉伸和压缩时,杆件横截面上产生的应力为A、正应力,B、拉应力,C、压应力,D、切应力。
6、胡克定律在下述哪个范围内成立?A、屈服极限,B、比例极限,C、强度极限,D、名义屈服极限。
时,试样将7、当低碳钢试样横截面上的实验应力σ =σsA、完全失去承载能力,B、断裂,C、产生较大变形,D、局部出现颈缩。
8、脆性材料具有以下哪种力学性质?A、试样拉伸过程中出现屈服现象,B、抗冲击性能比塑性材料好,C、若构件开孔造成应力集中现象,对强度没有影响。
D、抗压强度极限比抗拉强度极限大得多。
9、灰铸铁压缩实验时,出现的裂纹A、沿着试样的横截面,B、沿着与试样轴线平行的纵截面,C、裂纹无规律,D、沿着与试样轴线成45。
角的斜截面。
10、横截面都为圆的两个杆,直径分别为d和D ,并且d=0.5D。
两杆横截面上轴力相等两杆横截面上应力之比Ddσσ为 A 、2倍, B 、4倍, C 、8倍, D 、16倍。
二、填空题1、求内力常用的方法是 。
2、轴向拉伸和压缩时,虎克定律的两种表达形式为 ,3、通过低碳钢拉伸试验可知,反映材料抵抗弹性变形能力的指标是 ;反映材料强度的指标是 ;反映材料塑性的指标是 。
4、σ0.2表示材料的 。
5、与截面平行的应力称为 ;与截面垂直的应力称之为 。
6、 钢的弹性模量E=200Gpa ,铝的弹性模量E=71Gpa,试比较在同一应力作用下,哪种材料应变大? 。
7、轴向拉伸和压缩时,杆上所受外力或外力的合力与杆件的轴线 。
项目三 轴向拉压杆习题

项目三轴向拉伸与压缩一、填空题:1、内力是由引起的杆件内个部分间的。
2、求内力的基本方法是。
3、直杆的作用内力称。
其正负号规定为:当杆件受拉而伸长时为正,其方向截面。
4、截面法就轴力的步骤为:、、。
5、轴力图用来表达,画轴力图时用的坐标表示横截面位置,坐标表示横截面上的轴力。
6、轴力图中,正轴力表示拉力,画在轴的。
7、轴力的大小与外力有关。
与杆件截面尺寸、材料(有关、无关)。
8、应力是,反应了内力的分布集度。
单位,简称。
9、1pa= N/mm2 = N/m2。
1Mpa= pa。
10、直杆受轴力作用时的变形满足假设,根据这个假设,应力在横截面上分布,计算公式为。
11、正应力是指。
12、在荷载作用下生产的应力叫。
发生破坏是的应力叫。
许用应力是工作应力的;三者分别用符号、、表示。
13、当保证杆件轴向拉压时的安全,工作应力与许用应力应满足关系式:。
14、等截面直杆,受轴向拉压力作用时,危险截面发生在处。
而变截面杆,强度计算应分别进行检验。
15、轴向拉压杆的破坏往往从开始。
16、杆件在轴向力作用下长度的改变量叫,用表示。
17、胡克定律表明在范围内,杆件的纵向变形与及,与杆件的成正比。
18、材料的抗拉、压弹性模量用表示,反映材料的能力。
19、EA称作材料的,它反映了材料制成一定截面尺寸后的杆件的抗拉、压能力。
EA越大,变形越。
20、ε叫作,指单位长度的变形。
21、泊松比又叫,ν= ,应用范围为弹性受力范围。
二、计算题:1、试计算轴向拉压杆指定截面的轴力。
2、绘制图示杆件的轴力图。
3、求图示结构中各杆的轴力。
4、用绳索起吊管子如图所示。
若构件重W=10KN ,绳索的直径d=40mm ,许用30 20KNB 45C 455、图示支架中,荷载P=100KN。
杆1为圆形截面钢杆,其许用应力[σ]拉=150MPa,杆2位正方形截面木杆,其许用应力[σ]压=4MPa。
试确定钢杆的直径d和木杆截面的边长c。
C6、钢杆长l=2m,截面面积A=200 mm2,受到拉力P=32KN的作用,钢杆的弹性模量E=2.0×105MPa,试计算此钢杆的伸长量Δl。
工程力学:拉伸压缩 习题与答案

一、单选题1、拉压正应力计算公式s=F/A的适用条件是()。
A.应力小于弹性极限B.应力小于屈服极限C.应力小于比例极限D.外力的合力沿杆轴线正确答案:D2、材料经过冷作硬化后,其比例极限和塑性分别()。
A.提高,提高B.下降,不变C.下降,提高D.提高,下降正确答案:D3、假设一拉伸杆件的弹性模量E=300GPa,比例极限为 sp=300MPa,杆件受一沿轴线的拉力,测得轴向应变为e=0.0015,则该拉应力s的大小为()。
A.大于450MPaB.300MPa£s£450MPaC.450MPaD.小于300MPa正确答案:B4、受轴向拉伸的杆件,其最大切应力与轴线的角度为()。
A.30B.90C.45D.0正确答案:C5、一等直拉杆在两端承受拉力作用,若其一段为钢,另一段为铝,则两段的()。
A.应力不同,变形相同B.应力不同,变形不同C.应力相同,变形不同D.应力相同,变形相同正确答案:C6、脆性材料与塑性材料相比,其拉伸性能的最大特点是()。
A.没有明显的屈服阶段和塑性变形B.应力应变关系严格遵守虎克定律C.强度低、对应力集中不敏感D.强度极限比塑性材料高正确答案:A7、现有一两端固定、材料相同的阶梯杆,其大径与小径的横截面积之比为4:1, 杆的大径与小径长度相同,在大径与小径交界处施加一轴向力P,则杆的大径与小径所受轴力之比为()。
A.2:1B.1:1C.4:1D.1:2正确答案:C8、在低碳钢的拉伸实验中,材料的应力变化不大而变形显著增加的是()。
A.屈服阶段B.颈缩阶段C.强化阶段D.线弹性阶段正确答案:A9、现有两相互接触的平板,在垂直于板平面的方向上打一直径为d的销孔,使用直径d、许用切应力[τ]、许用挤压应力[sbs]的圆柱形销钉进行固定,两板的厚度均为h, 现分别在两板施加大小相同、方向相反的F,使两板有沿接触面相互错动的倾向,若要销钉不失效破坏,则要满足的条件是()。
材料力学 拉伸压缩 习题及参考答案

轴向拉伸和压缩 第二次 作业1. 低碳钢轴向拉伸的整个过程可分为 弹性阶段 、 屈服阶段 、 强化阶段 、 局部变形阶段 四个阶段。
2. 工作段长度100 mm l =,直径10 mm d =的Q235钢拉伸试样,在常温静载下的拉伸图如图所示。
当荷载F = 10kN 时,工作段的伸长∆l = 0.0607mm ,直径的缩小∆d = 0.0017mm 。
则材料弹性模量E = 210 GPa ,强度极限σb = 382 MPa ,泊松比μ = 0.28 ,断后伸长率δ = 25% ,该材料为 塑性 材料。
∆l / mmO0.0607253. 一木柱受力如图所示。
柱的横截面为边长20mm 的正方形,材料的弹性模量E =10GPa 。
不计自重,试求 (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱端A 的位移。
100kN260kN解:(1)轴力图如图所示 (2)AC 段 310010250MPa 2020NAC AC AC F A σ-⨯===-⨯ CB 段 326010650MPa 2020NCB CB CB F A σ-⨯===-⨯ (3)AC 段 69250100.0251010NAC AC AC AC F EA E σε-⨯====-⨯ CB 段 69650100.0651010NCB CB CBCB F EA E σε-⨯====-⨯ (4)AC 段 0.025150037.5mm NAC ACAC AC AC ACF l l l EA ε∆===-⨯=- CB 段 0.065150097.5mm NCB CBCB CB CB CBF l l l EA ε∆===-⨯=- 柱端A 的位移 37.597.5135mm A AC CB l l ∆=∆+∆=--=-(向下)4. 简易起重设备的计算简图如图所示。
已知斜杆AB 用两根63×40×4不等边角钢组成,63×40×4不等边角钢的截面面积为A = 4.058cm 2,钢的许用应力[σ] = 170 MPa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q=4.2kN/m
FN26.5kN ③ 由强度条件求直径
0.4m
F Ay
4.25m
C FCx
FCy FN
由F A N4F dN 2得
d4F N 42 1 6 7 .0 5 1 1 0 0 6 3P N a 0.0141 m 14.1 m m
为了经济起见,选用钢拉杆的直径为14mm。其值略小于计算 结果,但是其工作正应力超过许用应力不到5%。
F N 2 F 1 F 2 1 0 k N 2 5 k N 3 5 k N 拉 力
F1=10kN
1F2=25kN 2 F3=55kN 3 F4=20kN
A1 B
2
C
Fx 0 FN3F4 0
FN3
F N 3 F 4 2 0 k N 压 力
FN1 10kN FN2 35kN
第二章 轴向拉伸和压缩
例 一等直杆受四个轴向外力作用,如图所示。试作轴力图
F1=10kN
1F2=25kN 2 F3=55kN
F4=20kN
A1 B
2
C
D
F1=10kN
FN1
Fx 0 FN1 F1 0 F N 1 F 1 1 0 k N 拉 力
F2=25kN
F1=10kN
FN2
Fx 0 FN2F1F20
得F N 1 5 0 k N 拉 F N 1
2-2截面
1 B 2C 3 D 40kN 30kN 20kN
Fx 0 FN230200
得 F N 21 0k N (拉 )
F N2
30kN 20kN
3-3截面
Fx 0 FN3200
得F N 3 2 0k N (压 )
FN / kN 50
F N3 10
2 1 0 1 0 9 P a 5 0 0 1 0 6 m 2 2 0 0 1 0 6 m 2
0.0286103m0.0286m m (缩短)
计算结果为负,说明整根杆发生了缩短
例 已知三铰屋架如图,承受竖向均布载荷,载荷的分布集度为 :q =4.2kN/m,屋架中的钢拉杆材料为Q235钢,[σ]=170MPa, 试选择钢拉杆的直径。(不计钢拉杆的自重)
l1=300
求:(1)AB、BC段的伸长量及杆
的总伸长量;(2)C截面相对B截面
的位移和C截面的绝对位移。
B B′
解:(1) 变形:物体受力以后
l2=200
发生尺寸和形状的改变。
C
l1
F N l1 E A1
40103N 300103m
210109Pa 400106m2
C′
0 .1 4 3 1 0 3 m = 0 .1 4 3 m m (伸长) 杆的总伸长量
B
C
F=40 kN
l2
FN l2 E A2
40103N 200103m
210109Pa 250106m2
l l1l2 0 .1 4 3 m m + 0 .1 5 2 m m
0.295mm (伸长)
0 .1 5 2 1 0 3 m = 0 .1 5 2 m m (伸长)
课堂练习 1. 已知: AAB =500mm2
q
F Ax
A
0.4m
F Ay
C
钢拉杆 8.5m
B
F B 0.4m
解:① 整体平衡求支反力
Fx0 FAx0
M B 0-F A y 8 .5 4 .2 9 .3 8 2 .5 0
FAy19.53kN
② 局部平衡求轴力
MC 0
F N 1 .4 24 2 .24 .6 5 2 1 9 .5 3 4 .2 50A
20kN
O
x
20
例 设例中的等直杆为实心圆截面,直径d=20mm。试求此 杆的最大工作应力。
F1=10kN
F2=25kN F3=55kN
F4=20kN
A
B
FN / kN
35
10
O
C
D
FN,max=35kN (BC段)
x
20
m a x F N A ,m a x F d N ,2 m a x 4 4 3 0 5 .0 2 1 m 0 3 2 N 1 1 1 .4 1 0 6 P a 1 1 1 .4 M P a
Fx0 FAx0
M B0-F A y164 2 2162
A
8m
F Ay
③求应力
C FCx
FCy
FN
② 局部平衡求轴力
MC 0
FN24228233680
FN672kN
FN A
672103 N 42104 m2
160106Pa
160MPa
例
A
已知: AB段:A1 =400mm2 BC段:A2 =250mm2 ,E=210GPa
课堂练习 1. 已知:q=40kN/m, []=160MPa C
试选择杆件的面积。
解: (1)计算拉杆的轴力
MA0 F N Bsin4 5 2 2 q 10
FNB56.6kN
A
45
B
(2)选择等边角钢型号
A FNB [ ]
56.6 103 N 160 106 Pa
3.54104m 2
q
2m FN B
危险截面:在研究拉(压)杆的强度问题时,通常把最大工作 正应力所在的横截面称为危险截面。
练习: 已知三铰屋架如图,承受竖向均布载荷,载荷的分 布集度为:q =42kN/m,屋架中的钢拉杆截面面积为42cm2 ,试求钢拉杆横截面的正应力。(不计钢拉杆的自重)
q
C
F Ax
A
钢拉杆
B
F Ay
16m
FB
解:① 整体平衡求支反力
=3.54cm2
A
B
F Ax
F Ay
q
2. 图示杆系中BC、AC杆的直径分别为d1=12m B
m,d2=18mm,两杆材料均为Q235钢,许用应 力[] = 170MPa,试按强度条件确定容许F值。
1
解: 取C节点为研究对象 F N 1 0 .8 9 7 F , F N 2 0 .7 3 2 F
A
B30kN
ABC =200mm2 ,E=210GPa 求:杆的总变形量。
解:(1)作轴力图 (2)计算变形
0.1m 0.3m
FN 20kN
lAClABlBC
FNABlAB EAAB
FNBClBC EABC
10kN
C 10kN x
1
2 0 1 0 3 N 0 .1 m1 0 1 0 3 N 0 .2 m
FN / kN
10
35
FN3 20kN O
3D F4=20kN
x
几点说明:
20
(1)荷载将杆件分成几段,就取几段截面来研究 (2)轴力大小与截面面积无关 (3)集中力作用处轴力图发生突变,突变值等于该集中力
例 试作轴力图 解:1-1截面
1
2
3
40kN 30kN 20kN
Fx 0 F N 14030200A
