arc中值定理.ppt

合集下载

lecture 11_中值定理

O
a
x0
x02
b x
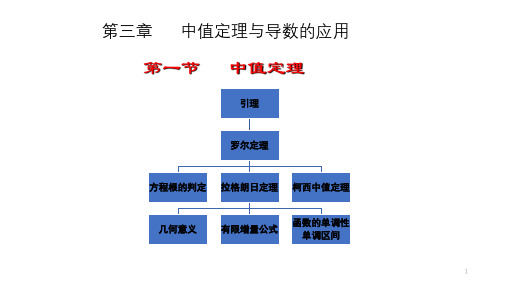
几何意义: 在两个高度相同的点之间的连续曲线上若除端点外，每一点都有不垂直于轴的切线，则其中必
有一条切线平行于x轴，也即平行于两个端点的连线。
证:
M 和最小值 m . 若M=m,则因此
故在[ a , b ]上取得最大值
若 M > m , 则 M 和 m 中至少有一个与端点值不等,
( 1 x 1).
x (1, 1)
由推论1 f ( x ) C ,
arcsin x arccos x .1 x [ 1, 1] (arccos x ) 2 2 1 , x 例5（p.96） arctan x arc cot x x ( , ).
其他求导公式都可由它们及求导法则推出; 2) 求分段函数在分界点处的导数 , 及某些特殊
函数在特殊点处的导数; 3) 由导数定义证明一些命题. 2.用导数定义求极限 3.微分在近似计算与误差估计中的应用
二、导数和微分的求法
1. 正确使用导数及微分公式和法则 2. 熟练掌握求导方法和技巧
(1) 求分段函数的导数注意讨论界点处左右导数是否存在和相等
f ( x 0 x ) f ( x 0 ) f ( x 0 ) x
令 x x0 x , 则
( x 很小时)
f ( x ) f ( x 0 ) f ( x 0 ) ( x x 0 ).
第一节中值定理
一、罗尔（Rolle）中值定理
二、拉格朗日（Lagrange）中值定理
(2) 隐函数求导法（对数微分法）
(3) 复合函数求导法（链式法则、可利用微分形式不变性)

高等数学第3章第一节中值定理

6 6
（函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数，且当
x
6
ln sin x 定义域内的一部分；
,
5
6
时，cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件，且：
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理，至少存在一点 ∈（a，b），
即：
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。注意到 f ' x 0 为三次方程，它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时， x ln1 x x
1 x
证设f x ln1 x, 显然，函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于： f f b f a
ba
或： f f b f a 0
ba
AB的方程为：

高等数学《中值定理》习题课课件一

ba
整理得e [ f () f ()] e
即证
(5) 若已知条件中含高阶导数 , 多考虑用泰勒公式 ,
有时也可考虑对导数用中值定理 . (6) 若结论为不等式 , 要注意适当放大或缩小的技巧.
例9. 设函数
在
上二阶可导,
且
证明
证: x [0, 1] , 由泰勒公式得
f
(1)
f
(x)
f
( x)(1
m f (0), f (1), f (2) M
m
f (0) f (1) f (2) 3
M
由介值定理, 至少存在一点 c [0, 2] , 使
由罗分f (尔c析) 定: 所想理f (f3给到知()c条找), 必1件一,且存f 可点(0在f)写c(xf,为)3(使1在)(cf[fc(,f(0,32(3)))c])上f 3(11(连)0f,(续3f0())2,,)在使f3(1(1)cf,,(f3f()(2)3内))可01.导 ,
1 f ( ) (0 1)
24
f ( ) 24
例11 求下列极限 :
1) lim [x2 ln(1 1) x];
x
x
2)
lim
x0
1 x100
e
1 x2
;
3) lim ln(1 x x2 ) ln(1 x x2 ).
x0
sec x cos x
解: 1) lim [x2 ln(1 1) x]
(2)所证式中出现两端点, 可考虑用拉格朗日定理 .
例5 设f (x)在[a,b]上连续，在 (a,b)内可导
证明至少存在一点 (a,b)使得 bf (b) af (a) f ( ) f ( )
ba

§3.1-微分中值定理PPT课件

1 x2
1 x2
f ( x) C , x [1,1]
又 f (0) arcsin 0 arccos 0 0 ,
即
C
.
arcsin
x
arccos
x
2
.
2
2
2
说明欲证x I , f ( x) C0 ,只需证在 I上
f ( x) 0,且 x0 自证 arctan x arc
则在开区间 (a, b)内至少存在一点 ,使得 f (b) f (a) f ( ) F (b) F (a) F ( )
广义微分中值定理
20
微分中值定理
柯西(1789 – 1857)
法国数学家, 他对数学的贡献主要集中在微积分学, 复变函数和微分方程方面 . 一生发表论文800余篇, 著书 7 本 ,《柯西全集》共有 27 卷. 其中最重要的的是为巴黎综合学校编写的《分析教程》,《无穷小分析概论》, 《微积分在几何上的应用》等, 有思想有创建, 对数学的影响广泛而深远 . 他是经典分析的奠人之一, 他为微积分所奠定的基础推动了分析的发展.
0
由条件,则 f ( x1 ) f ( x2 ), 即在区间I中任意两
点的函数值都相等,所以, f ( x) C.
17
微分中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证设 f ( x0) arcsin x0 arccos 0x, x [1,1]
f ( x) 1 ( 1 ) 0.由推论
f (1) 0 f (2) (2) 结论正确
方程f ( x) 0, 即3x2 8x 7 0有实根
x1
1 (4 3
37),

第三章中值定理与导数的应用课件

那么在(a,b)内至少有一点使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1：验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解：y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6：求
lim
x
xn ex
(n 0, 0)
解：lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7：求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2：证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数，且它存在直到n 1 阶的导数，那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒（Taylor)中值定理
泰勒(Taylor)中值定理如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个

中值定理

定理6.3 设 f ( x)在区间 I上可导，则 f ( x)在区间 I 上单调增(减)的充要条件是 : f ( x) 0 ( 0). 证若 f 为递增函数, 则当 x, x0 I , x x0 时,有
f ( x) f ( x0 ) 0. x x0
令 x x0 , 即得 f ( x0 ) 0. 反之,若 f ( x) 0, x I . x1, x2 I ,(设 x1 x2 )
ba 注当 f (a) f (b) 时,拉格朗日定理就是罗尔定理,
可见，罗尔定理是拉格朗日定理的一个特例.
几何意义如右图，曲线 y = f (x) 的两个端点 A, B 连线的斜率为
kAB
f (b) f (a) . b a
y B
y f (x)
A Oa
bx
用平行推移的方法,曲线上至少在一点 ( , f ( ))
所以 p( x0 ) 0, 矛盾.
定理6.2 (拉格朗日中值定理) 设函数 f (x) 满足： (i) f(x) 在闭区间 [a, b] 上连续; (ii) f(x) 在开区间 (a, b) 内可导.
那么在开区间 (a ,b)内 ( 至少 ) 存在一点 , 使得 f ( ) f (b) f (a) .
当 x 趋于时, 不趋于 , 而是趋于 1.
y
0.4
0.2
O 1 2 3 4 5 6 7 8 9 10 x
3.若 f(x) 在(a, b) 上可微, [a, b] 上连续, 则对于任意
x (a ,b], 存在 (a , x), 使 f ( x) f (a) f ( )(x a),
2x sin 1 cos 1 , x 0. 因此对每个 x > 0 , 存在使

3.1中值定理

［或 f ( x ) f ( x0 )］，则有f ( x0 ) 0 . 也说f(x)在x0取
y 水平切线
得了极大值。
y f (x) 几何意义：
若y=f(x)在x0取得极值，
且在( x0, f(x0))点存在
O
x0
x1
x 切线，则该切线平行于x轴。
2. 罗尔定理
若f(x)满足：1.在闭区间[a,b]上连续;2.在开区间(a,b)
f (b) f (a) f ( )(b a) , (a , b) 两个不 g (b ) g ( a ) g ( )( b a ) , ( a , b ) 一定相同
上面两式相比即得结论.
P88 3
小结: 1. 三个中值定理的条件、结论及关系
费马引理
f (a) f (b)
拉格朗日中值定理 g(x) x
f ( ) f (b) f (a) . g ( ) g (b) g (a)
F ( )
分析: 问题转化为证 f ( ) f (b) f (a) g ( ) 0
g (b) g (a)
作辅助函数 F ( x ) f ( x ) f (b) f (a) g ( x) g(b) g(a)
P88 1,2,5,7 并整理6的答案
3.令f(x)=xn，则f(x)在[a, b]上连续，在(a, b)内可导，
由拉格朗日中值定理，至少存在一点 ,使(a,b)
f (b) f (a) f ( )(b a)
即 bn an n n1(b a).
又 0 a b, n 1
故
0 an1 n1 bn1,
arccosx
2
推论2 若f(x)与g(x)在(a,b)内每一点的导数都相等，

高等数学第三章第一节中值定理课件.ppt

及满足 :
(1) 在闭区间 [ a , b ] 上连续
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内至少存在一点
使
f (b) f (a) F (b) F (a)
f ( ) . F( )
分析: F(b) F(a) F()(b a) 0 a b
要证 f (b) f (a) F( ) f ( ) 0
且 x0 I , 使 f (x0 ) C0.
自证: arctan x arccot x , x (, )
2
例3. 证明不等式 x ln(1 x) x (x 0). 1 x
证: 设 f (t) ln(1 t) ,
中值定理条件, 因此应有
即因为
故
三、柯西(Cauchy)中值定理
即
2. 设 f (x) 0 , f (0) 0 证明对任意 x1 0, x2 0 有
f (x1 x2 ) f (x1) f (x2 ) 证：不妨设 0 x1 x2
f (x1 x2) f (x2) f (x1)
f (x1 x2) f (x2) f (x1) f (0)
上面两式相比即得结论. 错!
柯西定理的几何意义:
弦的斜率切线斜率
注意:
x F (t)
y
f
(t)
d y f (t) d x F(t)
y
f (b)
f (a)
o F(a)F( )
F (b) x
例4. 设
至少存在一点
使
证: 结论可变形为
证明
设 F (x) x2, 则 f (x), F(x) 在 [0, 1] 上满足柯西中值定理条件, 因此在 ( 0 , 1 ) 内至少存在一点 , 使

微积分(第三版)课件：中值定理

例试证 | arctanb arctan a || b a |.
证
设f
(x)=arctan
x
,
(a<b)
.
(arctan
x)
1
1 x2
显然arctan x在[a,b]上满足拉格朗日中值定理条件.
可知必定存在一点 (a,b) , 使得
arctanb arctana
1
1
2
(b a),
a
b.
拉格朗日 Joseph-Loouis Lagrange
(1736-1813)
f (x) x (0 x 1)
f
(x)
x 0
0 x1 x 1
原点处不可导
端点处值不等
端点处不连续
例验证函数 f (x) x4 50x2 300 在区间 [ 8，8]符合罗尔定理.
显然多项式函数 f (x) 为偶函数，且连续可导.
满足罗尔定理条件 f (x) 4x3 100x
y
f (x) x4 50x2 300
微分中值定理
一、罗尔中值定理二、拉格朗日中值定理三、柯西中值定理
微分中值定理
导数在实际问题中具有广泛的应用，利用导数可以求解未定式的极限问题；利用导数可以研究函数的基本性态、函数图形的特征；利用导数可以解决实际生活中的优化问题.
微分中值定理是利用导数研究函数在区间上整体性质的有力工具和桥梁，微分中值定理主要包括罗尔定理、拉格朗日定理和柯西定理。
例 f (x) (x 1)2在[0,3]上不满足罗尔定理的条件
( f (0) f (3)), 但是存在 1(0,3)使 f ( ) 0.
(2)罗尔定理的三个条件缺少其中任何一个条件定

微分中值定理

导，由 Lagrange 中值定理，
f
(
x) x
f (x0 x0
)
=(x0+
(xx0))
， (0,1).
因为(x0+)存在，且当 x→x0+时，x0+ (xx0)→x0+，
limx x0来自f (x) xf (x0 ) = lim
x0
x x0
(x0+ (xx0))=(x0+)，
f 在 x0 点右可导且+(x0)=(x0+) .
+(x0)与(x0+)本是两个完全不同的概念，在一定条
件下，两者有密切的联系
2 ax x2, x 0 f (x)
sin x b, x 0
确定a、b的值使函数在点x=o处连续且可导
书上第64页
设 f 为[a,b]上的非常值函数.
f在[a,b]上连续，最小值m与最大值M. 中至少有一个
不在端点取到, 在内点取到。
故由Fermat定理得()=0 .
尽管 Rolle 定理的三个条件显然是其结论的充分条件，但是这些条件又缺一不可，试各举一例说明之.
验证 f (x) x2 2x 3在1,3
证明：“必要性”. 显然成立. “充分性”. 取定 x0I，则xI (0,1):
(x)=f(x0)+(x0+ (xx0))(xx0)=f(x0)，
设函数 f, g 均在区间 I 上可导，且(x)g(x)，则存在常数 c 使得(x)g(x)+c.
F(x) f (x) g(x)
证明 f (x) ln(x 1 x2 )在(, )上严格单调增
Lagrange 中值定理还有如下表示形式：

高等数学第一节微分中值定理

f ( x )
1 1 x
2

1 1 x
2
0
在 ( 1, 1 ) 内成立 .
所以 f ( x ) 在 ( 1, 1 ) 内取常数 c .
又 f (0) arcsin 0 arccos0 0 , 所以 c . 2 2 2 又 f ( 1) , 2 2 f ( 1) 0 . 2 2
2 2 为求 , 需解方程 cos x 2 . 1 sin x 2
9
设 y x, 2 y y 2 sin cos cos x sin y 2 2 cot y 2 . 则 2 2 1 sin x 1 cos y 2 sin 2 y 2 y tan 1 , y 2 arc tan 1 , 2 2 2 x y 2 arc tan 1 . 2 2 2 0 2 1 1 , 0 arctan 1 , 2 4 x 2 arc tan 1 0 , . 2 2 2 因此 , 取 2 arc tan 1 0 , . 2 2 2 ( ) ( 0) ( ) 2 确能使 ) (0) 成立 . 10 ( ) ( 2
使
或
y f (b) f (a ) f ( ) , ba f (b) f (a ) f ( ) (b a ) .
f (b) f (a ) 注 . 1. 弦的斜率 k . ba
2 . 若令 f (a ) f (b) ,
o
a

b
xБайду номын сангаас

【高数-微积分课件】4.1 微分中值定理(1)

练习证明 arctan x arccot x , x ( , )
2
应用拉格朗日中值定理证明不等式的步骤
1.由不等式选择恰当的f ( x)和区间[a,b] 2. f ( x)在[a,b]上使用拉氏定理.
3.由的介值性推出不等式.
例证明对任何常数 x1, x2, 恒有 | sin x1 sin x2 || x1 x2 | .
F(x)
f
(x)

f
(a)

f
(b) b

f a
(a)
(x

a)
容易验证 F ( x) 在 [a,b] 上满足罗尔中值定理的条件,
由罗尔中值定理可得
必存在 (a,b) 使得 F ( ) 0, 即
f ( ) f (b) f (a)
ba 由于拉格朗日中值定理的一般性, 我们常称其为微分中值定理.
例2 设 f ( x) 在 (a , b)内二阶可导, 若 f ( x) 0, x (a , b), 则 f ( x) 在 (a , b)内至多有一个驻点. 证明若 f ( x)在(a,b)内有两个驻点 x1, x2 , x1 x2 , 则
f ( x1) f ( x2 ) 0 又由 f (x) 在 (a , b)内二阶可导知 f (x) 可导,
但 f ( x) 3( x2 1) 0, ( x (0,1)) 矛盾, 假设不成立.
x1为方程f ( x) 0唯一的小于1的正实根.
例1 证明方程 sin x x cos x 0 在 (0, π)内必有实根. 证明由于 sin x x cos x 是 x sin x 的导函数, 考虑函数 F( x) x sin x, x [0, π]

中值定理(三步教学)

中值定理应用一．相关定理中值定理的本质其实是一组定理的总和，主要是围绕函数，零点，导函数之间的一些关系来展开，下面介绍最常用的7个定理[][]()μεεμ=∈≤≤≤≤f b a M m M x f m b a x f 使得必存在一点时当上连续在介值定理：设,,)(,,)( ()0)(,,0)()(=∈<•εεf b a b f a f 使得存在零点定理：当 0)(')(00=x f x x f 则有处满足可导且取极值，在费马定理：设[]()0)('),()()(,,)(=∈=εεf b a b f a f b a b a x f 使得则存在一点内可导且有上连续，开区间满足在闭区间罗尔定理：设[]())(')()()(),(,,)(εεf a b a f b f b a b a b a x f −=−∈使得则存在一点内可导上连续，开区间满足在闭区间拉格朗日中值定理：设[]())(')(')()()()(),(0)(',,)(),(εεεg f a g b g a f b f b a x g b a b a x g x f =−−∈≠使得则存在一点内可导且上连续，开区间满足在闭区间柯西中值定理：设之间介于均有域内的任一点阶导数存在，则对该邻的某个邻域内在点泰勒公式：010)1(00)(0000,,)()!1()())((!1))((')()(,1)(x x x x n f x x x f n x x x f x f x f x n x x f n n nn εε++−++−+−+=+ 二．具体使用步骤（定区间，定函数，定数值）第一步：确定做题的区间第二步：确定辅助函数及定理第三步：确定特殊点或条件隐含点处的函数值三．题目分析技巧用于找0)(=c f ：常用零点定理用于找0)('=c f ：常用费马定理，罗尔定理，导函数的零点定理用于找的关系和'f f ，或者题目出现)()(a f b f −：常用拉格朗日中值定理涉及到函数二阶导：常用泰勒公式涉及到之间的关系两个函数之间和',',g f g f ：柯西中值定理学四．具体例题分析[]⎰=−<xdt t f x x f x f 0)1,0(1)(21)(,1,0)(1.内有且仅有一个实根在证明：且上连续在设解：分析题目可以看到，要证明有实根，可以运用零点定理，而证明仅有一个实根，则需要判断函数的单调性。

微分中值定理与导数的应用课件

x
ex x
,
0
.
29
第30页/共112页
例6
tan x lim x tan3x
证设 f (t) ln(1 t),
f (t)在[0, x]上满足拉格朗日定理的条件,
f ( x) f (0) f ()(x 0), (0 x)
f (0) 0, f ( x) 1 , 由上式得 1 x
ln(1 x) x , 1
又0 x
111 x
1 1 1, 1 x 1
(2) 若 M m. f (a) f (b),
最值不可能同时在端点取得. 设 M f (a),
则 (a, b)，使 f ( ) M .
由费马引理,
f ( ) 0 .
5
第6页/共112页
注意：如果定理的三个条件有一个不满足，则定理的结论就可能不成立。
y
y
y
B
A
B
A
B
A
aO
bx a O c bx a O
而 f (0) , 且 f (1) f (1) ,
2
2
故 f ( x) , x 1,1 .
2
类似可得： arctan x arccot x , x R .
2 15
第16页/共112页
利用拉格朗日定理可证明不等式.
例5 证明： 1 ln b 罗尔(Rolle)定理如果函数yf(x)满足条件：(1)在闭区间[a, b]上连续，(2)在开区间(a, b)内可
导，(3) f(a)f(b)，则至少存在一点(a, b)，使得f () 0。
几何解释:
如果连续光滑的曲线 yf(x) 在端点 A、B 处的纵坐标相等。那么，在曲线弧上至少有一点

中值定理和洛必达法则

(ln x)
x 1
lim
x 1
1 x
1，
故此极限属于 0 型 .由洛必达法则Ⅰ得 0
ln x
(ln x)
lim
x 1
x
1
lim
x 1
x
1
1.
中值定理和洛必达法则
例4
解
属于 0 型，用洛必达法则Ⅰ得 0
原式 lim (ex cos x) lim ex sin x .
x0
x2
x0 2x
x
x2
lim
x0
3x2
1. 3
注意:
计算极限时，也可以将洛必达法则 I 和等价无穷小结合起来使用，以便简化计算. 该题用了两次等价无穷小代换，用了一次洛必达法则Ⅰ.
中值定理和洛必达法则
例6
解
原式 lim 1 e x0 x
2e2x ex 3x 1
lim
x0
x2
2e2x ex 3x 1
注意:
根据洛必达法则Ⅰ，求导后的结果可以是有限数A，也可以是，或 .
中值定理和洛必达法则
例5
解
属于 0 型，先将分母中的sin x用等价无穷小进行代换，原式变为lim x
0
x0
tan x x3
，然后
再使用洛必达法则Ⅰ进行求解，有
原式
1 sec2
lim
x0
3x2
x
lim
x0
tan2 3x2
经济数学
中值定理和洛必达法则
1.1 中值定理
引例
在区间 a ，b内可导函数y f (x)的图像如图3 1所示，它
是一条光滑的曲线.这条曲线的两个端点A、B的纵坐标相等，即

中值定理课件

( ) 0,
例 5 设 f ( x) 在 [a,b] 上连续, 在 (a,b) 内可导,
且 f (a) f (b) 0.
证明: 存在 (a,b), 使 f ( ) f ( ) 成立.
证
( x) f ( x)e x f ( x)e x ,
因此, 在 (a,b) 内至少存在一点 (a,b), 使
证因 f (a) f (b) 0, 故 f (a) 和 f (b) 同号, 不妨设 f (a) 0, f (b) 0. 又因为 f (a) f (c) 0, 所以 f (c) 0. 在 [a,c]和 [c,b] 上 f ( x) 连续, 由于 f (a) 和 f (c) 异号, f (c) 和 f (b) 异号, 所以, 至少存在一点 x1 (a,c), 使 f ( x1) 0;
x) x
f ( x0 )
0;
当
x
0
时， f ( x0
x) x
f
( x0 )
0.
由极限的保号性，
费马引理
证不妨设 x U( x0 )时，f ( x) f ( x0 ).
则对 x0 x U( x0 ), 有 f ( x0 x) f ( x0 ),
从而当 x 0
时，lxim0
f ( x0 x) x
(2, 3) 内.
完
例 3 证明方程 x 5 5 x 1 0 有且仅有一个小于
1的正实根.
证设 f ( x) x 5 5x 1 1, 则 f ( x) 在 [0,1]上连续, 且 f (0) 1, f (1) 3. 由介值定理, 存在
x0 (0,1), 使 f ( x0 ) 0,
则对 x0 x U( x0 ), 有 f ( x0 x) f ( x0 ),

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

' ( ' (
) )
几何解释:
在曲线弧AB上至少有一
点C(F ( ), f ( )),在该点
处的切线平行于弦 AB.
证1 作辅助函数
Y
CM
N
A
F(x)
o F(a) F(1)
X F(x)

Y

f
(x)
B
D
X F(2 )F (b)
(x) f (x) f (a) f (b) f (a) [F (x) F (a)].
二、试证明对函数 y px 2 qx r 应用拉氏中值定理
时所求得的点总是位于区间的正中间 . 三、证明等式arcsin 1 x2 arctan x
1 x2 2 ( x (0,1) ) . 四、设a b 0，n 1，证明
nb n1 (a b) a n b n na n1 (a b) .
证设 f (x) x5 5x 1, 则 f (x)在[0,1]连续, 且 f (0) 1, f (1) 3，异号由介值定理 x0 (0,1),使 f (x0 ) 0. 即为方程的小于1的正实根. 设另有 x1 (0,1), x1 x0, 使 f (x1) 0. f (x) 在 x0, x1 之间满罗尔定理的条件,
xn
f (n) (x)，（0
n!
1）.
七、设 f (x)在[a,b]内上连续，在(a,b)内可导，若
0 a b,则在(a,b)内存在一点，使
af (b) bf (a) [ f ( ) f ( )](a b)] .
点C , 在该点处的切线是
水平的.
o a 1
y f (x)
2 b x
证 f (x) 在 [a,b] 连续, 必有最大值 M 和最小值 m.
(1) 若 M m. 则 f (x) M .
由此得 f (x) 0. (a,b), 都有 f ( ) 0.
(2) 若 M m. f (a) f (b), 最值不可能同时在端点取得.
f (b) f (a) f '( )(b a) 拉格朗日中值公式
注意：
与罗尔定理相比条件中去掉了 f (a) f (b).
结论亦可写成 f (b) f (a) f ( ).
ba
几何解释:
在曲线弧 AB 上至少有一点 C,在该点处的切线平行于弦 AB.
y
C
y f (x)
∴由Rolle定理，至少存在ξ∈(a,b)，使得
g’(ξ)=0 ∴ f’(ξ)/F’(ξ)=[f(b)-f(a)]/[F(b)-F(a)]
例4 设函数f (x)在[0,1]上连续,在(0,1)内可导,证明: 至少存在一点 (0,1),使 f ( ) 2[ f (1) f (0)].
当 F (x) x, F(b) F(a) b a, F(x) 1,
f (b) f (a) f ( ) F (b) F (a) F( )
f (b) f (a) f ( ).
ba
证2 设g(x)=f(x)-[f(b)-f(a)]/[F(b)-F(a)]*F(x) 显然，g(x)在[a, b]上连续，(a, b)内可导且g(a)=g(b)
五、证明下列不等式：
1、 arctan a arctan b a b ；
2、当x 1时，e x ex .
六、设函数 y f ( x)在 x 0的某邻域内且有n阶导数，
且 f (0) f (0) f (n1) (0)试用柯西中值定理
证明：
f (x)
那末 f (x) 在区间 I 上是一个常数 .
例2 证明arcsin x arccos x (1 x 1).
2
证设 f (x) arcsin x arccos x,x [1,1]
f (x)
1 ( 1 x2
1 1
x2
)

0.
f (x) C,x [1,1]
即 f ( ) 2[ f (1) f (0)].
四、小结
罗尔定理、拉格朗日中值定理及柯西中值定理之间的关系；
Rolle f (a) f (b) Lagrange F(x) x Cauchy
定理
中值定理
中值定理
注意定理成立的条件；注意利用中值定理证明等式与不等式的步骤.
思考题
例如, y x , x [2,2];
在 [2,2] 上除 f (0) 不存在外,满足罗尔定理的一切条件, 但在区间[-2，2]内找不到一点能
使 f (x) 0.
又例如,
y

1 0,x
x,
x 0

(0,1] ;
y x, x [0,1].
例1 证明方程 x5 5x 1 0 有且仅有一个小于 1的正实根.
试举例说明拉格朗日中值定理的条件缺一不可.
思考题解答
x2, 0 x 1
f1(
x)

3,
x1
不满足在闭区间上连续的条件；
f2(
x)

1 x
,
x [a,b]
且 ab 0
不满足在开区间内可微的条件；
以上两个都可说明问题.
练习题
一、填空题： 1、函数 f ( x) x 4在区间[1,2]上满足拉格朗日中值定理，则ξ =_______. 2、设 f ( x) ( x 1)( x 2)( x 3)( x 4) ，方程 f ( x) 0有____________个根，它们分别在区间 _____________上. 3、罗尔定理与拉格朗日定理之间的关系是 _________________. 4、微分中值定理精确地表达函数在一个区间上的 _______与函数在这区间内某点处的_______之间的关系. 5、如果函数 f ( x)在区间 I 上的导数__________，那么 f (x)在区间 I 上是一个常数.
x

f( )

lim
x0
f
(

x) x

f
( )

0;
f( )

lim
x0
f
(

x) x

f
( )

0;
f ( )存在, f( ) f( ). 只有 f ( ) 0.
注意:若罗尔定理的三个条件中有一个不满足,其结论可能不成立.
第一节中值定理
一、罗尔中值定理二、拉格朗日中值定理三、柯西中值定理四、小结
一、罗尔(Rolle)定理
罗尔(Rolle)定理若函数f(x) （1）在闭区间[a,b]上连续；（2）在开区间(a,b)内可导；（3）在区间端点的函数值相等，即f(a)=f(b). 则在(a,b)内至少存在一点ξ(a<ξ<b)，使f’(ξ)=0.
三、柯西(Cauchy)中值定理
柯西(Cauchy)定理
若函数f(x)及F(x)
（1）在闭区间[a,b]上连续；
（2）在开区间(a,b)内可导；
（3）F(x)在(a,b)内每一点处的导数均不为0.
则在(a,b)内至少存在一点ξ(a<ξ<b)，使得
f F
(b) (b)

f (a) F (a)

f F
F(x) 满足罗尔定理的条件,
则在(a,b)内至少存在一点 ,使得 F( ) 0.
即 f ( ) f (b) f (a) 0
ba
或 f (b) f (a) f ( )(b a).
证2 设F(x)=f(x)-[f(b)-f(a)]/(b-a)*x 显然，F(x)在[a, b]上连续，(a, b)内可导且F(a)=F(b)
f (x) f (0) f ( )(x 0), (0 x)

f
(0)

0,
f
(
x)

1
1
x
,由上式得
ln(1

x)

1
x

,
又0 x 1 1 1 x 1 1 1, 1 x 1
x x x,
1 x 1
即 x ln(1 x) x. 1 x
分析: 结论可变形为
f (1) f (0) 1 0
f ( ) 2

f (x) (x2 )
x .
证设 g(x) x2,
则 f (x), g(x) 在[0,1]上满足柯西中值定理的条件,
在(0,1)内至少存在一点 ,有
f (1) f (0) 1 0
f ( ) 2
M
B
A
N
D
o a 1 x
2 b
x
分析1:
条件中与罗尔定理相差 f (a) f (b).
弦AB方程为 y f (a) f (b) f (a) (x a).
ba 曲线 f (x) 减去弦 AB, 所得曲线a,b两端点的函数值相等.
证1 作辅助函数
F (x) f (x) [ f (a) f (b) f (a) (x a)]. ba
至少存在一个 (在 x0, x1 之间),使得 f ( ) 0.
但 f (x) 5(x4 1) 0, (x (0,1)) 矛盾,
为唯一实根.
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)定理若函数f(x) （1）在闭区间[a,b]上连续；（2）在开区间(a,b)内可导. 则在(a,b)内至少存在一点ξ(a<ξ<b)，使得