中值定理和导数的应用.ppt.ppt
合集下载
3_1 微分中值定理与导数应用

第一节 微分中值定理与导数应用
罗尔(Rolle)定理 罗尔( ) 设函数 f ( x ) 满足条件: 满足条件: (1) f ( x )在闭区间[a , b] 上连续; 上连续; (2) 内可导; f ( x ) 在开区间 ( a , b ) 内可导; (3) 在区间端点的函数值相等,即 f (a ) = f (b ), 在区间端点的函数值相等, 那末在 ( a , b ) 内至少有一点ξ ( a < ξ < b ), 使得函数 在该点的导数等于零, f ( x ) 在该点的导数等于零,即
利用泰勒公式证明不等式
上二阶可导, 例1 设函数 y = f ( x ) 在区间 [0,1]0, max f ( x ) = 2, 证明在 证明在(0,1)至少存在一 至少存在一
0 ≤ x ≤1
点 ξ , 使得 f ′′(ξ ) ≤ −16. 证
0 ≤ x ≤1
矛盾, 但 f ′( x ) = 5( x 4 − 1) < 0, ( x ∈ (0,1)) 矛盾,∴ 为唯一实根 .
拉格朗日(Lagrange)中值定理 拉格朗日(Lagrange)中值定理 (Lagrange)
如果函数f 满足下列条件 如果函数 (x)满足下列条件 (1) 在闭区间 b]上连续; 在闭区间[a, 上连续 上连续; (2)在开区间(a, b)内可导; )在开区间( )内可导; 那末在(a , b ) 内至少有一点ξ ( a < ξ < b ), 使等式 f ( b ) − f (a ) = f ′(ξ )(b − a ) 成立. 成立.
即
f ′(ξ ) = 2ξ [ f (1) − f ( 0)].
泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
罗尔(Rolle)定理 罗尔( ) 设函数 f ( x ) 满足条件: 满足条件: (1) f ( x )在闭区间[a , b] 上连续; 上连续; (2) 内可导; f ( x ) 在开区间 ( a , b ) 内可导; (3) 在区间端点的函数值相等,即 f (a ) = f (b ), 在区间端点的函数值相等, 那末在 ( a , b ) 内至少有一点ξ ( a < ξ < b ), 使得函数 在该点的导数等于零, f ( x ) 在该点的导数等于零,即
利用泰勒公式证明不等式
上二阶可导, 例1 设函数 y = f ( x ) 在区间 [0,1]0, max f ( x ) = 2, 证明在 证明在(0,1)至少存在一 至少存在一
0 ≤ x ≤1
点 ξ , 使得 f ′′(ξ ) ≤ −16. 证
0 ≤ x ≤1
矛盾, 但 f ′( x ) = 5( x 4 − 1) < 0, ( x ∈ (0,1)) 矛盾,∴ 为唯一实根 .
拉格朗日(Lagrange)中值定理 拉格朗日(Lagrange)中值定理 (Lagrange)
如果函数f 满足下列条件 如果函数 (x)满足下列条件 (1) 在闭区间 b]上连续; 在闭区间[a, 上连续 上连续; (2)在开区间(a, b)内可导; )在开区间( )内可导; 那末在(a , b ) 内至少有一点ξ ( a < ξ < b ), 使等式 f ( b ) − f (a ) = f ′(ξ )(b − a ) 成立. 成立.
即
f ′(ξ ) = 2ξ [ f (1) − f ( 0)].
泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 (Taylor)
第3章微分中值定理与导数的应用第一节-PPT精选文档

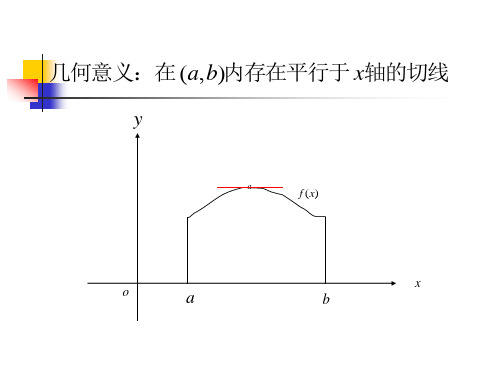
几何意义:
在曲线弧 至少有一点 该点处的切线平 行于弦 AB .
O y C1 y=f(x) C2 A a B
AB 上 C ,在
h
b
x
证明
作辅助函数
f ( b ) f ( a ) F ( x ) f ( x ) ( x a ) , b a
容 易 验 证 ,F 足 罗 尔 定 理 的 条 件 , (x)满
2. 罗尔(Rolle)定理
如果函数 yf(x) 满足条件: (1) 在闭区间 [a, b] 上 连续,(2)在开区间(a, b)内可导,(3) f(a)f(b),则至少 存在一点(a, b),使得f () 0。 几何解释:
如果连续光滑的曲线 yf(x) 在端点 A、B 处的 纵坐标相等。那么,在 曲线弧上至少有一点 C( , f()),曲线在 C点 的切线平行于 x 轴。 y A C yf(x) B
于是 a, b ,使
即
f ( b ) f ( a ) F ( ) f ( ) 0 , b a f (b) f (a) f ( ) . ba
例3
, 在 上 满 足 拉 格 朗 日 定 理 的 条 件 , f ( x ) ln x [ 1 , e]
f(x)不满足条件(1)
f(x)不满足条件(2)
f(x)不满足条件(3)
例1
f(x )sin x ,
在 上 连 续 , 内 可 导 , [ 0 ,] () f ( ) 0 ,
验证
f ( ) 0 , (0, ) . f (x ) cos x , 2 2
1 f ( x ) , x
f(e ) f( 1 ) 1 , e1 e1
e 1 ( 1 , e, )
在曲线弧 至少有一点 该点处的切线平 行于弦 AB .
O y C1 y=f(x) C2 A a B
AB 上 C ,在
h
b
x
证明
作辅助函数
f ( b ) f ( a ) F ( x ) f ( x ) ( x a ) , b a
容 易 验 证 ,F 足 罗 尔 定 理 的 条 件 , (x)满
2. 罗尔(Rolle)定理
如果函数 yf(x) 满足条件: (1) 在闭区间 [a, b] 上 连续,(2)在开区间(a, b)内可导,(3) f(a)f(b),则至少 存在一点(a, b),使得f () 0。 几何解释:
如果连续光滑的曲线 yf(x) 在端点 A、B 处的 纵坐标相等。那么,在 曲线弧上至少有一点 C( , f()),曲线在 C点 的切线平行于 x 轴。 y A C yf(x) B
于是 a, b ,使
即
f ( b ) f ( a ) F ( ) f ( ) 0 , b a f (b) f (a) f ( ) . ba
例3
, 在 上 满 足 拉 格 朗 日 定 理 的 条 件 , f ( x ) ln x [ 1 , e]
f(x)不满足条件(1)
f(x)不满足条件(2)
f(x)不满足条件(3)
例1
f(x )sin x ,
在 上 连 续 , 内 可 导 , [ 0 ,] () f ( ) 0 ,
验证
f ( ) 0 , (0, ) . f (x ) cos x , 2 2
1 f ( x ) , x
f(e ) f( 1 ) 1 , e1 e1
e 1 ( 1 , e, )
§3.1-微分中值定理PPT课件

1 x2
1 x2
f ( x) C , x [1,1]
又 f (0) arcsin 0 arccos 0 0 ,
即
C
.
arcsin
x
arccos
x
2
.
2
2
2
说明 欲证x I , f ( x) C0 ,只需证在 I上
f ( x) 0,且 x0 自证 arctan x arc
则在开区间 (a, b)内至少存在一点 ,使得 f (b) f (a) f ( ) F (b) F (a) F ( )
广义微分中值定理
20
微分中值定理
柯西(1789 – 1857)
法国数学家, 他对数学的贡献主要集中 在微积分学, 复变函数和微分方程方面 . 一生发表论文800余篇, 著书 7 本 ,《柯 西全集》共有 27 卷. 其中最重要的的是为巴黎综合学 校编写的《分析教程》,《无穷小分析概论》, 《微积 分在几何上的应用》 等, 有思想有创建, 对数学的影 响广泛而深远 . 他是经典分析的奠人之一, 他为微积分 所奠定的基础推动了分析的发展.
0
由条件,则 f ( x1 ) f ( x2 ), 即在区间I中任意两
点的函数值都相等,所以, f ( x) C.
17
微分中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x0) arcsin x0 arccos 0x, x [1,1]
f ( x) 1 ( 1 ) 0.由推论
f (1) 0 f (2) (2) 结论正确
方程f ( x) 0, 即3x2 8x 7 0有实根
x1
1 (4 3
37),
第三章中值定理与导数的应用课件
那么在(a,b)内至少有一点 使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
函数旳极大值与极小值统称为极值,使函数取得 极值旳点称为极值点.
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
第三章微分中值定理与导数应用第一节微分中值定理

f (b) f (a) f ( ) g(b) g(a) g( )
f (b) f (a) f ( ).
ba
例4 设函数f ( x)在[0,1]上连续, 在(0,1)内可导, 证明 :
至少存在一点 (0,1), 使 f ( ) 2[ f (1) f (0)].
则在(a, b)内至少存在一点, 使得 () 0.
即 f ( ) f (b) f (a) g( ) 0,
g(b) g(a)
f (b) f (a) f ( ) . g(b) g(a) g( )
当 g( x) x, g(b) g(a) b a, g( x) 1,
拉格朗了函数在一个区间 上的增量与函数在这区间内某点处的导数之间的关系.
定理 若函数 f ( x)在区间I 内的导数恒
等于零, 则在区间I 内,f ( x)恒为常量.
证 任取x1, x2 I , 由(1) 式知
f ( x2 ) f ( x1 ) f ( )( x2 x1 ) , 在x1, x2 之 间.
设 另有 x1 (0, 2), x1 x0 , 使 f ( x1 ) 0.
f ( x) 在 x0, x1 之间满足罗尔定理的条件,
至少存在一个 (在 x0, x1 之间),使得 f () 0. 但 f ( x) 5x4 1 0 x (0, 2) 矛盾, 为唯一实根.
那么在(a, b)内至少有一点(a b),使得函数 f ( x)在该点的导数等于零,
即 f '() 0
例如 f ( x) x2 2x 3
( x 3)(x 1). 在[1,3]上连续, 在(1,3)上可导, 且 f (1) f (3) 0, f (x) 2(x 1),
高中物理课件-第三章-微分中值定理、导数的应用

lim x3 1 . x x 1
一、 0 0 型不定式 定理:设函数 f (x) 与 F (x) 满足:
0
(1)在点 a 的某去心邻域U (a) 内可导且 F(x) 0;
(2)
lim
xa
f
(x)
0,
lim
x a
F ( x)
0;
f (x)
(3)
lim
xa
F
(
x)
存在(或
).
则
lim
xa
f F
(x) (x)
提示: f (2) f (1) f (0) f (1) 0, 且 f (x) 在三个区间 [2,1], [1,0] 和[0,1] 上都满足 Rolle 定理的条件.
在 (2,1), (1,0), (0,1) 内分别至少存在一点1, 2, 3 使 f (1) 0, f (2) 0, f (3 ) 0 .即 f (x) 0 至少有三个实根.
F( )
f
( ) 2
f
( )
由 F ( ) 0 得 f ( ) f ( ).
【例】设 f (x) 在[a,b]上连续,在(a, b) 内可导且 f (a) f (b) 0,
证明:在(a,b) 内至少存在一点 使 f ( ) f ( ). 提示:令 F(x) ex f (x) ,可验证 F (x) 在[a,b] 上满足 Rolle
g(x) 0, f (a) f (b) g(a) g(b) 0.
证明:(1)在(a,b)内 g(x) 0;
(2)在(a,b)内至少存在一点, 使得
f ( ) g( )
f ( ) . g( )
提示:(1)假设c (a,b) 使 g(c) 0, 则由 Rolle 定理,
微分中值定理与导数应用.ppt

拉格朗日中值公式又称有限增量公式. 拉格朗日中值定理又称有限增量定理.
定理 如果函数 f (x) 在区间 I 上的导数恒为零, 那末 f (x) 在区间 I 上是一个常数.
第一节 中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x) arcsin x arccos x, x [1,1]
f (b) F (b)
f (a) F (a)
f '( F '(
). )
第一节 中值定理
证: 作辅助函数
( x) f ( x) f (a) f (b) f (a) [F ( x) F (a)]. F(b) F(a)
( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 () 0.
弦AB方程为 y f (a) f (b) f (a) ( x a).
ba 曲线 f ( x) 减去弦 AB,
所得曲线a, b两端点的函数值相等.
第一节 中值定理
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 F () 0. 即 f () f (b) f (a) 0
y f (x)
2 b x
第一节 中值定理
第一节 中值定理
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)满足
(1)在闭区间[a, b]上连续; (2)在开区间(a, b) 内可导; 那么在(a, b)内至少有一点(a b) ,使得
f (b) f (a) f ' ()(b a) .
定理 如果函数 f (x) 在区间 I 上的导数恒为零, 那末 f (x) 在区间 I 上是一个常数.
第一节 中值定理
例2 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x) arcsin x arccos x, x [1,1]
f (b) F (b)
f (a) F (a)
f '( F '(
). )
第一节 中值定理
证: 作辅助函数
( x) f ( x) f (a) f (b) f (a) [F ( x) F (a)]. F(b) F(a)
( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 () 0.
弦AB方程为 y f (a) f (b) f (a) ( x a).
ba 曲线 f ( x) 减去弦 AB,
所得曲线a, b两端点的函数值相等.
第一节 中值定理
作辅助函数
F ( x) f ( x) [ f (a) f (b) f (a) ( x a)]. ba
F( x) 满足罗尔定理的条件, 则在(a, b)内至少存在一点,使得 F () 0. 即 f () f (b) f (a) 0
y f (x)
2 b x
第一节 中值定理
第一节 中值定理
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 如果函数 f(x)满足
(1)在闭区间[a, b]上连续; (2)在开区间(a, b) 内可导; 那么在(a, b)内至少有一点(a b) ,使得
f (b) f (a) f ' ()(b a) .
