介质波导色散
西北工业大学_光纤通信作业答案

答案第一章:光纤通信1、什么是光纤通信?光纤通信及系统的组成光纤通信使用光导纤维作为传输光波信号的通信方式。
光纤通信系统通常由电发射机、光发射机、光接收机、电接收机和由光纤构成的光缆等组成。
2、什么事光通信光通信就是以光波为载波的通信。
3、光纤通信的优点?①传输频带宽,通信容量大。
②传输衰减小,传输距离长。
③抗电磁干扰,传输质量好。
④体积小、重量轻、便于施工。
⑤原材料丰富,节约有色金属,有利于环保4、光纤通信的工作波长?光源:近红外区波长:0.8—1.8μm频率:167—375THz5、WDM是指什么?DWDM指什么?WDM:波分复用DWDM:密集波分复用6、光纤从材料上可以分为哪几种?从材料上分为石英光纤、多组份玻璃光纤、氟化物光纤、塑料光纤等7、光纤活动连接器从连接方式来看分为哪几种?常见的插针端面有哪几种?PC、APC、SPC(球面、斜面、超级抛光端面呈球面的物理接触)8、按缆芯结构分,光缆分为哪几种?层绞式、单位式、骨架式、带状式9、光线的制造分哪几个步骤?I 材料准备与提纯II 制棒III 拉丝、涂覆IV 塑套其中制棒分为:(1)MCVD改进的化学气相沉淀法(2)PCVD等离子化学气相沉淀法10、按材料光纤分几种?同611、无源器件的种类连接器、分路器与耦合器、衰减器、隔离器、滤波器、波分复用器、光开关和调制器等第二章:光纤通信的物理学基础1、通过哪些现象可以证明光具有波动性?光的波动性可以从光的干涉、光的衍射和光的偏振等现象证明2、什么叫光电效应?光电效应具有哪些试验规律?由于光的照射使电子从金属中溢出的现象称为光电效应⑴ 每种金属都有一个确定的截止频率γ0,当入射光的频率低于γ0 时,不论入射光多强,照射时间多长,都不能从金属中释放出电子。
⑵ 对于频率高于γ0的入射光,从金属中释放出的电子的最大动能与入射光的强度无关,只与光的频率有关。
频率越高释放出的电子的动能就越大。
⑶ 对于频率高于γ0的入射光,即使入射光非常微弱,照射后也能立即释放出电子。
光纤色散的分类

光纤色散的分类光纤的色散主要由模式色散、材料色散和波导色散组成。
其中,材料色散与波导色散都与波长有关,所以又统称为波长色散。
模式色散在多模光纤中,传输的模式很多,不同的模式,其传输路径不同,所经过的路程就不同,达终点的时间也就不同,这就引起了脉冲的展宽。
对模式色散进行的严密分析比较复杂,这里仅作简单讨论。
我们知道,在同一根光纤中,高次模到达终点走的路程长,低次模走的路程短,这就意味着高次模到达终点需要的时间长,低次模到达点需要的时间短。
在同一条长度为的光纤上,最高次模与最低次模到达终点所用的时间差,就是这段光纤产生的脉冲展宽。
影响光纤时延差的因素有两个:纤芯-包层相对折射率差和光纤的长度。
光纤的时延差与纤芯-包层相对折射率差成正比。
其中是纤芯的折射率,是包层的折射率。
越大,时延差就会越大,光脉冲展宽也越大。
从减小光纤时延差的观点上看,希望较小为好,这种小的光纤称为弱导光纤。
通信用光纤都是弱导光纤。
另外,光纤越长,时延差也越大,色散也越大。
材料色散材料色散是由光纤材料自身特性造成的。
石英玻璃的折射率,严格来说,并不是一个固定的常数,而是对不同的传输波长有不同的值。
光纤通信实际上用的光源发出的光,并不是只有理想的单一波长,而是有一定的波谱宽度。
当光在折射率n的为介质中传播时,其速度v与空气中的光速C之间的关系为:v=C/n光的波长不同,折射率n就不同,光传输的速度也就不同。
因此,当把具有一定光谱宽度的光源发出的光脉冲射入光纤内传输时,光的传输速度将随光波长的不同而改变,到达终端时将产生时延差,从而引起脉冲波形展宽。
波导色散光纤的第三类色散是波导色散。
由于光纤的纤芯与包层的折射率差很小,因此在交界面产生全反射时,就可能有一部分光进入包层之内。
这部分光在包层内传输一定距离后,又可能回到纤芯中继续传输。
进入包层内的这部分光强的大小与光波长有关,这就相当于光传输路径长度随光波波长的不同而异。
把有一定波谱宽度的光源发出的光脉冲射入光纤后,由于不同波长的光传输路径不完全相同,所以到达终点的时间也不相同,从而出现脉冲展宽。
光波在介质波导中的传播

射线法是把波导中的波看作是均匀平面波在薄膜两个界 面上全反射而形成的,故界面Ⅰ、Ⅱ上的入射角应满足
sinIc n3/n1 sinIIc n2/n1
若 n2 n3 , 则取 sin IIc 为波导的临界角。
波动理论法则是把薄膜波导中的波看作是满足介质平板波导边 界条件的麦克斯韦方程组的解。此时,在波导的中间介质层中波以 行波传输,衬底和覆盖层中则是一种倏逝波,光波能量就是由介质 表面引导下在波导内传输的,此时所传输的波称之为导行波。若当 入射角小于临界角时,一部分能量由界面折射后不再回到介质n1中, 此时无法导行光波。这种波成为辐射波。
x
E z x
i
0
H
z
E y x
E x y
针对现在讨论的无穷大平板介质波导,考虑到y方向无限大,
场在该方向不受限制,因而可得 0 ; 又考虑到光是沿z向传输, y
沿该方向场的变化可用一个传输因子e ik z z 来表示。为了普适地讨论
电磁波在三层介质中的情况,记 为 k1z、k2z、k3z,表示实波矢
是同一频率,各模式的群速度也是不同的。 波导色散
为满足特征方程,对同一个m值即同一个波导模,不同的波长对应于 不同的入射角。这就是说,对于不同波长的光,即使没有材料色散存在, 但由于波导的谐振条件的要求,波在波导内经过一段距离传输后,将因 为入射角不同而具有不同的相位、出射角及出射波导的时间,因此将引
d2Ey
dx2
(n22k02
2)Ey(x) 0
x0,在衬底层n2
dd2xE2y (n32k02 2)Ey(x)0
xh,在覆盖层n3
按前面的分析我们已知,导波在z方向按 e i z 传播。而在横向,
电磁波在材料中的色散特性研究

电磁波在材料中的色散特性研究电磁波是一种波动形式的能量传播,具有特定的频率和波长。
它在不同的材料中传播时会受到材料的影响,呈现出特定的色散特性。
色散是指不同频率的电磁波在材料中传播的速度不同。
对于材料的色散特性的研究,不仅有助于加深我们对电磁波的理解,还在很多应用领域中有着重要的意义。
一、色散现象的原理在介质中传播的电磁波,受到介质分子和电荷的相互作用影响,形成了色散现象。
这种相互作用导致电磁波的传播速度随频率变化,从而使得不同频率的电磁波在材料中的传播路径不同,呈现出色散效应。
二、光的色散特性光是一种电磁波,因此也受到色散的影响。
光在不同的材料中传播时,由于材料的光学性质的差异,会产生不同程度的色散。
常见的光的色散现象包括折射率的频率相关性、不同波长的光在材料中的传播速度差异等。
以折射率的频率相关性为例,当光通过一种材料时,不同频率的光会呈现出不同的折射率。
折射率随频率的增加而减小,这种现象被称为正常色散;而随频率的增加折射率增大,则被称为反常色散。
这种色散现象在精密光学仪器设计中起到重要作用,可以根据材料的色散特性来优化光学系统的性能。
三、电磁波在微波领域的色散特性研究除了光的色散特性研究外,电磁波在微波领域的色散特性研究同样重要。
微波是一种具有较长波长的电磁波,对于材料的色散特性研究可以帮助我们更好地理解微波信号的传输和材料的电磁性能。
在微波领域的色散特性研究中,一个关键概念是复介电常数和复磁导率。
这两个参数描述了材料对电磁波的响应能力。
在不同频率下,复介电常数和复磁导率会发生变化,从而产生色散现象。
在微波频率下,常见的色散现象包括介质损耗、复折射率频率关系等。
介质损耗是指材料对微波信号的吸收能力,随频率增加而增加。
复折射率频率关系描述了不同频率下材料对微波信号的相位延迟。
四、色散特性的应用色散特性的研究不仅能够加深对电磁波在材料中传播行为的理解,还有着广泛的应用前景。
其中一项重要应用是光通信领域。
光纤的色散及降低色散的措施

(3.20)
它决定一阶群(速度)色散,称作色散参量,它是由于Vg 与 有关引起的(许多
书中称此参量为二阶色散,它是从 () 对 的二阶微商定义的,而从式 ()
v 看, 与相速度对 的二阶微商有关,因此称作二阶色散;但是从群速度看 与
群速度对 的一阶微商有关,因此称作一阶群色散)。第三项系数 为二阶群色散 (有些人称此为三阶色散,这是从相速度对频率的三阶微商而得名)。
反常色散: 0 , dVg 0 , D 0 d
(3.23b)
1.2 色散位移光纤(DSF)和非零色散位移光纤(NZ—DSF)
由于总色度色散是由材料色散和波导色散构成的, 材料色散基本不能改变,而波导色散是由波导结构尺寸 决定的,最简单的改变波导色散的办法就是改变芯径尺 寸。纤芯直径下降可使波导色散下降(数值更负),从而 总色散零点就可向长波长移动,这就是色散位移光纤 (DSF)。更复杂的波导结构,如多包层结构也可使色散 零点向长波长移动。 人们一度认为色散位移光纤是最理想的光纤,限制光纤传 输特性(比特率距离积 )的两大因素,衰减和色散在
6. 用单模光纤消除模式色散 单模光纤是在给定工作波长内只能传输单一基模的光纤。前面有关
阶跃折射率光纤的讨论中已经指出,当满足单模传输条件时,光纤中只 能传输 LP01模(即矢量模的 HE11 模),此种光纤即称作单模光纤。
为了满足单模传输条件(归一化频率V 2.40483),V 要足够小,即在 光纤材料(包括纤芯和包层材料)和工作波长一定的条件下,纤芯半径 a
由式(3.20)可进一步得到
d
d
(1/Vg )
1 Vg2
dVg
d
(3.21)
在光纤通信技术中常用色散系数 D 表示群色散,定义为:
第7讲_波在损耗介质中的传播、色散、群速

分析方法: 导电介质中电导率为有限值, 可用复数介电系数表示
ε j
2
电磁场与电磁波 · 第七讲 波在损耗介质中的传播,色散,群速 · 章献民
有耗介质(导电介质)用复介电系数表示的麦氏方程
对于电导率为的各向同性导体 安培全电流定律的微分形式为
jkz
)e jkz
其中
k [1 j
| | e j
1/ 2 ] kr jki
将复数形式的k、代入E、H表达式
E x0 E0e
E的瞬时值为 z方向传播的速度为
ki z jkr z
e
Ex E0e ki z cos(t kr z )
电磁场与电磁波 · 第七讲 波在损耗介质中的传播,色散,群速 · 章献民
11120010 电磁场与电磁波
波在损耗介质中的传播
章献民
zhangxm@ 2012年3月6日星期二
1
色散,群速
电磁场与电磁波 · 第七讲 波在损耗介质中的传播,色散,群速 · 章献民
有耗介质(导电Biblioteka 质)中的平面波 设传播的信号只含两个频率分量,一个比载波 ������������ 略高,另一个比 ������������ 略低,其瞬
E (t ) E0 cos(c d )t E0 cos(c d )t
此信号沿波导传播z 距离后,两个波的合成为
E ( z, t ) E0 cos[(c d)t (kzc dkz ) z] E0 cos[(c d)t (k zc dk z ) z]
5
电磁场与电磁波 · 第七讲 波在损耗介质中的传播,色散,群速 · 章献民
第4章-介质波导
Ae
be
e r
A
g
b
ar
x y z
a
n1 n2 plane l of f incidence i id
a e a cos e a r a cos r a g a cos g b e br bg b Poyntingvector S E H
2 n1 cos g 1 2 sin 2 e n2 Eg 2n1 cos e Ee n1 cos e n 2 cos g
rTE
2 2 2 Er n1 cos e n 2 n1 sin e 2 2 Ee n1 cos e n 2 2 n 1 sin e
r cs e e
e
e
cc r
导波模
两个界面处全内反射 nf > ns > nc
2ΦS
17
nc nf ns
h
z
nc
z=h
cc
s
c e
radiation mode
x
y n=0
nf
ns
e
h
cc
r
substrate mode
h
s
2ΦC
e
h
e
cc r
rcs e
1
4.1 光的反射和折射
TE-Wave
He Ee ke e r Hr Er kr
n1 < n2
He
ke
TM-Wave
kr Er
Hr
n1 n2
x y z
Ee
e r
n1 n2
g
Eg
Hg kg
g
2.2介质光波导中的色散
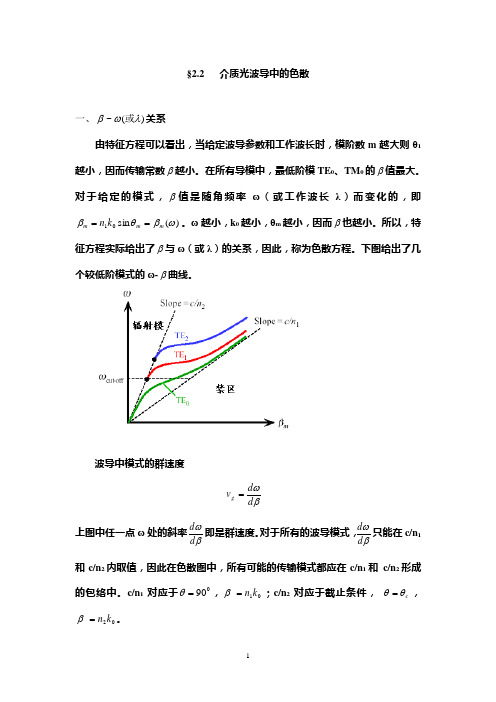
§2.2 介质光波导中的色散一、)(~λωβ或关系由特征方程可以看出,当给定波导参数和工作波长时,模阶数m 越大则θ1越小,因而传输常数β越小。
在所有导模中,最低阶模TE 0、TM 0的β值最大。
对于给定的模式,β值是随角频率ω(或工作波长λ)而变化的,即)(sin 01ωβθβm m m k n ==。
ω越小,k 0越小,θm 越小,因而β也越小。
所以,特征方程实际给出了β与ω(或λ)的关系,因此,称为色散方程。
下图给出了几个较低阶模式的ω-β曲线。
波导中模式的群速度βωd d v g = 上图中任一点ω处的斜率βωd d 即是群速度。
对于所有的波导模式,βωd d 只能在c/n 1和c/n 2内取值,因此在色散图中,所有可能的传输模式都应在c/n 1和 c/n 2形成的包络中。
c/n 1对应于090=θ,01k n =β;c/n 2对应于截止条件, c θθ=,02k n =β。
当光频率一定时,不同模式的光群速度不同。
当模式一定时,不同光频率的光群速度不同。
二、模式色散(intermodal dispersion )当波导中能够传输多个模式时,低阶模与高阶模的群速度不同。
最低阶模的群速度最小,接近于c/n 1,最高阶模的群速度最大。
这是因为高阶模渗透到包层中的能量较多,而包层的折射率小,因此传输快。
此现象称为模式色散(或模间色散)。
长距离传输时,将导致输出端的信号脉冲展宽。
脉冲展宽的大小取决于各个模式在波导中传输的时间差τ∆。
设传输距离为L ,模式色散量定义为g m a n g v Lv L -∆m i n =τ v gmin 是最慢模式的群速度,v gman 是最快模式的群速度。
估算:由上图,v gmin ≈ c/n 1,v gmax 不超过c/n 2,近似得传输单位长度的色散量 cn n L 21-≈∆τ n 1= 1.48, n 2= 1.46,km ns m s L /67/107.611=⨯≈∆-τ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
������������1 − ������������������������ ������������������������ − 1
(3.17) (3.18)
3.4 对称面1 2������
∙
1 ������������1 − ������������������������ ������������ + arctan ������������1 ∙
域的有效介电常数εeffi ,εeffo ,用下图所示的单层介质光波导去等效。习惯上用用������������������������ 表示 纵向传播常数:
������������������������ = (������������������������ )2
(4.1)
另 z 为纵向
kyi 2 = ������02εri − ������������ 2
2
jZ
2 1
tgk
z1l
0
Z0 Z1 1 tg 2k z1l jtgk z1l Z02 Z12 0
1 tg 2k z1l
jtgk
z1l
Z Z
0 1
Z1 Z0
0
Y0 jY1 tan k z1l Z0 jZ1 tan k z1l 0
两者的曲线,程序如下:
clear er1=12; eff=1:0.01:er1-0.01 l1=0.5/pi./sqrt(er1-eff).*atan(sqrt((er1-1)./(er1-eff))); l2=0.5/pi./sqrt(er1-eff).*(pi-atan(sqrt((er1-eff)./(er1-1)))); l3=0.5/pi./sqrt(er1-eff).*(pi-atan(1/er1*sqrt((er1-eff)./(er1-1)))); l4=0.5/pi./sqrt(er1-eff).*atan(er1*sqrt((er1-eff)./(er1-1))); plot(l1,eff); hold on plot(l2,eff,'r'); hold on plot(l3,eff,'g'); hold on plot(l4,eff,'k');
(4.5) (4.6) (4.7)
������g
������a ������g
+ +
j������g tan(kyg j������a tan(kyg
������g ) ������g )
+
������f
������s ������a
+ +
j������ftan(kyf ������f) j������stan(kyf ������f)
kzi k02ri kx2
(3.3) (3.4)
带入得到横向谐振条件:
Y0 jY1 tan kz1l 0
(3.5)
对于单层平板介质光波导,波限制在薄层中传播,kz1 是实数,kz0 是虚数,k1、k0 和 kx 满足 如下关系 :
此时对于 z >l 的区域 : 由 TE 模: 带入色散方程,得到: 引入有效介电常数定义: 上式成为:
4.2.3 最后利用 x 方向谐振:
这里应满足:
������o
+
������i
������o ������f
+ +
j������itan(kzo ω) j������itan(kzo ω)
=
0
(4.18)
4.2.4
k������i2 = ������02εeffi − ������������ 2
图1
二、平板介质波导的横向谐振原理
图2
横向谐振原理是分析介质波导的有效方法,以上图所以的非对称介质单层介质波导为例 证明,横向谐振包含限制在导模层中传播必要而充分的条件。
根据波导的传输线理论,z 方向波的传播可以用上图中的电路等效。在 z=0 处看进去输入阻 抗或输入导纳为 0,即:
Z0
Z1
Z0 Z1
(3.6) (3.7) (3.8) (3.9) (3.10) (3.11)
(3.12)
由: 带入上式得:
1
������0������ =
������������ + arctan ������������1 − ������������������������
������������������������ − 1 ������������1 − ������������������������
三、单层介质光波导色散特性曲线
3.1 以推导对称面开路为例: 由横向谐振条件:
Y Y 0
从 z=l 向右和向左看去的输入导纳为:
Y Y0 Y jY1 tan(kz1l)
(3.1)
(3.3) (3.2)
式中:
kzi Yi r0i0
kzi
TE模 TM模
(4.10) (4.11) (4.13)
4.2.2 外部区域有效介电常数������������������������������的计算
同样由 y 方向的横向谐振得到:
������s
+
������f
������a ������f
+ j������ftan(k������f������f) + j������a tan(kyf ������f)
带入方程得到:
������↑
=
������g
������a ������g
+ +
j������g tan j������a tan
kyg ������g kyg ������g
������↓
=
������f
������s ������a
+ +
j������f tan j������s tan
kyf ������f kyf ������f
对条形介质光波导的严格分析比平板介质光波导要苦难得多,业已发展了多种近似方法用于 条形介质光波导的分析。有效介电常数(EDC 法)就是比较成功的一种方法,不仅适用于介 质光波导,也适用于毫米波集成波导的分析。
4.2 EDC 法理论推导:
图5
用 EDC 法计算条形介质光波导的纵向波数时,先求条形介质光波导内部区域和外部区
=
0
同样需要满足:
定义: 各介质参量满足:
kyf > kxo > kz������、kz������ ε������������������������ = (k������x0o )2
kyi 2 = ������02εri − ������������������ 2
(4.14) (4.15) (4.16) (4.17)
3.3 对称面开路(TM 模)
������������������������ − 1 ������������1 − ������������������������
������′
=
1 2������
∙
1
1
������������1 − ������������������������ ������������ − arctan ������������1 ∙
=
0
(4.8)
由于波需要限制在薄层介质中传播,所以kzg 、kzf 为实数,而kz������ 、kz������应为虚数,要求满足
如下关系:
kyf = ������0 εrf > kxi > kz������ = ������0 εrs
(4.9)
定义: 此时,各参量应满足:
kyg = ������0 εrg > kxi > kz������ = ������0 εra ε������������������������ = (k������x0i )2 kyi 2 = ������02εri − ������������������ 2
������������������������ − 1 ������������1 − ������������������������
(3.19)
3.5 色散曲线仿真绘制 利用 MATLAB 绘制色散曲线时,我们可以从不同的������������������������ 得到不同的������′ 值,然后转而会出
最后得到:
Y0 jY1 tan kz1l 0
(2.2)
Z0 jZ1 tan kz1l 0
(2.3)
于是得到如下两种分布可能。一种是偶对称,对于电压来说,对称面(z=0)为波腹,相当 于开路;另一种是奇对称,对称面对于电压来说是波节,相当于短路。因此光沿对称结构的 单层平板介质波导的传播可以分为四种情况,即:对称面开路(TE 模),对称面开路(TM 模),对称面短路(TE 模),对称面短路(TM 模)。
得到图形如下:
图3 这样得到的额曲线有一个问题,因为有些 ������′ 的值超出了。所以我们对超过1的������′ 值舍去。最后 得到的色散曲线如下:
图4
四、条形介质光波导色散特性
4.1 综述:
对于平板介质光波导,光波限制在整个导模层中传播,而对下图所示的条形介质光波导, 光波主要限制在条形介质中传播,对光能的利用率大大提高。对于 x=0,a 侧面的不连续性
jZ1 2tgk z1l jZ 0 2tgk z1l
0
Z0 Z1 1 tg 2k z1l jZ0 2tgk z1l Z1 Z0 1 tg 2k z1l jZ1 2tgk z1l 0
