固体地球物理学概论第四章-02讲解
固体地球物理学概论Snell定律课件

固体地球物理学概论
第七章
弹性概念——应力 (续)
The stresses are symmetrical(对称的), i.e. only six components of the stress tensor p are independent because
P = - (pxx+ pyy+ pzz)/3 This is a general definition of the “pressure”. In the special case of a liquid at rest, pxx= pyy= pzz = - P, this is the hydrostatic pressure. In geology, lithostatic pressure is often estimated by using
When the material in the mantle is heated, it expands and becomes lighter. In spite of its high viscosity(粘性), it rises more or less vertically in some places, especially under the oceanic ridges. With its losing pressure and heat during traveling upward, the material is forced to travel horizontally. They drag the lithosphere motion.
固体物理学讲义4.1

第四章能带理论能带理论的出发点是固体中的电子不再束缚于个别原子,而是在整个固体内运动(这要求电子的平均自由程远大于晶格常数),称为共有化电子。
能带理论是近似理论。
由于固体中大量电子的运动是相互关联的,每个电子的运动受到其他电子和原子的影响,在如此大量粒子的多体系统严格求解是不可能的。
大多数情况下我们关心的是价电子的运动状态,在单原子结合成固体的过程中价电子的运动状态发生大的变化,而内层电子的变化较小,可以把内层电子和原子实近似看成离子实。
这样价电子的等效势场包括离子实的势场,其他价电子的平均势场以及电子波函数反对称性而带来的交换作用。
能带理论是单电子近似理论,即把每个电子的运动看成是独立的在一个等效势场中的运动。
单电子近似理论最早用于研究多电子原子,又称为哈特里(Hartree)-福克(κoΦ)自洽场方法。
把多体问题简化为单电子问题需要进行多次简化。
1、绝热近似:原子核或者离子实的质量比电子大的多,离子的运动速度慢,在讨论电子问题时可以认为离子是固定在瞬时位置上。
这样多种粒子的多体问题就简化为多电子问题;2、哈特里-福克自洽场方法:每个电子是在固定的离子势场以及其他电子的平静势场只运动;3、所有的离子势场和其他电子的平均场是周期性的势场。
对于三维的周期场中的单电子问题只能用各种近似方法求解。
通常选取某个布洛赫函数形式的集合作为完备的基本函数族,把晶体电子的波函数用此函数的集合展开,然后代入薛定谔方程,确定展开式的系数所满足的久期方程,据此求能量本征值,再依照逐个本征值确定波函数展开式的系数。
不同的方法仅在于选择不同的函数集合。
能带理论取得相当的成功,但也有他的局限性。
如过渡金属化合物的价电子迁移率较小,相应的自由程和晶格常数相当,这时不能把价电子看成共有化电子,周期场的描述失去意义,能带理论不再适用。
此外,长电子和晶格相互作用的强弱程度来看,在离子晶体中的电子的运动会引起周围晶格畸变,电子是带着这种畸变一起前进的,这些情况都不能简单看成周期场中单电子运动。
固体物理学第四章

0 CV exp 0 kBT
28
Einstein模型 金刚石热容量的实验数据
29
4.6 Debye模型 一、模型
假设:晶体是各向同性的连续弹性介质,格波可以看
l V
1 U (T ) s (q)[ns (q) ] 2 s ,q
色散关系
对于实际晶体,晶格振动波矢的代表点密集的均匀分布于布 里渊区内,因此可引入频率分布函数 ( ), 将上式改写为:
在 附近单位频率间隔内的振动模式的数目
ρ()d :频率在-+d之间的振动模式数
0
E 3/2 f ( E )dE
17
才有明显变化,因此 T 0 K 时只有能量在 EF 附近 kBT 范围内 f ( E )
1
(0 E EF kBT )
f ( E)
E EF k BT 2kBT
( EF kBT E EF kBT )
0
( E EF kBT )
1 ( , q) (q)[n( , q) ] 2
与同一波矢 q 相应的角频率 (q ) 可以不止一个——不同的 频支。因此与晶格振动相应的固体的内能为:
1 U (T ) s (q)[ns (q) ] 2 s ,q
23
则晶格振动的定容热容为:
U (T ) C T
与温度有关的内能: 绝缘体 金属
晶格振动能量 晶格振动能量+价电子的热动能
低温下才考虑
3
4.1 电子气的状态密度
金属的自由电子气Drude模型
4
固体地球物理学概论第四章-02

• 在高山附近,重力场方向应该是地球基 本场与高山引力场合力的方向。 • 1854年英国人普拉特(Pratt)在喜马拉雅 山附近,根据地形计算,估计垂线应有 28”(角秒)的偏斜。 • 但是,实测只有5”(角秒)!仅仅相当于应 有值的1/6! • 在图4· 3· 1中,A是由于山的质量引起的理 论偏斜,B是实测的偏斜,而C是不偏斜 的标准位置。
• 它表明在海洋下面反山根的剩余质量, 约为高山下面山根亏损质量的 61 %。 • 为了获得普拉特-海福特均衡异常,需要 在布格异常的基础上进行均衡改正 (又称 补偿改正),补偿改正(δC)往往与地形 改正 ( δ1 )同时进行。 • 实际改正工作是使用一套规格化的环带。 • 在29km以内,采用平面公式进行地形改 正和补偿改工; • 在29一116.7 km之间,要考虑地球曲率 做一些小的校正;
• 按照1855年艾里 (Airy)假说,喜马拉雅 山有山根,山越高则山根贯人较重的基 底应该越深。 • 如果基底的性能像流体一样,并且较轻 的山岳物质有点像冰山浮在水面上那样 浮在较厚的流体基底上,则上述情况是 完全可能的。 • 因此补偿深度是可变的,而且像是真实 地面地形的镜象投影 (图4· 3· 2(a))o
t ' h'{1 [2T ( 1)h' ] / r (2T h' ) [2T ( 1)h' ] / r 2 T (T h' ) / r [( 1)h' ] /(3r )}
2 2 2 2
• 式中,μ=( ρ0 - ρ海 )/Δρ=73
t ' ( 0 海 ) / h' 2.73h'
• 由此可知,反山根是水深的2· 7倍。 • 无论是陆地还是海洋,它们的补偿都是 建立在等压条件的基础上。 • 等压线的深度一般取为地球上最高峰(珠 峰)相应的补偿深度处:珠峰高度h≈8·8km, 代入相应式子,求出山根厚度 • t = 4.45x8.8 = 39.2 km
固体地球物理学概论复习重点答案

《固体地球物理学概论》第一章:引言1、地球物理学的定义。
解:地球物理学是以地球为研究对象的一门应用物理学。
2、地球物理学组成及研究内容。
解:组成包括:理论地球物理、应用地球物理A. 理论地球物理学着眼于基础理论方面的研究,研究的主要内容有:(1)研究地球形状与重力分布的重力学;(2)研究地震及弹性波在地球内部传播规律的地震学;(3)研究地球磁现象的地磁学;(4)研究地球电性质的地电学;(5)研究地球内部热过程和热状态的地热学;(6)深部探测和地球动力学等。
B. 应用地球物理学是解决勘察石油、金属、非金属矿或其它地质问题的。
3、地球物理学的基本特点。
解:1、入地的窗口:根据地面或空中的资料和信息,了解地球深部情况;2、地球物理方法反演的多解性:正演问题、反演问题、精度问题3、地球物理方法的间接性问题4、建模与简化:就是以数学公式或数值形式表征地球某种性质或规律,它是对复杂研究客体的合理抽象和简化,从而更能反映客体的内在本质。
5、地球物理学初值和边值的约束作用:现在的地球为地球演化提供了一个作为初值(终值)的时间条件,而地面观测又为地球内部的物理过程提供了一个边界条件。
6、对地球物理学结论的可靠性估计(1)可靠性高的:牛顿万有引力定律,球谐分析理论、地球形状、地球自转周期;(2)可靠性较高:GPS、地球的速度分层结构;(3)可靠性具中的:地球的年龄、地球的分层结构(4)可靠性差的:大陆漂移和板块构造、地球内部的温度分布、地震预报;(5)可靠性最差的:地幔对流假说、地球起源假说、地磁场起源假说第二章:地球的起源1、戴文赛新星云假说的要点。
解:行星的形成要经过“原始星云→星云盘→尘层→星子→行星”这样几个步骤。
(1)原始星云的形成:原始星云是由一块星际云块塌缩并瓦解而成的。
根据维里定理,星际云质量比太阳现质量大三个数量级,它才会塌缩。
(2)星云盘的形成:原始星云盘继续塌缩,半径逐渐减小,因角动量守恒,造成自转速度增大。
固体物理第四章总结1
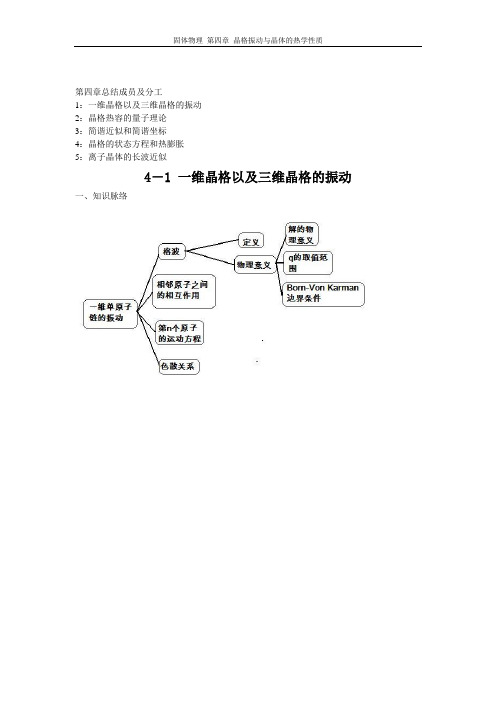
第四章总结成员及分工1:一维晶格以及三维晶格的振动2:晶格热容的量子理论3:简谐近似和简谐坐标4:晶格的状态方程和热膨胀5:离子晶体的长波近似4-1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义:晶格原子在平衡位置附近作振动时,将以前进波的形式在晶体中传播,这种波称为格波。
(2)物理意义:一个格波解表示所有原子同时做频率为ω的振动,不同原子之间有位相差。
相邻原子之间的位相差为aq 。
(3) q 的取值范围:-(π/a)<q ≤(π/a)这个范围以外的值,不能提供其它不同的波。
q 的取值及范围常称为布里渊区(Brillouin zones )。
(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation),也称为振动频谱或振动谱。
3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解(1)运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙(2)方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义(1)声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω+对应的格波称为光学波(optic wave )或光学支(optic branch) ;ω-对应的格波称为声学波(acoustic wave)或声学支(acoustic branch )(2)两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--(3)ω+ 与ω- 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论(1)一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波(一个波矢对应一个格波)— 声学波;而一维双原子链则有两支格波(一个波矢对应两个格波)— 声学波和光学波,两支格波的频率各有一定的范围:0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙,说明这种频率的格波不能被激发。
固体物理讲义第四章

第四章 晶格振动和晶体的热学性质● 晶格振动:晶体中的原子在格点附近作热振动● 原子的振动以波的形式在晶体传播(原子的振动波称为格波) ● 晶格振动对晶体的性质有重要影响 主要内容● 晶格动力学(经典理论,1912年由波恩和卡门建立)晶格振动的模式数量(有多少种基本的波动解) 晶格振动的色散关系(波动的频率和波数的关系)● 晶格振动的量子理论 ● 固体的热容量 4.1 一维单原子链的振动原子链共有N 个原胞,每个原胞只有一个原子,每个原子具有相同的质量m,平衡时原子间距等于晶格常数a,原子沿链方向运动,第n 个原子离开平衡位置的位移用x n 表示,第n 个原子和第n+1个原子间的相对位移为 一维单原子链原子振动时,相邻两个原子之间的间距: 基本假设● 平衡时原子位于Bravais 格点上 ● 原子围绕平衡位置作微振动●简谐近似:原子间的相互作用势能只考虑到平方项 微振动时:简谐近似:势能展开式保留到二次项微振动:原子离开平衡位置的位移与原子间距相比是小量。
晶体中原子的平衡位置由原子结合能(势)决定。
任何一种晶体,原子间的相互作用势能可以表述成原子之间距离的函数。
n n x x -=+1δδ+=a x ()()⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=+=222 21 )(δδδa ax d U d x d U d a U a U x U把qa改变一个2π的整数倍,原子的振动相同,因此可以把qa限制负pi和正pi之间,此范围以外的q值,并不提供新的物理内容.群速度是指波包的传播速度,dw/dq,也就是能量在介质中的传播速度。
在布里渊区的边界上,群速度为零,波是一个驻波。
4.2 一维双原子链的振动q趋于0时,w也趋于零,称为声学波4.3 三维晶格的振动(略) 一个原胞中有n 个原子晶格基矢: 原胞数目: 原子的质量: 对于一个波矢q,有3n 个ω(即有3n 支色散曲线) 在3n 支色散关系中,当q→0时(长波):有三支ω →0,且各原子的振幅趋于相同,这三支为声学波。
固体地球物理学导论(4-5)

固体地球物理学概论
第四章
地磁“自激发电机”假说 (续五)
现代的自激发电机效应假说认为: ①液态地核内部由于重力分异、温差、压差等原因产生涡旋运动; ②由于地球绕轴自转所引起的回旋磁效应就存在一微弱初始磁场,虽 比地磁场小10倍,但足以引起再生效应; ③地核电流体形成,通过感应方式电流自身形成的场又可连续不断地 再生磁场,从而增强了原来的磁场,由于地核电流体持续运动而不断提供 能量,因而引起一种自激发电机效应; ④由于能量的不断消耗和供应,磁场增强到一定程度就稳定下来,形 成现在的地球基本磁场; ⑤由于地核内涡流系统的复杂性,宏观上表现为一个不稳定的自激发 电系统,外界条件或内部因素有一定变化时,会出现极性倒转现象。 这种假说不仅能定性地解释地磁偶极子场和非偶极子场起源,而且解 释了地球磁轴倒转等现象,目前被认为是最可取的地磁成因理论。
固体地球物理学概论
第四章
地磁“自激发电机”假说 (续二)
然而实际地球磁场模型与上述这种均匀发电 盘的“模式”并不一样。但是它却形象直观地给 出了电流作功以维持磁场的过程。在地磁发电机 的理论中、首先假定在核内存在着一个所谓初始 A型磁场,电荷在初始磁场中发生X型运动,X型 运动感应出B型磁场的运动,由于这个运动将感 应出B型磁场。进而电荷在这个B型磁场中产生Y 型运动,……,如此下去,就形成了地磁场。
⑷地磁变化场
地磁的变化主要可分为长期变化和短期变化。长期变化主要由地球 内部幔核物质运动所引起的地磁场变化,如磁极漂移、磁极倒转等;短 期变化主要由太阳风作用与电离层扰动所引起的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 在大陆内部,最大地壳厚度位于前苏联的 科学院山脉! • 在海洋,最薄地壳厚度位于最深的海洋处, 而在海岭和海岛下面又趋向变厚。布格异 常的数量,大致反映了低密度地壳的厚度 补偿程度。 • 至此,铰大的布格异常得到解释,并且肯 定艾里模式是地壳均衡的基本模式,
• 但是,从图4.3.3会发现,根据均衡改正 而求出的均衡异常,有的地区补偿不足, 有的地区补偿过分,其均衡异常曲线有 10-3一IO-4 m/s2 的起伏。 • 这表明在基本均衡的背景上,允许有局 部的不均衡。造成这种不均衡的原因, 学者们的意见有分歧。 • 傅承义认为: • 地球介质在极长期载荷下,和真正的流 动有区别。
• 由此可得
t 0 h / 2.67 / 0.6h 4.45h
• 由此可知,山根是陆地高程的4· 5倍。 • 对于海洋, 设海水深度为h’, 反山根厚 度为 t’ ,则有以下关系
t ' ( 0 海 )h'
• 上式表明, 高度为 h’、密度差为 ρ0 - ρ 海 的柱体亏损,由厚度为t’、密度为Δρ的 反山根来补偿。由此可得·
t ' h'{1 [2T ( 1)h' ] / r (2T h' ) [2T ( 1)h' ] / r
2
T (T h' ) / r [( 1)h' ] /(3r )}
2 2 2 2
• 式中,μ=( ρ0 - ρ海 )/Δρ=2.73
• 海斯坎宁根据上述公式,得到补偿厚度, 并计算出相应的补偿改正量 (制成专用的 • 表)。经过这样改正后,将得到艾里-海斯 坎宁均衡异常。 • 3、二维准艾里均衡方法 • 沃泽尔 (J.L. Worzol)为了消除超过大陆边 缘的重力剖面中的地壳-地慢结构的边缘效 应,提出了两维准艾里均衡计算方法。 • 该方法依据艾里的山根-反山根概念,但不 是采用柱状体做局部补偿,而是采用连续 体做区域补偿。
• 然而,由于重力资料不能唯一确定地下密 度分布,因此,地壳均衡的具体模式问题, 仍有待进一步论证。 • 在这方面能发挥重要作用的是地震测深, 可通过地震方法得出地球外层的详细图象。 • 我们已知,莫氏面是地壳与地慢之分界面, 在此上下速度发生急剧变化 (从6.5km/s 变到8.O km/s),根据速度与密度的一般 关系,又根据地球内部密度随深度的变化,
二 几种均衡改正和均衡异常
• 1、普拉特-海福德均衡改正和均衡异常 在1909年和1910年海福德把普拉特的均 衡平衡概念发展成一种方法。 • 普拉特的均衡平衡概念如图4.3.4,所示。 其中,地面高程越高,下伏的岩石层密 度越低。 • 对于海洋,情况正好相反。
• 设从诲平面计起的补偿深度D(一般假定 l00km,严格说是1l3· 7km)之上,竖立着 若干柱体,各个柱体的重量相等,即柱 体底面积上的压强相等。 • 对于陆地,取其海拔高度为h, 因此该 柱体的高度为D+h, 密度为ρh 。另取海 拔高度为零的正常柱体,高度为D, 密 度为 ρ0。根据柱体重量相等的关系,可 得
• 在更远处,需用球面公式进行地形和补偿 改正。 • 关千地形效应和补偿效应,可从图4· 3· 5看 出两种效应的对比情况。 • 图中取陆地高度为1km和3km,分别给出 环状地形质量所产生的垂直引力(地形改 正)和补偿质量而产生的垂直引力(补偿改 正 )。 • 地形效应靠近测点比较大,远离测点比较 小,然而,补偿效应与此相反,靠近测点 比较小,而远离测点比较大。 • 这两种效应在15km处大约相等,
• 如果正常的地壳厚度取T=32 km,则等 压线的深度为 • t+h=71.2km • 通常取70km。应该注意,陆地的地壳厚 度为: T+h+t • 海洋的地壳厚度 T-h’-t’ • 海斯坎宁利用地形质量 (Δm1)与补偿质 量 (Δm2) 相等的条件,写出全球性大尺 度的补偿厚度 t 和 t’ 的公式。
§4.5 地壳均衡和均衡异常
• 一、均衡问题的产生 • 上面介绍的各项改正后所得完全布格异 常应很小。即仔细消除起因于高度和可 见地形影响之后的观测值,与正常值应 当差得很小。但事实并非如此。在广阔 的地区,布格异常显示出系统的与地形 的相关性。
• 在山区的异常值往住是负值,并且山区 地势越高,异常值下降得越严重。大约 每上升1000m,要降低l--2mm/s2! • 而在海洋地区异常值是正的,并且海水 越深,异常值上升得越历害。大约每加 深1000m,要提高2一4mm/s2! • 这是否地形改正过了头?经过反复核实所 用公式和数据没有错误,所得结果也在 允许的误差范围内。
• 它表明在海洋下面反山根的剩余质量, 约为高山下面山根亏损质量的 61 %。 • 为了获得普拉特-海福特均衡异常,需要 在布格异常的基础上进行均衡改正 (又称 补偿改正),补偿改正(δC)往往与地形 改正 ( δ1 )同时进行。 • 实际改正工作是使用一套规格化的环带。 • 在29km以内,采用平面公式进行地形改 正和补偿改工; • 在29一116.7 km之间,要考虑地球曲率 做一些小的校正;
• 图4.3.7是这种方法原理的示意图。 • 先假设一定深度 (30km)处的压力相等, 即为补偿深度。 • 然后依一般的局部补偿概念,由海水深 度确定海洋下面的反山根,得到地壳-地 慢边界的深度。 • 这样的结构是我们进行二维均衡改正的 出发点。为此,可分两步:
• 在高山附近,重力场方向应该是地球基 本场与高山引力场合力的方向。 • 1854年英国人普拉特(Pratt)在喜马拉雅 山附近,根据地形计算,估计垂线应有 28”(角秒)的偏斜。 • 但是,实测只有5”(角秒)!仅仅相当于应 有值的1/6! • 在图4· 3· 1中,A是由于山的质量引起的理 论偏斜,B是实测的偏斜,而C是不偏斜 的标准位置。
t ' ( 0 海 ) / h' 2.73h'
• 由此可知,反山根是水深的2· 7倍。 • 无论是陆地还是海洋,它们的补偿都是 建立在等压条件的基础上。 • 等压线的深度一般取为地球上最高峰(珠 峰)相应的补偿深度处:珠峰高度h≈8·8km, 代入相应式子,求出山根厚度 • t = 4.45x8.8 = 39.2 km
0 D h (D h)
• 从而求出陆地柱体与正常柱体的密度差 Δρ: • Δρ =ρh-ρ0=-[h / (D+h)]ρ0 • 对于海洋,设海水深度h’,海水密度ρ海, 该柱体包括一段水柱和一段岩柱,岩柱 密度可取ρh’。同样利用重量相等的关系, 可得: • ' '
0 D h' ( D h ) 海 h
• 2、艾里一海斯坎宁均衡改正和均衡异常 • 在1924年和1938年海斯坎宁把艾里的均 衡概念加以发展,成为易于确定均衡异 常和计算山根和反山根的方法。 • 艾里的概念如图4.3.6所示。 • 海斯坎宁所发展方法,其要点是:补偿直 接在地形下面,因而是局部的; • 取地壳(密度为2.67x103kg/m3 )浮在 地慢 (密度为3.27 x103kg/m3 )介质上.
• 有明显迹象表明这个界面也是一个发生 很大密度差的界面 (从2.9x1O3 kg/cm3变 到3.3x1O3 kg/cm3)。 • 图4.3.3给出大陆与海洋的折射地震研究 结果。其中,标出地形、地壳厚度和布 格异常,它们之间显示出极好的相关性。 • 不难得出结论,艾里模式与地震学结果 一致。 由莫氏面作为补偿面,恰恰是地 形的一个放大的镜象。 • 毫无疑问,莫氏面首先反映出海洋与大 陆的不同地形;
t {1 [2T ( 1)h] / r (2T h) [2T ( 1)h] / r
2
T (T h) / r [( 1)h ] /(3r )}
2 2 2 2
• 式中,λ= ρ0 /Δρ= 4.45; r为正常地壳厚 度(32km) ,r为地球平均半径 • (6371km)。
• 这两种假说的重要区别在于,普拉特认 为地壳底面的深度一致,但密度随地面 高度增加而减少; • 艾里认为地壳的密度一致,但底面深度 随地面高度增加而下降。但是,哪个合 • 理呢? • 1899年美国地质学家杜通(Dutto)在讨 论地球内部一定深度处的流体静压力时, 第一次引进“地壳均衡”一词。 • 地壳均衡的概念己经广泛地运用于地学 (地质学、地球物理学)领域。
• 地壳本身有一定弹性强度,因而局部不 匀衡是完全的,即是说补偿未必是完全 的。这就仿佛船在水里,虽然全船的重 量等于船所排出的水的重量,但由于船 本身有一定强度,船内的负荷还可以随 意安排。 • 意思是说,重力均衡从物理学角度分析, 主要是阿基米德原理在地球最上层 (岩石 层与软流层)的应用。
• 在补偿深度之下,较弱的软流层会发生 横向流动,对上覆岩石层产生浮力,这 是重力均衡部分。 • 但同时也应注意到岩石层自身并非刚体, 它可以在重力与浮力作用下发生弹性弯 曲、塑性蠕动或者局部断裂,以应力调 整方式参与力的平衡。 • 这部分应属于非重力均衡。
• 取某厚度(T) 厚度时不存在质量补偿问 题,即地壳不"插入"地慢。 • 对于陆地,若地形高度为 h, 其下部深 入地慢介质深度为 t (山根),根据阿基米 德原理可得: • t h
0
• 这里ρ0为地壳密度, Δρ为地慢与地壳的 密度之差。上式表明,高为 h, 密度为 ρ0的柱体,由厚为t、密度差为Δρ的山根 来补偿。
• 因此,这种高区负异常和低区正异常的 现象是可以肯定的。 • 上述异常的存在只能意味着在高山地区 下面的岩石密度小于平均密度。 • 而在海洋盆地下面的岩石密度则大于平 均密度。 • 这是一种由地下质量补偿地球表面形态 原理的例证。
• 应该指出,这种补偿原理远在采用重力 的详细测量之前,就已经提出来了。质 量补偿观念的最早提出者,应是16世纪 时具“天才的直觉” 的达· 芬奇。 • 直到18世纪,即l746年布格才得出同样 的结论。 • 然而,关于山下面的质量补偿的明确概 念,以及地球怎么支撑如此巨大地质体 的解释,迟至19世纪50年代,根据在北 印度大地测量资料,对于喜马拉雅山附 近的垂线偏差进行认真分析后才形成的。
