第4讲 枚举法一
高思3年级·3枚举法(一)(计数问题第1讲)·答案

第3讲 枚举法(一)(计数问题第1讲)【1】1~20共有多少个数相隔:20-1=19(个);个数:19+1=20(个)。
答:1~20共有20个数。
【2】20~40共有多少个数相隔:40-20=20(个);个数:20+1=21(个)。
答:20~40共有21个数。
【3】如图,桌上有一些围棋子,有多少枚黑子 正难则反一共:5×5=25(枚);白子:9枚;黑子:25-9=16(枚)。
答:有16枚黑子。
【4】小明决定去香山、颐和园、圆明园这3个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序 (1)香山、颐和园、圆明园;(2)香山、圆明园、颐和园;(3)颐和园、香山、圆明园;(4)颐和园、圆明园、香山;(5)圆明园、香山、颐和园;(6)圆明园、颐和园、香山。
3×2=6(种)答:他一共有6种不同的游览顺序。
【5】小王准备从青岛、三亚、桂林、杭州这4个地方中选2个地方去旅游,小王有多少种不同的选择 握手原则⎩⎨⎧÷⨯-2每个人握手次数所有人握手次数:人数1每个人握手次数:人数(1)青岛、三亚;(2)青岛、桂林;(3)青岛、杭州;(4)三亚、桂林;(5)三亚、杭州;(6)桂林、杭州。
4×3÷2=6(种)答:小王有6种不同的选择。
【6】小王准备从青岛、三亚、桂林、杭州这4个地方中选3个地方去旅游,小王有多少种不同的选择 正难则反:在4个地方里面选3个,也就是每次去掉1个地方不选。
(1)青岛、三亚、桂林(不选杭州);(2)青岛、三亚、杭州(不选桂林);(3)青岛、桂林、杭州(不选三亚);(4)三亚、桂林、杭州(不选青岛)。
答:小王有4种不同的选择。
【7】墨莫在一张纸上画了一些图形,如图所示,每个图形都是由若干条线段连接组成的。
数一数,纸上一共有多少条线段(最外面的大长方形是纸的边框,不算在内) 三角形个数:2;四边形个数:2;五边形个数:2。
(3+4+5)×2=24(条) 答:纸上一共有24条线段。
【墨漪高二985精编题】第4讲枚举法与加乘原理

枚举法与加乘原理1、若x、y均为正整数,且满足x+y⩽7,则平面上的点(x,y)共有()A. 18个B. 19个C. 20个D. 21个2、把10个苹果分成三堆,要求每堆至少1个,至多5个,则不同的分法共有()A. 4种B. 5种C. 6种D. 7种3、将长为15的木棒截成长为整数的三段,使它们构成一个三角形的三边,则得到的不同三角形的个数为()A. 8B. 7C. 6D. 54、设A是整数集的一个非空子集,对于k∈A,如果k−1∉A且k+1∉A,那么称k是A的一个“孤立元”.给定S={1,2,3,4,5,6,7,8},则S的3个元素构成的所有集合中,其元素都是“孤立元”的集合个数是()A. 6B. 15C. 20D. 255、如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有()A. 8种B. 12种C. 16种D. 20种6、现有5幅不同的国画,2幅不同的油画,7幅不同的水彩画.(1) 从中任选一幅画布置房间,有几种不同的选法?(2) 从这些国画、油画、水彩画中各选一幅布置房间,有几种不同的选法?(3) 从这些画中选出两幅不同种类的画布置房间,有几种不同的选法?7、已知a∈{0,3,4},b∈{1,2,7,8},r∈{8,9},则方程(x−a)2+(y−b)2=r2表示不同的圆的个数是.8、乘积(a+b+c+d)(m+n)(x+y+z)展开后共有多少项?9、6名学生争夺7项冠军,每项冠军只能由一人获得,获得冠军的可能的种数有.10、有5位同学各自独立地报名课外兴趣小组,可报名的小组有中华传统文化、生物技术(Biotechnology)、数学应用共3个.如果每位同学限报一个小组,小组招收人数没有上限,那么所有可能的不同的报名结果有种.11、如图所示,从A→B→C,有多少种不同的走法?从A→C,有多少种不同的走法?12、把4件不同的产品摆成一排.若其中的产品A与产品B都摆在产品C的左侧,则不同的摆法有种.(用数字作答)13、用数字0,2,3,4,6.(1) 能组成多少个没有重复数字的三位数?(2) 可以组成多少个可以被3整除的没有重复数字的三位数?(注:每小题结果都写成数字形式)14、用数字1,2,3,4,5构成没有重复数字的五位数,其中奇数的个数为()A. 24B. 48C. 60D. 7215、从黄瓜、白菜、油菜、扁豆4个蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法有()A. 24种B. 18种C. 12种D. 6种参考答案1 、【答案】 D【解析】 当x =1时,y =1,2,3,4,5,6,有6种情况;当x =2时,y =1,2,3,4,5,有5种情况;当x =3时,y =1,2,3,4,有4种情况;当x =4时,y =1,2,3,有3种情况;当x =5时,y =1,2,有2种情况;当x =6时,y =1,有1种情况.故平面上的点(x,y )共有6+5+4+3+2+1=21个.2 、【答案】 A【解析】 解:分类:三堆中“最多”的一堆为5个,其他两堆总和为5个,每堆至少1个,只有2种分法,即1和4,2和3两种方法.三堆中“最多”的一堆为4个,其他两堆总和为6个,每堆至少1个,只有2种分法,即2和4,3和3两种方法.三堆中“最多”的一堆为3个,那是不可能的.所以不同的分法共有2+2=4(种).故选:A .3 、【答案】 B【解析】 解:将长为15的木棒截成长为整数的三段,使它们构成一个三角形的三边,根据三角形三边之间的关系,可以列举出所有情况:1,7,7;2,6,7;3,5,7;3,6,6;4,5,6;4,4,7;5,5,5,共有7种结果,故选:B .4 、【答案】 C【解析】 135,136,137,138,146,147,148,157,158,168,246,247,248,257,258,268,357,358,368,468. 故选:C .5 、【答案】 C【解析】 解:分为以下两类:第一类,从一个村庄出发向其他三个村庄各修一条路,共有4种方法;第二类,一个村庄最多修两条路,但是像下面这样的两个排列对应一种修路方法,A −B −C −D ,D −C −B −A ,要去掉这样重复的排列,因此共有12A 44=12种方法.根据分类计数原理,可知共有4+12=16种,故选:C .6 、【答案】 (1) 14;(2) 70;(3) 59.【解析】 (1) 根据题意,共有5幅不同的国画,2幅不同的油画,7幅不同的水彩画,共有5+2+7=14幅画,从中任选一幅画布置房间,有14种选法.(2) 分三步完成,第一步选国画有5种,第二步选油画有2种,第三步选水彩画有7种,根据分步计数原理得,共有5×2×7=70种.(3) 根据题意,分三类情况讨论:第一类,选国画和油画共有5×2=10种,第二类,选国画和水彩画共有5×7=35种,第三类,选油画和水彩画共有2×7=14种,根据分类计数原理共有10+25+14=59种.7 、【答案】 24【解析】解:3×4×2=24.8 、【答案】24项【解析】4×2×3=24.9 、【答案】6710 、【答案】243【解析】5位同学中每位同学报名方式都有3种,∴总情况为35=243种.11 、【答案】从A→B→C共有4种走法.从A→C共有6种走法.【解析】从A→B→C分两步.第一步:从A→B,有2种走法;第二步:从B→C,有2种走法.所以从A→B→C共有2×2=4种走法.从A→C分两类.第一类:从A→B→C共有4种走法;第二类:从A→C (不经过B)有2种走法.所以从A→C共有4+2=6种走法.12 、【答案】 8【解析】解:根据题意,分2步分析:①将产品A与产品B全排列,都摆在产品C的左侧,有A22=2种情况,②三件产品放好后,有4个空位,在其中任选1个,安排最后一件产品,有4种情况,则4件产品有2×4=8种不同的摆法;13 、【答案】 (1) 48个;(2) 20个.【解析】 (1) 百位数字只能是2,3,4,6中之一.百位数字确定后,再排十位和个位数字.∴可以组成4×4×3=48个没有重复数字的三位数.(2) 能被3整除的没有重复数字的三位数分四类:①2,4,0;②2,4,3;③2,4,6;④0,3,6.共有2×2×1+3×2×1+3×2×1+2×2×1=20个,符合要求的三位数.14 、【答案】 D【解析】由题可知,五位数要为奇数,则个位数只能是1,3,5;分为两步:先从1,3,5三个数中选一个作为个位数有3种情况,再将剩下的4个数字排列得到4×3×2×1=24种情况,则满足条件的五位数有3×4×3×2×1=72种情况15 、【答案】 B【解析】解:解法1:第一步,选出3种蔬菜,由于黄瓜必选,所以选法有3种:第二步,将选出的3种蔬菜种植在3块土地上,种法有3×2×1=6(种),所以共有种植方法3×6=18(种),所以选择B.解法2:特殊元素优先考虑,由于黄瓜必须种植,所以整个种植过程分两步进行,第一步,种黄瓜,有3种方法;第二步,从白菜、油菜、扁豆中选两种种植在剩下的两块土地上,有3×2=6(种)方法.所以共有种植方法3×6=18(种),所以选择B.解法3:排除法:先计算从4种蔬菜中选3种种在3块不同的土地上,有4×3×2=24(种)方法;再计算除黄瓜外3种蔬菜种在3块不同的土地上有3×2×1=6(种)方法.所以,黄瓜必种的方法为24−6=18(种).。
部编版数学五年级暑假第4讲.枚举法进阶.优秀A版

第4讲四年级寒假几何计数初步四年级春季排列组合初步五年级暑假枚举法进阶五年级秋季排列组合进阶五年级秋季几何计数进阶用枚举法计算较复杂的几何,数论等问题漫画释义知识站牌枚举法虽然是一种最简单,最基本的计数方法,但在生活中有很多的应用.例如,破译电脑密码.破译密码最简单的原理,就是尝试所有可能的密码组合,直到得到正确的密码.只要有足够的时间和存储空间,枚举密码原则上是可行的.1.掌握枚举法不重不漏的方法:分类,有序2.灵活运用枚举法解决各种计数问题.枚举常用的方法有列表法、树形图、标数法、找规律及公式法.(1)列表法例:有一张伍拾元,4张贰拾元,8张拾元.要拿出80元,可以有多少种不同的拿法?取的张数4376548伍拾元1100000贰拾元0112340拾元316428(2)树形图例:暑假里,一个学生在A 、B 、C 三个城市游览.他今天在这个城市,明天就到另一个城市.假如他第一天在A 市,第五天又回到A 市,问他有几种不同的游览方案?经典精讲教学目标课堂引入第4讲B A AC A B A C B A AB A AC A C A BB A⎧⎧---⎧⎪⎨⎪---⎪⎩⎪⎨⎪⎧⎪⎪⎨⎪---⎪⎩⎪⎩⎨⎧---⎧⎪⎨⎪⎪---⎪⎩⎪⎨⎪⎧⎪⎪⎨⎪---⎩⎪⎩⎩第一天第二天第三天第四天第五天(3)标数法例:如图,从A 到B 的最短路线有多少条?BA(4)找规律:适用于规律性强,情形较多的题.例:从1到100的自然数中,每次取出两个数,要使它们的和大于100,共有多少种取法?(5)公式法:此法比较适合于题目涉及的对象比较富有规律性,且情形繁多,数目很大,不宜用逐一列举来解.但通过适当的分类,逐一分析后,可利用公式解答.模块1:例1-2,树形图,标数法;模块2:例3-4,分类,定序枚举;模块3:例5,较复杂的枚举.如图,从起点走到终点,要求取出每个站点上的旗子,并且每个站点只允许通过一次,有种不同的走法。
例题思路【分析】给这些点依次标上字母(如左图),然后采用枚举法(如右图):afbdefed f deff e c cd cba共4种不同的走法。
一年级第4讲 简单数图形(1)

一条直线 两个端点
数一数,下面各图中分别有几条线段8 ?几 个角?几个三角形?
数一数,下面各图中分别有几条线段?几 个角?你发现了什么?
下面的图形有几个小正方体?为什么?
下面的图形中有几个小正方体?
下图由3层正方形木块垒成的,求图中共有多 少个小正方体?
( 7 )个 ( 12 )个 ( 10 )个
2、在数数时,应养成顺序数数和分类数数的习惯,这对解决 数数问题很重要。
3、在解决数图形问题时,可以首先认真分析图形的组成规律 ,根据图形特点选择适当的方法,既可以逐个计数,也可以把 图形个数,再把他们的个数合起来。
3、数一数,下图中有几个三角形?
•休息到1:55
数一数,有多少个小正方体?你是怎么数的
数一数,下面分别有多少个小正方体?
要搭成正方体,至少还缺几个小正方体?
要搭成较大的正方体,至少还缺几个小正方体?
连接下面这四个点,你能够画出多 少条线段,并画出。
通过下面这五个点,你能够画出几条线段? 请画出所有线段。
总结
1、我们在数数的时候,遵循不重复、不遗漏的原则,才能使 数出的结果准确。分类数图形的方法能够帮助我们找到图形的 规律从而有秩序、有条理并且正确地数出图形的个数。
第 讲 简单数图形
1、学会用枚举法进行数图形,并能有序的数 出并计算出图形个数; 2、掌握立体图形计数的方法; 3、培养学生的分析能力,并养成有序思考的 习惯。
跳跳说,好久都没有出去野餐了,笨笨也 说,是啊,最近我们都没有出去玩,不如我们去 蘑菇森林野餐吧,也可以来一场蘑菇大餐,其他 小伙伴们都觉得这个提议很好。于是,奇奇、笨 笨、跳跳、乐乐和希博士准备好野餐需要带的东 西就出发了,我们也一起去蘑菇森林里看看吧。
2019秋二年级上册精英班讲义 第4讲-有序思考(教师版)
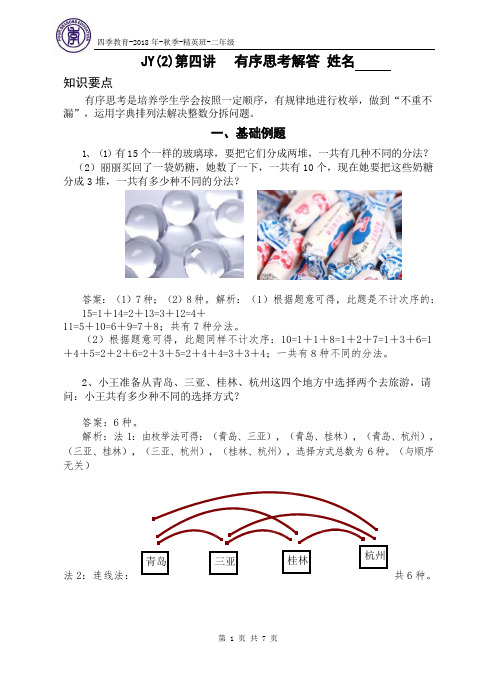
知识要点JY(2)第四讲 有序思考解答 姓名有序思考是培养学生学会按照一定顺序,有规律地进行枚举,做到“不重不 漏”,运用字典排列法解决整数分拆问题。
一、基础例题1、(1)有 15 个一样的玻璃球,要把它们分成两堆,一共有几种不同的分法? (2)丽丽买回了一袋奶糖,她数了一下,一共有 10 个,现在她要把这些奶糖 分成 3 堆,一共有多少种不同的分法?答案:(1)7 种;(2)8 种。
解析:(1)根据题意可得,此题是不计次序的:15=1+14=2+13=3+12=4+ 11=5+10=6+9=7+8;共有 7 种分法。
(2)根据题意可得,此题同样不计次序:10=1+1+8=1+2+7=1+3+6=1 +4+5=2+2+6=2+3+5=2+4+4=3+3+4;一共有 8 种不同的分法。
2、小王准备从青岛、三亚、桂林、杭州这四个地方中选择两个去旅游,请 问:小王共有多少种不同的选择方式?答案:6 种。
解析:法 1:由枚举法可得:(青岛、三亚),(青岛、桂林),(青岛、杭州),(三亚、桂林),(三亚、杭州),(桂林、杭州),选择方式总数为 6 种。
(与顺序 无关)法 2:连线法:共 6 种。
: 3、在一次知识抢答比赛中,小月和冬冬两个人一共答对了 10 道题,并且每 人都有答对的题目,如果每道题 1 分,那么小月和冬冬两人有多少种不同的得 分?答案:9 种。
解析:两人得分的可能:10=1+9=2+8=3+7=4+6=5+5=6+4=7+3=8+2=9 +1。
(有顺序)二、举一反三4、妈妈买了 10 盒酸奶,需要放在两个相同的塑料袋里,并且她在每个袋子 里至少放了两盒,那么妈妈一共有多少种不同的放法?答案:4 种。
解析:每袋至少放两盒,所以为:10=2+8=3+7=4+6=5+5 共 4 种放法。
5、有 4 个小朋友一起玩握手游戏,每 2 人握手 1 次,一共要握几次手?答案:6 次。
解析:法 1:设这 4 个小朋友分别为 1 号,2 号,3 号,4 号。
四年级数学思维能力拓展专题突破系列(十五)枚举法讲义(含答案)

四年级数学思维能力拓展专题突破系列(十五)枚举法------枚举法基础(1)1、能用枚举法熟练解决一般的计数问题。
2、掌握枚举法的几种解题方法。
1、掌握枚举法的概念。
2、学会分类枚举。
例题1:用数字1,2,3可以组成多少个不同的数?分别是哪几个数?例题2:用一台天平和重1克、3克、9克的砝码各一个(不再用其他物体当砝码),当砝码只能放在一个盘内时,可称出多少种不同的重量?例题3:将三个相同的小球放入A、B、C三个盒子中,一共有多少种放法?例题4:商店出售苹果5千克重的有5筐,6千克重的有4筐,9千克重的有3筐,王阿姨要买20千克重的苹果有多少种买法?(筐不能被打开)即是该课程的课后测试练习1:小帅有面值为5角,8角的邮票各两枚。
他用这些邮票能付多少种不同的邮资(寄信时,所需邮票的钱数)?练习2:用长56厘米的铁丝围成各种长方形(长和宽都是整厘米数,且长和宽不相等),围成的最大一个长方形的面积是多少平方厘米?练习3:如图,有8张卡片,上面分别写着自然数1至8。
从中取出3张,要使这3张卡片上的数字之和为9。
问有多少种不同的取法?练习4:课外小组组织30人做游戏,按1—30号排队报数。
第一次报数后,单号全部站出来;以后每次余下的人中第一个人开始站出来,隔一人站出来一个人。
到第几次这些人全部站出来了?最后站出来的人应该是第几号?练习5:商店出售饼干,现存10箱5千克重的,4箱2千克重的,8箱1千克重的。
一位顾客要买9千克饼干,为了便于携带要求不开箱。
营业员有多少种发货的方法?练习1:解析:一枚:5角,8角二枚:两个5角=1元,两个8角=1元6角,一个5角和一个8角=1元3角三枚:两个5角和一个8角=1元8角,两个8角和一个5角=2元1角四枚:两个5角和两个8角=2元6角答:有8种不同的邮资。
练习2:解析:比如有一下几种情况作为例子:10+18=28(厘米) S=10⨯18=180(平方厘米)11+17=28(厘米) S=11⨯17=187(平方厘米)12+16=28(厘米) S=12⨯16=192(平方厘米)…13+15=28(厘米) S=13⨯15=195(平方厘米)14+14=28(厘米) S=14⨯14=196(平方厘米)但是长和宽不相等,且有长和宽都是整数所以S=13⨯15 =195(平方厘米)答:围成的最大一个长方形的面积是195平方厘米。
红棉杯冲刺讲义第四讲---计数综合
HM 冲刺讲义第四讲——计数综合知识汇编:1.加法原理和分类计数法加法原理:做一件事,完成它可以有n 类办法,在第一类办法中有1M 种不同的方法,在第二类办法中有2M 种不同的方法,……,在第n 类办法中有n M 种不同的方法,那么完成这件事共有N=n M M M M ++++ 321种不同方法。
分类计数法:第一类办法的方法属于集合1A ,第二类办法的方法属于集合2A ,……,第n 类办法的方法属于集合n A ,那么完成这件事的方法属于集合n A A A A ++++ 321。
分类的要求:每一类中的每一种方法都可以独立地完成此任务;两类不同办法中的具体方法,互不相同(即分类不重);完成此任务的任何一种方法,都属于某一类(即分类不漏)。
加法原理的常用方法:(1)枚举法:数出来的种类分类枚举找规律(2)树形图:“树形图法”实际上是枚举的一种,但是它借助于图形,可以使枚举过程不仅形象直观,而且有条理又不重复遗漏,使人一目了然。
(3)标数法:平面图形标数法立体图形标数法适用于最短路线问题,需要一步一步标出所有相关点的线路数量,最终得到到达终点的方法总数.标数法是加法原理与递推思想的结合。
2.乘法原理乘法原理:做一件事,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法,……,做第n 步有m n 种不同的方法,那么完成这件事共有N=m 1×m 2×m 3×…×m n 种不同的方法。
合理分步的要求:任何一步的一种方法都不能完成此任务,必须且只须连续完成这n 步才能完成此任务;各步计数相互独立;只要有一步中所采取的方法不同,则对应的完成此事的方法也不同。
3.排列组合(1)排列就是指从给定个数的元素中取出指定个数的元素进行排序。
排列的定义:从n 个不同元素中,任取m(m≤n,m 与n 均为自然数,下同)个元素按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列;从n 个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号m nA 表示。
《数量关系》2015最新李委明讲义
式?
A. 9
B. 12
C. 14
D. 16
● 题型三:分配插板型
【例 5】把 9 个苹果分给 5 个人,每人至少一个苹果,那么不同的分法一共有多少种?
A.30
B.40
C.60
D.70
【例 6】(陕西 2013-80)某领导要把 20 项任务分给三个下属,每个下属至少分得三项
任务,则共有( )种不同的分配方式。
A.101
B.175
C.188
D.200
第 06 讲 拓展牛吃草
一、题型评述
牛吃草问题还可能出现新的变化,这类考题不是牛吃草问题的重点,但仍然值得关注。
二、破题密钥
仍然使用表格法来解题,但需要做一些修正。
三、例题精析
核心提示 如果草场有面积区别,如“M 头牛吃 W 亩草”时,N 用“M/W”代入,此时 N 代表单位面 积上的牛数。
● 题型二:归纳法
【例 2】十阶楼梯,小张每次只能走一阶或者两阶,请问走完此楼梯共有多少种方法?
A.55
B.67
C.74
D.89
【例 3】(深圳 2011-13)已知一对幼兔能在一月后长成一对成年兔子,一对成年兔子能 在一个月后生出一对幼兔,如果现在给你一对幼兔,问一年后共有( )对兔子。(假设每对
三、例题精析
● 题型一:枚举法
【例 1】(国家 2011-80)一个班的学生排队,如果排成 3 人一排的队列,则比 2 人一排
的队列少 8 排;如果排成 4 人一排的队列,则比 3 人一排的队列少 5 排。这个班的学生如果
按 5 人一排来排队的话,队列有多少排?
A. 9
B. 10
C. 11
D. 12
人教版三年级下册春季第四讲《除数是一位数的除法应用题》(知识精讲+典型例题+同步练习+进门考)
人教版三年级数学春季《除数是一位数的除法应用题》除数是一位数的除法应用题知识点一:除法算式中的应用复习:一个除法算式,除数是8,商是85,余数是6,那么被除数是多少?答案:85×8+6=686复习小马虎计算一道除数是5的除法算式的时候,把被除数的百位和个位看反了。
他算出来的商是115,余数是2,那么正确的商应该是多少?答案:小马虎看错的被除数:115×5+2=577正确的被除数:775正确的结果:775÷5=155正确的商应该是155知识讲解:小高正在计算一道除法题小猫不小心打翻了墨水瓶弄脏了纸张,小高计算的算式中被除数是129,商是6,余数是3,除数看不清楚了,请问:除数应该是多少?步骤:(被除数-余数)÷商(129-3)÷6=21总结:除数=(被除数-余数)÷商思考:小高发现一个除法算式的被除数和余数都看不清楚了。
只能看到除数是6,商是28,而且肯定有余数,你知道被除数最大可能是多少吗?步骤:除法算式中,被除数=除数×商+余数要让被除数最大,需要余数最大,而且除法算式中余数一定比除数小。
除数是6,余数最大是5被除数最大的可能:28×6+5=173总结:余数一定比除数小练习:把下面的除法算式补充完整⑴102÷4=() (2)⑵()÷6=175 (1)⑶273÷()=9 (3)答案:25 451 30在除法算式中,除数是9,商是105,那么被除数有可能是()A:955B:950C:944在算式♤÷4=52......♡中被除数♤最大可能是()答案:B 211知识点二根据下面的题目,判一判1.4.6能组成多少个各位数字不重复的两位数?答5个。
分别是61.64.14.16.41×4.5.6.能组成多少个各位不重复的三位数?答:7个。
分别是456、654、546、645、465、546、564。
第4 讲 枚举法
枚举法学习数学的唯一方法是做数学。
——哈尔莫斯 老奶奶数鸡蛋,她小心翼翼地把鸡蛋从篮子里一个一个地往外拿,边拿边数.篮子里的鸡蛋拿光了。
有多少个鸡蛋也就数出来了。
这种最简单的计数方法就叫做枚举法。
对于一组需要计算总数的东西,如果它们的数量不太多多,我们可以运用枚举法把它们一一列举出来,从而求出这个总数。
例1 将一个整数分成若干个小于它的整数之和,叫做分拆。
比如4=1+1+2,4=1+3,是两种不同的分拆。
但4=l+1+2,4=1+2+1,4=2+1+l ,它们只有加数的顺序不同,应算是同一种分拆,请问:整数6有多少种不同的分拆方式?分析与解1 整数6小大,可以考虑直接运用枚举法求解。
由于6=1+1+1+1+1+1,这说明6最多拆为6个数,又6=1++5=2+4=3+3,最少拆为两个数之和,因此我们可按分拆后整数个数分类,除上述两类情形外,另外还有: 拆成三个数的:6=1+1+4=1+2+3=2+2+2; 拆成四个数的:6=1+1+1+3=1+1+2+2; 拆成五个数的:6=1+1+1+1+2.可见,一共有10种不同的分拆方式。
我们在列举分拆的整数时,先写较小的数,再写较大的数,这样有规律地写,可以防止遗漏任何一种情形。
分析与解2还有一种更好的分类方法:按分拆中的最大整数来穷举。
最大数足5: 6=5+1;最大数是4:6=4+2=4+l+1;最大数是3:6=3+3=3+2+1=3+1+1+1;最大数是2:6=2+2+2=2+2+1+1=2+1+1+1+1; 最大数是1:6=l+1+1+1+1+1。
因此,一共有10种不同的分拆方式。
为什么不按分拆中的最小数来分类呢?可以想象到,分拆中最小整数1出现的次数最多,如果按最小数来分类,就会使分类流于繁琐,从而失去了它的意义,而分类的主要目的在于简化问题。
运用枚举法必须注意两个方面:第一,我们应初步估计总的数目不是太大。
因为若需要计算数目的情况太多时,把它们一一列举出来将是非常费时、困难的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲枚举法一
内容概述
掌握枚举的一般方法,学会按照一定顺序,有规律地进行枚举,做到“不重不漏”;应用字典排列法解决整数分拆的问题,学会分辨“计次序”与“不计次序”的情形。
典型问题
兴趣篇
1. 冬冬在一张纸上画了一些图形,如图4-1所示,每个图形都是由若干条线段连接组成的。
请你数一数,纸上一共有多少条线段?(最外面的大长方形是纸的边框,不算在内)
2. 要沿着如图2-4所示的道路从A点走到B点,并且每段路最多只能经过一次,一共有多少种不同的走法?
3. 小明决定去香山、颐和园、圆明园这三个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序?
4. 小王准备从青岛、三亚、桂林、杭州这4个地方中选2个去旅游,小王有多少种不同的选择方式?如果小王想去其中的3个地方,又有多少种选择方式?
5. 小烧饼每个5角钱,大烧饼每个2元钱,冬冬一共有6元钱,如果把这些钱全部用来买烧饼,一共有多少种不同的买法?
6. 在一次知识抢答比赛中,小悦和冬冬两个人一共答对了10道题,并且每人都有答对的题目。
如果每道题1分,那么小悦和冬冬分别可能得多少分?请把所有的可能填写到下面的表格里:
小悦的总分
冬冬的总分
7. 两个海盗分20枚金币。
请问:
(1)如果每个海盗最少分5枚金币,一共有多少种不同的分法?
(2)如果每个海盗最多分到16枚金币,一共有多少种不同的分法?
8. 有15个玻璃球,要把它们分成两堆,一共有几种不同的分法?这两堆球的个数可能相差几个?
9. 张奶奶去超市买了12盒光明牛奶,发现这些牛奶需要装在2个相同的袋子里,并且每个袋子最多只能装10盒。
张奶奶一共有几种不同的装法?
10. 小悦、冬冬、阿奇三个人一共有7本课外书,每个人至少有一本。
小悦、冬冬、阿奇分别有几本课外书?请写出全部可能的情况。
拓展篇
1. 如图4-3,小悦画了一个小房子,如果每画一笔都不能拐弯,那么她最少画了几笔?
2. 小悦把8块绿豆糕摆成如图4-4所示的图形,让冬冬挑两块挨在一起的绿豆糕。
请问:冬冬一共有多少种不同的挑法?
3. 小悦、冬冬、阿奇三个人去看电影,他们买了三张座位相邻的票。
他们三人的座位顺序一共有多少种不同的安排方法?
4. 小李摆摊卖货,小木偶每个卖1元,大木偶每个卖2元。
他今天一共卖出了5个木偶。
小李今天一共可能卖了多少钱?
5. (1)老师给小悦14个相同的练习本。
如果小悦把这些本子全都分给冬冬和阿奇,有多少种不同的分法?(2)老师给小悦14个相同的练习本,如果小悦只需要把这些本子分成2堆,又有多少种不同的分法?
6. 盘子里一共有20颗花生,小悦和冬冬一起吃,每人一口吃2颗,两个人一起把花生吃完(每人至少吃一口),他们分别可能吃了多少颗花生?
7. 如图4-5,有7个按键,上面分别写着:1、2、3、4、5、6、7这七个数字。
请问:
(1)从中选出2个按键,使它们上面数字的差等于2,一共有多少种选法?
(2)从中选出2个按键,使它们上面数字的和大于9,一共有多少种选法?
8. 小王有5个相同的飞机模型,他要把它们放在一个3层的货架上,每层至少要放1个。
小王一共有多少种不同的放法?过了几天,他又要把18个相同的汽车模型放到另一个3层货架上,每层最少要放5个,这时有多少种不同的放法?
9. (1)小明买回了一袋糖豆,他数了一下,一共有10个。
现在他要把这些糖豆分成3堆,一共有多少种不同的分法?
(2)如果小明有两袋糖豆,每袋10个。
要把这两袋糖豆分成3堆,每堆最少要有5个,一共有多少种不同的分法?
10. A、B、C、D、E这五个人一起回答一道题目,结果只有两个人答对了。
所有可能的回答情况一共有多少种?
11. (1)有2个相同的白球和1个红球。
如果把这3个小球排成一排,有多少种不同的排法?
(2)有2个相同的白球和3个相同的红球,把这5个小球排成一排,有多少种不同的排法?
12. 班主任要从甲、乙、丙、丁、戊这五个小朋友里面选出四个人参加乒乓球赛,有多少种不同的选法?如果已尼选出甲、乙、丙、丁,现在要把他们分成两组,进行双打比赛,有多少种不同的分法?
超越篇
1. 小明参加了一次小测验,每个小题2分,每个大题5分,两种题目各有3道,小明的得分一共有多少种不同的可能?
2. 几个小朋友在屋子里玩石头剪子布。
冬冬在门外问他们一共有几个人。
其中一个小朋友说:“不能直接告诉你人数,不过我们现在一共伸出来了22根手指,并且有3个人出石头。
”请问:屋子里可能有几个人在玩游戏?(出石头的不伸手指,出剪子的伸2根,出布的伸5根)
3. 一次小测验一共4道题,最初每位同学都有4分的基础分,然后每答对一道题加3分,每答错一道题加1分,不答不扣分,同学们的得分可能是多少?
4. 现在有分、2分、5分的硬币各5枚,要用这些硬币凑出2角钱,一共有多少种不同的凑法?
5. 如图4-6,妈妈在5张卡片上分别写了1、1、1、2、2这5个数字,让小明从里面挑出3张来组成一个三位数,小明可能组成多少个不同的三位数?
6. 刘老师在一个星期中要去3次健身馆,但是为了防止运动过量,不能连续两天都去,刘老师一共有多少种满足条件的时间安排?
7. 在算盘上,用两颗珠子可以表示多少个不同的四位数?
8. 一座99层摩天大楼的电梯上,有显示楼层的液晶屏,如图4-7,由于屏幕受到损坏,显示左边数字的7根线段中有1根不能亮了,显示右边数字的7根线段中有3根不能亮了。
请问:电梯在运行的过程中,最多还
有多少个楼层的显示是正确的?。
